Dynamical integrity assessment of stable equilibria: a new rapid iterative procedure

Abstract

A new algorithm for the estimation of the robustness of a dynamical system’s equilibrium is presented. Unlike standard approaches, the algorithm does not aim to identify the entire basin of attraction of the solution. Instead, it iteratively estimates the so-called local integrity measure, that is, the radius of the largest hypersphere entirely included in the basin of attraction of a solution and centred in the solution. The procedure completely overlooks intermingled and fractal regions of the basin of attraction, enabling it to provide a significant engineering quantity in a very short time. The algorithm is tested on four different mechanical systems of increasing dimension, from 2 to 8. For each system, the variation of the integrity measure with respect to a system parameter is evaluated, proving the engineering relevance of the results provided. Despite some limitations, the algorithm proved to be a viable alternative to more complex and computationally demanding methods, making it a potentially appealing tool for industrial applications.

1 Introduction

Stability is one of the most important properties of a dynamical state. Although several definitions of stability exist [30], it can be stated that if a motion is stable, small perturbations have only a transient effect on the system dynamics, which tends to return to the stable motion. Engineers heavily exploit this concept, and, indeed, the study of the stability of the working conditions of a device is an indispensable step of the design. For linear systems, in a dynamical sense, stability is a sufficient condition to guarantee the safe operation of a device. However, this is not necessarily true for nonlinear systems. While linear dynamical systems have only one solution, nonlinear systems have, in general, many. If more than one solution is stable, the system dynamics will converge to one of them depending on the initial conditions. The set of initial conditions in the phase space from which the system converges to a particular solution is called basin of attraction (BOA) of the solution, which is bounded for multi-stable systems. This concept is fundamental for assessing the robustness of a stable solution.

The fact that a BOA is bounded has obvious critical implications for real systems. Let us assume that a system (for instance, an aeroplane) is correctly working in the desired dynamical state (steady flight conditions). Suddenly, a short impulse (a violent wind gust) perturbs the system and moves it away from this state. If the system remains in its BOA, it will again converge to the original state after a short transient. Considering the aeroplane example, the transient might consist of vanishing oscillations of the wings, causing no real danger. Conversely, suppose the perturbation makes the system cross its BOA boundaries. In that case, it will converge towards another dynamical state, which, for an aeroplane, might consist of flutter wing oscillations, representing a danger for the system integrity. As a matter of fact, the assessment of flutter-free flight conditions for aeroplanes involves several lengthy tests [24, 34].

This phenomenon exists in many and various dynamical systems, ranging from mechanical ones, such as braking systems (generating brake squeal [22, 51]) and aircraft landing gears (causing the generation of shimmy vibrations [2, 56]), to very different systems such as traffic flow or power grids, where the escape from the BOA can cause traffic jams [41] and power blackouts [11, 37, 42]. The implications of limited BOA are well-known to scientists dealing with dynamical systems, and indeed several quantitative measures of system robustness exist (often referred to as dynamical integrity measures [44, 48, 53, 54]). However, in industrial approaches, they are usually overlooked if not ignored. This is mainly related to the difficulty of computing BOAs.

A few methods for the identification of BOAs of continuous dynamical systems exist [23, 32]. Analytical methods are generally based on Lyapunov functions [13]. A Lyapunov function is a continuously differentiable locally positive definite function whose time derivative is locally negative semi-definite around the equilibrium point. The region of space in which these properties are verified is part of the BOA of the equilibrium [38]. However, there is no general procedure to find Lyapunov functions [38], and their computation is practically impossible for large-dimensional systems; therefore, it is not a feasible option for the majority of real applications [23].

The most intuitive and commonly implemented numerical method consists of performing direct numerical simulations, imposing a grid of points of the system’s phase space as initial conditions and verifying if the system converges or not to the desired solution. Assuming that the mesh is sufficiently fine, this method accurately identifies BOAs of the system. However, it is computationally very costly since it requires a large number of numerical simulations, which increases exponentially with the dimension of the system, becoming practically infeasible even for medium size systems. For this reason, BOA representations are often limited to bidimensional sections [45]. This method is intrinsically very inefficient since from each numerical simulation it extracts only one bit of information. Furthermore, it is practically unusable experimentally. Probabilistic approaches, based on Monte Carlo sampling, are an alternative method for reducing computational cost [39, 50, 51, 63]; however, they do not provide any insight about the system dynamics, and their outcome is not comparable with integrity measures [32]. The cell mapping method, first developed by Hsu [20, 21, 52], is probably the most efficient numerical method for BOA estimation; its basic idea is to consider the state space not as a continuum, but rather as a collection of a large number of state cells, with each cell taken as a state entity; this method is computationally very efficient, having the advantage of being perfectly suited for parallel computation [1]. Developments of the method, such as the generalized cell mapping [18, 19], the subdivision cell mapping [5,6,7] and the multi-degree-of-freedom cell mapping method [26, 57, 58, 64], enable to investigate even relatively large dynamical systems. A first attempt to extend the method to a data-driven model-free approach, therefore implementable also in experimental environments, was recently proposed by Li et al. [33].

Virgin and co-workers [60, 61] obtained remarkable results developing an experimental method for BOA estimation based on stroboscopic surface crossing. However, this method is intrinsically limited to 3-dimensional systems (or to systems reducible to 3 dimensions [62]). Despite a significant effort by the scientific community, thus far, there is no method effectively implementable in an industrial environment for the thorough computation of dynamical system robustness.

1.1 Dynamical integrity measures

A procedure to quantify the robustness of a dynamical state was first proposed in [53]. Several measures of robustness, called dynamical integrity measures, were defined. Thompson [53] first introduced the global integrity measure (GIM). This was rapidly re-examined by Soliman and Thompson [48], who introduced the local integrity measure (LIM), the impulsive integrity measure (IIM) and the stochastic integrity measure (SIM). Later, in a series of papers, Rega and Lenci [31, 44] carefully evaluated the relevance of these integrity measures and proposed new ones, such as the integrity factor (IF) and the actual global integrity measure (AGIM). These dynamical integrity measures proved to be a valuable tool to quantitatively investigate phenomena of BOA erosion, particularly important for safe engineering design [32, 40, 45].

Figure 1 illustrates the BOA of two coexisting equilibria of a Duffing oscillator, which enable us to illustrate the difference between the various integrity measures proposed in the literature.

Fig. 1

Basin of attraction of the unforced Duffing oscillator $\ddot{x}+0.1\dot{x}-x+x^3=0$. The black and white regions indicate the basin of attraction of the equilibria at $(-1,0)$ and (1, 0), respectively. The white circle indicates the LIM (0.7683), the white line the IIM (0.7725) and the red dashed circle the IF (0.8049)

• The GIM is the extent of the area of one solution’s BOA within a specific range of the phase space. In the figure, it is given by the total extent of the black region.

• The LIM is the minimum distance from an equilibrium point to its basin boundary in any direction. Generally, if extended to periodic or quasiperiodic solutions, one point of the solution is chosen for measuring the LIM. In Fig. 1 the LIM is given by the radius of the white circle.

• The IIM is analogous to the LIM; however, it considers perturbations only in directions related to the system velocity, acknowledging that an impulse causes variations of the velocity of a mechanical system. In Fig. 1, the IIM is given by the solid white line; for this specific case, the difference between LIM and IIM is quantitatively negligible.

• The SIM is a stochastic quantity, defined in terms of the mean escape time when the attractor is subject to additive white noise excitation of prescribed intensity.

• The IF is given by the radius of the largest hypersphere that lies entirely in the BOA. In Fig. 1 it is given by the red circle, which is slightly larger than the circle referring to the LIM, and it is not centred in the equilibrium point.

• The AGIM is analogous to the GIM; however, it excludes points surrounded by not converging points in the phase space. This integrity measure acknowledges that BOAs are obtained from a finite number of discrete points and aims at not counting fractal regions.

Integrity measures provide significant engineering quantities, characterizing the robustness of a dynamical state. Apart from the GIM (and partially also the SIM), they all neglect intermingled and fractal regions of the BOA, which are not practically useful because of their intrinsic uncertain character.

2 Basic idea and objective

The objective of the present study is to develop an algorithm for the rapid assessment of the robustness of a stable equilibrium point. For addressing this task, the algorithm should iteratively quantify an integrity measure, disregarding intermingled and fractal regions of the BOA. Let us consider the integrity measures presented in Sect. 1.1. The SIM is based on a probabilistic quantity; therefore, it requires a sufficiently large number of samples to be computed. The GIM and the AGIM depend on the global extent of the BOA; hence it is computationally expensive to evaluate them. On the contrary, the LIM, the IIM and the IF depend only on the local geometry of the BOA. However, the IIM is conceived explicitly for mechanical systems, where perturbations related to impacts affect the system’s velocity; accordingly, it does not have a general character. The LIM and the IF are similar measures of the system integrity; however, for the designed algorithm’s objective, the LIM presents several advantages. First of all, the IF is relatively expensive to be exactly calculated in large-dimensional systems; it corresponds to the largest empty sphere problem [3] in geometry, and its computation is based on the definition of the Voronoi diagram [46, 55]. Although faster approximate methods to compute the IF exists [27], the computation of the LIM is significantly simpler and faster. Furthermore, in view of an iterative procedure, the LIM provides the important advantage that, if at an iteration step a particular value of the LIM is defined, all the phase space external to the hypersphere defined by the LIM (that we call hypersphere of convergence) can be immediately disregarded; this is not true for the IF. As illustrated in [48] and in [45], in most cases the various integrity measures provide qualitatively similar results. This fact allows us to use the most convenient one for our purposes, which is the LIM.

Acknowledging these premises, the algorithm is based on a simple framework. Subsequent iterative steps consist of performing a time simulation of the system and estimating the LIM value. The estimated LIM value either decreases or remains constant at each iteration. It defines a hypersphere in the phase space, which limits the region of interest of the analysis. Initial conditions of each simulation are defined within this hypersphere, as described in Sect. 3.3.3.

Although relatively simple and intuitive, this framework presents various challenges, which, if not correctly addressed, might significantly increase computational time. The first problem is related to each simulation’s stopping criterion, which directly impacts computational time. Then, an intelligent choice of initial conditions for each simulation is required for a faster convergence to an acceptable estimate of the true LIM value. Finally, since the procedure is iterative, a stopping criterion for the whole algorithm is also required. These aspects are investigated in the remaining part of the paper.

The developed algorithm, as explained later, is applicable only for the robustness assessment of equilibrium points and not for other types of solutions (such as periodic and quasiperiodic). The implementation of the algorithm to periodic solutions will be the subject of future studies. The research’s long-term objective is to provide an algorithm potentially implementable in experiments and appealing for industrial applications.

3 Algorithm description

The algorithm can be divided into three main phases: data input, preprocessing and iterative computation. The various phases are described in details below.

3.1 Data input

Data input includes: (i) the equations governing the dynamics of the system, either autonomous ordinary differential equations or difference equations, (ii) the boundaries of the phase space, (iii) the discretization interval of the phase space (required for convergence analysis, as explained later), (iv) the definition of other quantities, such as the maximal simulation time, the simulation tolerances and the utilized time integrator (in the case of ordinary differential equations). The boundaries of the phase space indicate limits beyond which the system is assumed as diverged. In other words, if during a simulation the state of the system crosses the phase space boundary, the simulation is immediately interrupted, and the algorithm assumes that the trajectory does not converge to the equilibrium of interest. The cases of non-autonomous systems, partial or delayed differential equations are not addressed here. However, we plan to extend the present procedure for those cases in future studies.

3.2 Preprocessing

The preprocessing consists of various steps; not all of them are always necessary. Namely:

• Reorganization of the equations of motion. In most cases, it is convenient to transform the system in modal coordinates of the underlying linear system for the equilibrium point of interest. In particular, this helps for the definition of the distance in the phase space, as explained in Sect. 3.2.1.

• Identification of the equilibrium point of interest, if not directly provided by the user. Equilibrium point can be computed through a numerical simulation utilizing initial conditions, which are known to be within the basin of attraction of the equilibrium point. Alternatively, it can be directly calculated from the equations of motion utilizing numerical methods.

• Define a time integration interval. This is needed to have trajectories defined by a finite number of points equidistributed in time.

• Initialize LIM value. The initial LIM value is calculated as the minimal distance between the equilibrium point and the phase space boundary.

• Define initial conditions for the first simulation. A random point of the phase space (within the given boundary) is a reasonable choice. Initial conditions of subsequent simulations are computed according to the procedure described in Sect. 3.3.3.

3.2.1 Distance definition

Identifying an integrity measure requires the definition of distance in the phase space because the system variables are, in general, physically diverse. Keeping in mind the practical purposes of the analysis, defining a distance in a significant engineering way is convenient. Since the algorithm is tested only on mechanical systems in this study, we define the distance accordingly. We assume that two points in the phase space are equidistant from the equilibrium point of interest if the energetic level of the underlying linear system at those points is the same.

Let us consider a generic autonomous n-DoF mechanical system, whose linearized equations of motion around a stable equilibrium are

$$\begin{aligned} {\mathbf {M}}\ddot{{\mathbf {x}}}+{\mathbf {C}}\dot{{\mathbf {x}}}+\mathbf {K x}={\mathbf {0}}, \end{aligned}$$

(1)

where ${\mathbf {M}}$ and ${\mathbf {K}}$ are symmetric and positive definite. Performing a modal analysis of the system and neglecting damping, the system can be reduced to

$$\begin{aligned} \ddot{q}_i+\omega _i^2q_i=0,\quad \text {for }i=1,\ldots ,n. \end{aligned}$$

(2)

The system in Eq. (2) has the same energy level $E=1/2$ for the following states

• $\dot{q}_l=1$, $q_i=0$, $\dot{q}_j=0$, for $i=1,\ldots ,n$, $j=1,\ldots ,n$, $j\ne l$

• $q_l=1/\omega _l$, $q_i=0$, $\dot{q}_j=0$, for $i=1,\ldots ,n$, $j=1,\ldots ,n$, $i\ne l$,

which are therefore assumed equidistant from the equilibrium. Accordingly, in the phase space of the system in modal coordinates, the distance between a generic point and the equilibrium is computed as

$$\begin{aligned} d=\sqrt{\sum _{i=1}^n\left( \omega _i^2q_i^2+\dot{q}_i^2\right) }, \end{aligned}$$

(3)

and, in general, the distance between two points A and B is computed as

$$\begin{aligned} d_{\text {AB}}=\sqrt{\sum _{i=1}^n\left( \alpha _i\left( q_{i\text{ A }}-q_{i\text{ B }}\right) ^2\right) +\sum _{i=1}^n\left( \alpha _{n+i}\left( \dot{q}_{i\text{ A }}-\dot{q}_{i\text{ B }}\right) ^2\right) }, \end{aligned}$$

(4)

where $q_{i\text{ A }}$ and $q_{i\text{ B }}$ are the coordinates of the two points and $\alpha _i$ are the weights. In the case of an n-dimensional mechanical systems, defined in the underlying linear modal space, the vector $\varvec{\alpha }=\left[ \alpha _1,\ldots ,\alpha _{2n}\right]$ has the from $\varvec{\alpha }=\left[ \omega _1^2,\ldots ,\omega _n^2,1,\ldots ,1\right]$. We remark that the adopted definition of distance loses significance far from the equilibrium point because of the nonlinear nature of the dynamical systems studied.

Although engineering significant, this definition is arbitrary and not applicable in many dynamical systems, for which the $\alpha _i$ coefficients should be chosen according to appropriate criteria. Despite being relevant for the practical meaning of the result provided, the definition of distance does not affect the algorithm’s effectiveness.

3.3 Iterative computation

Once all input data are provided and preprocessing is performed, the iterative computation can be started. This is the core of the algorithm and it includes the following steps:

• I perform a time integration of the system

• II classify the obtained trajectory as:

  • (a) converging to the desired solution

  • (b) non-converging to the desired solution

• III if the trajectory does not converge to the desired solution, recompute the LIM

• IV verify if the stopping criterion is fulfilled; if yes, then terminate the procedure

• V define initial conditions for the next simulation and go to step I.

3.3.1 Time series classification

Since time integration is, computationally, the most expensive operation of the algorithm, it is critical to limit the integration to the minimal essential time. For this purpose, a strategy inspired by the cell mapping method is implemented. In practice, the whole phase space is subdivided into cells. Each point of a trajectory is associated with the cell it lies in. Assuming that the cell occupied by the desired equilibrium point is known, if a trajectory reaches that cell, it is classified as “converging” to the desired solution (Fig. 2, trajectory 1). Consequently, all the cells containing points of that trajectory are also classified as “converging” (green cells in Fig. 2). If a trajectory crosses the boundary of the phase space admissible region, it is classified as “non-converging” (or “diverging” from the phase space, as trajectory 2 in Fig. 2), and similarly all cells containing points of that trajectory. These two cases are straightforward to be recognized and do not present any particular difficulty. If the convergence to the desired equilibrium is too slow, or if the cells are excessively small, a certain number of cells surrounding the one containing the desired equilibrium point can be, by default, classified as “converging”. In this way, time-series reaching those cells are interrupted, saving computational time.

Fig. 2

Illustrative examples of trajectory classification. (1) Converging to a known equilibrium; (2) leaving the considered phase space region; (3) converging to an unknown equilibrium; (4) converging to a periodic solution; (5) converging to an already tracked cell

For the recognition of fixed points different from the desired equilibrium, we consider that, if several subsequent points of a trajectory lie in the same cell, then the trajectory is assumed to have converged to a previously unknown fixed point (Fig. 2, trajectory 3); therefore, it is classified as “non-converging”. If a trajectory passes through a very slow region (for instance, close to a saddle point), then many points might lie in the same cell, leading to detecting a non-existent fixed point. In order to avoid this occurrence, a sufficiently large number of subsequent points lying in the same cell are required to classify the cell as a fixed point (40 points by default). Although this slightly slows down the computation, the detection of each new solution is performed only once during the iterations; therefore, it is not a practical issue.

The recognition of periodic motions is somehow more troublesome. We consider that, if non-subsequent points pass through the same cell, then the trajectory is considered converged to a previously unknown periodic solution (Fig. 2, trajectory 4), and it is classified as “non-converging”. However, a trajectory might encounter cells already tracked by previous points of the same trajectory even if there is no periodic solution. This usually happens, for instance, while a trajectory spirals around a stable fixed point. In order to avoid the detection of non-existent periodic solutions, the algorithm requires that a cell must be touched by non-consecutive points several times (5 by default) before the algorithm stops the simulation and assumes that it identified a periodic solution. We also remark that since, in general, the time step utilized is not an integer fraction of the period of a solution, there is no guarantee that a periodic trajectory, after one period, will reach a cell already tracked. Therefore, the detection of a periodic solution might require the time series to travel along the periodic path for several loops. Furthermore, the algorithm might confuse very small periodic solutions with fixed points; however, this does not compromise the algorithm’s effectiveness, which needs only to distinguish between trajectories converging and not converging to the desired solution. Cell dimension and time-step duration are also parameters affecting the correct classification of trajectories.

Quasiperiodic and chaotic attractors are detected and classified as periodic solutions if a point of their trajectory passes through the same cell several times. The algorithm is unable to distinguish between chaotic, quasiperiodic or periodic solutions. However, the identification of such solutions might require more time than the predefined maximal time for each time series. If a trajectory does not reach any of the conditions mentioned above within the available time, then the developed algorithm offers two possibilities: supervised and automatic classification. In supervised classification, the computation is interrupted, and the algorithm asks the user to decide, based on a representation of the trajectory in the phase space and in time, if the trajectory converges or not to the equilibrium. In the automatic classification case, the trajectory is directly marked as “non-converging”. Ultimately, for the scope of the algorithm, it is sufficient to classify cells as either converging or non-converging. Referring to Fig. 2, yellow and red cells are “non-converging” cells, while green cells are “converging” ones.

If a point of a trajectory lies in a cell already tracked by a previous time series, the simulation stops and all the cells touched by the present simulation are assumed to have the same convergence properties of the cell reached. This case is illustrated by trajectory 5 in Fig. 2. Because of the different time scales of a dynamical system’s modes, trajectories usually rapidly approach an invariant manifold before converging towards an attractor [4, 16, 17]; therefore, they tend to gather around these invariant manifolds, reaching already investigated cells within a short time. This dynamical phenomenon enables the algorithm to proceed relatively quickly after the computation of the first few trajectories, as will be illustrated in Sect. 4.

If stable solutions, different from the desired one, are known from previous analysis, then cells containing these solutions are classified as “non-converging” in advance. This facilitates the classification of the trajectories and reduces computational time.

On the one hand, the proposed classification criterion can lead to even significant inaccuracies if the cells are too large. On the other hand, smaller cells increase computational time since they reduce the probability of reaching already investigated cells (this behaviour is validated in Sect. 4). Therefore, a trade-off between accuracy and rapidity must be reached while choosing cells’ dimension. Nevertheless, the LIM is not computed according to the cell classification but directly from the points of the time series, as the shortest distance between the equilibrium and any “non-converging” point; thus, the cell dimension is not strictly related to the LIM resolution. We also remark that the algorithm does not require to store information about all the cells, as it is for the cell mapping method, but it is necessary only to save the tracked cells; therefore, in general, memory is not a particular issue for the algorithm.

3.3.2 Stopping criteria

We consider three different stopping criteria:

• 1. The algorithm performs a predefined number of iterations.

• 2. The algorithm stops if the estimated LIM value does not decrease for a given number of iterations.

• 3. The algorithm stops if the density of the points in the hypersphere of convergence reaches a predefined value.

In this study, we always let run the algorithm for a predefined number of iterations. However, for a general user, it might be convenient to use a different criterion. In light of the numerical results illustrated in Sect. 4, the other two criteria are discussed later.

Fig. 3

Illustrative example of initial condition selection. red dashed line: hypersphere of convergence; black dots: points of previous trajectories; red, blue and green dots: potential initial condition points (individuals), green dots mark the best performing individual, blue dots mark best individuals after the first one. a Points directly tracked by previous simulations; b remaining points after nearby points are eliminated; c first generation of genetic algorithm; d second generation of genetic algorithm. (Color figure online)

3.3.3 Define initial conditions for next simulation

The definition of the initial conditions of each simulation is a pretty critical step for the algorithm. Since the algorithm aims to iteratively reduce the LIM value until a good approximation is obtained, initial conditions are chosen within the hypersphere of convergence, according to the latest LIM value calculated. Additionally, we aim to fill the space within the hypersphere of convergence in a relatively homogeneous way; this suggests choosing initial conditions as the most remote point of the phase space from points already tracked within the hypersphere of convergence. However, this is a computationally expensive procedure, which corresponds to solve the largest empty sphere problem [3] (as for computing the IF). Nevertheless, there is no need for precisely identifying the most remote point; therefore, an approximate procedure based on a genetic algorithm is developed for this purpose [27]. First, all tracked points within the hypersphere of convergence and slightly outside of it are considered (Fig. 3a). Then, points very close to each other are merged in order to reduce computational time in the following steps (Fig. 3b). After that, a given number of potential initial conditions are randomly generated within the hypersphere of convergence; these are the “individuals” of the first generation of the genetic algorithm (red and green dots in Fig. 3c). The coordinates of these points are their “chromosomes”, and the “fitness function” is given by the minimal distance from any point previously tracked (black dots in the figure). The individual with the highest fitness function (green dot) is kept as an individual of the next generation. The new generation also includes individuals generated from random variations of the best individuals’ chromosomes of the previous generation and fully randomly generated new individuals (red dots in Fig. 3c, d). The procedure continues for a prescribed number of generations.

4 Algorithm validation

In this section, the proposed algorithm is applied to four different systems of increasing dimension. First, a Duffing oscillator, encompassing a negative linear stiffness and a positive cubic one, is considered, which is the same system utilized for the generation of the BOA in Fig. 1. Then, a two-DoF system, consisting of a van der Pol-Duffing oscillator with an attached tuned mass damper (TMD) [12, 15], is studied. Later, a pitch and plunge wing profile with an attached nonlinear tuned vibration absorber is considered [36]. Finally, the algorithm is applied on a chain of four masses presenting a bistability related to a geometrical nonlinearity.

Table 1 Main algorithm parameters used for the computations

4.1 Duffing oscillator

We consider an unforced Duffing oscillator, whose dynamics is governed by the equation of motion

$$\begin{aligned} \ddot{x}+2\zeta \dot{x}-x+ax^3=0. \end{aligned}$$

(5)

The system has three fixed points, ${\mathbf {x}}_{01}=(x_{01},\dot{x}_{01})=(0,0)$, ${\mathbf {x}}_{02}=(-1/\sqrt{a},0)$ and ${\mathbf {x}}_{03}=(1/\sqrt{a},0)$; if $\zeta >0$ and $a>0$, the trivial equilibrium is unstable and the other two are stable [25].

We apply the proposed algorithm to this system, utilising the fixed point ${\mathbf {x}}_{02}$ as the desired solution, while any other steady-state solution, i.e. the fixed point ${\mathbf {x}}_{03}$, is considered undesired. The position of the undesired equilibrium point is not provided to the algorithm.

Before initializing the procedure, the distance in the phase space is normalized according to the definition in Eq. (4), with $\varvec{\alpha }=\left[ \omega _1^2, 1\right]$ and $\omega _1=2$, that is the natural frequency of the system linearized around ${\mathbf {x}}_{02}$. Initially, the parameter values $\zeta =0.05$ and $a=1$ are utilized, making the system identical to the one used for obtaining Fig. 1. The results are presented in Fig. 4. For the computation, we utilized the parameters indicated in Table 1.

Fig. 4

a Trajectories in the phase space for the system in Eq. (5); red and black crosses mark desired and undesired equilibrium solutions, respectively; blue dots: converging trajectories, orange dots: non-converging trajectories, black dots: initial conditions, dashed red circle marks LIM. b Iterative estimated LIM. c Computational time per iteration; black line: total step time, blue line: simulation time, red line: time for defining following initial condition. (Color figure online)

Figure 4a illustrates all the points tracked during the entire computation in the phase space. Blue points mark trajectories converging to the desired equilibrium; orange points indicate non-converging points. Black points mark the initial conditions utilized, while the red and black crosses represent the desired and undesired equilibrium points, respectively; the undesired equilibrium was found directly by the algorithm. Finally, the red dashed circle is the hypersphere of convergence (which is 2-dimensional and reduces to a circle).

Studying the robustness of one of the stable equilibrium of this system is not challenging because of its small dimension. However, it is ideal for illustrating how the algorithm works, and it enables us to perform a first evaluation of the algorithm’s effectiveness. Figure 4b depicts the trend of the estimated LIM value at each iteration. We notice that the estimated LIM value decreases very rapidly. After only one simulation, it decreases to 0.788, which closely approximates the real LIM value, which is 0.768 (obtained from the BOA in Fig. 1). The trajectory corresponding to the first simulation (whose initial condition is marked by the number 1 in Fig. 4a) starts from a point in the right half-plane, and its trajectory makes almost one complete loop around ${\mathbf {x}}_{02}$ before converging to ${\mathbf {x}}_{03}$. Therefore, it provides a reasonable estimate of the LIM value, and it enables the algorithm to identify ${\mathbf {x}}_{03}$. The following ten simulations all converge to the desired solution; therefore, they cannot reduce the LIM value. The twelfth simulation (initial conditions marked by number 12), instead, does not converge to ${\mathbf {x}}_{02}$, and improves the estimation of the LIM value to 0.7791, which has a difference of less than 1 % from the exact LIM value. All the remaining simulations converge to ${\mathbf {x}}_{02}$; accordingly, they do not reduce the estimated LIM value.

Figure 4c illustrates the time required for the various steps of the procedure. The red line, marking the time required for defining each initial condition, has a clear increasing linear trend due to the increasing number of points included in the hypersphere of convergence. For the case under study, this time is not very large; however, it can increase significantly for large-dimensional systems. In those cases, as illustrated later, it is required to correctly choose the parameters of the genetic algorithm procedure for defining the initial conditions in order to limit it. The blue line indicates the time required for each simulation. The first two simulations require, on average, much more time than the following ones. That occurs because, once the cells near the stable solutions have already been tracked, new simulations are rapidly interrupted as soon as they reach a cell already tracked, significantly reducing computational time. The black line depicts the total time of each iteration step, which is mainly given by the sum of the simulation time and the time required for choosing the initial conditions, plus some additional operation, such as defining the new LIM value. The whole procedure, performed on a single core of a commercial personal computer (processor i5-10600 3.30 GHz), took 5.04 seconds. Although this time is minimal if compared with a brute force computation of the BOA or with a Monte Carlo approach for robustness evaluation, the cell mapping method is significantly faster [1]. Nevertheless, we remark that we did not try to reduce the computational time in any way, if not by rationally planning the basic logic of the algorithm. Indeed, time integrations were performed utilizing the standard ODE45 function in MATLAB, which is relatively slow compared to other solvers [43]. Some advantages of the present approach over the cell mapping method will be addressed while referring to larger-dimensional systems.

Fig. 5

Considering the system in Eq. (5), a estimated value for each iteration; b final estimated value for various number of cells (n is the number of cells in each dimension); c time required for the computation for various number of cells. Black lines indicate the average value, shaded areas mark the standard deviation obtained from 40 computations (a) and 150 computations for each n value (b, c)

Figure 5a illustrates the trend of the estimated LIM as an average of 40 computations. The shaded area indicates the standard deviation from the average value, marked by the black line. Although the selection of the initial conditions is partially random, the figure illustrates that the trend of the estimated LIM value is relatively uniform for all the different computations. Figure 5b, c illustrates the trend of the final estimated LIM value and the time taken for the whole computation, considering different numbers of cells (n indicates the number of cells for each dimension, and the total number of cell is $n^2$). The figures are obtained from 150 different repetitions for each considered n value. According to Fig. 5b, the estimated LIM value is relatively accurate even for a very small number of cells, and precision does not significantly improve, even increasing n from 400 to 1300. On the contrary, computational time increases practically linearly with n, as illustrated in Fig. 5c. This observation suggests that the number of cells is critical for having a fast and accurate evaluation.

Fig. 6

Considering the system in Eq. (5), estimated LIM for various values of a (a) and $\zeta$ (b)

Figure 6 illustrates the trend of the LIM for variations of a and $\zeta$ parameters. The results confirm the expectation that increasing a the LIM decreases, in fact ${\mathbf {x}}_{02}$ and ${\mathbf {x}}_{03}$ get closer and closer; while, for $a\rightarrow 0$, ${\mathbf {x}}_{02}$ and ${\mathbf {x}}_{03}$ diverge to ±infinity, therefore also the LIM value increases unboundedly. Similarly, increasing the damping ratio $\zeta$, the energy required to go from one equilibrium to the other one increases, which explain the trend of the LIM value in Fig. 6b. To some extent, this result illustrates the possibility of utilizing the proposed algorithm for design purposes.

4.2 Duffing-van der Pol oscillator with an attached tuned mass damper

We now consider a Duffing-van der Pol oscillator with an attached TMD, as the one studied in [12, 15]. The equation of motion of the system is

$$\begin{aligned} {\mathbf {M}}\ddot{{\mathbf {x}}}+{\mathbf {C}}\dot{{\mathbf {x}}}+\mathbf {Kx}+{\mathbf {b}}\left( {\mathbf {x}},\dot{{\mathbf {x}}}\right) ={\mathbf {0}}, \end{aligned}$$

(6)

where

$$\begin{aligned} \begin{aligned}&{\mathbf {x}}=\left[ \begin{array}{c}x_1\\ x_2\end{array}\right] ,\,{\mathbf {M}}=\left[ \begin{array}{cc}1&{} 0\\ 0 &{} r \end{array}\right] ,\, {\mathbf {K}}=\left[ \begin{array}{cc} 1+\gamma ^2 r&{}-\gamma ^2 r\\ -\gamma ^2 r &{} \gamma ^2 r\end{array}\right] ,\\&{\mathbf {C}}=\left[ \begin{array}{cc} -2\left( \mu _1+\gamma \mu _2 r\right) &{}-2\gamma \mu _2 r\\ -2\gamma \mu _2 r&{}2\gamma \mu _2 r \end{array}\right] ,\,{\mathbf {b}}=\left[ \begin{array}{c}\alpha x_1^3+2\mu _1x_1^2\dot{x}_1\\ 0\end{array}\right] , \end{aligned} \end{aligned}$$

(7)

$x_1$ and $x_2$ are the displacements of the primary system and the TMD, respectively, r is the mass ratio between the primary system and the TMD, $\mu _1$ is the negative damping of the primary system, $\mu _2$ is the TMD’s damping ratio, $\gamma$ is the natural frequency ratio between the primary system and the TMD, and $\alpha$ is the cubic stiffness coefficient of the primary system. Before applying the algorithm for LIM estimation, we transform the system in modal coordinates by implementing a standard modal analysis of the undamped system, linearized around its trivial equilibrium. This leads to the system of equations

$$\begin{aligned} \ddot{{\mathbf {q}}}+{\mathbf {U}}^{\text{ T }}\mathbf {CU}\dot{{\mathbf {q}}}+\varvec{\Omega }{\mathbf {q}}+{\mathbf {U}}^{\text{ T }}{\mathbf {b}}\left( {\mathbf {q}},\dot{{\mathbf {q}}}\right) ={\mathbf {0}}, \end{aligned}$$

(8)

where ${\mathbf {U}}$ contains the eigenvectors of the system, ${\mathbf {q}}$ indicates the modal displacements and $\varvec{\Omega }=\text {diag}\left( \omega _1^2,\omega _2^2\right)$, with $\omega _1$ and $\omega _2$ natural frequencies of the undamped system. The modal analysis enables us to identify the vector $\varvec{\alpha }=\left[ \omega _1^2,\omega _2^2, 1, 1\right]$, necessary for defining the distance in the phase space.

For this study, we fixed the parameter values at $r=0.05$, $\gamma =0.97$, $\mu _2=0.12$ and $\alpha =0.3$, which provide $\omega _1=0.8815$ and $\omega _2=1.1004$, while we initially set $\mu _1=0.075$ (all quantities are assumed dimensionless). For these parameter values, the trivial solution is stable; however, the bifurcation analysis performed in [15] showed that it coexists with a stable and an unstable periodic solution.

Fig. 7

a, b Projection of the collected points in the phase space for the system in Eq. (8); blue dots: converging trajectories, orange dots: non-converging trajectories, black dots: initial conditions, dashed green lines: sections of the hypersphere of convergence, black lines: coexisting periodic attractor. c Iteratively estimated LIM (various computations). d Computational time per iteration; black line: total step time, blue line: simulation time, red line: time for defining following initial condition. (Color figure online)

The results of the algorithm for LIM estimation are illustrated in Fig. 7. For the computation, we utilized the parameters indicated in Table 1. Figures 7a and 7b depict all the collected points in the phase space, projected in the $q_1,\dot{q}_1$ and $q_2,\dot{q}_2$ spaces. Orange and blue points mark diverging and converging points to the trivial solution, respectively; the green dashed circle represents a section of the hypersphere of convergence; the black line is a projection of the limit cycle oscillation identified by the algorithm. Since Fig. 7a, b is the projection on a 2-dimensional plane of objects existing in a 4-dimensional space, lines are overlapping, and it is not easy to distinguish them. However, we notice that the algorithm was able to identify the limit cycle oscillation correctly.

Fig. 8

a bifurcation diagram of the system in Eq. (8), b estimated LIM over a range of $\mu _1$ values

Figure 7c shows the trend of the estimated LIM value. The solid black line refers to the computation which produced Fig. 7a, b, while the blue dashed lines indicate the trend of LIM obtained repeating the computation multiple times. First, we notice that, also for this system, few simulations are sufficient for providing a somewhat accurate estimate of the LIM value. Furthermore, all plotted lines have a very similar trend, which suggests that this behaviour of the algorithm is general and consistent, despite the partial randomness in the selection of the initial conditions of the simulations. Figure 7d indicates the computational time of the procedure, where red and blue lines indicate the time required for defining the initial conditions and for the simulations, respectively, while the black line marks the total time of each iteration. Similarly to the case studied in the previous section, the time utilized for defining the initial conditions increases linearly, and the simulation time is much more significant for the first few simulations than for the following ones, even though the system is now 4-dimensional. The total time required for the computation was 40.3 seconds.

Figure 8a depicts the bifurcation diagram of the system, whose trivial solution loses stability for $\mu _1=0.1005$ through a subcritical Andronov-Hopf bifurcation. The generated branch of unstable periodic solutions coexists with the stable trivial solution for $\mu _1<0.1005$; then, it turns back and becomes stable at $\mu _1=0.0619$, in correspondence of a fold bifurcation. According to this bifurcation diagram (generated through the continuation toolbox MatCont [8], extensive results of the bifurcation analysis are provided in [15]), and we expect that for $\mu _1\in \left( 0.0619,\,0.1005\right)$ the robustness of the trivial solution is bounded. Also, the trend of the branch of unstable solutions suggests that the robustness of the trivial solution decreases for increasing $\mu _1$ values. Implementing the algorithm for LIM estimation over this range of $\mu _1$ values, the expected behaviour is fully confirmed. As it is illustrated in Fig. 8b, for $\mu _1<0.0619$ the LIM value obtained is limited only by the imposed boundaries of the phase space, while for $\mu _1\in \left( 0.0619,\,0.1005\right)$ the LIM value decreases as $\mu _1$ increases, reaching zero for $\mu _1=0.01005$. However, we remark that the line depicting LIM values reaches zero with a non-vertical tangent, differently from the branch of unstable solutions. This difference suggests that the algorithm might have been inaccurate in estimating the LIM value in the vicinity of the Andronov-Hopf bifurcation.

4.3 Pitch and plunge wing with an attached nonlinear tuned vibration absorber

Let us consider a pitch and plunge wing profile with an attached nonlinear tuned vibration absorber, as the one studied in [36]. The pitch and plunge model considered, used to describe an airfoil motion, was implemented in various studies [10, 28, 29], while the nonlinear tuned vibration absorber is practically a tuned mass damper also encompassing a nonlinear restoring force [14, 15]. Equations of motion governing the dynamics of the system are

$$\begin{aligned} {\mathbf {M}}\ddot{{\mathbf {x}}}+{\mathbf {C}}\dot{{\mathbf {x}}}+\mathbf {Kx}+{\mathbf {b}}\left( {\mathbf {x}}\right) ={\mathbf {0}}, \end{aligned}$$

(9)

where

$$\begin{aligned}&{\mathbf {x}}=\left[ \begin{array}{c} y\\ \alpha \\ {\tilde{x}} \end{array}\right] ,\,{\mathbf {K}}=\left[ \begin{array}{ccc} \Omega ^2+\varepsilon \gamma &{}\beta u^2-\varepsilon \gamma \lambda &{}-\varepsilon \gamma \\ -\varepsilon \gamma \lambda &{}r_\alpha ^2-\nu u^2+\varepsilon \gamma \lambda ^2&{}\varepsilon \gamma \lambda \\ -\gamma &{}\gamma \lambda &{}\gamma \end{array}\right] ,\nonumber \\&{\mathbf {C}}=\left[ \begin{array}{ccc} \zeta _h+\varepsilon \zeta +\beta u&{}-\varepsilon \zeta \lambda &{}-\varepsilon \zeta \\ -\nu u-\varepsilon \zeta \lambda &{}\zeta _\alpha +\varepsilon \zeta \lambda ^2&{}\varepsilon \zeta \lambda \\ -\zeta &{}\zeta \lambda &{}\zeta \end{array}\right] ,\nonumber \\&{\mathbf {M}}=\left[ \begin{array}{ccc} 1&{}x_\alpha &{} 0\\ x_\alpha &{}r_\alpha ^2&{}0\\ 0&{}0&{}1\end{array}\right] ,\,{\mathbf {b}}=\left[ \begin{array}{c} \varepsilon \xi \left( y-{\tilde{x}}-\lambda \alpha \right) ^3\\ \xi _\alpha \alpha ^3+\varepsilon \lambda \xi \left( {\tilde{x}}+\lambda \alpha -y\right) ^3\\ \xi \left( {\tilde{x}}+\lambda \alpha -y\right) ^3 \end{array}\right] ,\nonumber \\ \end{aligned}$$

(10)

y indicates the heave displacement, $\alpha$ the pitch rotation and ${\tilde{x}}$ the absorber displacement, non-dimensionalized with respect to the semichord of the airfoil, while u is the non-dimensional flow velocity. For the physical meaning of all the other parameters, we address the interested reader to [36]. The adopted parameter values are $x_\alpha =0.2$, $r_\alpha =0.5$, $\beta =0.2$, $\nu =0.08$, $\Omega =0.5$, $\zeta _\alpha =0.01$, $\zeta _h=0.01$, $\xi _\alpha =1$, $\varepsilon =0.05$, $\lambda =1$, $\zeta =0.11$, $\gamma =0.462$ and $\xi =0.218$; initially, u is set at 1.236.

Since a standard modal analysis cannot be applied to the case under study because the stiffness matrix ${\mathbf {K}}$ is not symmetric (although alternative methods exist [35]), we applied a different approach for defining the distance in the phase space. We first transform the system in first order form, i.e.

$$\begin{aligned} \dot{{\mathbf {y}}}=\mathbf {Ay}+\tilde{{\mathbf {b}}}\left( {\mathbf {y}}\right) , \end{aligned}$$

(11)

where

$$\begin{aligned} {\mathbf {y}}=\left[ \begin{array}{c} {\mathbf {x}}\\ \dot{{\mathbf {x}}}\end{array}\right] ,\, {\mathbf {A}}=\left[ \begin{array}{cc} {\mathbf {0}}&{}{\mathbf {I}}_3\\ -{\mathbf {M}}^{-1}{\mathbf {K}}&{}-{\mathbf {M}}^{-1}{\mathbf {C}}\end{array}\right] ,\,\tilde{{\mathbf {b}}}=\left[ \begin{array}{c} {\mathbf {0}}\\ -{\mathbf {M}}^{-1}{\mathbf {b}}\end{array}\right] . \end{aligned}$$

(12)

Then, we transform it in Jordan normal form by applying the coordinate transformation ${\mathbf {y}}=\mathbf {Tq}$, where

$$\begin{aligned} {\mathbf {T}}=\left[ \begin{array}{cccccc} \text {Re}({\mathbf {s}}_1)&\text {Im}({\mathbf {s}}_1)&\text {Re}({\mathbf {s}}_2)&\text {Im}({\mathbf {s}}_2)&\text {Re}({\mathbf {s}}_3)&\text {Im}({\mathbf {s}}_3) \end{array}\right] , \end{aligned}$$

(13)

and ${\mathbf {s}}_1$, ${\mathbf {s}}_2$, ${\mathbf {s}}_3$ are the eigenvectors of ${\mathbf {A}}$, reducing the system to

$$\begin{aligned} \dot{{\mathbf {q}}}=\mathbf {Wq}+{\mathbf {T}}^{-1}\tilde{{\mathbf {b}}}\left( {\mathbf {q}}\right) , \end{aligned}$$

(14)

where ${\mathbf {W}}$ is a block-diagonal matrix. In ${\mathbf {q}}$, variables are not organized anymore as displacements and velocities. We, therefore, define the distance in the phase space, weighting it with respect to the damping of each mode, provided by the real part of the eigenvalues of ${\mathbf {A}}$, indicated with $\lambda _1$, $\lambda _2$ and $\lambda _3$. Therefore we have $\varvec{\alpha }=\left[ \lambda _1\quad \lambda _1\quad \lambda _2\quad \lambda _2\quad \lambda _3\quad \lambda _3\right]$. This procedure enables us to reasonably balance the effect of perturbations in each direction in the phase space. Nevertheless, it is not required to compute these transformations to apply the algorithm for LIM estimation; instead, one can directly utilize physical coordinates, normalizing the distance based on practical considerations relevant for the system under study.

The application of the algorithm was particularly troublesome for this system because of its low damping. In fact, although various parameter setting were tried, either the algorithm required very long simulations for identifying limit cycles, or it confused the spiralling trajectories converging towards the stable trivial solution as converged to a non-existent limit cycle. Therefore, we manually identified new solutions. In other words, if the algorithm could not recognize if a trajectory converges towards the desired solution or to an unknown one, the computation paused, and we could indicate to the software if the cells encountered by the trajectory had to be marked as “converging” or “not-converging” (for the identification of the LIM value, it is irrelevant if a solution diverges from the considered portion of the phase space or it converges to another solution). We remark that also for other numerical techniques, such as cell-mapping, distinguishing between a centre (surrounded by infinitely many limit cycle) and a sink equilibrium point in slightly damped systems is very challenging [59].

The result of the computation is illustrated in Fig. 9. For the computation, we utilized the parameters indicated in Table 1.

Fig. 9

a–c Projection of the collected points in the phase space for the system in Eq. (14); blue dots: converging trajectories, orange dots: non-converging trajectories, black dots: initial conditions, dashed green lines: sections of the hypersphere of convergence. d Iteratively estimated LIM. e Bifurcation diagram, solid lines: stable solutions, dashed lines: unstable solutions. f Estimated LIM over a range of u values. (Color figure online)

Figure 9a–c shows all the tracked points of the various numerical simulations, projected in the $q_1,q_2$, $q_3,q_4$ and $q_5,q_6$ spaces. Blue and orange points indicate converging and non-converging points, respectively, black points mark initial conditions of the simulations, and green dashed lines represent sections of the hypersphere of convergence. Although the stable limit cycle coexisting with the trivial solution was not directly identified, in all the projection, it can be clearly recognized that the orange points are enclosed by a smooth curve, which marks a limit cycle. The figures are rather hard to interpret because of the multiple overlapping lines. However, the projection on the $q_3,q_4$ plane seems to provide a pretty clear view of the BOA of the trivial solution. We tried to plot two-dimensional sections of the phase space instead of projections; however, points are not dense enough to provide a meaningful image; therefore, we omitted such figures. As depicted in Fig. 9d, the estimated LIM value rapidly decreases in few iterations, immediately providing a reasonable estimate of the LIM value. After iteration 12, only iteration 30 did not converge to the trivial solution, improving the estimate of the LIM value.

Figure 9e illustrates the bifurcation diagram of the system (generated through the continuation software AUTO [9], extensive results of the bifurcation analysis are provided in [36]). The trivial solution loses stability through a supercritical Andronov-Hopf bifurcation for $u=1.255$, which in general does not mine the robustness of a stable fixed point. However, the branch of periodic solutions undergoes various other bifurcations. First, a couple of Neimark–Sacker bifurcations generates a branch of quasiperiodic solutions for $u\in (1.264,\,1.279)$ (not illustrated in the figure). Then a fold bifurcation at $u=1.313$ makes the branch turn back, reaching the region of stability of the trivial solution. Overall, the bifurcation diagram shows that the trivial solution is not globally stable for $u>1.212$. This behaviour was perfectly confirmed by the algorithm when applied for u ranging from 1.21 to 1.255, as shown in Fig. 9f. For $u<1.212$, the LIM value was limited uniquely by the set boundaries of the phase space. For $u\in (1.212,\,1.254)$, the LIM value has a trend, which closely resembles the trend of the branch of unstable periodic solutions in Fig. 9e. This similarity suggests that the algorithm can provide significant information for design purposes. We remark that a classical local bifurcation analysis would not directly illustrate that the trivial solution has bounded stability in the investigated range of u values because of its supercritical characteristic.

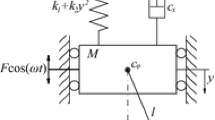
4.4 Chain of four masses

The last model considered in this study is a chain of four lumped masses, as the one illustrated in Fig. 10. Four identical masses, connected by identical linear springs and dampers, are free to move in the horizontal direction. The second mass is attached to two other springs positioned vertically, as illustrated in the figure. $l_0$ is the vertical elongation of the spring, whose elongation at rest is $l_r$, where $l_r>l_0$. k, m and c indicates the stiffness of the springs, the masses and the damping coefficients of the dampers, respectively.

Fig. 10

Mechanical model of the chain of four masses

Assuming, without loss of generality, that $k=1$ and $m=1$ (all quantities are assumed dimensionless), the equation of motion of the system is

$$\begin{aligned} {\mathbf {M}}\ddot{{\mathbf {x}}}+{\mathbf {C}}\dot{{\mathbf {x}}}+\mathbf {Kx}+{\mathbf {b}}\left( {\mathbf {x}}\right) ={\mathbf {0}}, \end{aligned}$$

(15)

where

$$\begin{aligned}&{\mathbf {x}}=\left[ \begin{array}{c} x_1\\ x_2\\ x_3\\ x_4 \end{array}\right] ,\,{\mathbf {M}}=\left[ \begin{array}{cccc} 1&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1 \end{array}\right] ,\,{\mathbf {C}}=c\left[ \begin{array}{cccc} 2&{}-1&{}0&{}0\\ -1&{}2&{}-1&{}0\\ 0&{}-1&{}2&{}-1\\ 0&{}0&{}-1&{}2 \end{array}\right] \nonumber \\&{\mathbf {K}}=\left[ \begin{array}{cccc} 2&{}-1&{}0&{}0\\ -1&{}2&{}-1&{}0\\ 0&{}-1&{}2&{}-1\\ 0&{}0&{}-1&{}2 \end{array}\right] ,\,{\mathbf {b}}=\left[ \begin{array}{c} 0\\ 2x_2\left( 1-\frac{l_r}{\sqrt{l_0^2+x_2^2}}\right) \\ 0\\ 0 \end{array}\right] . \nonumber \\ \end{aligned}$$

(16)

Imposing that $l_0=1$, the system has the equilibrium points

$$\begin{aligned} {\mathbf {x}}_{01}=\left[ \begin{array}{c} 0\\ 0\\ 0\\ 0 \end{array}\right] ,\,{\mathbf {x}}_{02}=-\left[ \begin{array}{c} \frac{\sqrt{144 l_r^2-289}}{34}\\ \frac{\sqrt{144 l_r^2-289}}{17}\\ \frac{2\sqrt{144 l_r^2-289}}{51}\\ \frac{\sqrt{144 l_r^2-289}}{51} \end{array}\right] ,\, {\mathbf {x}}_{03}=-{\mathbf {x}}_{02}, \end{aligned}$$

(17)

${\mathbf {x}}_{01}$ is real for any $l_r$ value, while ${\mathbf {x}}_{02}$ and ${\mathbf {x}}_{03}$ are real for $l_r>17/12$. If ${\mathbf {x}}_{02}$ and ${\mathbf {x}}_{03}$ are real, they are stable, while ${\mathbf {x}}_{01}$ is unstable. In the following, we aim at studying the robustness of ${\mathbf {x}}_{02}$.

First, we centre the coordinates of the system around ${\mathbf {x}}_{02}$ by defining the coordinates ${\mathbf {y}}={\mathbf {x}}-{\mathbf {x}}_{02}$. Then, we perform a classical modal analysis, considering the underlying undamped linear system, in order to obtain the distance weight vector $\varvec{\alpha }=\left[ \omega _1^2,\omega _2^2,\omega _3^2,\omega _4^2,1, 1,1,1\right]$, where the natural frequencies depend on $l_r$.

Initially, we set $c=0.05$ and $l_r=2$, for which we have $\omega _1=0.7455$, $\omega _2=1.21$, $\omega _3=1.6409$ and $\omega _4=1.9662$. Applying the algorithm for LIM estimation, we obtain the results illustrated in Fig. 11. For the computation, we utilized the parameters indicated in Table 1.

Fig. 11

a, b Projection of the collected points in the phase space for the system in Eq. (15); blue dots: converging trajectories, orange dots: non-converging trajectories, black dots: initial conditions, dashed red lines: sections of the hypersphere of convergence, black cross: coexisting stable equilibrium. c Iteratively estimated LIM (various computations). d Computational time per iteration; black line: total step time, blue line: simulation time, red line: time for defining following initial condition. e Distance of each initial condition from the closest tracked point in the phase space various computations). f Estimated LIM computed over a range of $l_r$ values. (Color figure online)

Fig. 12

a, b Projection of the collected points in the phase space for the system in Eq. (15); blue dots: converging trajectories, orange dots: non-converging trajectories, black dots: initial conditions, dashed red lines: sections of the hypersphere of convergence, black cross: coexisting stable equilibrium. c Iteratively estimated LIM. d Distance of each initial condition from the closest tracked point in the phase space various computations. (Color figure online)

Figure 11a, b shows the projection of collected points in the $q_1,\dot{q}_1$ and $q_3,\dot{q}_3$ spaces. Blue and orange points mark converging and non-converging points, respectively; black points indicate initial conditions of the simulations; the red dashed lines represent sections of the hypersphere of convergence; the black cross marks the coexisting stable equilibrium ${\mathbf {x}}_{03}$ (found automatically by the algorithm). Although lines overlap because of the projection, the $q_1,\dot{q}_1$ plane offers a pretty clear picture of the compact region of the BOAs of the two attractors. Nevertheless, Fig. 11b suggests that the high dimensionality of the system significantly complicates the global analysis of the system. In fact, in that projection, ${\mathbf {x}}_{03}$ seems to be within the hypersphere of convergence of ${\mathbf {x}}_{02}$ (obviously, it is not within it).

Figure 11c shows the trend of the estimated LIM value, where the light blue lines refer to other computations of the algorithm. The trend is similar to the previous systems, i.e. the first few simulations are the most revealing for the estimation. Nevertheless, we notice that the final estimated LIM values in the various computations, after 100 iterations, have a significant variation.

Figure 11d illustrates the time required for the various phases of the algorithm, organized for each iteration. The red and blue lines indicate the time required for choosing the initial conditions of each simulation and the time required for the numerical integration, respectively; the black line marks the total iteration time. The trend of the simulation time (blue line) qualitatively reminds the results obtained for the systems previously studied. Initially, simulations are relatively long; then, they require less time since trajectories rapidly reach cells already tracked. The time required for choosing the initial conditions increases linearly with the iterations because of the increasing number of points within the hypersphere of convergence. It is still relatively short because we purposely reduced the number of generations in the genetic algorithm. This parameter represents a trade-off between finding initial conditions really as remote as possible and the time required to find them. The entire computation took 108 seconds.

Figure 11e indicates the distance d between each initial condition and the closest tracked point in the hypersphere of convergence. Because of the increasing density of points, the value of d naturally decreases after each iteration (in average), and it is an indicator of the density of points in the hypersphere of convergence. However, we notice that its decreasing trend is very slow, and after 100 iterations, it still has a value larger than half of the LIM. This result explains how empty and unexplored the phase space is, even after so many simulations, which is related to the relatively large dimension of the system. This fact suggests that, although the proposed algorithm provides a quantity significant from an engineering point of view, it gives no guarantee that other undetected attractors exist.

Concerning the engineering pertinence of the result provided, Fig. 11f illustrates how the LIM value varies with $l_r$. As $l_r$ tends to 17/12, the value of the LIM tends to zero, since for $l_r=17/12$ ${\mathbf {x}}_{02}$ and ${\mathbf {x}}_{03}$ merge. On the contrary, increasing $l_r$ the value of the LIM increases, as the energy required to reach ${\mathbf {x}}_{03}$ from ${\mathbf {x}}_{02}$ increases. This result confirms the engineering relevance of the outcome of the computation.

Considering the low density of points in the phase space, we repeated the computation in Fig. 11 increasing the number of iteration from 100 to 1000.

Fig. 13

Comparison of estimated LIM and time required for the computation utilizing various stopping criteria. Results relative to the system in Eq. (15). a, b Predefined number of iterations; c, d computation stopped when N consecutive iterations do not reduce the estimated LIM value; e, f computation stopped when the average d value decreases below a predefined $d_{\text {lim}}$ value. The solid lines mark the average of 1000 computations, while the grey areas indicate the standard deviation

The results, illustrated in Fig. 12, show that the additional simulations did not significantly improve the estimation of the LIM value (after the first 50 iterations, only iteration 79 and 757 were not converging), whose final value was 0.8136. This value is larger than the value provided by the best performing computation in Fig. 11c after only 100 iteration, that is 0.7481. This fact, together with the general observation that most of the simulations, after the first few ones, converge to the desired solution, provides relevant indications about the strategy for the definition of the initial conditions. In fact, on the one hand, selecting, as initial conditions, remote points of the hypersphere of convergence enables to homogeneously fill the hypersphere, potentially revealing attractors hidden in pockets of the phase space. On the other hand, this is probably not an efficient strategy for increasing the accuracy of the estimated LIM value in a short time. For this objective, selecting points closer to the boundary of the hypersphere is probably more efficient. This observation suggests that the algorithm for selecting initial conditions should be adapted to the objective of the analysis, that is, either obtaining an accurate estimation of the LIM (but potentially wrong, if an attractor is unrevealed) or having a more rough estimation but still more reliable.

Although not desirable from the point of view of the safety of the estimation because of the large unexplored space, the low density of points in the phase space clearly illustrates how the proposed algorithm has no memory issues. In contrast, the cell mapping method requires significant memory for large-dimensional systems [1].

4.5 Comparison of stopping criteria

We now aim at investigating the different stopping criteria proposed in Sect. 3.3.2. Namely, (i) interrupt the computation after a predefined number of iterations, (ii) when a given number of consecutive iterations do not reduce the estimated LIM, or (iii) when the tracked points within the radius of convergence reach a specific density. The three criteria are compared for the analysis of the chain of four masses.

For the comparison, we ran the algorithm 1000 times for 100 iterations. Based on the results obtained, we computed the LIM value that the algorithm would have estimated adopting a different stopping criterion and the time it would have taken. Results are illustrated in Fig. 13.

Figure 13a, b depicts the estimated LIM value and the required time for a predefined number of iterations. The black lines mark the average value, while the grey areas indicate the standard deviation. Considering Fig. 11c, the trend of Fig. 13a is not surprising. After about 30 iterations, the estimated LIM value decreases very slowly; besides, the standard deviation remains relatively large for any number of iterations considered. After 100 iterations, the LIM value still has a slightly decreasing trend, meaning that a much larger number of iterations is needed to approximate the actual LIM value correctly. Conversely, the required time for the computation increases linearly, and it is highly predictable, as proved by its small standard deviation.

Figure 13c, d refers to the second proposed stopping criterion. Namely, the computation is interrupted if N consecutive iterations fail to reduce the LIM value. According to the results in Fig. 13c, $N\approx 10$ is probably the lower limit for a reliable computation. Further increasing N reduces the LIM value only slightly. As in the previous case, the computational time increases linearly with N; however, it has a significant standard deviation, making it hardly predictable.

Results of the third stopping criterion are presented in Fig. 13e, f. In this case, the computation is interrupted if d (the distance between each initial condition and the closest tracked point) is below a predefined $d_{\text {lim}}$ value on average. The average of d is computed according to the last ten d values measured. Indeed, d is strictly related to the density of tracked points in the hypersphere of convergence; a smaller d value indicates a higher density of tracked points. According to Fig. 13e, for small values of $d_{\text {lim}}$, the trend of the estimated LIM value becomes steeper. This phenomenon is due to the slowly decreasing trend of d for increasing iterations, as illustrated in Figs. 11e and 12d. Accordingly, as d decreases, the computational time increases with an increasing steepness. Consequently, it is very hard to set a proper $d_{\text {lim}}$ value. In fact, if $d_{\text {lim}}$ is too large, the standard deviation of the estimated LIM is too large to provide reliable results. Conversely, if $d_{\text {lim}}$ is too small, computational time might be excessively large. Additionally, the suitable choice of the $d_{\text {lim}}$ value strongly depends on the system under study.

Fig. 14

Comparison of the three stopping criteria with respect to the average estimated LIM value and computational time. The data are the same as in Fig. 13

Considering the illustrated results, the third criterion is the most complicated to implement, while the first and second are somewhat similar and easy to implement. An advantage of the first criterion over the second one is that it allows one to predict the required computational time accurately. A direct comparison of the three criteria in terms of their efficiency is provided in Fig. 14, where the average computational time is plotted against the average estimated LIM value. The figure clearly shows that the first and second criteria are computationally equivalent since the two corresponding curves almost overlap. Besides, Fig. 14 also illustrates that the third criterion is more efficient than the other two since it provides lower LIM estimates in less time, on average. These contradictory results suggest that the best choice of the stopping criterion might depend on practical constraints and the specific system at hand.

5 Discussion

5.1 Algorithm evaluation

Applying the proposed algorithm to various systems, presented in Sect. 4, illustrated its effectiveness but also highlighted some of its limitations. Regarding the advantages of the procedure, we remark:

• The algorithm provided a value, which could quantitatively characterize the robustness of a stable equilibrium. Applying the algorithm on a Duffing oscillator showed that this value is indeed a good estimation of the LIM. For the other, larger systems, the obtained LIM value was not compared with the exact one; however, its trend for variations of one parameter illustrated that the provided value has engineering relevance.

• The algorithm converges to a meaningful estimation of the LIM in very few steps, which makes it potentially very quick.

• Simulations after the first few ones are relatively short, even for large-dimensional systems, enabling one to set a large number of iterations keeping the required time reasonable.

• The procedure does not require much memory, even for large-dimensional systems, differently from other methods for computing BOAs.

• The algorithm neglects intermingled and fractal region, contrary to probabilistic approaches [37, 39, 49, 50], which might overestimate the safe robust region.

About the limitations of the procedure, we highlight the following:

• The procedure is not well-suited for parallel computation. Each iteration is computed after the previous one is completed. Some operations can be parallelized, such as the algorithm for defining the initial conditions; however, this would not significantly speed up the computation. Nevertheless, if the algorithm is implemented for parametric analysis, it can be easily parallelized for the various considered values of the parameter. The author obtained Figs. 6, 8b and 11f in a similar way.

• The procedure provides information about one attractor only, while other methods for studying global dynamics generally produce information relative to all the detected attractors at the same time. This limitation might be overcome with a proper redesign of the algorithm, which will be the subject of future studies.

• Simulations after the first few ones improve the estimation of the LIM value very slowly. This problem is related to the algorithm utilized for defining initial conditions, which looks for empty regions of the hypersphere of convergence, and does not aim at finding the boundary of the BOA.

• In high-dimensional systems, the phase space is filled very slowly. Unless a considerable number of simulations are run, stable solutions existing within the estimated hypersphere of convergence may be undetected. This limitation is an intrinsic issue of large-dimensional systems, which can hardly be solved utilizing a purely numerical approach, as done in this study. Probably, the best strategy is to reduce the dimension of the system as much as possible before applying the algorithm, neglecting modes that seem less relevant for the system’s robustness. Although the algorithm was able to provide a quantitatively significant result also for an 8-dimensional system in a very short time, industrial systems might be significantly larger. This aspect should be carefully evaluated in future developments of this research.

5.2 Future developments

Several decades of research optimized existing method for robustness assessment, such as the cell mapping method, which is now very efficient. On the contrary, up to the author’s knowledge, this is the first attempt to study robustness, directly aiming to find an integrity measure in a multi-dimensional system. Therefore, we believe that the proposed algorithm can be significantly improved and, in the future, might become a valid alternative to the cell mapping method. Probably, the main aspects which should be improved are the following:

• Numerical simulations were performed with the MATLAB function ODE45, which is one of the less efficient algorithms in terms of velocity of computation [43]. Adopting a more efficient time integrator could reduce the computational time by one order of magnitude or more.

• The problem of the choice of each simulation’s initial conditions was already partially discussed in this paper. The approach utilized in this study aims at homogeneously filling the hypersphere of convergence. However, this is probably not the best way to quickly obtain an accurate LIM value. Besides, choosing initial conditions becomes significantly time-consuming for large-dimensional systems if many iterations are required and the number of points inside the hypersphere of convergence increases. Alternative strategies should be tested. In some cases, it might be possible to define a critical section of the phase space, limiting the system robustness, and choose initial conditions in that subspace. For example, considering the pitch and plunge wing studied in Sect. 4.3, the analysis clearly revealed that the system’s eigenvectors associated with the eigenvalue with the smaller real part spanned a critical section of the phase space concerning the robustness of the trivial solution. Another approach for defining the initial conditions is to choose them on a single line, aiming at precisely identifying one point of the stability boundary, which might generate a trajectory particularly revealing in terms of the maximum extent of the hypersphere of convergence. Finally, a random choice of initial conditions has the advantage of being very rapid, and it might be advantageous in large-dimensional systems. All of these possibilities present advantages and disadvantages, depending on the dimension of the system, on the shape of its basin of attraction and on the number of iterations performed. In future studies, these different methods should be investigated, aiming at programming an algorithm to choose the best strategy for each given situation automatically. However, the individualistic nature of nonlinear systems makes it very hard to define a general procedure that is at the same time rapid and reliable.

• The proposed algorithm has already several parameters which strongly affect the computational speed. The main ones are the relative and absolute tolerance of the time integration, the number of cells in the phase space, the parameters of the genetic algorithm for initial condition selection. In this study, the relevance of some of them was investigated; the others should also be studied to optimize the performance of the algorithm.

• At the moment, the algorithm can study the robustness of equilibrium points only. In the future, it should be extended to other types of solutions, such as periodic and quasiperiodic motions. Also, the robustness of chaotic solutions is worth investigating, although it might be excessively challenging.

• The algorithm is defined for numerical computations. However, we plan to extend it to experimental investigations, as well, for which no well-established alternative exists [47, 61, 65]. That would require some modifications, for instance, regarding the choice of the initial conditions, which should obey some practical limitations. Furthermore, the subdivision of the phase space in cells might be unnecessary. These aspects will be the subject of future studies.

• The algorithm can be implemented for parametric analysis, i.e. studying how the LIM value varies with one (or more) parameter. In the absence of global bifurcations, the variation of LIM is smooth, and two close values of the varying parameter produce similar LIM values. The similarity of the LIM values could be exploited as it is usually done in continuation analysis, where the previously computed solution is used as an initial guess for the following one. Such an approach might significantly accelerate the computation. However, so far, no strategy is proposed for this purpose.

Concerning the results shown in Sect. 4, we notice that for all the systems under study, a bifurcation analysis, combined with continuation techniques, provides already very extensive information about the robustness of the stable equilibrium. This observation highlights the importance of such well-established techniques for the global analysis of dynamical systems.

6 Conclusions

In this study, a new algorithm for estimating the robustness of a stable equilibrium was developed. The algorithm utilizes an approach different from existing numerical methods for global analysis. It does not aim at studying the whole basin of attraction of a solution; instead, it directly tries to estimate the local integrity measure (LIM) [48], which defines the largest hypersphere in the phase space of the system, centred in the equilibrium, fully included in the basin of attraction of the equilibrium of interest. From an engineering point of view, this quantity has obvious relevance for the safety of a dynamical system.

The algorithm was then tested on four different mechanical systems of increasing dimension (from 2 to 8). For each of the systems, the algorithm produced a meaningful estimation of the LIM in a relatively short time. In particular, the results highlighted that a few numerical simulations are already sufficient for providing a rough but practically relevant estimation of the LIM. This outcome suggests that the algorithm has the potentiality to be utilized in industrial environments, where rapid solutions are generally pursued. The algorithm still presents several drawbacks, detailed in Sect. 5.1, which is not surprising, considering that it is the first time that the problem of robustness of a solution is faced with a similar approach. Nevertheless, several ways of improving the algorithm, concerning the speed of computation and reliability of the result were discussed and will be the subject of future studies.