Spatiotemporal distortion effects and interaction properties for certain nonlinear waves of the generalized AB system

Abstract

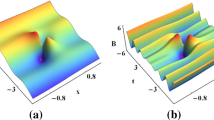
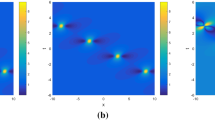
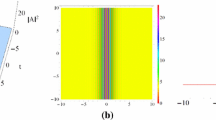
Under investigation in this paper is the generalized AB system, which is extended from the well-known AB system that is used to describe the evolution of the wave packets in a marginally stable or unstable baroclinic shear flow. Introducing an auxiliary function $\alpha (\tau )$, we construct the Nth-order vector solitary waves for the generalized AB system, which are different from the regular vector solitary waves in the existing literature. We find that the vector solitary waves are subject to spatiotemporal distortion (SD) effects in the evolution. Influenced by the SD effects, the vector solitary waves would evolve with the shape changes or the appearances, splits, combinations and disappearances of certain bulges. It is revealed that the SD effects do not change the interaction properties of the vector solitary waves. Excluding from the SD effects, we find that the interacting vector solitary waves not only exhibit the same local and global oscillations as the scalar solitary waves of AB system, but also lead to certain unique inelastic interactions as they possess different velocities. It is also found that two vector solitary waves with the same velocity may degenerate into a parallel-state solitary wave while two scalar solitary waves can not. For the interactions among the multi vector solitary waves, we observe that the symmetric parallel-state solitary waves interacting with standard bell-shaped solitary waves may bring about the destruction of the symmetric structures as well as the generation of the bound-state solitary waves, and that two symmetric parallel-state solitary waves interacting with each other may cause the broken symmetric structures for both ones. Moreover, the vector breathers and rogue waves of the generalized AB system are presented. Taking vector rogue waves in consideration, we demonstrate that the SD effects manifest themselves in two aspects: one is the destruction of the conventional one-peak-two-valley or four-petal symmetric structure; the other is the split of the rogue wave into some small ones with the adjustable number. Besides, modulation instability analysis presents the conditions under which the perturbed plane waves can develop into the distorted rogue waves.

Appendix

The $\Theta ^{(n)}_{\Gamma _1,\Gamma _2,\cdots ,\Gamma _j;\Gamma '_1,\Gamma '_2,\cdots ,\Gamma '_{j-1}}$ and $\Theta _{\Gamma _1,\Gamma _2,\cdots ,\Gamma _j;\Gamma '_1,\Gamma '_2,\cdots ,\Gamma '_{j}}$ are expressed as follows:

$$\begin{aligned}&\Theta ^{(n)}_{\Gamma _1,\Gamma _2,\cdots ,\Gamma _j;\Gamma '_1,\Gamma '_2,\cdots ,\Gamma '_{j-1}}\\&= \frac{\prod \limits _{1\le \imath<\jmath \le j}\left( k_{\Gamma _\imath }{-}k_{\Gamma _\jmath }\right) \prod \limits _{1\le \imath<\jmath \le j-1}\left( k_{\Gamma '_\imath }{-}k_{\Gamma '_\jmath }\right) }{\prod \limits _{1\le \imath<\jmath \le j}\left( k_{\Gamma _\imath }{+}k_{\Gamma _\jmath }\right) \prod \limits _{1\le \imath<\jmath \le j-1}\left( k_{\Gamma '_\imath }{+}k_{\Gamma '_\jmath }\right) \prod \limits _{1\le \imath \le j,1\le \jmath \le j-1}\left( k_{\Gamma _\imath }+k_{\Gamma '_\jmath }\right) ^2 }\\&\quad \times \sum _{\gamma =1}^j \left[ \sum _{\begin{array}{c} 1\le p_1<p_2<\cdots<p_\gamma \le j\\ 1\le q_1<q_2<\cdots<q_{\gamma -1}\le j-1 \end{array}} ^{\begin{array}{c} \{q_\gamma<q_{\gamma +1}<\cdots<q_{j-1} \}=\{1,2,\cdots ,j-1\} \backslash \{q_1, q_2,\cdots ,q_{\gamma -1}\}\\ \{p_{\gamma +1}<p_{\gamma +2}<\cdots<p_{j}\}=\{1,2,\cdots ,j\} \backslash \{p_1, p_2,\cdots ,p_\gamma \} \end{array}}\right. \\&\quad \left. \left( (-1)^{{\tilde{t}}_1+{\tilde{t}}_2} \prod _{r=1}^{\gamma } \varrho ^{(n)}_{\Gamma _{p_{r}}} \prod _{r=1}^{\gamma -1} { \varrho ^{(n)}_{\Gamma '_{q_{r}}} }^*\prod _{s=1}^{j-\gamma } {\varrho ^{(3-n)}_{\Gamma _{p_{\gamma +s}}} } \prod _{s=1}^{j-\gamma } {\varrho ^{(3-n)}_{\Gamma '_{q_{\gamma +s-1}}}}^*\tilde{\Delta }\right) \right] ,\\&\quad {\tilde{t}}_1=t\left( \Gamma _{p_1},\Gamma _{p_2},\cdots ,\Gamma _{p_\gamma },\Gamma _{p_{\gamma +1}},\Gamma _{p_{\gamma +2}},\cdots , \Gamma _{p_j}\right) ,\\&\quad {\tilde{t}}_2=t\left( \Gamma '_{q_1},\Gamma '_{q_2},\cdots ,\Gamma '_{q_{\gamma -1}},\Gamma '_{q_{\gamma }}, \Gamma '_{q_{\gamma +1}},\cdots ,\Gamma '_{q_{j-1}} \right) ,\\&\quad \tilde{\Delta }=\prod _{1\le \imath<\jmath \le \gamma }\left( {k_{\Gamma _{p_\imath }}}^2-{k_{\Gamma _{p_{\jmath }}}}^2 \right) \prod _{1\le \imath<\jmath \le \gamma -1}\left( {k_{\Gamma '_{q_\imath }}^*}^2-{k_{\Gamma '_{q_{\jmath }}}^*}^2 \right) \\&\quad \times \prod _{\gamma +1\le \imath<\jmath \le j}\left( {k_{\Gamma _{p_\imath }}}^2-{k_{\Gamma _{p_{\jmath }}}}^2 \right) \prod _{\gamma \le \imath<\jmath \le j-1}\left( {k_{\Gamma '_{q_\imath }}^*}^2-{k_{\Gamma '_{q_{\jmath }}}^*}^2 \right) \\&\qquad \prod _{1\le \imath \le \gamma \le \jmath \le j-1}\left( {k_{\Gamma _{p_\imath }}}^2-{k_{\Gamma '_{q_{\jmath }}}^*}^2 \right) \prod _{1\le \imath \le \gamma -1<\gamma +1\le \jmath \le j}\left( {k_{\Gamma '_{q_\imath }}^*}^2-{k_{\Gamma _{p_{\jmath }}}}^2 \right) ,\\&\quad \Theta _{\Gamma _1,\Gamma _2,\cdots ,\Gamma _j;\Gamma '_1,\Gamma '_2,\cdots ,\Gamma '_{j}}\\&\quad = \frac{\prod \limits _{1\le \imath<\jmath \le j}\left( k_{\Gamma _\imath }-k_{\Gamma _\jmath }\right) \prod \limits _{1\le \imath<\jmath \le j}\left( k_{\Gamma '_\imath }-k_{\Gamma '_\jmath }\right) }{\prod \limits _{1\le \imath<\jmath \le j}\left( k_{\Gamma _\imath }+k_{\Gamma _\jmath }\right) \prod \limits _{1\le \imath<\jmath \le j}\left( k_{\Gamma '_\imath }+k_{\Gamma '_\jmath }\right) \prod \limits _{1\le \imath \le j,1\le \jmath \le j}\left( k_{\Gamma _\imath }+k_{\Gamma '_\jmath }\right) ^2 }\\&\quad \times \sum _{\gamma =1}^j \left[ \sum _{\begin{array}{c} 1\le p_1<p_2<\cdots<p_\gamma \le j\\ 1\le q_1<q_2<\cdots<q_{\gamma }\le j \end{array}} ^{\begin{array}{c} \{q_{\gamma +1}<q_{\gamma +2}<\cdots<q_{j}\}=\{1,2,\cdots ,j\} \backslash \{q_1, q_2,\cdots ,q_\gamma \}\\ \{p_{\gamma +1}<p_{\gamma +2}<\cdots<p_{j}\}=\{1,2,\cdots ,j\} \backslash \{p_1, p_2,\cdots ,p_\gamma \} \end{array}}\right. \\&\quad \left. \left( (-1)^{{\hat{t}}_1+{\hat{t}}_2} \prod _{r=1}^{\gamma } \varrho ^{(1)}_{\Gamma _{p_{r}}} \prod _{r=1}^{\gamma } { \varrho ^{(1)}_{\Gamma '_{q_{r}}} }^*\prod _{s=1}^{j-\gamma } {\varrho ^{(2)}_{\Gamma _{p_{\gamma +s}}} } \prod _{s=1}^{j-\gamma } {\varrho ^{(2)}_{\Gamma '_{q_{\gamma +s}}}}^*{\hat{\Delta }}\right) \right] ,\\&\quad {\hat{t}}_1=t\left( \Gamma _{p_1},\Gamma _{p_2},\cdots ,\Gamma _{p_\gamma },\Gamma _{p_{\gamma +1}},\Gamma _{p_{\gamma +2}},\cdots , \Gamma _{p_j}\right) ,\\&\quad {\hat{t}}_2=t\left( \Gamma '_{q_1},\Gamma '_{q_2},\cdots ,\Gamma '_{q_{\gamma }},\Gamma '_{q_{\gamma +1}}, \Gamma '_{q_{\gamma +2}},\cdots ,\Gamma '_{q_{j}} \right) ,\\&\quad {\hat{\Delta }}=\prod _{1\le \imath<\jmath \le \gamma }\left( {k_{\Gamma _{p_\imath }}}^2-{k_{\Gamma _{p_{\jmath }}}}^2 \right) \prod _{1\le \imath<\jmath \le \gamma }\left( {k_{\Gamma '_{q_\imath }}^*}^2-{k_{\Gamma '_{q_{\jmath }}}^*}^2 \right) \\&\quad \times \prod _{\gamma +1\le \imath<\jmath \le j}\left( {k_{\Gamma _{p_\imath }}}^2-{k_{\Gamma _{p_{\jmath }}}}^2 \right) \prod _{\gamma +1\le \imath<\jmath \le j}\left( {k_{\Gamma '_{q_\imath }}^*}^2-{k_{\Gamma '_{q_{\jmath }}}^*}^2 \right) \\&\quad \prod _{1\le \imath \le \gamma< \jmath \le j}\left( {k_{\Gamma _{p_\imath }}}^2-{k_{\Gamma '_{q_{\jmath }}}^*}^2 \right) \prod _{1\le \imath \le \gamma <\jmath \le j}\left( {k_{\Gamma '_{q_\imath }}^*}^2-{k_{\Gamma _{p_{\jmath }}}}^2 \right) ,\\ \end{aligned}$$

where $t\left( \Gamma _{p_1},\Gamma _{p_2},\cdots ,\Gamma _{p_\gamma },\Gamma _{p_{\gamma +1}},\Gamma _{p_{\gamma +2}},\cdots , \Gamma _{p_j}\right)$ denotes the inversion number of the sequence $\left( \Gamma _{p_1},\Gamma _{p_2},\cdots ,\Gamma _{p_\gamma },\Gamma _{p_{\gamma +1}},\Gamma _{p_{\gamma +2}},\cdots , \Gamma _{p_j}\right)$.