Modeling and staged assessments of the controllability of spread for repeated outbreaks of COVID-19

Abstract

SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2) has been causing an outbreak of a new type of pneumonia globally, and repeated outbreaks have already appeared. Among the studies on the spread of the COVID-19, few studies have investigated the repeated outbreaks in stages, and the quantitative condition of a controllable spread has not been revealed. In this paper, a brief compartmental model is developed. The effective reproduction number (ERN) of the model is interpreted by the ratio of net newly infectious individuals to net isolation infections to assess the controllability of the spread of COVID-19. It is found that the value of the ERN at the inflection point of the pandemic is equal to one. The effectiveness of the quarantine, even the treatment, is parametrized in various stages with Gompertz functions to increase modeling accuracy. The impacts of the vaccinations are discussed by adding a vaccinated compartment. The results show that the sufficient vaccinations can make the inflection point appear early and significantly reduce subsequent increases in newly confirmed cases. The analysis of the ERNs of COVID-19 in the United States, Spain, France, and Peru confirms that the condition of a repeated outbreak is to relax or lift the interventions related to isolation and quarantine interventions to a level where the ERN is greater than one.

1 Introduction

As of April 27, 2021, SARS-CoV-2 has caused 3 116 444 deaths globally, and nearly 147.54 million cumulative confirmed cases worldwide have been reported [1]. With such a severe global pandemic, the preventions of the pandemic are uneven across countries, and the occurrence of repeated outbreaks in many countries is becoming the current urgent concern and a problem that needs to be resolved. Fortunately, several COVID-19 vaccines have been put into vaccination.

In the study of the spread of the COVID-19, the assessments and predictions of the pandemic have provided some useful references for health policymaking. From the viewpoint of the spread of the pandemic in population, many compartmental models were effectively developed from the SIR (Susceptible-Infectious-Removed) model [2] and the SEIR (Susceptible-Exposed-Infected-Removed) model [3] to describe the spread dynamics of the pandemic considering different preventive measures or negative actions [4,5,6,7,8,9,10,11,12]. A developed SEIR model considering asymptomatic individuals has been proposed to estimate the spread risk of the COVID-19 and assess the impact on public health [4]. Liu et al. [5] have modeled a variant SIR model that evaluates the effects of the isolation with an exponential decline in transmission rate in China. Rong et al. [6] have established a model taking the effect of delay in diagnosis into account and studied the dependence of model parameters on the basic reproduction number. Moreover, the impacts of zoonotic spread and emigration have also been considered in a conceptual model [7]. Nonetheless, dynamic models have been rarely established from the perspective of infection controllability to assess the controllability of the pandemic.

The ERN denoting the average number of infected cases caused by an infected individual in the infectious period [13] and measuring the instantaneous situation of the spread of the infectious disease has always been analyzed in the studies. Wilasang et al. [13] investigated the pandemic development of COVID-19 of several countries and found that the countries employing active case detection with prompt isolation have a higher reduction in the ERN. Peng et al. [14] quantified the critical interventions of COVID-19 to the changes of the ERNs in China, Italy, Iran, South Korea, and Japan. However, these studies have not analyzed the ERN on the controllability of infection, such as the correspondece between the inflection point and ERN.

Most countries of the world have been severely suffering from COVID-19. Therefore, the research on the prevention and predictions for the second outbreak, even the repeated outbreaks, are still hotpots [15,16,17,18,19,20]. Wang et al. [15] investigated the impact of asymptomatic individuals on the second outbreak. The study of the pandemic in China outside Hubei [16] indicated that carefully monitoring the confirmed case-fatality risk, extremely restrict quarantine measures and instantaneous reproduction number can provide a reference for preventing the potential repeated outbreaks. The second outbreak in Spain and India was also predicted by relaxing the control measures to various extents [17, 18]. Ho et al. [19] developed a mobile app named Social distancing 2.0, to avoid the repeated outbreaks, and assessed the impact of the adoption rate of this app on the basic reproduction number. Nevertheless, the assessments or predictions of the pandemic have been rarely linked to staged public health interventions or the staged change of the newly confirmed cases, and few studies have explored the relationship between the ERN and the dominant interventions to control the outbreak. We found that for repeated outbreaks, it is difficult to simulate the complete evolution of the pandemic without staged investigation and functional parameterization.

So far, a variety of COVID-19 vaccines have been put into pandemic prevention; 961.23 million vaccine doses have been administered globally [1]. As the number of people vaccinated against COVID-19 worldwide increases, people who develop antibodies due to vaccination will gradually become a large immune compartment, which will greatly reduce the number of susceptible individuals and ease the pressure on medical and health care. Thus, the impact of vaccination cannot be ignored.

In this paper, the novelty and main contributions are as follows:

• 1. A compartmental model specifically considering the controllability of infections is given to study the spread dynamics of COVID-19.

• 2. The effects of quarantine and treatment are parametrized with Gompertz functions rather than constants according to the interventive stages or the change of newly confirmed cases.

• 3. The quantitative correspondence of the ERN and the evolution of the newly confirmed cases are revealed.

• 4. The impacts of the daily vaccinated cases of COVID-19 on newly confirmed cases and the ERN reflecting inflection point are also investigated.

This paper consists of five sections. In Sect. 2, a compartmental model is proposed, the effects of quarantine and treatment are parametrized with Gompertz functions, and the ERN in the model is reasonably explained and illustrated. In Sect. 3, the evolution of the pandemic in Italy is completely fitted and assessed in stages according to the evolution of the ERN and fitting results. Section 4 presents the discussion on the impacts of the vaccinations and the quantitative condition of a repeated outbreak. The findings of the controllability of the pandemic and limitations of the study are summarized in Sect. 5.

2 Compartmental model for the spread of COVID-19

2.1 Dynamic model

Considering the spread pattern of COVID-19 before the vaccination or with a small number of vaccinators, firstly, it is assumed that:

• 1. The region investigated is approximately a closed system in population.

• 2. The unvaccinated population is susceptible due to the high infectivity of COVID-19 [21].

• 3. The confirmed individuals can receive treatment and be thoroughly isolated in time.

• 4. Since rare zoonotic cases have been reported, the spread way is limited to human-to-human.

• 5. The healed cases are immune to the SARS-CoV-2.

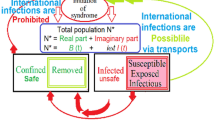
As shown in Fig. 1, the population of the investigated region consists of six compartments. S(t) means the susceptible individuals that are uninfected without immunity to SARS-CoV-2. I(t) refers to the infectious individuals with free infectivity, who have not been isolated. T(t) indicates the treated individuals with isolation, also known as existing confirmed cases with controlled infectivity. C(t) refers to the cumulative confirmed cases. R(t) refers to the recovered or healed cases, and D(t) the deceased or fatal cases. S(t), R(t), and D(t) are non-infectious. For an investigated region with population size N, $N = S(t) + I(t) + T(t) + R(t) + D(t)$, and $C(t) = T(t) + R(t) + D(t)$.

Fig. 1

Propagation path of COVID-19

The complete model describing the spread dynamics of COVID-19 is built as

$$\left\{ \begin{aligned} \dot{S} &= - \frac{\alpha (t)I \cdot S}{N}, \hfill \\ \dot{I} &= \frac{\alpha (t)I \cdot S}{N} - \beta (t)I, \hfill \\ \dot{T} &= \beta (t)I - (\gamma (t) + d(t))T, \hfill \\ \dot{R} &= \gamma (t)T, \hfill \\ \dot{D} &= d(t)T, \hfill \\ \dot{C} &= \beta (t)I, \hfill \\ \end{aligned} \right.$$

(1)

where $\dot{x}$ is the time derivate of x. Since the unit of count is day⁻¹, Eq. (1) can also be discretized as

$$\left\{ \begin{aligned} S(t + 1) &= S(t) - \frac{\alpha (t)I(t)S(t)}{N}, \hfill \\ I(t + 1) &= I(t) + \frac{\alpha (t)I(t)S(t)}{N} - \beta (t)I(t), \hfill \\ T(t + 1) &= T(t) + \beta (t)I(t) - (\gamma (t) + d(t))T(t), \hfill \\ R(t + 1) &= R(t) + \gamma (t)T(t), \hfill \\ D(t + 1) &= D(t) + d(t)T(t), \hfill \\ C(t + 1) &= C(t) + \beta (t)I(t). \hfill \\ \end{aligned} \right.$$

(2)

The descriptions of model parameters are listed in Table 1.

Table 1 Description and value range of model parameters

2.2 Parameter estimations and approximate solutions

To date, the staged public health interventions generally are determined by the development of the pandemic. Therefore, it is necessary to stage the evolution of the pandemic for accurately assessing the controllability of the spread of the pandemic.

In certain countries or regions with distinct and uniform interventions, the interventive stages can be identified by iconic public health interventions. Not uniquely, we can divide the evolution of the pandemic into multiple interventive stages. For example, the first stage (S₁) refers to the outbreak period before the lockdown. The date interval between the start date of lockdown and the start date of the first relaxation of the lockdown is the second stage (S₂), also named the lockdown period. The third stage (S₃) is the period of the first relaxation of lockdown or critical interventions. If the pandemic situation is well controlled, some countries will further relax certain influential interventions, and the pandemic will enter the fourth stage (S₄), and so on.

Furthermore, for certain countries or regions with unbalanced or unsystematic interventions, if the evolutions of the pandemic presented a rather convoluted performance, it is hard to segment interventive stages. In this case, we can roughly stage the pandemic situation according to the trend of the newly confirmed cases; for example, in certain countries where the repeated outbreaks have occurred, we may divide the pandemic into the periods of the first outbreak, transition, second outbreak, and so on.

We then rationale the rates mathematically according to the staged health public interventions in certain countries or regions that have taken lockdowns. In S₁, the interventions were relatively weaker, the self-isolation was very limited, the spread environment was relatively stable, and the pandemic was basically free to spread; thus the COVID-19 spread at a higher constant $\alpha (t)$. After the lockdown began, the pandemic entered S₂. Lockdown remarkably reduced the human-to-human contact in the fastest way, which suddenly caused $\alpha (t)$ to drop to a lower constant. In S₃, $\alpha (t)$ is still estimated as a constant that mainly depends on the specific measures and intensity of the interventions after relaxing the lockdown and whether the time point for relaxing the lockdown is appropriate, and so is $\alpha (t)$ in S₄, and so on. Consequently, a switch function is proposed to describe the change of $\alpha (t)$ at different stages as follows:

$$\alpha (t) = \left\{ {\begin{array}{*{20}c} {a_{1} , \, t \in {{S}}_{1} ,} \\ {a_{2} , \, t \in {{S}}_{{2}} ,} \\ {a_{3} , \, t \in {{S}}_{{3}} ,} \\ \begin{gathered} a_{4} , \, t \in {{S}}_{{4}} , \hfill \\ \ldots \hfill \\ \end{gathered} \\ \end{array} } \right.$$

(3)

where ${{S}}_{1} :t < \tau_{lock} ,\;{{S}}_{2} :\tau_{lock} \le t < \tau_{relax} ,\;{{S}}_{3} :\tau_{relex} \le t < \tau_{frelax} ,\;{{S}}_{4} :t \ge \tau_{frelax}$, $\tau_{lock} ,\tau_{relax} ,$ and $\tau_{frelax}$ indicate the start time of lockdown, first relaxation of the lockdown and further relaxation of the lockdown, respectively.

In each stage of the pandemic, we assumed that the interventions taken have roughly effectuated monotonous effectiveness. For instance, increased quarantine coverage contributes to an increase in $\beta (t)$. Thus, $\beta (t)$ should be monotonously bounded. Note that $\gamma (t)$ and d(t) are severely dependent on the level of treatment of the COVID-19 and medical resources, they may not be monotonous in each stage. However, in certain countries where the number of healed cases is steadily increasing, $\gamma (t)$ and d(t) can also be monotonous.

To match the change trends of $\beta (t)$ more closely in each stage, growth curve functions are good choices of estimation functions for their advantages of well-defined asymmetric monotonicity and boundness [23], and also are well-drawn depictions for predicting the progression of the COVID-19 [24]. We here estimate that the rates increase or decrease in the patterns consistent with Gompertz functions, which is of the form

$$g(t) = b_{1} e^{{ - b_{2} e^{{ - b_{3} (t + b_{4} )}} }} .$$

(4)

As depicted in Fig. 2a, Gompertz functions show the advantageous characterization of plasticity in monotonicity and boundness. b₁ defines the upper boundary, b₂, b₃ jointly define the amplitude of the change rate of Gompertz function, b₄ is a translation coefficient. In the estimation, if the estimated rate presents a relatively apparent increase, then b₃ is estimated to a value that is greater than zero; otherwise, b₃ is less than zero. For an extremely slow increase or decrease in the estimated rate, b₂ will be adapted to a relatively larger value that makes the rate of change of the estimated rate exceedingly close to zero. For the estimated rate being a constant, b₂ will be adapted to zero. Hence, the properties of Gompertz functions essentially satisfy the requirements of $\beta (t)$ at each stage. We then have

$$\beta (t) = \left\{ {\begin{array}{*{20}c} {b_{11} e^{{ - b_{12} e^{{ - b_{13} (t + b_{14} )}} }} , \, t \in {{S}}_{1} ,} \\ {b_{21} e^{{ - b_{22} e^{{ - b_{23} (t + b_{24} )}} }} , \, t \in {{S}}_{{2}} ,} \\ {b_{31} e^{{ - b_{32} e^{{ - b_{33} (t + b_{34} )}} }} , \, t \in {{S}}_{{3}} ,} \\ \begin{gathered} b_{41} e^{{ - b_{42} e^{{ - b_{43} (t + b_{44} )}} }} , \, t \in {{S}}_{{4}} , \hfill \\ \ldots \hfill \\ \end{gathered} \\ \end{array} } \right.$$

(5)

Fig. 2

Estimation functions, a curves of Gompertz functions, b curves of time derivate of Gompertz functions

The option of estimation function is not unique. Other growth curve functions, even other functions, such as the Logistic model, Sigmoid function, also are alternatives to estimate $\beta (t)$. Besides, we can obtain the approximate solution analytically under $S(t) \approx N$. From Eq. (1), we approximately have

$$\dot{I} = (\alpha (t) - \beta (t))I,$$

(6)

For taking the Gompertz functions as the estimation functions, one obtains

$$I = I_{i} (0)e^{{\varepsilon_{i} (\chi (u(t), \, t), \, t)}} .$$

(7)

Here, $I_{i} (0)$ represents the initial value of I(t) of on the ith stage and $\varepsilon_{i} (\chi (t), \, t) = a_{i} t + {{(b_{i1} + \chi (t))} \mathord{\left/ {\vphantom {{(b_{i1} + \chi (t))} {b_{i3} }}} \right. \kern-\nulldelimiterspace} {b_{i3} }}$. $\chi (u(t),t)$ denotes the one-argument exponential integral given by

$$\chi (u(t), \, t) = \int\limits_{ - \infty }^{u(t)} {\frac{{e^{t} }}{t}dt} ,$$

(8)

where $u(t) = - b_{i2} e^{{ - b_{i3} (t + b_{i4} )}}$. Also, the approximate solution of newly confirmed cases is

$$\dot{C} = \Delta C(t + 1) = I_{i} (0)\beta_{i} (t)e^{{\varepsilon_{i} (\chi (u(t), \, t), \, t)}} .$$

(9)

Here, $\Delta x(t) = x(t) - x(t - 1)$, that is, $\Delta x(t)$ indicates the newly increased or decreased cases of x(t) at the time t.

2.3 Indictors of controllability of the spread

From the perspective of controllability of the spread of the pandemic, the basic reproduction number (R₀) measures the potential for an infectious disease to spread through an immunologically naive population [6], and a real-time indicator in measuring the spread risk and the controllability of the spread is the ERN, i.e., $R_{e} (t)$. In Eq. (1), we define the ERN $R_{e} (t) \, (R_{e} > 0)$ straightforwardly as

$$R_{e} (t) = \frac{ - \Delta S(t)}{{\Delta C(t)}}.$$

(10)

$- \Delta S(t)$ refers to the newly reductive cases in S(t), also the net newly infectious individuals who have not been isolated. $\Delta C(t)$ refers to the newly cumulative confirmed cases, also the net newly isolated infections with controllable infectivity.

Remark 1

$R_{e} (t) > 1$ indicates that if net newly infectious individuals outnumber the net newly isolated cases, the spread of pandemic is risky. A substantial medical burden will be imposed to an unbearable level if this situation has a long continuity. $R_{e} (t) = 1$ indicates that all net newly infectious individuals can just happen to be medically isolated under the current quarantine and diagnosis level. The controllable spread of the pandemic satisfying $R_{e} (t) < 1$ means that medical resources and the intensity of quarantine are sufficient to handle the net newly infectious individuals.

We here give an exemplification to precisely interpret the role of $R_{e} (t)$ in reflecting the spread dynamics of the COVID-19. Assume that an investigated region has 10,000,000 people, 300 infectious individuals without isolation, and 50 cumulative confirmed cases at the initial time of the outbreak. The simulated results with varying $\alpha (t)$ and fixed $\beta (t) = 0.10$ are shown in Fig. 3.

Fig. 3

Newly confirmed cases and ERN with varying $\alpha (t)$ and fixed $\beta (t) = 0.10$, a evolution of the newly confirmed cases, b evolution of the ERN

When $\Delta C(t)$ shows a single wave (Fig. 3a), the corresponding $R_{e} (t)$ (Fig. 3b) declines from a value greater than one to a value less than one, and the points of $R_{e} (t) = 1$ are just the inflection point of $\Delta C(t)$, where $\Delta C(t)$ starts to decline. Moreover, $R_{e} (t) > 1$ corresponds to the increase in $\Delta C(t)$, the lager $R_{e} (t)$, the faster the growth of $\Delta C(t)$. Conversely, $R_{e} (t) < 1$ indicates the decline of $\Delta C(t)$, the smaller $R_{e} (t)$, the faster the decrease in $\Delta C(t)$. Especially, if $R_{e} (t) \equiv 1$ (purple curve in Fig. 3b), $\Delta C(t)$ will be a constant (purple curve in Fig. 3a), indicating that the number of cumulative confirmed cases will linearly increase. Therefore, $R_{e} (t)$ accurately depicts the controllability of the spread of the pandemic.

Remark 2

When susceptible individuals make up the vast majority of the population, i.e., $S(t) \approx N$, according to model (2), the ERN $R_{e} (t)$ can be approximately estimated as

$$R_{e} (t) = \frac{ - \Delta S(t + 1)}{{\Delta C(t + 1)}} = \frac{\alpha (t)I(t)S(t)}{{N\beta (t)I(t)}} \approx \frac{\alpha (t)}{{\beta (t)}}.$$

(11)

In this case, it is noted that $\alpha (t)$ and $\beta (t)$ almost determine the value of $R_{e} (t)$, which means that the public health interventions influencing $\alpha (t)$ and $\beta (t)$ nearly determine the spread dynamics of the pandemic. Generally, these interventions mainly are isolation, quarantine measures including lockdown, travel ban, contact tracing, implementation of social distance, the establishment of testing sites and implementation of universal nucleic acid detection, etc.

Remark 3

Differing from the model of Eq. (1), for general SIR model, its ERN is defined by the ratio of net newly infectious individuals to net removed infections, which characterizes the eradication situation of the pandemic rather than controllability of the spread; in other words, the ERN of the SIR model less than one is merely a sufficient condition for a controllable spread.

Besides, an indicator characterizing the strength of the spread of an infectious disease is the infection period, which means the days it takes for an infection to infect the next one. The number of individuals infected by each infector per day follows

$$n(t) = \frac{ - \Delta S(t + 1)}{{I(t)}},$$

(12)

the infection period is the reciprocal of $n(t)$, one obtains

$$\tau_{g} (t) = \frac{I(t)}{{ - \Delta S(t + 1)}}.$$

(13)

For $S(t) \approx N$, $n(t)$ can be approximated as

$$n(t) = \frac{ - \Delta S(t + 1)}{{I(t)}} = \frac{\alpha (t)I(t)S(t)}{{NI(t)}} \approx \alpha (t),$$

(14)

thus,

$$\tau_{g} (t) \approx \frac{1}{\alpha (t)}.$$

(15)

$\tau_{g} (t)$ almost is inversely proportional to $\alpha (t)$, which means that the stages with higher $\alpha (t)$ correspond to shorter $\tau_{g} (t)$, the faster the pandemic spreads.

3 Staged assessments of the evolution of COVID-19 in Italy

3.1 Data analysis

As one of the early countries to declare a lockdown, Italy has distinct staged health public interventions of the pandemic, and has presented a good performance in healed, newly confirmed cases in the first break. Hence, we study the complete dynamics of the COVID-19 in Italy using Eqs. (1) and (2). Since WHO did not report the healed cases, the pandemic data used are reported by [25], which has reliable data sources, as detailed in its data description.

We here divide the pandemic in Italy from February 22, 2020 to March 31, 2021 into ten stages according to the iconic dates of interventions and the evolution of newly confirmed cases. For example, three iconic dates of the early pandemic intervention in Italy are March 10, 2020, May 4, 2020, and May 18, 2020, on which Italy issued the lockdown and the relaxation of lockdown, further relaxation of lockdown [26], respectively. The date interval and the corresponding description of each stage are listed in Table 2.

Table 2 Date interval and description of the development stages of COVID-19 in Italy

In the data fitting, the least square method is applied. Optimization functions fmincon and lsqnonlin in MATLAB are adopted to minimize the objective functions. To fit the complete dynamics of the pandemic, the objective function can be given by

$$f({{\varvec{\upnu}}},t) = \sum\limits_{{i = t_{s} }}^{{t_{e} }} {(C(t) - \hat{C}(t))^{2} } + \sum\limits_{{i = t_{s} }}^{{t_{e} }} {(T(t) - \hat{T}(t))^{2} } + \sum\limits_{{i = t_{s} }}^{{t_{e} }} {(R(t) - \hat{R}(t))^{2} } + \sum\limits_{{i = t_{s} }}^{{t_{e} }} {(D(t) - \hat{D}(t))^{2} } .$$

(16)

For merely investigating the spread dynamics, the objective function follows

$$f({{\varvec{\upnu}}},t) = \sum\limits_{{i = t_{s} }}^{{t_{e} }} {(C(t) - \hat{C}(t))^{2} } ,$$

(17)

where ${{\varvec{\upnu}}}$ represents the parametric vector to be fitted, which is composed of the coefficients in Eqs. (3) and (5), $t_{s}$ and $t_{e}$ are the start and end time of the corresponding stage interval, respectively. $y(t)$ denotes the fitted result of pandemic data $\hat{y}(t)$.

Figure 4a, b show the fitted individuals of various compartments. It is visible that the fitting results excellently conform to the reported data with high determination coefficients ($R^{2}$) and small root means squared errors (RMSE) of various compartments listed in Table 3. Correspondingly, the values of fitted parameters are shown in Table 4.

Fig. 4

Fitting results of cumulative confirmed, treated, healed, and fatal cases, a black dotted curves represent the fitted results of the reported cumulative confirmed cases and treated cases filled with orange and green stem lines, respectively, b black dotted curves represent the fitted result of the reported healed cases and fatal cases filled with blue and purple stem lines, respectively

Table 3 Determination coefficients and root mean squared errors of various compartments

Table 4 Model parameters at various stages

Note that the estimated values of $\alpha (t)$ and $\beta (t)$ have a serious dependence on $I(t_{0} )$, that is, these two values may not be coherent to real data due to $I(t_{0} )$ is unknown. However, the estimated trends of $\alpha (t)$ and $\beta (t)$ are consistent with the real data when the data fit well. In particular, it does not significantly impact the ERN estimated from Eq. (11).

3.2 Assessment of evolution of the pandemic in Italy

During the first outbreak, it can be seen from the fitting results shown in Table 4 that $\alpha (t)$ gradually becomes smaller, indicating that the pandemic interventions like lockdown, restricting the social distance, etc., have effectively reduced the infective contacts. However, at the beginning of the first outbreak, the ERN was as high as 4.81, shown in Fig. 5b. The color bar indicates the value of the ERN, which illustrates that the pandemic spread at an uncontrollable level and weak pandemic interventions were taken. As shown in Fig. 5a, if the first lockdown had not been implemented on March 10, 2020, and the medical system was affordable, as of March 25, 2020, there would be nearly 400,000 existing infectors and 40,000 newly confirmed cases. The approximate solutions of $I(t)$ and $\Delta C(t)$ show good accuracies when $S(t) \approx N$. In Fig. 5b, S₅ shows a steady fluctuation in newly confirmed cases, $\alpha (t)$ rises to 0.11 (Table 4), and the ERN in S₅ is approximately equal to 1; thus, S₅ is a transition period between the first wave and the second wave.

Fig. 5

Prediction of infectious individuals and newly confirmed cases without lockdown and the evolution of the ERN with newly confirmed cases of the COVID-19 in Italy, a infectious individuals and newly confirmed cases without lockdown, b evolution of the ERN with newly confirmed cases of the COVID-19 in Italy

For the second wave, the pandemic entered the early stage when it reached S₆, which showed a slight rebound in newly confirmed cases and an increase in the ERN, $\alpha (t)$ continues to rise to 0.26 (Table 4), indicating that influential contacts were increasing. Approximately after October 6, 2020, the newly confirmed cases increased rapidly with a highest $\alpha (t) = 0.39$ in S₇ (Table 4). The frequent infections occurred, and the daily increase exceeded 20,000, while the ERN has not increased much due to better quarantine measures and an already more mature medical system. During S₉, a weak rebound in newly confirmed cases appeared with a increased the ERN compared to that of S₈, while $\alpha (t)$ decreased which illustrates that although the pandemic spread at a lower $\alpha (t)$, the spread controllability of the pandemic was weaken caused by the drop of the quarantine intensity.

From Table 4 and Fig. 5b, it is evident that S₁₀ corresponds to the third outbreak with decreased $\alpha (t) = {{0.29}}$ (Table 4), and the ERN generally fluctuates around one, reflecting that the spread of the pandemic has not been significantly alleviated, but the overall quarantine intensity has increased so that the spread was not too violent.

It can be seen from Fig. 5b that the ERN of inflection points of the pandemic is almost equal to one. Among them, the inflection point of the first outbreak occurred roughly on March 22, 2020, and the second November 14, 2020, the third March 18, 2021. Correspondingly, these dates are very close to the points that $\Delta C(t)$ started to decrease.

Figure 6 shows the complete evolution of various compartments in Italy from February 22, 2020 to March 31, 2021. The overall situation shows multiple waves of the pandemic. During repeated outbreaks, the infectious proportion and the healed proportion have significantly decreased and increased, respectively, demonstrating that the controllability of the spread of the pandemic and the treatment level has been dramatically enhanced compared to the initial period of the first outbreak. This is why the ERN in the subsequent outbreaks is smaller than that in the initial period of the first outbreak. However, there are still a large number of infectious individuals in the subsequent outbreaks, indicating that there is no direct correspondence between the controllability of the pandemic and the number of the infectious individuals.

Fig. 6

Complete spread evolution of COVID-19 created by model (1) in Italy from February 22, 2020 to March 31, 2021

4 Discussion of vaccination and prevention using ERN

4.1 Impacts of the daily vaccinated cases

So far, several vaccines have been put into the prevention of COVID-19. Susceptible individuals will develop antibodies after vaccination and will not be infected during the immunization cycle. Additionally, the growth rate of vaccinators should be equal to the number of daily vaccinated cases. Therefore, based on the model of Eq. (1), we propose the modified model to merely describe the spread of the pandemic after sufficient vaccinations can be provided as follows

$$\left\{ \begin{aligned} \dot{S} &= - \frac{\alpha (t)I \cdot S}{N} - v(t), \hfill \\ \dot{I} &= \frac{\alpha (t)I \cdot S}{N} - \beta (t)I, \hfill \\ \dot{C} &= \beta (t)I, \hfill \\ \dot{V} &= v(t) \hfill \\ \end{aligned} \right.$$

(18)

where compartment $V$ denotes that the individuals have been vaccinated and $v(t)$ is the newly or daily vaccinated cases. For an investigated region with population size $N$, $N = S(t) + I(t) + C(t) + V(t)$.

For the modified model of Eq. (18), the ERN $R_{e} (t)$ becomes

$$R_{e} (t) = \frac{\alpha (t)I(t)S(t)}{{N\beta (t)I(t)}} = \frac{\alpha (t)S(t)}{{N\beta (t)}}.$$

(19)

Remark 4

Since susceptible individuals become immune-resistant people within the validity period after being vaccinated, the number of susceptible people is no longer approximately equal to the total population. Thus, the ERN can no longer be estimated by Eq. (11).

Assume that a pandemic has spread in a region with a 20 million population, including 300 infected and 50 confirmed cases. If the pandemic spreads with $\alpha (t) = {{0.22}}$, $\beta {{(t)}} = 0.1$ according to Eq. (18), and there is a corresponding vaccine to prevent the pandemic, we then investigate the impacts of the daily vaccinated cases shown in Fig. 7.

Fig. 7

Impacts of the daily vaccinated cases on newly confirmed cases and ERN, a evolution of the newly confirmed cases varying $v(t)$ from 300,000 to 420,000, b evolution of the ERN varying $v(t)$ from 300,000 to 420,000

When vaccines are relatively sufficient, vaccination dominates the development trend of the pandemic. As the number of people being vaccinated increases, the inflection points of the pandemic appeared early, and the number of daily cases decreased significantly. The ERN decreases faster, which means that the rate at which the pandemic subsides increases.

Moreover, people with immunity against SARS-CoV-2 may dilute the density of susceptible people to a certain extent, resulting in decreased transmission rate. Large-scale vaccination can reduce long-term treatment expenditure and medical resources, accelerate the recovery of economic production, education, and teaching, etc.

4.2 Characteristics of repeated outbreaks

The fact is that most people in the world have not been vaccinated for COVID-19. At present, the development of epidemic control is still mainly based on non-vaccine methods. Therefore, it is necessary to discuss the characteristics and prevention of repeated outbreaks.

A repeated outbreak generally refers to a quantitative rebound in newly confirmed cases for a period caused by relaxing the interventions or lifting the interventions. Due to insufficient vaccine production, incomplete vaccination and other reasons, repeated outbreaks still exist in various countries worldwide. As of April 27, 2021, the pandemic of the COVID-19 in many countries has appeared a situation of repeated outbreaks, such as the United States, Peru, Spain, France, Iran, Turkey, Germany, Canada, etc.

From the analysis of the ERN, an increase in newly confirmed cases indicates $R_{e} (t) > 1$, while a decrease in newly confirmed cases indicates $R_{e} (t) < 1$. Therefore, strictly speaking, a repeated outbreak with an increase in newly confirmed cases indicates a repeated period with $R_{e} (t) > 1$. Note that two decisive parameters governing $R_{e} (t)$ are $\alpha (t)$ and $\beta (t)$ when $S(t) \approx N$; thus, a repeated outbreak can only be triggered when the interventions, such as lockdown, restriction of social distance, contact tracing, quarantine at traffic gates, that have great impacts on $\alpha (t)$ and $\beta (t)$, are relaxed or lifted to a certain level with $R_{e} (t) > 1$, and the weaker the intervention is relaxed or lifted, the stronger the rebound will be.

Figure 8 shows the evolutions of newly confirmed cases with the color bar marking the ERN in the United States, Spain, France, and Peru from March 20, 2020 to March 31, 2021, the reason for not updating the data to April is to eliminate the impact of the vaccine as much as possible. As shown in Fig. 8, the ERNs of all four countries become less than one from the inflection point, fluctuate near one in the transition period, and are greater than one again in subsequent outbreaks. Overall, the ERN of repeated outbreaks is essentially smaller than that of the early period of the first outbreak because the COVID-19 response mechanism has already matured. Therefore, although the situation of repeated outbreaks varies from country to country, it is clear that the ERN exactly characterizes of the controllability of the spread of the pandemic. $R_{e} (t) > 1$ definitely indicates the occurrence of a repeated outbreak, and the controllability of subsequent outbreaks is generally better than the first outbreak due to various pandemic preventions.

Fig. 8

Illustration of repeated outbreaks in the United States, Spain, France, and Peru colored with ERN, a the change in ERN with reported newly confirmed cases in the United States and Spain, b the change in ERN with reported newly confirmed cases in the France and Peru

4.3 Preventions of large-scale repeated outbreaks

Before sufficient vaccines are provided, from the discussion of the ERN, it is vital to maintain or enhance the interventions influencing $\alpha (t)$ and $\beta (t)$ to prevent a large-scale repeated outbreaks. A re-lockdown is unlikely for the countries with a slight rebound in newly confirmed cases, contrary to the original intention of deregulation to restore the economy. However, interventions like contact tracing, quarantine of cross-regional traffic ports and imported products, etc., are necessary to be implemented. Contact tracing quickly identifies sources of newly infections and isolates the suspected infections, contributing to the decrease in $\alpha (t)$ and meanwhile, the increase in $\beta (t)$. Quarantine of cross-regional traffic ports and imported products prevents the trans-regional spread of undiagnosed cases and imported infections from overseas, which prevents a large-scale outbreak; a localized outbreak is still possible. For heavily affected areas, an extension of the coverage of nucleic acid testing is even necessary and more thorough action of screening potential infections, especially for diagnosing asymptomatic infections.

Indeed, the thorough prevention is to complete the vaccination of most susceptible people as soon as possible. Vaccination can quickly reduce the susceptible population, form an effective immune group, dilute the transmission process, and save treatment costs, etc.

5 Conclusion

This paper assessed the controllability of the large-scale spread of COVID-19 in different stages based on an epidemic model. In data fitting, Gompertz functions were introduced to estimate the effectiveness of quarantine interventions and treatment; the results completely simulate the development of the pandemics. The development of the pandemic was quantified as the evolution of the ERN, and the simulated results illustrated that the ERN being greater than one caused by the relaxation or lift of isolation or quarantine interventions would lead a repeated pandemic. Furthermore, we modified the model considering the impacts of the vaccinations, the results showed that the increase in the daily vaccinated cases of COVID-19 can apparently suppress the uptrend in newly confirmed cases and quickly prevent the pandemic to a controllable level. We also advised maintaining or strengthening the interventions like contact tracing, quarantine of cross-regional traffic ports and imported products, etc., to prevent a large-scale repeated outbreak before most people are vaccinated. In this study, some factors such as economics and case import have not been taken into consideration, and the coherence between parameters and real data needs to be improved.