Resonant modal interactions in micro/nano-mechanical structures

Abstract

This paper considers nonlinear interactions between vibration modes with a focus on recent studies relevant to micro- and nanoscale mechanical resonators. Due to their inherently small damping and high susceptibility to nonlinearity, these devices have brought to light new phenomena and offer the potential for novel applications. Nonlinear interactions between vibration modes are well known to have the potential for generating a “zoo” of complicated bifurcation patterns and a wide variety of dynamic behaviors, including chaos. Here, we focus on more regular, robust, and predictable aspects of their dynamics, since these are most relevant to applications. The investigation is based on relatively simple two-mode models that are able to capture and predict a wide range of transient and sustained dynamical behaviors. The paper emphasizes modeling and analysis that has been done in support of recent experimental investigations and describes in full detail the analysis and attendant insights obtained from the models that are briefly described in the experimental papers. Standard analytical tools are employed, but the questions posed and the conclusions drawn are novel, as motivated by observations from experiments. The paper considers transient dynamics, response to harmonic forcing, and self-excited systems and describes phenomena such as extended coherence time during transient decay, zero dispersion response, and nonlinear frequency veering. The paper closes with some suggested directions for future studies in this area.

1 Introduction

Vibratory mechanical structures of microscale dimensions are ubiquitous in modern sensing and time-keeping technologies and are used in virtually every smart phone, tablet, automobile, and more [1, 2]. Fabrication and transduction technologies are now pushing resonant devices to even smaller dimensions, for example, using carbon nanotubes and two-dimensional structures (thickness of a few nanometers or less) made from graphene and other materials. These nanoscale devices, which can have dimensions down to a single atomic layer, hold promise for enhanced sensing [3,4,5,6], but are yet to see widespread application. Collectively, in this work we refer to this group of systems as micro/nano-resonators, or MNRs. In addition to their practical utility, these tiny resonators have proven to be a rich source of nonlinear dynamic behaviors. Some of the nonlinear phenomena observed in MNRs, especially related to modal interactions, had not been previously seen in vibrations of macroscale structures, primarily because MNRs have significantly smaller damping. In fact, such extremely light damping, with damping ratios as small as $10^{-8}$ at room temperature [7], is desirable for many sensing and time-keeping applications, where devices operate near resonance and require high frequency selectivity, that is, a very sharp resonance peak. Another attractive feature of MNRs is that their linear and nonlinear characteristics can be designed a priori and are also easily tunable, for example, using electrostatic bias. These characteristics allow access to parametric studies not easily accessible to macroscale resonators, thus opening doors to new and potentially useful phenomena.

MNRs have a wide range of geometries, materials, and means of transduction. Fortunately, under most situations, including all current applications in the marketplace, the behavior of MNRs is well described using the laws of classical physics, specifically, classical mechanics and classical electrodynamics. Thus, a variety of approaches are available for determining models and parameter values for describing and predicting the dynamics of MNRs. Commercial devices, which require precise and repeatable device characteristics, are designed using sophisticated computational tools that require comparison against experimental characterization [8, 9]. For more academic studies of devices with simple geometries, one can start with a distributed parameter model (a partial differential equation) and project it onto the vibration modes of interest to obtain the desired model [10]. To account for nonlinearities in such a process necessitates knowledge about the nonlinear field equations, which for MNRs typically involve multiple physical sources [11, 12]. This approach is challenging, in terms of a priori prediction of device parameters, even for the simplest geometries, since features like boundary conditions and electrostatic fields are always necessarily idealized. Such an approach is useful for determining the effects of parameter changes, e.g., how a beam thickness or electrode gap affects model coefficients, but is rarely able to precisely predict parameter values that are measured in the lab. Another approach is more phenomenological, in which one postulates a form of the model based on knowledge of device physics. In this approach, which requires some experience, if one is trying to compare model results to experimental measurements, coefficients are obtained by fitting with experimental data. This is straightforward for linear resonators operating in a single mode since one needs to know only the natural frequency, damping, and a parameter that captures the susceptibility of the device to applied forces, that is, an effective modal mass or stiffness. This approach is very fruitful for determining linear frequency response characteristics.

Until recently, interest in the nonlinear behavior of MNRs was focused on single-mode dynamics, for example, Duffing and other stiffness (conservative) nonlinearities and nonlinear damping, cf. [13,14,15,16]. In terms of modeling nonlinear behavior near resonance, one is guided by generic models. For single-mode operation, one can use standard models from nonlinear vibration, such as the Duffing equation, to capture nonlinear stiffness, or van der Pol terms for nonlinear damping. This approach is quite straightforward and has been widely and successfully employed. Here, the characterization is relatively straightforward, by first determining the linear resonance characteristics and then comparing results with the anticipated generic model to obtain values for nonlinear model coefficients [14, 15]. With such a nonlinear resonator model, one can predict the system response to different inputs, such as shocks, harmonic forcing, and closed-loop operation.

More recently, as described in a recent survey [17] and many other papers noted below, nonlinear interactions between modes in MNRs have been receiving significant attention. Some of these studies explore previously known dynamics in a new setting with unprecedented fidelity, but others describe previously unknown phenomena and new applications. When more than one mode is needed to describe the dynamics, the situation requires a more sophisticated view of modeling, since a brute force approach can lead to an unwieldy number of model coefficients. Here, one is guided by the theory of normal forms from dynamical systems, which dictates which are the essential coupling terms for the model. Once the form of the essential coupling terms is known, the problem of device characterization for coupled-mode behavior becomes tractable, cf. [18]. It should be noted that we do not rigorously follow normal form theory but use it to help select resonant terms for our models. We also use additional knowledge about the effects of various terms in the normal form in order to distill the minimum number of coefficients required to describe experimental observations.

We noted that due to the extremely small size of NMRs and their coupling with electronics, these devices are highly susceptible to thermal fluctuations and other sources of noise. Consideration of these effects is important from both fundamental and application points of view. From an applications view, noise is a limiting factor in the precision of sensors and frequency sources. From a fundamental view, the devices provide platforms for studying noise sources and device limitations imposed by noise [19,20,21,22]. These effects, while important, are outside the scope of this paper, but will be pointed to when relevant to the discussion.

Our development will focus on systems with lightly damped modes, that is, high-Q modes or, equivalently, modes for which the decay rate is much slower than the eigenfrequency. This is a primary feature required for many applications and is also the realm in which dynamically rich behavior can occur. Also, our references to the literature will focus on MNRs papers, even when there are relevant classical papers, in order to maintain focus on the applications of interest. And, while nonlinear-mode interactions can involve coupling between any number of modes, two-mode interactions will be our focus since they offer plenty of interesting and useful dynamics. For a broader discussion of modal interactions and examples from macroscale systems, the reader is referred to [23].

We consider systems with two modes and an approximately rational frequency ratio of n : m, a condition known as internal resonance (IR). Such conditions on eigenfrequencies can, in lightly damped systems, allow for dynamic energy exchange between eigenmodes. Several such internal resonances have been studied in MNRs, including 1:3 IR, as featured in this paper and in Refs. [18, 24,25,26,27,28,29,30,31]. This particular IR has received attention in the nonlinear dynamics literature for many years (see [23] and references cited therein) and remains of interest in macroscale structures, cf. [32]. Other works on IR in MNRs include studies of 1:2 IR [33,34,35,36,37,38,39,40,41,42,43,44,45,46] and 1:1 IR [47,48,49,50,51,52,53]. Also, some MNRs can exhibit multiple IRs, depending on how they are tuned [54,55,56,57,58,59], or involve interactions among more than two modes [46, 60, 61]. Applications of IR in MNRs have also been considered, including rate gyros [38, 51, 62,63,64,65], mass sensing [66, 67], AFM operation [68, 69], frequency conversion [46], frequency stabilization for time-keeping [40, 41, 44, 70, 71], and frequency comb generation [31, 35, 72,73,74,75,76]. Any one of these IRs or applications could be the basis for an in-depth review.

This paper considers only 1:3 IR in MNRs and is organized as follows: The model to be used throughout the paper is developed in Sect. 2. We then consider free vibrations in Sect. 3. Response to an externally imposed harmonic drive is considered in Sect. 4, which is the standard way of thinking about frequency response. Section 5 considers closed-loop operation that generates self-sustained vibrations, which is the most commonly used form of excitation for sensing and time-keeping applications. For each type of operation, we demonstrate and analyze new and useful types of responses and point to relevant experimental papers. Section 6 provides some closing thoughts and ideas about where the field of coupled-mode MNRs may be headed in the coming years.

2 Coupled-mode model for IR

Generally, when driving a MNRs near its eigenfrequency, at sufficiently small amplitudes only the corresponding eigenmode responds with appreciable amplitude. This is true even when that mode is driven into its nonlinear range. However, nonlinearities necessarily couple the eigenmodes. In many cases, this coupling does not affect operation of the MNRs. However, there are two situations in which the single-mode assumption breaks down. The first is when the energy of the MNRs increases and the modal amplitudes become large together with the overtones of the fundamental harmonic, i.e., deep in the strongly nonlinear range [77]. The second situation, of interest here, which does not require large amplitudes, is that of internal resonance (IR), for which eigenfrequencies are (exactly or nearly) rationally related, that is, $\omega _1/\omega _2\approx n/m$ where n and m are integers, a so-called n-to-m IR [23]. These IRs promote energy exchange between modes, even at small (weakly nonlinear) amplitudes, and these effects are most prominent in systems with small dissipation, such as MNRs.

The behaviors of interest involve two lightly damped modes operating near their eigenfrequencies, either decaying or sustained by a weak drive. The dynamics of such systems are conveniently described by a weakly nonlinear two-mode model expressed in terms of the eigenmode coordinates $x_n(t)$, $n=1,2$, as follows,

$$\begin{aligned} \ddot{x}_1+\omega _1^2x_1&=\epsilon F_1(x_1,x_2,\dot{x}_1,\dot{x}_2,t), \end{aligned}$$

(1)

$$\begin{aligned} \ddot{x}_2+\omega _2^2x_2&=\epsilon F_2(x_1,x_2,\dot{x}_1,\dot{x}_2,t) \end{aligned}$$

(2)

where $\omega _n$ are the mode eigenfrequencies, the $F_n$ include the effects of dissipation, nonlinearities, and drive, and $\epsilon (\ll 1)$ is a scaling parameter used to keep track of small effects, which generally include damping, external forcing, and nonlinearities. As Eqs. (1)-(2) are close to those of a pair of linear uncoupled oscillators, we expect that their solutions have nearly harmonic form with generally time-varying amplitudes and phases. Hence, we seek solutions in the form of $x_{n}(t)=A_{n}(t)e^{i\omega _{n} t}+c.c.,~n=1,2$, where c.c. denotes the complex conjugate of the preceding term. The complex amplitude (also known as a phasor) $A_{n}(t)$ conveniently describes the amplitude and relative phase of mode n in a frame of reference that rotates with $\omega _{n}$ relative to the $(x_n,{\dot{x}}_n)$ coordinates. Note that we make no restriction on $x_{1,2}(t)$ here, as both the observed amplitudes $|A_n|$ and frequencies $\omega _n+d(\arg A_n)/dt$ may deviate from the constant amplitudes and frequencies $\omega _n$ of the linear uncoupled, undamped oscillators. Furthermore, since we represent each unknown real solution $x_n(t)$ with a complex function $A_n(t)$, we must impose an additional condition—a constraint—in order to close the problem. A convenient form for the constraint is to represent the time derivatives of $x_n(t)$ as $\dot{x}_{n}=i\omega _{n}A_{n}e^{i\omega _{n}t}+c.c.,~n=1,2$. With this, the conversion from $(x_n,{\dot{x}}_n)$ to $A_n$ amounts to a change to a complex vector in a reference frame that rotates with frequency $\omega _n$. This transformation is standard in the method of averaging. Applying it to Eqs. (1)-(2), one obtains the following equations that govern the evolution of the complex amplitudes

$$\begin{aligned} \dot{A}_1&=\epsilon \frac{e^{-i\omega _{1} t}}{2i\omega _1} F_1(A_1e^{i\omega _{1} t},A_2e^{i\omega _{2} t},t), \end{aligned}$$

(3)

$$\begin{aligned} \dot{A}_2&=\epsilon \frac{e^{-i\omega _{2}t}}{2i\omega _2} F_2(A_1e^{i\omega _{1} t},A_2e^{i\omega _{2} t},t). \end{aligned}$$

(4)

Up to this point, the transformations are exact and no approximations have been made. We now use the small parameter $\epsilon$ (essentially, the previously described physical characteristics of the system) to obtain approximate equations that govern the slow evolution of $A_{1,2}$. As the right-hand sides (RHSs) of the pair of equations in Eqs. (3)-(4) are small (of order $\epsilon$), the variations of $A_1$ and $A_2$ can be either slow (if they are large) or small (if they are fast, e.g., with the frequencies $\omega _1$ and $\omega _2$). We restrict ourselves to large and slow variations, i.e., terms containing the fast oscillations ($e^{i n \omega _1 t}, ~e^{i m \omega _2 t},~n,m=\pm 1,\pm 2,...$) on the RHS of Eqs. (3)-(4) are neglected, which is equivalent to averaging over the period of the oscillations $T_{1,2} = 2\pi /\omega _{1,2}$ [78].

The resulting averaged model is convenient since it is autonomous, thus significantly simplifying the analysis of the response. For example, one can use it to solve for periodic responses of the original system, which are fixed points of the averaged system. In addition, the stability and most bifurcations of these steady responses are captured by the averaged model [78]. Other types of responses are also captured by the averaged system; for example, limit cycles of the averaged equations correspond to amplitude-modulated responses of the original model. Moreover, transient decay of the unforced system is also conveniently modeled with these equations. The approach does have limitations, however, especially when dealing responses with long timescales, such as some of the bifurcations that result in chaotic motions [78].¹

To illustrate the predictive capabilities of the averaged model and the types of responses of interest, we consider in detail the case of 1:3 IR. Schematics of two systems exhibiting this IR are depicted in Fig. 1, the second of which is for device that is referred to throughout the paper. As noted above, this choice is motivated by a number of recent experimental and analytical studies, which have demonstrated a variety of interesting dynamics. Note that while we consider the specific case of 1:3 IR, the same general approach can be, and has been, implemented in a systematic manner for other low-order IRs.

Fig. 1

Schematics of systems with 1:3 IR. In both cases, the coupling parameter is denoted as $\alpha$. Upper panel: A taut nano/micro-wire in which the first and third flexural modes can interact resonantly via the geometric nonlinearity of the wire or by electrostatic and other effects. Lower panel: A computational model of the MNRs from [18, 30, 31, 70] in which the primary in-plane flexural and primary torsional modes interact

In the sequel, we consider the case with no external forcing (free vibration), as well as the case in which one mode is driven near resonance with an imposed external harmonic excitation or using a feedback loop. For forced vibration, we examine the system in which the lower-frequency mode (mode 1) is driven and is coupled to a nonlinear high-frequency mode (mode 2) with a frequency ratio $\omega _2 \approx 3\omega _1$. A generic model capable of describing the dynamics of this system is motivated by the theory of normal forms [78] and is given by

$$\begin{aligned} \ddot{x}_1 \!+\! \omega _1^2x_1=&F\cos (\varPhi _F (t))-2\varGamma _1 \dot{x}_1\!-\!\gamma _1 x_1^3-3\alpha x_2 x_1^2, \end{aligned}$$

(5)

$$\begin{aligned} \ddot{x}_2+\omega _2^2x_2=&-2\varGamma _2 \dot{x}_2-\gamma _2x_2^3-\alpha x_1^3. \end{aligned}$$

(6)

It should be noted that this model may appear to be special but is, in fact, quite generic. If one develops a model for a system with 1:3 IR from first principles, it may have a different form. For example, if the degree of freedom (DOF) coordinates employed for the model are linearly coupled, the first step is to decouple the system at linear order by converting to the eigenmode coordinates. This transformation generally introduces several additional nonlinear terms, even if only a Duffing term is present in one mode, and possibly coupled damping terms, but most of these are not important for the dynamics. Specifically, if the damping terms are small, they can be lumped into equivalent modal decay rates $\varGamma _1$ and $\varGamma _2$; this is most easily formulated for systems with Caughey damping [79], in which case the modes are standing waves, but it can also be done in the more general case of non-Caughey damping, which corresponds to complex modes and traveling waves [80]. In terms of the conservative coupling terms, most of them are non-resonant and will not survive the averaging process, since they are composed of fast oscillating terms after the transformation. The terms that survive provide the normal form for the resonance at hand, a type of minimal nonlinear model [78]. In this way, the above model captures the two most essential features: (i) the nonlinear amplitude–frequency dependence of the individual modes, i.e., they are Duffing oscillators with nonlinear coefficients, $\gamma _{1,2} x_{1,2}^3$ arising from potentials $V_{\mathrm{Duff1,2}}=\gamma _{1,2} x_{1,2}^4$/4, and (ii) a channel for the exchange of energy between modes, captured by the essential coupling term arising from a single-term potential $V_\mathrm{cpl}=\alpha x_1^3x_2$. Another nonlinear coupling term, the so-called dispersive coupling, will survive the averaging process and is described below in a more general context. In terms of the external drive, the form presented above allows one to choose open- or closed-loop operation. Also, if the external drive is dominated by a frequency close to $\omega _1$, it will not directly affect the second mode, a fact borne out by the averaging process. The most important fact about the presented model is that virtually all of the dynamics that have been observed in experiments involving the 1:3 IR in MNRs are captured by this deceptively simple dynamical system. The equations governing the slow dynamics of the averaged complex amplitudes for this 1:3 IR are given by

$$\begin{aligned}&\dot{A}_1\!=\!-(\varGamma _1+i\varDelta \omega _1)A_{1}\!+\!\frac{3i\gamma _1 }{2\omega _F}|A_1|^2A_{1} \!+\! \frac{3i\alpha }{2\omega _{F}} A_2A_1^{*2}\nonumber \\&-\frac{iF}{4\omega _{F}}\left( c_1+c_2 \frac{A_{1}}{|A_{1}|}e^{i\varDelta } \right) , \end{aligned}$$

(7)

$$\begin{aligned}&\dot{A}_2=-(\varGamma _2+i\varDelta \omega _2)A_2+\frac{i\gamma _2}{2\omega _F}A_2^3+\frac{i\alpha }{6\omega _F}A_1^3, \end{aligned}$$

(8)

where for the free response we remove the drive by setting $c_1=0~,c_2=0$ and take $\omega _F=\omega _1$. For open-loop forced operation, we set $c_1=1~,c_2=0$, where F and $\omega _F$ are the imposed drive amplitude and frequency, that is, $F\cos (\omega _F t)$, and $\varDelta \omega _1=\omega _F-\omega _1,~\varDelta \omega _2=3\omega _F-\omega _2$ are the frequency detunings of modes 1 and 2 relative to the drive, respectively. The model for closed-loop operation is obtained by setting $c_1=0,~c_2=1$, in which case F is the closed-loop amplifier output amplitude, $\omega _F=\omega _1$ since there is no imposed forcing frequency, and $\varDelta$ is the phase shift imposed in the feedback loop. One can view the open-loop case as having an imposed frequency from which the system dynamics selects a response phase relative to the input, whereas in the closed-loop case the relative phase is imposed and the system selects a frequency.

Note that the coupling potential can contain more than a single term, e.g., $V_{\mathrm{cpl}}=\alpha x_1^3x_2+\beta x_1^2x_2^2$, the latter of which is dispersive coupling that can be used to tune device characteristics [62, 81,82,83,84]. However, the inclusion of dispersive and other low-order terms of the form $x_1^n x_2^m,~m+n<4$ do not promote modal energy exchange via amplitude modulations, and they only shift the modal frequencies and the locations of the bifurcation conditions in parameter space. In fact, for both 1:2 and 1:3 IRs, only a single term in the coupling potential $V_{\mathrm{cpl}}$ is responsible for nonlinear resonant interactions. (This can be seen by considering the dominant harmonics of the coupling terms in the two modes and whether or not they generate resonances.) The ultimate justification for the model employed herein for analyzing 1:3 internal resonance, specifically one that does not include dispersive coupling, is found in its ability to accurately describe a wide range of experimental results in both qualitative and quantitative terms. For 1:1 IR, there are more than one essential coupling terms, including dispersive coupling, which promotes energy exchange in that IR, making the analysis significantly more involved. However, the symmetry of the 1:1 IR can be used in order to simplify the analysis [85, 86]. We now turn to analysis of free vibrations with 1:3 IR.

3 Free response

The free vibration, or ringdown, of a linear system with lightly damped modes is necessarily composed of components at the system’s damped eigenfrequencies that decay at the modal decay rates, a fact that follows from the fundamental principles of superposition and the invariance of eigenmodes. While the response of system coordinates associated with the DOF (typically physical coordinates) can appear to be complicated, e.g., involving beats, this is merely an artifact of the coordinates being used to measure the system response [87]. Fundamentally, the system response, when decomposed into the individual eigenmode components, is a set of simple decaying oscillations.

It is well known how typical nonlinearities affect the free response of a single-mode response; namely the stiffness nonlinearities result in a relationship between the instantaneous frequency and amplitude of vibration, and damping nonlinearities result in non-exponential decay of the amplitude, cf. [15]. The amplitude–frequency curve of the undamped system, i.e., the backbone curve, provides the underlying structure of how the frequency changes as the system rings down with a small decay rate. The canonical single-mode model of this type is the Duffing oscillator, which in its simplest form with a cubic stiffness term provides a monotonic dependence of the frequency on amplitude. However, mixed nonlinearities are quite common in MNRs and result in non-monotonic backbone curves [15, 88, 89]. The backbone also forms the underlying structure of the frequency response under weak excitation near resonance [90]. When the backbone is non-monotonic, it generally results in interesting frequency responses with multiple jumps and desirable operating conditions for reducing frequency fluctuations [89, 91, 92].

Under IR conditions, the eigenmodes can strongly interact during free vibration, resulting in phenomena that cannot be captured by linear models, nor by simple single-mode backbone analyses. A simple test to see whether an IR exists is to drive the system into a given mode (assuming it is possible to maintain the driven response in a single mode) and turn off the drive to observe the free vibration, and do so for a range of initial energies. An IR will be characterized by energy exchange between the mode of interest and one or more other modes, typically resulting in a beating response (although, as we describe subsequently, other non-intuitive transient responses can also occur).²

The experimental studies in Refs. [29, 30] reported such observations of the free response of very lightly damped MNRs with 1:3 IR. The results in Ref. [29] demonstrate that within the 1:3 IR, the second mode can act as an energy sink for the first mode and, hence, increase the effective dissipation rate of the first mode during the first part of a ringdown, similar to the behavior used for nonlinear vibration sinks [93]. This phenomenon was also observed in a driven MNRs with a 1:2 IR [36]. In direct contrast, the experimental results in Ref. [30] demonstrate that within the 1:3 IR, the second mode can also act as a type of mechanical battery for the first mode and compensate for energy losses in the first mode during ringdown, thus supporting, or even amplifying, its oscillation amplitude for a certain period of time (until the second mode is exhausted), called the coherence time, $t_{\mathrm{coherent}}$.

In an analytical study, which was carried out in parallel with these experimental studies, we showed that these seemingly contradicting behaviors are both feasible at the 1:3 IR conditions and can be understood from the undriven counterpart of Eqs. (7)-(8) [94]. The key to understanding this situation is to examine the manner in which the modes exchange energy in the transient response, during which the total system energy must be decreasing. If energy flows from one mode to another and does so on a timescale that does not allow the energy to flow back, then the source mode will decay faster than its linear rate and the sink mode will decay slower than its linear rate. So, the apparently contradictory phenomena described in [30] and [29] are simply a matter of considering which mode is being measured, the source mode or the sink mode.

The details of this process can be captured by the free vibration version of the present model, that is,

$$\begin{aligned}&\dot{A}_1=-\varGamma _1A_{1}+\frac{3i\gamma _1}{2\omega _1}|A_1|^2A_{1}+\frac{3i\alpha }{2\omega _{1}} A_2A_1^{*2}, \end{aligned}$$

(9)

$$\begin{aligned}&\dot{A}_2=-(\varGamma _2+i\varDelta \omega _2)A_2+\frac{i\gamma _2}{2\omega _1}A_2^3+\frac{i\alpha }{6\omega _1}A_1^3. \end{aligned}$$

(10)

Before examining the general case, we consider a special case, where the modal interaction is non-trivial but can be captured by a reduced, single-mode model.

3.1 The adiabatic approximation

A simple scenario in which the dissipation of the first mode is nonlinearly, and non-uniformly, enhanced due to the 1:3 IR, can be readily obtained from the model in Eqs. (9)-(10), if the second mode is linear ($\gamma _2=0$) and decays much faster than the first mode $\varGamma _1\ll \varGamma _2$ (with both $\ll \omega _{1,2}$), which is common in MNRs [95,96,97,98]. In such a case, the second mode adiabatically follows the first mode; that is, it quasi-statically tracks the first mode. Under these assumptions, in the model we set the time derivative of the second mode to zero ($\dot{A}_2\approx 0$), while the first mode decays to zero. Thus, we find from Eq. (10) that $A_2=i\alpha A_1^3/[6\omega _1(\varGamma _2+i\varDelta \omega _2)]$, which can be substituted into Eq. (9) to yield a dynamic model for the first mode,

$$\begin{aligned} \dot{A}_1=&-\left[ \varGamma _1+\left( \frac{\alpha }{2\omega _{1}}\right) ^2\left( \frac{\varGamma _2}{\varGamma _2^2+\varDelta \omega _2^2}\right) |A_1|^4 \right] A_{1}\nonumber \\&+i\left[ 3\gamma _1+ \frac{\alpha ^2}{2\omega _{1}}\left( \frac{\varDelta \omega _2}{\varGamma _2^2+\varDelta \omega _2^2}\right) |A_1|^2\right] \frac{|A_1|^2A_{1}}{2\omega _1}. \end{aligned}$$

(11)

From Eq. (11), we deduce that under the adiabatic approximation, the resonant interaction of the modes modifies the nonlinearities of mode 1. Specifically, we see that the 1:3 IR leads to the addition of a quintic nonlinear damping term $-\alpha ^2\varGamma _2|A_1|^4A_1/[4\omega _1^2(\varGamma _2^2+\varDelta \omega _2^2)]$ and an effective “conservative” restoring force $i\alpha ^2\varDelta \omega _2|A_1|^4A_1$ $/[4\omega _1^2(\varGamma _2^2+\varDelta \omega _2^2)]$. Hence, Eq. (11) is consistent with the complex amplitude equation that one gets from the averaging method for the following phenomenological model,

$$\begin{aligned} \ddot{x}_1+\omega _{1}^2 x_1=&-\left( \gamma _1 +\frac{\alpha ^2\varDelta \omega _2}{20\omega _{1}(\varGamma _2^2+\varDelta \omega _2^2)}x_1^2\right) x_1^3\nonumber \\&-\left( 2\varGamma _1+\frac{\alpha ^2\varGamma _2}{4\omega _{1}^2(\varGamma _2^2+\varDelta \omega _2^2)}x_1^4\right) \dot{x}_1. \end{aligned}$$

(12)

We note that the additional conservative restoring force changes sign as the frequency mismatch $\varDelta \omega _2$ is swept through zero during decay, which means that on one side of the IR condition, where $\varDelta \omega _2>0$, it acts as a stiffening nonlinearity, while on the other side, where $\varDelta \omega _2<0$, it acts as a softening nonlinearity. This effect leads to a mixed type of nonlinearity, even though the only stiffness nonlinearity is the Duffing effect in the first mode. This is associated with a nonlinear frequency anti-crossing/veering, which is discussed in more detail in the following sections, since it has a dramatic effect on the frequency response in both open- and closed-loop operation.

The presence of the Lorentzian-like term $\varGamma _2/(\varGamma _2^2+\varDelta \omega _2^2)$ in the additional dissipation force means that the force is enhanced near the IR condition and is in fact maximal at $\varDelta \omega _2=0$. The effective IR-induced decay rate can be understood in terms of the Fermi golden rule from quantum mechanics [99], where $\alpha /(2\omega _1)$ is the “matrix element” of the interaction and $\varGamma _2/[\varGamma _2+(3\omega _1-\omega _2)^2]$ is the “density of states” of the effective reservoir provided by mode 2 at triple the eigenfrequency of mode 1.

Using a polar representation for the complex amplitude $A_1=a_1e^{i\phi _1}/2$, we find that the model for the real amplitude for this adiabatic decay is given by

$$\begin{aligned} \dot{a}_1=&-a_{1} \left[ \varGamma _1+\left( \frac{\alpha }{8\omega _{1}}\right) ^2\left( \frac{\varGamma _2}{\varGamma _2^2+\varDelta \omega _2^2}\right) a_1^4 \right] , \end{aligned}$$

(13)

and therefore, the relaxation of mode 1 as its amplitude goes to zero is given by

$$\begin{aligned}&a_1(t)=a_1(0)\exp (-\varGamma _1t)\nonumber \\&\times \left[ 1-\left( \frac{\alpha }{8\omega _{1}}\right) ^2\left( \frac{\varGamma _2/\varGamma _1}{\varGamma _2^2+\varDelta \omega _2^2}\right) a_1^4(0)\exp (-4\varGamma _1t) \right] ^{-1/4}. \end{aligned}$$

(14)

Note that the decay of $a_1(t)$ is initially faster than exponential (Fig. 2, lower panel). This is due to the fact that the second mode is “dragged” along with the first mode and also dissipates energy, thereby increasing the effective damping of the first mode. The decay eventually becomes exponential, after the amplitudes become sufficiently small that the coupling is no longer important, specifically when

$$\begin{aligned} \left( \frac{\alpha }{8\omega _{1}}\right) ^2\left( \frac{\varGamma _2/\varGamma _1}{\varGamma _2^2+\varDelta \omega _2^2}\right) a_1^4(0)\exp (-4\varGamma _1t) \ll 1. \end{aligned}$$

Fig. 2

Ringdown response of mode 1 with resonantly induced nonlinear damping. Upper panel: The envelope of the ringdown response (red curve) is the analytical solution of Eq. (14), and the fast oscillating response (black) is obtained from numerical integration of Eqs. (5)-(6) in the absence of drive. Lower panel: The variation of the amplitude decay as a function of the coupling parameter $\alpha$: ($\alpha =100$) magenta, ($\alpha =87.5$) blue, ($\alpha =75$) red, ($\alpha =0$) dashed black. The system parameters are $\omega _1=\omega _2/3=1000,~\varGamma _1=0.01,~\varGamma _2=10,~\alpha =20,~\gamma _1=50,~\gamma _2=0$, which satisfy the conditions for the adiabatic approximation

3.2 Validity of the adiabatic approximation

To understand the conditions under which the adiabatic approximation holds, it is helpful to express Eqs. (9)-(10) in dimensionless form. Therefore, we take $\varGamma ^{-1}_1$ to be the timescale of the dynamics of interest, $\ell _1=\sqrt{2\omega _1\varGamma _1/(3\gamma _1)}$ as the typical amplitude scale of the first mode, $\ell _2=\sqrt{2\omega _1\varGamma _1^2/(27\gamma _1\varGamma _2)}$ as the typical amplitude scale of the second mode, and obtain the following non-dimensional equations

$$\begin{aligned}&A_{1\mathrm n}'=-A_{1\mathrm n}+i|A_{1\mathrm n}|^2A_{1\mathrm n}+\frac{i\kappa }{3} A_{2\mathrm n}A_{1\mathrm n}^{*2}, \end{aligned}$$

(15)

$$\begin{aligned}&\mu A_{2\mathrm n}'=-(1+i\varDelta \omega _{2\mathrm n})A_{2\mathrm n}+\frac{i\kappa }{3}A_{1\mathrm n}^3, \end{aligned}$$

(16)

where the prime symbol denotes derivative with respect to the dimensionless time $\tau =\varGamma _1 t$, and $\ell _{1,2}A_{1\mathrm n,2\mathrm n}=A_{1,2}$, $\mu =\varGamma _1/\varGamma _2$, $\varDelta \omega _{2\mathrm n}=\varDelta \omega _2/\varGamma _2, \kappa =(\alpha /\gamma _1)\sqrt{\varGamma _1/\varGamma _2}$. Consequently, for small damping ratio $\mu \ll 1$, and $\varDelta \omega _{2\mathrm n}$ and $\kappa$ are of O(1), the LHS of Eq. (16) is approximately zero and our adiabatic approximation is valid.

We note that in the foregoing dimensionless equations, Eqs. (15)-(16), we have implicitly assumed that the amplitude of the second mode is smaller than the amplitude of the first mode by the introduction of different length scales $\ell _2/\ell _1=\sqrt{\mu }/3$, and that the timescale of interest is the relaxation of the uncoupled first mode $\varGamma _1^{-1}$. However, for shorter timescales $t\ll \varGamma _1^{-1}$ our analysis is invalid even if $\alpha \approx O(\gamma _1\sqrt{\varGamma _2/\varGamma _1})$ and $\varDelta \omega _{2}\approx O(\varGamma _1)$. This failure at very short times can be understood, since Eqs. (15)-(16) give rise to a singular boundary layer problem. That is, for the time interval $0<t\ll \varGamma _1^{-1}$, the adiabatic approximation is unable to satisfy the initial conditions of the second mode $A_2(0)$ due to the elimination of its time derivative. Hence, in this narrow time interval, $0<t\ll \varGamma _1^{-1}$ (i.e., the boundary layer), the adiabatic approximation breaks down, namely $A_{2\mathrm n}\ne i\kappa A_{1\mathrm n}^3/[3(1+i\varDelta \omega _{2\mathrm n})]$, and we have a slow–fast dynamical system in which $A_{1\mathrm n}'\approx O(1)$ and $A_{2\mathrm n}'\approx O(1/\epsilon )\gg 1$. Therefore, the second mode experiences a rapid transition from its initial state $A_2(0)$ to adiabatically following the first mode, that is, with $A_{2\mathrm n}(\tau )= i\kappa A_{1\mathrm n}^3(\tau )/[3(1+i\varDelta \omega _{2\mathrm n})]$ (see Fig. 3).

Fig. 3

The rapid time evolution of mode 2. In the narrow time interval $0<t\ll \varGamma _1^{-1}$, mode 2 experiences rapid transient dynamics (red curve) due to its initial condition $A_2(0)=1$ and its inability to initially follow mode 1 adiabatically (black curve). The system parameters are $\mu =0.001,~\varDelta \omega _{2\mathrm n}=0,~\kappa =0.0211$, which satisfy the conditions for the adiabatic approximation for $t>\sim \varGamma _1^{-1}$

Another phenomenon associated with adiabatic decay of this resonance involves the system passing through an IR, which interrupts its usual decay along the backbone. The analysis needed to describe this behavior is more involved and essentially accounts for the fact that the term $\varDelta \omega _2=3 \omega _1- \omega _2$ actually depends on the amplitude of mode 1 due to its Duffing nonlinearity and can be replaced by a term of the form $\varDelta \omega _{2\mathrm eff}=3 \omega _{1\mathrm eff}- \omega _2$, where $\omega _{1\mathrm eff}=\omega _1+3\gamma _1|A_1|^2/(2\omega _1)$³. In this case, the effective damping of the first mode is unaffected except where the Lorentzian term comes into play, corresponding to a frequency window of scale $\varDelta \omega _{2\mathrm eff}\sim \varGamma _2$, during which the effective damping of mode 1 is significantly increased [94]. This has been experimentally observed, where the effective quality factor of a high-Q Lamé mode resonator has a temporary and repeatable dip from its expected behavior during ringdown [100].

3.3 The quasi-conservative approximation

We next consider a more general case, where the relaxation rates of the two modes are not necessarily drastically different; however, they are still significantly smaller than the vibration frequencies $\omega _{1,2}$. MNRs are usually lightly damped systems, and hence, we can consider Eqs. (9)-(10) as a nearly conservative system with small perturbations from dissipation.

The modal dynamics in the absence of decay is interesting on its own, and understanding it provides a framework for describing the response of the weakly damped system. To this end, we set $\varGamma _{1,2}=0$, normalize the complex amplitude equations by $\ell _{1,2}A_{1,2\mathrm n}=A_{1,2}$, where $\ell _1=\ell _2/\sqrt{3}=3^{1/4}\omega _1\sqrt{2/\gamma _1}$, the time by $\tau =\omega _1 t$, and obtain the following dimensionless conservative system

$$\begin{aligned} A_{1\mathrm n}'&=3\sqrt{3}i|A_{1\mathrm n}|^2A_{1\mathrm n}+3i\kappa A_{2\mathrm n} A_{1\mathrm n}^{*2}=-i\frac{\partial {\mathcal {H}}}{\partial { A_{1\mathrm n}^*} }, \end{aligned}$$

(17)

$$\begin{aligned} A_{2\mathrm n}'&=i\frac{\gamma _{21}}{\sqrt{3}}|A_{2\mathrm n}|^2A_{2\mathrm n}-i\varDelta \omega _{2\mathrm n}A_{2\mathrm n}+i\kappa A_{1\mathrm n}^3 =-i\frac{\partial {\mathcal {H}}}{\partial { A_{2\mathrm n}^*} }, \end{aligned}$$

(18)

where $\varDelta \omega _{2\mathrm n}=\varDelta \omega _2/\omega _1$, $\gamma _{21}=\gamma _2/\gamma _1$, $\kappa =\alpha /\gamma _1$, and ${\mathcal {H}}=\varDelta \omega _{2\mathrm n}|A_{2\mathrm n}|^{2}-\gamma _{21}|A_{2\mathrm n}|^{4}/(2\sqrt{3})-3\sqrt{3}|A_{1\mathrm n}|^{4}/2-\kappa ( A_{2\mathrm n} A_{1\mathrm n}^{*3}+ A_{2\mathrm n}^*A_{1\mathrm n}^3 )$ is the averaged Hamiltonian of the system which, by construction, is a conserved quantity (since ${\mathcal {H}}$ is Hermitian). To see this, consider

$$\begin{aligned} \frac{d{\mathcal {H}}}{d\tau }=&\frac{\partial {\mathcal {H}}}{\partial A_{1\mathrm n}} A_{1\mathrm n}'\!+\!\frac{\partial {\mathcal {H}}}{\partial A_{1\mathrm n}^*} A_{1\mathrm n}^{*'}\!+\!\frac{\partial {\mathcal {H}}}{\partial A_{2\mathrm n}} A_{2\mathrm n}'\!+\!\frac{\partial {\mathcal {H}}}{\partial A_{2\mathrm n}^*} A_{2\mathrm n}^{*'}\\ =&-i\left( \frac{\partial {\mathcal {H}}}{\partial A_{1\mathrm n}} \frac{\partial {\mathcal {H}}}{\partial A_{1\mathrm n}^*}-\frac{\partial {\mathcal {H}}}{\partial A_{1\mathrm n}^*}\frac{\partial {\mathcal {H}}}{\partial A_{1\mathrm n}}\right) \\&-i\left( \frac{\partial {\mathcal {H}}}{\partial A_{2\mathrm n}}\frac{\partial {\mathcal {H}}}{\partial A_{2\mathrm n}^*}-\frac{\partial {\mathcal {H}}}{\partial A_{2\mathrm n}^*}\frac{\partial {\mathcal {H}}}{\partial A_{2\mathrm n}}\right) \equiv 0. \end{aligned}$$

There is a second conserved quantity for Eqs. (17)-(18), which is an analog of the Manley–Rowe invariant used in nonlinear optics [101] and has the form of ${\mathcal {M}}=I+3|A_{2\mathrm n}|^{2}$, where $I=|A_{1\mathrm n}|^{2}$ is the action of the first mode. Thus, with these two conserved quantities, the system is integrable and its dynamics are conveniently described by two canonically conjugate variables I and $\psi$, where $\psi =3\arg (A_{1\mathrm n})-\arg (A_{2\mathrm n})$ is the modal phase difference, a quantity that arises naturally in the study of this IR and will be encountered again in the analysis of the closed-loop system. Consequently, the Hamiltonian of the system can be rewritten as

$$\begin{aligned} {\mathcal {H}}=&\frac{\varDelta \omega _{2\mathrm n}}{3}({\mathcal {M}}-I)-\frac{\gamma _{21}}{18\sqrt{3}}({\mathcal {M}}-I)^2-\frac{3\sqrt{3}}{2}I^2\nonumber \\&-\frac{2\kappa }{\sqrt{3}}({\mathcal {M}}-I)^{1/2}I^{3/2}\cos \psi , \end{aligned}$$

(19)

and the Hamiltonian equations for these variables read

$$\begin{aligned} I'=&\frac{\partial {\mathcal {H}}}{\partial \psi }=\frac{2\kappa }{\sqrt{3}} ({\mathcal {M}}-I)^{1/2}I^{3/2}\sin \psi , \end{aligned}$$

(20)

$$\begin{aligned} \psi '=&-\frac{\partial {\mathcal {H}}}{\partial I}=\frac{\varDelta \omega _{2\mathrm n}}{3}-\frac{\gamma _{21}}{9\sqrt{3}}({\mathcal {M}}-I)\nonumber \\&+3\sqrt{3}I+\frac{\kappa }{\sqrt{3}}\sqrt{\frac{I}{{\mathcal {M}}-I}}(3{\mathcal {M}}-4I)\cos \psi . \end{aligned}$$

(21)

We note that these two canonically conjugate variables, I and $\psi$, are singular when $I\rightarrow 0$ and $I\rightarrow {\mathcal {M}}$ (i.e., when either of the mode amplitudes goes to zero) since the phase difference $\psi$ is ill-defined in such cases; therefore, transformation to Cartesian coordinates ($q=I\cos \psi ,~p=I\sin \psi$) is required near the singularities. Nevertheless, the use of I and $\psi$ helps to gain insight into the dynamics of the amplitude of mode 1 ($I\propto a_1^2$), obtained by considering their phase portraits (Fig. 4) for varying ${\mathcal {M}}$. Once the dynamics of I ($|A_{1\mathrm n}|^2$) and $\psi$ are determined, those of mode 2 follow from $|A_{2\mathrm n}|^{2}=({\mathcal {M}}-I)/3$.

Fig. 4

Phase trajectories of the resonating modes in the absence of decay. Motion along the trajectories (thin black curves) corresponds to oscillations in time of the squared amplitudes I and $({{\mathcal {M}}}-I)/3$ of modes 1 and 2, respectively, and of the mode phase difference $\psi$. The pattern is $2\pi$-periodic in $\psi$. The Hamiltonian ${\mathcal {H}}$ is constant on a given trajectory. The scaled system parameters are $\varDelta \omega _{2\mathrm n}=-91,~\gamma _{21}=-1,~\kappa =1$. The extrema of the Hamiltonian and the separatrices that go in to or out of the saddle point are indicated in red. The blue trajectories correspond to the energy levels shown in Fig. 5 for the attendant effective potentials. The different panels show how the phase portrait evolves as ${\mathcal {M}}$ decreases: upper panel ${\mathcal {M}}=10$, middle panel ${\mathcal {M}}=8$, and lower panel ${\mathcal {M}}=5$. When dissipation is present, the system follows trajectories that are close to those shown and continuously evolve through such phase portraits, with both ${\mathcal {M}}$ and the total energy both decreasing

Shown in Fig. 4 are the contours of constant ${\mathcal {H}}$, which are, essentially, parametric plots of the trajectories $I(\tau )$ and $\psi (\tau )$. Clearly, the fixed points correspond to special vibrations where both modes have constant amplitude. The closed loops, known as librations, correspond to oscillations of I and $\psi$ about the stationary states, where ${\mathcal {H}}(I,\psi ;{\mathcal {M}})$ is maximal or minimal (see the red crosses in Fig. 4). These oscillations correspond to an back and forth exchange of energy between the modes with oscillating relative phase $\psi$. In contrast, the open trajectories, known as rotations, correspond to the accumulation of phase $\psi$ in time, which is also accompanied by oscillations of the mode amplitudes. The librations around different extrema of ${\mathcal {H}}$ are separated from each other and from the rotations by separatrices (see the red curves in Fig. 4). We note that, in the absence of resonant-mode coupling, the phase trajectories are just straight horizontal lines, since in this case the amplitudes of the modes are both constant.

The dynamics of Eqs. (20)-(21) can be mapped onto the motion of a particle in a potential well. This can be readily seen by squaring and adding Eqs. (19)-(20), which yields an analogous equation to the conservation of energy of a unit mass “particle” with a coordinate I that oscillates in a potential well $U_{\mathrm{eff}}(I)$ with zero total energy

$$\begin{aligned}&\frac{1}{2}I'^2+U_{\mathrm{eff}}(I)=0, \nonumber \\&U_{\mathrm{eff}}(I)=-\frac{2\kappa ^2}{3}({\mathcal {M}}-I)I^{3}\nonumber \\&+\frac{1}{2}\left[ {\mathcal {H}}-\frac{\varDelta \omega _{21}}{3}({\mathcal {M}}-I)+\frac{\gamma _{21}}{18\sqrt{3}}({\mathcal {M}}-I)^2+\frac{3\sqrt{3}}{2}I^2 \right] ^2. \end{aligned}$$

(22)

The potential $U_{\mathrm{eff}}$ is a quartic polynomial in I parameterized by ${\mathcal {M}}$ and ${\mathcal {H}}$. It can have a single well or two wells separated by a local maximum (Fig. 5).

Fig. 5

Effective potential $U_{\mathrm{eff}}$ and time evolution of I and $\psi$. The upper, middle, and lower panels are the effective potentials for the cases corresponding to the blue trajectories in the upper, middle, and lower panels of Fig. 4. The insets show the time evolution of I and $\psi$, where in the upper panel the motion is associated with librations; in the middle panel, the motion could be associated with either librations (around the smaller well with larger amplitudes) or rotations (around the larger well with lower amplitudes), and in the lower panel, the motion is associated with rotations

In the latter scenario, if the local maximum of the double well potential lies below zero (Fig. 5, upper panel), then the equation $U_{\mathrm{eff}}(I)=0$, which yields the turning points $I'=0$, has a pair of real solutions $I_1>I_2$, and a pair of complex conjugate solutions $I_4=I_3^*$. Therefore, the motion $I(\tau )$ is qualitatively the same as the motion of a particle in a single well potential (Fig. 5, lower panel), where $I(\tau )$ oscillates non-uniformly between $I_1$ and $I_2$, and can be described in terms of Jacobi elliptic functions

$$\begin{aligned} I(u)= & {} \frac{I_{1}z^{(2)}+I_{2}z^{(1)}-(I_{1}z^{(2)}-I_{2}z^{(1)}){\text {cn}}(u|m)}{z^{(1)}+z^{(2)}+(z^{(1)}-z^{(2)}){\text {cn}}(u|m)},\nonumber \\ u= & {} \frac{\tau -\tau _0}{18}\sqrt{\frac{1296\kappa ^2+(81+\gamma _{21})^2}{3}z^{(1)}z^{(2)}},\nonumber \\ m= & {} \frac{1}{4}\frac{(I_{1}-I_{2})^2-(z^{(1)}-z^{(2)})^2}{z^{(1)}z^{(2)}},\nonumber \\ z^{(j)}= & {} \sqrt{(I_{3}-I_{j})(I_{4}-I_{j})},\qquad j=1,2. \end{aligned}$$

(23)

where $z^{(1,2)}$ are the zeros of the elliptic function. On the other hand, if the local maximum of the double well potential is above zero (Fig. 5, middle panel), then the equation $U_{\mathrm{eff}}(I)=0$ has four real solutions $I_1>I_2>I_3>I_4$. Therefore, depending on the initial condition I(0), the “particle” $I(\tau )$ oscillates non-uniformly either between $I_1$ and $I_2$, or between $I_3$ and $I_4$. (And these motions can also be described in terms of Jacobi elliptic functions.) We note that the period of the oscillations is given by,

$$\begin{aligned} T=72K(m)/\sqrt{\frac{1296\kappa ^2+(81+\gamma _{21})^2}{3}z^{(1)}z^{(2)}}, \end{aligned}$$

where K(m) is the elliptic integral of the first kind, which is invariant under the replacement of $I_1$ with $I_3$ and $I_2$ with $I_4$. Therefore, the period of the oscillations in both wells (i.e., the motions $I_1\geqslant I(\tau )\geqslant I_2$ and $I_3\geqslant I(\tau )\geqslant I_4$) is the same. However, the oscillations $I_1\geqslant I(\tau )\geqslant I_2$ are librations with a bounded phase $\psi$ occurring in the interior of the separatrix loop, while the oscillations $I_3\geqslant I(\tau )\geqslant I_4$ are rotations with free-running phase $\psi$ occurring exterior to the separatrix loop (see Fig. 4, middle panel).

Fig. 6

Time evolution of $I/{\mathcal {M}}_0$, the normalized first-mode action, and $[{\mathcal {M}}-I]/(3{\mathcal {M}}_0)$, the normalized second-mode action, in the presence of light damping, along with samples of the corresponding slowly varying effective potential $U_{\mathrm{eff}}$. Here, ${\mathcal {M}}_0\equiv {\mathcal {M}}(t=0)$ and $\varGamma _{1\mathrm n}=\varGamma _{2\mathrm n}=0.01$. Resonance capture is exhibited in region (i) of the upper and middle panels, where mode 1 oscillates without much (if any) decay, while draining energy from mode 2 as the energy flows between them in the oscillations. A sample of the effective potential associated with resonance capture is shown in the left inset of the lower panel, and the time duration of the resonance capture is denoted by $t_{\mathrm{coherent}}$. The transition region (ii) of the upper and middle panels is associated with the bifurcation condition $dU_{\mathrm{eff}}/dI|_{I=I_{2,3}}=0$, where the local maximum of the double-well potential approaches zero, as shown in the center inset of the lower panel. Region (iii) of the upper panel is associated with the motion after escape from the resonance capture, where the modes are effectively decoupled, and thus decay exponentially; a sample effective potential for this situation is shown in the right inset of the lower panel

In the presence of dissipation, ${\mathcal {H}}$ and ${\mathcal {M}}$ are no longer conserved quantities. If the modes are lightly damped, these two quantities are slowly varying in time and their evolution equations are given by

$$\begin{aligned} {\mathcal {H}}'=&-(3\varGamma _{1\mathrm n}+\varGamma _{2\mathrm n}){\mathcal {H}}-\frac{2}{3}(3\varGamma _{1\mathrm n}-\varGamma _{2\mathrm n})\varDelta \omega _{2\mathrm n}({\mathcal {M}}-I)\nonumber \\&-\frac{\sqrt{3}}{18}(\varGamma _{2\mathrm n}-\varGamma _{1\mathrm n})[27I^{2}-\gamma _{21}({\mathcal {M}}-I)^2], \end{aligned}$$

(24)

$$\begin{aligned} {\mathcal {M}}'=&-2\varGamma _{1\mathrm n}I-2\varGamma _{2\mathrm n}({\mathcal {M}}-I), \end{aligned}$$

(25)

where $\varGamma _{1\mathrm n,2\mathrm n}=\varGamma _{1,2}/\omega _1$. We note that Eqs. (23)-(25) give a complete description of the system dynamics under the quasi-conservative approximation. Also, note that since ${\mathcal {M}}>I$, ${\mathcal {M}}'<0$ for any positive damping, so that ${\mathcal {M}}$ decays. Furthermore, as the RHSs of Eqs. (24)-(25) are small (of order $\varGamma _{1\mathrm n,2\mathrm n}$ in magnitude), the variations of ${\mathcal {M}}$ and ${\mathcal {H}}$ can be either slow, if they are large, or small, if they are fast, e.g., oscillating with the frequency $\omega =(\pi /36K(m))$ $\times \sqrt{\frac{1296\kappa ^2+(81+\gamma _{21})^2}{3}z^{(1)}z^{(2)}}$. By restricting the analysis to large and slow variations, i.e., we can remove all the fast terms on the RHS of Eqs. (24)-(25) by averaging over the period of the oscillations 4K(m) with respect to the argument u, we obtain a slowly varying dynamical system for the averages of ${\mathcal {H}}$ and ${\mathcal {M}}$. The resulting averaged equations, not presented here but given in [94], cannot be solved in closed form. Moreover, as the parameter m of the elliptic function approaches unity $(m\rightarrow 1)$, the period becomes infinitely long and the averaging process becomes invalid. However, for finite period of oscillations, these averaged equations only depend on the slow dynamics of the roots $I_j$ (with $j=1,2,3,4$) of the equation $U_{\mathrm{eff}}(I)=0$. Of particular interest are the bifurcation points in which a pair of turning points coincide with a fixed point, corresponding to $dU_{\mathrm{eff}}/dI|_{I=I_{2,3}}=0$. Transition through such points results in dramatic qualitative changes in the system dynamics (Fig.6). This bifurcation point marks the very rapid transition from a resonance capture [102] in a neighborhood of the 1:3 IR manifold [Fig. 6, upper panel, region (i)] to the decoupled exponentially decaying modes [Fig. 6, upper panel, region (iii)].

The coherent time of the resonance capture, i.e., the time spent inside the separatrix, explains the experimental results of Ref. [30]. Namely, the first-mode amplitude remains nearly constant, possibly with oscillations whose period increases until escape, as observed in the experiments of Ref. [30]. Note that at the resonance capture, the second mode [Fig. 6, middle panel, region (i)] provides the energy to sustain the amplitude dwell of the first mode, and hence, it experiences enhanced nonlinear damping, thus describing the phenomenon observed by Ref. [29]. Therefore, as noted above, this model is able to describe both enhanced damping and coherence time that have been observed in experiments.

4 Open loop operation—response to harmonic drive

Here, we consider the usual external harmonic drive applied to a MNRs near a resonance frequency, for which one imposes a force of amplitude F and frequency $\omega _F$. In this situation, the system steady-state response of interest is at the same frequency with a constant amplitude and a shifted phase. We refer to this as open-loop operation, which is commonly used for system characterization.

The open-loop analysis of systems with a 1:3 IR is by no means new or unknown, cf., [32, 103,104,105,106]. However, its implications for MNRs have only recently become of interest. These include experimental observations of various phenomena, such as frequency-veering/anti-crossing [57], a region of drive parameter space where the desired steady-state oscillations are not possible [18], and generation of frequency combs due to a saddle node on an invariant circle (SNIC) and Hopf bifurcations [31, 35, 72,73,74,75,76].

To explore the dynamics of open-loop operation, we take a similar approach to the analysis of Sect. 3, where we consider the adiabatic and the diabatic (non-adiabatic) cases of the externally driven counterpart of Eqs. (7)-(8) with a linear secondary mode, that is, $\gamma _2=0$,

$$\begin{aligned} {\dot{A}}_1=&-(\varGamma _1+i\varDelta \omega _1)A_{1}+\frac{3i\gamma _1 }{2\omega _F}|A_1|^2A_{1}\nonumber \\&+\frac{3i\alpha }{2\omega _{F}} A_2A_1^{*2}-\frac{iF}{4\omega _{F}}, \end{aligned}$$

(26)

$$\begin{aligned} {\dot{A}}_2=&-(\varGamma _2+i\varDelta \omega _2)A_2+\frac{i\alpha }{6\omega _F}A_1^3. \end{aligned}$$

(27)

Generally speaking, as is always the case with such perturbation methods, the results from the approximate analysis are expected to be less accurate as the drive level is increased and/or as the frequencies move away from the resonance conditions, both external and internal. To that end, as is standard in such analyses, we replace $\omega _F$ with $\omega _1$ when its correction will be at higher order.

In the adiabatic case, the steady-state analysis can be reduced to that of an effective single mode by elimination of mode 2. Taking $\dot{A}_2=0$, we find from Eq. (27) that $A_2=i\alpha A_1^3/[6\omega _1(\varGamma _2+i\varDelta \omega _2)]$, which can then be substituted into Eq. (26) with $\dot{A}_2=0$ to yield an equation for the steady-state conditions for the first mode (where $\dot{A}_1=0$ as well), $A_{1ss}$, which can be any solution of the algebraic equation

$$\begin{aligned} A_{1ss}{\mathcal {I}}=\frac{F}{4\omega _{F}}, \end{aligned}$$

(28)

where

$$\begin{aligned} {\mathcal {I}}&=-\left[ \!\varDelta \omega _1\!-\!\frac{3\gamma _1}{2\omega _F}|A_{1ss}|^2\!-\!\left( \!\frac{\alpha }{2\omega _{1}}\!\right) ^2\!\left( \!\frac{\varDelta \omega _2}{\varGamma _2^2\!+\!\varDelta \omega _2^2}\!\right) \! |A_{1ss}|^4 \!\right] \nonumber \\&\quad +i\left[ \varGamma _1+\left( \frac{\alpha }{2\omega _{1}}\right) ^2\left( \frac{\varGamma _2}{\varGamma _2^2+\varDelta \omega _2^2}\right) |A_{1ss}|^4 \right] \end{aligned}$$

(29)

is the impedance of mode 1 modified by its coupling to mode 2. Consequently, the amplitude $a_{1ss}$ and phase $\phi _{1ss}$ of the steady-state response expressed as $A_{1ss}=a_{1ss}e^{i\phi _{1ss}}/2$ are given implicitly by

$$\begin{aligned} a_{1ss}&=\frac{F}{2\omega _1 |{\mathcal {I}}|}\nonumber \\ =&\frac{F}{2\omega _1}\left\{ \left[ \!\varDelta \omega _1\!-\!\frac{3\gamma _1}{8\omega _1}a_{1ss}^2\!-\!\left( \!\frac{\alpha }{8\omega _{1}}\!\right) ^2\!\left( \!\frac{\varDelta \omega _2}{\varGamma _2^2\!+\!\varDelta \omega _2^2}\!\right) \! a_{1ss}^4 \!\right] ^2\right. \nonumber \\&+\left. \left[ \varGamma _1+\left( \frac{\alpha }{8\omega _{1}}\right) ^2\left( \frac{\varGamma _2}{\varGamma _2^2+\varDelta \omega _2^2}\right) a_{1ss}^4 \right] ^2\right\} ^{-1/2}, \end{aligned}$$

(30)

$$\begin{aligned} \tan \phi _{1ss}&=\frac{\mathfrak {R}\{{\mathcal {I}}\}}{\mathfrak {I}\{{\mathcal {I}}\}} \nonumber \\&=\frac{\!\varDelta \omega _1\!-\!\frac{3\gamma _1}{8\omega _1}a_{1ss}^2\!-\!\left( \!\frac{\alpha }{8\omega _{1}}\!\right) ^2\!\left( \!\frac{\varDelta \omega _2}{\varGamma _2^2\!+\!\varDelta \omega _2^2}\!\right) \! a_{1ss}^4 \!}{\varGamma _1+\left( \frac{\alpha }{8\omega _{1}}\right) ^2\left( \frac{\varGamma _2}{\varGamma _2^2+\varDelta \omega _2^2}\right) a_{1ss}^4}. \end{aligned}$$

(31)

Note that we replaced the drive frequency $\omega _F$ with the eigenfrequency of the first mode $\omega _1$ in Eqs. (30)-(31), since it leads to higher-order corrections that can be ignored in the first-order approximation.

The above steady-state conditions take advantage of the linearity of the second mode, $\gamma _2=0$, and do not require adiabaticity. Thus, the structure of the frequency response curves will be identical in the adiabatic and diabatic cases, but the stabilities and bifurcations will generally differ, with the diabatic case being dynamically more complicated, as expected and described below.

To show the main effect of the IR, sample frequency response curves of $a_{1ss}$ are shown in Fig. 7, with coupling ($\alpha \ne 0$, black curves) and without coupling ($\alpha =0$, blue curves). The coupled and uncoupled response curves overlap outside of the IR zone but diverge near it in a form of nonlinear frequency repulsion (or veering, or anti-crossing). Note that due to the very light damping there are pairs of response curves that are very close to one another.

In the absence of mode coupling, $\alpha =0$, we obtain the amplitude response curve of a standard Duffing resonator (with a positive Duffing nonlinearity), which is shown by the dark blue curves in Fig. 7. These follow the usual backbone curve, which is computed from the conservative forces of the first mode and can be calculated by setting the real part of the impedance to zero ($\mathfrak {R}\{{\mathcal {I}}\}=0$), resulting in $\omega _{p}=\omega _1+3\gamma a_{1p}^2/(8\omega _1)$. The backbone curve is shown by the light blue dashed line in the Figure. The frequency response follows the backbone and monotonically increases with increasing frequency until the peak amplitude $a_{1p}$ is reached at the corresponding drive frequency $\omega _{p}$. The peak amplitude is given by $a_{1p}=F/(2\omega _1\varGamma _1)$ and is dictated by a balance of the non-conservative forces (specifically, the ratio between the external drive magnitude and the dissipation), and it can be calculated from Eq. (30) by setting the drive frequency in the impedance to the peak frequency ${\mathcal {I}}(\omega _{p})$. This peak condition, which occurs off scale in Fig. 7, occurs on the backbone curve.

Fig. 7

The steady-state mode 1 amplitude versus the normalized excitation frequency. The dark blue and black curves are the amplitude response with solid representing stable response and dashed representing unstable response. The backbone curve of the isolated mode 1 ($\alpha =0$) response is shown in the light blue dashed line. The black lines show the coupled-mode amplitude response with $\alpha =0.5$, where the insets are provided to show details about stability. The dashed gray curves are the corresponding backbone curves. The IR condition is shown by the red vertical line. Due to its non-monotonic behavior in the vicinity of the IR, the backbone curve of the coupled-mode case contains a zero-dispersion point, where $d\omega _p/da_{1p}=0$. Note that due to the hardening to softening transition below the IR, for this level of damping the response has three SN bifurcations near the IR and a corresponding frequency window of bistability. The system parameters are: $\varGamma _1=9.5\times 10^{-6},~\varGamma _2=2.5\times 10^{-5},~\omega _1=1,~\omega _2=3.1,~\gamma _1=0.5,~F=1.1\times 10^{-4}$

For nonzero coupling, $\alpha \ne 0$, the response becomes more intricate due to the presence of effective quintic nonlinearities in the reduced first-mode model. These are shown as black curves in Fig. 7. In particular, the coupled-mode backbone curve ($\mathfrak {R}\{{\mathcal {I}}\}=0$), shown as the gray dashed line in Fig. 7, yields the following bi-quadratic equation in $a_{1p}$

$$\begin{aligned}&\omega _{p}-\omega _1-\frac{3\gamma _1}{8\omega _1}a_{1p}^2-\left( \!\frac{\alpha }{8\omega _{1}}\!\right) ^2\nonumber \\&\qquad \frac{3\omega _{p}-\omega _2}{\varGamma _2^2+(3\omega _{p}-\omega _2)^2} a_{1p}^4 =0. \end{aligned}$$

(32)

Therefore, in contrast to the standard Duffing resonator, in this case it is possible that two different peak amplitudes can occur at the same peak frequency. When this occurs, it implies that the slope of the coupled-mode backbone curve changes sign. Furthermore, when $3\omega _p\approx \omega _2$ (i.e., in the vicinity of the IR), the highest-order nonlinear term (the coupling term) in the backbone curve equation [Eq. (32)] vanishes. Hence, there is a singular behavior in the vicinity of the IR condition that results in a frequency gap in which no peak frequency can be found. The effect of this gap is that the response curves terminate on either side of the IR in saddle node (SN) bifurcations (where the solid curves merge and terminate at the backbone). For any level of damping, resonant response (that is, on the upper branch of the Duffing response curve) at the drive frequency is not possible in the gap; more about this follows.

Inspection of the highest-order nonlinear frequency shift $\alpha ^2 a_{1p}^4(3\omega _{p}-\omega _2)/\{64\omega _{1}^2[\varGamma _2^2+(3\omega _{p}-\omega _2)^2]\}$ reveals that at one side of the IR, for which $3\omega _{p}-\omega _2<0$, the system has an effective softening nonlinearity, while on the other side of the IR, $3\omega _{p}-\omega _2>0$, the effective nonlinearity is hardening. This phenomenon is intimately related to the free response dynamics, which we described in subsection 3.1 where, due to the coupling, the system cannot sustain periodic vibrations in which the frequencies are close to a 1:3 ratio. Hence, the backbone curve of the coupled system admits a nonlinear version of anti-crossing of the frequencies, a classical analog to the quantum nonlinear Landau–Zener formula [107] that has been observed in mechanical systems [57, 108, 109].

Note that the frequency anti-crossing leads to a zero-dispersion (ZD) point in the frequency–amplitude relation, i.e., a vertical tangency on the backbone curve described by $d\omega _p/da_p=0$ for a nonzero amplitude (Fig. 7). Such a point is highly beneficial for phase noise reduction in closed-loop oscillators, as considered in Sect. 5.

In the adiabatic case, $\varGamma _1\ll \varGamma _2$, the second mode tracks the first mode and the dynamics are described by the reduced single-mode model

$$\begin{aligned} \dot{A}_1=&-(\varGamma _1+i\varDelta \omega _1)A_{1}+\frac{3i\gamma _1 }{2\omega _F}|A_1|^2A_{1}\nonumber \\&-\frac{\alpha ^{2}}{6\omega _{F}^2} (\varGamma _2+i\varDelta \omega _2)^{-1}|A_1|^4A_{1}- \frac{iF}{4\omega _{F}}. \end{aligned}$$

(33)

Here, the stability of the response curves is relatively straightforward, involving pairs of stable and unstable branches that merge at SN bifurcations on or near the backbone curves. Specifically, due to the relatively fast decay of the second mode, no dynamic energy exchange between the modes is possible, the result of which is that no Hopf bifurcations occur in this case. The stability of the response in the diabatic case is considered next.

4.1 Bifurcation analysis of the diabatic system

When the relaxation rates of the modes are not vastly different, we need to consider the dynamics of the second mode. This leads to new dynamical outcomes that are impossible in the adiabatic approximation, in particular, Hopf and SNIC bifurcations and the resulting dynamic energy transfer between the modes that result in amplitude modulations [23, 24, 31, 35, 45, 72,73,74,75,76, 86, 103]. The steady-state amplitudes and phases are identical to those of the adiabatic approximation, where $A_{1ss}$ is determined from Eq. (28) and $A_{2ss}=i\alpha A_{1ss}^3$ $/[6\omega _1(\varGamma _2+i\varDelta \omega _2)]$. Therefore, we can use these steady-state solutions with the fully coupled dynamic model to study the stability and local bifurcations of the steady-state responses of the diabatic system.

The stability analysis follows the standard approach in which one considers the linearized dynamics of small perturbations to the steady-state response. In the diabatic case, the system is four dimensional (in contrast to two dimensional in the adiabatic case), and this leads to the solution of the eigenvalues of a four-by-four matrix, described by a quartic equation, as described in more detail in Ref. [18]. As the device and/or excitation parameters are varied, it is found that both SN and Hopf bifurcations occur near the IR. Bifurcation conditions are determined by numerical solution of the steady-state amplitudes and phases and using these to evaluate SN and Hopf conditions on the eigenvalues. From this analysis, one can generate diagrams of the steady-state responses and their stability, as well as bifurcation diagrams.

Fig. 8

Bifurcation conditions and first-mode frequency responses derived from the model. System parameters are: $\varGamma _1=2\varGamma _2=0.001,\gamma _1=0.001, \alpha =0.0009,\omega _1=1,\omega _2=3.09$. Upper panel: Local bifurcation conditions in a normalized parameter space for the drive amplitude versus the drive frequency. Green curves are SN conditions, and red curves are Hopf bifurcation conditions. The light green segment SN3 is a SN condition for an already unstable steady-state response. Lower panel: Frequency response curves and bifurcation conditions for different levels of the drive amplitude. Solid (dashed) curves represent stable (unstable) responses. The inset shows details near the IR

To make a clear connection between a bifurcation diagram and the response curves, we show in Fig. 8 a bifurcation diagram and mode 1 frequency response plots for a sample set of parameters. The parameters are selected so that the system response is qualitatively the same as the device of Ref. [18]. However, for Fig. 8, we select significantly higher damping values, $\varGamma _1=2\varGamma _2=0.001$, in order to obtain better visibility of the different branches of the response curve. The upper panel of Fig. 8 shows the SN and Hopf bifurcation conditions in a normalized space of the driving amplitude versus the frequency detuning from resonance. The two green curves represent, outside of the IR region, the usual SN bifurcations associated with the Duffing model. Specifically, the upper green curve labeled as SN2 represents the SN on the lower part of the Duffing response curve since it occurs at a lower drive frequency. Similarly, curve SN1 represents the SN on the upper part of the Duffing response curve. In the vicinity of the IR, the bifurcation structure becomes quite complicated and involves Hopf bifurcations, shown as red curves. Note that the light green curve labeled as SN3 (it is really just a part of SN1) between Hopf branches is a bifurcation involving an already unstable steady state, therefore it will not be experimentally observable. Also, note that where Hopf branches meet SN branches, a double zero (DZ) condition exists, which corresponds to co-dimension two bifurcations that necessarily involve additional, non-local bifurcations not captured by the eigenvalue analysis [78].

We now consider frequency sweeps at different levels of drive amplitude F. To link the bifurcation diagram of Fig. 8(upper panel) to the system frequency response, we show in the lower panel of Fig. 8 samples of the frequency response for the first-mode steady-state amplitude for different levels of drive amplitude, along with SN (green) and Hopf (red) bifurcation conditions. In the frequency response curves of Fig. 8, solid (dashed) lines represent stable (unstable) steady-state responses. For very small values of F, below the cusp point C in Fig. 8(upper panel), the frequency response is essentially linear, without any bistability. This is verified by the lowest level frequency response curve depicted in Fig. 8(lower panel). For the next larger range of F values, the system behaves like the usual Duffing system, exhibiting bistability, also verified by the frequency response curves depicted in Fig. 8(lower panel). For the next larger range of F values, the SN1 curve in Fig. 8(upper panel), corresponding to the larger amplitude Duffing response branch, is encountered at a drive frequency much lower than anticipated by the Duffing response, due to the “bump” in the SN curves near the IR. The SN1 and SN3 branches merge at a DZ eigenvalue point labeled DZ1 in Fig. 8(upper panel), above which a Hopf branch emerges, labeled H2. For values of F above DZ1, the response encounters H2. For these ranges of F, after crossing SN1 or H2, a complicated sequence of bifurcations are encountered, including those that lead to amplitude modulated motions and even chaos. Generally, in this range of F, sweeping up in frequency leads to the SN1 or H2 bifurcation that does not allow the system to continue in the usual Duffing manner. As one sweeps down in frequency for this range of F values, the system encounters the H1 Hopf bifurcation. It is worth noting the that drive frequency corresponding to the SN1 and H2 bifurcations essentially saturates just before the IR, well below the expected Duffing SN1 condition. In fact, it was the experimental observation that the frequency response was interrupted at a nearly constant drive frequency, independent of the drive level, that first signaled the IR in the MNRs device described in Refs. [18, 30, 31, 70]. The dynamics in the IR gap can be very complicated, as partially explored below. At very large levels of F, even the SN2 branch can have Hopf segments, labeled as H3 and shown in both the upper and lower panels of Fig. 8.

Some general comments about this complicated picture of the response are in order. First, the reader is reminded that these bifurcations are for the slow flow equations so, for example, Hopf bifurcations lead to amplitude modulated equations in the original system. Also, there are several parameters that influence the bifurcation diagram and quite different bifurcation structures are possible. For example, as one varies the coupling parameter $\alpha$, the bifurcation diagram evolves from the simple Duffing picture to the one shown in the upper panel of Fig. 8 and can become even more complicated as $\alpha$ is increased further. Finally, as described next, the model and its complicated bifurcation structure are clearly observed in experiments.

To illustrate that this intricate bifurcation structure and its non-trivial dynamical consequence occur in a physical MNRs device, we reproduce in Fig. 9 the bifurcation diagram of Ref. [18], from the device shown in the lower panel of Fig. 1. The bifurcation diagram uses the same color scheme as Fig. 8(upper panel), but has a slightly different structure due to the differing damping levels and coupling coefficients.

Fig. 9

Theoretical and measured bifurcation diagrams with experimental parameters and data taken from Ref. [18] for the device depicted in the lower panel of Fig. 1. The upper panel shows an extended bifurcation diagram depicting the remarkable agreement between the model predictions from Eqs. (26)-(27) and the experimental results. The green solid curves are the predicted location of SN bifurcations; the dashed red curve is the predicted location of Hopf bifurcations; and the solid squares of various colors indicate the experimental data. The upper panel shows two green curves that correspond to the SN bifurcations of the usual Duffing resonator, the lower/upper of which corresponds to the SN at large/small amplitudes. The lower curve is interrupted by the IR, and the region in the vicinity of the IR is shown in detail in the lower panel, where the thin black vertical line indicates the location of the IR condition. For discussion in subsection 4.2, the left inset schematically depicts the phase space with stable/unstable (solid/open circles) constant amplitude responses to the left of the IR. The right inset schematically depicts the phase space with a limit cycle and no fixed amplitudes, beyond the SN, which corresponds to amplitude modulations that occur to the right of the IR; note that this is not a simple limit cycle as it exists in four dimensions and arises as part of a saddle-connection bifurcation in that space

The colors of the solid squares indicate different types of transitions, as follows. Black squares indicate the SN bifurcation encountered as the frequency is swept upward, showing both the usual Duffing situation and the IR. Some details of the IR transition beyond the SN are described below. The light blue squares indicate Hopf bifurcations encountered as the frequency is swept down from above the IR. The dark blue squares indicate Hopf bifurcations seen as the frequency is swept up. Of course, a “zoo” of bifurcations, including global bifurcations, occur in the IR zone, one of which is described below. Also, note that the range of drive amplitudes is limited by the experimental apparatus to the values shown, so that the upper parts of the bifurcation diagram cannot be explored.

We note that while the considered model is perhaps the most simplified for 1:3 IR [Eqs. (26)-(27)], it captures the intricate experimental bifurcation structure near the IR remarkably well. For example, the bifurcation conditions describe the regions of parameter space where the Duffing response is observed and where it breaks down and the manner in which it does so. Note that the IR causes a saturation of the SN bifurcations at a frequency close to one-third of the second mode, the low frequency boundary of the Duffing breakdown, which has implications for the closed-loop operation considered in Sect. 5. Additionally, note that the model describes bifurcations that are not experimentally accessible, e.g., curve SN3 in Fig. 8.

One interesting result of this IR is the creation of a gap in the excitation frequency near the IR, where stable oscillations cannot be sustained. For drive voltages above 15 mV and below 260 mV, as the driving frequency is increased through SN1, the amplitude of the resonator will decay to very small amplitudes (essentially, to the noise floor since the system is sufficiently far from resonance) and remain there as the frequency increases. Due to hysteresis, once this occurs, if the frequency is decreased, it will not recover oscillations until reaching SN2. This gap in the operating parameter space is created by the presence of mode coupling in the resonator, i.e., mode 2 drains mechanical energy from mode 1, reducing its amplitude to the point where oscillations at that frequency are unstable, thus causing the amplitude to drop to the lower branch of the resonant curve. If the excitation amplitude is above 260 mV and the frequency is increased through SN1, sustained motions with interesting amplitude modulations are observed, a behavior considered in detail in subsection 4.2.

It is important to note that in order to characterize a physical device with 1:3 (or 1:2) IR, one needs only to characterize the two modes in their uncoupled operation, including their Duffing nonlinearities, and then determine the single essential coupling coefficient, $\alpha$. In the device reported in [18, 31], this parameter was determined by a fit of the SN bifurcation curves. If one can a priori measure it in another way, say from ringdown measurements, this would allow one to predict the full driven response with good confidence.

4.2 Bifurcation generated frequency comb

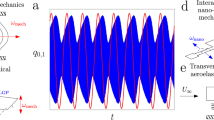
Here, we describe an interesting dynamic response that results from global features of the dynamical system that arise just beyond the SN1 transitions corresponding to the black squares. For sufficiently large driving amplitude (above the threshold of 260 mV) in the gap near the IR, the response does not transition to the lower branch beyond the SN, but exhibits complex periodic amplitude modulations, as shown in the upper panel of Fig. 10.

Fig. 10

Experimental amplitude modulation and its corresponding frequency comb. (Data are taken from Ref. [31].) Upper panel: Temporal amplitude response of mode 1 (blue) and mode 2 (red); the responses showing the fast–slow dynamics on the limit cycle (associated with the time scales $T_f$ and $T_s$, respectively), which correspond to periodic but non-harmonic modulations. Lower panel: Frequency spectrum of the temporal response measured in the upper panel showing the generation of a frequency comb

The timescale of these modulations is approximately 5(!) orders of magnitude larger than the drive period $2\pi /\omega _F$, and their period is observed to vary in a systematic manner as the excitation period is varied away from the SN1 point.⁴. From the upper panel of Fig. 10, we see that the amplitudes of modes 1 and 2 exhibit fluctuations with distinct transitions from quiescent spells of constant amplitude to periods of large modulations. In the frequency domain, this response results in a frequency comb with equidistant spacing of the spectral lines, as shown in lower panel of Fig. 10 and derived below. This transition from constant amplitude to periodic, harmonically rich, amplitude modulations is associated with a form of a SNIC bifurcation, also known as a saddle-node-loop, or SNL, bifurcation [110]. In the present system, as the drive frequency crosses the SN1 frequency, the stable and unstable fixed amplitude solutions annihilate one another and the amplitude starts to oscillate due to the generation of a periodic cycle near the bifurcation SN point [31]. The remnant, or ghost, of the SN1 bifurcation leads to slow passage through a bottleneck near its location in phase space (see insets of the lower panel in Fig. 9). Consequently, the period of the amplitude modulations T is composed from two timescales: $T_f$, the duration of the fast burst around the loop, and $T_s\propto (\omega _F-\omega _{SN})^{-1/2}$, the slow passage near the remnant of the SN, where $\omega _F-\omega _{SN}$ is the detuning of the frequency from the SN1/SNIC bifurcation [31]. The scaling of $T_s$ with the bifurcation parameter $(\omega _F-\omega _{SN})$ is generic for a saddle node bifurcation [111] and provides a convenient parameter for tuning the modulation period.

The transition from a usual SN to the SNIC bifurcation as the driving voltage is increased is due to a global bifurcation involving the saddle point involved in bifurcation SN1. Specifically, at a drive level near 260 mV, its one-dimensional unstable manifold becomes connected to the nearby stable node that is also involved in the SN1 bifurcation; see the insets in Fig. 9. This is part of a complicated set of bifurcations in the four-dimensional phase space that results in the periodic response shown in Fig. 10. While the SNIC bifurcation occurs at the SN1 condition, it requires a condition on the global system dynamics that is not captured by a simple, local, SN analysis.

To understand how the periodic fast–slow dynamics of the amplitude leads to a frequency comb, we briefly present the spectral analysis of the amplitude modulations. We derive an expression for the Fourier transform (FT) of a signal $x_{T}(t)$ consisting of train of identical bursts of general shape and duration $T_f$ that are separated by time segments of length $T_s$ of nearly constant response, resulting in a total period $T=T_s+T_f$. Note that as the SNIC bifurcation point is approached from above (in frequency), both the period T and duration $T_s$ approach infinity, while $T_f$ remains nearly constant. Here, the goal is to express the FT of this periodic signal in terms of the FT of an isolated burst and T. Such a relationship allows one to predict how the spectrum of the periodic response changes as parameters, and thus, T varies under the assumption that the burst shape does not change. We start by considering a single-burst signal $x_{T_f}(t)$ that is zero except in the interval $0< t < T_f$ and has a general shape in that interval. The FT of $x_{T_f}(t)$ is continuous and is expressed as

$$\begin{aligned} X_{T_f}(\varOmega )&=\int ^{\infty }_{-\infty }e^{-i\varOmega t}x_{T_f}(t)dt\nonumber \\&=\int ^{T_f}_{0}e^{-i\varOmega t}x_{T_f}(t)dt, \end{aligned}$$

(34)

which has a scale of $2\pi /T_f$ in the frequency domain. Next, we consider the T-periodic extension of $x_{T_f}(t)$, which can be expressed as $x_{T}(t)=\sum ^{\infty }_{k=-\infty } x_{T_f}(t-kT),$ and also as a Fourier series $x_{T}(t)=\sum ^{\infty }_{n=-\infty } c_n e^{in\omega _0 t}$, where $\omega _0=2\pi /T$ is the base frequency and the Fourier coefficients (FC) are given by

$$\begin{aligned} c_n&=\frac{1}{T}\int ^{T}_{0}e^{-in\omega _0 t}x_{T}(t)dt\nonumber \\&=\frac{1}{T}\int ^{T_f}_{0}e^{-in\omega _0 t}x_{T_f}(t)dt. \end{aligned}$$

(35)

Comparing Eq. (34) with Eq. (35) yields

$$\begin{aligned} c_n={T^{-1}}X_{T_f}(n\omega _0). \end{aligned}$$

(36)

Equation (36) shows that the FC of $x_T (t)$ are simply a discretized version of the FT of the single burst evaluated at the frequencies $n\omega _0$ and divided by T.

To make the relationship between the FTs of the isolated individual burst and the sequence of bursts explicit, we consider the inverse FT of $x_T (t)$ and compare it to its Fourier series

$$\begin{aligned} x_T(t)&=\frac{1}{2\pi }\int ^{\infty }_{-\infty }e^{-\varOmega t}X_{T}(\varOmega )d\varOmega =\sum ^{\infty }_{n=-\infty } c_n e^{in\omega _0 t}. \end{aligned}$$

(37)

Therefore, we find that

$$\begin{aligned} X_T(\varOmega )&=2\pi \sum ^{\infty }_{n=-\infty } c_n \delta (\varOmega -n\omega _0). \end{aligned}$$

(38)

Substituting Eq. (36) into Eq. (38), we find the following explicit connection between the FTs,

$$\begin{aligned} X_T(\varOmega )&=\omega _0\sum ^{\infty }_{n=-\infty } X_{T_f}(n\omega _0) \delta (\varOmega -n\omega _0). \end{aligned}$$

(39)

This is a discrete spectrum with spectral lines at $n\omega _0$ whose amplitudes are set by the continuous FT of the single burst $X_{T_f}(\varOmega )$ evaluated at those frequencies. In fact, as $T \rightarrow \infty ~(\omega _0 \rightarrow 0)$, the lines become closer together and $X_{T}(\varOmega )\rightarrow X_{T_f}(\varOmega )$. In terms of the spectrum shown in the lower panel of Fig. 10, this analysis shows that the envelope of the spectral peaks is determined by the shape of an individual burst, and that as the period of the signal is increased, this envelope is filled with more closely spaced peaks, approaching a continuous spectrum of the shape of the envelope in the limit $T \rightarrow \infty$.

This analysis demonstrates how one can tune the comb spacing by changing the system parameters, since the signal frequency $\omega _0$ varies continuously with the bifurcation parameter $(\omega _F-\omega _{SN})$. The range of tuning is, as noted above, limited by the noise level. Another important feature of this frequency comb is that it does not exhibit hysteresis; that is, it can be continuously varied over its tuning range without losing the signal, which requires resetting of the limit cycle. This highly desirable robustness stems from the inherent nature of the SNIC bifurcation. This is in contrast to other studies of frequency combs in MNRs, which are associated with amplitude modulated motions arising from Hopf bifurcations, which are generally hysteretic and therefore less robust to noise [35, 72,73,74,75,76].

5 Closed-loop operation—self-sustained response

Here, we consider a situation where a MNRs is used in a feedback loop in which its output is amplified (or attenuated, as appropriate) to a desired amplitude and phase shifted by a set amount, and this signal is fed back and used to drive the MNRs. The conditions of interest here are those that result in self-sustained oscillations of constant amplitude and frequency. We refer to this as closed-loop operation, which is commonly used to maintain resonant vibrations in sensors and time-keeping oscillators. It is important to note that in this case, the system has no externally imposed frequency. In fact, the parameters of the MNRs and the feedback loop elements determine the steady-state amplitude and frequency of the MNRs output, which is maintained near resonance.

In applications of MNRs-based self-sustained oscillators, frequency resolution is a key metric for precision and the level of frequency fluctuations is a key limitation on their performance [112]. Generally, to improve frequency stability, one operates the system such that the frequency-selective element, that is, the MNRs, vibrates at a large amplitude in order to attenuate the effects of thermal noise, thereby improving the signal-to-noise ratio. However, this amplitude is limited by the onset of nonlinear effects, where amplitude-to-frequency ($A-f$) noise conversion comes into play [113]. It has been known that noise spectra can be narrowed at certain amplitudes by reducing this effect, specifically by operating at a ZD point at which, local to the operating point, $A-f$ effects are eliminated, even though the operating point is well into the nonlinear regime. This has been suggested and analyzed as a means of reducing noise in self-sustained oscillators [92], and quite recently, this effect has been experimentally demonstrated [89]. These works utilize a ZD point associated with single-mode operation, in which the mode nonlinearity goes from hardening to softening, for example, as nonlinear effects transition from mechanical to electrostatic dominant sources [15, 88]. Here, we show how the ZD effects described above for open-loop operation of a coupled-mode IR system can also be realized in closed-loop operation, and how one can broaden the range of ZD effects by varying the strength of the intermodal coupling.

Frequency stabilization in a MNRs-based oscillator operating near an 1:3 IR was first experimentally demonstrated in Ref. [70]. As the amplifier output level was varied, the system exhibited hysteresis between single and dual mode operation, with both possible over a range of feedback conditions. A remarkable difference of $\sim 3$ orders of magnitude in the level of frequency fluctuations between the two operating conditions was measured [70]. The mechanism for this frequency stabilization is that the coupled-mode dynamics exhibit a saturation phenomenon in which the operation frequency is nearly constant over a range of oscillator amplitudes. This effect, which is linked to the nature of the SN1 curve depicted in the upper panel of Fig. 9, results in a ZD condition. This provides a mechanism for reducing $A-f$ noise conversion in a system with an MNRs that has a purely hardening or softening nonlinearity. Clearly, this behavior is intimately related to the frequency anti-crossing associated with the IR. As shown in the following, there is another feature of IR that suppresses frequency noise: the inter-modal phase locking constraint that is inherent in IRs. This provides a separate mechanism for reducing frequency noise, similar to the case of coupled oscillators [114]. These two effects combine to achieve the reduction in frequency fluctuations.

To explicitly calculate the frequency noise reduction from the model, one needs to include noise effects and use stochastic methods, such as the method of stochastic averaging [115], which are outside the scope of this paper. However, a deterministic analysis enables one to uncover and understand the underlying mechanisms of the observed frequency stabilization. To this end, we consider the closed-loop version ($c_1=0,~c_2=1$) of Eqs. (7)-(8) with a linear secondary mode, $\gamma _2=0$,

$$\begin{aligned} {\dot{A}}_1=&-\varGamma _1A_{1}+\frac{3i\gamma _1 }{2\omega _F}|A_1|^2A_{1}+\frac{3i\alpha }{2\omega _{F}} A_2A_1^{*2}\nonumber \\&-\frac{iF}{4\omega _{F}} \frac{A_{1}}{|A_{1}|}e^{i\varDelta }, \end{aligned}$$

(40)

$$\begin{aligned} {\dot{A}}_2=&-(\varGamma _2+i\varDelta \omega _2)A_2+\frac{i\alpha }{6\omega _F}A_1^3. \end{aligned}$$

(41)

Again, we employ $A_j(t)=a_j(t) e^{i \phi _j(t)}/2$ to express the equations in terms of the amplitudes and phases,

$$\begin{aligned} \dot{a}_1&=-\varGamma _1 a_1+\frac{F}{2\omega _{1}}\sin \varDelta +\frac{3\alpha }{8\omega _1}a_2 a_1^2\sin \psi , \end{aligned}$$

(42)

$$\begin{aligned} {\dot{\phi }}_1&=\frac{1}{2\omega _1}\left( \frac{3\gamma _1}{4}a_1^2+\frac{3\alpha }{4}a_2 a_1\cos \psi -\frac{F\cos \varDelta }{a_1}\right) , \end{aligned}$$

(43)

$$\begin{aligned} \dot{a}_2&=-\varGamma _2 a_2-\frac{\alpha }{24\omega _1}a_1^3\sin \psi , \end{aligned}$$

(44)

$$\begin{aligned} {\dot{\phi }}_2&=-\varDelta \omega _2+\frac{\alpha }{24\omega _1}\frac{a_1^3}{a_2} \cos \psi . \end{aligned}$$

(45)

Note that in closed-loop operation, only the phase difference $\psi =3 \phi _1-\phi _2$ appears in the RHS of Eqs. (42)-(45), since there is no external drive to independently fix the individual phases. This free running nature of the phase of each mode is what leads to the inherent susceptibility of the system to fluctuations in frequency. For the analysis, it is convenient to replace Eqs. (43) and (45) with a single equation for the phase difference

$$\begin{aligned} {\dot{\psi }}=&\frac{9\gamma _1}{4\omega _1}a_1^2+\frac{9\alpha }{4\omega _1}a_2 a_1\left( 1-\frac{a_1^2}{27a_2^2}\right) \cos \psi \nonumber \\&-\frac{3F\cos \varDelta }{2\omega _1a_1}+\varDelta \omega _2. \end{aligned}$$

(46)

The desired steady-state operation has constant amplitudes for both modes and constant phase difference $\psi$. Corresponding to this operating state, we introduce ${\dot{\phi }}_{1ss}=\nu$ so that $\varOmega =\omega _1+\nu$ is the steady-state frequency of the first mode, and thus of the closed-loop oscillator. The second-mode phase is therefore given by ${\dot{\phi }}_{2ss}=3 \nu$ so that ${\dot{\psi }}=0$, as required for steady-state operation. We then set $\dot{a}_1=\dot{a}_2={\dot{\psi }}=0$ in Eqs. (42), (44), (46) and seek a solution ${\mathbf {u}}=(a_{1ss},~ a_{2ss},~\psi _{ss})^T$ to the corresponding algebraic equations. Again, the analysis is simplified since mode 2 is linear. By setting Eq. (44) to zero and Eq. (45) equal to $3 \nu$ and using $\sin \psi ^2+\cos ^2 \psi =1$, we find that

$$\begin{aligned} a_{2ss}=\alpha a_{1_{ss}}^3/(24\omega _1\sqrt{\varGamma _2^2+(3\nu +\varDelta \omega _2)^2}) \end{aligned}$$

and

$$\begin{aligned} \tan \psi _{ss}=-\varGamma _2/(3\nu +\varDelta \omega _2). \end{aligned}$$

Numerical solutions are required for a detailed analysis of $a_{1_{ss}}$, and thus the full response, but we can gain some insights by considering the oscillator frequency, which is given by the first-mode resonant frequency $\varOmega$. Using $a_2=a_{2ss}$ and $\psi =\psi _{ss}$ above in Eq. (43), $\varOmega$ can be expressed implicitly in terms of $a_{1ss}$ and the system parameters, as follows,

$$\begin{aligned} \varOmega =&\omega _1+\frac{3\gamma _1}{8\omega _1}a_{1ss}^2+\left( \!\frac{\alpha }{8\omega _{1}}\!\right) ^2\frac{3\varOmega -\omega _2}{\varGamma _2^2+(3\varOmega -\omega _2)^2} a_{1ss}^4\nonumber \\&-\frac{F\cos \varDelta }{2\omega _1 a_{1ss}}. \end{aligned}$$

(47)

Note that the peak amplitude is achieved in the closed-loop operation when the phase shift in the feedback is $\varDelta =\pi /2$ [i.e., all the energy from the feedback is directed toward amplitude enhancement; see Eq. (42)]. Therefore, the backbone condition, expressed in terms of the peak amplitude $a_{1p}$ at frequency $\varOmega _p$, is identical to that of open-loop operation [Eq. (32)], namely

$$\begin{aligned}&\varOmega _p-\omega _1-\frac{3\gamma _1}{8\omega _1}a_{1p}^2 \nonumber \\&\qquad -\left( \!\frac{\alpha }{8\omega _{1}}\!\right) ^2\frac{3\varOmega _p-\omega _2}{\varGamma _2^2+(3\varOmega _p-\omega _2)^2} a_{1p}^4=0. \end{aligned}$$

(48)

Hence, the closed-loop response also admits a ZD point at which $d\varOmega _p/da_{1p}=0$ (see Fig. 7), and by operating at that point, we can effectively eliminate the $A-f$ noise conversion. We next show that there can exist a range of very small dispersion near the ZD point, offering a more robust range of desirable operating conditions.

An explicit condition for the backbone curve is easily obtained by solving Eq. (48), the bi-quadratic equation for $a_{1p}$ in terms of $\varOmega _p$. The result is a pair of positive values for $a_{1p}$, and these merge at the ZD points. Setting to zero the discriminant of the $a_{1p}^2$ quadratic equation yields a pair of expressions for two values of $\varOmega _{ZD}$. These simplify significantly in the limit $\varGamma _2 \rightarrow 0$, to

$$\begin{aligned} \varOmega _{ZD}= \frac{4 \alpha ^2 \omega _1 + 9 \gamma _1^2 \omega _2}{4 \alpha ^2 + 27 \gamma _1^2}~,~\frac{\omega _2}{3}. \end{aligned}$$

Only the first (and smaller) of which yields a nonzero amplitude $(a_{1p}\ne 0)$ and hence is the ZD point of interest. This result also allows one to compute the frequency gap width as

$$\begin{aligned}{}[\![\omega ]\!]_{\mathrm{gap}}=\frac{\omega _2}{3}- \frac{4 \alpha ^2 \omega _1 + 9 \gamma _1^2 \omega _2}{4 \alpha ^2 + 27 \gamma _1^2}= -\frac{4 \alpha ^2 \varDelta \omega _2}{12 \alpha ^2 + 81 \gamma _1^2}, \end{aligned}$$

which is valid only for $\varDelta \omega _2=3 \omega _1-\omega _2<0$ and $\gamma _1>0$. (The other scenario of $\varDelta \omega _2>0$ will lead to a ZD point only for a softening first mode, $\gamma _1<0$.) Thus, the gap width $[\![\omega ]\!]_{\mathrm{gap}}$ varies from zero at $\alpha =0$ to $-\varDelta \omega _2/3$ as $\alpha \rightarrow \infty$. The $\varGamma _2=0$ steady-state amplitude at the ZD point of interest is found to be

$$\begin{aligned} a_{1_{ss},ZD}=4 \sqrt{3} \sqrt{\frac{-\gamma _1 \omega _1\varDelta \omega _2}{4 \alpha ^2 + 27 \gamma _1^2}}. \end{aligned}$$

Figure 11 shows backbone curves for sample values of the coupling strength, showing that the right limit of the gap is fixed, while the left limit, given by the ZD point of interest, moves to smaller frequencies and smaller amplitudes as the coupling strength increases. It is seen that for small values of the coupling strength the gap is, of course, smaller, and the system also has a broader, presumably more robust and effective, range of amplitudes with small dispersion. This may be useful in the design of systems that use this effect for frequency stabilization.

Fig. 11

Backbone curves, showing the relationship between closed-loop first-mode vibration amplitude and operating frequency, for different coupling strengths: $\alpha =10^{-4}$ (black), 0.1 (blue), 0.5 (magenta), and 1 (red). The system parameters are: $\varGamma _1=9.5\times 10^{-6},~\varGamma _2=2.5\times 10^{-5},~\omega _1=1,~\omega _2=3.1,~\gamma _1=0.5$

The second mechanism of frequency stabilization is the locking of the phase difference, which hybridizes the phases of the two modes, and therefore enables the system to clean the “noisy” phase of mode 1, which includes noise from the circuitry of the feedback loop in addition to thermal noise in the mechanical resonator, with the relatively “clean” phase of mode 2, which is largely uncoupled from the feedback loop since it is far off resonance. The analysis proceeds by first considering the dynamics of the phase difference $\psi$, and then features of the phase sum, from which one can glean the behavior of the phase of interest, $\phi _1$. To see how this mechanism works, we make the assumption that the phase dynamics are relatively slow in comparison with the amplitude dynamics, which is commonly the case in self-sustained oscillators [116,117,118,119,120]. Thus, Eq. (46) reduces to the well-known Adler equation [67],

$$\begin{aligned} {\dot{\psi }}=&\varDelta \varOmega +\kappa \cos \psi , \end{aligned}$$

(49)

where

$$\begin{aligned} \varDelta \varOmega =\frac{9\gamma _1}{4\omega _1}a_1^2-\frac{3F\cos \varDelta }{2\omega _1a_1}+\varDelta \omega _2,\\ \kappa =\frac{9\alpha }{4\omega _1}a_2 a_1\left( 1-\frac{a_1^2}{27a_2^2}\right) . \end{aligned}$$

The dynamics of the Adler equation can be mapped onto the motion of an overdamped particle trapped in a washboard potential, i.e., ${\dot{\psi }}=-d{\mathcal {V}}(\psi )/d\psi$, where ${\mathcal {V}}(\psi )=-\varDelta \varOmega \psi -\kappa \sin \psi$; see Fig.12. Thus, for a stable operating point ${\mathbf {u}}=(a_{1ss},~ a_{2ss},~\psi _{ss})^T$, where $|\varDelta \varOmega |<|\kappa |$, the phase difference $\psi$ will remain at one of the minima of the potential and will rattle back and forth due to the presence of noise $\eta _{\psi }(t)$, with small and confined variance (Fig.12).

Fig. 12

Qualitative view of the phase-difference fluctuations. The phase-difference fluctuations are associated with the motion of a randomly forced overdamped particle trapped in a washboard potential. Therefore, the variance of $\psi$ is small and confined, in contrast to the strongly diffusive random walk motion of the individual mode phases $\phi _{1,2}$

The phase of mode 1, $\phi _1$, is a linear combination of the phase difference, $\psi$, and the phase sum, $\varphi =\phi _1+\phi _2$, as

$$\begin{aligned} \phi _1&=\frac{1}{4}(\psi +\varphi ). \end{aligned}$$

(50)

In contrast to the phase difference $\psi$, which has a stabilizing restoring force $-d{\mathcal {V}}(\psi )/d\psi$, the phase sum $\varphi$ is unconstrained and runs freely with a variance that increases linearly in time. However, it is affected by both $\phi _1$ and $\phi _2$, where $\phi _2$ is far less noisy than $\phi _1$ since it is purely mechanical and unexposed to the noise that stems from the circuitry of the feedback loop. Hence, the noise of $\phi _2$ can be neglected in the noise of the phase sum $\varphi$. Moreover, due to the 3:1 ratio between $\phi _1$ and $\phi _2$ [Eq. (50)], the effective noise intensity [115] of the coupled-mode 1 response is approximately (when neglecting also the phase diffusion of $\psi$) sixteen times smaller than the noise of the uncoupled version of mode 1,

$$\begin{aligned} D_{\phi _1}^{\mathrm{coupled}}&=\left( \frac{1}{4} \right) ^2[D_{\psi }+D_{\varphi }]\approx \left( \frac{1}{4} \right) ^2D_{\phi _1}^{\mathrm{uncoupled}}. \end{aligned}$$

(51)

It is these two effects, the reduction of $A-f$ conversion due to ZD and the phase constraint, that are responsible for the dramatic reduction in frequency fluctuations measured when operating in IR [70]. The fundamental knowledge presented here will be essential if one is to design self-sustaining oscillators that exploit IR for noise reduction. This has yet to occur in commercial devices, but the idea is quite compelling given the importance of frequency stability in sensing and time-keeping applications.

6 Conclusion

The sampling of results presented here is biased toward the interests and activities of the authors in the area of IR in MNRs. There are many groups working in this area, and several papers have recently appeared that describe interesting dynamics of these systems. Most of these studies are experimental observations, and some are backed up by models and simulations, but most often without any detailed analysis. It is hoped that the successes of modeling and analysis done in support of experimental work, such as those described herein, will motivate others to make use of the tools of nonlinear dynamics, not only to describe what is observed, but to gain a deeper understanding of the underlying sources of these rich dynamics. This approach also allows one to explore new phenomena and applications using mathematical models, which complements the essential exploratory work of experimentalists.

The model employed does a remarkable job in capturing the dynamics associated with the 1:3 IR, in spite of the fact that it neglects the dispersive coupling term that appears in the formal version of the attendant normal form. The included coupling term, which promotes inter-modal energy exchange, appears to be sufficient for capturing the dynamics of the devices of interest. This observation raises an interesting issue about the relevance of normal forms for predicting and describing the nonlinear response of physical systems, namely how one decides which terms in a normal form are really essential. This subject deserves consideration from a mathematical view, with physics in mind.

In order to utilize IR in devices, it is interesting to consider how one might design for desired IR features. This is part of the general topic of designing nonlinearity into MNRs. The design and tuning of single-mode Duffing-like nonlinearity using mechanics, electrostatics, and material properties have received quite a bit of attention, cf. [10, 88, 121]. However, there are very few studies that describe the design of the coupling nonlinearity in structures, as needed to design for IR. Here, knowledge of the associated normal forms makes such an approach possible, since it focuses the design on a relatively small number of parameters [40, 122, 123]. Refinement of computational tools, in conjunction with a good understanding of nonlinear dynamics, should allow for the eventual implementation of IR in applications.

In terms of future developments, there will, of course, be new phenomena uncovered in experiments, as researchers push MNRs into new operating realms. Many of these groups will be motivated to observe dynamics at low temperatures, to the point where quantum behavior will emerge. The nature of nonlinear dynamics in the quantum domain is a topic of current and envisioned research, cf. [49, 55, 124, 125], and it seems quite natural that IRs in the quantum domain will become a research topic of interest. Another topic of interest is the development of methods for characterizing IR models. Previous work has used ad hoc fitting methods, cf. [31], but there are no doubt other, less cumbersome, methods, for example, using ringdown properties. Such methods could utilize a set of measured transient responses that activate the IR and from which one could distill normal form coefficients by comparing the response to model predictions.