A parametric study of an unbalanced Jeffcott rotor supported by a rolling-element bearing

Abstract

Rolling-element bearings are widely used in industrial rotating machines, and hence there is a strong need to accurately predict their influence on the response of such systems. However, this can be challenging due to an interaction between the dynamics of the rotor and the bearing nonlinearities, and it becomes difficult to provide a physical explanation for the nonlinear response. A novel approach, combining a Jeffcott rotor supported by a detailed bearing model with the generalised harmonic balance method, is presented, enabling an in-depth study of the complex rotor–stator interaction. This allows the quasi-periodic response of the rotor, due to variable compliance, to be captured, and the impact of clearance, ring and stator compliance, and centrifugal loading of the bearing on the response to be investigated. A strongly nonlinear response was observed due to the bearing, leading to large shifts in frequency as the excitation amplitude was increased, and the emergence of stable and unstable operating regions. The variable compliance effect generated sub-synchronous forcing, which led to sub-resonances when the ball pass frequency coincided with the frequency of one of the modes. Radial clearance in the bearing had by far the largest influence on the unbalance response, the self-excitation due to variable compliance, and the stability. Introducing outer ring compliance was found to slightly soften the system, and centrifugal loading on the bearing elements marginally increased the system’s region of instability, but neither of these effects had a significant impact on the response for the investigated bearing. When the bearing was mounted on a sufficiently compliant stator, the system was found to behave linearly.

1 Introduction

Rotating machines are used in a wide variety of applications, ranging from large-scale power-generation and aero-engines, to small-scale consumer goods such as computer hard drives. Vibration in such rotating systems can lead to performance reduction, malfunction, or even catastrophic failure. Consequently, there has been a strong research focus on modelling and understanding their dynamic behaviour, and the fundamental theory is now well established. One of the first attempts to model a simple rotor system was introduced by Jeffcott [1] more than a century ago, consisting of a single rotor connected to ground via a bearing. The rotor is assumed to move only in-plane, but is sufficient to investigate the unbalance response of the rotor, and can display resonance at certain critical speeds. Consequently, this model has become a useful test case for the development of new modelling and analysis techniques.

Every rotating machine is supported by bearings of some form, which allow free rotation and transfer loads to the stator. They are a key source of both compliance and damping in the system and therefore have a large influence on the response of the rotor [2, 3]. Rolling-element bearings (REB) are one of the most widely used types of bearing in heavy machinery, because of their high load capacity and low friction [4]. Every REB consists of the same key components: multiple rolling elements, a cage which holds them, and finally inner and outer races on which the elements roll. The elements can be either spherical or cylindrical, termed “ball” and “roller’ bearings, respectively, where balls are additionally free to pivot about the contact. In most the basic bearing models, the bearings will be represented with linear springs and dampers [2, 3],enabling conventional modal analysis. However, due to the complexity of REBs, this is a gross simplification which has led to the introduction of a large range of more advanced bearing models [5], most of which are based on the quasi-static approach originally presented in [6].

Clearance is one of the largest sources of nonlinearity in a bearing [7,8,9,10], caused by a gap opening up between the elements and races. Bearings are often preloaded in some way, to prevent this from occurring, but this is not always possible. It is simple to incorporate axial and radial clearance into existing models [11, 12], and these have been used to show that the clearance can unload some of the elements [13], amplify the radial and axial coupling [14], and even introduce local instability for very loose bearings [15]. Nonlinear dynamic analyses have shown that the clearance can lead to changes in the resonant frequencies of a rotor system as well as introduce jump phenomena [16]. In the extreme case chaotic responses can be observed [17, 18], which are heavily dependent on the applied axial preload [19]. Although the impact of the bearing clearance on the rotor response is well recorded in the literature, there is only a limited physical understanding of the underlying physical mechanisms that drive these phenomena.

The rings of the bearing are often considered as rigid [11], but it has been shown that ring compliance can significantly change the load distribution between the rolling elements [20] leading to a reduction in the peak ball load [21, 22]. Several different approaches have been developed to include this effect in bearing models, including the introduction of springs in series for each element [22], reduced order models [21, 23], and high-order FE models [24]. However, little is known about the influence in rotor-bearing systems. It has been shown that ring flexibility can attenuate the higher harmonics in the response [25], but this effect is otherwise often neglected.

If the rotor system operates at high speeds, the dynamic loads on the bearing elements, including centrifugal loads and gyroscopic moments [6, 11], can significantly change the bearing stiffness [11]. These loads can lead to a reduction in the bearing stiffness with increasing speed [26] and an increase in the effective clearance [27]. A few studies have included such dynamic loads when investigating the nonlinear dynamics of a rotor system [28,29,30,31], but no comparison was made between the behaviour with and without them. Therefore, there is little understanding of the specific influence of these dynamic loads.

When modelling a rotor system, the structure supporting the bearing, known as the stator, is often assumed to be rigid. However, in real applications, the rotor is typically integrated into some larger flexible system, such as the casing around an aero-engine, which introduces additional compliance to the system and potentially modifies the influence of any bearing nonlinearities. Lim et al. investigated the response of plate-shaft systems using a linearised analysis and were able to accurately predict the vibration transmission [12, 15]. Sinou investigated the nonlinear response of a flexible rotor, where each bearing was supported by compliant supports [32], and various nonlinear effects such as sub- and super-harmonic responses were observed. However, the properties of the support structure were kept constant in these studies and consequently did not provide a physical understanding of the interaction with the bearing nonlinearities.

The combination of the above bearing features leads to a strongly nonlinear bearing stiffness, which strongly influences the response of a rotor-bearing system. However, the stiffness will also depend on the angular position of the elements so will vary as the cage rotates. This “variable compliance” (VC) [4] can introduce extra harmonics into the response of the rotor system [30, 33,34,35], or even lead to chaotic behaviour [30, 36, 37]. It has been shown that VC can be neglected when there is a large radial load on the bearing [13], in which case an alternative integral-based model can be used [38,39,40], but this is no longer the case when there is large dynamic loading from a rotor unbalance [41].

In order to study the effect of different bearing nonlinearities on a rotating system in an isolated manner, the basic Jeffcott rotor has been, and still is, widely used in the literature due to its simplicity and ease of computation [42]. A variety of numerical techniques have been employed to obtain the vibration response of such systems, where the most common approach is time-integration of the equations of motion [19, 25, 27, 30, 34,35,36,37]. This approach allows all forms of nonlinear dynamic response to be captured, including chaos, but it comes at high computational cost, which somewhat limits its use. Alternatively, the nonlinear unbalance response of the rotor system can be obtained by the harmonic balance method (HBM) [10, 16, 32, 43] which allows periodic responses to be captured very efficiently. However, conventional HBM cannot capture quasi-periodic responses, and therefore recent studies have neglected VC to ensure the response remains periodic. The generalised HBM (GHBM) overcomes this limitation and is able to additionally capture quasi-periodic responses very efficiently [44,45,46]. This technique has been recently applied to a dual-shaft system with REBs [47].

The effect of rolling-element bearings on the nonlinear dynamic response of a rotor system has been studied in great detail, but little attention has been paid to the influence of the different physical mechanisms. Previous studies have also been limited by the available numerical techniques, and often only individual effects were investigated. This paper will combine a high fidelity rolling-element bearing model with a simple unbalanced Jeffcott rotor, to study the influence of the bearing on the nonlinear dynamic response of the system. The GHBM will be applied in a novel way to include the effect of variable compliance in the prediction of the nonlinear dynamic response. An extensive parameter study will be performed to identify the influence of the different physical effects in the bearing and provide explanations for the observed behaviour of the rotor system.

2 Bearing model

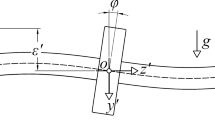
To accurately predict the nonlinear dynamic response of a rotor system supported by rolling-element bearings, a detailed bearing model is required that can capture its time-varying stiffness, as well as the influence of features such as clearance, ring compliance, and dynamic loading on the elements, whilst remaining fast to evaluate. The presented bearing model is based on the well-established approach first introduced by Jones [6] but will be simplified to consider only the case of deep groove ball bearings. These bearings typically consist of a single row of spherical elements held in place by a cage and are designed to resist primarily radial load. If the bearing is only loaded radially, it can be assumed without loss of accuracy that the contacts will remain collinear, since the rings will only move in plane. The number of bearing elements will be denoted by Z, and the key dimensions are defined in Fig. 1.

Fig. 1

Bearing dimensions

The values are shown for a SKF6002 bearing in Table 1. This particular bearing was chosen as it has already been examined in the literature by multiple authors [18, 28, 34, 48] and has known parameters. The radial clearance is denoted by $c_\mathrm{r}$, but this can vary depending on the bearing. Small clearance corresponds to the SKF designation C2, whereas large clearance corresponds to C5.

Table 1 SKF 6002 dimensions.

2.1 Kinematics

In order to compute the bearing forces, the displacements between all the involved components must be defined. It will be assumed that the elements remain evenly distributed around the circumference since they are adequately constrained by the cage [6].

With reference to Fig. 2a, the angular position of each ball $\psi _j$ is given by [32, 34]:

$$\begin{aligned} \psi _j = (j-1)\varDelta \psi + \psi _\mathrm{c} \end{aligned}$$

(1)

where $\psi _\mathrm{c}$ is the angle through which the cage has rotated from its initial position. This is zero when the first element is directly under the bearing centre. The angle between each adjacent pair of elements is denoted by $\varDelta \psi = \frac{2\pi }{Z}$.

The cage rotation speed ${\dot{\psi }}_\mathrm{c}$ linearly depends on the rotation speed of the inner and outer rings, denoted by $\varOmega _\mathrm{i}$ and $\varOmega _\mathrm{o}$:

$$\begin{aligned} {\dot{\psi }}_\mathrm{c} = (1-\gamma ) \varOmega _\mathrm{o} + \gamma \varOmega _\mathrm{i} \end{aligned}$$

(2)

where the speed ratio $\gamma$ relates the shaft speeds to the cage speed. This is given by [4]:

$$\begin{aligned} \gamma = \frac{1}{2} \left( 1 - \frac{D}{d_m} \right) \end{aligned}$$

This ratio has a value of $\gamma = 0.40$ for the SKF6002 bearing considered in this study. If the rotational speeds of the rings remain constant, then the cage rotation speed, ${\dot{\psi }}_\mathrm{c}$, will also remain constant so that $\psi _\mathrm{c} = {\dot{\psi }}_\mathrm{c} t$. In most applications, either the inner or outer rings will be fixed to the stator, which means $\varOmega _\mathrm{i}$ or $\varOmega _\mathrm{o}$ can be set to zero, respectively.

The bearing deflections $x_\mathrm{b}$ and $y_\mathrm{b}$ shown in Fig. 2b are defined as the inner ring relative to the outer ring. This means the outer ring can be considered fixed for the remainder of the derivation of the bearing properties [11, 12]. However, this is without loss of generality, since the values of $x_\mathrm{b}$ and $y_\mathrm{b}$ are equally sensitive to movements of either ring.

In order to determine the contact deflections at the jth element, it is necessary to first compute the radial ring deflection $r(\psi )$ around the bearing which is given by [12]:

$$\begin{aligned} r(\psi ) = x_\mathrm{b} \sin {\psi } - y_\mathrm{b} \cos {\psi } - c_\mathrm{r} \end{aligned}$$

(3)

where $c_\mathrm{r}$ is the radial clearance, which can be positive or negative, corresponding to a loose or radially preloaded bearing, respectively. With reference to Fig. 2b, the deflections at the inner, $\delta ^\mathrm{i}_j$, and outer, $\delta ^\mathrm{o}_j$, contacts can then be expressed as:

$$\begin{aligned} \delta ^\mathrm{i}_j&= r(\psi _j) - v^\mathrm{i}_j - u_j \end{aligned}$$

(4)

$$\begin{aligned} \delta ^\mathrm{o}_j&= - v^\mathrm{o}_j + u_j \end{aligned}$$

(5)

where $v^\mathrm{i}_j$ and $v^\mathrm{o}_j$ are the ring deformations at each contact due to their compliance, and $u_j$ is the radial deflection of each element as depicted in Fig. 2b. The total contact deflection is given by the sum of (4) and (5):

$$\begin{aligned} \delta _j = \delta ^\mathrm{i}_j + \delta ^\mathrm{o}_j = r(\psi _j) - \left( v^\mathrm{i}_j + v^\mathrm{o}_j\right) \end{aligned}$$

(6)

It should be noted that this eliminates the elemental deflection $u_j$ and consequently the deflection $\delta _j$ depends only on the ring deflection $r(\psi _j)$ and the ring compliance deformations $v^\mathrm{e}_j$. With all the contact deflections defined, the contact forces can now be evaluated.

Fig. 2

Bearing forces and geometry

2.2 Contact forces

The contacts between the balls and the races are assumed to be Hertzian, so that the ball loads $Q^\mathrm{e}$ can be computed from [19]:

$$\begin{aligned} Q^\mathrm{e}_j = C_\mathrm{e} \left[ \delta ^\mathrm{e}_j \right] ^n_+ \end{aligned}$$

(7)

where the subscript e denotes the race under consideration and can be replaced with either i for the inner, and o for the outer race.

The constant $C_\mathrm{e}$ is the Hertzian contact stiffness constant of the race and $[\cdot ]_+$ denotes saturation to positive values and ensures that there are no attractive contact forces. The local stiffness of each Hertzian contact can then be found from the relationship:

$$\begin{aligned} \frac{\partial Q^\mathrm{e}_j}{\partial \delta ^\mathrm{e}} = C_\mathrm{e} n \left[ \delta ^\mathrm{e}_j \right] ^{n-1}_+ \end{aligned}$$

(8)

The values of the inner and outer race contact stiffness parameters for the SKF6002 bearing considered in this paper were obtained from [48] and are given in Table 2.

Table 2 SKF 6002 contact parameters.

2.3 Equilibrium

The interaction between the two rings and the elements, considering a wide range of effects, can be described by enforcing the radial equilibrium of the jth ball and the rings:

$$\begin{aligned}&Q^\mathrm{i}_j - Q^\mathrm{o}_j + F^\mathrm{c}_j = 0 \end{aligned}$$

(9)

$$\begin{aligned}&Q^\mathrm{e}_j - N^\mathrm{e}_j = 0 \end{aligned}$$

(10)

where $Q^\mathrm{e}_j$ are the contact loads, $N^\mathrm{e}_j$ are the radial loads reacted by the rings, and $F^\mathrm{c}$ are the centrifugal loads on each element as shown in Fig. 2b.

Now that the contact loads and stiffnesses have been defined, attention can move onto determining the load and stiffness at each element.

2.4 Elemental load and stiffness

The last step before computing the bearing loads and stiffness is to solve for the unknown deflections $u_j$, $v^\mathrm{i}_j$, and $v^\mathrm{o}_j$, when then allows the bearing loads to be computed. In this section, it will be demonstrated how to solve for these unknowns, so that it is then possible to express the contact loads as a function of the ring deflection $r(\psi _j)$only:

$$\begin{aligned} Q^\mathrm{e} = h_\mathrm{e}\left( r(\psi )\right) \end{aligned}$$

where the subscript j has been neglected for brevity. This notation will be maintained for the remainder of this section. The function $h_\mathrm{e}(r)$ defines what will be referred to as the “elemental compliance model”. This expression can be substituted into the equilibrium relation (9) and differentiated with respect to r to give:

$$\begin{aligned} K = h'_\mathrm{i}\left( r(\psi )\right) = h'_\mathrm{o}\left( r(\psi )\right) \end{aligned}$$

which is the total elemental stiffness and is the stiffness of the inner contact, outer contact, and rings in series with each other. It can be observed that this property is the same at either ring.

In the following sections, different types of elemental compliance model will be derived, based upon different assumptions.

2.4.1 Simplified model

If the centrifugal loads are neglected so that $F^\mathrm{c}=0$, it can be seen from (9) that the inner and outer contact loads must be equal. In this case the contacts can be combined, so that the contact loads can be computed directly:

$$\begin{aligned} Q = Q^\mathrm{i} = Q^\mathrm{o} = C \left[ \delta \right] ^n_+ \end{aligned}$$

(11)

where the parameter C is the combined Hertzian coefficient of the inner and outer race contacts given by [4]:

$$\begin{aligned} C = \left( C_\mathrm{i}^{-\frac{1}{n}} + C_\mathrm{o}^{-\frac{1}{n}} \right) ^{-\frac{1}{n}} \end{aligned}$$

and $\delta$ is the total contact deflection from (6). If it is assumed that ring compliance is negligible so $v^\mathrm{e} = 0$, then it can be seen from (6) that $\delta = r$.

The elemental stiffness can be found by differentiating (11) this relation with respect to r:

$$\begin{aligned} K = \frac{\partial Q}{\partial r} = \frac{\partial Q}{\partial \delta } = C n \left[ \delta \right] ^{n-1}_+ \end{aligned}$$

(12)

Thus, (11) and (12) yield a fully defined elemental compliance model, which will be fast to evaluate. However, this model may give inaccurate results if the ring compliance or centrifugal loading become significant, in which case a more complex solution process is required. This will be introduced in the following sections.

2.4.2 Ring compliance

If ring compliance is to be included in the model, the value of the ring deflections $v^\mathrm{e}$ in Eq. 6 is an unknown to be found. A simplified ring compliance model based on the recently presented work by Leontiev et al. [22] will be used here, where each ring is divided into Z segments of angle $\varDelta \psi$, one for each element in the bearing. Each segment is then allowed to deflect radially by a uniform amount $v^\mathrm{e}$, which leads to a deformation pattern similar to the one shown in Fig. 3. Under this assumption, the radial load $N^\mathrm{e}$ can then be computed [22]:

$$\begin{aligned} N^\mathrm{e} = \left[ \frac{E A_\mathrm{e} v^\mathrm{e}}{R_\mathrm{e}} + \frac{E I_\mathrm{e} v^\mathrm{e}}{\left( R_\mathrm{e} \mp v^\mathrm{e}\right) ^3} \right] \varDelta \psi \end{aligned}$$

(13)

Fig. 3

Ring compliance model from [22]

where E is the Young’s Modulus, A is the area and I is the second moment of area of the outer ring. The first term in (13) is due to circumferential compression of the ring, and the second is due to the change in radius of the curvature where the negative sign applies for the case of the inner ring (e = i), and the positive sign applies for the case of the outer ring (e = o). The race radius $R_\mathrm{e}$ can be calculated from:

$$\begin{aligned} R_\mathrm{e} = \frac{d_m \mp \left( D + c_\mathrm{r}\right) }{2} \end{aligned}$$

Differentiating Eq. 13 with regards to the radial displacement $v^\mathrm{e}$ leads to an expression for the ring stiffness for the segment:

$$\begin{aligned} \frac{\partial N^\mathrm{e}}{\partial v^\mathrm{e}} = \left[ \frac{E A_\mathrm{e}}{R_\mathrm{e}} + \frac{E I_\mathrm{e}}{\left( R_\mathrm{e}\!\mp \!v^\mathrm{e} \right) ^3} \left( 1 \mp \frac{3 v^\mathrm{e}}{R_\mathrm{e}\!\mp \!v^\mathrm{e}}\right) \right] \varDelta \psi \end{aligned}$$

(14)

Since the effect of inner and outer ring compliance will be qualitatively very similar, it will be assumed that only the outer ring is compliant in this work, and consequently the inner ring deflections $v^\mathrm{i}$ will be set to zero but the outer ring deflections $v^\mathrm{o}$ must be computed. The outer ring cross-section will be approximated as rectangular with width B, and an effective thickness t, as shown in Fig. 3, which will be varied during the analysis. It will be assumed to be made of steel with Young’s modulus $E_\mathrm{steel} = {200}\,\hbox {GPa}$.

The contact loads will still be equal as in 2.4.1 since centrifugal loads are being neglected. This means the contact loads can be computed from (11), except that the total contact deflection $\delta$ from (6) now has a contribution from the compliance of the outer ring:

$$\begin{aligned} \delta = r - v_\mathrm{o} \end{aligned}$$

There is no contribution from the inner ring as it is assumed to be rigid.

In order to solve for the value of $v_\mathrm{o}$, Eqs. (11) and (13) describing the contact and ring forces, respectively, can be substituted into (10) to enforce ring equilibrium. This leads to a nonlinear algebraic equation in $v^\mathrm{o}$ which can be solved numerically using the Newton–Raphson method:

$$\begin{aligned} \left[ v^\mathrm{o}\right] _{k+1} = \left[ v^\mathrm{o}\right] _k + \left[ \frac{Q - N^\mathrm{o}}{\frac{\partial Q}{\partial \delta } +\frac{\partial N^\mathrm{o}}{\partial v^\mathrm{o}}}\right] _k. \end{aligned}$$

(15)

where the terms in the denominator can be found from (12) & (14), respectively. Starting from an initial guess $\left[ v^\mathrm{o}\right] _0 = 0$ only a few iterations were needed until the equilibrium equation in (10) was satisfied to a tolerance of ${1 \times 10^{-8}\,\hbox {N}}$.

Once the ring deflections and contact loads have been found, the stiffness can be computed from:

$$\begin{aligned} K = \left( \left[ \frac{\partial Q}{\partial \delta }\right] ^{-1} + \left[ \frac{\partial N^\mathrm{o}}{\partial v^\mathrm{o}}\right] ^{-1}\right) ^{-1} \end{aligned}$$

(16)

where there is now a contribution from the ring compliance. Equation 16 yields a much more accurate estimate of the contact stiffness than Eq. 12 when the rings are compliant.

2.4.3 Centrifugal loading

The rotation of the cage during operation generates an outward centrifugal load $F^\mathrm{c}$ on each element, given by [11]:

$$\begin{aligned} F^\mathrm{c} = \frac{1}{12} \rho \pi D^3 d_m {\dot{\psi }}_\mathrm{c}^2 \end{aligned}$$

(17)

where $\rho$ is the ball density, and ${\dot{\psi }}_\mathrm{c}$ is the rotation speed of the cage from (2). In this investigation it will be assumed that the balls are made of steel with $\rho = \rho _\mathrm{steel} = {7800}\,\hbox {kg m}^{-3}$.

The influence of centrifugal loads will only be considered for the case with rigid rings for which $v^\mathrm{e}=0$, so that the influence of the centrifugal loads can be studied in isolation. This has the additional benefit that it simplifies the analysis. However, it is possible that in real applications both effects could be significant.

In order to find the contact loads, the inner and outer contacts can no longer be combined as the contact loads will be unequal. Instead, Eq. (7) must be used, where the contact deflections $\delta ^\mathrm{e}$ from (4) & (5) reduce to:

$$\begin{aligned} \delta ^\mathrm{i}&= r - u \\ \delta ^\mathrm{o}&= u \end{aligned}$$

since the rings are assumed rigid so $v^\mathrm{i} = v^\mathrm{o} = 0$.

In order to solve for u, Eqs. (7) and (17) can be substituted into the equilibrium relation in (9) to yield an algebraic problem in the elemental deflection u. This can also be solved using a Newton–Raphson approach:

$$\begin{aligned} \left[ u\right] _{k+1} = \left[ u\right] _k + \left[ \frac{Q^\mathrm{i} + F^\mathrm{c} - Q^\mathrm{o}}{\frac{\partial Q^\mathrm{i}}{\partial \delta ^\mathrm{i}} + \frac{\partial Q^\mathrm{o}}{\partial \delta ^\mathrm{o}}}\right] _k. \end{aligned}$$

(18)

where the derivatives in the denominator are given in (8). This relation is iterated until the equilibrium equation in (9) is satisfied to a tolerance of $1 \times 10^{-8}\,\hbox {N}$. The initial guess $\left[ u\right] _0$ was set to the elemental deflection in case of no centrifugal loading:

$$\begin{aligned} \left[ u\right] _0 = \frac{C_\mathrm{o}^{\frac{1}{n}}}{C_\mathrm{i}^{\frac{1}{n}} + C_\mathrm{o}^{\frac{1}{n}}} \left[ r\right] _+ \end{aligned}$$

Once the elemental deflection has been found, the contact stiffness at each ring is simply determined by the stiffness of the Hertzian contacts in series with each other:

$$\begin{aligned} K = \left( \left[ \frac{\partial Q^\mathrm{i}}{\partial \delta ^\mathrm{i}}\right] ^{-1} + \left[ \frac{\partial Q^\mathrm{o}}{\partial \delta ^\mathrm{o}}\right] ^{-1}\right) ^{-1} \end{aligned}$$

(19)

Equation (19) gives a much more accurate estimate of the contact stiffness when the centrifugal loading on the elements is significant.

2.5 Time-varying load and stiffness

Once the contact loads $Q^\mathrm{e}_j$ and elemental stiffnesses $K_j$ have been evaluated using the appropriate elemental compliance model from Sect. 2.4, the total load on the inner ring, $\mathbf {f}^\mathrm{i}_\mathrm{b}$, and outer ring, $\mathbf {f}^\mathrm{o}_\mathrm{b}$, can be computed. The contributions from each element can be summed up, taking their angular position into account (see Fig. 2a):

$$\begin{aligned} \mathbf {f}^\mathrm{e}_\mathrm{b}(\mathbf {x}_\mathrm{b},\psi _\mathrm{c}) = \begin{bmatrix} f^\mathrm{e}_x \\ f^\mathrm{e}_y \end{bmatrix}= \sum _{j=1}^{Z} Q^\mathrm{e}_j \begin{bmatrix} \sin {\psi _j} \\ -\cos {\psi _j} \end{bmatrix} \end{aligned}$$

(20)

where $\mathbf {x}_\mathrm{b} = \begin{bmatrix} x_\mathrm{b}&y_\mathrm{b} \end{bmatrix}^\mathrm{T}$ is the bearing deflection vector. It should be noted that the total ring load, $\mathbf {f}^\mathrm{e}_\mathrm{b}$, depends on cage position and rotational speed due to variable compliance and centrifugal loading, respectively.

The bearing stiffness matrix $\mathbf {K}_\mathrm{b}$ can be found in a similar way by summing up all the previously introduced contributions from each element:

$$\begin{aligned}&\mathbf {K}_\mathrm{b}(\mathbf {x}_\mathrm{b},\psi _\mathrm{c}) = \begin{bmatrix} k_{xx} &{} k_{xy}\\ k_{yx} &{} k_{yy} \end{bmatrix} = \begin{bmatrix} \frac{\partial f^\mathrm{e}_x}{\partial x} &{} \frac{\partial f^\mathrm{e}_x}{\partial y}\\ \frac{\partial f^\mathrm{e}_y}{\partial x} &{} \frac{\partial f^\mathrm{e}_y}{\partial y} \end{bmatrix} \nonumber \\&\quad = \sum _{j=1}^{Z} K_j \begin{bmatrix} \sin ^2{\psi _j} &{} -\sin {\psi _j}\cos {\psi _j} \\ -\sin {\psi _j}\cos {\psi _j} &{} \cos ^2{\psi _j} \end{bmatrix} \end{aligned}$$

(21)

With expressions for the total load $\mathbf {f}^\mathrm{e}_\mathrm{b}$, and stiffness $\mathbf {K}_\mathrm{b}$, available, the bearing model is now fully described. However, both the load and stiffness depend on the cage angle $\psi _\mathrm{c}$ and will therefore vary over time which is known as “variable compliance” (VC). As an example, the variation of the horizontal, vertical, and cross-stiffnesses with cage angle has been plotted in Fig. 4, in the case that a constant vertical load is applied; the horizontal stiffness is typically at a maximum when there are elements either side of the bearing centre as shown in Fig. 4a, and the vertical stiffness is at a maximum when there is a ball directly under the bearing centre shown in Fig. 4b. The cross-stiffness is zero at both of these cage angles, because the elements are then symmetrically distributed either side of the vertical plane. However, it becomes non-zero at all other cage angles when the symmetry is broken. For this particular bearing, the horizontal stiffness was found to vary by around 20%, and the vertical stiffness by around 2%, so these effects are significant.

Due to the cyclic-symmetry of the cage, an element will pass a particular location at a frequency $\omega _\mathrm{BPF} = Z {\dot{\psi }}_\mathrm{c}$, which is known as the “ball pass frequency” (BPF). This is also the VC frequency at which the bearing load and stiffness will oscillate, which can lead to a harmonic forcing on the structures connected via the bearings, even without any external excitation. To identify the impact of this often neglected excitation source on the rotor-dynamic response, a particular focus will be placed on this behaviour during simulation.

Fig. 4

Variation of bearing stiffness with cage position

2.6 Average load and stiffness

Although the VC can be significant, the compliance oscillations are often ignored in the first instance, by computing the average load and stiffness in each direction. This decouples the influence of the bearing displacement $\mathbf {x}_\mathrm{b}$, from the influence of the cage angle $\psi _\mathrm{c}$, on the bearing load and stiffness [39, 40].

The average properties can be computed by considering the case of an infinite number of elements where the discrete ball locations $\psi _j$ are replaced with a continuous domain $\psi$ in the equations from Sects. 2.3 to 2.4.3. Denoting the deflection at each angle by $r(\psi )$, the load and stiffness per unit angle around the bearing can then be computed from:

$$\begin{aligned} {\bar{Q}}^\mathrm{e}\left( \psi \right)&= \frac{Z}{2\pi } h_\mathrm{e} \left( r\left( \psi \right) \right) \\ {\bar{K}}\left( \psi \right)&= \frac{Z}{2\pi } h'_\mathrm{e} \left( r\left( \psi \right) \right) \end{aligned}$$

where $h_\mathrm{e}\left( r\right)$ is the elemental compliance model being used from Sect. 2.4.

A comparison of this continuous load distribution, denoted by the shaded area, and the discrete element loads, shown by the arrows, is plotted in Fig. 5, for the same applied load. It can be observed that the load is more unevenly distributed when there are discrete elements, with those at the bottom of the bearing being most highly loaded in this particular example.

Using a Sjovall integral formulation [38], the average ring load $\bar{\mathbf {f}}^\mathrm{e}_\mathrm{b}$ can then be computed as follows:

$$\begin{aligned} \bar{\mathbf {f}}^\mathrm{e}_\mathrm{b}(\mathbf {x}_\mathrm{b}) = \begin{bmatrix} {\bar{f}}^\mathrm{e}_{x} \\ {\bar{f}}^\mathrm{e}_{y} \end{bmatrix} = \int _0^{2\pi } {\bar{Q}}^\mathrm{e}\left( \psi \right) \begin{bmatrix} \sin {\psi } \\ -\cos {\psi } \end{bmatrix} d\psi \end{aligned}$$

(22)

Fig. 5

Comparison of continuous load distributions and discrete element loads

and similarly the average stiffness matrix becomes:

$$\begin{aligned} \bar{\mathbf {K}}_\mathrm{b}(\mathbf {x}_\mathrm{b})= & {} \begin{bmatrix} {\bar{k}}_{xx} &{} {\bar{k}}_{xy}\\ {\bar{k}}_{yx} &{} k_{yy} \end{bmatrix} = \begin{bmatrix} \frac{\partial {\bar{f}}^\mathrm{e}_x}{\partial x} &{} \frac{\partial {\bar{f}}^\mathrm{e}_x}{\partial y}\\ \frac{\partial {\bar{f}}^\mathrm{e}_y}{\partial x} &{} \frac{\partial {\bar{f}}^\mathrm{e}_y}{\partial y} \end{bmatrix}\nonumber \\= & {} \int _0^{2\pi } {\bar{K}}(\psi ) \begin{bmatrix} \sin ^2{\psi } &{} -\sin {\psi }\cos {\psi } \\ -\sin {\psi }\cos {\psi } &{} \cos ^2{\psi } \end{bmatrix} d\psi \nonumber \\ \end{aligned}$$

(23)

The resulting average stiffnesses are shown in Fig. 4. With this formulation the average load and stiffness is independent of the cage position which simplifies the computation, but it comes at the cost of lost accuracy. However, this formulation still allows a dependence on cage speed, which will be the case when there is significant centrifugal loading.

2.7 Bearing damping

REBs also introduce some damping to the system. Energy can be dissipated through material damping in the elements and rings, friction at the contacts, or viscous losses in the lubricant. However, REBs are typically quite lightly damped components, so these effects are not as significant as those already introduced in this paper. For this reason, instead of a physical damping model, a simple viscous damping term $\mathbf {f}^\mathrm{e}_{b,d}$ will be added. The damping load on the inner ring is given by:

$$\begin{aligned} \mathbf {f}^\mathrm{e}_{b,d} = \begin{bmatrix} f^\mathrm{e}_{x} \\ f^\mathrm{e}_{y} \end{bmatrix}_d = \pm c_\mathrm{b} \begin{bmatrix} {\dot{x}}_\mathrm{b}\\ {\dot{y}}_\mathrm{b} \end{bmatrix} = \pm \mathbf {C}_\mathrm{b} \dot{\mathbf {x}}_\mathrm{b} \end{aligned}$$

where $\mathbf {C}_\mathrm{b} = c_\mathrm{b} \mathbf {I}$, and the positive sign is for the inner ring and the negative sign for the outer ring. The constant $c_\mathrm{b}$ is the viscous damping coefficient and was arbitrarily set to ${400}\,\mathrm{Nsm}^{-1}$ throughout, which is comparable to experimentally measured values for similar sized bearings [49].

This completes the derivation of the detailed bearing model, incorporating the effect of clearance, ring compliance centrifugal loads, and variable compliance. In the next section, the bearing model will be combined with a Jeffcott rotor model.

3 Jeffcott rotor

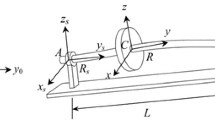
In order to assess the significance of the different bearing nonlinearities on a rotor-dynamic system, the response of a rigid Jeffcott rotor will be considered, as shown in Fig. 6. The rotor is assumed to spin at a constant speed $\varOmega$ and is supported by the SKF6002 bearing with the parameters from Tables 1 and 2 . Gyroscopic effects were not included. The bearing is connected to ground via linear spring and viscous damping elements, representing a generic support structure, similar to the configuration considered by Saito [16]. The horizontal and vertical deflections of the rotor centroid are denoted by $x_\mathrm{r}$ and $y_\mathrm{r}$, respectively, in Fig. 6 whilst the stator deflection is expressed by $x_\mathrm{s}$ and $y_\mathrm{s}$. The rotation angle of the rotor is denoted by $\varTheta = \varOmega t$. When the supports are rigid, the damping ratio is around 2% purely due to the bearing damping.

Fig. 6

Jeffcott rotor mounted on a REB

All the relevant parameters for the computation are summarised in Table 3.

Table 3 Baseline Jeffcott rotor parameters

3.1 Equations of motion

Describing the rotor and stator motion with vectors $\mathbf {x}_\mathrm{r} = \begin{bmatrix} x_\mathrm{r}&y_\mathrm{r} \end{bmatrix}^\mathrm{T}$ and $\mathbf {x}_\mathrm{s} = \begin{bmatrix} x_\mathrm{s}&y_\mathrm{s} \end{bmatrix}^\mathrm{T}$, respectively, the equations of motion of the rotor and stator can be written as:

$$\begin{aligned}&\mathbf {M}_\mathrm{r}\ddot{\mathbf {x}}_\mathrm{r} + \mathbf {C}_\mathrm{b} \left( \dot{\mathbf {x}}_\mathrm{r} - \dot{\mathbf {x}}_\mathrm{s} \right) + \mathbf {f}^\mathrm{i}_\mathrm{b}(\mathbf {x}_\mathrm{r}-\mathbf {x}_\mathrm{s},{\dot{\psi }}_\mathrm{c} t) = \mathbf {f}_\mathrm {ex}(t) \end{aligned}$$

(24)

$$\begin{aligned}&\begin{aligned} \mathbf {C}_\mathrm{s}\dot{\mathbf {x}}_\mathrm{s}&+ \mathbf {K}_\mathrm{s} \mathbf {x}_\mathrm{s} \\&- \mathbf {C}_\mathrm{b} \left( \dot{\mathbf {x}}_\mathrm{r} -\dot{\mathbf {x}}_\mathrm{s} \right) - \mathbf {f}^\mathrm{o}_\mathrm{b}(\mathbf {x}_\mathrm{r}-\mathbf {x}_\mathrm{s},{\dot{\psi }}_\mathrm{c} t) = \mathbf {0} \end{aligned} \end{aligned}$$

(25)

where $\mathbf {M}_\mathrm{r} = m_\mathrm{r} \mathbf {I}$, $\mathbf {C}_\mathrm{s} = c_\mathrm{s} \mathbf {I}$, and $\mathbf {K}_\mathrm{s} = k_\mathrm{s} \mathbf {I}$. The vectors $\mathbf {f}^\mathrm{i}_\mathrm{b}$ and $\mathbf {f}^\mathrm{o}_\mathrm{b}$ are the nonlinear bearing forces from (20), and the terms involving $\mathbf {C}_\mathrm{b}$ are due to the bearing damping. The vector $\mathbf {f}_\mathrm{ex}$ contains the external forces on the rotor. Equations (24) and (25) can then be combined to the general form:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {x}} + \mathbf {C}\dot{\mathbf {x}} + \mathbf {K}\mathbf {x} + \mathbf {f}_\mathrm{nl}\left( \mathbf {x}, t \right) = \mathbf {u}(t) \end{aligned}$$

(26)

where $\mathbf {M}$, $\mathbf {C}$, and $\mathbf {K}$ are the global mass, damping, and stiffness matrices, respectively, $\mathbf {x} = \begin{bmatrix} {\mathbf {x}_\mathrm{r}}^\mathrm{T}&{\mathbf {x}_\mathrm{s}}^\mathrm{T} \end{bmatrix}^\mathrm{T}$ is the global position vector and $\mathbf {u} = \begin{bmatrix} \mathbf {f}_\mathrm{ex}^\mathrm{T}&\mathbf {0} \end{bmatrix}^\mathrm{T}$ is the global excitation vector. The time dependence of the nonlinear forces $\mathbf {f}_\mathrm{nl}$ is being introduced by the variable compliance discussed in Sect. 2.5. To obtain the nonlinear dynamic response of the rotor system in the time domain, the equations of motion can be integrated using an ODE solver such as ode15s in MATLAB.

3.2 External forces

The rotor in Fig. 6 is excited by a small mass unbalance, which will be expressed in terms of an offset $\epsilon$ between the rotor centre of gravity (CoG) and centroid, leading to an unbalance force $f_\mathrm{ub} = m_\mathrm{r} \epsilon \varOmega ^2$. The rotor also experiences a static downward load $m_\mathrm{r} g$ due to its self-weight. The total force on the rotor $\mathbf {f}_\mathrm{ex}$ in (24) can therefore be written as:

$$\begin{aligned} \mathbf {f}_\mathrm{ex}(t) = \mathbf {f}_\mathrm{g} + \mathfrak {R}{\left( \mathbf {f}_\mathrm{ub} e^{i\varOmega t}\right) } \end{aligned}$$

(27)

where $\mathbf {f}_\mathrm{g} = \begin{bmatrix} 0&-m_\mathrm{r} g \end{bmatrix}^\mathrm{T}$ is due to the self-weight and $\mathbf {f}_\mathrm{ub} = f_\mathrm{ub} \begin{bmatrix} 1&-i \end{bmatrix}^\mathrm{T}$ represents the unbalance force.

3.3 Performance metrics

To quantify the vibration behaviour of the rotor, three different performance metrics will be used.

The first will be the synchronous transmissibility, denoted by $T_x$ & $T_y$, defined as the ratio between the unbalance force and the load transmitted to the stator. Mathematically, this can be written as:

$$\begin{aligned} T_x = \frac{\left\{ f^\mathrm{o}_x\right\} _\text {1X}}{f_u} \qquad \qquad T_y = \frac{\left\{ f^\mathrm{o}_y\right\} _\text {1X}}{f_u} \end{aligned}$$

where only the synchronous component of the stator load is included, denoted by the subscript 1X, since the unbalance excitation must be synchronous by definition. For a rotor mounted on rigid bearings, this metric would be unity; if the magnitude is less than unity, it indicates attenuation of vibrations; and if it is greater than unity, it suggests amplification The transmissibility will remain independent of the forcing amplitude if a system is linear, but this will no longer be true when nonlinearity is present in the system.

The second metric assesses the self-excitation due to the variable compliance effect in the bearing. This may excite both the rotor and stator, and in turn impact the overall dynamic behaviour. The performance metric used here will be the load transmitted to the stator at the BPF:

$$\begin{aligned} F^\mathrm{b}_x = \left\{ f^\mathrm{o}_x\right\} _\text {BPF} \qquad \qquad F^\mathrm{b}_y = \left\{ f^\mathrm{o}_y\right\} _\text {BPF} \end{aligned}$$

If the bearing had an infinite number of elements, or the average loads from Sect. 2.6 were used, this forcing would be 0 and hence no response would be expected at this frequency. However, if the time-varying loads from Sect. 2.5 are used, the load will vary as the cage rotates, leading to additional harmonic forcing and this metric will be non-zero.

The last metric is the position of the centre of the rotor orbit. This is given by the ${0}\,\hbox {Hz}$ component of the horizontal x, and vertical y components of the rotor response, denoted by the subscript DC:

$$\begin{aligned} {\bar{x}} = \left\{ x\right\} _\text {DC} \qquad \qquad {\bar{y}} = \left\{ y\right\} _\text {DC} \end{aligned}$$

For a linear system, this would not vary with excitation frequency or amplitude, since the response to static loads on the structure would be independent of the dynamic response. However, this is no longer true for nonlinear systems.

3.4 Summary

A model of a Jeffcott rotor supported by nonlinear bearings has been introduced. The presented physical bearing model allows the impact of a wide range of bearing parameters on the dynamic response of the system to be assessed, including the clearance, centrifugal loading, or ring compliance, whilst incorporating the variable compliance effect. However, due to the nonlinear nature, advanced numerical methods are required to analyse the frequency response in an efficient way.

4 Numerical methods

The equation of motion in (26) for the Jeffcott rotor has a nonlinear form, preventing the use of standard linear solution techniques to compute the response. Time domain solvers, such as ode15s in MATLAB, are widely used to solve such nonlinear equations, and although they are a powerful tool for capturing all forms of response, convergence issues can make them very slow and computationally expensive. Alternatively, the nonlinear response can be analysed much more efficiently in the frequency domain using the harmonic balance method (HBM) [50]. Due to its high efficiency, standard HBM has been used successfully to compute the nonlinear dynamic response of rotor-bearing systems [32, 43] under the assumption that the response of the system will be periodic with the fundamental frequency equal to the rotation speed $\varOmega$.

However, if the VC effect from Sect. 2.5 is to be included in the analysis, as is the intention of this study, an additional periodicity is being introduced via the bearing stiffness matrix which varies at the BPF. Unless the BPF happens to be comensurate with the shaft rotation frequency, the response will in fact be quasi-periodic, for which conventional HBM is inadequate. Instead of resorting to computationally expensive time-integration, an alternative approach is to apply the GHBM which can capture quasi-periodic responses and has already been applied to rotor dynamic systems [44, 46].

To the authors’ knowledge no attempts have been made in the literature to date to study the combined effect of unbalance and VC on a rotor-bearing system using harmonic balance. This paper will introduce a new approach to achieve this using GHBM, which will be discussed in the following sections.

4.1 Generalised harmonic balance method

For a nonlinear dynamic rotor system with unbalance and VC excitation, two base frequencies will be present, (i) the rotation speed $\omega _1 = \varOmega$, arising from the synchronous excitation, and (ii) the ball pass frequency $\omega _2 = \omega _\mathrm{BPF}$. These base frequencies are both proportional to the rotor speed $\varOmega$:

$$\begin{aligned} \omega _1 =\varOmega&\omega _2 = \omega _\mathrm{BPF} = Z {\dot{\psi }}_\mathrm{c} = Z \gamma \varOmega \end{aligned}$$

Unless the speed ratio $\gamma$ happens to be rational, the ratio between the two base frequencies $\omega _1$ and $\omega _2$ will be irrational. The nonlinear response will consequently contain components at the fundamental harmonics of each base frequency, and at various linear combinations of each base frequency. Mathematically, each frequency component $\omega _{k_1,k_2}$ can be expressed as:

$$\begin{aligned} \omega _{k_1,k_2} = \left( k_1\omega _1 + k_2\omega _2\right) \end{aligned}$$

where $k_1$ and $k_2$ are integers, representing the harmonic coefficients. The total quasi-periodic response of the rotor-bearing system can then be approximated by [51]:

$$\begin{aligned} \mathbf {x}(t) =\sum _{k_1,k_2 \in P} \mathfrak {R}{\left( \tilde{\mathbf {x}}_{k_1 k_2} e^{i \left( k_1 \omega _1 + k_2 \omega _2\right) t}\right) } \end{aligned}$$

(28)

where the complex vectors $\tilde{\mathbf {x}}_{k_1 k_2}$ contain the harmonic component in $\mathbf {x}$ at the frequency $\omega _{k_1,k_2}$. In the GHBM, the set of frequencies specified by the set of integers P must be somehow truncated. There are several strategies for achieving this [51]. For this rotor-dynamic problem, the approach taken in [10] was used, since this includes the most frequencies so is the most thorough. In this case, the set P includes all integers $\left| k_1\right| \le M^\mathrm{H}_1$ and $\left| k_2\right| \le M^\mathrm{H}_2$ for which the frequency $\omega _{k_1,k_2}$ is positive. This set is depicted in Fig. 7 for the case of $M^\mathrm{H}_1 = 5, M^\mathrm{H}_2 = 3$.

Fig. 7

Set of harmonics included in GHBM $\left( M^\mathrm{H}_1 = 5, M^\mathrm{H}_2 = 3\right)$

This leads to a total of $M^\mathrm{H}_\mathrm{tot}$ included harmonics, given by [51]:

$$\begin{aligned} M^\mathrm{H}_\mathrm{tot} = \frac{(2M^\mathrm{H}_1+1)(2M^\mathrm{H}_2+1) + 1}{2} \end{aligned}$$

Typically, the larger the values of $M^\mathrm{H}_1,M^\mathrm{H}_2$, the greater the accuracy, at the expense of computational cost.

The truncated series of the total response $\mathbf {x}(t)$ from (28) and its derivatives can then be combined with the equation of motion in (26), and upon equating the terms at each frequency $\omega _{k_1,k_2}$, $M^\mathrm{H}_\mathrm{tot}$ equations of the following form are obtained:

$$\begin{aligned} \left[ -\omega _{k_1,k_2}^2\mathbf {M} + i \omega _{k_1,k_2}\mathbf {C} + \mathbf {K}\right] \tilde{\mathbf {x}}_{k_1 k_2} + \tilde{\mathbf {f}}_{k_1 k_2} = \tilde{\mathbf {u}}_{k_1 k_2}\nonumber \\ \end{aligned}$$

(29)

where the excitation term $\tilde{\mathbf {u}}_{k_1 k_2}$ is known explicitly, but the term arising from the nonlinear forces $\tilde{\mathbf {f}}_{k_1 k_2}$ remains unknown. It will be shown how to compute $\tilde{\mathbf {f}}_{k_1 k_2}$ in the following section.

The complex vectors $\tilde{\mathbf {x}}$ containing the component at each harmonic can then be assembled into a single vector $\mathbf {z}$ defined as:

$$\begin{aligned} \mathbf {z} = \begin{bmatrix} \tilde{\mathbf {x}}_{0,0} \\ \mathfrak {R}{\left( \tilde{\mathbf {x}}_{1,0}\right) } \\ \mathfrak {I}{\left( \tilde{\mathbf {x}}_{1,0}\right) } \\ \mathfrak {R}{\left( \tilde{\mathbf {x}}_{0,1}\right) } \\ \mathfrak {I}{\left( \tilde{\mathbf {x}}_{0,1}\right) } \\ \vdots \\ \mathfrak {R}{\left( \tilde{\mathbf {x}}_{k_1,k_2}\right) } \\ \mathfrak {I}{\left( \tilde{\mathbf {x}}_{M^\mathrm{H}_1,M^\mathrm{H}_2}\right) } \end{bmatrix}. \end{aligned}$$

Similar vectors $\mathbf {h}$ and $\mathbf {g}$ can be formed from both $\tilde{\mathbf {f}}$ and $\tilde{\mathbf {u}}$, respectively, allowing the equation of motion from (29) to be written in its final vector form [51]

$$\begin{aligned} \mathbf {r}(\mathbf {z},\varOmega ) = \mathbf {L}(\varOmega ) \mathbf {z} + \mathbf {h}\left( \varOmega , \mathbf {z}\right) + \mathbf {g}\left( \varOmega \right) = \mathbf {0} \end{aligned}$$

(30)

where $\mathbf {r}(\mathbf {z},\varOmega )$ is the residual to be minimised, $\mathbf {L}$ contains the linear parts of the model, $\mathbf {h}\left( \varOmega , \mathbf {z}\right)$ contains the nonlinear terms, and $\mathbf {g}\left( \varOmega \right)$ contains the excitation. The matrix $\mathbf {L}$ is block-diagonal and given by [46, 51, 52]:

$$\begin{aligned} \mathbf {L} = \begin{bmatrix} \mathbf {L}_{0,0} &{} \mathbf {0} &{} \dots &{} \dots &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {L}_{1,0} &{} \dots &{} \dots &{} \mathbf {0} \\ \vdots &{} \vdots &{} \mathbf {L}_{0,1} &{} \dots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \mathbf {0} &{} \dots &{} \dots &{} \dots &{} \mathbf {L}_{M^\mathrm{H}_1,M^\mathrm{H}_2} \\ \end{bmatrix} \end{aligned}$$

(31)

with $\mathbf {L}_{0,0} = \mathbf {K}$, and for all other $k_1$ and $k_2$

$$\begin{aligned} \mathbf {L}_{k_1,k_2} = \begin{bmatrix} \mathbf {K} - \omega _{k_1,k_2}^2\mathbf {M} &{} -\omega _{k_1,k_2}\mathbf {C}\\ \omega _{k_1,k_2}\mathbf {C} &{} \mathbf {K} - \omega _{k_1,k_2}^2\mathbf {M} \end{bmatrix} \end{aligned}$$

It is now necessary to specify how to compute the nonlinear vector $\mathbf {h}$, comprised from the nonlinear phasors $\tilde{\mathbf {f}}_{k_1 k_2}$.

4.2 Alternating frequency-time

The most common approach to compute the nonlinear forces is to use the alternating frequency/time (AFT) method [46], where the displacements in the frequency domain are converted to the time domain in which the nonlinear forces can be evaluated, before converting them back to the frequency domain to yield $\tilde{\mathbf {f}}_{k_1 k_2}$. This can then be substituted into the harmonic balance Eq. (29). One way this can be achieved for quasi-periodic problems is to introduce a multi-dimensional time domain (or hyper-time) [45], so that the response can be written as:

$$\begin{aligned} \mathbf {x}(t_1,t_2) =\sum _{k_1,k_2 \in P} \mathfrak {R}{\left( \tilde{\mathbf {x}}_{k_1 k_2} e^{i \left( k_1 \omega _1 t_1 + k_2 \omega _2 t_2\right) }\right) } \end{aligned}$$

(32)

Applying this concept to a rotor-bearing system with unbalance and VC, means that along the domain $t_1$ the rotor spins at a speed $\varOmega = \omega _1$ whilst the cage is fixed. Conversely, the cage rotates along the domain $t_2$ at speed ${\dot{\psi }}_\mathrm{c} = \frac{\omega _2}{Z}$, with the rotor held fixed. This idea is depicted in Fig. 8, where the x axis represents $t_1$ with the rotor rotation, whilst the y-axis represents $t_2$ with the cage rotation. The true time domain, t, where both the rotor and cage will rotate but at different speeds, is represented by a diagonal line in hyper-time where $t = t_1 = t_2$.

Fig. 8

Depiction of hyper-time for the Jeffcott rotor

The whole AFT process can now be summarised as [46]:

$$\begin{aligned} \tilde{\mathbf {x}}_{k_1,k_2} \xrightarrow {\text {IFFT}} \mathbf {x}(t_1,t_2) \rightarrow \mathbf {f}_\mathrm{nl}(\mathbf {x}(t_1,t_2),t_2) \xrightarrow {\text {FFT}} \tilde{\mathbf {f}}_{k_1,k_2} \end{aligned}$$

where the fast Fourier transform (FFT) and inverse fast Fourier transform (IFFT) operations are carried out over both $t_1$ and $t_2$. It should be noted that the nonlinear force $\mathbf {f}_\mathrm{nl}$ has an explicit dependence on $t_2$ and not $t_1$. This is because the nonlinear bearing forces vary with cage angle, which varies with $t_2$ only, according to the definition of hyper-time.

4.3 Frequency response

The equation of motion in multi-harmonic terms can then be used to compute the frequency response characteristic for a range of frequencies. For nonlinear systems, more than one solution may be present for a given frequency, requiring the use of a continuation algorithm to obtain the full response curve. A linear predictor with a pseudo arc-length corrector [53] has been used in this case to compute the quasi-periodic response of the Jeffcott rotor, where the continuation parameter was the rotor speed $\varOmega$.

4.4 Stability

In nonlinear systems, some portions of the nonlinear frequency response curve can become unstable. The stability can be assessed with Hill’s method [52], which yields approximate values of the Floquet exponents $\lambda$ using a standard HBM formulation. If these are in the right half-plane, then the solution is unstable, and vice versa. It was demonstrated in [52] that, under the assumption that the perturbation varies slowly with time, the Floquet exponents for a periodic response can be computed from the following quadratic eigenvalue problem:

$$\begin{aligned} \mathbf {A} \lambda ^2 + \mathbf {B} \lambda + \frac{\partial \mathbf {r}}{\partial \mathbf {z}} = 0 \end{aligned}$$

(33)

The terms involving $\mathbf {A}$ and $\mathbf {B}$ arise from the linear parts of the model, whilst the HBM Jacobian $\frac{\partial \mathbf {r}}{\partial \mathbf {z}}$ contains additional contributions from the nonlinearities. The matrix $\mathbf {A}$ is block-diagonal and given by $\mathbf {A} = \mathbf {I} \otimes 2\mathbf {M}$ [52]. The matrix $\mathbf {B}$ is of a very similar form to the matrix $\mathbf {L}$ in (31) [52]:

$$\begin{aligned} \mathbf {B} = \begin{bmatrix} \mathbf {B}_{0} &{} \mathbf {0} &{} \dots &{} \dots &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {B}_{1} &{} \dots &{} \dots &{} \mathbf {0} \\ \vdots &{} \vdots &{} \mathbf {B}_{2} &{} \dots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \mathbf {0} &{} \dots &{} \dots &{} \dots &{} \mathbf {B}_{M_\mathrm{H}}\\ \end{bmatrix} \end{aligned}$$

where $\mathbf {B}_{0} = \mathbf {C}$ but for all other k:

$$\begin{aligned} \mathbf {B}_{k} = \begin{bmatrix} \mathbf {C} &{} - 2\omega _{k}\mathbf {M}\\ 2\omega _{k}\mathbf {M} &{} \mathbf {C} \end{bmatrix} \end{aligned}$$

(34)

where $\omega _{k}$ denotes the kth frequency component included in the HBM problem, and $M_\mathrm{H}$ is the number of harmonics included.

Hill’s method is only valid for periodic responses, but there is no direct equivalent when the response is quasi-periodic, so it is not possible to directly apply Hill’s method to the solution found from GBHM in Sect. 4.1. However, it is possible to make the “adjusted HBM” approximation [51], where the two base frequencies are adjusted to be commensurate so that the response becomes periodic. Applying this approach to the Jeffcott rotor in this paper, the ratio between the BPF and rotor speed $\gamma Z$ was approximated as the ratio of two integers p and q (to an accuracy of ${1 \times 10^{-4}}$), such that $Z \gamma \approx \frac{p}{q}$. This means that the two base frequencies $\omega _1 = \varOmega$ and $\omega _2 = \omega _\mathrm{BPF} = Z \gamma \varOmega$ are no longer incommensurate. Using this approximation, each frequency component in the solution from GHBM can be written as:

$$\begin{aligned} \omega _{k_1,k_2}&= k_1 \omega _1 + k_2 \omega _2 \\&= \left( k_1 + k_2 Z \gamma \right) \varOmega \\&\approx (k_1 + k_2 \frac{p}{q}) \varOmega \\&\approx (k_1q + k_2p) \frac{\varOmega }{q}\\ \end{aligned}$$

It can be observed that the base frequency of adjusted HBM is given by $\omega _0 = \frac{\varOmega }{q}$, and each approximated frequency component $\omega _k$ can therefore be written as:

$$\begin{aligned} \omega _k = (k_1 q + k_2 p) \omega _0 \end{aligned}$$

The approximate frequencies $\omega _k$ can then be substituted into (34) to compute the value of the matrix $\mathbf {B}$. They can then also be used to compute the adjusted HBM Jacobian $\frac{\partial \mathbf {r}}{\partial \mathbf {z}}$, allowing the approximate Floquet exponents to be found by solving (33). Note that Jacobian was evaluated at the solution vector $\mathbf {z}$ found from GHBM; the solution was not recomputed using adjusted HBM. This approach couples the improved accuracy of GHBM for computing the frequency response, with the ability of adjusted HBM to assess the stability in an efficient manner, without resorting to time-integration.

4.5 Summary

The proposed application of the GHBM, in combination with the pseudo arc-length continuation and Hill’s method for stability, provides, for the first time, an efficient way to study the nonlinear unbalance response of a rotor-bearing system whilst including the VC effect. This therefore represents a more complete and accurate method for computing the nonlinear dynamic response of a rotor-bearing system than previous approaches.

Fig. 9

Comparison of the orbits obtained from integrating the ODE and GHBM

5 Results

The previously introduced model of the Jeffcott rotor from Sect. 3 supported by the nonlinear time-varying bearing model from Sect. 2 will be analysed in detail using the GHBM approach presented in Sect. 4, in order to obtain a better understanding of the rotor-bearing interaction. In particular, the impact of the VC and the nonlinear bearing stiffness on the rotor response will be investigated.

Initially, the results from a baseline configuration will be presented and discussed in detail to highlight the underlying mechanisms that drive the nonlinear response. This will be followed by a study of the effect of the individual bearing parameters on the response.

5.1 Baseline

The input parameters of the baseline model are given in Tables 1, 2 and 3. Centrifugal loads were neglected, and both rings and the stator were assumed to be rigid, in order to keep the complexity of the base line to a minimum. The clearance was set to the C2 level given in Table 1, corresponding to a radial clearance of ${2.5}\,\upmu \hbox {m}$.

5.1.1 Validation of GHBM

In a first step the novel implementation of the GHBM for rotating systems from Sect. 4.1 had to be validated, to ensure that the predictions were accurate. For this purpose, the solution from GHBM was compared to the solution from time-integration of the equations of motion in (26), with use of ode15s in MATLAB.

The number of harmonics $M^\mathrm{H}$ for each frequency $\omega _{1,2}$ in the GHBM computation was chosen so that the dominant peaks in the spectrum of the response could be captured, across a range of speeds and unbalance levels, ensuring the results would be sufficiently accurate. The set of included harmonics was the same as shown in Fig. 7. The number of discrete time points $M_{1,2}^\mathrm{T}$ was set to be $4 \times$ the minimum dictated by the Nyquist frequency for each $\omega _{1,2}$, in order to minimise aliasing, leading to the GHBM parameters in Table 4. It is important to note that the multi-dimensional FFT/IFFT operations were evaluated over $M^\mathrm{T}_1 \times M^\mathrm{T}_2 = 40 \times 24 = 960$ points; leading to accurate results with relatively few points over each dimension [51]. The rational approximation of the ratio between the base frequencies $Z\gamma$ used in adjusted HBM for stability analysis is also given in Table 4.

Table 4 Harmonic balance parameters

The resulting rotor orbits from time-integration and GHBM are shown in Fig. 9 for three rotation speeds $\varOmega$ and three unbalance levels $\epsilon$. The two methods provide identical results for the first two excitation levels and show a very similar behaviour at the highest excitation level, although small differences are visible. Both approaches accurately capture the clearly quasi-periodic nature of the response, which leads to the rotor never retracing exactly the same orbit. This is due to the time dependence introduced by the VC effect, which is in agreement with results from [41]. Based on the comparison of the solutions from GHBM and time solution, it can be concluded that GHBM, with the selected number of harmonics, is indeed able to capture the quasi-periodic response of the rotor system accurately.

Both solutions where found on a Windows PC with an 8-Core i7 processor and 32GB of memory using MATLAB 2018b, where approximately 16sec of computation time were needed to compute the solution at a given frequency using ode15s, whilst only 2sec were needed using the GHBM approach. This $8\times$ increase in computational speed, in combination with the ability to apply continuation to the analysis, highlighted the great potential the GHBM has for quasi-periodic rotor-dynamic problems, and all of the following results will be consequently based on the GHBM approach.

5.1.2 Stiffness

The dynamic response of the rotor system is heavily dependent on the bearing stiffness, which in turn depends on the rotor deflection, and the cage angle of the bearing. In order to evaluate the nonlinear stiffness characteristic of the baseline bearing, independent of the cage angle, the average bearing stiffness from Sect. 2.6 has been computed for different horizontal and vertical rotor positions and the results are shown in Fig. 10.

The variation of the average horizontal stiffness ${\bar{k}}_{xx}$ with rotor position was computed by varying the horizontal rotor position, whilst maintaining vertical equilibrium. It can be observed in the top graph of Fig. 10a that the stiffness increases monotonically as the rotor moves away from the centre, $x=0$, in either direction. This is due to an increase in the size of the loaded zone, as well as the hardening characteristic of the Hertzian contacts. The variation of the cross-stiffness ${\bar{k}}_{xy}$ with horizontal rotor motion x is shown in the bottom graph of Fig. 10a. The cross-stiffness is zero when the rotor is in the centre, due to the symmetry of the system, but as the rotor moves horizontally away from the centre, the load distribution becomes asymmetric and the cross-stiffness becomes non-zero. As the rotor displaces even further, the coupling stiffness, ${\bar{k}}_{xy}$, tends back to zero, since the influence of the self-weight becomes negligible compared to the large horizontal rotor deflection, and the load distribution becomes symmetric about the x-axis once more.

Fig. 10

Variation of the average bearing stiffness with rotor position for the baseline system

The average vertical stiffness ${\bar{k}}_{yy}$ is plotted in Fig. 10b where the rotor was moved vertically whilst maintaining horizontal equilibrium. The position where the rotor is in vertical equilibrium with its self-weight is marked with a diamond. The rotor sags by approximately ${6}\,\upmu \hbox {m}$ due to the self-weight.

When the rotor moves further downwards, the vertical stiffness increases due to an increase in the size of the loaded zone and Hertzian contact stiffening. However, when the rotor moves upwards from its equilibrium position, the stiffness initially reduces as the effect of the self-weight is removed. When the rotor is near the central position $y=0$, there is a dead-band where the stiffness is zero, which is due to the radial clearance. If the rotor deflects even further upward, the stiffness increases once more as the elements at the top of the bearing become loaded. There is no such dead-band in the horizontal stiffness, since the presence of the self-weight ensures that there is always some contact. The cross-stiffness ${\bar{k}}_{xy}$ remains zero if the rotor moves vertically because the load distribution remains symmetric about the y-axis and has therefore not been plotted.

The dependence of the time-varying stiffness from Sect. 2.5 on the cage angle was computed with the rotor in its equilibrium position. These results are shown in Fig. 11, and it is clear that the stiffness strongly depends on the cage angle, and can vary quite differently in each direction. In the vertical direction it reaches its maximum when a ball is directly under the rotor, whilst in the horizontal direction the maximum stiffness is reached when there are balls either side. It is important to note that the variation in stiffness is larger in the horizontal than the vertical direction. The horizontal stiffness has its main contribution from the elements at the edges of the loaded zone since these contact loads have the greatest horizontal component, and the overall stiffness is consequently very sensitive to their angular position since their contribution is proportional to $\sin ^2{\psi _j}$. The vertical stiffness on the other hand is mainly determined by the elements underneath the rotor, which have a small angle $\psi _j$. Their contribution to the vertical stiffness is proportional to $\cos ^2{\psi _j}$, but this is much less sensitive to variations in $\psi _j$.

The cross-stiffness is zero when the balls are positioned symmetrically about the vertical plane, but non-zero otherwise. This occurs when $\psi _\mathrm{c} = 0$ or $\frac{\pi }{Z}$. The strong change in stiffness behaviour around $\psi _\mathrm{c} = \frac{\pi }{Z}$ corresponds to a region where there is an extra element in the loaded zone. There is a non-smooth transition when an element enters or leaves the load zone.

Fig. 11

Variation of the stiffness with cage angle for the baseline system

Fig. 12

Frequency response of the baseline system

The results show that the stiffness varies considerably as the rotor deflects leading to a highly nonlinear characteristic. In addition, the stiffness varies as the cage rotates, leading to the time-dependent VC effect, which can further excite the rotor.

5.1.3 Frequency response

With the accuracy of the GHBM implementation confirmed, and an understanding of the bearing stiffness behaviour obtained, the frequency response of the baseline rotor was computed for increasing levels of rotor unbalance, leading to the results in Fig. 12. The displacement of the centre of the rotor orbit (${\bar{x}}, {\bar{y}}$) is shown in the left hand column, the unbalance transmissibility ($T_x$, $_y$) across the bearing in the central column, and the self-excitation due to VC ($F^\mathrm{b}_x$, $F^\mathrm{b}_y$) in the right hand column. The dashed lines denote where the periodic solution is unstable.

It can be observed that there are distinct resonances in the horizontal (x) and vertical (y) directions. At low excitation levels, the horizontal resonance is at ${213}\,\hbox {Hz}$ and the vertical resonance is higher at ${376}\,\hbox {Hz}$, which is consistent with the different stiffnesses in each direction discussed in the previous section. At resonance, the vertical position of the centre of the rotor orbit approaches the line ${\bar{y}} = 0$. The horizontal position ${\bar{x}}$ is always zero, and only becomes non-zero when the quasi-periodic solution loses stability. It can also be observed the forcing due to VC has resonances at speeds well below the primary resonances.

In order to condense and highlight the most important information contained in the frequency plots in Fig. 12 the variation of the resonance frequency, $\varOmega _\text {max}$, the peak horizontal and vertical transmissibilities, $\left| T_x\right| _\text {max}$ and $\left| T_y\right| _\text {max}$, and the vertical position of the orbit centre ${\bar{y}}_\text {max}$ can be plotted over the unbalance level, $\epsilon$, leading to Fig. 13. Similarly, the maximum forcing amplitude at the BPF due to VC, and the frequency at which this occurs can be plotted over the unbalance level, $\epsilon$, leading to Fig. 14.

Synchronous transmissibility The unbalance transmissibility in the central column of Fig. 12 shows that the horizontal peaks start to lean to the right as the unbalance level is increased due to the horizontal stiffness increasing as the rotor oscillates with larger amplitudes, as shown in Fig. 10a. Interestingly, the vertical resonance leans to the left at low unbalance levels due to the initial reduction in stiffness as the rotor enters the dead-band region in Fig. 10b. At higher unbalances, the rotor deflects so much that it passes through to the other side of the dead-band, so that the effective stiffness is actually increased and the peak starts to lean to the right. This softening/stiffening effect of the nonlinear bearing is in agreement with the literature [32] and highlights the strongly nonlinear nature of the problem.

Fig. 13

Unbalance transmissibility of the baseline system at resonance

The stiffening effect of the bearings is so strong that “jump phenomena” start to appear at the higher unbalance levels, where the periodic solution becomes unstable under the peak, denoted by the dotted lines. Additionally, both resonant peaks become unstable for certain medium excitation levels, before regaining stability at higher unbalance levels. Using time-integration, the system was found to respond chaotically in these unstable regions which is in good agreement with the literature [18, 28, 30, 34, 48, 54]. These unstable regions are clearly identifiable in Fig. 13, where they are marked as dashed lines.

It can also be observed in Fig. 12 that cross-resonances start to appear at higher unbalance levels. At the horizontal resonance frequency, a peak starts to appear in the vertical response. In this case the cross-stiffness becomes non-zero as the rotor oscillates horizontally, which excites the rotor in the vertical direction. As the unbalance level is further increased, this cross-resonance becomes larger and the primary vertical resonance becomes smaller. Eventually, the cross-resonance forms the dominant part of the vertical response, leading to a single resonance with circular orbits and equal motion in the horizontal and vertical directions. In this regime, the effect of the self-weight of the rotor is negligible compared to the dynamic loads, so the resonance frequencies and amplitudes are identical in both directions as clearly shown in Fig.  13. The resonance frequency more than doubles for the highest load case and the peak response increases significantly in this regime. This can be attributed to the fact that the effective damping ratio is given by $\zeta _\mathrm{r} \approx \frac{c_\mathrm{b}}{2 m \omega _n}$, where the bearing damping $c_\mathrm{b}$ is constant but the effective natural frequency $\omega _n$ increases due to the nonlinear bearing stiffness, and therefore the effective damping ratio is reduced.

Another feature to observe in Fig. 12 are the small sub-resonances in the horizontal transmissibility around ${180}\,\hbox {Hz}$, which only appear at the highest excitation levels. This is approximately half of the vertical natural frequency, so is therefore evidence of $2\times$ components in the response.

Centre of rotor orbit The position of the centre of the rotor orbit is shown in the left hand column of Fig. 12. The horizontal position ${\bar{x}}$ remains near zero, since the system is symmetric in the vertical plane, but the vertical position ${\bar{y}}$ varies considerably, which can be more clearly seen in Fig. 13. At higher unbalance levels, the rotor moves upward towards the centre position at resonance, because the self-weight becomes negligible compared to the dynamic loads, and no longer impacts the rotor motion.

Self-excitation due to variable compliance Due to the novel use of the GHBM in this paper, the forcing due to VC could be computed and is shown in the right hand column of Fig. 12. There are prominent peaks in the forcing in both the vertical and horizontal directions, when the BPF coincides with the natural frequency $\omega _n$ of the underlying linear system of either the vertical or horizontal mode. The mathematical relation is given by $\varOmega = \frac{\omega _n}{\gamma Z}$.

The frequency of maximum forcing varies very little with the excitation level, but the magnitude of the peaks reduce slightly at very high excitation levels as Fig. 14 clearly shows. The latter indicates an influence of the unbalance forces even at these lower speeds and suggests that the VC phenomenon is most relevant for small unbalance levels. Surprisingly, the forcing is greater in the vertical direction, despite the fact that the horizontal stiffness was found to be more sensitive to cage position (see Fig. 11). This effect could be attributed to the variations in cross-stiffness which can also excite the rotor in the vertical direction.

Fig. 14

VC forcing of the baseline system at resonance

Table 5 Configurations for each section of the parameter study

The results from the baseline configuration show that the REB leads to a highly nonlinear unbalance response. In addition, the VC effect introduces further sub-synchronous forcing, leading to sub-resonances at low frequencies. In order to identify which of the bearing features particularly influence the observed behaviour, a parameter study will be presented next.

5.2 Parameter study

The influence of four key bearing features on the Jeffcott rotor response will be further investigated. In each section, the parameter of interest will be varied whilst keeping all others fixed at the baseline values, which is outlined in Table 5. For each parameter, the impact on the stiffness will be discussed initially to support the understanding and interpretation of the frequency response.

Fig. 15

Variation of the average bearing stiffness with rotor position for different clearance levels

5.2.1 Clearance

The clearance is one of the largest sources of nonlinearity in a bearing, so the radial clearance $c_\mathrm{r}$ was chosen for the first parameter study. It was increased from its nominal C2 value of ${2.5}\,\upmu \hbox {m}$ to the C5 level of ${20}\,\upmu \hbox {m}$, and decreased to ${0}\,\upmu \hbox {m}$ corresponding to a perfect fit. In addition, the effect of a radial preload on the bearing was considered by setting $c_\mathrm{r}$ to ${-2.5}\,\upmu \hbox {m}$.

Stiffness The horizontal and vertical stiffness variation was computed in the same way as outlined in Sect. 5.1. The results for the average horizontal stiffness in Fig. 15a show a high sensitivity to the clearance level.

The preload case ($c_\mathrm{r} = {-2.5}\,\upmu \hbox {m}$) has a higher overall stiffness level as the loaded zone encompasses the whole of the bearing as shown in Fig. 16. The stiffness initially reduces as the rotor moves away from the centre as the loaded zone initially decreases in size due to loss of preload on the lightly loaded side of the bearing. At larger displacements the stiffness starts to increase again since the effect of the stiffening Hertzian contact dominates. For the cases of a loose bearing ($c_\mathrm{r} > {0}\,\upmu \hbox {m}$), the size of the loaded zone is smaller as seen in Fig. 16. This means the overall stiffness level is reduced. However, the loaded zone increases in size as the rotor moves horizontally, so the stiffness increases monotonically.

The cross-stiffness in Fig. 15a is near zero for the preloaded case but reaches higher values when the bearing is loose. This can be attributed to the load distribution becoming more asymmetric as the rotor moves horizontally. It is interesting to note that the maximum cross-stiffness is reached at a greater deflection as the clearance is increased, but the maximum value does not seem to be affected, although it is always larger than in the preload case. As was found in the baseline case, the cross-stiffness tends back to zero for very large displacements.

Fig. 16

Variation of elemental stiffness distribution in equilibrium position for different clearance levels

The radial clearance has a very similar effect on the vertical stiffness, as shown in Fig. 15b. The most noticeable difference is that for the loose bearings, a dead-band around the centre of the bearing where the stiffness is zero; the size of the dead-band depends directly on the clearance level. For the preload case, it can also be observed that the vertical stiffness is very close to the horizontal stiffness in Fig. 15a. This is because the radial preload dominates over the self-weight, so the bearing stiffness is nearly axisymmetric.

In order to understand if the clearance changes the sensitivity of the bearing stiffness to cage angle, the stiffness in the rotor equilibrium position is plotted over a range of cage angles $\psi _\mathrm{c}$ in Fig. 17. It can be seen that larger clearances lead to a greater sensitivity to cage angle. To explain this behaviour, Fig. 18 shows the number of loaded elements that are in contact as the cage rotates. When the bearing is preloaded, all elements remain in contact at all times, leading to a bearing stiffness independent of cage angle, whilst increasing clearance leads to a smaller and a changing number of loaded elements.

Although the variation in the vertical and cross-stiffnesses increases as the bearing clearance is increased, this is not the case for the horizontal stiffness. The level of horizontal stiffness variation is similar for all of the cases with bearing clearance ($c_\mathrm{r} \ge {0}\,\upmu \hbox {m}$) and only reduces when the bearing is radially preloaded ($c_\mathrm{r} = {-2.5}\,\upmu \hbox {m}$). This highlights a complex interaction between the clearance level and VC, since the variations in stiffness as the cage rotates are not only determined by the number of loaded elements at each cage angle, but also the angular positions of each element.

Fig. 17

Variation of the bearing stiffness with cage angle for different clearance levels

Fig. 18

Variation of number of loaded elements with cage angle for different clearance levels

The clearance appears to have a significant impact on the stiffness of the bearing, and consequently it is expected to also have a strong impact on the frequency response of the system.

Frequency response The frequency response was computed for all clearance levels, but only the condensed variation of the response at resonance is shown in Fig. 19. Considering first the linear response at low unbalance levels, $\epsilon$, it can be seen that the resonance frequencies in both directions, $\varOmega _\text {max}$, are reduced when the bearing is loose, and increased when the bearing is preloaded. This behaviour can be attributed to the changes in the bearing stiffnesses observed in Fig. 15.

Fig. 19

Variation of unbalance transmissibility at resonance with clearance

At higher excitation levels the resonance frequencies become much more dependent on the clearance. For the preload case ($c_\mathrm{r} = {-2.5}\,\upmu \hbox {m}$), some softening can be observed as the excitation increases, which is followed by a hardening effect, consistent with the more complex stiffness variation in Fig. 15. The resonance frequencies of the vertical and horizontal mode are similar for all unbalance levels, due to similar stiffness values in each direction.

For the smaller clearance case ($c_\mathrm{r} = {2.5}\,\upmu \hbox {m}$), the resonance frequencies $\varOmega _\text {max}$, increase with the excitation level, which is consistent with the hardening effect shown in Fig. 15. At very large clearance ($c_\mathrm{r} = {20}\,\upmu \hbox {m}$) the vertical mode shows a softening behaviour. This is because the size of the dead-band in the vertical bearing stiffness is increased, so the rotor does not deflect enough to reach the stiffening regime. If the unbalance level was increased even further, it would eventually display a stiffening effect.

An unstable region appears for all clearance cases, indicated by a dashed line, which is caused by the dead-band in the stiffness characteristic. As the clearance is increased, these unstable regions are shifted to higher excitation levels. This can be attributed to a smoother change in stiffness at the edges of the dead-band so that the system must be excited harder to initiate instability. If the excitation level is further increased, the system is once more stabilised by the addition of the radial preload as observed in [19]. In summary, these results show that the bearing instability due to increasing excitation levels is strongly influenced by the radial clearance, but that it can be potentially controlled by applying a preload.

The peak transmissibility curves shows significantly lower values for increasing clearance. Since the damping in the system is kept constant, this increase in response amplitude can be directly linked to the change in resonance frequency, which is quite apparent from Fig. 19. As the resonance frequency reduces, the effective damping ratio increases due to the simple relationship of $\zeta _\mathrm{r} \approx \frac{c_\mathrm{b}}{2 m \omega _n}$.

It can also be observed from the bottom graphs in Fig. 19 that the centre of the rotor orbit at low unbalance levels moves downward as the clearance is increased. This is because the rotor must sag more for the bearing to become loaded, in order to resist the self-weight and reach equilibrium. However, the orbit centre moves upward towards 0 in all cases at high unbalance levels, since the influence of the unbalance loading starts to negate the impact of the self-weight.

The variation of the VC forcing at resonance can be seen in Fig. 20 for different excitation and clearance levels. The magnitude of the forcing generally increases with the radial clearance, which can be attributed to the increased sensitivity of the stiffness to the cage position, as shown in Fig. 17.

When the bearing is preloaded, there is no VC forcing at all, since the stiffness does not vary with the cage angle. The frequency of the maximum forcing reduces with clearance, which is consistent with the above-mentioned reduction in bearing stiffness. The VC forcing generally remains constant for most of the excitation range, both in frequency and amplitude. Only at very large excitation levels in the vertical direction, some variations can be observed, where smaller clearance values ($c_\mathrm{r} = {2.5}\,\upmu \hbox {m}$) lead to a small drop in VC forcing, whilst a large clearance ($c_\mathrm{r} = {20}\,\upmu \hbox {m}$) leads to an increase in forcing. This is likely due to some interaction with the unbalance excitation. Another interesting point to note is that the vertical forcing is higher for low clearance ($c_\mathrm{r} = {2.5}\,\upmu \hbox {m}$), whereas the horizontal forcing is greater for larger clearance ($c_\mathrm{r} = {20}\,\upmu \hbox {m}$). This is likely affected by the significant changes in the cross-stiffness shown in Fig. 17. Based on these results it can be observed that radial clearance generally amplifies the significance of VC, and that non negligible forces can be generated by it.

Fig. 20

Variation of VC forcing at resonance with clearance

It has been shown that bearing clearance has a large influence on the rotor response. It controls whether there is a stiffening or softening effect in the response, strongly impacts the bearing stability, and it amplifies the VC forcing that a bearing experiences.

5.2.2 Ring compliance

The influence of ring compliance on the dynamic response of the Jeffcott rotor will be investigated next. For this purpose, the outer ring of the bearing will be made compliant, and its thickness t will be varied from ${25}\,\hbox {mm}$ down to ${2.5}\,\hbox {mm}$ to control its stiffness.

Fig. 21

Variation of the average bearing stiffness with rotor position for different levels of ring compliance

Fig. 22

Elemental stiffness distribution in equilibrium position for different levels of ring compliance

Stiffness The average stiffness variation with regards to the rotor position is shown in Fig. 21. It can be seen that reducing the ring thickness, and hence increasing the ring compliance, leads to only a small reduction in bearing stiffness which applies in both the horizontal and vertical direction. The ring compliance has a tendency to reduce the maximum elemental load, as depicted in Fig. 22, which agrees with results from the literature [21, 22]. When the rotor moves very far in either direction, the contact loads and hence stiffnesses increase, which in turn makes the rings the dominant sources of compliance leading to a slight increase in stiffness reduction for softer rings.

The cross-coupling reduces very slightly as the rings are made more compliant, as can be observed in Fig. 21a. This stiffness term mainly arises from a transfer of load from the most heavily loaded elements underneath the rotor to the adjacent ones, making the load distribution around the bearing asymmetric. However, the ring compliance distributes the loads between the elements more evenly so that the load distribution remains more symmetric as the rotor moves horizontally.

Fig. 23

Variation of the bearing stiffness with cage angle for different levels of ring compliance

The sensitivity of the bearing stiffness to cage angle is plotted in Fig. 23 for different ring thicknesses. It can be observed that the central lobes around $\psi _\mathrm{c} = \frac{\pi }{Z}$ are wider when the rings are more compliant. The ring compliance transfers more load to the elements at the edge of the loaded zone as shown in Fig. 22, so that these elements remain loaded for a wider range of cage angles. This can be confirmed by examining the number of loaded elements which is shown in Fig. 24.

The peak horizontal stiffness $k_{xx}$ at $\psi =\frac{\pi }{Z}$ is actually increased as the rings are made more compliant, which is again because more load is transferred to the elements at the edges of the loaded zone by the ring compliance, so they add a greater contribution to the horizontal stiffness. On the other hand, the horizontal stiffness $\psi =0$ is reduced as the rings are made more compliant, due to the general softening effect of the ring compliance. This means that the horizontal stiffness varies over a greater range as the rings are made more compliant.

The vertical stiffnesses $k_{yy}$ varies over a smaller range as the rings are made more compliant. However, the mean vertical stiffness also reduces with ring compliance, so that the vertical stiffness, like the horizontal stiffness, actually varies over a greater range when normalised by its average value.

Fig. 24

Variation of number of loaded elements with cage angle for different levels of ring compliance

In summary it can be observed, that the bearing stiffness is reduced very slightly as the rings are made more compliant, but this becomes more significant as the rotor deflects further. The bearing stiffness becomes slightly more sensitive to cage position, which particularly applies to the horizontal stiffness.

Frequency response As with the previous cases, the frequency response was computed for different ring compliance levels, and the variation of the synchronous response at resonance is shown in Fig. 25. The resonance frequencies for the horizontal and vertical mode reduce slightly as the rings are made more compliant, but the effect only becomes of relevance at higher excitation levels. This is consistent with the larger stiffness reduction due to the ring compliance in Fig. 21. The peak response very much mirrors the frequency behaviour, which can once more be linked to the effective damping ratio in the system. The vertical position of the rotor, $y_\text {max}$, in Fig. 25 is slightly lower at resonance for more compliant rings due to an overall reduction in the bearing stiffness.

The stable region of the system is unchanged by ring compliance since the unstable regions appear at the same excitation levels as in the baseline case. This indicates that the ring compliance does not impact the stability of the system and further supports the conclusions from Sect. 5.2.1 that the instability is mainly driven by the bearing clearance.

Fig. 25

Variation of unbalance transmissibility at resonance with ring compliance

The variation of the VC forcing due to ring compliance is plotted in Fig. 26. The magnitude of the forcing increases slightly as the rings are made more compliant which is consistent with the larger stiffness variations with cage position shown in Fig. 23. There is a drop in forcing at high excitation levels for all levels of ring compliance, due to an interaction with the unbalance excitation. The frequency of maximum forcing drops as the rings are made more compliant, since the linearised natural frequency of the system is reduced by the ring compliance.

Fig. 26

Variation of VC forcing at resonance with ring compliance

Generally it can be said that the ring compliance leads to a small drop in the resonance frequency, which becomes more significant at higher amplitudes. It does not seem to affect the instability of the system, and its effect on the VC behaviour of the bearing is relatively small.

5.2.3 Centrifugal loading

No other studies in the literature were found to focus on the effect on the rotor-dynamic response of centrifugal loading on the bearing elements, and consequently their impact was investigated in some detail. The ball density $\rho$ was set to the true value for steel ($\rho _\mathrm{steel} ={7800}\,\hbox {kg m}^{-3}$), and then doubled and quadrupled in order to artificially scale the centrifugal loads. The baseline case corresponding to neglecting centrifugal loads was also considered by setting $\rho ={0}\,\hbox {kg m}^{-3}$.

Stiffness The stiffness computation was performed at a speed of $\varOmega = {600}\,\hbox {Hz}$ to ensure the centrifugal loads will be strong enough to influence the bearing behaviour. The resulting average horizontal stiffness, $k_{xx}$, in Fig. 27a shows only a small dependence on the centrifugal load, where higher centrifugal loading leads to a slightly softer behaviour. Looking at the load distribution plot in Fig. 28 it can be seen that higher centrifugal loads have a tendency to slightly unload the contacts at the edge of the loaded zone and hence reduce their contribution to the horizontal stiffness. With increasing horizontal rotor displacement, the reduction in stiffness becomes smaller, since the elastic loads dominate over the centrifugal loads.

Fig. 27

Variation of the average bearing stiffness with rotor position at $\varOmega = {600}\,\hbox {Hz}$ for different levels of centrifugal loading

Fig. 28

Elemental stiffness distribution in equilibrium position at $\varOmega = {600}\,\hbox {Hz}$ for different levels of centrifugal loading

The cross-stiffness variation is shown in the bottom graph of Fig. 27a and is increased very slightly by the introduction of centrifugal loads. As the rotor moves horizontally, the more lightly loaded side of the bearing is further unloaded by the centrifugal loading on the elements, which increases the asymmetry of the load distribution around the bearing (see Fig. 28), thereby slightly increasing the cross-stiffness.

The average vertical stiffness in Fig. 27b shows that the dead-band around the centre of the bearing is wider with centrifugal loads, leading to an increase in the effective clearance. This can be attributed to an unloading of the inner contacts due to the centrifugal forces, leading to a larger displacement of the inner race before it comes into contact with the elements. As an interesting side effect, the rotor equilibrium position is slightly lower when centrifugal loads are introduced. Although the effective clearance is increased, the stiffness in the equilibrium position is counter-intuitively increased very slightly. This can be related to load distribution being more focused on the elements underneath the bearing (see Fig. 28), which provide the greatest contribution on the vertical stiffness.

The stiffness variation with the cage position is shown Fig. 29. It can be seen that the bearing stiffness is much more sensitive to cage position when centrifugal loads are included. For the horizontal stiffness, $k_{xx}$ the lobe of the baseline case around $\psi _\mathrm{c} = \frac{\pi }{Z}$, where an extra element becomes loaded, is replaced by a flat region with a much lower stiffness. This behaviour can be attributed to a decrease in the number of loaded elements due to the centrifugal loading, as shown in Fig. 30 where higher centrifugal loads lead to wider areas of reduced element contact. As a result the load distribution is distorted in the presence of centrifugal loads (see Fig. 28), and consequently the cage must rotate further for the next contact to enter the loaded zone. This effect also amplifies the cross-stiffness in this regime. The maximum horizontal stiffness values are much less affected by the cage position.

The vertical stiffness is also heavily affected by the cage position, with a similar flat section around $\psi _\mathrm{c} = \frac{\pi }{Z}$. The maximum vertical stiffness, which occurs at $\psi _\mathrm{c} = 0$ and $\psi _\mathrm{c} = \frac{2\pi }{Z}$, is increased by the centrifugal loads which once more can be linked to the previously discussed more focussed load distribution in this case (see Fig. 28).

Fig. 29

Variation of the bearing stiffness with cage angle at $\varOmega = {600}\,\hbox {Hz}$ for different levels of centrifugal loading

Fig. 30

Variation of number of loaded elements with cage angle at $\varOmega = {600}\,\hbox {Hz}$ for different levels of centrifugal loading

In summary the centrifugal loading has a very limited influence on the bearing stiffness, but it significantly increases the sensitivity towards cage position, potentially leading to greater self-excitation due to VC.

Fig. 31

Variation of unbalance transmissibility at resonance with centrifugal loading

Frequency response The variation of the peak frequency responses in Fig. 31 shows that the centrifugal loads have a very small influence on the rotor response. As the centrifugal loading level is increased, there is a very slight reduction in the resonance frequencies for both modes, which is consistent with the drop in stiffness shown in Fig. 27. This reduction in the resonance frequency becomes less significant at the highest excitation levels where the elastic forces at the contacts start to dominate. Although the resonance frequencies themselves are not affected much, the unstable regions at medium excitation levels are influenced by the centrifugal loading. Particularly for the vertical mode in Fig. 31b, larger centrifugal loads lead to a loss of stability at smaller unbalance levels. This effect is driven by the centrifugal loads increasing the effective clearance which has previously been shown to destabilise the system (see Sect. 5.2.1).

The stability of the horizontal mode in 31a is unaffected, as the self-weight of the rotor prevents the centrifugal loads from increasing the effective clearance in this direction.

The behaviour of the VC forcing with regards to the centrifugal loading can be seen in Fig. 32 where an increase in the centrifugal load leads to an increase in the VC forcing. The increase in forcing is smaller than might be expected from the relatively significant changes in bearing stiffness shown in Fig. 29. This is due to the VC resonances occurring at lower frequencies around ${100}\,\hbox {Hz}$, where the centrifugal loads are much less significant than the results in Fig. 29 at ${600}\,\hbox {Hz}$. It should be kept in mind that this is application specific, and consequently this effect may be quite strong for other rotors and bearings.

Fig. 32

Variation of VC forcing at resonance with centrifugal loading

Another feature of the increasing centrifugal loading was a quite strong downward motion of the equilibrium position of the rotor with increasing rotational speed (see Fig. 33). This could be once more attributed to the speed dependent increase in clearance due to the centrifugal ball loading.

Fig. 33

Variation of mean vertical rotor position with centrifugal loading for different speeds with $\epsilon = {1 \times 10^{-8}}\,\hbox {m}$

The inclusion of the centrifugal loading into the bearing model shows very small effect on the actual dynamic response of the Jeffcott rotor, but it slightly destabilises the system and can lead to a different equilibrium position, potentially impacting the safe operation of the rotor.

5.2.4 Stator compliance

The final parameter study focused on the effect of a flexible stator. For this purpose the support stiffness $k_\mathrm{s}$ of the symmetric stator was varied over a wide range. The limiting case of a rigid stator, as in the baseline configuration, was also considered by setting $k_\mathrm{s} = \infty$.

Stiffness The overall stiffness of the bearing including the previously stator stiffness, $k_\mathrm{s}$ can be seen in Fig. 34. Not surprisingly as the stator compliance is increased, the vertical and horizontal stiffnesses reduce considerably and become less and less dependent on the displacement since the linear stator compliance starts to dominate. This has the additional consequence that the cross-stiffness is also reduced and leads to a generally more linear behaviour of the bearing. However, it should be noted that the dead-band in the vertical stiffness remains, since this purely depends on the clearance of the bearing, which is not affected by the support stiffness.

Fig. 34

Variation of the average bearing stiffness with rotor position for different levels of stator compliance

Figure 35 shows the variation of the overall bearing stiffness with cage angle. As the stator becomes more compliant, the sensitivity of the stiffness to the cage position is reduced in all directions, since the stator compliance dominates the behaviour, which is axisymmetric and independent of the cage position.

Fig. 35

Variation of the bearing stiffness with cage angle for different levels of stator compliance

In summary, considerable changes to the stiffness behaviour of the bearing can be observed when the stator compliance is increased. The rotor support becomes much softer and more linear.

Frequency response Given the strong changes in the bearing support stiffness due to stator compliance, a significant change in the frequency response would be expected. Figure 36 shows that as the stator becomes more compliant, the resonance frequencies reduce and the linear regime extends to higher excitation amplitudes. For the softest case of $k_\mathrm{s} = {10}\,\hbox {MN}\,\hbox {m}^{-1}$, there is no change in the resonance frequency even at the highest excitation level, which is in agreement with the full linearisation of the stiffness characteristic in Fig. 34. This also means that the peak transmissibility remains constant.

Stator compliance has the additional consequence that the mean rotor position, $y_\text {max}$, does not move upward so much at resonance, since static response of the linearised system is unaffected by the unbalance response.

Fig. 36

Variation of unbalance transmissibility at resonance with stator compliance

The unstable regions in Fig. 36 move to higher unbalance levels as the stator becomes more compliant with the lowest stiffness level $k_\mathrm{s} = {10}\,\hbox {MN}\,\hbox {m}^{-1}$ leading to a totally stable system. Previous results in Sect. 5.2.1 have shown that the instability predominantly depends on the clearance and its effect on the stiffness behaviour (dead-band). As the support gets softer, the transition from the dead-band region to the contact zone in Fig. 34b becomes smoother and smoother, hence stabilising the system.

The maximum VC forcing is shown in Fig. 37. It reduces considerably when the stator becomes compliant since the stator compliance dominates, making the system less sensitive to the cage position (see Fig. 35). The frequency of maximum forcing also reduces significantly with increasing stator compliance, since the overall system is softer.

Fig. 37

Variation of VC forcing at resonance with stator compliance

Increasing stator compliance has a significant effect on the rotor-dynamic response, by linearising the system and reducing the resonance frequency. In addition, the system is also stabilised, and VC effects become less relevant.

6 Discussion

The presented study on the influence of a nonlinear rolling-element bearing on the unbalance response of a Jeffcott rotor has highlighted the relative importance of different features from a modelling perspective.

When there is a static load on the bearing, it can no longer be considered symmetric, leading to different stiffnesses in the horizontal and vertical directions. In the case investigated in this paper, the vertical stiffness was approximately $2\times$ higher than the horizontal direction due to the weight of the rotor, which agrees with the literature [55]. This asymmetry leads to a splitting of the resonance frequencies, where the vertical mode has a higher frequency (${376}\,\hbox {Hz}$) than the horizontal mode (${213}\,\hbox {Hz}$). The frequency response showed an extremely nonlinear behaviour, where the vertical mode initially decreases in frequency as the unbalance load is increased, before eventually increasing significantly, whereas the resonant frequency of the horizontal mode increases monotonically. At the highest excitation levels, the two modes converged towards a single resonance frequency of ${674}\,\hbox {Hz}$.

At medium unbalance levels, the response of the horizontal and vertical modes can become unstable, which was attributed to the radial clearance. At very high unbalance levels the influence of the self-weight is negligible, so that the rotor exhibits circular orbits around the centre. This also means the effect of the clearance becomes negligible so that the response can regain stability.

A particular feature of this investigation was the introduction of VC to investigate its effect on the rotor response. The GHBM proved to be an effective tool to study rotor-bearing systems which display quasi-periodic responses due to VC. It was shown that VC leads to sub-synchronous excitation, which generates extra resonances at lower frequencies, where the VC frequency coincides with the natural frequency of the horizontal and vertical modes of the underlying linear system. The forcing due to VC is generally insensitive to unbalance level, as it is driven purely by the cyclic-symmetry of the bearing. The resulting forcing amplitude was in the range 10N to 40N, and is determined by the sensitivity of the bearing stiffness is to cage position.

Clearance was found to have the largest influence on the bearing characteristic and is the greatest source of bearing nonlinearity. When the bearing is loose, the response in the horizontal direction displays hardening behaviour, whereas the vertical response displays an initial softening then hardening behaviour. If the bearing is radially preloaded, both modes increase in frequency significantly (by around ${300}\,\hbox {Hz}$) and display softening then hardening behaviour. Clearance was identified as the main driver of instability in the system, due to the sudden change in stiffness when the clearance gap is closed. These unstable regions cover a wider range of unbalance levels as the clearance is increased, but can be controlled by radially preloading the bearing. It was also observed that bearing clearance magnifies the variation in compliance as the cage rotates, leading to a $8\times$ increase in VC forcing.

Ring compliance is rarely included in bearing models, but the results in Sect. 5.2.2 showed that this phenomenon can lead to a small reduction in bearing stiffness (up to 7% in the vertical direction). The reduction in stiffness becomes more significant as the bearing is more highly loaded (where there can be up to a 16% drop in stiffness), so it is particularly important that attention is paid to how the rings are supported in applications where the vibration levels are high. Ring compliance can also increase the self-excitation from the VC effect somewhat (by up to 5N), but was not found to change the overall softening/hardening characteristic of the nonlinearity.

Centrifugal loading on the bearing elements was found to have a very small effect on the rotor-dynamic response in Sect. 5.2.3, leading to a very small reduction in resonant frequency (up to 2%) and no change to the nonlinear stiffness characteristic. For very heavy balls, the unstable region extended to higher unbalance levels due to an increase in effective clearance, but this corresponded to non-physical ball densities. The most significant effect of the centrifugal loading was that the rotor drifts downward as the rotor speed is increased (up to 15% of the static deflection), which can strongly affect rotor and disc clearances in high accuracy applications. Centrifugal loading was found to slightly increase the self-excitation due to VC (by around 2N), due to the increase in effective clearance.

The results in Sect. 5.2.4 show that increasing the level of stator compliance reduces the resonant frequency of both modes, and more importantly, the system becomes more linear because the influence of the bearing is reduced. Additionally the instability induced by the bearing clearance disappears when the supports are very soft, and the self-excitation from VC becomes negligible. As a result it is acceptable to model a relatively stiff bearing on a soft support as a linear system, as long as the support stiffness is significantly softer than the bearing stiffness; in this case, the system behaved linearly once the stator stiffness was approximately $\frac{1}{5}$ of the vertical bearing stiffness.

In summary it can be said that support stiffness and bearing clearance are the two most important features that need to be considered when attempting to accurately model the response of a rotor-dynamic system. The effect of the centrifugal loading on the bearing elements is only relevant for high precision or high speed applications, and ring compliance can generally be neglected as long as the bearing housing is significantly stiff and the rotor remains reasonably well balanced. VC can generate significant sub-synchronous excitation forces in the bearing, which may not directly impact the rotor dynamics due to their low frequency nature, but may lead to unexpected resonances on the rotor or support structure.

7 Conclusions

Developing a deep understanding of the dynamic response of a rotor is of fundamental importance, due to their wide application in engineering structures. Bearings form a fundamental part of such rotating machines, potentially introducing significant nonlinearity to the system. To ensure accurate predictions, a sufficiently detailed bearing model was introduced to capture the main nonlinear and time-varying aspects of the bearing behaviour. The bearing model was coupled with a novel implementation of the generalised harmonic balance method, enabling a detailed study of the rotor-dynamic behaviour of a Jeffcott rotor. The approach allowed the interaction of bearing clearance, centrifugal loads, ring compliance, and support stiffness with VC to be studied for the first time, providing much better physical insight into the quasi-periodic rotor response.

The system was found to have distinct horizontal and vertical resonances due to the asymmetry introduced by the rolling-element bearing, both of which were highly dependent on the forcing level. The response was found to be highly nonlinear, with both softening and stiffening behaviour present. In addition, zones of stability loss could be identified, which strongly depended on the bearing parameters. The presented application of GHBM was able to capture the sub-synchronous self-excitation from the VC effect, which led to sub-resonances where the ball pass frequency coincided with the frequency of the horizontal and vertical modes. Such phenomena could not be captured with a linearised bearing model.

A systematic parameter study showed that bearing clearance has by far the largest influence on the dynamic response of the rotor, leading to strong nonlinear effects and controlling the stability of the system. It was also found to amplify the self-excitation due to the VC effect. Only the addition of a soft support compliance around the bearing was found to limit this nonlinear behaviour by linearising the system. Ring compliance and centrifugal loading had only a small impact on the nonlinear dynamic response of the rotor, suggesting that they may generally be neglected in the analysis, although they may become of relevance for heavily unbalanced machines and high accuracy applications, respectively. A much improved understanding of the different physical mechanisms within the bearing was developed.

The results from this work have highlighted the need to use a bearing model that can at least capture the radial clearance. However, if the support structure is very low, a linearised analysis is sufficient. The results also showed that the VC can lead to significant forcing at lower frequencies, which may excite rotor sub-structures, such as bladed discs, or any other stationary sub-systems. The current study could be extended to consider the effect of axially preloading the bearing, which is very common in industrial applications, or to include a physical bearing damping model to investigate the influence of different energy dissipation mechanisms.