1 Introduction

Nowadays, digitally controlled devices are becoming more and more popular, as the field of automation, smart devices, and the Internet of Things continuously grows.

The three main digital effects: sampling, quantization and processing delay are usually present in all kinds of digitally controlled devices [13, 18]. Because of high-performance applications are featuring fast CPUs, high resolution analog-to-digital (adc) and digital-to-analog converters (dac), these effects were often negligible—in the last years—thanks to the small sampling time, fast computation and high resolution of quantizers.

Currently, however, low- and medium-cost controllers (from Atmel\(^{\copyright }\) AVRs in Arduinos to ARM Cortex\(^{\copyright }\) ST microcontrollers) are becoming widespread in several applications, which usually use 8–12 bit adcs/dacs and communicate in larger and wider networks which often introduce noticeable lags. That is, the corresponding digital effects: sampling, quantization and delay are becoming more significant.

We have shown in our previous works [2, 4] that in case of rounding and sampling, digitally controlled systems can exhibit small amplitude chaotic oscillations—the so-called micro-chaos. Rounding partitions the state space into bands corresponding to different control effort values, and sampling adds irregularity to switching events. Trajectories are allowed to cross switching lines unnoticed for a random amount of time—until the next sampling occurs. It can happen that multiple chaotic attractors appear in the state space of these systems and—depending on the initial conditions—the system may arrive to an attractor far away from the desired state. Thus, the control errors becomes large. Usually, the size of the chaotic attractor is so small that the solution is practically stable [14]. Depending on the nature of the instability of the uncontrolled system, periodic orbits with superimposed chaotic oscillations can also appear [6, 7, 12].

Note that the explicit control of chaos itself is not our goal with the PD-control. However, an elegant feedback control approach was introduced in [17] and applied to a simple system in [1].

The single quantization cases—where either only the measured state or only the outgoing control effort is quantized—are well known [3, 5]. In some cases, when both quantizations are present, the less significant can be neglected, and one can return to a single quantization case.

Our current aim is to create a model for twofold quantization from which the single quantization cases can be inherited, and to discover the range of quantization resolutions for which the effect of the less important quantizer is negligible.

In this paper, the effects of twofold quantization are presented on an inverted pendulum with a simple PD-control. Two new types of bifurcations are also introduced: deadzone crisis (Sect. 3.3) and collision of switching lines (Sect. 4.1).

2 Digitally controlled inverted pendulum

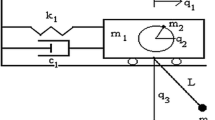
Consider a single degree-of-freedom (DoF) inverted pendulum with digital control, i.e. the measured states and the output control torque are sampled and quantized. The processing delay is neglected and the controller realizes zero-order-hold, see Fig. 1. The measured angle \(\varphi \) and angular velocity \({\dot{\varphi }}\) are quantized according to input resolution \(r_{{\mathrm {I}}}\), and the calculated control effort M is quantized with output resolution \(r_{{\mathrm {O}}}\).

After linearization, the equation of motion of the inverted pendulum assumes the following form:

$$\begin{aligned} \begin{aligned}&{\ddot{\varphi }}(t)+2\delta \alpha {\dot{\varphi }}(t)-\alpha ^2\varphi (t)=-(P\varphi _i+D{\dot{\varphi }}_i), \\&\quad t\in [i\tau ,(i+1)\tau ), \end{aligned} \end{aligned}$$
(1)

where \(\alpha \) is the reciprocal of the time constant characterizing the instability of the upper equilibrium position, \(\delta \) is the relative damping, P and D are control gains, \(\tau \) is the sampling period and Eq. (1) is valid between subsequent sampling instants.

Fig. 1
figure 1

The digitally controlled inverted pendulum with the schematic representation of the zero-order-hold and quantization at the input (measured angle, angular velocity) and output (control torque)

Full size image
Fig. 2
figure 2

Rounding towards zero (Int); mid-tread quantization with double deadzone

Full size image

Introducing the dimensionless time \(T=t/\tau \) and using the notation \(\square '={\mathrm d \square }/{\mathrm dT}\), Eq. (1) can be rewritten as

$$\begin{aligned} \begin{aligned}&\varphi ''(T)+2\delta {\hat{\alpha \varphi }}'(T)-{\hat{\alpha }}^2\varphi (T)=-({\hat{P}}\varphi _i+{\hat{D}}\varphi '_i), \\&\quad T\in [i,i+1), \end{aligned} \end{aligned}$$
(2)

where

$$\begin{aligned} {\hat{\alpha }}=\alpha \tau ,\quad {\hat{P}}=P\tau ^2,\quad {\hat{D}}=D\tau . \end{aligned}$$
(3)

Taking input and output quantization into account, and temporarily returning to the original control parameters (P and D) introduced in Eq. (1), we arrive at the following:

$$\begin{aligned} \begin{aligned}&\varphi ''(T)+2\delta {\hat{\alpha }}\varphi '(T)-{\hat{\alpha }}^2\varphi (T) \\&\quad = -r_{{\mathrm {O}}}\,\tau ^2\,{\mathrm {Int}}\left( \frac{P\,r_{{\mathrm {I}}}}{r_{{\mathrm {O}}}}{\mathrm {Int}}\left( \frac{\varphi _i}{r_{{\mathrm {I}}}}\right) +\frac{D\,r_{{\mathrm {I}}}}{\tau \,r_{{\mathrm {O}}}}{\mathrm {Int}}\left( \frac{\varphi '_i}{r_{{\mathrm {I}}}}\right) \right) , \\&T\in [i,i+1). \end{aligned} \end{aligned}$$

In this paper, we use a mid-tread quantizer with double deadzone, that is \({\mathrm {Int}}(x)\) yields the integer part of x (see Fig. 2).

Note, that the resolution of the angular velocity \({\dot{\varphi }}_i\) is \(r_{{\mathrm {I}}}/\tau \). Thus, according to the definition of the dimensionless time T, one can write \({\dot{\varphi }}_i\,\tau /r_{{\mathrm {I}}} = \varphi '_i/r_{{\mathrm {I}}}\). This results in the same dimension in displacement and velocity with the same quantization resolutions, \(r_{{\mathrm {I}}}\) at the input and \(r_{{\mathrm {O}}}\) at the output.

In some cases, one of the quantizations is dominant over the other, and therefore, the quantization with higher resolution can be neglected, and one of the single quantization models can be used (where either the input or the output is quantized) [3]. However, our goal is to analyse the joint effect of twofold quantization and examine the transition between the twofold and single quantization cases. Doing so, we can also highlight those ranges, where neglecting the less influential quantizer is valid.

In order to reduce the number of resolution parameters, we re-scale the space coordinate with a properly chosen (see Sects. 2.1, 2.2) characteristic displacement X. Introducing the notations \(x=\varphi /X\), \(x'=\varphi '/X\) and \(x''=\varphi ''/X\), the equation of motion can be rewritten as

$$\begin{aligned} \begin{aligned}&x''(T)+2\delta {\hat{\alpha }} x'(T){-}{\hat{\alpha }}^2 x(T)\\&\quad =-\frac{r_{{\mathrm {O}}}\,\tau ^2}{X}\,{\mathrm {Int}}\left( \frac{P\,r_{{\mathrm {I}}}}{r_{{\mathrm {O}}}}{\mathrm {Int}}\left( \frac{x_i\,X}{r_{{\mathrm {I}}}}\right) {+}\frac{D\,r_{{\mathrm {I}}}}{\tau \,r_{{\mathrm {O}}}}{\mathrm {Int}}\left( \frac{x'_i\,X}{r_{{\mathrm {I}}}}\right) \right) . \end{aligned} \end{aligned}$$

If we want to transform the output quantizer to a unit resolution one, \(X_{{\mathrm {O}}}=r_{{\mathrm {O}}}\,\tau ^2\) characteristic displacement should be used. Similarly, using \(X_{{\mathrm {I}}}=r_{{\mathrm {I}}}\) results in unit resolution input quantization.

2.1 Characteristic displacement for unit resolution output quantization

Using \(X_{{\mathrm {O}}}\), the equation of motion assumes the following form:

$$\begin{aligned} \begin{aligned}&x''(T)+2\delta {\hat{\alpha }} x'(T)-{\hat{\alpha }}^2 x(T)\\&\quad =-\,{\mathrm {Int}}\left( \frac{P\,r_{{\mathrm {I}}}}{r_{{\mathrm {O}}}}{\mathrm {Int}}\left( \frac{x_i\,r_{{\mathrm {O}}}\,\tau ^2}{r_{{\mathrm {I}}}}\right) {+}\frac{D\,r_{{\mathrm {I}}}}{\tau \,r_{{\mathrm {O}}}}{\mathrm {Int}}\left( \frac{x'_i\,r_{{\mathrm {O}}}\,\tau ^2}{r_{{\mathrm {I}}}}\right) \right) . \end{aligned} \end{aligned}$$

Introducing \(\rho _{{\mathrm {I}}}=r_{{\mathrm {I}}}/(r_{{\mathrm {O}}}\,\tau ^2)=r_{{\mathrm {I}}}/X_{{\mathrm {O}}}\) one can write:

$$\begin{aligned} \begin{aligned}&x''(T)+2\delta {\hat{\alpha }} x'(T)-{\hat{\alpha }}^2 x(T)\\&\quad = -\,{\mathrm {Int}}\left( P\,\tau ^2\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( \frac{x_i}{\rho _{{\mathrm {I}}}}\right) +D\,\tau \,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( \frac{x'_i}{\rho _{{\mathrm {I}}}}\right) \right) , \end{aligned} \end{aligned}$$

where \({\hat{P}}\) and \({\hat{D}}\) can be recognized [see Eq. (3)] and it can be seen that \(\rho _{{\mathrm {I}}}\) acts as a resolution for the input quantization and the output quantizer has unit resolution:

figure a

2.2 Characteristic displacement for unit resolution input quantization

Using \(X_{{\mathrm {I}}}\) and \(\rho _{{\mathrm {O}}}=r_{{\mathrm {O}}}\,\tau ^2/r_{{\mathrm {I}}}=1/\rho _{{\mathrm {I}}}\), a similar derivation leads to:

$$\begin{aligned} \begin{aligned}&x''(T)+2\delta {\hat{\alpha }} x'(T)-{\hat{\alpha }}^2 x(T)\\&\quad =-\rho _{{\mathrm {O}}}\,{\mathrm {Int}}\left( \frac{P\,r_{{\mathrm {I}}}}{r_{{\mathrm {O}}}}{\mathrm {Int}}\left( x_i\right) +\frac{D\,r_{{\mathrm {I}}}}{\tau \,r_{{\mathrm {O}}}}{\mathrm {Int}}\left( x'_i\right) \right) . \end{aligned} \end{aligned}$$

Exploiting the definition of \({\hat{P}}\), \({\hat{D}}\) and \(\rho _{{\mathrm {O}}}\) we arrive at the following equation:

figure b

where the input quantizer has unit resolution and \(\rho _{{\mathrm {O}}}\) acts as a resolution for the output quantization.

In Equations (\(4_{{\mathrm {I}}}\)–\(4_{{\mathrm {O}}}\)), a single quantization ratio (\(\rho \)) characterizes the ratio of input and output quantization resolutions. For large \(\rho _{{\mathrm {I}}}\) or small \(\rho _{{\mathrm {O}}}\) values, the input quantization dominates, and the outer quantization can be practically neglected. Similarly, for large \(\rho _{{\mathrm {O}}}\) or small \(\rho _{{\mathrm {I}}}\) values, the output quantization is more significant. Lastly, when the characteristic displacements \(X_{{\mathrm {I}}}\) and \(X_{{\mathrm {O}}}\) are equal, \(\rho _{{\mathrm {O}}} = \rho _{{\mathrm {I}}} = 1\), therefore both quantizations have the same unit resolution.

It may seem that one could continue by choosing one of the characteristic displacements \(X_{{\mathrm {I}}}\) (and the corresponding resolution \(\rho =\rho _{{\mathrm {O}}}\)) or \(X_{{\mathrm {O}}}\) (with \(\rho = \rho _{{\mathrm {I}}}\)) and examine the \(\rho \rightarrow 0\) and \(\rho \rightarrow \infty \) limits to express the single quantization cases. However, neither of the two choices are perfect, as the upper limit of quantization is

$$\begin{aligned} \lim \limits _{\rho \rightarrow \infty }\rho \,{\mathrm {Int}}(x/\rho ) = 0, \end{aligned}$$
(5)

consequently the control effort turns to zero in Equations (\(4_{{\mathrm {I}}}\)–\(4_{{\mathrm {O}}}\)); thus, this model does not reflect the physical properties of the single quantization controller.

Taking the lower limit, we obtain

$$\begin{aligned} \lim \limits _{\rho \rightarrow 0}\rho \,{\mathrm {Int}}(x/\rho ) = x, \end{aligned}$$
(6)

which means that the twofold quantization turns to single quantization because the infinitely fine resolution quantizer yields the original signal itself (see Fig. 3).

Consequently, it can be firmly stated that none of the single-parameter twofold quantization equations (\(4_{{\mathrm {I}}}\)) or (\(4_{{\mathrm {O}}}\)) can be solely used to analyse the transition to both single quantization cases.

Therefore, we use Eq. (\(4_{{\mathrm {I}}}\)) to examine the transition from twofold quantization to single quantization at the output (\(\rho _{{\mathrm {I}}} \rightarrow 0\)), and similarly Eq. (\(4_{{\mathrm {O}}}\)) to inspect the transition to the single quantization at the input (as \(\rho _{{\mathrm {O}}} \rightarrow 0\)):

$$\begin{aligned} \begin{aligned}&{\mathrm {Int}}\left( \hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x_{i}/\rho _{{\mathrm {I}}}\right) +\hat{D}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x'_{i}/\rho _{{\mathrm {I}}}\right) \right) \xrightarrow [\rho _{{\mathrm {I}}} \rightarrow 0]{} \qquad \\&\quad {\mathrm {Int}}\left( \hat{P}\,x_{i}+\hat{D}\,x'_{i}\right) , \\&\rho _{{\mathrm {O}}}\,{\mathrm {Int}}\left( \frac{\hat{P}}{\rho _{{\mathrm {O}}}}{\mathrm {Int}}\left( x_i\right) +\frac{\hat{D}}{\rho _{{\mathrm {O}}}}{\mathrm {Int}}\left( x'_i\right) \right) \xrightarrow [\rho _{{\mathrm {O}}} \rightarrow 0]{} \qquad \\&\quad \hat{P}\,{\mathrm {Int}}(x_{i})+\hat{D}\,{\mathrm {Int}}(x'_{i}). \end{aligned} \end{aligned}$$

It is worth noting that one can trivially switch between (\(4_{{\mathrm {I}}}\)) and (\(4_{{\mathrm {O}}}\)) at \(\rho _{{\mathrm {I}}} = \rho _{{\mathrm {O}}} = 1\) or also can use one of the representations to examine the effect of rather large values of \(\rho \), without switching to the other representation.

Fig. 3
figure 3

Visualization of \(\lim \limits _{\rho \rightarrow 0}\rho \, {\mathrm {Int}}(x/\rho ) = x\) (for \(x=1\)) and \(\lim \limits _{\rho \rightarrow \infty }\rho \,{\mathrm {Int}}(x/\rho )\). The values of the non-smooth function \(\rho \,{\mathrm {Int}}(x/\rho )\) are between the bounds x and \(x-\rho \)

Full size image

3 Numerical analysis of the micro-chaos map

3.1 Micro-chaos map

Equations (\(4_{{\mathrm {I}}}\)–\(4_{{\mathrm {O}}}\)) characterize the behaviour of the inverted pendulum with sampling, PD-control and quantization at both input and output. Rewriting it as a system of first-order differential equations, one can formulate its solution as:

$$\begin{aligned} {\mathbf {y}}(T)={\mathbf {U}}(T){\mathbf {y}}(0)+{\mathbf {b}}(T)\,F(T),\quad T\in [0,1), \end{aligned}$$
(7)

where \({\mathbf {y}}=[x(T)\quad x'(T)]^T\), \({\varGamma }=\sqrt{1+\delta ^2}\), F is the control effort,

$$\begin{aligned} \begin{aligned}&{\mathbf {U}}(T)=\frac{e^{-\hat{\alpha } \delta T}}{{\varGamma }} \,\cdot \\&\left[ \begin{array}{cc} {\varGamma } {\,{\mathrm {ch}}}\left( \hat{\alpha } {\varGamma } T\right) +\delta {\,{\mathrm {sh}}}\left( \hat{\alpha } {\varGamma } T\right) &{} {\,{\mathrm {sh}}}\left( \hat{\alpha } {\varGamma } T\right) /\hat{\alpha } \\ \hat{\alpha } {\,{\mathrm {sh}}}\left( \hat{\alpha } {\varGamma } T\right) &{} {\varGamma } {\,{\mathrm {ch}}}\left( \hat{\alpha } {\varGamma } T\right) -\delta {\,{\mathrm {sh}}}\left( \hat{\alpha } {\varGamma } T\right) \\ \end{array} \right] , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} {\mathbf {b}}(T)=\frac{1}{{{\hat{\alpha }}}^2 {\varGamma }}\left[ \begin{array}{cc} {\varGamma } -e^{-\hat{\alpha } \delta T} \left( {\varGamma } {\,{\mathrm {ch}}}\left( \hat{\alpha } {\varGamma } T\right) +\delta {\,{\mathrm {sh}}}\left( \hat{\alpha } {\varGamma } T\right) \right) \\ -\hat{\alpha } e^{- \hat{\alpha } \delta T}{\,{\mathrm {sh}}}\left( \hat{\alpha } {\varGamma } T\right) \end{array}\right] . \end{aligned}$$

Substituting \(T=1\), the so-called micro-chaos map [10] is obtained, which is valid at sampling instants:

$$\begin{aligned}&{\mathbf {y}}_{i+1} {=}{\mathbf {U}}(1) \, {\mathbf {y}}_i+{\mathbf {b}}(1)\,F_i, \quad {\mathrm {where}} \nonumber \\&F_i{=}{\mathrm {Int}}\left( \rho _{{\mathrm {I}}}\,({\hat{P}}\,{\mathrm {Int}}(x_{i}/\rho _{{\mathrm {I}}}){+}{\hat{D}} \,{\mathrm {Int}}(x'_{i}/\rho _{{\mathrm {I}}})) \right) \ \text{ if } \ X {=} X_{{\mathrm {I}}}, \nonumber \\&\quad {\mathrm {or}} \nonumber \\&F_i{=}\rho _{{\mathrm {O}}}\,{\mathrm {Int}}\left( \frac{1}{\rho _{{\mathrm {O}}}}\,({\hat{P}}\,{\mathrm {Int}}(x_{i}){+}{\hat{D}} \,{\mathrm {Int}}(x'_{i})) \right) \ \text{ if } \ X {=} X_{{\mathrm {O}}}.\nonumber \\ \end{aligned}$$
(8)

Here \(F_i\) is the control effort between the dimensionless sampling instants \(T = i\) and \(T=i+1\).

Note, that the Lyapunov exponents of the micro-chaos map are known analytically, as they are the eigenvalues of \({\mathbf {U}}(1)\):

$$\begin{aligned} \lambda _{1,2} = e^{\hat{\alpha }(-\delta \pm {\varGamma })} = e^{\hat{\alpha }(-\delta \pm \sqrt{1+\delta ^2})}. \end{aligned}$$
(9)

As \({\varGamma } > \delta \), the Lyapunov exponents are always real numbers with opposite signs.

It is clear that the quantization causes the control effort \(F_i\) to be a piecewise constant function over the state space, which consists of domains, each corresponding to a specific \(F_i\) value. When the output quantization is dominant, \(F_i = {\mathrm {Int}}\left( \hat{P}\,x_{i}+\hat{D}\,x'_{i}\right) \). Thus, the aforementioned domains are parallel bands separated by parallel switching lines that can be given as

$$\begin{aligned} x' = \frac{m-Px}{D}, \quad m \in {\mathbb {Z}}, \end{aligned}$$
(10)

(see Figs. 4 and 6).

For the input quantization case, however, these domains are rectangular areas since \(F_i = \hat{P}\,{\mathrm {Int}}(x_{i})+\hat{D}\,{\mathrm {Int}}(x'_{i})\). Consequently, the quantization results in a grid of horizontal and vertical switching lines (see Figs. 5 and 6).

Based on former research [3, 8], in the case of single quantization at the output, multiple chaotic attractors can be found in the state space, at the intersections of switching lines and the x-axis, as it is illustrated in Fig. 4. Depending on system and control parameters, attractors may appear or disappear due to border collision bifurcation, or some of them may become repellers, and form one or more bigger attractors, by pushing the trajectory towards each other [2].

Fig. 4
figure 4

Output quantization. State space of the micro-chaos map at \(\hat{\alpha }=0.07\), \(\delta =0.03\), \(\hat{P}=0.007\), \(\hat{D}=0.02\), \(r_{{\mathrm {I}}}\rightarrow 0\) and \(r_{{\mathrm {O}}}=1\). Three example trajectories are shown starting from \(x=0\) and : \(x'=10\), : \(x'=13\), : \(x'=15\). The first trajectory ( ) ends up in an attractor on the switching line between control effort bands \(F=2\) and \(F=3\), the second one ( ) ends up in an attractor between bands \(F=0\) and 1, while the third ( ) ends up in an attractor between bands \(F=1\) and 2. Close-up images of the attractors are also provided in the balloons with the corresponding colour. (Color figure online)

Full size image

In case of input quantization, our general observation is that a periodic orbit (with superimposed chaotic oscillations) appears around the internal structure of repellers. Depending on the parameters, one or more chaotic attractors spanning over multiple control effort bands can be found, see Fig. 5.

3.2 Cell mapping results

In order to explore the effect of varying the quantization ratio and examine the transitions from twofold to single quantization cases, Cell Mapping Methods [11] were utilized. Simple Cell Mapping (SCM) is suitable to obtain a global picture of a certain state space region, i.e. to find periodic orbits, fixed points and their domains of attraction. Chaotic attractors are usually covered by one or more high-period cell groups [11].

Fig. 5
figure 5

Input quantization. Switching lines and example periodic orbits with superimposed chaotic oscillations at \(\hat{\alpha }=0.007\), \(\delta =0.\), \(\hat{P}=0.027\), \(\hat{D}=0.02\) and \(\rho _{{\mathrm {I}}}=0.8\). Two example trajectories are shown starting from \(x'=0\) and : \(x=8\) and : \(x=15\). They end up in separated periodic orbits with superimposed chaotic oscillations. (Color figure online)

Full size image
Fig. 6
figure 6

Top switching lines and control effort bands in case of output quantization. Bottom switching line grid and control effort tiles in case of input quantization

Full size image

Utilizing Clustered Simple Cell Mapping [9], it is possible to automatically extend the analysed state space region and also execute cell mapping in a parallel computing environment.

Our primary goal is to express the control error; therefore, we extract the location (centre of mass; \(x_{{\mathrm {attr}}}\), \(y_{{\mathrm {attr}}}\)) and size (\(S_x,S_y\)) of chaotic attractors (see Fig. 7). In the output quantization case, the attractors reside on the x-axis (\(y_{{\mathrm {attr}}}=0\)). Since the desired control state is the origin, any solution arriving to a specific attractor will yield a mean control error of \(x_{{\mathrm {attr}}}\).

Fig. 7
figure 7

Top example attractor obtained by SCM and illustration of extracted properties, location of attractor’s centre of mass (\(x_{{\mathrm {attr}}}\), \(y_{{\mathrm {attr}}}\)) and the extent along x and \(x'\) axes: (\(S_x,S_y\)). Bottom the same attractor obtained by numerical simulation

Full size image

We have generated a series of SCM solutions by sweeping the parameter \(\rho _{{\mathrm {I}}}\) for some fixed \(\alpha , \beta , \hat{P}\) and \(\hat{D}\) values. Figure 8 shows the transition from \(\rho _{{\mathrm {I}}}=0\) to \(\rho _{{\mathrm {I}}}=16\) at \(\hat{P}=0.007, \hat{D}=0.02, \alpha = 0.074\) and \(\delta = 0\), which correspond to the parameters of a realistic experimental device. Here the output quantization case has eight separated chaotic attractors (four-four on both sides, see Fig. 9top) and as the quantization ratio increases, these attractors eventually become repellers. At \(\rho _{{\mathrm {I}}}=1.28\) (see Fig. 9bottom), the outermost attractors disappear resulting in a more favourable state space configuration in terms of control error.

We trace back the aforementioned results to two phenomena: as it can be seen in Fig. 7, the switching lines become jagged, and consequently regions appear in the state space corresponding to only-P and only-D control (so-called input deadzones, see Fig. 6), due to the quantization of measured values. In the next section, we examine the effect of these new deadzones.

3.3 Deadzone crisis

For output quantization, the deadzone of the output quantizer creates an unstable band between switching lines \({\textsc {sw}}_{-1}\) and \({\textsc {sw}}_{1}\) (see Figs. 4 and 6). On the other hand, in case of input quantization the two deadzones (corresponding to the measured values’ quantizers) around the x and \(x'\) axes will cause the PD-control to work as only-P control for small velocities and only-D control for small displacements (see Fig. 6).

Fig. 8
figure 8

Transition from output quantization to twofold quantization. At \(\rho _{{\mathrm {I}}}\approx 1.3\), the outermost chaotic attractors, while at \(\rho _{{\mathrm {I}}}\approx 2.4\), the innermost attractors disappear due to deadzone crisis (denoted by X). At \(\rho _{{\mathrm {I}}}\approx 4.7\) the chaotic attractors merge (denoted by arrows) on both sides, and lastly at \(\rho _{{\mathrm {I}}}\approx 12\), they merge again resulting in a single recurring orbit with superimposed chaotic vibrations

Full size image
Fig. 9
figure 9

SCM results illustrating deadzone crisis. Top 4–4 separated attractors and their domains of attraction are highlighted at \(\rho _{{\mathrm {I}}}=1.247\). Bottom outermost attractors disappear via deadzone crisis at \(\rho _{{\mathrm {I}}}=1.287\). Coloured regions indicate domains of attractions, pink circles highlight chaotic attractors, white crosses denote unstable fixed points. (Color figure online)

Full size image

In the case of twofold quantization, during the variation of the quantization ratio, the borders of the output deadzone (uncontrolled region between the \({\textsc {sw}}_{\pm 1}\) switching lines, where the control effort is \(F=0\)) and input deadzones (deadzones around x and \(x'\) axes, where either part of the PD-control is offline) move, thus state space objects (e.g. attractors or periodic orbits) can disappear or qualitatively change. This is called deadzone crisis.

To illustrate a possible scenario, consider Fig. 10. As the quantization ratio \(\rho _{{\mathrm {I}}}\) increases, the steps on the switching lines grow. At the intersection of the x-axis and the switching line, the switching line becomes locally vertical in the range of the input quantizer’s deadzone and the attractor adapts to this by expanding proportionally. At a certain point—as the switching line gets close to the stable manifold of the nearby saddle point—a deadzone crisis happens, and the solution will be able to escape from the chaotic attractor, leaving a transient chaotic repeller behind.

During the transition from the output quantization to twofold quantization, a series of deadzone crises occur and eventually all chaotic attractors turn to repellers. The interactions of the repellers lead to a newly formed recurring orbit with superimposed chaotic oscillations (see Sect. 3.2 and Fig. 8).

Based on these results, it is obvious that the non-smooth, stair-like shape of the switching lines play an important role in manipulating state space objects by opening up escape possibilities from the previously closed domains of chaotic attractors.

To gain a deeper insight in this phenomenon, the following section examines the topology of switching lines.

4 Analysis of switching lines

4.1 Switching line collision

For the single quantization cases, the switching lines corresponding to different efforts of the PD-control are simple to express: parallel lines ( \(\hat{P}\,x+\hat{D}\,x'=m, m \in {\mathbb {Z}}\)) for the output quantization, and a grid of lines (\(x=i\,\rho _{{\mathrm {I}}},\)\(x'=j\,\rho _{{\mathrm {I}}},\)\(i,j \in {\mathbb {Z}}\)) for the input quantization. In the twofold quantization case, however, their explicit expression is not straightforward.

Fig. 10
figure 10

Deadzone crisis increasing the quantization ratio changes the switching line and the chaotic attractor around it. As the step around the x-axis becomes larger, the switching line becomes locally vertical. Top row\({{\rho }}_{\mathrm{I}}=0.1\) and \({{\rho }}_{\mathrm{I}}=0.5\). Bottom row\({{\rho }}_{\mathrm{I}}=1\), \({{\rho }}_{\mathrm{I}}=2.5\). The last subfigure illustrates the crisis, when transient chaotic solution escapes by jumping over the stable manifold (indicate by blue arrow) of the neighbouring fixed point. (Color figure online)

Full size image
Fig. 11
figure 11

Conjugated integer part function Int\(^*()\), i.e. rounding towards infinity

Full size image

For this section of the paper, we use Eq. (\(4_{{\mathrm {I}}}\)) and \(\rho _{{\mathrm {I}}}\). Starting with the implicit equation of the control effort:

$$\begin{aligned} {\mathrm {Int}}\left( \hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x/\rho _{{\mathrm {I}}}\right) {+}\hat{D}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x'/\rho _{{\mathrm {I}}}\right) \right) =m, \quad m \in {\mathbb {Z}}. \end{aligned}$$

The domain of control effort band \(F_i = m\) is bounded by two switching lines: \({\textsc {sw}}_{{\mathrm {m}}}\) and \({\textsc {sw}}_{\mathrm {m+1}}\), see Fig. 4. The equation of the lower bounding switching line is

$$\begin{aligned} \begin{aligned}&{\textsc {sw}}_{{\mathrm {m}}}: \quad \hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x/\rho _{{\mathrm {I}}}\right) {+}\hat{D}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x'/\rho _{{\mathrm {I}}}\right) {=}m,\quad m \in {\mathbb {Z}}, \end{aligned}\nonumber \\ \end{aligned}$$
(11)

while the upper bounding switching line can be expressed implicitly as

$$\begin{aligned} \begin{aligned} {\textsc {sw}}_{\mathrm {m+1}}{\mathrm {:}}\quad \hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x/\rho _{{\mathrm {I}}}\right) +\hat{D}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x'/\rho _{{\mathrm {I}}}\right)&=m+1,\\&\quad m \in {\mathbb {Z}}. \end{aligned}\nonumber \\ \end{aligned}$$
(12)

Expressing the quantized velocity (\(\rho _{{\mathrm {I}}}\,{\mathrm {Int}}(x'/\rho _{{\mathrm {I}}})\)) from Eq. (11):

$$\begin{aligned} \rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x'/\rho _{{\mathrm {I}}}\right) =\frac{m-\hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x/\rho _{{\mathrm {I}}}\right) }{\hat{D}}, \quad m \in {\mathbb {Z}}, \end{aligned}$$

and applying the conjugated version (\({\mathrm {Int}}^*\)) of the rounding function used in quantizers, i.e. rounding towards infinity without deadzone (see Fig. 11), yields the explicit formula of the switching lines:

$$\begin{aligned} x'=\rho _{{\mathrm {I}}}\,{\mathrm {Int}}^* \left( \frac{m-\hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x/\rho _{{\mathrm {I}}}\right) }{\hat{D}\,\rho _{{\mathrm {I}}}}\right) , \quad m \in {\mathbb {Z}}. \end{aligned}$$
(13)

One can similarly derive the inverse expression:

$$\begin{aligned} x=\rho _{{\mathrm {I}}}\,{\mathrm {Int}}^* \left( \frac{m-\hat{D}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x'/\rho _{{\mathrm {I}}}\right) }{\hat{P}\,\rho _{{\mathrm {I}}}}\right) , \quad m \in {\mathbb {Z}}. \end{aligned}$$
(14)

As the quantization ratio increases further, the stairs on the switching lines become larger, and at some point, the jagged switching lines will touch each other (see Fig. 12). This event—which will be referred to as Switching Line Collision (slc)—changes the topology of control effort bands in the state space, regardless of the dynamics of the system under control as the switching lines depend only on the control strategy.

When switching line collision occurs, trajectories gain the ability to bypass certain control bands by passing through a switching line intersection point. In the case of PD-control—if there is no switching line collision—bands corresponding to the same control effort are connected domains. However, if the switching lines \({\textsc {sw}}_{{\mathrm {m}}}\) and \({\textsc {sw}}_{\mathrm {m+1}}\) collide, the band \(F_i = m\) becomes disconnected (see Fig. 12).

Observing the collision of \({\textsc {sw}}_m\) and \({\textsc {sw}}_{m+1}\) at \(x=i\,\rho _{{\mathrm {I}}}\), \(x'=j\,\rho _{{\mathrm {I}}}\), one can write the following condition:

$$\begin{aligned} \begin{aligned}&\lim \limits _{\varepsilon \rightarrow 0} \rho _{{\mathrm {I}}}\,{\mathrm {Int}}^* \left( \frac{m-\hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}(i-\varepsilon )}{\hat{D}\,\rho _{{\mathrm {I}}}}\right) \\&\quad = \lim \limits _{\varepsilon \rightarrow 0} \rho _{{\mathrm {I}}}\,{\mathrm {Int}}^* \left( \frac{(m+1)-\hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}(i+\varepsilon )}{\hat{D}\,\rho _{{\mathrm {I}}}}\right) . \end{aligned} \end{aligned}$$

Here the left and right hand sides correspond to switching lines \({\textsc {sw}}_m\) and \({\textsc {sw}}_{m+1}\), respectively (see Eq. (11–12)), both sides equal to \(x' = j\,\rho _{{\mathrm {I}}}\) and \(\{i,j,m\} \in {\mathbb {Z}}\).

Fig. 12
figure 12

Switching lines at \(\hat{P}=2/5\), \(\hat{D}=2/9\) and \(\rho _{{\mathrm {I}}}=0.33\) (left) \(\rho _{{\mathrm {I}}}=1.0\) (centre), \(\rho _{{\mathrm {I}}}=1.65\) (right). The latter value is slightly above \(\rho _{{\mathrm {I}}}^{L,i} = 1/(\hat{P}+\hat{D}) \approx 1.61\). Black lines indicate the switching lines for the output quantization case, gray gridlines indicate the \(\rho _{{\mathrm {I}}}\)-spaced grid corresponding to the input quantization. Red point highlights switching line collision, pink and blue points highlight upper corners of \({\textsc {sw}}_2\) and lower corners of \({\textsc {sw}}_3\), respectively. Green region indicates control effort band \(F = 2\) which becomes disconnected due to slc. (Color figure online)

Full size image
Fig. 13
figure 13

Switching lines at \(\hat{P}=2/5\), \(\hat{D}=2/9\) and critical quantization ratios \(\rho _{{\mathrm {I}}}=2.0\) (left), \(\rho _{{\mathrm {I}}}=\rho _{{\mathrm {I}}}^{1,i}=1/\hat{P}\) (centre), \(\rho _{{\mathrm {I}}}=\rho _{{\mathrm {I}}}^{2,i}=2/\hat{P}\) (right). Trajectories going through intersection points may bypass certain control effort bands. Orange points highlight \(2{{\mathrm {nd}}}\) order switching line collisions. (Color figure online)

Full size image

Since the quantization \({\mathrm {Int}}(i)\) has a discontinuity (see Fig. 14), we analyse a small neighbourhood \(\varepsilon \) around \(x=i\,\rho _{{\mathrm {I}}}\) and express the collision between the upper corner of the lower switching line (\({\textsc {sw}}_m\)) and the lower corner of the upper switching line (\({\textsc {sw}}_{m+1}\)).

Expressing the limits, we can substitute \(\lim _{\,\varepsilon \rightarrow 0}{\mathrm {Int}}(i-\varepsilon )=i-1\) for \({\textsc {sw}}_m\) and use \(\lim _{\,\varepsilon \rightarrow 0}{\mathrm {Int}}(i+\varepsilon )=i\) for \({\textsc {sw}}_{m+1}\), resulting in the following equation:

$$\begin{aligned} \begin{aligned}&{\mathrm {Int}}^* \left( \frac{m-\hat{P}\,\rho _{{\mathrm {I}}}\,(i-1)}{\hat{D}\,\rho _{{\mathrm {I}}}}\right) =j\\&\quad = {\mathrm {Int}}^* \left( \frac{(m+1)-\hat{P}\,\rho _{{\mathrm {I}}}\,i}{\hat{D}\,\rho _{{\mathrm {I}}}}\right) ,&\quad \{i,j,m\} \in {\mathbb {Z}}. \end{aligned} \end{aligned}$$
(15)

Resolving the quantization to infinity (\({\mathrm {Int}}^*\)) in Eq. (15), the following inequalities can be written:

$$\begin{aligned} \begin{aligned}&(j-1)< \frac{m-\hat{P}\,\rho _{{\mathrm {I}}}\,(i-1)}{\hat{D}\,\rho _{{\mathrm {I}}}}&< j, \\&(j-1)< \frac{(m+1)-\hat{P}\,\rho _{{\mathrm {I}}}\,i}{\hat{D}\,\rho _{{\mathrm {I}}}}&< j. \end{aligned} \end{aligned}$$
(16)

The inequalities in Eq. (16) can be reformulated as

$$\begin{aligned}&\frac{1}{\hat{D}+\hat{P}}<\rho _{{\mathrm {I}}} \le \frac{1}{\hat{P}} \quad \wedge \quad \nonumber \\&\quad \frac{(m+1)-\hat{P}\,\rho _{{\mathrm {I}}}\,i}{\hat{D}\,\rho _{{\mathrm {I}}}} {\le } j{<} \frac{m-\hat{P}\,\rho _{{\mathrm {I}}}\,(i-1)+\hat{D}\,\rho _{{\mathrm {I}}}}{\hat{D}\,\rho _{{\mathrm {I}}}},\nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned}&\frac{1}{\hat{P}}< \overbrace{\rho _{{\mathrm {I}}}<\frac{1}{\hat{P}-\hat{D}}}^{{\mathrm {if}}\,\hat{P}>\hat{D}>0} \quad \wedge \quad \nonumber \\&\quad \frac{m-\hat{P}\,\rho _{{\mathrm {I}}}\,(i-1)}{\hat{D} \rho _{{\mathrm {I}}} }{\le } j{<}\frac{(m+1) - \hat{P}\,\rho _{{\mathrm {I}}}\,i+\hat{D}\, \rho _{{\mathrm {I}}}}{\hat{D} \rho _{{\mathrm {I}}} }.\nonumber \\ \end{aligned}$$
(18)

For a given m and i, Eq. (17–18) can be solved for \(j \in {\mathbb {Z}}\) to find switching line collisions between \({\textsc {sw}}_m\) and \({\textsc {sw}}_{m+1}\) at \([x,x']=\rho _{{\mathrm {I}}}\,[i,j]\).

These kind of slcs will be referred to as first-order switching line collisions (while in general, the \(k{{\mathrm {th}}}\) order slc means the collision of \({\textsc {sw}}_m\) and \({\textsc {sw}}_{m+k}\)).

It can be observed that there is a lowest quantization ratio for first-order switching line collisions to appear at a certain value of i in the state space:

$$\begin{aligned} \rho _{{\mathrm {I}}}^{L,i}=1/(\hat{P}+\hat{D}), \end{aligned}$$
(19)

When \(\rho _{{\mathrm {I}}} \ge \rho _{{\mathrm {I}}}^{L,i}\), first-order slcs are present in the state space and by increasing \(\rho _{{\mathrm {I}}}\), they become more and more frequent (see Fig. 13). Equation (17) reveals the value of the critical quantization ratio for which there is a solution for every i:

$$\begin{aligned} \rho _{{\mathrm {I}}}^{1,i}=1/\hat{P}. \end{aligned}$$
(20)

When \(\rho _{{\mathrm {I}}} = \rho _{{\mathrm {I}}}^{1,i}\), every switching line collides with its neighbour at coordinates \(x = i\,\rho _{{\mathrm {I}}}\), for all i. To prove this statement, one can substitute \(\rho _{{\mathrm {I}}}^{1,i}\) into Eq. (17), and the four inequalities are reduced to two relations:

$$\begin{aligned} (j-1)< \frac{m+1-i}{\hat{D}\,\rho _{{\mathrm {I}}}} < j. \end{aligned}$$
(21)

This result shows that there is a solution \(j\in {\mathbb {Z}}\) for every \(\{i,m\}\in {\mathbb {Z}}\):

$$\begin{aligned} j={\mathrm {Int}}^{*}\left( \frac{m+1-i}{\hat{D}\,\rho _{{\mathrm {I}}}}\right) . \end{aligned}$$
(22)

Note, that it does not imply that collision occurs for every \(x' = j\,\rho _{{\mathrm {I}}}\), too (see Fig. 13centre panel).

Fig. 14
figure 14

Illustration of switching line collision of \({\textsc {sw}}_m\) ( ) and \({\textsc {sw}}_{m+1}\) ( ) at \((i,j)\,\rho _{{\mathrm {I}}}\). The upper corner of \({\textsc {sw}}_m\) touches the lower corner of \({\textsc {sw}}_{m+1}\). (Color figure online)

Full size image

It follows from (18) that one can introduce the highest quantization ratio corresponding to the disappearance of first-order switching line collisions:

$$\begin{aligned} \rho _{{\mathrm {I}}}^{H,i}=1/(\hat{P}-\hat{D}) \quad {\mathrm {when}}\quad 0< \hat{D} < \hat{P}. \end{aligned}$$
(23)

When \(\rho _{{\mathrm {I}}} > \rho _{{\mathrm {I}}}^{H,i}\), first-order switching line collisions no longer present, because higher-order collisions take their place.

Expressing the condition for the collision of \({\textsc {sw}}_m\) and \({\textsc {sw}}_{m+1}\) for i (instead of j, similarly to Eq. (15)), one can write:

$$\begin{aligned} \begin{aligned}&{\mathrm {Int}}^* \left( \frac{m-\hat{D}\,\rho _{{\mathrm {I}}}\,(j-1)}{\hat{P}\,\rho _{{\mathrm {I}}}}\right) =i \\&\quad = {\mathrm {Int}}^* \left( \frac{(m+1)-\hat{D}\,\rho _{{\mathrm {I}}}\,j}{\hat{P}\,\rho _{{\mathrm {I}}}}\right) ,&\quad \{i,j,m\} \in {\mathbb {Z}}, \end{aligned} \end{aligned}$$
(24)

which yields the following inequalities:

$$\begin{aligned}&\frac{1}{\hat{P}+\hat{D}}<\rho _{{\mathrm {I}}} \le \frac{1}{\hat{D}} \quad \wedge \quad \nonumber \\&\quad \frac{(m+1)-\hat{D}\,\rho _{{\mathrm {I}}}\,j}{\hat{P}\,\rho _{{\mathrm {I}}}} {\le } i{<} \frac{m-\hat{D}\,\rho _{{\mathrm {I}}}\,(j-1)+\hat{P}\,\rho _{{\mathrm {I}}}}{\hat{P}\,\rho _{{\mathrm {I}}}},\nonumber \\ \end{aligned}$$
(25)
$$\begin{aligned}&\frac{1}{\hat{D}}< \overbrace{\rho _{{\mathrm {I}}}<\frac{1}{\hat{D}-\hat{P}}}^{{\mathrm {if}}\,\hat{D}>\hat{P}>0} \quad \wedge \quad \nonumber \\&\quad \frac{m-\hat{D}\,\rho _{{\mathrm {I}}}\,(j-1)}{\hat{P} \rho _{{\mathrm {I}}} }{\le } i{<}\frac{(m+1) - \hat{D}\,\rho _{{\mathrm {I}}}\,j+\hat{P}\, \rho _{{\mathrm {I}}}}{\hat{P} \rho _{{\mathrm {I}}} }.\nonumber \\ \end{aligned}$$
(26)

Here another critical quantization ratio is revealed for which Eqs. (25–26) have a solution for every j (but not necessarily for every \(x = i\,\rho _{{\mathrm {I}}}\)):

$$\begin{aligned} \rho _{{\mathrm {I}}}^{1,j}=1/\hat{D}. \end{aligned}$$
(27)

Combining Eqs. (20) and (27), one can express a combined critical quantization ratio:

$$\begin{aligned} \rho _{{\mathrm {I}}}^{1}={\mathrm {max}}(\rho _{{\mathrm {I}}}^{1,i},\rho _{{\mathrm {I}}}^{1,j})={\mathrm {max}}(1/\hat{P},1/\hat{D}). \end{aligned}$$
(28)

If \(\rho _{{\mathrm {I}}} \ge \rho _{{\mathrm {I}}}^{1}\), switching line collisions occur for all i and j.

Expressing higher-order switching line collisions in a similar fashion, one can arrive at the formulae of k-th order critical quantization ratios for the collision of \({\textsc {sw}}_m\) and \({\textsc {sw}}_{m+k}\) at \(\forall \,i \in {\mathbb {Z}}\) and \(\forall \,j \in {\mathbb {Z}}\), respectively:

$$\begin{aligned} \rho _{{\mathrm {I}}}^{k,i}= & {} k/\hat{P},\end{aligned}$$
(29)
$$\begin{aligned} \rho _{{\mathrm {I}}}^{k,j}= & {} k/\hat{D}. \end{aligned}$$
(30)

It is important to note that due to the double deadzone of the mid-tread quantizer (see Fig. 2), switching line collisions of \({\textsc {sw}}_{-1}\) and \({\textsc {sw}}_{+1}\) are \(2{{\mathrm {nd}}}\) order ones.

Here we considered only the case of positive \(\hat{P}\) and \(\hat{D}\), but a similar analysis can be carried out for negative control parameters, as well.

In the following sections, we show how the transition between the twofold and single quantization cases affects the switching lines.

4.2 Transition from twofold quantization to output quantization

It is clear—based on Sect. 4, and Eq. (13)—that refining the input quantizer (\(\rho _{{\mathrm {I}}} \rightarrow 0\)) means smaller steps on the jagged switching lines, and eventually the transition to output quantization leads to a set of parallel lines.

$$\begin{aligned} \begin{aligned}&\rho _{{\mathrm {I}}}\,{\mathrm {Int}}^* \left( \frac{m-\hat{P}\,\rho _{{\mathrm {I}}}\,{\mathrm {Int}}\left( x/\rho _{{\mathrm {I}}}\right) }{\hat{D}\,\rho _{{\mathrm {I}}}}\right) \xrightarrow [\rho _{{\mathrm {I}}} \rightarrow 0]{} \frac{m-\hat{P}\,x}{\hat{D}} \\&\quad m \in {\mathbb {Z}}. \end{aligned} \end{aligned}$$
(31)

One can imagine this kind of transition by looking at Fig. 12. The transition from twofold quantization to input quantization, however, is not this trivial.

4.3 Transition from twofold quantization to input quantization

Switching lines corresponding to input quantizations form a regular grid of horizontal (Int(y)) and vertical (Int(x)) lines (see Fig. 6right). The square shaped domains (or rectangle shaped domains around the axes) between switching lines correspond to integer value linear combination of the control parameters, e.g. \(F=i\,\hat{P}+j\,\hat{D}\) control effort at \({\mathrm {Int}}(x)=i,\,{\mathrm {Int}}(x')=j\).

If we would like to achieve the same structure of switching lines in the twofold quantization case, the following conditions must be satisfied:

  • Condition 1 switching lines must partition the state space into square shaped domains, i.e. for every \(x'\) value, crossing \(x=i,\,(i\in {\mathbb {Z}})\) values must result in a switch in the control effort value. Similarly, for every x value, crossing \(x'=j,\,(j\in {\mathbb {Z}})\) must also result in a switch.

  • Condition 2 for each domain between the switching lines, the control effort value should be the same as in the case of input quantization.

Condition 1 can be satisfied by using \(\rho _{{\mathrm {O}}} \le \rho _{{\mathrm {O}}}^{1}\) (where \(\rho _{{\mathrm {O}}}^{1} = 1/\rho _{{\mathrm {I}}}^{1}={\mathrm {min}}(\hat{P},\hat{D})\)), which corresponds to \(\rho _{{\mathrm {I}}} \ge {\mathrm {max}}(1/\hat{P},1/\hat{D})\) (see Eq. (28)), because in this case, for all \(i,j \in {\mathbb {Z}}\)—at least first order—switching line collision takes place.

It can be seen, that once Condition 1 is satisfied (and the structure of the state space matches the input quantization case), the control effort value of twofold quantization will be within an error of \(\rho _{{\mathrm {O}}}\) to the control effort value of the input quantization case [see Eq. (8)]. It follows therefore, that \(\rho _{{\mathrm {O}}}\rightarrow 0\) will satisfy Condition 2.

5 Conclusion

We have shown that twofold quantization in digital control can be characterized by the quantization ratio, corresponding to the ratio of input and output quantizers’ resolution. We have presented that twofold quantization can be reduced to a single quantization case (input or output quantization) if an appropriate quantization ratio \(\rho \) is used and its limit \(\rho \rightarrow 0\) is analysed.

The micro-chaos map corresponding to a digitally controlled inverted pendulum was presented and the Clustered Simple Cell Mapping method was used to analyse the effect of varying the quantization ratio. Numerical results revealed, that the chaotic attractors disappear or merge due to the change of the switching lines and deadzones corresponding to input quantization.

We have presented, that deadzone crisis occurs, when the innermost stair on the switching line—governed by the input quantization deadzone—grows large enough to collide with other state space objects. Analysing an example transition from output to twofold and finally input quantization, we have highlighted that a series of deadzone crises happen and separated chaotic attractors merge into a single recurring orbit.

Another interesting effect, the switching line collision was also introduced, which can induce qualitative changes in the state space of continuous flows. Since the solutions of maps are allowed to “jump” in the phase-space, the effects of slc are less pronounced in the case of maps. This is the reason why no slc-related sudden bifurcations were detected during the analysis of the micro-chaos map.

From practical point of view, it is possible to improve the properties of the control for a given application, by carrying out an analysis of the quantization ratio and selecting a favourable range as illustrated in Sect. 3.2. Doing so, one can also find out how to improve a certain controlled system, i.e. which quantizer should be replaced by a higher-resolution one. In some cases one can even arrive to an unnatural conclusion, that using lower-resolution output quantizer or larger sampling time will actually result in lower control error. Similar results were found in [15, 16], where the quantization improved the stability properties of the controlled system.