Chaos control in the fractional order logistic map via impulses

Abstract

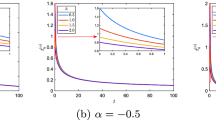
In this paper, the chaos control in the discrete logistic map of fractional order is obtained with an impulsive control algorithm. The underlying discrete initial value problem of fractional order is considered in terms of Caputo delta fractional difference.Every $\Delta$ steps, the state variable is instantly modified with the same impulse value, chosen from a bifurcation diagram versus impulse. It is shown that the solution of the impulsive control is bounded. The numerical results are verified via time series, histograms and the 0-1 test. Several examples are considered.

Appendix

1.1 The ‘0-1’ test

The ’0-1’ test has its roots in [41] been developed in [42] (see also [43] or [44]). It is designed to distinguish chaotic behavior from regular behavior in deterministic systems. The input being a time series, the test is easy to implement and does not need the system equations. Consider a discrete or continuous-time dynamical system and a one-dimensional observable dataset, constructed from a time series, $\phi (j)$, $j=1,2,\ldots ,N$, with N some positive integer. The ‘0-1’ test bases on a theorem, which states that a nonchaotic motion is bounded, while a chaotic dynamic behaves like a Brownian motion [41].

• (1) First, for $c\in [0,2\pi ]$, one computes the translation variables p and q [42]

  $$\begin{aligned} p(n)=\sum _{j=1}^n\phi (j)\cos (jc),~~~ q(n)=\sum _{j=1}^n\phi (j)\sin (jc), \end{aligned}$$

  for $n=1,2,\ldots ,N$. The choice of c represents an important and sensible algorithm variable (see, for example, [43] where for c, the interval $[\pi /5,4\pi /5]$ is proposed).

• (2) To determine the growths of p and q, the mean square displacement M is determined:

  $$\begin{aligned} M(n)= & {} \lim _{N\rightarrow \infty }\frac{1}{N}\sum _{j=1}^N[p(j+n)-p(j)]^2\\&+\,[q(j+n)-q(j)]^2. \end{aligned}$$

  where $n\ll N$ (in practice, $n=N/10$ represents a good choice).

• (3) Next, the asymptotic growth rate K is defined as

  $$\begin{aligned} K=\lim _{n\rightarrow \infty }\log M(n)/\log n. \end{aligned}$$

If the underlying dynamics is regular (i.e., periodic or quasiperiodic), then $K \approx 0$; if the underlying dynamics is chaotic, then $K \approx 1$.

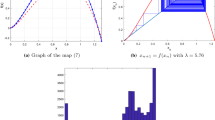
In Fig. 7, the case of the logistic map of integer order is presented. In Fig. 7a are presented the plots of q and p while in Fig. 7b the mean square displacement M as a function of n. In Fig. 1, the regular orbit of the logistic map $x_{n+1}=\mu x_n(1-x_n)$ for $\mu =3.55$ while Fig. 2 presents the chaotic orbit of the logistic map for $\mu =4$.