1 Introduction

Capsule endoscopy has been widely used in clinical practice for diagnosing gastrointestinal (GI) diseases, including obscure GI bleeding, Crohn’s disease, coeliac disease, angiodysplasia, tumours and polyposis syndromes [1,2,3]. It uses a swallowable capsule equipped with a miniature camera to screen the lining of the GI tract, visualising suspected lesions to clinicians. Capsule endoscopy has been considered as the gold standard for diagnosing disease in the small bowel [2], which was historically difficult to examine due to its small diameter and lengthy size. Compared with conventional endoscopies, e.g. colonoscopy and gastroscopy, capsule endoscopy provides a safe, minimally invasive, sedation-free, patient-friendly and accurate diagnostic modality. However, it is still an immature technique [4, 5] due to the following flaws: (i) The capsule endoscope is passively propelled by GI peristalsis. (ii) Real-time positioning and control are required for precise screening [6]. (iii) Biopsy and therapy are required for clinical treatment [7]. (iv) There is no unified and realistic model for capsule–intestine interaction [6], thus lacking the understanding of capsule’s locomotion in the small intestine. This paper will study the modelling of capsule–intestine contact when a capsule endoscope moves inside the small intestine and validate the modelling approach through experimentation, which will provide design and optimisation guidelines for the vibro-impact self-propelled capsule robot [8].

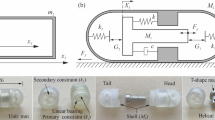
In the past decade, several locomotion mechanisms were developed to provide active propulsion for capsule endoscopes, including the rotating spiral [9], inchworm-like [10], legged [11], paddle-based [12] and vibro-impact [8] locomotion mechanisms. The vibro-impact capsule robot is self-propelled without any external moving parts. As shown in Fig. 1a, the vibro-impact capsule robot consists of a rigid shell (\(M_{\mathrm{c}}\)) and an inner mass (\(M_m \)) connecting to the shell via a spring (\(k_1\)) and a damper (c). A secondary spring (\(k_2\)), attached to the shell, provides impacts for the inner mass when the relative displacement between the capsule and the inner mass is equal to or larger than the gap (G). As the inner mass is driven by a harmonic force (\(P_d {\mathrm{cos}} (\omega t)\)), the interaction force between the shell and inner mass may exceed the environmental resistance (\(P_f\)) leading to a forward or backward motion of the whole capsule. The detailed mathematical modelling of the vibro-impact capsule robot can be found from [8]. Dimensions of the capsule prototype used in this study are presented in Fig. 1b, where the capsule is 26 mm in length and 11 mm in diameter.

Fig. 1
figure 1

(Color online) a Physical model of the vibro-impact self-propelled capsule robot and b photograph of the 3D printed capsule

Full size image

For prototyping the capsule robot, it is very important to know how much resistance will the capsule encounter from the small intestine, so a realistic capsule–intestine contact model is required. Recent studies on capsule–intestine interaction suggest that frictional resistance from the small intestine ranged from 10 to 200 mN depending on capsule’s shape, dimension and instantaneous velocity [13,14,15], and the friction coefficient between the capsule and the intestine could vary from 0.08 to 0.2 [13]. In order to increase the frictional resistance, capsule surface can be coated using micro-patterned adhesives [16, 17] or micro-pillar arrays [18], which could increase the friction coefficient up to 0.49 . Furthermore, analytical modelling of frictional resistance between a capsule endoscope and the intestine was considered and validated by experiments [19,20,21]. Peristaltic motion of the small intestine can induce contraction pressure on the capsule robot, and a capsule of 12 mm in diameter and 30 mm in length with two pressure sensors was studied in [22] to measure such a pressure. In vitro tests by using a 72 kg live pig found that the contraction rate was 9.4–11 times per minute, and the peak contraction pressure was \(0.24 \pm 0.05\) kPa. On the other hand, for some capsule robots with external moving parts, such as the legged and the paddle-based robots, the contact pressure between the robots and the intestine could be very large to cause trauma on the intestine, due to the limited contact area or the sharp edges of the legs and paddles. In vivo tests of rabbit’s small intestine under reciprocal sliding conditions [23] revealed that the increase in pressure aggravated the damage degree, from hyperaemia to haemorrhage, and even to degeneration. Therefore, such a contact model is vital for assessing the damage induced by the vibro-impact motion of the capsule robot on the intestine. The outcomes of this work will eventually provide design guidelines for the robot.

In addition, these aforementioned studies have not considered different contact conditions for the moving capsule, e.g. partial or full contact with the intestine, since the contact condition may change according to the gesture of the capsule and GI peristalsis. This in turn will affect the control strategy of the capsule robot causing the capsule unstable during a screening procedure. Therefore, our focus in this work will be on measuring the contact pressure between the capsule and the intestine under various contact conditions, and use experimental and numerical results to build a realistic capsule–intestine contact model. Since the contact pressure can directly reflect the capsule–intestine interaction, the findings from this work could be used to predict the frictional resistance between the capsule and the intestine. This will be practically crucial for clinicians to estimate the location of the capsule endoscope in the small intestine which is at the moment underrepresented.

The rest of this paper is organised as follows. Section 2 details the modelling of the contact pressure for three typical contact cases. The experimental and numerical set-ups are given in Sects. 3 and 4, respectively. In Sect. 5, experimental, analytical and numerical results are compared and discussed. Finally, conclusions are drawn in Sect. 6.

2 Modelling of capsule–intestine contact

The contact situation between the capsule and the small intestine may vary all the time due to the gesture of the capsule and GI peristalsis. To date, few studies have considered these contact conditions. In this section, three typical contact cases are investigated based on the realistic environment of the small intestine under the peristalsis, including partial and full contacts, as presented in Fig. 2.

Fig. 2
figure 2

(Color online) Three contact cases considered in this study, where the small intestine and the capsule are marked by dark and light grey, respectively. a Case 1: the capsule moves on a flat small intestinal surface; b Case 2: the capsule slides inside a collapsed intestine; c Case 3: the capsule is surrounded by the small intestine. Photographs on the right panels show the experimental set-ups for these contact cases

Full size image

Case 1: When the small intestine is expanding due to the peristalsis, the external radius of the capsule, \(R_{\mathrm{c}}\), will be much smaller than the internal radius of the intestine, \(R_{\mathrm{i}}\), i.e. \(R_{\mathrm{c}} \ll R_{\mathrm{i}}\). Capsule–intestine contact can be treated as the cylinder–cylinder contact as shown in Fig. 3a, and the contact pressure, \(P_{\mathrm{c}_1} \), is induced by the gravity of the capsule, which can be written as

$$\begin{aligned} P_{\mathrm{c}_1}=P_{\mathrm{c}}, \end{aligned}$$
(1)

where \(P_{\mathrm{c}}\) represents the contact pressure due to capsule’s gravity.

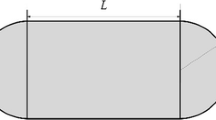
When the capsule robot is stationary, the Hertz contact theory [24] can be used to compute the analytical solution of the contact pressure between the capsule and the small intestine. Such a contact surface and its pressure distribution are shown in Fig. 3b, where 2a and L represent the width and length of the contact area, respectively, and r is the distance of the contact position from its central axis.

Fig. 3
figure 3

a Sectional view of contact Case 1, b top view of the contact area and contact pressure distribution

Full size image

According to the Hertz contact theory [24], the semi-contact width, a, can be expressed as

$$\begin{aligned} a=\sqrt{\frac{4FR_e}{\pi LE_e}}, \end{aligned}$$
(2)

where \(F=M_{\mathrm{c}}g\), \(R_e=(\frac{1}{R_{\mathrm{c}}}+\frac{1}{R_{\mathrm{i}}})^{-1}\) and \(E_e=(\frac{1-\nu _{\mathrm{c}}^2}{E_{\mathrm{c}}}+\frac{1-\nu _{\mathrm{i}}^2}{E_{\mathrm{i}}})^{-1}\) represent the load acting on the capsule, the equivalent radius and the equivalent Young’s modulus, respectively. \(E_{\mathrm{c}}\) and \(E_{\mathrm{i}}\) are Young’s moduli of the capsule and the small intestine, respectively. \(\nu _{\mathrm{c}}\) and \(\nu _{\mathrm{i}}\) are Poisson’s ratios of the capsule and the small intestine, respectively. It is worth noting that L is the length of the contact area, which equals to the length of the cylindrical body of the capsule as shown in Fig. 1b.

As the contact pressure distributes elliptically along the direction of the contact width, it can be written as

$$\begin{aligned} P=P_\mathrm{max}\sqrt{1-\left( \frac{r}{a }\right) ^2}, \end{aligned}$$
(3)

where \(P_\mathrm{max}\) is the maximum contact pressure along the central axis of the contact area given as [24]

$$\begin{aligned} P_\mathrm{max}=\frac{2F}{\pi a L}. \end{aligned}$$
(4)

Since it is difficult to measure the maximum contact pressure practically, the average contact pressure over the contact area,

$$\begin{aligned} P_\mathrm{avg}=\frac{F}{2aL}, \end{aligned}$$
(5)

was measured in our experiments and simulation studies. Therefore, \(P_\mathrm{avg}\) will be used as an analytical prediction of the contact pressure for Case 1 and will be compared with its contour parts of experimental testing and finite element analysis (FEA) in Sect. 5.

In order to use the Hertz contact theory, the following four conditions must be satisfied. (i) The contact surface is continuous and non-conforming, \(a \ll R_e\). (ii) The strain is small, \(a \ll R_e\). (iii) Each solid can be considered as an elastic half-space, \(a \ll R_{\mathrm{i}}\), \(a \ll R_{\mathrm{c}}\), and \(a \ll L\). (iv) The surface is frictionless, \(\mu =0\). For our Case 1 experiment, \(R_{\mathrm{i}}=\infty \) mm, \(R_{\mathrm{c}}=5.5\) mm, \(a=0.2359\) mm, and \(L =15\) mm, which satisfy the first three conditions. For a moving capsule in the small intestine, the friction coefficient, \(\mu \), could vary from 0.08 to 0.20 [13]. Since the influence of tangential traction on the normal pressure and contact area is small [24], the Hertz contact theory is still valid for predicting the contact pressure of Case 1 under various capsule velocities.

Case 2: When the small intestine stops expanding and falls down on the capsule, the external radius of the capsule is smaller or equal to the internal radius of the intestine, i.e. \(R_{\mathrm{c}} \le R_{\mathrm{i}}\). There are two contact surfaces, with one on the top and the other at the bottom of the capsule, as shown in Fig. 2b. Under this condition, in addition to capsule’s gravity, the gravity of the small intestine also contributes to the contact pressure. Thus, the contact pressure, \(P_{\mathrm{c}_2}\), can be written as

$$\begin{aligned} P_{\mathrm{c}_2}=P_{\mathrm{c}}+P_{\mathrm{i}}, \end{aligned}$$
(6)

where \(P_{\mathrm{i}}\) represents the contact pressure due to the gravity of the small intestine falling on the capsule. However, the analytical representation of \(P_{\mathrm{i}}\) is difficult to be obtained since only a small varying part of the intestine acts on the capsule. For this contact case, \(P_{\mathrm{c}_2}\) will be numerically calculated through FEA only and compared with experimental measurements in Sect. 5.

Case 3: When the intestine is contracting, the capsule will be surrounded by the intestine leading to \(R_{\mathrm{c}}>R_{\mathrm{i}}\). The viscoelastic deformation of the intestinal wall will induce hoop pressure on the capsule as shown in Fig. 2c. Under this condition, the contact pressure, \(P_{\mathrm{c}_3}\), can be written as

$$\begin{aligned} P_{\mathrm{c}_3}=P_{\mathrm{c}}+P_{\mathrm{i}}+P_{\mathrm{h}}, \end{aligned}$$
(7)

where \(P_{\mathrm{h}}\) represents the hoop pressure caused by the hoop stress of the expanded small intestine.

In order to model the hoop pressure for Case 3 analytically, the small intestine can be considered as a viscoelastic material [15, 19], and the following assumptions are made: (i) the internal surface of the small intestine surrounds capsule’s external surface when they are in contact; (ii) the intestinal material is incompressible; (iii) the intestinal deformation is isotropic and symmetrical.

To model the hoop pressure, a local coordinate system [19, 25] is built in Fig. 4, with x and R(x) representing the axial and radial directions, respectively. As shown in the figure, the capsule is divided into three segments: a semi-sphere head, a cylindrical body and a semi-sphere tail. In the local coordinate system, \(x_{\mathrm{c}}\) is the distance from the contact point to the centre of the head in the axial direction.

Fig. 4
figure 4

a Geometric dimensions of the capsule in the small intestine for Case 3, b sectional view at the centre of capsule–intestine interaction, which is perpendicular to the x axis

Full size image

Based on Assumption (i), the internal radius of the expanded intestine contacting the capsule body, R(x), is the same as the external radius of the capsule, i.e. \(R(x)=R_{\mathrm{c}}\), and \(x_{\mathrm{c}}\) can be expressed as

$$\begin{aligned} x_{\mathrm{c}}=\sqrt{R_{\mathrm{c}}^2-R_{\mathrm{i}}^2}. \end{aligned}$$
(8)

Based on Assumption (ii), the thickness of the intestinal wall attenuates when the capsule body expands the intestine radially. So, the thickness of the expanded intestine, \(t_{\mathrm{i,e}}\), can be expressed as

$$\begin{aligned} t_{\mathrm{i,e}}=\sqrt{(R_{\mathrm{i}}+t_{\mathrm{i}})^2+R^2_{\mathrm{c}}-R_{\mathrm{i}}^2}-R_{\mathrm{c}}, \end{aligned}$$
(9)

where \(t_{\mathrm{i}}\) is the original thickness of the intestinal wall. According to Assumption (iii), hoop strain can be expressed as

$$\begin{aligned} \epsilon =\frac{R_{\mathrm{i}}-R_{\mathrm{c}}}{R_{\mathrm{i}}}. \end{aligned}$$
(10)

In [15, 19, 21], the viscoelastic property of small intestinal lining was studied, and the stress–strain relationship of the small intestine was represented by the Maxwell model, including three elastic springs and two viscous dampers as shown in Fig. 5a, where \(E_j\) (\(j=1,2,3\)) and \(\eta _k\) (\(k=1,2\)) represent the Young’s moduli of the springs and the damping coefficients of the dampers, respectively. In our study, the Maxwell model with two elastic springs and one viscous damper as shown in Fig. 5b was used, since it fits better with our stress relaxation test. Therefore, the viscoelastic property of the synthetic small intestine used in our experiment can be written as

$$\begin{aligned} \tau (t)=\epsilon (E_1e^{-\frac{E_1}{\eta _1}t}+E_2), \end{aligned}$$
(11)

where \(E_1\) and \(E_2\) are the Young’s moduli of the springs and \(\eta _1\) is the viscosity coefficient of the damper.

Fig. 5
figure 5

Maxwell models for depicting the stress–strain relationship of the small intestine: a the five-element model [19] and b the three-element model used in our experiment

Full size image

For a capsule robot moving at a constant velocity, v, the hoop stress can be written as

$$\begin{aligned} \tau (x)=\epsilon (E_1e^{-\frac{E_1x}{\eta _1v}}+E_2). \end{aligned}$$
(12)

The relationship between the hoop pressure and the hoop stress of Case 3 is the same as the pressure vessels [26], which can be expressed as

$$\begin{aligned} P_h(x)=\frac{t_{\mathrm{i,e}}}{R_{\mathrm{c}}}\tau (x). \end{aligned}$$
(13)

Since the capsule is small, the dimensions of the strain gauges used to measure the hoop pressure in Eq. (13) are similar to the dimensions of the capsule. So, the average hoop pressure on the capsule body,

$$\begin{aligned} P_h=\frac{1}{L} \int _{x_{\mathrm{c}}}^{x_{\mathrm{c}}+L} P_h(x) \mathrm{d}x, \end{aligned}$$
(14)

is applied as the analytical prediction of hoop pressure in this study and will be compared with experimental and FEA results in Sect. 5.

Fig. 6
figure 6

(Color online) Photograph of the experimental set-up, where a DC motor was used to drive the capsule moving inside the intestine and the contact pressure was measured by using the strain gauges attached to the capsule. A synthetic small intestine, produced by the SynDaver Labs [27], was used in this experiment

Full size image
Fig. 7
figure 7

Schematic diagram of the experimental set-up. A DC motor was used to drive the capsule to move inside a synthetic small intestine at a constant speed. The speed was varied by adjusting the DC power supply for each experimental trial. Two pairs of strain gauges were attached to the external surface of the capsule, and their signals were amplified and then collected by a National Instrument data acquisition (DAQ) card via a graphic user interface (GUI) in LabVIEW

Full size image
Table 1 Geometric dimensions and mechanical properties of the capsule and the synthetic small intestine [27]
Full size table

3 Experimental set-up

An experimental rig was designed and assembled, and extensive experiments were conducted to measure the contact pressure on the capsule for the three contact cases depicted in Fig. 2. The photograph of the rig is shown in Fig. 6, where a DC motor was used to drive the capsule to move inside a synthetic small intestine [27] at a constant speed. Two pairs of strain gauges were attached to the external surface of the capsule, forming a full Wheatstone bridge, and their signals were collected at the sampling rate of 1 kHz using a National Instrument data acquisition (DAQ) card (USB6210) through a graphic user interface (GUI) in LabVIEW. The schematic diagram of the experimental set-up is presented in Fig. 7. The capsule was made by polyethylene with 11 mm in diameter, 26 mm in length and 0.5 mm for shell thickness. The capsule can be driven either forward or backward inside the small intestine, which is 0.69 mm in thickness and 26 mm in diameter. The mechanical properties of the polyethylene and the synthetic small intestine are summarised in Table 1. The friction coefficient between the capsule and the small intestine was experimentally identified at \(\mu =0.2293\) by lifting up one end of the workbench and making the capsule slide freely.

Calibration of strain gauges was conducted repeatedly before any contact pressure measuring. The schematic diagram of the calibration set-up is presented in Fig. 8a, where the capsule was fully submerged in water. The pressure on the capsule can be varied by adjusting the depth of the capsule. Meanwhile, the voltage output of the strain gauges was recorded by the DAQ system. An example of the calibration data is shown in Fig. 8b, where black dots and red solid line represent the measured voltage output as a function of the calculated water pressure and the linear fit for all the recorded data, respectively. By using this linear relationship, contact pressure on the capsule can be calculated using the voltage output of the strain gauges.

Fig. 8
figure 8

(Colour online) a Schematic diagram for calibrating the strain gauges, b an example of the calibration data. Black dots represent experimental measurements, and red solid line represents their linear fit

Full size image

The synthetic small intestine consists of synthetic human tissue analogs and woven fibres. When the small intestine is compressed, its mechanical properties are dominant by the synthetic human tissue analogs with Young’s modulus varying from 21 to 29 kPa. Thus, Young’s modulus of the small intestine was set at \(E_{\mathrm{i}}=25\) kPa for our experimental and numerical (analytical and FEA) investigation for Cases 1 and 2. When the small intestine is expanded by the capsule, the woven fibres dominate its mechanical properties and the stress relaxation phenomenon was clearly observed in experiments. Therefore, four trials of relaxation experiments were conducted by pushing the capsule into the small intestine quickly and forcing it to stop at the middle of the intestine suddenly. Then this measured contact pressure was used to estimate the parameters of the three-element model using Eqs. (11)–(14). As shown in Fig. 9, the fitted curve shows a good agreement with the experimental data with the r-squared fitting goodness at 0.9803, where a value of 1.0 represents perfect fitting. The identified values of \(E_1\), \(\eta _1\) and \(E_2\) are given in Table 1.

Fig. 9
figure 9

(Color online) A typical time histories of the measured and fitted contact pressure for relaxation test. The fitting model is based on Eq. (13), and the identified parameters are given in Table 1

Full size image

Three sets of experiments were conducted to investigate the contact pressure between the capsule and the intestine. The snapshots of the three contact cases are presented on the right panel of Fig. 2. As shown in the figure, the small intestine was cut-open for Case 1 and fixed onto a steel workbench. Therefore, the internal radius of the capsule can be written as \(R_{\mathrm{i}}:=R_1=\infty \) mm. For Case 2, the small intestine was put in a semi-tubular slot with the radius of \(R_{\mathrm{i}}:=R_2=13\) mm made by polyvinyl chloride, and the upper half of the small intestine collapses on the capsule. For Case 3, the internal radius of the small intestine was shrank to \(R_{\mathrm{i}}:=R_3=5\) mm. For each testing run, the experimental procedure was carried out as follows: (i) Turn on the DC power supply for strain gauges. (ii) Run the GUI in LabVIEW to log the voltage output of the strain gauges. (iii) Turn on the DC power supply for the DC motor to drive the capsule move forward or backward at a constant speed. The progression speed was measured using a stopwatch manually. (iv) Disable the data logging and save the experimental results.

As the strain gauges were noise-sensitive, a low-pass filter with bandwidth of 10 Hz was used to smooth the measured data. An example of typical measurement and data processing for the contact pressure of Case 3 is presented in Fig. 10, where the time interval marked by blue lines defines a time span \(\Delta T\) indicating the data used for averaging. The averaged experimental data will be compared with the analytical and the FEA results in Sect. 5.

Fig. 10
figure 10

(Color online) A typical time histories of measured contact pressure for Case 3, where the solid black line represents the measured data and red line shows the filtered data. The time span \(\Delta T\) marked by blue lines indicates the area of contact pressure used for averaging. In this example, the capsule was pushed to move forward by using the DC motor at a constant speed of 10.60 mm/s

Full size image

4 Numerical set-up

Four sets of FEA testing were conducted using ANSYS to study the contact pressure of Cases 1–3. The geometric dimensions and material properties of the capsule and the intestine are given in Table 1, and the set-up for each FEA testing set is detailed as follows.

First FEA testing set: The FEA set-up for Case 1 (\(R_1=\infty \) mm) is presented in Fig. 11a. The capsule moved on a piece of flat cut-open small intestine with a total length of 100 mm supported by a steel workbench. The contact pair between the capsule and the small intestine was frictional with the friction coefficient \(\mu =0.2293\) identified experimentally, and the contact pair between the small intestine and the supporting steel was bonded. Standard gravity was applied, and the weight of the capsule was 0.4 g. Young’s modulus of the small intestine was configured as \(E_{\mathrm{i}}=25\) kPa.

Fig. 11
figure 11

(Color online) a FEA set-up for Case 1, the capsule moving on a piece of flat cut-open small intestine supported by a steel workbench. b FEA set-up for Case 2, the capsule moving inside a piece of collapsed small intestine supported by a steel workbench. c FEA set-up for hoop pressure testing and Case 3, the capsule moving inside the small intestine whose internal radius is smaller than the external radius of the capsule. All the simulation parameters are summarised in Table 1

Full size image

Second FEA testing set: The FEA set-up for Case 2 is shown in Fig. 11b. The capsule moved inside a piece of collapsed small intestine with an inner radius \(R_2=13\) mm and a total length of 250 mm, supported by a steel workbench. Standard gravity was applied, and the Young’s modulus of the small intestine was configured as \(E_{\mathrm{i}}=25\) kPa in the simulation. The contact pairs among the capsule, the small intestine and the supporting steel were frictional with the friction coefficient \(\mu =0.2293\). The reason for setting the contact pair between the small intestine and the steel workbench as frictional rather than bonded is to match our experimental set-up of Case 2. Otherwise, the small intestine cannot collapse under the load of standard gravity.

Third FEA testing set: The FEA set-up for Case 3 is shown in Fig. 11c. The capsule was surrounded by the small intestine with an inner radius \(R_3=5\) mm and a total length of 100 mm. The contact pair between the capsule and the small intestine was frictional with the friction coefficient \(\mu =0.2293\). This testing set was designed to verify the hoop pressure model in Eq. (14), so standard gravity was not applied for this scenario. Young’s modulus of the synthetic small intestine was configured according to the three-element model in Fig. 5b with the experimentally identified parameters in Table 1.

Fourth FEA testing set: The FEA set-up for this testing set was the same as the third FEA testing set shown in Fig. 11c, but the standard gravity was applied for this scenario in order to match the contact pressure of Case 3 given in Eq. (7).

Table 2 Convergence test of the hoop pressure for Case 3 by using four different mesh set-ups
Full size table

Convergence test for each FEA testing set was conducted. By taking the third FEA testing set as an example, the convergence of four mesh set-ups was tested which is summarised in Table 2, and the results are illustrated in Fig. 12. In this figure, the red solid line represents the analytical prediction of the hoop pressure calculated from Eq. (14) when the capsule moves at a constant speed of 10 mm/s. As shown in the figure, the first and second mesh set-ups are too coarse to converge, and refining the mesh size will lead to better converged results. The results of the third and fourth mesh set-ups are almost the same as the analytical prediction with errors banded within ± 0.5%, but the third set-up has much less elapsed time than the fourth one. So, the third mesh set-up was adopted for the third FEA testing set. For the other FEA testing sets, similar convergence test was conducted to ensure the accuracy of FEA simulation with the numerical error banded within ± 0.5%.

Fig. 12
figure 12

(Color online) Convergence test of the hoop pressure for Case 3 by using four different mesh set-ups summarised in Table 2. The capsule moves in the intestine at a constant speed of 10 mm/s

Full size image
Fig. 13
figure 13

(Color online) Typical time histories of contact pressures for a Case 1 with the capsule’s velocity at 7.01 mm/s, b Case 2 with the capsule’s velocity at 14.96 mm/s and c Case 3 with the capsule’s velocity at 13.76 mm/s. The measured data between the two red lines were averaged as the experimental result for each trial

Full size image
Fig. 14
figure 14

(Color online) Typical contact pressures as functions of capsule’s displacement with capsule’s velocity at 10 mm/s for a Case 1, b Case 2, c the hoop pressure of Case 3 and d Case 3. The contact pressures between the two red lines were averaged as the FEA result for each trial

Full size image
Fig. 15
figure 15

(Color online) Contact pressures for Case 1 under a wide range of capsule velocities. Blue dots denote experimental measurements, and their linear fit is presented by blue solid line. Red triangles with solid line represent FEA results, and green dashed line indicates the analytical predictions obtained by using the Hertz contact theory in Eq. (5)

Full size image
Fig. 16
figure 16

(Color online) Maximum contact pressures for Case 1 under a wide range of capsule velocities. Red triangles with solid line represent FEA results, and green dashed line denotes the analytical prediction calculated by using the Hertz contact theory in Eq. (4)

Full size image
Fig. 17
figure 17

(Color online) Contact pressures for Case 2 with various capsule velocities. Blue dots denote experimental measurements, and their linear fit is shown by blue solid line. Red triangles with solid lines represent FEA results

Full size image
Fig. 18
figure 18

(Color online) Comparison of hoop pressures on the capsule between the analytical and FEA results under various capsule velocities. Analytical predictions are shown by green dashed line, and FEA results are denoted by red triangles with solid lines

Full size image
Fig. 19
figure 19

(Color online) Comparison of contact pressures between FEA and experimental testing for Case 3 under various capsule velocities. Blue dots represent experimental measurements, and their linear fit is shown by blue solid line. The FEA results with consideration of gravity are marked by red triangles with solid lines, and the FEA results without consideration of gravity, i.e. the hoop pressures only, are denoted by green squares with solid lines

Full size image

5 Results and discussion

In this section, analytical, experimental and FEA results are compared for each contact case. Typical time histories of experimental and FEA testing are presented in Figs. 13 and 14, respectively. Detailed comparisons of contact pressures under a wide range of capsule velocities are shown in Figs. 15, 16, 17, 18 and 19.

Figure 13 illustrates typical time histories of measured contact pressures for Cases 1–3. Figure 13a shows the measurement of Case 1 with the capsule’s velocity at 7.01 mm/s, and the average pressure between the two red lines is about 0.75 kPa, which is small as the contact pressure is only caused by capsule’s weight in this case. Figure 13b shows the measurement of Case 2 with the capsule’s velocity at 14.96 mm/s, and the average pressure for this case is about 2.38 kPa, which is twice larger than that of Case 1. It is because for this case partial intestine’s weight contributes to the contract pressure. Figure 13c shows the measurement of Case 3 with the capsule’s velocity at 13.67 mm/s, and the averaged pressure for this case is about 14.38 kPa. In this scenario, the expanded intestine suffers large hoop stress, so it introduces large hoop pressure on the capsule.

Figure 14 presents typical contact pressures in FEA simulations as functions of capsule’s displacement with capsule’s velocity at 10 mm/s. As shown in Fig. 14a, the average contact pressure is about 0.38 kPa for Case 1, which is smaller than the experimental result in Fig. 13a. Figure 14b illustrates the contact pressure for Case 2, and the average contact pressure is about 1.85 kPa, which is close to the experimental testing in Fig. 13b. Figure 14c presents the numerical result of the hoop pressure for Case 3, and its average hoop pressure is about 11.87 kPa, which fits well with its analytical prediction by Eq. (14). In Fig. 14d, the contact pressure for Case 3 is shown with an average value at 12.95 kPa, which is slightly smaller than the experimental results in Fig. 13c.

Comparison of analytical, experimental and numerical contact pressures for Case 1 under a wide range of capsule’s velocities is presented in Fig. 15. As the contact pressure is generated by capsule’s gravity only according to Eq. (1), it does not vary significantly as the capsule’s velocity increases. As shown in the figure, the analytical prediction denoted by green dashed line shows a high accordance with the linear fit of the experimental results marked by blue solid line at about 0.55 kPa. The FEA results shown by red triangles are around 0.38 kPa, which is lower than the analytical and experimental results. Such a difference may be caused by the accuracy of FEA simulation, and our investigation has shown that the smaller the mesh size, the closer the FEA and experimental results. For example, the analytical semi-contact width was obtained at \(a=0.24\) mm for Case 1 by using Eq. (2), but this parameter was observed at \(a=0.40\) mm in our FEA simulation. Further refining the mesh size could improve this semi-contact width more accurate, but the computational time will be increased dramatically.

Figure 16 shows the maximum contact pressures of the analytical prediction and FEA results for Case 1. The analytical prediction was calculated at about 0.70 kPa by using the Hertz contact theory in Eq. (4). The maximum contact pressures obtained from FEA simulation vary slightly from 0.63 to 0.68 kPa, fitting well with the analytical prediction.

Figure 17 presents the FEA and experimental results for Case 2, where the average contact pressures are about 1.85 kPa and 2.00 kPa for the FEA and experimental results, respectively. Compared with the experimental results of Case 1 shown in Fig. 15, the contact pressures for Case 2 are twice larger due to the collapsed intestine on the capsule. As the velocity of the capsule increases, the contact pressures for both the FEA and experimental results are slightly reduced.

To verify the analytical model of the hoop pressure in Eq. (14), five FEA simulations were conducted and their results are compared with analytical predictions. In this scenario, the simulation was set as Case 3 but without consideration of intestine and capsule’s gravity. As shown in Fig. 18, analytical predictions using Eq. (14) represented by green dashed line show a good agreement with the FEA results denoted by red triangles with solid lines.

To consider the effect of intestine and capsule’s gravity, the contact pressures for Case 3 obtained by FEA and experiments are shown in Fig. 19, whereas the FEA and experimental contact pressures were recorded at 13 kPa and 16 kPa, respectively. The figure shows that the hoop pressure calculated by FEA at about 12 kPa, marked by green squares with solid lines, dominates the contact pressure of Case 3, which is about 13 kPa indicated by the red triangles with solid lines in the figure.

Comparing the experimental results in Figs. 15, 17 and 19, the average contact pressures for Cases 1–3 are 0.5 kPa, 2 kPa and 16 kPa, respectively. This correlation indicates that the contact pressure between the capsule and the small intestine is very sensitive to the condition of the small intestine. When the external radius of the capsule is larger than the internal radius of the small intestine, the hoop pressure will dominate the contact pressure, which may increase significantly. This brings a challenging control issue for the capsule robot. For example, in order to drive the capsule, the driving force should be sufficiently large when the small intestine fully contacts with the capsule. However, such a large force may induce transient high speed to the capsule causing inaccurate positioning at the area of interest when the small intestine is released due to periodic peristalsis. Therefore, a suitable control strategy or a robust stabilising mechanism, which can accommodate such a high pressure drop subjected to a wide range of environmental variations, is crucial for the capsule robot.

6 Conclusions

In this work, the contact pressure of the capsule robot when moving through a small intestine was investigated analytically, experimentally and numerically. The purpose of this work is to deepen our understanding in capsule–intestine interaction in order to design a robust control strategy or an efficient locomotion mechanism for stabilising the self-propelled capsule robot [8] in the presence of peristalsis of the small intestine.

Three typical contact cases were considered to reproduce the complex environment of the small intestine with peristalsis. When the small intestine is expanding, the external radius of the capsule is much smaller than the internal radius of the intestine. The Hertz contact theory [24] was used to calculate the analytical solution of the contact pressure. As the contact pressure in this case is generated by capsule’s gravity only, it does not change significantly as the speed of the capsule increases. This trend is consistent with the FEA and experimental results, but the difference between the experimental result, 0.55 kPa, and the FEA result, 0.38 kPa, has been observed. However, our investigation has shown that this difference was caused by the mesh size used in FEA simulation. Further refining the mesh size could improve the accuracy, but this in turn will increase the computational time drastically.

When the small intestine stops expanding, it falls down on the capsule, and the external radius of the capsule will be smaller or equal to the internal radius of the intestine. In this condition, in addition to capsule’s gravity, the gravity of the small intestine falling on the capsule will contribute to the contact pressure. Our experimental and FEA results show a good agreement on the contact pressure of this case, which is twice larger than the case when the small intestine is expanding. Our investigation also indicates that as the speed of the capsule increases, this contact pressure will be slightly reduced.

When the small intestine is contracting, the capsule will be fully surrounded by the intestine, so the contact pressure on the capsule is induced by the hoop pressure, the gravity of the intestine and the capsule. In this case, the expanded intestine suffers large hoop stress, so it introduces large contact pressure on the capsule. Our investigation from FEA and experiment indicates that the hoop pressure at about 12 kPa dominates the contact pressure, which is about 13 kPa in average. Thus, the hoop pressure model given by Eq. (14) can be used to analytically predict the contact pressure for this case.

Finally, our studies reveal that the contact pressure between the capsule and the intestine is very sensitive to different contact conditions, i.e. expanding or contracting due to intestinal peristalsis. The contact pressure may vary from 0.5 to 16 kPa based on our experimental measurement using a synthetic small intestine. Therefore, a proper control method or a robust stabilising mechanism, which can accommodate such a high pressure difference, is crucial for designing the self-propelled capsule robot.

Our future work will focus on experimental testing of the vibro-impact self-propelled capsule robot by using the synthetic intestine and study of dynamic interactions between the capsule robot and the small intestine through FEA simulation and experimental investigation.