Evaluating the resistant force of an endoscopic capsule self-propelling in the small intestine

Abstract

In this paper, we study a mathematical model for evaluating the resistant force of endoscopic devices self-propelling in the small intestine with a consideration of its anatomy. Circular fold is the main source of intestinal resistance that needs to be overcome during the endoscopic procedure. Our model is able to calculate the resistances of such folds in different dimensions. Finite element analysis and experimental testing are presented to validate the proposed model by using a pulling-type endoscopic capsule. Our investigation shows that the resistance reaches its maximum immediately after the capsule is pulled against the fold, and drops off gradually during the crossing motion. The proposed method is further demonstrated by using a magnetic pulling-type capsule prototype in an intestine simulator. The findings of this study provide a better insight into the biomechanics of the small intestine and advance the understanding of capsule–intestine interaction for robotic and endoscopic engineers.

1 Introduction

The small intestine, an anatomical site previously considered inaccessible to clinicians due to its small diameter and lengthy size, is the part of the gastrointestinal (GI) tract between the stomach and the colon. Since its introduction into clinical practice 20 years ago, capsule endoscopy [1, 2] has become established as the primary modality for examining the surface lining of the small intestine. However, its reliance on peristalsis for passage through the intestine leads to significant limitations [3], in particular due to the unpredictable and variable locomotion speed [4]. Significant abnormalities, e.g. small-bowel bleeding, may be missed, due to intermittent high transit speeds that lead to incomplete visualization of the intestinal surface. Furthermore, each case produces up to 100,000 still images, from which video footage is generated, taking 30–90 min for the clinician to examine in its entirety. The current procedure is considered both time-consuming and burdensome for clinicians.

Building a reliable propulsive mechanism in a capsule, which is 26 mm in length and 11 mm diameter, for active endoscopy is a challenging task [5]. Different propulsion methods were proposed in the past few decades for GI diagnosis [6,7,8] and therapy [9, 10]. For example, an integrated untethered swimming capsule with on-board camera and battery was designed by Falco et al. [11]. The device has four propellers enabling locomotion in a liquid environment and generating a maximum propulsive force of 25.5 mN. Carta et al. [12] employed an on-board vibratory motor with a wireless powering unit for active capsule endoscopy. Liu et al. [13] developed a vibrational capsule with periodic impact motions that can achieve the progression speed up to 14.4 mm/s. More recently, Erin et al. [14] proposed an MRI-powered untethered robot integrated with a camera and an on-board battery for wireless capsule endoscopy. However, like these designs, robotic and endoscopic engineers have barely considered the anatomy of the small intestine, in particular the intestinal resistance, when designing and validating their devices. Preliminary simulation and experimental studies [15, 16] indicate that the capsule’s transit speed and power efficiency for self-propulsion significantly rely on the intestinal resistance acting on the capsule. Therefore, considering the anatomy of the small intestine and estimating the required driving force for self-propulsion are vital for endoscopic designs.

Fig. 1

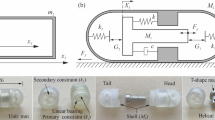
(Colour online) a Anatomy of the GI tract and b the small intestine. The small intestine is about 6 m in length and 3.5 cm in diameter, consisting of the duodenum, the jejunum and the ileum. The duodenum is about 25 cm in length. The jejunum, connecting the duodenum and the ileum, is about 2.5 m in length [17]. The circular fold of the small intestine is a large valvular flap projected on the lumen of the intestine, which is about 2 mm in thickness [18]. It normally extends for about one half or two thirds of circumference of the small intestine showing in a crescent shape, but some may form a complete circle or in a spiral direction [17, 19]. The folds mainly distribute in the horizontal and ascending parts of the duodenum and the upper part of the jejunum per 25 mm in average [20, 21] and diminishes considerably in size and quantity once reaching the middle of the ileum

The small intestine, the main screening area for capsule endoscopy, which is about 6 m in length and 3.5 cm in diameter, consists of the duodenum, the jejunum and the ileum, coiling around the abdomen and extending the stomach to the colon, as illustrated in Fig. 1a. The duodenum is about 25 cm in length as the first portion of the small intestine with no mesentery. The jejunum, connecting the duodenum and the ileum, is about 2.5 m in length [17]. The circular fold of the small intestine, see Fig. 1b, is a large valvular flap projected on the lumen of the intestine, which is about 2 mm in thickness [18]. It normally extends for about one half or two thirds of circumference of the small intestine showing in a crescent shape, but some may form a complete circle or in a spiral direction [17, 19]. Unlike the gastric fold in the stomach, the circular fold is permanent and does not disappear when the intestine is distended. The folds mainly distribute in the horizontal and ascending parts of the duodenum and the upper part of the jejunum per 25 mm in average [20, 21] and diminishes considerably in size and quantity once reaching the middle of the ileum. Therefore, it is the main resistant mechanism for the endoscopic devices progressing in the small intestine. These devices need to overcome the resistant force induced by the circular fold providing a key design factor for endoscopic engineers. Compared to our previous studies that only a flat intestine was considered [16, 22, 23], the present study will provide further insight into the biomechanics of the small intestine for designing self-propelled endoscopic devices.

To develop new endoscopic devices capable of self-propelling in the small intestine, endoscopic engineers need to take the complex anatomy of the small intestine into account, in particular the circular fold of the small intestine, when evaluating the performance of their designs. Thus, the purpose of the present work is to provide a systematic method for accurately predicting the resistant force of the capsule-type devices moving in the small intestine. According to the peristalsis of the small intestine, most of the research works (e.g. [24,25,26]) assume that the capsule distends the intestine in the radial direction when assessing the intestinal resistance. However, this assumption is only valid for a very short interval during the intestinal movement. For most of the time of diagnosis, the capsule is in one-sided contact with the intestinal wall, so the resistance from the hoop pressure does not apply. For this reason, Guo et al. [15, 16] estimated the intestinal resistance for a self-propelled capsule by considering both partial and full capsule–intestine contacts. In the present work, we use the cylindrical capsule as an example and take the circular fold of the small intestine into consideration to evaluate the required driving force for self-propulsion. Similar work has been done by Sliker et al. [27] who developed an analytical model for predicting the resistant force on the capsule when passing through the gastrointestinal tract. Their study assumes that the maximum resistant force on the capsule occurs at the time when the spherical surface of the capsule reaches the tip of the circular fold. While for a moving capsule, the maximum resistance might be encountered earlier before reaching the tip depending on the geometric and mechanical properties of the circular fold. In addition, Sliker et al. [27] only considered a single static state of capsule–fold interaction, while the other motions, such as climbing and crossing over, were omitted. Therefore, taking the entire motion of the capsule into account in the presence of the circular fold is vital to precisely predict the required driving force for self-propulsion as well as the capsule’s dynamics in clinical scenario. Nevertheless, very few studies have considered the anatomy of the small intestine when evaluating their devices, which could lead inaccurate assessment of their designs.

In the present work, we study a general method for evaluating the resistant force of endoscopic devices self-propelling in the small intestine with the consideration of intestinal anatomy. This work, is built on our previous studies on capsule–intestine modelling [15, 22] and intestinal friction [16]. We thus demonstrate the utility of our approach to predict the resistant force of an endoscopic capsule when passing through the small intestine. This is done by (1) mathematical modelling, (2) finite element (FE) analysis and (3) experimental validation of capsule–intestine interaction. This study exemplifies our ability to replicate the clinical scenario of small-intestine endoscopy, mimicking the underlying biomechanics, thus providing accessible ways to study and understand the capsule’s real dynamics in the small intestine. Overall, this study advances the understanding of capsule–intestine interaction and provides a further insight into biomechanics of the small intestine for endoscopic engineers.

The rest of the paper is organised as follows. Section 2 studies the mathematical model of the capsule–intestine interaction, where a pulling-type endoscopic capsule is considered to interact with a circular fold on a tissue substrate. Section 3 presents the FE modelling of such an interaction model. The purpose of studying this FE model to provide a supplementary comparison for the proposed mathematical model. It also provides a further insight into the capsule–intestine interaction which cannot be uncovered by the proposed model, such as the pressure distribution on the intestine. In Sect. 4, the experimental setup and procedure for testing the capsule–intestine interaction are introduced. Then, comparison of the mathematical, FE and experimental results is made in Sect. 5, and the driving force required for overcoming the fold’s resistant force is validated using an intestine simulator in Sect. 6. According to the comparison, the FE model can provide a better prediction, but its computational cost is extremely high. Thus, the proposed mathematical model can be a compromise between the accuracy of prediction and computational efficiency. Finally, conclusions are drawn in Sect. 7.

2 Mathematical modelling of the capsule–intestine interaction

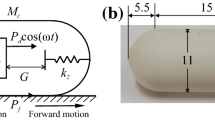
The interaction between a capsule and tissue substrate is schematically illustrated in Fig. 2a. As seen, the capsule’s hemispheric head and tail are connected by a cylindrical body with a length of L and a radius of R. When the capsule moves horizontally in x-direction, it may engage with the circular fold of the small intestine, resulting in complex interactive forces and capsule motion. To simplify the corresponding analysis, we introduce the assumption used by Sliker et al. [27] as follows:

• The capsule is rigid as the tissue substrate is very soft compared with the capsule.

• The capsule does not rotate, but only translates along the xoy plane.

• The tissue is incompressible and isotropic, and its deformation conforms to the capsule profile.

Front view of cross section A–A is illustrated in Fig. 2b, showing that the capsule penetrates into the tissue substrate with a depth of $\delta _\text {max}$ due to its weight. The intestinal tract has a thickness of H, with N circular folds distributed on its surface. The ith fold located at $x=x_i$ has a width of $2 w_i$ and a height of $h_i$ ($i=1, 2, \cdots , N$). In the xoy coordinate, the shape function for the ith fold can be approximated by

$$\begin{aligned} f_i(x) = {\left\{ \begin{array}{ll} h_i \cos \left( \frac{\pi }{2 w_i}(x-x_i)\right) , &{} |x-x_i|\le w_i,\\ 0, &{} |x-x_i|> w_i. \end{array}\right. } \end{aligned}$$

(1)

Given all circular folds, the overall shape function of the tissue substrate is described by

$$\begin{aligned} f(x) = \max \limits _{i=1,\cdots ,N} f_i(x). \end{aligned}$$

(2)

Fig. 2

(Colour online) a 3D schematic of an endoscopic capsule moving towards a circular fold on a flat tissue substrate. b Cross section A–A shows the horizontal and vertical location of the capsule by $x_0$ and $\delta _\text {max}$, and the location, width and height of the ith fold by $x_i$, $w_i$ and $h_i$. c Cross section B–B shows the capsule–substrate contact angle, $\theta \in [-\alpha (x), \alpha (x)]$. d The stress, $\sigma (x,\theta )$, is exerted on the capsule shell as a normal pressure. e Integrating the x and y components of the pressure yields the horizontal and vertical reactions, where $F_y$ is balanced by the capsule’s gravity, G, and $F_x$ resists the capsule’s motion

Except the inertial frame xoy fixed with the substrate, another moving frame ucv located at the centre of the capsule’s head, ${\mathbf {r}}_c = (x_0,R-\delta _\text {max})$, is introduced. The two frames shown in Fig. 2b can be transformed by

$$\begin{aligned} u = x - x_0 \quad \text {and} \quad v = y - R + \delta _\text {max}. \end{aligned}$$

(3)

At a given point, u, the capsule has a round cross section with a radius of

$$\begin{aligned} \rho (u) = {\left\{ \begin{array}{ll} \sqrt{R^2 - u^2}, &{} 0< u \le R,\\ R, &{} -L \le u \le 0,\\ \sqrt{R^2 - (u+L)^2}, &{} -R-L \le u < -L. \end{array}\right. } \end{aligned}$$

(4)

Combining Eqs. (3) and (4) results in the shape function of capsule bottom described in the fixed xoy frame as follows

$$\begin{aligned} \begin{aligned} p(x)&= R-\delta _\text {max} - \rho (x-x_0) \\&= {\left\{ \begin{array}{ll} R-\delta _\text {max} - \sqrt{R^2 - (x-x_0)^2}, &{} x_0< x \le x_0+R,\\ -\delta _\text {max}, &{} x_0-L \le x \le x_0,\\ R-\delta _\text {max} - \sqrt{R^2 - (x-x_0+L)^2}, &{} x_0-R-L \le x < x_0-L. \end{array}\right. } \end{aligned} \end{aligned}$$

(5)

Side view of cross section B–B is illustrated in Fig. 2c, where the vertical distance from the capsule’s axis to the substrate is

$$\begin{aligned} d(x) = R - \delta _\text {max} - f(x). \end{aligned}$$

(6)

The capsule does not engage with the fold when $d(x)>\rho (x)$. For $d(x)\le \rho (x)$, they are engaged with a contact angle $\theta \in [-\alpha (x), \alpha (x)]$, where the limit of the contact angle, $\alpha (x)$, is given by

$$\begin{aligned} \alpha (x,\delta _\text {max}) = \cos ^{-1}\left( \min \left( 1,\frac{d(x)}{\rho (x)}\right) \right) . \end{aligned}$$

(7)

Given the contact angle, $\theta$, the shape function of the capsule bottom, Eq. (5), is revised to be

$$\begin{aligned} p(x,\theta ) = R-\delta _\text {max} - \rho (x)\cos (\theta ). \end{aligned}$$

(8)

Compared with Eq. (5), one can see that $p(x,0) = p(x)$.

When the capsule is in contact with the fold, the tissue conforms to the capsule’s profile. As a result, the substrate yields deformation given by the difference between the shape functions of the substrate and the capsule bottom as follows

$$\begin{aligned} \delta (x,\theta ) = \max \left( 0, f(x) - p(x,\theta )\right) . \end{aligned}$$

(9)

Given the original thickness of the substrate, the strain corresponding to the tissue deformation is

$$\begin{aligned} \epsilon (x,\theta ) = \frac{\delta (x,\theta )}{H + f(x)}, \end{aligned}$$

(10)

and the corresponding stress is

$$\begin{aligned} \sigma (x,\theta ) = \epsilon (x,\theta ) E(x), \end{aligned}$$

(11)

where E is the Young’s module of the tissue.

As shown in Figs. 2(d-e), the stress exerts normal pressure on the capsule shell. It has $x-$ and $y-$components as follows:

$$\begin{aligned} \begin{aligned} \sigma _x(x,\theta )&= \sigma (x,\theta )\sin (\varphi ),\\ \sigma _y(x,\theta )&= \sigma (x,\theta )\cos (\varphi )\cos (\theta ), \end{aligned} \end{aligned}$$

(12)

where $\varphi$ is the angle of anticlockwise rotation from R to $\rho (x)$, given by

$$\begin{aligned} \varphi (x) = {\left\{ \begin{array}{ll} - \sin ^{-1}\left( \frac{x - x_0}{R} \right) , &{} x_0< x \le x_0+R,\\ 0, &{} x_0-L \le x \le x_0,\\ - \sin ^{-1}\left( \frac{x - x_0 + L}{R} \right) , &{} x_0-R-L \le x < x_0-L. \end{array}\right. } \end{aligned}$$

(13)

Integrating $\sigma _y(x,\theta )$ over the capsule shell yields the vertical reaction force exerted by the tissue on the capsule as follows:

$$\begin{aligned} F_y (x_0,\delta _\text {max}) = \int _{x_0 - L - R}^{x_0 + R}\int _{-\alpha (x,\delta _\text {max})}^{\alpha (x,\delta _\text {max})}{\sigma _y(x,\theta )}\rho (x) \text {d}\theta \frac{\text {d}x}{\cos (\varphi (x))}. \end{aligned}$$

(14)

The vertical force cancels the capsule’s gravity as

$$\begin{aligned} F_y(x_0,\delta _\text {max}) = G, \end{aligned}$$

(15)

which can be used to solve the penetration depth, $\delta _\text {max}$, for a given position, $x_0$. It is worth noting that $\delta _\text {max}(x_0)$ is an implicit function of $x_0$ governed by Eq. (15). Once the capsule moves, Coulomb friction is involved in the x-directional capsule–intestine’s reaction force, yielding

$$\begin{aligned} F_x (x_0) = {-\mu G} + \int _{x_0 - L - R}^{x_0 + R}\int _{-\alpha (x,\delta _\text {max}(x_0))}^{\alpha (x,\delta _\text {max}(x_0))}{\sigma _x(x,\theta )}\rho (x) \text {d}\theta \frac{\text {d}x}{\cos (\varphi (x))}, \end{aligned}$$

(16)

where $\mu$ is the frictional coefficient.

3 Finite element modelling of the capsule–intestine interaction

FE analysis has been carried out to study the interaction between the capsule and the small intestine by considering the contact pressure and resistant force on the capsule under different contact conditions [23]. In this section, the capsule–intestine interaction model with the consideration of circular folds was developed by using ANSYS WORKBENCH transient structural module for which the implicit dynamics was adopted.

3.1 Geometrical modelling and material description

In order to improve computational efficiency, a two-dimensional model as presented in Fig. 3 was developed for FE analysis. As can be seen from the figure, the cross-sectional profile of the circular fold is elliptical, and the height and width of the circular folds can be adjusted by changing the lengths of the semi-major and the semi-minor axes. The material of the capsule in the FE model was set as polyethylene. According to the model assumptions in Sect. 2 and Eq. (11), the intestine was configured as an isotropic linear elastic material with the consideration of Young’s modulus.

Fig. 3

(Colour online) Two-dimensional FE model with the definitions of geometric parameters and boundary conditions. The cross-sectional profile of the circular fold is elliptical, and the height, $h_i$, and width, $w_i$, of the circular fold can be adjusted by changing the lengths of the semi-major and the semi-minor axes. The material of the capsule was set as polyethylene, and the intestine was configured as an isotropic linear elastic material with the consideration of Young’s modulus. The capsule and the intestine were modelled by using the 4-node plane element (PLANE182) and the 8-node plane element (PLANE183), and their mesh sizes were set as 0.5 [mm] and 0.3 [mm], respectively. The mesh of the small intestine was built in three layers, and its bottom surface was fixed. For the first 0.3 s of the simulation, standard gravity was applied to the capsule, and a constant speed of 8 [mm/s] was applied to the capsule’s head along the x axis

3.2 Meshing and boundary conditions

Because of the requirement of deformation, the proposed model was meshed with two types of elements. The capsule was modelled by using the 4-node plane element (PLANE182), and a higher-order 8-node plane element (PLANE183) with quadratic displacement behaviour was adopted for the small intestine. Convergence tests using different mesh sizes were implemented. As the mesh size gradually decreases, the maximum frictional force tends to stabilization, and the mesh size for every two results within $\pm 5 \%$ was used later in the FE model. In order to obtain the best performance for the FE model, the mesh sizes for the capsule and the small intestine were set as 0.5 [mm] and 0.3 [mm], respectively, and the mesh of the small intestine was built in three layers. For the boundary condition of the FE model, the bottom surface of the small intestine was fixed. The displacement of the capsule along the y axis and the rotation of the capsule on the xoy plane were set as free. For the first 0.3 [s] of the simulation, standard gravity was applied to the capsule, and a constant speed of 8 [mm/s] was applied to the head of the capsule along the x axis after the capsule settled down on the y axis. In addition, the friction coefficient between the capsule and the small intestine was set as 0.2293, which was identified via experiment in [15].

4 Experimental setup

To validate the mathematical and FE models proposed in Sects. 2 and 3, a self-assembled apparatus was developed for experimental testing of fold’s resistant force, and this section details the experimental apparatus and procedure, as follows.

4.1 Experimental apparatus

The schematic diagram of the self-assembled experimental apparatus is presented in Fig. 4a, with its photographs shown in Fig. 4b. The testing apparatus was composed of: (i) a micro controller unit (MCU) with the model number of Ardunio Uno Rev3, (ii) a DC stepper motor with the model number of 28BYJ-45 and its drive circuit, (iii) a load cell with the series number of YZC-133 100g, (iv) an signal amplifier with the series number of AD627, and (v) other mechanical and electrical accessories.

Fig. 4

(Colour online) The self-assembled experimental apparatus, a schematic diagram, and b photographs. A self-designed graphic user interface (GUI) in a personnel computer (PC) is used to control an Arduino micro-controller unit (MCU) by sending commands (CMDs) via a USB cable. The MCU sends pulse width modulation (PWM) signals to a drive circuit, and the drive circuit generates pluses to control a DC stepper motor operating at a constant speed. The DC motor uses a gear and a rack to pull a load cell moving forward, and the signal from the load cell is amplified, and converted to digital signals by the MCU, and the MCU sends the digital data to the GUI via the USB cable for data logging. A capsule is connected to the load cell via a nylon rope and can be pulled moving forward on a piece of flat-open synthetic small intestine at a preset constant speed, while the synthetic small intestine is fixed onto a solid holder with two circular folds

As shown in Fig. 4, a graphic user interface (GUI) in a personnel computer (PC) was developed to achieve bi-way real-time communication with the MCU via a USB cable, which sent commends (CMD) to the MCU for setting motor speed, and received digital data from the MCU for recording data. According to the preset motor speed, the MCU generated desired pulse width modulation (PWM) signals to the motor drive circuit, which further generated pluses to control the DC stepper motor operating at the preset constant speed. The rotation of the DC stepper motor was converted to linear translation via a gear and a sliding rack, on which the load cell was fixed. The load cell was connected to the capsule using a nylon rope, and thus, the capsule was pulled moving forward on a piece of cut-open synthetic small intestine in a preset constant speed. Then, the friction force acting on the capsule was measured via the load cell. As the signal from the load cell was at the scale of millivolt, an amplifier was applied to condition the signal to the level of volt. The MCU was configured to acquire the amplified signal via its on-chip analogue-to-digital converter (ADC) before sending the collected digital data to the GUI for data logging.

4.2 Experimental procedure

After initialising the MCU, the load cell was calibrated by standard weight. For each testing trial, the motor speed was set as a constant. After initialising the capsule position, the data log function of the MCU was enabled before switching on the motor. The rotating motor pulled the capsule on a cut-open synthetic small intestine with two circular folds in different dimensions. After the capsule moving to the terminal position, the DC stepper motor was switched off and the collected data were saved. To ensure the validity of this testing, the completeness of the collected data were checked. If the data were incomplete, this testing trail was repeated until complete data were collected. If the data were valid, the speed of the DC stepper motor was set to another constant value for a new trial, until sufficient data were acquired.

Fig. 5

Experimental procedure with flowchart in (a) and capsule moving stages in (b)

As shown in Fig. 4, the capsule moved on a flat-open synthetic small intestine fixed on a solid holder with two circular folds, of which the small fold’s dimensions were 3.33 [mm] in width and 1.67 [mm] in height, and the large fold’s dimensions were 3.09 [mm] in width and 2.34 [mm] in height. The distance between the two folds was 50 [mm]. Those dimensions were selected according to the measurement of a real GI tract in [27]. According to experimental observation, the capsule’s motion was divided into ten stages, as follows: Stages ${\textcircled {1}}$–${\textcircled {4}}$ described how the capsule passed the small fold; Stage ${\textcircled {5}}$ detailed the capsule moving on the flat section between the two folds; Stage ${\textcircled {6}}$–${\textcircled {9}}$ illustrated how the capsule climbed over the large fold; Stage ${\textcircled {10}}$ shown that the capsule reached the end point.

5 Results and discussions

5.1 Model validation

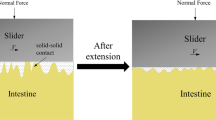
In order to validate the analysis, the mathematical and FE models adopted the parameters listed in Fig. 6 corresponding to the experimental setup described in Sect. 4. Under the same position, the one-to-one correspondence between the capsule’s posture and the resistant force is shown in Fig. 6. According to the FE result, the process of capsule’s crossing over a circular fold can be divided into six stages. Although some stages were missed by the mathematical model or the experiment due to their limitations, here we are interested with the maximum resistant force experiencing by the capsule when it crosses over the fold. As can be seen from Fig. 6, all of the results included Stage ${\textcircled {1}}$, in which the capsule’s resistance was purely due to the intestinal friction as the capsule moved on the small intestine. Stage ${\textcircled {2}}$ reveals that when the capsule’s head encountered the fold, the resistance increased rapidly. In both the FE and experimental results, Stage ${\textcircled {2}}$ terminated when the pulling force overcame the maximum resistance of the fold, and the capsule entered Stage ${\textcircled {3}}$ after its head was lifted up. As the capsule in the mathematical model cannot rotate according to the assumption, it entered Stage ${\textcircled {4}}$ from Stage ${\textcircled {2}}$ directly by retaining its horizontal posture but moving forward and vertically simultaneously during the crossing. In the FE result, we observed a slight increase in the resistant force during Stage ${\textcircled {4}}$, as the tail of the capsule tended to leave the intestinal surface. After the centre of mass of the capsule crossed the fold, the head of the capsule sank and contacted with the intestinal surface, at which point the first valley value of the resistant force was recorded in Stage ${\textcircled {5}}$. In the experiment, Stage ${\textcircled {4}}$ was not recorded, in which the capsule’s body was only supported by the fold, without either the head or tail contacted with the intestine. In the theoretical analysis, Stage ${\textcircled {5}}$ was absent since the capsule cannot sink its head by rotation. Next, a further drop of the resistance was recorded by both of the mathematical and FE models in Stage ${\textcircled {6}}$. This stage started when the capsule tail was engaged with the fold, and the fold exerted pressure on the tail to push the capsule forward. However, this stage was not recorded in the experiment, which could be due to two experimental factors. Firstly, the folds were formed by the 3D-printed holder shown in Fig. 4b, so their geometrical and mechanical properties were not exactly the same as the ideal circular folds. Secondly, the capsule was pulled by a nylon rope that cannot record a negative resistant force when the capsule slid down from the fold.

Fig. 6

(Colour online) Resistant force acting on the capsule as a function of capsule’s displacement when the capsule was pulled on a cut-open synthetic small intestine consisting of two different circular folds in a constant speed of 8 [mm/s] obtained from the mathematical model (blue line), the FE model (red line) and the experiment (black line). FE model can capture all of the six stages of the capsule’s motion. Due to the limitations, experiment missed Stages ${\textcircled {4}}$ and ${\textcircled {6}}$, and the mathematical model cannot capture Stages ${\textcircled {3}}$ and ${\textcircled {5}}$. Parameters for the mathematical and FE models were chosen as $E = 100$ [kPa], $G=33.96$ [mN], $\mu =0.2293$, $R = 5.50$ [mm], $L=15$ [mm], $H=0.69$ [mm], $x_1 = 12.66$ [mm], $h_1 = 1.67$ [mm], $w_1 = 1.665$ [mm], $x_2=62.66$ [mm], $h_2 = 2.34$ [mm] and $w_2 = 1.545$ [mm], which were identified from the experimental setup

Fig. 7

(Colour online) FE contour maps of the intestinal contact pressure in six stages when the capsule crossed over the first circular fold. When the capsule moved forward at a uniform speed in Stage ${\textcircled {1}}$, the maximum contact pressure appeared on the head of the capsule. The maximum contact pressure, 5.962 [kPa], was encountered in Stage ${\textcircled {2}}$ when the capsule moved against the fold, and in this stage, this maximum contact pressure appeared on the fold rather on the tail of the capsule. In Stage ${\textcircled {5}}$, when the capsule’s head tilted down, the maximum contact pressure appeared on its head, leading the capsule to experience a fluctuated resistant force

To further study the resistant forces generated in different stages of crossing, the distribution of contact pressure between the capsule and the small intestine in each stage is displayed in Fig. 7. When the capsule moved forward at a uniform speed in Stage ${\textcircled {1}}$, the maximum contact pressure appeared on the head of the capsule. This is due to the fact that the capsule sank in the small intestine, leading its head’s contact pressure greater than the tail. According to the FE simulation, the maximum contact pressure, 5.962 [kPa], was encountered in Stage ${\textcircled {2}}$ when the capsule moved against the fold. Compared with Stage ${\textcircled {2}}$ in Fig. 6b, the maximum contact pressure and the maximum resistant force are consistent correspondingly. In addition, in Stage ${\textcircled {2}}$, the maximum contact pressure appeared on the fold rather on the tail of the capsule, while in Stage ${\textcircled {5}}$, when the capsule’s head sank, the maximum contact pressure appeared on its head, leading the capsule to have a reversed motion trend. This explains why the FE’s resistant force in Stage ${\textcircled {5}}$ shown in Fig. 6b fluctuated and tended to be negative, although the contact pressure was still relatively large.

Experimental results are shown in Fig. 8, with the friction-displacement recording shown in Fig. 8a, and the peak and average frictions shown in Fig. 8b. As shown in Fig. 8a, the friction force increased dramatically to its peak value at Stage ${\textcircled {1}}$ when the capsule head contacted the small fold. Then, the friction decreased at Stage ${\textcircled {2}}$ when the capsule started to pass the small fold with a small dip angle. As the capsule moves further with its centre of gravity align with the small fold vertically, the friction decreases dramatically to its minimum value at Stage ${\textcircled {3}}$. After the capsule head contacting the synthetic small intestine again, the friction increased until the whole capsule passed the small fold at Stage ${\textcircled {4}}$. At Stage ${\textcircled {5}}$, capsule moved on a flat section between two folds. The Stages ${\textcircled {6}}$–${\textcircled {10}}$ depicted the process of the capsule passed the larger fold, which were similar to the process of passing the small fold, as described at Stages ${\textcircled {1}}$–${\textcircled {5}}$.

In Fig. 8a, the peak value for the small fold at Stage ${\textcircled {1}}$, the average value for the flat span at Stage ${\textcircled {5}}$, and the peak value for the large fold at Stage ${\textcircled {6}}$ are selected as characteristic parameters to depict the procedure of capsule passing folds. Fourteen testing trials, with a wide range of capsule speed, were conducted, and the characteristic parameters are shown in Fig. 8b. In general, the peak and average values were not sensitive to the speed. The peak value for the large fold is much larger than that for the small fold.

Fig. 8

Experimental results of the measured friction. In (a), the measured friction force varies with the capsule displacement at a constant speed of 12 [mm/s], of which the peak value for the small fold, the average value for the flat span (shadowed region), and the peak value for the large fold are marked by red dot, blue triangle, and black square, respectively. These three values are selected as characteristic parameters to depict the procedure of capsule passing folds. For a wide range of capsule speed, these characteristic parameters are shown in (b)

5.2 Influence of parameters

As discussed above, both the theoretical and FE models yield consistent results compared with the experimental study. Thus, we can use these two methods to predict the influence of various geometric and mechanical parameters of the small intestine and the capsule on the resistant force. As seen in Fig. 9a–b, increase of the fold’s height strengthens the resistant force. For a higher fold, the maximum becomes larger and shows up earlier for a larger region of capsule–fold contact when the capsule moves towards it. With respect to the increase of the fold’s width, as seen in Figs. 9c–d, the maximum is decreased, while the region for capsule–fold contact becomes wider. Namely, increasing the fold’s width flattens the fluctuation in the resistant force. With respect to the increase of the fold’s Young’s modulus, as seen in Fig. 9e–f, the maximum resistant force increases, and the jump in Stage ${\textcircled {2}}$ becomes sharper. However, the width the of capsule–fold contact region is unchanged.

Fig. 9

(Colour online) Resistant forces as functions of the capsule’s position under various heights, widths and Young’s moduli of the circular fold calculated by the mathematical (left panels) and FE models (right panels), with the maximums marked by blue circles and red squares, respectively. a–b The fold’s height was increased from 1.0 [mm] to 5.5 [mm], c–d the fold’s width was increased from 1.0 [mm] to 10.0 [mm], and e–f the Young’s module was changed from 10 [kPa] to 200 [kPa]. Increase of the fold’s height strengthens the resistant force, while increasing the fold’s width flattens the fluctuation in the resistant force. Once the fold is stiffer, the increase of the maximum resistant force becomes more rapid

The maximum resistant forces are plotted as functions of several parameters in Fig. 10. The influence of the fold’s height, width and Young’s modulus, which corresponds with Fig. 9, is shown in Fig. 10a–c, showing that increasing the height, decreasing of the width, or enhancing the fold’s stiffness results in larger forces. It is seen in Fig. 10d that the maximum force decreases with respect to the increase of the tissue’s thickness. With respect to the increases of the frictional coefficient and the capsule’s weight, as seen in Fig. 10e–f, the resistance increases due to the enhancement of the frictional force. In terms of the capsule’s size, Fig. 10g shows a decline of the maximum resistant force with respect to the increase of its radius, while the capsule’s length in Fig. 10h does not show a strong influence on the maximum force, especially for $L>10$ [mm]. It is worth noting that, in Fig. 10a, g and h, there exists a discrepancy between the theoretical and FE results in case of large h, small R and small L, respectively. This could be induced by the assumption in the theoretical model that the capsule does not rotate, but the tilted angle becomes significant for a higher fold or a shorter capsule.

Fig. 10

(Colour online) Maximum resistant forces as functions of a fold’s height, h, b fold’s width, w, c Young’s module of the fold, E, d tissue’s thickness, H, e frictional coefficient, $\mu$, f capsule’s weight, G, g capsule’s radius, R and h capsule’s length, L calculated by the mathematical (blue dot line) and FE models (red square line). Increasing the fold’s height, decreasing the width, or enhancing the stiffness may result in larger maximum resistant force. The maximum force decreases as the tissue’s thickness increases. When the frictional coefficient and the capsule’s weight increase, the maximum resistance increases due to the enhancement of the frictional force. For the capsule’s size, the maximum resistant force declines with respect to the increase of its radius, while the capsule’s length does not show a strong correlation with the maximum, especially for $L>10$ [mm]. Also, there exists a discrepancy between the theoretical and FE results in case of large h, small R and small L, which could be induced by the assumptions in the mathematical model

6 Validation of the maximum resistant force using an intestine simulator

To evaluate the force needed for crossing the folds in a relatively real environment, an additional experiment was carried out by using an intestine simulator as shown in Fig. 11a. The simulator manufactured by the Chamberlain Group has its soft internal wall simulating the real intestinal environment with the folds in random dimensions and an interfold distance of 30 [mm] approximately. A stereolithography 3D-printed capsule prototype with a length of 26 [mm] and an outer diameter of 11 [mm] was placed inside the intestinal tract. The capsule contains an inner permanent neodymium magnet to be dragged by the external magnetic field generated by a self-assembled electromagnetic coil. The coil was placed on the same axis with the magnet to gain a calculable magnetic force acting on the capsule. This force was calculated from a combination of the coil’s supplying current and the distance between the coil and magnet. Such a force-distance relationship has been measured through experiment and validated by analytical calculation in [13].

Fig. 11

(Colour online) (a) A self-assembled electromagnetic coil generated magnetic field to drive the capsule (with an inner permanent neodymium magnet) to cross over various folds in an intestine simulator, where the capsule has a weight of 34.2 [mN], a radius of 5.5 [mm] and a length of 15 [mm], and the intestine has a Young’s modulus of 25 [kPa] and a frictional coefficient of 0.2105. (b) Minimum magnetic forces required for the capsule to cross over eight randomly selected folds (Fold no. 1-8), which have the heights of 1.91 [mm], 4.03 [mm], 2.68 [mm], 2.41 [mm], 2.81 [mm], 2.46 [mm], 2.32 [mm] and 2.91 [mm], and the widths of 2.63 [mm], 1.39 [mm], 2.30 [mm], 2.66 [mm], 2.175 [mm], 2.615 [mm], 2.4 [mm] and 1.99 [mm], respectively. For each fold, the experiment was repeated for five times to get a more reliable result. Between each repeat, the intestinal surface was moisturised constantly by using the clinical lubricant to keep similar friction environment, mimicking the environment of a real and live intestine

During the experiment, the capsule was placed 50 [mm] away from the centre of the coil and was just in contact with the testing fold. A low voltage was applied to the coil initially to provide a magnetic force for the capsule, and then the voltage was gradually increased until the capsule started to cross over the fold. If the coil’s current reaches its limit and the capsule still cannot cross over the fold, the coil was moved closer to the capsule gradually until it started the crossing. Then, the instant current of the coil and the coil-magnet distance were recorded for calculating the magnetic force at that moment. To validate the theory proposed in Sect. 2, the maximum resistant forces during crossing eight randomly selected circular folds in the intestine simulator were recorded for comparison. For each fold, the experiment was repeated for five times to get a more reliable result. Between each repeat, the intestinal surface was moisturised constantly by using the clinical lubricant to keep similar friction environment, mimicking the environment of a real and live intestine. As the results shown in Fig. 11b, the resistant forces obtained from this experiment prove to be consistent with the theoretical predictions, no matter the variation of the fold’s height and width.

7 Conclusions

This paper studied the capsule–intestine interaction during an endoscopic capsule crossing over the circular fold in the small intestine. To this end, an analytical model for the resistant force exerted by the small intestine on the capsule was proposed, which was then validated by comparing with a 2-dimensional FE model and an experimental study. All of the three methods yielded consistent results, especially in the prediction of the maximum resistant force which is critical for the capsule to cross the “barrier”. Finally, a capsule prototype equipped with an inner permanent magnet and dragged by an external magnetic field was used to validate the maximum resistant force that should be overcome for crossing over the fold. Tested with eight randomly selected folds, the theoretical model yielded consistent predictions of the force compared with the experiment.

According to the capsule–intestine interaction, the crossing procedure was divided into six stages, and all of the theoretical, FE and experimental analyses found the maximum resistant force in Stage ${\textcircled {2}}$ where the capsule’s head was engaged with the fold. However, Stages ${\textcircled {3}}$ and ${\textcircled {5}}$ in which the capsule rotated to climb up and down the fold were absent in the theoretical model due to the assumption that the capsule can only translate without rotation. The experiment, by contrast, did not unveil Stage ${\textcircled {6}}$ for a sudden drop of the resistant force when the capsule’s tail was in contact with the fold. In general, the FE model captured all of the crossing stages, but the computation was so time-consuming that we only adopted a 2-dimensional model by sacrificing its accuracy. Nonetheless, all these three methods yielded consistent results for the maximum resistant force, which is a key design parameter for endoscopic engineers when considering the new endoscopic device design. The predicted maximum resistant force was finally validated by another experiment using a magnetic-driven capsule prototype moving in an intestine simulator.

It was found that the resistant force depends on various geometric and mechanical parameters of the fold and the capsule. In terms of the fold, increasing the fold’s height, decreasing its width, enhancing the Young’s modulus of the fold or decreasing the tissue’s thickness yielded a larger resistant force. Besides, the resistant force can also be raised by increasing the frictional coefficient and capsule’s weight, or decreasing the capsule radius. Beside the magnitude of the maximum resistant force, it was found that the location for the appearance of the maximum is not constant, but is dependent on the fold’s properties. For example, the maximum resistant force may show up earlier for a higher, wider and stiffer fold.

Major limitations of the proposed mathematical model are twofold. First, the actual intestine structure was simplified based on our previous studies on the anatomy of the small intestine [15, 16]. The small intestine has two types of movements, peristalsis and segmentation. However, the frequencies of these two movements are extremely low, so they were ignored in this study. Also, the distance between each circular fold increases from the beginning section (duodenum) to the end section of the small intestine (terminal ileum). While in this work, we did not consider such a distance as a system parameter to study the locomotion of the capsule. Furthermore, tubular and twisted lumen was simplified as a plane tissue substrate in this work. All of these simplifications in structure may cause inaccuracies in prediction. Second, the capsule was assumed to be without any rotation during its crossing motion, which led to the missing of a few key stages of the crossing motion compared to the FE results. All these limitations could be mitigated by developing a more comprehensive model, including the capsule’s rotation and the complex structure of the small intestine, which could be the future work of this research.