Localized discrete breather modes in neuronal microtubules

Abstract

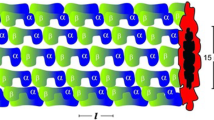
We made an attempt to provide a realistic picture of the localization of energy in microtubules (MTs), and we intend to model the nonlinear dynamics of MTs using the “double-well” $\phi ^4$ form of the potential describing the dipole–dipole interactions. We investigate the modulational instability (MI) of the nonlinear plane wave solutions by considering both the wave vector (q) of the basic states and the wave vector (Q) of the perturbations as free parameters. A set of explicit criteria of MI is derived, and under the plane-wave perturbation, the constant amplitude solution becomes unstable and localized discrete breathers (DBs) solutions appear. We show numerically that MI is also an indicator of the presence of discrete breathers. We suggest that an electric field favourably leads the DB excitations towards the properly aligned end triggering a dissembly of the protofilament due to the energy release. These DBs could catalyse MT-associated proteins attachment/detachment and promote or inhibit the kinesin walk. We establish that the electromechanical vibrations in MTs can generate an electromagnetic field in the form of an electric pulse (breathers) which propagates along MT serving as signalling pathway in neuronal cells. The DBs in MT can be viewed as a bit of information whose propagation can be controlled by an electric filed. They might perform the role of elementary logic gates, thus implementing a subneuronal mode of computation. The generated DBs present us with novel possibilities for the direct interaction between the local electromagnetic field and the cytoskeletal structures in neurons. Thus, we emphasize that the effect of discreteness and electric field plays a significant role in MTs.

Appendices

Appendix 1

$$\begin{aligned} Im(\varOmega )= & {} \pm \Bigg [-768X_1X_2u_0^2\cos (q+Q)\\&-\,768X_1X_2u_0^2 \cos (q-Q)+27648X_2^2u_0^4\\&+\,8X_1^2\cos (q+Q)\omega \cos (q-Q)\\&-\,384\omega _0X_2u_0^2+768X_0X_2u_0^2\\&+\,384 X_2 u_0^2 +4X_1\omega _0\cos (q+Q)\\&+\,4X_1\omega _0\cos (q-Q)-8X_1 X_0\cos (q+Q)\\&-\,8X_1X_0\cos (q-Q) -4X_1 \omega \cos (q+Q)\\&-\,4X_1\omega \cos (q-Q)+\omega _0^2 -2\omega _0\omega \\&+\,4X_0^2 +4X_0\omega +\omega ^2\\&+\,4X_1^2\cos (q+Q)^2 +4X_1^2\cos (q-Q)^2\\&-\,\Big [\frac{192X_1X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ]\cos (q+Q)\\&-\,\Big [\frac{192X_1X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ]\cos (q-Q)\\&-\,\frac{96\omega _0X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\\&+\,\frac{96(\varepsilon +\frac{24X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2})X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\\&+\,\frac{192X_0X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\\&+\,\frac{96X_2X_3^2\omega }{(4X_1-\varepsilon -2X_0)^2} +\frac{18{,}432X_2^2X_3^2u_0^2}{(4X_1-\varepsilon -2X_0)^2}\\&+\,384\Big [\varepsilon +\frac{24X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ]X_2u_0^2\\&-\,4X_1\Big [\varepsilon +\frac{24X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ]\cos (q-Q)\\&-\,4X_1\Big [\varepsilon +\frac{24X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ] \cos (q+Q)\\&+\,\frac{2304X_2^2X_3^4}{(4X_1-\varepsilon -2X_0)^4}\\&+\,\Big [\varepsilon +\frac{24X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ]^2\\&-\,2\omega _0 \Big [\varepsilon +\frac{24X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ] \\&+\,4X_0\Big [\varepsilon +\frac{24X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ]\\&+\,2\omega \Big [\varepsilon +\frac{24X_2X_3^2}{(4X_1-\varepsilon -2X_0)^2}\Big ]\Bigg ]^{\frac{1}{2}}. \end{aligned}$$

Appendix 2

Consider a system of M polynomial NDDEs

$$\begin{aligned}&\Delta \mathbf {(u_{n+p1}(X),\ldots ,u_{n+pk}(X),\ldots ,u_{n+p1}^{'}(X),\ldots ,}\nonumber \\&\mathbf {u_{n+pk}^{'}(X),\ldots ,u_{n+p1}^{(r)}(X),\ldots ,u_{n+pk}^{(r)}(X)=0,} \end{aligned}$$

(37)

where the dependent variable $\mathbf {u_n}$ has M components $u_{i,n}$, the continuous variable $\mathbf {x}$ has N components $x_{i}$, the discrete variable $\mathbf {n}$ has Q components $n_j$, the k shift vectors $\mathbf {p_i} \in Z^{Q}$ and $\mathbf {u}^{(r)}\mathbf {(X)}$ denotes the collection of mixed derivative terms of order r.

According to the tanh-function method, the main steps of the extended tanh-function method for NDDEs are outlined as follows.

Step 1 When we seek the travelling wave solutions of Eq. (37), the first step is to introduce the wave transformation $\mathbf {u_{n+ps}(X)~=~U_{n+ps}}(\xi _n)$, $\xi _n~=~\sum _{i=1}^{Q}d_i n_i+\sum _{j=1}^{N}c_j x_j+\chi$ for any $s(s~=~1,\ldots ,k)$, where the coefficients $c_{1},c_{2},\ldots , c_{N},d_{1},d_{2},\ldots ,d_{Q}$ and the phase $\chi$ are all constants. In this way, Eq. (37) becomes

$$\begin{aligned}&\Delta \mathbf {(U_{n+p1}(\xi _n),\ldots ,U_{n+pk}(\xi _n),\ldots ,U_{n+p1}^{'}(\xi _n),\ldots ,}\nonumber \\&\mathbf {U_{n+pk}^{'}(\xi _n),\ldots ,U_{n+p1}^{(r)}(\xi _n),\ldots ,U_{n+pk}^{(r)}(\xi _n)=0,} \end{aligned}$$

(38)

Step 2 We propose the following series expansion as a solution of Eq. (38):

$$\begin{aligned} U_{n}(\xi _{n})=\sum _{j=-l}^{l}a_{j}\phi ^{j}(\xi _{n}), \end{aligned}$$

(39)

where $\phi (\xi _{n})$ satisfies the following Ricatti equation:

$$\begin{aligned} \frac{d\phi (\xi _{n})}{d\xi _{n}}=\delta +\phi ^{2}(\xi _{n}), \end{aligned}$$

(40)

where $\delta$ is an arbitrary constant. It is known that Eq. (40) possesses the solutions,

$$\begin{aligned}&\phi (\xi _{n})= \nonumber \\&\Bigg \{-\sqrt{-\delta }\tanh (\sqrt{-\delta }\xi _{n}), {-}\sqrt{-\delta }\coth (\sqrt{-\delta }\xi _{n}),\delta <0,\nonumber \\&\sqrt{\delta }\tan (\sqrt{\delta }\xi _{n}),{-}\sqrt{\delta }\cot (\sqrt{\delta }\xi _{n}),\delta > 0.\Bigg \}. \end{aligned}$$

(41)

At present, one should note the identities

$$\begin{aligned}&\tanh (x+y)=\frac{\tanh (x)+\tanh (y)}{1+\tanh (x)\tanh (y)}, \nonumber \\&\coth (x+y)= \frac{\coth (x)+\tanh (y)}{1+\coth (x)\tanh (y)}, \end{aligned}$$

(42)

and

$$\begin{aligned}&\tan (x+y)=\frac{\tan (x)+\tan (y)}{1-\tan (x)\tan (y)},\nonumber \\&\cot (x+y)= \frac{\cot (x)-\tan (y)}{1+\cot (x)\tan (y)}. \end{aligned}$$

(43)

One can obviously rewrite the expressions Eq. (42) and Eq. (43) in an uniform formula by using the expression Eq. (41)

$$\begin{aligned} \phi (\xi _{n}+y)=\frac{\phi (\xi _{n})+\mu \sqrt{\mu \delta }f(\sqrt{\mu \delta }y)}{1-\frac{1}{\sqrt{\mu \delta }}\phi (\xi _{n})f(\sqrt{\mu \delta }y)}, \end{aligned}$$

(44)

where $\mu =\pm {1}$ and

$$\begin{aligned} f(\sqrt{\mu \delta }y)= \left\{ \begin{array}{lll} &{}\tanh (\sqrt{-\delta }y), &{}\quad \mu = -1,\\ &{}\tan (\sqrt{\delta }y), &{}\quad \mu = 1. \end{array} \right. \end{aligned}$$

(45)

Thus

$$\begin{aligned}&u_{n}(\xi _{n+p_{s}})\nonumber \\&\quad = a_{0} + \sum _{j=-l}^{l} a_{j}\Bigg [\frac{\phi (\xi _{n})+\mu \sqrt{\mu \delta }f(\sqrt{\mu \delta }\varphi _{s})}{1-\frac{1}{\sqrt{\mu \delta }}\phi (\xi _{n})f(\sqrt{\mu \delta }\varphi _{s})}\Bigg ]^j,\nonumber \\ \end{aligned}$$

(46)

where

$$\begin{aligned} \varphi _{s}=p_{s1}d_{1}+p_{s2}d_{2}+\ldots +p_{sQ}d_{Q}, \end{aligned}$$

(47)

and $p_{sj}$ is the jth component of shift vector $p_{s}$.

Step 3 Determine the degree l of the polynomial solutions Eqs. (39) and (46). We are interested in balancing the term $\phi (\xi _{n})$, with the leading terms of $\mathbf {U_{n}(\xi _{n+p_{s}})}$, $(\mathbf {p_{s}\ne 0})$ will not affect the balance since $U_{n}(\xi _{n+p_{s}})$ can be interpreted as being of degree zero in $\phi (\xi _{n})$. So we can easily get the degree l in the ansatz Eqs. (39) and (46) by balancing the highest nonlinear terms and the highest-order derivative term in $\mathbf {U_{n}(\xi _n)}$ as in the continuous case.

Step 4  Substituting the ansatzs Eqs. (39) and (46) into (38), then setting the coefficients of all independent terms in $\phi (\xi _{n})$ to zero, we will get a series of algebraic equations, from which the constants $a_0, a_j(j=1,2\ldots ,l)$ are explicitly determined by the help of Maple.

Step 5 Substitute the values solved in Step 4 with Eq. (41) into expression Eq. (39), and one can find the solutions of Eq. (37).