1 Introduction

The idea of the finite-time stability of systems originated in Soviet scientific literature in the mid-20th century [19] and has since been applied to various real-world systems, such as biochemical reactions and communication networks, etc. [4, 12, 27]. The main goal of this analysis is to determine whether a system can maintain its desired behavior within a given time interval, which may be very short. By using the L–K functional approach and LMI techniques, a series of research works on stability, boundedness, stabilization, and \(H_\infty \) control over a finite time interval for both linear and nonlinear discrete-time systems were announced of late, e.g., see [3, 32, 38, 41, 44, 45].

NNs with delays are a type of artificial NNs that can model the temporal dynamics of complex systems. They can capture the effects of past inputs and outputs on the current state of the network and thus can handle non-Markovian processes. NNs with delays can learn the patterns and trends of time series data, such as stock prices, weather, or traffic, and forecast future values based on historical data; NNs with delays can be also used to design adaptive controllers for nonlinear systems, such as robots, vehicles, or power plants; and at last, NNs with delays can be applied to various signal-processing tasks, such as speech recognition, image processing, or biomedical signal analysis [5, 10, 17, 25, 26, 39, 40]. Especially, for the class of discrete-time NNs, there are a number of fascinating articles [1, 27, 37, 40] that deal with one of the topics of stability, passivity, or boundedness in a finite time interval. The paper [14] highlighted the importance of considering both discrete and leakage delays in the analysis of NNs. In particular, leakage delay in the negative feedback term can lead to instability and complex behaviors in NNs. Therefore, it is essential to investigate the effects of leakage delay on the stability and performance of NNs. Based on that fact, stability and passivity for several different classes of continuous-time NNs with leakage delay were studied in [5, 11, 21, 31], while the stability and dissipativity for some discrete-time analogs were considered in [6,7,8, 16, 22, 29, 34,35,36]. Delay-dependent stability criteria for complex-valued NNs with leakage delay were also established, e.g., see [9, 33]. The works mentioned seem to be enough to demonstrate the considerable attractiveness of leakage delay for researchers who have been working in various fields over the years. However, despite that, for the sake of convenience of analysis, leakage delay was unfortunately ignored while studying the finite-time stability, passivity, and boundedness of the systems mentioned in the papers [27, 40]. The same situation also holds for \(H_\infty \) FTB of the systems discussed in [1, 37]. On the other hand, from [15, 20], we know that nonlinear functions satisfying the sector-bounded condition are more general than the usual class of Lipschitz functions. However, up to this point, very few authors have investigated general NNs with activation functions satisfying the sector-bounded condition, and [10, 30] are some typical works among them.

To the best of our knowledge, in the literature, there are no results on the problem of \(H_\infty \) FTB for discrete-time NNs with leakage delay and discrete delay as well as different generalized activation functions. That is the main reason why we want to fill that gap in the existing literature. More specifically, in this paper, by a logical combination of appropriately constructed L–K functionals and an extended reciprocally convex matrix inequality, we first suggest conditions that ensure not only FTB of the involved NNs but also a finite-time \(H_\infty \) performance. With the same technique, the FTS of the corresponding nominal system is also obtained. Some numerical examples are offered to demonstrate the validity of the achieved conditions. The core contributions of this paper consist of:

  • It is the first time to propose delay-dependent criteria for \(H_\infty \) FTB and FTS of discrete-time NNs with a pair of time-varying delays (leakage delay and discrete delay). These criteria contain information about the upper and lower bounds of both types of delay.

  • The neuron activation functions are different and are supposed to satisfy the sector-bounded conditions, which are known to be more general than the usual Lipschitz conditions.

  • The extended reciprocally convex technique is entirely exploited, so the number of decision variables is limited as much as possible.

The arrangement of the rest of this paper is as follows. In Sect. 2, some relevant definitions and technical propositions are presented in detail, including the problem we aim to handle. Delay-dependent criteria in the form of matrix inequalities for \(H_\infty \) FTB and FTS, respectively, together with two illustrative examples, are delivered in Sect. 3. Sections on conclusion and references close the paper.

Notation \(\mathbb Z_+\) represents the set of all non-negative integers; \(\mathbb {R}^{n}\) and \(\mathbb {R}^{m \times n}\) symbol for the n-dimensional Euclidean space and the set of real matrices of size \(m\times n\) respectively; \(A^{-1}\) and \(A^{\textsf{T}}\) are the inverse and transpose of a matrix A respectively; \(A > 0\) means that A is a positive-definite matrix and \(A > B\) implies \(A - B > 0\). The symbol \(*\) stands for entries of a matrix implied by symmetry (in a symmetric matrix).

2 Preliminaries

Let us take the following discrete-time NNs with a pair of time-varying delays and any external disturbance into consideration

$$\begin{aligned} x(k+1)&= Ax(k-\sigma (k)) + Bf(x(k)) + B_1g(x(k-h(k))) + C\omega (k),\quad k\in \mathbb Z_+, \nonumber \\ z(k)&= A_1x(k) + Dx(k-h(k)) + D_1x(k-\sigma (k)) + C_1\omega (k), \nonumber \\ x(k)&= \phi (k),\quad k\in \{-\rho ,-\rho +1,\dots ,0\}, \end{aligned}$$
(1)

where \(x(k)\in \mathbb {R}^n\) is the state vector; n is the number of neurons; \(z(k)\in \mathbb {R}^r\) is the observation output; the diagonal matrix \(A \in \mathbb {R}^{n\times n}\) characterizes the self-feedback terms; \(B,\, B_1\in \mathbb {R}^{n\times n}\) are connection weight matrices; \(C\in \mathbb {R}^{n\times s}, C_1\in \mathbb {R}^{r\times s}\) are known matrices; \(A_1, D, D_1\in \mathbb {R}^{r\times n}\) are the observation matrices. The discrete delay function h(k) and leakage delay function \(\sigma (k)\) satisfy the condition

$$\begin{aligned} 0< h_1 \leqslant h(k) \leqslant h_2, \quad 0&< \sigma _1 \leqslant \sigma (k) \leqslant \sigma _2 \quad \forall k\in \mathbb Z_+, \end{aligned}$$
(2)

where \(h_1, h_2, \sigma _1\) and \(\sigma _2\) are given natural numbers; \(\rho := \max \{\sigma _2, h_2\}\) and \(\phi (k)\) is the initial function. \(\omega (k)\in \mathbb {R}^s\) is the external disturbance that is assumed to satisfy

$$\begin{aligned} \sum _{k=0}^N\omega ^{\textsf{T}}(k)\omega (k) < d, \end{aligned}$$
(3)

where d is a given positive scalar. Besides, in the framework of this article, we adopt the following assumption for neuron activation functions \( f(\cdot ) \) and \( g(\cdot ) \).

Assumption 1

[10, 30] The diagonal neuron activation functions

$$\begin{aligned} f(x(k))&= \begin{bmatrix} f_1(x_1(k))&f_2(x_2(k))&\dots&f_n(x_n(k))\end{bmatrix}^{\textsf{T}},\\ g(x(k-h(k)))&= \begin{bmatrix} g_1(x_1(k-h(k)))&g_2(x_2(k-h(k)))&\dots&g_n(x_n(k-h(k))) \end{bmatrix}^{\textsf{T}} \end{aligned}$$

are assumed to be continuous and satisfy \( f_i(0) = 0,\, g_i(0) = 0 \) for \(i=1,\dots , n\) as well as the sector-bounded conditions

$$\begin{aligned} {[} f(x) - f(y) - F_1(x-y) ]^{\textsf{T}} [ f(x) - f(y) - F_2(x-y) ]&\leqslant 0, \nonumber \\ {[} g(x) - g(y) - G_1(x-y) ]^{\textsf{T}} [ g(x) - g(y) - G_2(x-y) ]&\leqslant 0, \end{aligned}$$
(4)

where \( F_1, F_2, G_1 \) and \( G_2 \) are real matrices of appropriate dimensions.

Remark 1

As the authors explained in detail in the articles [10, 30], the sector-bounded condition covers the standard Lipschitz condition as a special case, so the NNs model (1) is more general than those were depicted in [17, 25, 26, 36, 37, 39].

Definition 1

(FTB [2, 40]) Suppose that \(c_1, c_2, N\) are given scalars with \(0<c_1<c_2,\, N\in \mathbb {Z}_{+}\), and that \(R>0\) is a symmetric matrix. The discrete-time delay NNs with exogenous disturbances \(\omega (k)\) satisfying (3)

$$\begin{aligned} x(k+1)&= Ax(k-\sigma (k)) + Bf(x(k))+B_1g(x(k-h(k))) + C\omega (k),\quad k\in \mathbb Z_+,\nonumber \\ x(k)&= \phi (k),\ k\in \{-\rho ,-\rho +1,\dots ,0\}, \end{aligned}$$
(5)

is FTB w.r.t. \((c_1, c_2, R, N)\) if

$$\begin{aligned} \max _{k\in \{-\rho ,-\rho +1,\dots ,0\}}\phi ^{\textsf{T}}(k)R\phi (k) \leqslant c_1 \; \Longrightarrow \; x^{\textsf{T}}(k)Rx(k) < c_2 \quad \forall k\in \{1, 2,\dots ,N\}. \end{aligned}$$

Remark 2

FTS w.r.t. \((c_1, c_2, R, N)\) is a special case of FTB w.r.t. \((c_1, c_2, R, N)\) which happens when \(\omega (k)=0\).

Definition 2

(\(H_{\infty }\) FTB [32, 37]) Suppose that \(c_1, c_2, N\) are given scalars with \(0< c_1<c_2, \, N\in \mathbb {Z}_{+}\), and that \(R>0\) is a symmetric matrix. System (1) is \(H_\infty \) FTB w.r.t. \((c_1, c_2, R, N)\) if the following two conditions hold:

  1. 1.

    System (5) is FTB w.r.t. \((c_1, c_2, R, N)\).

  2. 2.

    Under zero initial condition, for any nonzero \(\omega (k)\) satisfying (3), the output z(k) satisfies the condition

    $$\begin{aligned} \sum _{k=0}^Nz^{\textsf{T}}(k)z(k) \leqslant \gamma \sum _{k=0}^N\omega ^{\textsf{T}}(k)\omega (k) \end{aligned}$$
    (6)

    with a prescribed scalar \(\gamma >0\).

Proposition 1

(Discrete Jensen inequality, [18]) Suppose that \(M > 0 \) is a symmetric matrix of order n, \(k_1, k_2\) are positive integers satisfying \(k_1 \leqslant k_2,\) and \(\chi : \{k_1, k_1 + 1, \dots , k_2\} \rightarrow \mathbb {R}^{n}\) is a vector function. Then

$$\begin{aligned} \left( \sum _{i=k_1}^{k_2}\chi (i)\right) ^{\textsf{T}} M \left( \sum _{i=k_1}^{k_2}\chi (i)\right) \leqslant (k_2 - k_1 + 1)\sum _{i=k_1}^{k_2}\chi ^{\textsf{T}}(i)M\chi (i). \end{aligned}$$

Proposition 2

(Extended reciprocally convex matrix inequality, [42]) Suppose that \(R > 0 \) is a symmetric matrix of order n. Then the following matrix inequality

$$\begin{aligned} \begin{bmatrix} \frac{1}{\alpha }R &{} 0\\ 0&{}\frac{1}{1-\alpha }R\\ \end{bmatrix} \geqslant \begin{bmatrix} R+(1-\alpha )T_1&{}S\\ S^{\textsf{T}}&{}R+\alpha T_2\\ \end{bmatrix}, \end{aligned}$$

holds for some matrix S (of order n) and for all \( \alpha \in (0,1) \), where \( T_1 = R- SR^{-1}S^{\textsf{T}},\; T_2 = R- S^{\textsf{T}}R^{-1}S. \)

3 Main Results

Let \(y(k) = x(k+1) - x(k)\) and assume that \(\max _{k\in \{-\rho ,-\rho +1,\dots ,-1\}}y^{\textsf{T}}(k)y(k) < \tau \) with \(\tau \) is given positive real constant. For \( p, q \in \{1,2\}\), the following notations are used to facilitate the statement of the main results.

Theorem 1

Suppose that \(c_1, c_2, \gamma , N\) are given scalars such that \(0<c_1<c_2,\, \gamma > 0,\, N\in \mathbb {Z}_{+}\), and that \(R>0\) is a symmetric matrix. If there exist some positive-definite symmetric matrices \(P, Q, R_1, R_2, \) \( S_1, S_2\in \mathbb {R}^{n\times n},\) two any matrices \(Y_1, Y_2\in \mathbb {R}^{n\times n}\) and some positive scalars \(\lambda _i, \; i = \overline{1,7}\), \(\delta \geqslant 1\), such that the following matrix inequalities are satisfied

$$\begin{aligned}&\lambda _1R< {P}< \lambda _2R, \; {Q}< \lambda _3R,\; {R_1}< \lambda _4I,\; {R_2}< \lambda _5I,\; {S_1}< \lambda _6I,\; {S_2} < \lambda _7I, \end{aligned}$$
(7)
$$\begin{aligned}&\Sigma _{h_p,\sigma _q} = \begin{bmatrix} \Sigma _{h_p,\sigma _q}^{ij} \end{bmatrix}_{18\times 18} < 0 \quad \textit{for} \quad p, q \in \{1,2\}, \end{aligned}$$
(8)
$$\begin{aligned}&\Pi = \begin{bmatrix} \Pi ^{ij} \end{bmatrix}_{7\times 7} < 0, \end{aligned}$$
(9)

then system (1) is \(H_\infty \) FTB w.r.t. \((c_1, c_2, R, N)\).

Proof

Consider the L–K functional candidate \( V(k) = \displaystyle \sum \limits _{i=1}^{4}V_{i}(k)\), where

$$\begin{aligned} V_{1}(k)&= x^{\textsf{T}}(k){P}x(k),\\ V_{2}(k)&= \sum _{s=-\sigma _2+1}^{-\sigma _1+1}\sum _{t=k-1+s}^{k-1}\delta ^{k-1-t}x^{\textsf{T}}(t){Q}x(t),\\ V_{3}(k)&= \sum _{s=-h_1+1}^{0}\sum _{t=k-1+s}^{k-1}h_1\delta ^{k-1-t}y^{\textsf{T}}(t){R}_1y(t) \\&\quad +\sum _{s=-h_2+1}^{-h_1}\sum _{t=k-1+s}^{k-1}h_{12}\delta ^{k-1-t}y^{\textsf{T}}(t){R}_2y(t),\\ V_{4}(k)&= \sum _{s=-\sigma _1+1}^{0}\sum _{t=k-1+s}^{k-1}\sigma _1\delta ^{k-1-t}y^{\textsf{T}}(t){S}_1y(t) \\&\quad + \sum _{s=-\sigma _2+1}^{-\sigma _1}\sum _{t=k-1+s}^{k-1}\sigma _{12}\delta ^{k-1-t}y^{\textsf{T}}(t){S}_2y(t). \end{aligned}$$

Denote

$$\begin{aligned} \xi (k)&= \big [\begin{array}{l} x^{\textsf{T}}(k) \; x^{\textsf{T}}(k - h_1) \; x^{\textsf{T}}(k-h(k)) \; x^{\textsf{T}}(k - h_2) \; x^{\textsf{T}}(k - \sigma _1) \end{array}\\&\quad \begin{array}{l} x^{\textsf{T}}(k-\sigma (k)) \; x^{\textsf{T}}(k - \sigma _2) \; f^{\textsf{T}}(x(k)) \; g^{\textsf{T}}(x(k-h(k))) \; \omega ^{\textsf{T}}(k) \end{array}\big ]^{\textsf{T}},\\ \varUpsilon&:= \begin{bmatrix} 0&\; 0&\; 0&\; 0&\; 0&\; A&\; 0&\; B&\; B_1&\; C\end{bmatrix}, \end{aligned}$$

then it is not hard to get the following evaluation

$$\begin{aligned} V_1(k+1) -\delta V_1(k)&=\xi ^{\textsf{T}}(k)\varUpsilon ^{\textsf{T}}P\varUpsilon \xi (k)- \delta x^{\textsf{T}}(k)Px(k), \end{aligned}$$
(10)
$$\begin{aligned} V_2(k+1) -\delta V_2(k)&\leqslant (\sigma _{12}+1)x^{\textsf{T}}(k){Q}x(k) - \delta ^{\sigma _1}x^{\textsf{T}}(k-\sigma (k)){Q}x(k-\sigma (k)), \end{aligned}$$
(11)
$$\begin{aligned} V_3(k+1) -\delta V_3(k)&\leqslant y^{\textsf{T}}(k)\bigl [h_1^2{R}_1+ h_{12}^2{R}_2\bigl ]y(k) - h_1\delta \sum _{s=k-h_1}^{k-1}y^{\textsf{T}}(s){R}_1y(s) \nonumber \\&\quad -h_{12}\delta ^{h_1+1}\sum _{s=k-h_2}^{k-1-h_1}y^{\textsf{T}}(s){R}_2y(s), \end{aligned}$$
(12)
$$\begin{aligned} V_4(k+1) -\delta V_4(k)&\leqslant y^{\textsf{T}}(k)\bigl [\sigma _1^2{S}_1+ \sigma _{12}^2{S}_2\bigl ]y(k) - \sigma _1\delta \sum _{s=k-\sigma _1}^{k-1}y^{\textsf{T}}(s){S}_1y(s) \nonumber \\&\quad -\sigma _{12}\delta ^{\sigma _1+1}\sum _{s=k-\sigma _2}^{k-1-\sigma _1}y^{\textsf{T}}(s){S}_2y(s). \end{aligned}$$
(13)

By discrete Jensen inequality (Proposition 1),

$$\begin{aligned} -h_1\delta \sum _{s=k-h_1}^{k-1}y^{\textsf{T}}(s){R}_1y(s)&\leqslant -\delta \bigl [x(k)-x(k-h_1)\bigl ]^{\textsf{T}}{R}_1\bigl [x(k)-x(k-h_1)\bigl ], \end{aligned}$$
(14)
$$\begin{aligned} -\sigma _1\delta \sum _{s=k-\sigma _1}^{k-1}y^{\textsf{T}}(s){S}_1y(s)&\leqslant -\delta \bigl [x(k)-x(k-\sigma _1)\bigl ]^{\textsf{T}}{S}_1\bigl [x(k)-x(k-\sigma _1)\bigl ], \nonumber \\ -h_{12}\delta ^{h_1+1}\sum _{s=k-h_2}^{k-1-h_1}y^{\textsf{T}}(s){R}_2y(s)&\leqslant -\delta ^{h_1+1}\begin{bmatrix} \zeta _1\\ \zeta _2\\ \end{bmatrix}^{\textsf{T}}\begin{bmatrix} \frac{1}{\alpha _1}{R}_2 &{} 0\\ 0 &{} \frac{1}{1-\alpha _1}{R}_2 \end{bmatrix}\begin{bmatrix} \zeta _1\\ \zeta _2\\ \end{bmatrix}, \end{aligned}$$
(15)

where \(\zeta _1 = x(k-h_1)-x(k-h(k)), \; \zeta _2 = x(k-h(k))-x(k-h_2)\) and \( \alpha _1 = \frac{h(k)-h_1}{h_{12}} \). Using Proposition 2 to further evaluate the right hand side of the last inequality, we gain

$$\begin{aligned}&- h_{12}\delta ^{h_1+1}\sum _{s=k-h_2}^{k-1-h_1}y^{\textsf{T}}(s){R}_2y(s) \nonumber \\&\quad \leqslant - \delta ^{h_1+1}\begin{bmatrix} \zeta _1\\ \zeta _2\\ \end{bmatrix}^{\textsf{T}}\begin{bmatrix} {R}_2 + (1-\alpha _1)M_1 &{} Y_1\\ * &{} {R}_2 + \alpha _1 M_2 \end{bmatrix}\begin{bmatrix} \zeta _1\\ \zeta _2\\ \end{bmatrix}\nonumber \\&\quad = - \delta ^{h_1+1}\bigl [\zeta _1^{\textsf{T}}(R_2 + (1-\alpha _1)M_1)\zeta _1 + \zeta _1^{\textsf{T}}{Y_1}\zeta _2 + \zeta _2^{\textsf{T}}{Y_1}^{\textsf{T}}\zeta _1 + \zeta _2^{\textsf{T}}({R}_2 + \alpha _1 M_2)\zeta _2\bigl ], \end{aligned}$$
(16)

where \( M_1 = R_2- Y_1 R_2^{-1}Y_1^{\textsf{T}}\) and \( M_2 = R_2- Y_1^{\textsf{T}}R_2^{-1}Y_1. \)

In an entirely similar way, we obtain

$$\begin{aligned}&-\sigma _{12}\delta ^{\sigma _1+1}\sum _{s=k-\sigma _2}^{k-1-\sigma _1}y^{\textsf{T}}(s){S}_2y(s)\nonumber \\&\quad \leqslant - \delta ^{\sigma _1+1}\begin{bmatrix} \eta _1\\ \eta _2\\ \end{bmatrix}^{\textsf{T}}\begin{bmatrix} {S}_2 + (1-\alpha _2)N_1 &{} Y_2\\ * &{} {S}_2 + \alpha _2 N_2 \end{bmatrix}\begin{bmatrix} \eta _1\\ \eta _2\\ \end{bmatrix}\nonumber \\&\quad = -\delta ^{\sigma _1+1}\bigl [\eta _1^{\textsf{T}}(S_2 + (1-\alpha _2)N_1)\eta _1 + \eta _1^{\textsf{T}}{Y_2}\eta _2 + \eta _2^{\textsf{T}}{Y_2}^{\textsf{T}}\eta _1 + \eta _2^{\textsf{T}}({S}_2 + \alpha _2 N_2)\eta _2\bigl ], \end{aligned}$$
(17)

where \(\eta _1 = x(k-\sigma _1)-x(k-\sigma (k)), \; \eta _2 = x(k-\sigma (k))-x(k-\sigma _2),\; \alpha _2 = \frac{\sigma (k)-\sigma _1}{\sigma _{12}},\; N_1 = S_2- Y_2 S_2^{-1}Y_2^{\textsf{T}}\) and \( N_2 = S_2- Y_2^{\textsf{T}}S_2^{-1}Y_2. \)

Insert (14), (16) into (12) and (15), (17) into (13) then put (10)–(13) together, we have

$$\begin{aligned}&V(k+1) -\delta V(k)\nonumber \\&\quad \leqslant \xi ^{\textsf{T}}(k)\varUpsilon ^{\textsf{T}}P\varUpsilon \xi (k) + x^{\textsf{T}}(k)\bigl [-\delta ( {P} + {R}_1 + {S}_1) + (\sigma _{12}+1){Q} + A_1^{\textsf{T}}A_1 \bigl ]x(k) \nonumber \\&\qquad + x^{\textsf{T}}(k)\bigl [2\delta {R}_1 \bigl ]x(k-h_1) + x^{\textsf{T}}(k)\bigl [2A_1^{\textsf{T}}D \bigl ]x(k-h(k)) \nonumber \\&\qquad +x^{\textsf{T}}(k)\bigl [2\delta {S}_1 \bigl ]x(k-\sigma _1) + x^{\textsf{T}}(k)\bigl [2A_1^{\textsf{T}}D_1 \bigl ]x(k-\sigma (k)) + x^{\textsf{T}}(k)\bigl [2A_1^{\textsf{T}}C_1 \bigl ]\omega (k) \nonumber \\&\qquad + x^{\textsf{T}}(k-h_1)\bigl [ -\delta {R}_1 - \delta ^{h_1+1}({R}_2 + (1-\alpha _1)M_1) \bigl ]x(k-h_1) \nonumber \\&\qquad + x^{\textsf{T}}(k-h_1)\bigl [2\delta ^{h_1+1}\bigl ({R}_2 + (1-\alpha _1)M_1 - {Y_1}\bigl )\bigl ]x(k-h(k)) \nonumber \\&\qquad + x^{\textsf{T}}(k-h_1)\bigl [ 2\delta ^{h_1+1}{Y_1} \bigl ]x(k-h_2) \nonumber \\&\qquad + x^{\textsf{T}}(k-h(k))\bigl [- \delta ^{h_1+1}\bigl (2{R}_2 + (1-\alpha _1)M_1 + \alpha _1 M_2 - {Y_1} - {Y_1}^{\textsf{T}} + D^{\textsf{T}}D\bigl )\bigl ]x(k-h(k)) \nonumber \\&\qquad + x^{\textsf{T}}(k-h(k))\bigl [2\delta ^{h_1+1}\bigl ({R}_2 +\alpha _1 M_2 - {Y_1}\bigl )\bigl ]x(k-h_2) \nonumber \\&\qquad + x^{\textsf{T}}(k-h(k))\bigl [2D^{\textsf{T}}D_1 \bigl ]x(k-\sigma (k)) + x^{\textsf{T}}(k-h(k))\bigl [2D^{\textsf{T}}C_1 \bigl ]\omega (k) \nonumber \\&\qquad + x^{\textsf{T}}(k-h_2)\bigl [- \delta ^{h_1+1}({R}_2 + \alpha _1 M_2) \bigl ]x(k-h_2) \nonumber \\&\qquad + x^{\textsf{T}}(k-\sigma _1)\bigl [ -\delta {S}_1 - \delta ^{\sigma _1+1}({S}_2 + (1-\alpha _2)N_1) \bigl ]x(k-\sigma _1) \nonumber \\&\qquad + x^{\textsf{T}}(k-\sigma _1)\bigl [2\delta ^{\sigma _1+1}\bigl ({S}_2 + (1-\alpha _2)N_1 - {Y_2}\bigl )\bigl ]x(k-\sigma (k)) \nonumber \\&\qquad + x^{\textsf{T}}(k-\sigma _1)\bigl [ 2\delta ^{\sigma _1+1}{Y_2} \bigl ]x(k-\sigma _2) \nonumber \\&\qquad + x^{\textsf{T}}(k-\sigma (k))\bigl [- \delta ^{\sigma _1}Q - \delta ^{\sigma _1+1}\bigl (2{S}_2 + (1-\alpha _2)N_1 + \alpha _2 N_2 - {Y_2} - {Y_2}^{\textsf{T}}\bigl ) \nonumber \\&\qquad + D_1^{\textsf{T}}D_1\bigl ]x(k-\sigma (k)) \nonumber \\&\qquad + x^{\textsf{T}}(k-\sigma (k))\bigl [2\delta ^{\sigma _1+1}\bigl ({S}_2 +\alpha _2 N_2 - {Y_2}\bigl )\bigl ]x(k-\sigma _2) + x^{\textsf{T}}(k-\sigma (k))\bigl [2D_1^{\textsf{T}}C_1 \bigl ]\omega (k)\nonumber \\&\qquad + x^{\textsf{T}}(k-\sigma _2)\bigl [- \delta ^{\sigma _1+1}({S}_2 + \alpha _2 N_2) \bigl ]x(k-\sigma _2) + \omega ^{\textsf{T}}(k)\Bigl [ - \frac{\gamma }{\delta ^N}I + C_1^{\textsf{T}}C_1 \Bigl ]\omega (k)\nonumber \\&\qquad + y^{\textsf{T}}(k)\bigl [h_1^2{R}_1 + h_{12}^2{R}_2 + \sigma _1^2{S}_1 + \sigma _{12}^2{S}_2\bigl ]y(k) +\frac{\gamma }{\delta ^N}\omega ^{\textsf{T}}(k)\omega (k) - z^{\textsf{T}}(k)z(k). \end{aligned}$$
(18)

In addition, we receive the following evaluations from constraint (4)

$$\begin{aligned} 0&\leqslant f^{\textsf{T}}(x(k))[-I]f(x(k)) + x^{\textsf{T}}(k)[-2\overline{F}_2]f(x(k)) + x^{\textsf{T}}(k)[-\overline{F}_1]x(k),\nonumber \\ 0&\leqslant g^{\textsf{T}}(x(k-h(k)))[-I]g(x(k-h(k))) + x^{\textsf{T}}(k-h(k))[-2\overline{G}_2]g(x(k-h(k)))\nonumber \\&\quad + x^{\textsf{T}}(k-h(k))[-\overline{G}_1]x(k-h(k)). \end{aligned}$$
(19)

Thenceforth, by the combination of (18) and (19), we get

$$\begin{aligned} V(k+1) -\delta V(k)&\leqslant \xi ^{\textsf{T}}(k)\left( \Xi _{h(k),\sigma (k)} + \Lambda ^{\textsf{T}}\begin{bmatrix} {P} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} h_1^2{R}_1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} h_{12}^2{R}_2 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \sigma _{1}^2{S}_1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \sigma _{12}^2{S}_2 \end{bmatrix}^{-1}\Lambda \right) \xi (k)\nonumber \\&\quad + \frac{\gamma }{\delta ^N}\omega ^{\textsf{T}}(k)\omega (k) - z^{\textsf{T}}(k)z(k), \end{aligned}$$
(20)

where

$$\begin{aligned} \Lambda =\begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} PA &{} 0 &{} PB &{} PB_1 &{} PC \\ -h_1^2R_1 &{} 0&{} 0 &{} 0 &{} 0 &{} h_1^2R_1A &{} 0 &{} h_1^2R_1B &{} h_1^2R_1B_1 &{} h_1^2R_1C\\ -h_{12}^2R_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} h_{12}^2R_2A &{} 0 &{} h_{12}^2R_2B &{} h_{12}^2R_2B_1 &{} h_{12}^2R_2C\\ -\sigma _1^2S_1 &{} 0&{} 0 &{} 0 &{} 0 &{} \sigma _1^2S_1A &{} 0 &{} \sigma _1^2S_1B &{} \sigma _1^2S_1B_1 &{} \sigma _1^2S_1C\\ -\sigma _{12}^2S_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} \sigma _{12}^2S_2A &{} 0 &{} \sigma _{12}^2S_2B &{} \sigma _{12}^2S_2B_1 &{} \sigma _{12}^2S_2C\\ \end{bmatrix}, \end{aligned}$$

and

$$\begin{aligned} \Xi _{h(k),\sigma (k)} = \begin{bmatrix} \Xi _{h(k),\sigma (k)}^{ij} \end{bmatrix}_{10\times 10} \end{aligned}$$

with the entries of the last matrix are defined as

$$\begin{aligned} \Xi _{h(k),\sigma (k)}^{11}&= \Sigma _{h_1,\sigma _1}^{11} + A_1^{\textsf{T}}A_1,\; \Xi _{h(k),\sigma (k)}^{12} = \Sigma _{h_1,\sigma _1}^{12},\;\Xi _{h(k),\sigma (k)}^{13} = A_1^{\textsf{T}}D,\\ \Xi _{h(k),\sigma (k)}^{15}&= \Sigma _{h_1,\sigma _1}^{15},\; \Xi _{h(k),\sigma (k)}^{16} = A_1^{\textsf{T}}D_1,\; \Xi _{h(k),\sigma (k)}^{18} = \Sigma _{h_1,\sigma _1}^{18},\\ \Xi _{h(k),\sigma (k)}^{1,10}&= A_1^{\textsf{T}}C_1,\; \Xi _{h(k),\sigma (k)}^{22} = - \delta R_1 - \delta ^{h_1 + 1}[R_2 + (1-\alpha _1)M_1],\\ \Xi _{h(k),\sigma (k)}^{23}&= \delta ^{h_1 + 1}[R_2 + (1-\alpha _1)M_1 - Y_1], \; \Xi _{h(k),\sigma (k)}^{24} = \Sigma _{h_1,\sigma _1}^{24},\\ \Xi _{h(k),\sigma (k)}^{33}&= -\delta ^{h_1 + 1}[2R_2 + (1-\alpha _1)M_1 + \alpha _1 M_2 - Y_1 - Y_1^{\textsf{T}}] - \overline{G}_1 + D^{\textsf{T}}D,\\ \Xi _{h(k),\sigma (k)}^{34}&= \delta ^{h_1 + 1}[R_2 + \alpha _1 M_2 - Y_1],\; \Xi _{h(k),\sigma (k)}^{36} = D^{\textsf{T}}D_1,\; \Xi _{h(k),\sigma (k)}^{39} = \Sigma _{h_1,\sigma _1}^{39},\\ \Xi _{h(k),\sigma (k)}^{3,10}&= D^{\textsf{T}}C_1,\; \Xi _{h(k),\sigma (k)}^{44} = -\delta ^{h_1 + 1}[R_2 + \alpha _1 M_2],\\ \Xi _{h(k),\sigma (k)}^{55}&= - \delta S_1 - \delta ^{\sigma _1 + 1}[S_2 + (1-\alpha _2)N_1],\\ \Xi _{h(k),\sigma (k)}^{56}&= \delta ^{\sigma _1 + 1}[S_2 + (1-\alpha _2)N_1 - Y_2], \\ \Xi _{h(k),\sigma (k)}^{66}&= -\delta ^{\sigma _1}Q -\delta ^{\sigma _1 + 1}[2S_2 + (1-\alpha _2)N_1 + \alpha _2 N_2 - Y_2 - Y_2^{\textsf{T}}] + D_1^{\textsf{T}}D_1,\\ \Xi _{h(k),\sigma (k)}^{57}&= \Sigma _{h_1,\sigma _1}^{57},\; \Xi _{h(k),\sigma (k)}^{67} = \delta ^{\sigma _1 + 1}[S_2 + \alpha _2 N_2 - Y_2],\;\Xi _{h(k),\sigma (k)}^{6,10} = D_1^{\textsf{T}}C_1,\\ \Xi _{h(k),\sigma (k)}^{77}&= -\delta ^{\sigma _1 + 1}[S_2 + \alpha _2 N_2],\; \Xi _{h(k),\sigma (k)}^{88} = \Xi _{h(k),\sigma (k)}^{99} = -I,\\ \Xi _{h(k),\sigma (k)}^{10,10}&= -\frac{\gamma }{\delta ^N}I + C_1^{\textsf{T}}C_1,\; \Xi _{h(k),\sigma (k)}^{ij} = 0 \; \text {for any other} \; i, j:\; j> i,\\ \Xi _{h(k),\sigma (k)}^{ij}&= \;\left( \Xi _{h(k),\sigma (k)}^{ji}\right) ^{\textsf{T}}\; \text {for}\; i > j. \end{aligned}$$

Next, well-known Schur Complement Lemma gives us

$$\begin{aligned} \Xi _{h(k),\sigma (k)} + \Lambda ^{\textsf{T}}\begin{bmatrix} {P} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} h_1^2{R}_1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} h_{12}^2{R}_2 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \sigma _{1}^2{S}_1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \sigma _{12}^2{S}_2 \end{bmatrix}^{-1}\Lambda< 0 \quad \Longleftrightarrow \quad \Theta _{h(k),\sigma (k)} < 0, \end{aligned}$$

where

$$\begin{aligned} \Theta _{h(k),\sigma (k)}:= \begin{bmatrix} \Theta _{h(k),\sigma (k)}^{ij} \end{bmatrix}_{16\times 16} \end{aligned}$$

possesses its entries which are defined as follows

$$\begin{aligned} \Theta _{h(k),\sigma (k)}^{11}&= \Sigma _{h_1,\sigma _1}^{11},\; \Theta _{h(k),\sigma (k)}^{12} = \Sigma _{h_1,\sigma _1}^{12},\; \Theta _{h(k),\sigma (k)}^{15} = \Sigma _{h_1,\sigma _1}^{15},\; \Theta _{h(k),\sigma (k)}^{18} = \Sigma _{h_1,\sigma _1}^{18},\\ \Theta _{h(k),\sigma (k)}^{1,12}&= \Sigma _{h_1,\sigma _1}^{1,12},\; \Theta _{h(k),\sigma (k)}^{1,13} = \Sigma _{h_1,\sigma _1}^{1,13},\; \Theta _{h(k),\sigma (k)}^{1,14} = \Sigma _{h_1,\sigma _1}^{1,14},\; \Theta _{h(k),\sigma (k)}^{1,15} = \Sigma _{h_1,\sigma _1}^{1,15},\\ \Theta _{h(k),\sigma (k)}^{1,16}&= \Sigma _{h_1,\sigma _1}^{1,16},\; \Theta _{h(k),\sigma (k)}^{22} = \Xi _{h(k),\sigma (k)}^{22},\; \Theta _{h(k),\sigma (k)}^{23} = \Xi _{h(k),\sigma (k)}^{23}, \\ \Theta _{h(k),\sigma (k)}^{33}&= -\delta ^{h_1 + 1}[2R_2 + (1-\alpha _1)M_1 + \alpha _1 M_2 - Y_1 - Y_1^{\textsf{T}}] - \overline{G}_1,\\ \Theta _{h(k),\sigma (k)}^{24}&= \Sigma _{h_1,\sigma _1}^{24},\; \Theta _{h(k),\sigma (k)}^{34} = \Xi _{h(k),\sigma (k)}^{34},\; \Theta _{h(k),\sigma (k)}^{39} = \Sigma _{h_1,\sigma _1}^{39},\\ \Theta _{h(k),\sigma (k)}^{3,16}&= \Sigma _{h_1,\sigma _1}^{3,16},\; \Theta _{h(k),\sigma (k)}^{44} = \Xi _{h(k),\sigma (k)}^{44},\; \Theta _{h(k),\sigma (k)}^{55} = \Xi _{h(k),\sigma (k)}^{55},\\ \Theta _{h(k),\sigma (k)}^{56}&= \Xi _{h(k),\sigma (k)}^{56}, \; \Theta _{h(k),\sigma (k)}^{57} = \Sigma _{h_1,\sigma _1}^{57},\;\Theta _{h(k),\sigma (k)}^{67} = \Xi _{h(k),\sigma (k)}^{67},\\ \Theta _{h(k),\sigma (k)}^{66}&= -\delta ^{\sigma _1}Q -\delta ^{\sigma _1 + 1}[2S_2 + (1-\alpha _2)N_1 + \alpha _2 N_2 - Y_2 - Y_2^{\textsf{T}}],\\ \Theta _{h(k),\sigma (k)}^{6,11}&= \Sigma _{h_1,\sigma _1}^{6,11},\; \Theta _{h(k),\sigma (k)}^{6,12} = \Sigma _{h_1,\sigma _1}^{6,12},\; \Theta _{h(k),\sigma (k)}^{6,13} = \Sigma _{h_1,\sigma _1}^{6,13},\; \Theta _{h(k),\sigma (k)}^{6,14} = \Sigma _{h_1,\sigma _1}^{6,14},\\ \Theta _{h(k),\sigma (k)}^{6,15}&= \Sigma _{h_1,\sigma _1}^{6,15},\; \Theta _{h(k),\sigma (k)}^{6,16} = \Sigma _{h_1,\sigma _1}^{6,16},\; \Theta _{h(k),\sigma (k)}^{77} = \Xi _{h(k),\sigma (k)}^{77},\\ \Theta _{h(k),\sigma (k)}^{88}&= \Theta _{h(k),\sigma (k)}^{99} = \Theta _{h(k),\sigma (k)}^{16,16} = -I,\; \Theta _{h(k),\sigma (k)}^{8,11} = \Sigma _{h_1,\sigma _1}^{8,11},\\ \Theta _{h(k),\sigma (k)}^{8,12}&= \Sigma _{h_1,\sigma _1}^{8,12},\; \Theta _{h(k),\sigma (k)}^{8,13} = \Sigma _{h_1,\sigma _1}^{8,13},\; \Theta _{h(k),\sigma (k)}^{8,14} = \Sigma _{h_1,\sigma _1}^{8,14},\; \Theta _{h(k),\sigma (k)}^{8,15} = \Sigma _{h_1,\sigma _1}^{8,15},\\ \Theta _{h(k),\sigma (k)}^{9,11}&= \Sigma _{h_1,\sigma _1}^{9,11},\; \Theta _{h(k),\sigma (k)}^{9,12} = \Sigma _{h_1,\sigma _1}^{9,12},\; \Theta _{h(k),\sigma (k)}^{9,13} = \Sigma _{h_1,\sigma _1}^{9,13},\; \Theta _{h(k),\sigma (k)}^{9,14} = \Sigma _{h_1,\sigma _1}^{9,14},\\ \Theta _{h(k),\sigma (k)}^{9,15}&= \Sigma _{h_1,\sigma _1}^{9,15},\; \Theta _{h(k),\sigma (k)}^{10,10} = \Sigma _{h_1,\sigma _1}^{10,10},\; \Theta _{h(k),\sigma (k)}^{10,11} = \Sigma _{h_1,\sigma _1}^{10,11},\; \Theta _{h(k),\sigma (k)}^{10,12} = \Sigma _{h_1,\sigma _1}^{10,12},\\ \Theta _{h(k),\sigma (k)}^{10,13}&= \Sigma _{h_1,\sigma _1}^{10,13},\; \Theta _{h(k),\sigma (k)}^{10,14} = \Sigma _{h_1,\sigma _1}^{10,14},\; \Theta _{h(k),\sigma (k)}^{10,15} = \Sigma _{h_1,\sigma _1}^{10,15},\; \Theta _{h(k),\sigma (k)}^{10,16} = \Sigma _{h_1,\sigma _1}^{10,16},\\ \Theta _{h(k),\sigma (k)}^{11,11}&= \Sigma _{h_1,\sigma _1}^{11,11},\; \Theta _{h(k),\sigma (k)}^{12,12} = \Sigma _{h_1,\sigma _1}^{12,12},\; \Theta _{h(k),\sigma (k)}^{13,13} = \Sigma _{h_1,\sigma _1}^{13,13},\; \Theta _{h(k),\sigma (k)}^{14,14} = \Sigma _{h_1,\sigma _1}^{14,14},\\ \Theta _{h(k),\sigma (k)}^{15,15}&= \Sigma _{h_1,\sigma _1}^{15,15},\; \Theta _{h(k),\sigma (k)}^{ij} = 0 \; \text {for any other} \; i, j:\; j> i,\\ \Theta _{h(k),\sigma (k)}^{ij}&= \left( \Theta _{h(k),\sigma (k)}^{ji}\right) ^{\textsf{T}}\; \text {for}\; i > j. \end{aligned}$$

The convex combination technique allows us to assert that \(\Theta _{h(k),\sigma (k)} < 0 \) if the following four inequalities

$$\begin{aligned} \Theta _{h_1,\sigma _1}< 0, \quad \Theta _{h_1,\sigma _2}< 0, \quad \Theta _{h_2,\sigma _1}< 0 \quad \text {and}\quad \Theta _{h_2,\sigma _2} < 0 \end{aligned}$$

hold. In turn, by Schur Complement Lemma again, these inequalities hold if the inequalities stated in (8) hold. Combine these remarks with (20), we have

$$\begin{aligned} V(k+1) -\delta V(k) \leqslant \frac{\gamma }{\delta ^N}\omega ^{\textsf{T}}(k)\omega (k) \quad \forall k\in \mathbb {Z}_{+}. \end{aligned}$$

This implies that

$$\begin{aligned} V(k)&\leqslant \delta V(k-1) + \frac{\gamma }{\delta ^N}\omega ^{\textsf{T}}(k-1)\omega (k-1) \\&\leqslant \delta ^2 V(k-2) + \frac{\gamma }{\delta ^{N-1}}\omega ^{\textsf{T}}(k-2)\omega (k-2) + \frac{\gamma }{\delta ^N}\omega ^{\textsf{T}}(k-1)\omega (k-1) \\&\leqslant \dots \\&\leqslant \delta ^k V(0) + \frac{\gamma }{\delta ^N}\sum _{s=0}^{k-1}\delta ^{k-1-s}\omega ^{\textsf{T}}(s)\omega (s) \quad \forall k\in \mathbb {N}. \end{aligned}$$

By condition (3), it is obvious that

$$\begin{aligned} V(k) < \delta ^N V(0) + \frac{\gamma }{\delta }d \quad \forall k\in \{1,\dots , N\}. \end{aligned}$$
(21)

Moreover, according to condition (7), we can estimate

$$\begin{aligned} V_1(0)&= x^{\textsf{T}}(0){P}x(0)< \lambda _2 c_1,\\ V_2(0)&= \sum _{s=-\sigma _2+1}^{-\sigma _1+1}\sum _{t=-1+s}^{-1}\delta ^{-1-t}x^{\textsf{T}}(t){Q}x(t)<\lambda _3\delta ^{\sigma _2-1}\frac{\sigma _2(\sigma _2+1)-\sigma _1(\sigma _1-1)}{2}c_1,\\ V_3(0)&= \sum _{s=-h_1+1}^{0}\sum _{t=-1+s}^{-1}h_1\delta ^{-1-t}y^{\textsf{T}}(t){R}_1y(t) +\sum _{s=-h_2+1}^{-h_1}\sum _{t=-1+s}^{-1}h_{12}\delta ^{-1-t}y^{\textsf{T}}(t){R}_2y(t)\\&< \left[ \lambda _4 \delta ^{h_1-1}h_1\frac{h_1(h_1+1)}{2} + \lambda _5 \delta ^{h_2-1}h_{12}\frac{h_2(h_2+1)-h_1(h_1+1)}{2}\right] \tau ,\\ V_4(0)&= \sum _{s=-\sigma _1+1}^{0}\sum _{t=-1+s}^{-1}\sigma _1\delta ^{-1-t}y^{\textsf{T}}(t){S}_1y(t) +\sum _{s=-\sigma _2+1}^{-\sigma _1}\sum _{t=-1+s}^{-1}\sigma _{12}\delta ^{-1-t}y^{\textsf{T}}(t){S}_2y(t)\\&< \left[ \lambda _6 \delta ^{\sigma _1-1}\sigma _1\frac{\sigma _1(\sigma _1+1)}{2} + \lambda _7 \delta ^{\sigma _2-1}\sigma _{12}\frac{\sigma _2(\sigma _2+1)-\sigma _1(\sigma _1+1)}{2}\right] \tau . \end{aligned}$$

Substitute these upper bounds of \(V_i(0), i= 1,\dots , 4,\) into (21), it can be derived that

$$\begin{aligned} V(k) < \delta ^N \kappa + \frac{\gamma }{\delta }d\quad \forall k\in \{1,\dots , N\}, \end{aligned}$$
(22)

where

$$\begin{aligned} \kappa&:= c_1\lambda _2 + \frac{1}{2}c_1(\sigma _1+\sigma _2)(\sigma _{12}+1)\delta ^{\sigma _2-1}\lambda _3 + \frac{1}{2}\tau h_{1}^2(h_1+1) \delta ^{h_1-1}\lambda _4\\&\quad + \frac{1}{2}\tau h_{12}^2(h_1+h_2+1)\delta ^{h_2-1}\lambda _5 + \frac{1}{2}\tau \sigma _{1}^2(\sigma _1+1) \delta ^{\sigma _1-1}\lambda _6\\&\quad + \frac{1}{2}\tau \sigma _{12}^2(\sigma _1+\sigma _2+1)\delta ^{\sigma _2-1}\lambda _7. \end{aligned}$$

Furthermore, by (7), we see that (for \(k\in \mathbb {Z}_{+}\))

$$\begin{aligned} V(k)\geqslant x^{\textsf{T}}(k){P}x(k) \geqslant \lambda _1x^{\textsf{T}}(k)Rx(k). \end{aligned}$$
(23)

Using Schur Complement Lemma to perform equivalent transformations on (9), we find

$$\begin{aligned} \gamma d - c_2\delta \lambda _1 + c_1\delta ^{N+1}\lambda _2&+ \frac{1}{2}c_1(\sigma _1+\sigma _2)(\sigma _{12}+1)\delta ^{N+\sigma _2}\lambda _3\\&+ \frac{1}{2}\tau h_{1}^2(h_1+1)\delta ^{N+h_1}\lambda _4+ \frac{1}{2}\tau h_{12}^2(h_1+h_2+1)\delta ^{N+h_2}\lambda _5 \\&+ \frac{1}{2}\tau \sigma _{1}^2(\sigma _1+1)\delta ^{N+\sigma _1}\lambda _6 + \frac{1}{2}\tau \sigma _{12}^2(\sigma _1+\sigma _2+1)\delta ^{N+\sigma _2}\lambda _7 < 0, \end{aligned}$$

or

$$\begin{aligned} \gamma d - c_2\delta \lambda _1 + \delta ^{N+1} \kappa < 0. \end{aligned}$$
(24)

As a result of (22)–(24), it can be concluded that

$$\begin{aligned} x^{\textsf{T}}(k)Rx(k)< \frac{1}{\delta \lambda _1}\bigl [\delta ^{N+1}\kappa + \gamma d \bigl ] < c_2 \quad \forall k = 1, 2, \dots , N. \end{aligned}$$

According to Definition 1, we can confirm that system (5) is FTB w.r.t. \((c_1, c_2, R, N)\). The rest of the proof is to show the system (1) has a finite-time \(l_2\)-gain \(\gamma \), i.e., the condition (6) is satisfied. However, this step can be done in the same way as in [37]. The theorem has been completely proved. \(\square \)

Corollary 2

Suppose that \(c_1, c_2, N\) are given scalars such that \(0<c_1<c_2, N\in \mathbb {Z}_{+}\), and that \(R>0\) is a symmetric matrix. Then, the nominal system, which is the system in Eq. (5) without any disturbance (\(\omega (k) = 0\)), is FTS w.r.t. \((c_1, c_2, R, N)\) if there exist some positive-definite symmetric matrices \(P, Q, R_1, R_2, S_1, S_2\in \mathbb {R}^{n\times n}\), two any matrices \(Y_1, Y_2\in \mathbb {R}^{n\times n}\) and some positive scalars \(\lambda _i, \; i = \overline{1,7}\), \(\delta \geqslant 1\), that satisfy the LMIs in Eq. (7) and also the following matrix inequalities

$$\begin{aligned} \overline{\Sigma }_{h_p,\sigma _q}&= \begin{bmatrix} \overline{\Sigma }_{h_p,\sigma _q}^{ij} \end{bmatrix}_{16\times 16} < 0 \quad \textit{for} \quad p, q \in \{1,2\}, \end{aligned}$$
(25)
$$\begin{aligned} \overline{\Pi }&= \begin{bmatrix} \overline{\Pi }^{ij} \end{bmatrix}_{7\times 7} < 0, \end{aligned}$$
(26)

where \(\overline{\Sigma }_{h_p,\sigma _q}\) as a submatrix of \(\Sigma _{h_p,\sigma _q}\) that is obtained by removing the 10th and 16th rows and columns and \(\overline{\Pi }^{11}= - c_2\delta \lambda _1, \) \( \overline{\Pi }^{ij} = \Pi ^{ij} \; \text {for any other} \; i, j.\)

Proof

We can omit the proof of this result, since it follows the same steps as the one given for Theorem 1. \(\square \)

Remark 3

Theorem 1 and Corollary 2 provide theoretical analysis for \({H}_\infty \) FTB and FTS for a class of discrete-time NNs with leakage delay, discrete delay, and sector-bounded neuron activation functions. Leakage delay is the time-delay in leakage term of the systems and a significant factor that influences the network dynamics; in other words, the influence of leakage delay is not trivial. However, since the time-delay in the leakage term is often not easy to deal with, up to this point, such delay has yet to receive sufficient attention in the qualitative study of NNs. Moreover, in contrast to most existing literature, where the neuron activation functions are assumed to satisfy standard Lipschitz conditions [17, 25, 26, 36, 37, 39], in this paper, we consider more general sector-bounded nonlinearities that include the Lipschitz case as a special one. In short, the criteria stated in Theorem 1 and Corollary 2 are fresh and meaningful contributions.

Remark 4

To verify the practicability of the matrix inequalities in (8), (9), (25), and (26), we can fix the value of \(\delta \) and transform them into LMIs. Then, we can use the LMI Toolbox in MATLAB [13] to solve them efficiently.

Remark 5

The reciprocally convex combination technique, proposed in [24], is a method that minimizes the number of decision variables in matrix inequalities. In the proof of Theorem 1, we have applied a modified version of this technique to deal with double summation terms, which has the potential to achieve less conservative solutions than the widely used original method [42]. Namely, the matrix inequalities (8) and (25) contain only two free-weighting matrices each. Another advantage of Theorem 1 is that the results are derived without using any model transformations or other free-weighting matrix methods. We will demonstrate that the criteria given in Theorem 1 and Corollary 2 are succinct, valid, and practical through some examples.

Example 1

Considering the NNs (1) with its parameters are as follows

$$\begin{aligned} A&=\begin{bmatrix} 0.2 &{} 0\\ 0 &{} 0.175 \end{bmatrix},\quad B=\begin{bmatrix} -0.02 &{} 0.03\\ 0.03 &{} 0.05 \end{bmatrix},\quad B_1=\begin{bmatrix} 0.05 &{} 0.045\\ -0.05 &{} 0.05 \end{bmatrix}, \quad C=\begin{bmatrix} 0.05 \\ 0.1 \end{bmatrix},\\ A_1&=\begin{bmatrix} 0.3&-0.4 \end{bmatrix},\quad D=\begin{bmatrix} 0.2&-0.15 \end{bmatrix},\quad D_1=\begin{bmatrix} 0.12&-0.055 \end{bmatrix},\quad C_1 = \begin{bmatrix} 0.1 \end{bmatrix}, \\ \sigma (k)&= 1 + 3\cos ^2\frac{k\pi }{2},\quad h(k) = 1 + 6\sin ^2\frac{k\pi }{2},\quad k\in \mathbb Z_+. \end{aligned}$$

Moreover, the nonlinear activation functions f(x(k)) and \(g(x(k-h(k)))\) are chosen as

$$\begin{aligned} f(x(k))&= \begin{bmatrix} 0.2x_1(k)+\tanh (0.4x_1(k))\\ 0.3x_2(k)+\tanh (0.2x_2(k)) \end{bmatrix},\\ g(x(k-h(k)))&= \begin{bmatrix} 0.1x_1(k-h(k))+\tanh (0.2x_1(k-h(k)))\\ 0.1x_2(k-h(k))+\tanh (0.2x_2(k-h(k))) \end{bmatrix}. \end{aligned}$$

Then we can confirm that (4) is satisfied with

$$\begin{aligned} F_1 = \begin{bmatrix} 0.2 &{} 0\\ 0 &{} 0.3 \end{bmatrix},\quad F_2 = \begin{bmatrix} 0.6 &{} 0\\ 0 &{} 0.5 \end{bmatrix}, \quad G_1 = 0.1I,\quad G_2 = 0.3I. \end{aligned}$$

Since \( \overline{F}_1 = \begin{bmatrix} 0.12 &{} 0\\ 0 &{} 0.15 \end{bmatrix},\; \overline{F}_2 = -0.4I\ne 0,\; \overline{G}_1 = 0.03I,\; \overline{G}_2 = -0.2I\ne 0 \), the neuron activation functions \(f(\cdot ), \, g(\cdot ) \) in this case are sector-bounded.

For given \(h_1=1,\; h_2=7,\; \sigma _1=1,\; \sigma _2=4,\; d=1,\; \tau =1,\; \gamma = 1,\; c_1=1,\; c_2=9,\; N=90\) and \(R = \begin{bmatrix} 2.25 &{} 0.35 \\ 0.35 &{} 1.75 \end{bmatrix}\), the LMIs (7)–(9) are feasible with \(\delta =1.0001\) and the following values of the decision variables

$$\begin{aligned} P&= \begin{bmatrix} 39.0159 &{} -5.0480\\ -5.0480 &{} 26.4993 \end{bmatrix},\quad Q=\begin{bmatrix} 5.4035 &{} 0.0171\\ 0.0171 &{} 3.6365 \end{bmatrix}, \quad R_1=\begin{bmatrix} 1.4784 &{} -0.6092\\ -0.6092 &{} 1.0255 \end{bmatrix}, \\ R_2&=\begin{bmatrix} 0.1473 &{} -0.0496\\ -0.0496 &{} 0.1064 \end{bmatrix}, \quad S_1=\begin{bmatrix} 0.6555 &{} -0.1779\\ -0.1779 &{} 0.5015 \end{bmatrix},\quad S_2 =\begin{bmatrix} 0.1324 &{} -0.0359\\ -0.0359 &{} 0.1028 \end{bmatrix},\\ Y_1&=\begin{bmatrix} 0.002 &{} 0.0002\\ 0 &{} 0.002 \end{bmatrix},\quad Y_2 =\begin{bmatrix} 0.0008 &{} -0.0003\\ -0.0001 &{} 0.001 \end{bmatrix},\quad \lambda _1 = 11.4154,\quad \lambda _2 = 24.1403,\\ \lambda _3&= 2.8687,\quad \lambda _4 = 4.9184, \quad \lambda _5 = 0.1908,\quad \lambda _6 = 4.4446, \quad \lambda _7 = 0.2454. \end{aligned}$$

As a result of this, the system under consideration is \({H}_\infty \) FTB w.r.t. (1, 9, R, 90) according to Theorem 1.

Example 2

Considering the nominal system with the same matrices \(A, B, B_1, F_1, F_2,\) \(G_1, G_2, R\) as in Example 1. Also, we choose parameters \(h_1,\) \( \sigma _1, \sigma _2, c_1, c_2, \tau \) and N as in Example 1 except for \(h_2 = 11\). By solving the LMIs (7), (25) and (26) with \(\delta =1.0001\), we can gain the solution matrices and scalars as follows:

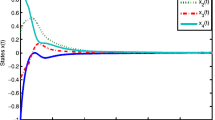
$$\begin{aligned} P&= \begin{bmatrix} 42.5262 &{} 1.5871\\ 1.5871 &{} 33.8294 \end{bmatrix},\quad Q=\begin{bmatrix} 6.1590 &{} 0.4737\\ 0.4737 &{} 4.4940 \end{bmatrix}, \quad R_1=\begin{bmatrix} 0.9622 &{} -0.0022\\ -0.0022 &{} 0.9291 \end{bmatrix}, \\ R_2&=\begin{bmatrix} 0.0579 &{} 0.0005\\ 0.0005 &{} 0.0586 \end{bmatrix}, \quad S_1=\begin{bmatrix} 0.6917 &{} -0.0161\\ -0.0161 &{} 0.6249 \end{bmatrix},\quad S_2 =\begin{bmatrix} 0.1473 &{} -0.0042\\ -0.0042 &{} 0.1340 \end{bmatrix},\\ Y_1&=\begin{bmatrix} 0.0028 &{} 0\\ -0.0002 &{} 0.0029 \end{bmatrix},\quad Y_2 =\begin{bmatrix} 0.0015 &{} 0.0001\\ 0.0001 &{} 0.0019 \end{bmatrix},\quad \lambda _1 = 16.4062,\quad \lambda _2 = 25.3133,\\ \lambda _3&= 3.5150,\quad \lambda _4 = 9.6686, \quad \lambda _5 = 0.0732,\quad \lambda _6 = 9.5124, \quad \lambda _7 = 0.5622. \end{aligned}$$

Therefore, by Corollary 2, we can affirm that the nominal system is FTS w.r.t. (1, 9, R, 90). With the initial condition is chosen as

$$\begin{aligned} \phi (k)=\begin{bmatrix} 0.25 \\ 0.55 \end{bmatrix} \quad \forall k\in \{-11,-10,\dots ,0\}, \end{aligned}$$

the trajectories of the system are described in Fig. 1.

Fig. 1
figure 1

The trajectories of the system are considered in Example 2

Full size image

Remark 6

In the proof of Theorem 1, we have applied the Jensen inequality without applying the Wirtinger-based summation inequality or any refined Jensen summation inequalities to obtain better conditions, although they are useful tools for this purpose, see [23, 28, 43] and references therein. The reason is that system (1) is a nonlinear system with leakage delay and discrete delay, which makes the analysis more complicated than the linear systems or NNs with lonely discrete delay in [23, 27, 28, 42, 43]. Therefore, we have used the Jensen inequality and the extended reciprocally convex technique in this paper which are more suitable for our problems. However, we think that trying the use of Wirtinger-based summation inequality or some refined Jensen summation inequalities in qualitative analysis for system (1) are some potential directions for future research to reduce conservatism. Moreover, our results can be also extended to switched NNs or Markovian jump NNs such as [30, 40].

4 Conclusion

This paper addresses the FTB and finite-time \(H_\infty \) performance for a general class of discrete-time NNs subjected to leakage time-varying delay, discrete time-varying delay, and different sector-bounded neuron activation functions. We have developed some novel delay-dependent criteria based on designing suitable L–K functionals and applying an enhanced reciprocally convex technique. These criteria can be easily implemented and solved by MATLAB software in a fast and efficient way.