1 Introduction

With the emergence of the big data era, machine learning methods have experienced rapid development, and artificial intelligence has achieved significant research breakthroughs in recent years. Its application has rapidly expanded to numerous fields of economic and social development. However, researchers have recognized that most existing machine learning models are primarily based on the study of variable correlations, disregarding the underlying causality in the data. This not only compromises the interpretability of the models but also diminishes their inference capabilities [17]. Understanding the causality between variables and leveraging causal relationships for inference is a crucial aspect of human intelligence. Intelligence that is built upon causal reasoning is a key criterion for assessing the gap between machine models and human intelligence. The fundamental distinction between causality and correlation lies in the inherent structural asymmetry of causality [24]. While correlation primarily focuses on describing the similarity in changing trends between variables, causality emphasizes the directional cause-and-effect relationship among samples. This distinction offers the potential for achieving accurate reasoning. Presently, there is a growing interest among researchers in causal reasoning based on causal relationships. The objective of causal research is to unveil the causal relationships between variables and construct causal models (causal discovery), followed by predicting causal effects and estimating variable changes based on this knowledge (causal inference). Causal research holds wide applicability in various domains, including social computing [10], policy evaluation [12], medical diagnosis [19], and financial market forecasting [11].

Causal discovery, as a crucial prerequisite for causal reasoning, has garnered significant attention in the academic community in recent years [8]. Traditionally, a common approach to causal discovery is through randomized controlled trials (RCTs), which involve interventions or random experiments to obtain sample data and unveil the causal structure between variables. However, RCTs often encounter issues such as high costs and limited practicality [26]. For instance, it is impractical to impose smoking or smoking cessation interventions on the subjects under investigation to study the impact of smoking on health. With the diversification of data acquisition methods and the increasing availability of abundant data, fields like sociology, biomedicine, economics, and environmental science have amassed large amounts of observational data. This data consists of direct observations of facts or phenomena and encompasses the underlying true distribution patterns. Although observational data may contain hidden variables and selection biases, researchers still believe that unaltered observational data can better reflect the true distribution of samples compared to intervention data, making them more generalizable. Consequently, the direct exploration of causal relationships between variables from observational sample data has emerged as a research focal point in statistics and artificial intelligence [4]. In order to address the challenges posed by observational data, researchers have developed various causal relationship models based on a series of fundamental assumptions (such as the sufficiency assumption and Markov assumption) to characterize the causal relationships between random variables [18, 21]. Among these models, the Structural Causal Model (SCM) proposed by J. Pearl has gained wide adoption in the field of explainable artificial intelligence. In SCM, a DAG is utilized to depict the causal relationships between multiple variables, where nodes represent random variables and directed edges signify causal relationships between variables. The objective of causal structure discovery is to learn a DAG that accurately represents the causal relationships between variables from the observed sample data. This task is commonly referred to as DAG structure learning or the Bayesian network structure learning problem [18].

Traditional algorithms for causal discovery based on SCM often approach the problem of learning causal structures as an optimization task involving scoring function values. Acyclicity constraints are introduced on sets of directed graphs, and candidate weight adjacency matrices are iteratively adjusted to optimize the scoring values and determine the final graph structure [5]. However, as the number of nodes increases, the exponential growth of the search space for DAGs makes this problem NP-hard [6], posing a significant challenge for researchers. In the 2018 NIPS conference, Zheng et al. [31] proposed a novel approach that employs continuous optimization under acyclicity constraints to solve the graph structure. This approach cleverly exploits the relationship between the diagonal elements in the kth power of the adjacency matrix and acyclicity, and by leveraging the convergence properties of matrix exponentiation, a continuous function is introduced to characterize the features of DAG structures. Consequently, the problem of DAG structure learning is recast as a continuous optimization problem under acyclicity constraints. This innovative approach has paved the way for new research directions and has generated considerable interest from researchers, establishing continuous optimization methods as a prominent focus in the field of causal structure discovery. Although this method exhibits elegant mathematical form, the computation of acyclicity constraints requires high-order power operations on the weight adjacency matrix, and the coefficients of high order terms can affect their numerical values. If the coefficients are too large, it may lead to numerical exploding. Therefore, some research efforts [27, 31] have attempted to use very small coefficients for high-order terms to mitigate this issue. However, another study [30] argues that high-order terms contain crucial information about larger cycles. If the coefficients are too small, there is a higher likelihood for the cycle information and gradient information within the higher-order terms to disappear. This leads to unstable convergence conditions and deviations from the true graph structure. Conversely, they argue that using larger coefficients can help detect larger cycles in the graph.

To address the aforementioned contradiction, this paper introduces the M-matrices [15] and its properties to propose a new acyclic constraint continuous function. This function allows for adaptive adjustment of the coefficients of higher-order terms. During the initial stage of optimization, where a significant disparity exists between the candidate graph and the target graph (as indicated by a large spectral radius for the candidate graph and a zero spectral radius for the target DAG), smaller coefficients are assigned to the higher-order terms to prevent numerical instability. As the optimization progresses and the candidate graph approaches the target graph, with the spectral radius approaching zero, larger coefficients are assigned to the higher-order terms to prevent numerical instability and facilitate the identification of larger cycle information in the DAG structure. Based on the aforementioned analysis, the proposed acyclic constraint with adjustable coefficients addresses both the potential issues of numerical instability and gradient disappearance during optimization. Building upon this acyclic constraint, this paper presents a novel causal structure discovery algorithm called LeCaSiM (learning causal structure via inverse of M-matrices with adjustable coefficients). Experimental results on both synthetic and real datasets demonstrate that LeCaSiM effectively learns the causal structure between variables from observational data, surpassing the efficiency and accuracy of existing algorithms.We present the following summary of our contributions:

  • In order to precisely characterize the structural features of DAGs, we present a summary of seven algebraic representations that are proven to be equivalent to DAGs. Additionally, concise proofs are provided for each of these representations.

  • We present theoretical proofs of the potential issues of numerical exploding and gradient vanishing that can arise in existing acyclicity constraints. To overcome these challenges, the concept of M-matrices is introduced, and a novel acyclicity constraint function based on the trace of the inverse of M-matrices is proposed. Furthermore, we offer rigorous theoretical analyses to substantiate the effectiveness of the newly proposed constraint function in addressing the aforementioned issues.

  • Based on the newly introduced acyclic constraint function and linear structural equation models, we utilize the augmented Lagrangian framework and present the LeCaSiM algorithm to transform the problem of learning DAG structures into a continuous optimization problem.

  • To evaluate the accuracy and efficiency of the LeCaSiM algorithm for DAG structure learning, we perform extensive experiments on both synthetic and real-world datasets. The experimental results unequivocally indicate that our proposed algorithm surpasses existing methods in terms of accuracy and efficiency.

The remaining structure of this paper is organized as follows: Sect. 2 introduces the background and related work of causal discovery and DAG structure learning. Section 3 uses algebraic graph theory to provide several equivalent conditions and brief proofs for characterizing the structural characteristics of DAG, and it derives a new continuous optimization constraint function based on the M-matrices. Section 4 introduces and analyzes the proposed causal structure learning algorithm, LeCaSiM. Section 5 presents the experimental verification and result analysis. Section 6 concludes the paper with a brief discussion and outlines possible future research directions.

2 Background and Related Work

2.1 Symbols and Notations

To ensure clarity, we present Table 1, which provides the symbols used throughout this article along with their corresponding meanings.

Table 1 Symbols and meanings
Full size table

2.2 Structural Causal Model

The SCM proposed by J. Pearl comprises two components: the causal graph and the structural equation model (SEM). The causal graph is a DAG used to represent the causal relationships between variables, denoted as \(\mathcal {G}=\left( \mathbb {V},\mathbb {E}\right) \), where \(\left| \mathbb {V}\right| =d\). For a d-dimensional random vector \({{\varvec{x}} =(x_1,x_2,\ldots ,x_d\ )\in \mathbb {R}^d}\), let \(\mathcal {P}({\varvec{x}})\) represents the joint probability distribution of \(\mathcal {G}\). Node \({i\in \mathbb {V}}\) corresponds to the random variable \({x_i\in {\varvec{x}}}\), and a directed edge \({\left( i,j\right) \in \mathbb {E}}\) indicates a causal relationship between \(x_i\) and \(x_j\). The set of parent nodes of node i is denoted as \({pa\left( i\right) }\). Under the assumptions of sufficiency and faithfulness [21], if all variables satisfy the property of first-order Markov [33], \(\mathcal {P}\left( {\varvec{x}}\right) \) can be decomposed as \(\mathcal {P}({\varvec{x}})=\prod _{i=1}^{d}{p\left( x_i\Big | x_{pa\left( i\right) }\right) }\). If we consider \(x_i\) as a specific function of \(x_{pa\left( i\right) }\), the causal relationships implied by the DAG correspond to a set of structural equations. Let e be a noise variable (or exogenous variable), then, the causal relationships between variables can be represented by the following SEM:

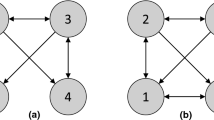
$$\begin{aligned} x_i=f_i\left( x_{pa\left( i\right) },e_i\right) \ , e_i\bot x_{pa\left( i\right) } \end{aligned}$$
(1)

where \({i\in \left\{ 1,\ldots ,d\right\} }\). As previously mentioned, the faithfulness assumption establishes a one-to-one correspondence between \({\mathcal {P}\left( {\varvec{x}}\right) }\) and the DAG, which also corresponds to a set of structural equations. Figure 1 illustrates an example of an SCM with three variables.

Fig. 1
figure 1

a The causal graph of the three variables. b SCM corresponding to the three variables. c The corresponding set of structural equations

Full size image

2.3 DAG Structure Learning

As described in Sect. 2.1, the problem of learning the DAG structure based on SCM can be defined as follows: Given the data matrix \({\varvec{X}}\), the goal is to learn the causal graph \({\mathcal {G}\in \mathbb {S}_\mathcal {G}}\) under the joint probability distribution \(\mathcal {P}\left( {\varvec{X}}\right) \).

Following prior research, we also employ the linear structural equation model (LSEM) to depict the causal relationships between variables. Let \({{\varvec{W}}\in \mathbb {R}^{d\times d}}\) as the weighted adjacency matrix corresponding to graph \(\mathcal {G}\) (the weight values are used to characterize the causal strength), where \({{\varvec{w}}_i\in \mathbb {R}^d}\), then in LSEM, \({\varvec{x}}={\varvec{W}}^T{\varvec{x}}+{\varvec{e}}\), \({\varvec{e}}=(e_1,e_2,\ldots ,e_d)^T\) denotes d i.i.d. noise terms. Correspondingly, the structural equations of the three nodes in the DAG in Fig. 1 can be expressed as follows (\({w_{ij}\in \mathbb {R}}\) represents the weight value of the directed edge between nodes i and j):

$$\begin{aligned}{} & {} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} =\begin{bmatrix} 0 &{}w_{12} &{} w_{13}\\ 0 &{} 0 &{}w_{23} \\ 0 &{}0 &{}0 \end{bmatrix}^T \begin{pmatrix} x_1\\ x_2 \\ x_3 \end{pmatrix}+\begin{pmatrix} e_1\\ e_2 \\ e_3 \end{pmatrix} \\{} & {} \quad \text {then} \left\{ \begin{array}{lr} x_1=e_1&{} \\ x_2=w_{12}x_1+e_2\\ x_3=w_{13}x_1+w_{23}x_2+e_3&{} \end{array} \right. \end{aligned}$$

Let \({\mathbb {G}({\varvec{W}})}\) denotes the directed graph corresponding to \({\varvec{W}}\), \({\mathbb {S}}_\mathcal {G}\) indicates the search space of the DAG, and the scoring function \(Q({\varvec{W}},{\varvec{X}})\) is utilized to evaluate the similarity between \(\mathbb {G}({\varvec{W}})\) and the observed data \({\varvec{X}}\). Consequently, the problem of learning the DAG structure can be formalized as the following optimization problem:

$$\begin{aligned} \min _{{\varvec{W}}\in \mathbb {R}^{d\times d}}{Q\left( {\varvec{W}},{\varvec{X}}\right) }\ \ \ \ s.t.\ \ \ \ \mathbb {G}\left( {\varvec{W}}\right) \in {\ \mathbb {S}}_\mathcal {G}\ \end{aligned}$$
(2)

2.4 Related Work

Algorithms aimed at learning causal structures between variables from observational data can generally be classified into two types: constraint-based algorithms and score-based algorithms. Constraint-based algorithms initiate the process with an undirected complete graph and systematically examine the conditional independence between variable pairs. Eventually, they produce a completed partially directed acyclic graph (CPDAG). The CPDAG represents a Markov equivalence class of the true DAG and does not provide a deterministic causal relationship. Prominent algorithms in this category include the PC (Peter–Clark) algorithm [21] and the IC (inductive causation) algorithm [23].

Fig. 2
figure 2

Left The counts of DAGs and directed graphs for specific nodes. Right The proportion of DAGs within the directed graphs for specific nodes

Full size image

In this research, we adopt a score-based approach for DAG structure learning. The traditional scoring-function-based algorithms employ combinatorial optimization to optimize the scoring function while adhering to the acyclicity constraint (such as Eq. 2). The scoring function is employed to evaluates the fit of the weighted adjacency matrix to the observed data. To enforce the acyclicity constraint, various implementation strategies involving combinations, search methods, and other techniques are utilized. Commonly used scoring functions include the Bayesian Information Criterion (BIC) [14], Minimum Description Length (MDL) [3], and Bayesian Dirichlet equivalent uniform (BDeu) [9]. Search strategies often encompass the hill climbing algorithm proposed by Heckerman et al. [9], A* search [29], integer programming [7], and greedy algorithm [5]. However, Since the search space of DAGs grows super-exponentially with the number of nodes, the task of learning specific graph structures using combinatorial optimization-based algorithms is known to be NP-hard [6]. Robinson [20] gives a recursive formula for calculating the number of DAGs that can be constructed from d nodes: \(\left| \mathcal {G}_d\right| =\sum _{i=1}^{d}{\left( -1\right) ^{i-1}\left( {\begin{array}{c}d\\ i\end{array}}\right) 2^{i(d-i)}\left| \mathcal {G}_{d-i}\right| }\), where \({\left| \mathcal {G}_0\right| =1}\). It is evident from Fig. 2 that as the number of nodes increases, both the counts of directed graphs and DAGs exhibit exponential growth, while the proportion of DAGs in the directed graphs decreases rapidly. As a result, the computational effort required to learn the desired DAG in such a vast space of directed graphs using the aforementioned combinatorial optimization algorithms is substantial.

To improve the accuracy and scalability of algorithms for learning directed acyclic graph (DAG) structures, Zheng et al.[31] discover that the trace of the matrix exponential effectively captures cycle information in a directed graph. Leveraging this finding, they develop a continuous acyclicity function denoted as \(h\left( {\varvec{W}}\right) \) that serves as a replacement for the combinatorial constraint \(G\left( {\varvec{W}}\right) \) in the optimization process. This transformative step converts the DAG structure learning problem into a continuous optimization problem, allowing for iterative solving through the utilization of existing numerical optimization algorithms[2]. However, a challenge arises in the form of high-order information loss during the solution process.

$$\begin{aligned} \min _{{\varvec{W}}\in \mathbb {R}^{d\times d}}{Q\left( {\varvec{W}},{\varvec{X}}\right) }\ \ \ \ \ \ s.t.\ \ \ \ h\left( {\varvec{W}}\right) =0 \end{aligned}$$
(3)

Building upon the aforementioned research, Yu et al. [27] introduce a novel acyclicity constraint for DAG learning that utilizes matrix binomials. Their approach is based on the important observation that a directed graph with d nodes does not contain any maximal cycles exceeding d steps. As a result, it is only necessary to compute powers of the weight adjacency matrix up to order d. This reduction in computational burden enhances the efficiency of the algorithm. However, this approach does not address the problem of high-order information loss. Wei et al. [25] introduce a combined polynomial constraint, replacing the Hadamard product with matrix absolute values, which is utilized for structure learning. Similarly, Lee et al. [13] and Zhu et al. [33] propose alternative constraints based on the spectral radius of the weighted adjacency matrix. These constraints have the notable effect of significantly reducing the computational complexity of the algorithm. In the algorithm proposed by Yu et al. in 2021 [28], there is a departure from previous methods that relied on the relationship between matrix powers and cycles in the graph to enforce acyclicity constraints. Instead, they employ a set of weighted graph potentials with gradients to describe the space of DAGs, enabling direct continuous optimization in algebraic space. Other related works include the extension of Zheng et al.’s work to implement DAG structure learning using time-series data [16] and the utilization of reinforcement learning methods to search for the optimal DAG [34], among other approaches.

3 Algebraic Characterization of DAGs

The construction of smooth acyclicity constraint functions plays a crucial role in converting the problem of learning the structure of a DAG from combinatorial optimization to continuous optimization (Eq. 2\(\rightarrow \) Eq. 3). In this section, we present various algebraic characterizations of DAG from the viewpoint of algebraic graph theory. Utilizing these algebraic characterizations, our objective is to devise smooth acyclicity constraint functions that facilitate the creation of continuous optimization algorithms for discovering causal graphs.

Let \({\mathbb {U}_{\mathbb {G}}=\left( \mathbb {V},\mathbb {E}\right) }\) denote an undirected graph defined on a node set \(\mathbb {V}\), where \({\left| \mathbb {V}\right| =d}\) and \({\mathbb {E}\subseteq \left( {\begin{array}{c}d\\ 2\end{array}}\right) }\). The adjacency matrix of \({\mathbb {U}_{\mathbb {G}}}\) is represented by \({{\varvec{A}}=\left( a_{i,j}\right) } ({i,j\in \mathbb {V}})\), where \({a_{i,j}=1}\) indicates the presence of an edge between nodes i and j, while \({a_{i,j}=0}\) indicates the absence of an edge. Specifically, \({a_{i,i}=0}\) signifies that there are no self-loops in the graph. A fundamental observation is that \({\left( {\varvec{A}}\right) ^k}_{ij}\) (where \({k\in \mathbb {Z}^+}\)) characterizes the number of walks of length k between nodes i and j, while \({\left( {\varvec{A}}\right) ^k}_{ii}\) characterizes the number of closed walks of length k that start and end at node i. It is important to note that a walk can pass through the same node multiple times. Correspondingly, in the case of a directed graph \({\mathbb {G} = (\mathbb {V}, \mathbb {E})}\), where \({|\mathbb {V}|=d}\) and \({\mathbb {E}\subseteq \mathbb {V}\times \mathbb {V}}\), if \({\left( {\varvec{A}}\right) ^k}_{ii}\ne 0\), it indicates the existence of at least one closed walk in \({\mathbb {G}({\varvec{A}})}\) that starts from node i, traverses \({k-1}\) nodes along directed edges, and returns to node i. Furthermore, the length of the cycle is less than or equal to k. This observation serves as the foundation for the algebraic characterization of cycles and the derivation of continuous constraint functions using algebraic methods.

As shown in Fig. 3, there are two cycles originating from node \(v_2\) and returning to itself after 6 steps. The cycles are as follows: \(v_2\rightarrow v_1\rightarrow v_6\rightarrow v_5\rightarrow v_4\rightarrow v_3\rightarrow v_2\) and \(v_2\rightarrow v_4\rightarrow v_3\rightarrow v_2\rightarrow v_4\rightarrow v_3\rightarrow v_2\).

Fig. 3
figure 3

Left A directed graph with 6 nodes. Right The diagonal elements of the 6th power of the adjacency matrix represent the cycle information of length 6 in the graph

Full size image

3.1 Algebraic Equivalence Condition for DAGs

This section provides a summary of six algebraic characterizations of equivalent DAG based on cycle information obtained from the adjacency matrix powers. The aim is to derive a continuous function as an acyclicity constraint based on these algebraic characterizations.

Proposition 1

\({\mathbb {G}\left( {\varvec{A}}\right) \in {\ \mathbb {S}}_\mathcal {G}}\) iff \({\varvec{A}}\) satisfies one of the following six conditions:

  1. (1)

    \(\sum _{k=1}^{d}{\text {tr}({\varvec{A}}^k) = 0}\).

  2. (2)

    \({\lambda _i\left( {\varvec{A}}\right) =0}\), \({i\in \left\{ 1,2,\ldots ,d\right\} }\), \(\lambda _i({\varvec{A}})\) denotes the i-th eigenvalue of matrix \({\varvec{A}}\).

  3. (3)

    \({\varvec{A}}\) is a nilpotent matrix that \({\varvec{A}}^m=\textbf{0}(m\in \mathbb {Z}^+, m \le d)\).

  4. (4)

    \(\rho ({\varvec{A}})=0\).

  5. (5)

    \({\varvec{A}}\) can be transformed by a similarity transformation into a strictly upper(or lower) triangular matrix.

  6. (6)

    \(({\varvec{I}}- {\varvec{A}})^{-1}\) exists and \(({\varvec{I}}- {\varvec{A}})^{-1}\ge 0\)(i.e., all elements of the matrix are greater than 0, the same as below).

We provide a brief proof of the equivalence of each item in Proposition 1 to \(\mathbb {G}\left( {\varvec{A}}\right) \in \ \mathbb {S}_\mathcal {G}\) in the “Appendix A.1”. Researchers in [27, 31] have introduced acyclicity constraints based on item (1). Similarly, in the study by [1], the acyclicity constraint is grounded in item (2). Moreover, the acyclicity constraints proposed in the research works [13, 33] are derived from item (4).

The key to formulating the DAG structure learning problem as a continuous optimization problem is to find a continuous acyclicity constraint function. However, the current propositions regarding acyclicity rely on the binary adjacency matrix \({\varvec{A}}\) (with entries limited to 0 and 1) and cannot facilitate the creation of a continuous acyclicity constraint function. To overcome this limitation, this paper adopts an approach similar to previous studies [27, 31], replacing \({\varvec{A}}\) with a weighted adjacency matrix \({\varvec{W}}\). \({\varvec{W}} \circ {\varvec{W}}\) ensures the weighted adjacency matrix remains nonnegative. This operation also maps W to a positively weighted adjacency matrix while preserving the same structure. In this formulation, \(({\varvec{W}} \circ {\varvec{W}})_{ij} > 0\) indicates the existence of a directed edge from node i to node j in the graph \(\mathbb {G}({\varvec{W}})\), while \(({\varvec{W}} \circ {\varvec{W}})_{ij} = 0\) indicates the absence of such an edge. Therefore, the problem of learning DAG structures using continuous optimization methods reduces to constructing a continuous function \(h({\varvec{W}}):\mathbb {R}^{d\times d}\rightarrow \mathbb {R}\) that can serve as an acyclicity constraint. \(h\left( {\varvec{W}}\right) \) should satisfy the following conditions:

  1. (1)

    \(h\left( {\varvec{W}}\right) \) quantifies the “distance" or dissimilarity between candidate graphs and the target DAG;

  2. (2)

    \(\mathbb {G}\left( {\varvec{W}}\right) \in {\ \mathbb {S}}_\mathcal {G}\)iff\(h\left( {\varvec{W}}\right) =0\);

  3. (3)

    The calculation of \(h\left( {\varvec{W}}\right) \) and its gradient \(\nabla h\left( {\varvec{W}}\right) \) is straightforward and convenient.

3.2 Analysis of Acyclicity Constraints in Existing Work

In Sect. 3.1, we summarize six equivalent conditions for DAGs based on the adjacency matrix of directed graphs. In the subsequent discussion, we present three continuous acyclicity constraint functions that are constructed in recent research, utilizing the aforementioned propositions. Additionally, we address the associated issues with these functions.

Zheng et al. [31] first define the following continuous acyclicity constraint based on item (1) of Proposition 1 and the trace function of matrices:

$$\begin{aligned} h_{TI}({\varvec{W}}) = tr\left[ ({\varvec{I}} - {\varvec{W}} \circ {\varvec{W}})^{-1}\right] - d \end{aligned}$$
(4)

where \(\rho ({\varvec{W}} \circ {\varvec{W}})<1\). The power series of \({\left( {\varvec{I}}-{\varvec{W}} \circ {\varvec{W}}\right) ^{-1}}\) is given by \(\sum _{k=0}^{\infty }({\varvec{W}} \circ {\varvec{W}})^k\), \(k\in \mathbb {Z}^+\). However, Zheng et al. find that the function \(h_{TI}({\varvec{W}})\) suffers from numerical explosion and other issues. Therefore, they propose a new acyclicity constraint based on the matrix exponential, which has better convergence properties. The new constraint is as follows:

$$\begin{aligned} h_{NT}({\varvec{W}}) = {tr}\left( e^{{\varvec{W}} \circ {\varvec{W}}}\right) - d \end{aligned}$$
(5)

where \({e^{{\varvec{W}} \circ {\varvec{W}}}}\) is the matrix exponential,which can be expressed as a power series \(\sum _{k=0}^{\infty }{\frac{1}{k!}({\varvec{W}} \circ {\varvec{W}})}^k\).

To reduce computational complexity, Yu et al.[27] proposed an improved constraint function based on item (1) of Proposition 1 and the matrix binomial to the power of d. The function is defined as follows:

$$\begin{aligned} h_{DG}({\varvec{W}}) = tr\left[ \left( {\varvec{I}}+\frac{1}{d}{\varvec{W}} \circ {\varvec{W}}\right) ^d\right] - d \end{aligned}$$
(6)

The power series expansion of \([{\varvec{I}}+\frac{1}{d}({\varvec{W}} \circ {\varvec{W}})]^d\) is given by \(\sum _{k=0}^{d}\left( {\begin{array}{c}d\\ k\end{array}}\right) / {d}^k ({\varvec{W}} \circ {\varvec{W}})^k\). The presence of the dth power signifies that in a directed graph with d nodes, there are no cycles of length greater than d.

However, it should be noted that in order to ensure the convergence of the power series expansion, the constraints defined by Eqs. 4, 5, and 6 can lead to numerical explosion or vanishing gradients for higher-order terms. As a result, when these constraints are utilized in iterative solving, there is a risk of the resulting target graph deviating from the true graph structure. To further illustrate this problem, we will analyze the power series expansions of \(h_{TI}({\varvec{W}})\), \(h_{NT}({\varvec{W}})\) and \(h_{DG}({\varvec{W}})\), along with their respective gradient terms as follows:

$$\begin{aligned} h_{TI} ({\varvec{W}})&= tr\left[ \sum _{k=1}^{\infty } ({\varvec{W}} \circ {\varvec{W}})^k\right] \end{aligned}$$
(7)
$$\begin{aligned} \nabla h_{TI}\left( {\varvec{W}}\right)&= 2\left[ \left( {\varvec{I}}-{\varvec{W}} \circ {\varvec{W}}\right) ^{-2}\right] ^T\circ {\varvec{W}} =2\left[ \sum _{k=0}^{\infty }{\left( k+1\right) ({\varvec{W}} \circ {\varvec{W}})^k}\right] ^T\circ {\varvec{W}} \end{aligned}$$
(8)
$$\begin{aligned} h_{NT} ({\varvec{W}})&= tr\left[ \sum _{k=1}^\infty \frac{1}{k!} ({\varvec{W}} \circ {\varvec{W}})^k\right] \end{aligned}$$
(9)
$$\begin{aligned} \nabla h_{NT} ({\varvec{W}})&= 2\left( e^{{\varvec{W}} \circ {\varvec{W}}}\right) ^T \circ {\varvec{W}} = 2\left[ \sum _{k=0}^\infty \frac{1}{k!} ({\varvec{W}} \circ {\varvec{W}})^k\right] ^T \circ {\varvec{W}} \end{aligned}$$
(10)
$$\begin{aligned} h_{DG} ({\varvec{W}})&= tr\left[ \sum _{k=1}^d \frac{\left( {\begin{array}{c}d\\ k\end{array}}\right) }{d^k} ({\varvec{W}} \circ {\varvec{W}})^k\right] \end{aligned}$$
(11)
$$\begin{aligned} \nabla h_{DG} ({\varvec{W}})&= 2\left[ \left( {\varvec{I}} + \frac{1}{d} {\varvec{W}} \circ {\varvec{W}}\right) ^{d-1}\right] ^T \circ {\varvec{W}} = 2\left[ \sum _{k=0}^{d-1} \frac{\left( {\begin{array}{c}d-1\\ k\end{array}}\right) }{(d-1)^k} ({\varvec{W}} \circ {\varvec{W}})^k\right] ^T \circ {\varvec{W}} \end{aligned}$$
(12)

Applying \({h_{TI}({\varvec{W}})}\) as the acyclicity constraint in DAG structure learning, the coefficients of the terms in the expansions of Eqs. 7 and 8 are 1 and \((k+1)\), respectively. However, when \(\rho ({\varvec{W}} \circ {\varvec{W}})\) is large, there may be numerical explosion issues when computing \(({\varvec{W}} \circ {\varvec{W}})^k\) and \((k+1)({\varvec{W}} \circ {\varvec{W}})^k\) as k increases. This can adversely affect the convergence stability of the algorithm. In contrast, \(h_{NT}({\varvec{W}})\) and \(h_{DG}({\varvec{W}})\), along with their gradient expansions, have coefficients of 1/k! and \(\left( {\begin{array}{c}d\\ k\end{array}}\right) /d^k\), respectively. As the optimization progresses, \(\rho ({\varvec{W}} \circ {\varvec{W}})\) approaches zero, causing the coefficients of the terms in the expansion to rapidly decrease with increasing k. Consequently, the k-th order term in the expansion becomes infinitesimal, leading to the loss of cycle information and gradient information in higher-order terms. This reduction in accuracy negatively impacts the algorithm.

In fact, \(h_{DG}\left( {\varvec{W}}\right) \) is not suitable for discovering DAG structures with a large number of nodes. For example, if we apply \(h_{DG}\left( {\varvec{W}}\right) \) to a DAG with 100 nodes, even for a relatively small value of k (such as \(k=10\)), the coefficient of the k-th term in the power series expansion becomes \(\left( {\begin{array}{c}100\\ 10\end{array}}\right) /{100}^{10}\). This can result in the failure to detect cycles in the graph with a length exceeding 10.

3.3 New Acyclicity Constraint

3.3.1 Background and Motivation

The acyclicity constraints \(h_{TI}\left( {\varvec{W}}\right) \), \(h_{NT}({\varvec{W}})\), and \(h_{DG}\left( {\varvec{W}}\right) \) can all be expressed as matrix polynomials. They share a general form \(\sum _{k=1}^{d}l(k)tr[({\varvec{W}} \circ {\varvec{W}})^k]\), where \({l\left( k\right) >0}\). As mentioned earlier, \(\sum _{k=1}^{d}l(k)tr[({\varvec{W}} \circ {\varvec{W}})^k]=0\) signifies the absence of cycles of length less than or equal to d in \(\mathbb {G}\left( {\varvec{W}}\right) \). While these three functions achieve the acyclicity constraint in a similar manner, the distinction lies in the coefficient term \(l\left( k\right) \). As previously discussed, selecting a relatively “large" coefficient may lead to numerical explosion, while opting for a relatively “small" coefficient may result in information loss and gradient vanishing. Therefore, in this paper, we utilize item (6) of Proposition 1 to establish a new equivalent condition for DAG and propose an acyclicity constraint function with adaptively adjustable coefficient terms \({l\left( k\right) }\).

Proposition 2

\({\mathbb {G} ({\varvec{W}} \circ {\varvec{W}})\in {\ \mathbb {S}}_\mathcal {G}}\) iff \((\alpha {\varvec{I}}-{\varvec{W}} \circ {\varvec{W}})^{-1}\) exists and \((\alpha {\varvec{I}}-{\varvec{W}} \circ {\varvec{W}})^{-1}\ge 0\).

Proposition 2 relaxes the constraint condition from \({\rho ({\varvec{W}} \circ {\varvec{W}})<1}\) to \({\rho ({\varvec{W}} \circ {\varvec{W}})<\alpha }\). Based on Proposition 2, the premise for defining the continuous acyclicity constraint function is to find a set of weighted adjacency matrices \({\varvec{W}}\), where Proposition 2 holds true for any \({\varvec{W}}\) in this set. In fact, if \({\varvec{W}}\) is a matrix defined in this set, then \(\alpha {\varvec{I}}-{\varvec{W}}\circ {\varvec{W}}\) is characterized as an M-matrix[15] (first introduced by Swiss mathematician Ostrowski in 1937). The definition of an M-matrix is as follows:

Definition 1

(M-matrix) Let \({\varvec{B}}\in \mathbb {R}^{d\times d}\ge 0\),\(\ \ {\varvec{C}}\in \mathbb {R}^{d\times d}\), if \({\varvec{C}}=\alpha {\varvec{I}}-{\varvec{B}}\), where \(\alpha >\rho \left( {\varvec{B}}\right) \), then \({\varvec{C}}\) is an M-matrix.

If \({\varvec{C}}\) is an M-matrix, it possesses the following properties:

  1. (1)

    \( \lambda _i\left( {\varvec{C}}\right) >0\),\(i\in \left\{ 1,\ldots ,d\right\} \);

  2. (2)

    \( {\varvec{C}}^{-1}\ge 0\).

The mentioned properties are evident: From the equation \({\lambda _i({\varvec{C}}) = \alpha - \lambda _i({\varvec{B}})}\) and the fact that \({\alpha > \rho ({\varvec{B}})}\), it follows that \({\lambda _i({\varvec{C}}) > 0}\). Moreover, from the power series expansion of \({\varvec{C}}^{-1}\), it is clear that \({{\varvec{C}}^{-1} \ge 0}\). Additionally, it is worth noting that \({\varvec{B}}\) can be equivalently replaced by \({\varvec{W}} \circ {\varvec{W}}\). Thus, when \(\alpha > \rho ({\varvec{W}} \circ {\varvec{W}})\), \({\alpha {\varvec{I}} - {\varvec{W}}\circ {\varvec{W}}}\) is an M-matrix, ensuring that Proposition 2 holds true. This clever connection between Proposition 2 and M-matrices allows us to determine the desired set of matrices \({\varvec{W}}\) based on the characteristics of M-matrices.

Definition 2

(\(\mathbb {W}^\alpha \) ) \({\mathbb {W}^\alpha =\left\{ {\varvec{W}} \in \mathbb {R}^{d\times d}\Big | \alpha >\rho \left( {\varvec{W}}\circ {\varvec{W}}\right) \right\} }\).

The set \(\mathbb {W}^\alpha \) refers to the aforementioned set that we seek to solve for, and it exhibits the following crucial properties:

Proposition 3

Let \(\mathbb {W}^{{\ \mathbb {S}}_\mathcal {G}}\) be the space of weighted adjacency matrices corresponding to \({\ \mathbb {S}}_\mathcal {G}\), when \(\alpha > 0\):

  1. (1)

    \(\mathbb {W}^{{\ \mathbb {S}}_\mathcal {G}}\subset \mathbb {W}^\alpha \);

  2. (2)

    \(\mathbb {W}^\alpha \subset \mathbb {W}^t\), where \(\alpha <t\).

For any \({{\varvec{W}} \in \mathbb {W}^{{\ \mathbb {S}}_\mathcal {G}}}\), it holds that \({\rho \left( {\varvec{W}}\circ {\varvec{W}}\right) < \alpha }\). item (1) indicates that feasible solutions to the DAG structure learning problem must lie within \(\mathbb {W}^\alpha \). item (2) suggests that the size of \(\mathbb {W}^\alpha \) can be adjusted by changing the value of \(\alpha \). As the optimization progresses, gradually decreasing \(\alpha \) narrows down the search space for feasible solutions, which in turn leads to faster convergence of the algorithm.

Based on the analysis above, the proposed continuous constraint function \({h\left( {\varvec{W}}\right) :\mathbb {W}^\alpha \rightarrow \mathbb {R}}\) is constructed as follows:

$$\begin{aligned} h({\varvec{W}})=tr\left[ (\alpha {\varvec{I}}-{\varvec{W}} \circ {\varvec{W}})^{-1}\right] -{d}/{\alpha } \end{aligned}$$
(13)

3.3.2 Theoretical Analysis

In this section, we will analyze the new acyclicity constraint proposed in the previous section (Eq. 13) from three aspects: acyclicity, continuity, and dynamic parameter adjustment. We will provide a brief theoretical analysis and offer a concise proof to support our findings.

Corollary 1

For any \({{\varvec{W}} \in \mathbb {W}^\alpha }\), it holds that \(h({\varvec{W}}) \ge 0\). Moreover, \(h({\varvec{W}}) = 0\) iff \(\mathbb {G}({\varvec{W}}) \in \mathbb {S}_\mathcal {G}\).

See “Appendix A.3” for detailed proof. Corollary 1 states that for any \({\varvec{W}} \in \mathbb {W}^\alpha \), we have \(h({\varvec{W}}) \ge 0\), which implies that \(\mathbb {W}^{{\ \mathbb {S}}_\mathcal {G}}\) corresponds to the set of local minima of \(h({\varvec{W}})\). This also helps us prove \({\mathbb {W}^{{\ \mathbb {S}}_\mathcal {G}} \subset \mathbb {W}^\alpha }\) from another perspective. During the optimization process, as the value of \(h({\varvec{W}})\) approaches 0, it indicates that \(\rho ({\varvec{W}})\) tends to 0, which means that \(\mathbb {G}({\varvec{W}})\) is getting closer to the optimal solution, satisfying the first condition mentioned in Sect. 3.1. \({h({\varvec{W}}) = 0}\) if and only if \({\mathbb {G}({\varvec{W}}) \in {\ \mathbb {S}}_\mathcal {G}}\), corresponding to the second condition in Sect. 3.1.

Corollary 2

The gradient of \(h({\varvec{W}})\), denoted as \(\nabla h({\varvec{W}})\), is defined as \(\nabla h({\varvec{W}}) = 2[(\alpha {\varvec{I}}-{\varvec{W}}\circ {\varvec{W}})^{-2}]^T\circ {\varvec{W}}\). For any \(i, j \in \mathbb {V}\), the element \({\nabla h({\varvec{W}})}_{ij}\) shares the same sign as \({\varvec{W}}_{ij}\). If \({\nabla h({\varvec{W}})}_{ij} \ne 0\), it indicates the presence of a cycle in \(\mathbb {G}({\varvec{W}})\).

See “Appendix A.4” for detailed proof. Corollary 2 states that \(\nabla h({\varvec{W}})\) satisfies the third condition in Sect. 3.1. Since \(2[\left( \alpha {\varvec{I}}-{\varvec{W}}\circ {\varvec{W}}\right) ^{-2}]^T\ge 0\), the sign of each element in \(\nabla h({\varvec{W}})\) depends on the sign of the corresponding element in \({\varvec{W}}\). If \({\nabla h({\varvec{W}})}_{ij} \ne 0\), it indicates that \([{{(\alpha {\varvec{I}}-{\varvec{W}}\circ {\varvec{W}})^{-2}}]^T_{ij} \ne 0}\) and \({\varvec{W}}_{ij} \ne 0\). Here, \({[(\alpha {\varvec{I}}-{\varvec{W}}\circ {\varvec{W}})^{-2}}]_{ij}^T=[\sum _{k=0}^{\infty }{\frac{k+1}{\alpha ^{k+2}}{({\varvec{W}}\circ {\varvec{W}}})^k}]_{ij}^T\) represents the sum of weights from node j to node i, indicating the existence of a path (possibly through one or more nodes) from node j to node i in the graph. Furthermore, \({\varvec{W}}_{ij} \ne 0\) represents the existence of a directed path from node i to node j. Therefore, the presence of a cycle in the graph can be inferred as \(i \rightarrow j \rightarrow \ldots \rightarrow i\).

Corollary 3

For any \({{\varvec{W}}\in \mathbb {W}^\alpha }\), let \(\alpha =\rho \left( {\varvec{W}}\circ {\varvec{W}}\right) +\xi \), where \(\xi \in \mathbb {R}^+\). Then, we have \(h\left( {\varvec{W}}\right) =tr[\left( \alpha {\varvec{I}}-{\varvec{W}}\circ {\varvec{W}}\right) ^{-1}]-{d}/{\alpha }=\sum _{k=1}^{\infty }{1}/{\alpha ^{k+1}}{\left( {\varvec{W}}\circ {\varvec{W}}\right) }^k\). The dynamic adjustment of \(\mathbb {W}^\alpha \) and \({1}/{\alpha ^{k+1}}\) in the optimization process ensures that the computation of \(h\left( {\varvec{W}}\right) \) and \(\nabla h\left( {\varvec{W}}\right) \) neither leads to numerical explosion nor loses the cycle information and gradient information in the higher-order terms.

\(h({\varvec{W}})\) shares the same form as \(h_{TI}({\varvec{W}})\), \(h_{NT}({\varvec{W}})\), and \(h_{DG}({\varvec{W}})\), which is \(\sum _{k=1}^{d}l(k)tr[({\varvec{W}} \circ {\varvec{W}})^k]\). The distinction lies in the coefficient l(k) of the power series in \(h({\varvec{W}})\), which depends on \(\alpha \), enabling it to adjust dynamically during the optimization process. Specifically, in the initial stages of optimization when \(\rho ({\varvec{W}}\circ {\varvec{W}})\) is large, the computation of \(h_{TI}({\varvec{W}})\) and its gradient may encounter numerical explosion. By setting \(\alpha =\rho ({\varvec{W}}\circ {\varvec{W}})+\xi \), the coefficients \({1}/{\alpha ^{k+1}}\) in the power series of \(h({\varvec{W}})\) diminish rapidly, effectively avoiding numerical explosion. As the optimization progresses and \(\rho ({\varvec{W}}\circ {\varvec{W}})\) approaches zero, there is a risk of losing cycle information and gradients in the higher-order terms of \(h_{NT}({\varvec{W}})\) and \(h_{DG}({\varvec{W}})\). To address this, setting \(\alpha =\rho ({\varvec{W}}\circ {\varvec{W}})+\xi \) (where \(\xi =1\)) ensures that s and \({1}/{\alpha ^{k+1}}\) are approximately 1. This preserves the true values of each term in the power series and resolves the issue of losing information in the higher-order terms. Additionally, \(\mathbb {W}^\alpha \) adjusts correspondingly as \(\rho ({\varvec{W}}\circ {\varvec{W}})\) decreases throughout the optimization process, narrowing down the search space for the DAGs. Consequently, the dynamic adjustment of \(\mathbb {W}^\alpha \) and \({1}/{\alpha ^{k+1}}\) enhances the efficiency and accuracy of DAG structure learning algorithm.

3.3.3 Computational Complexity Analysis

From the previous discussion, it is evident that the proposed acyclicity constraint function \(h({\varvec{W}})\) shares a similar power series form \({\sum _{k=1}^{d}{l(k)\text {tr}[({\varvec{W}} \circ {\varvec{W}})^k]}}\) with \(h_{TI}({\varvec{W}})\), \(h_{NT}({\varvec{W}})\), and \(h_{DG}({\varvec{W}})\). Therefore, the computational complexity of calculating these acyclicity constraints and their gradients is \(O(d^3)\) for each of them. As shown in Fig. 4, \(h({\varvec{W}})\) and its gradient have slightly higher average computation time, this is primarily due to the additional computation of the spectral radius of the matrix before calculating \(h({\varvec{W}})\), which incurs extra time. However, in Sect. 5, we will demonstrate through experiments that the algorithm based on \(h({\varvec{W}})\) has the shortest average runtime. This indicates that \(h({\varvec{W}})\) enables the algorithm to converge faster to an approximately optimal solution.

Table 2 provides a concise summary of the acyclicity constraint functions mentioned above, aiming to enhance comparison and comprehension.

Fig. 4
figure 4

The average computation time required for calculating the acyclicity constraints and their gradients at different node sizes

Full size image
Table 2 Comparison of acyclicity constraint functions
Full size table

4 Structure Learning Algorithm

Based on the newly introduced acyclicity constraint function \(h({\varvec{W}})\), this section presents a causal structure learning algorithm named LeCaSiM.

4.1 LeCaSiM Algorithm

Like previous studies, this paper utilizes the mean squared error (MSE) as the loss function \(q({\varvec{W}}, {\varvec{X}})\) in the LSEM:

$$\begin{aligned} q({\varvec{W}},{\varvec{X}})=\frac{1}{n}\Vert {\varvec{X}}-{\varvec{X}}{\varvec{W}}\Vert _{F}^{2} =\frac{1}{n} \sum _{i=1}^{n} \sum _{j=1}^{d}\left( {\varvec{X}}-{\varvec{X}}{\varvec{W}}\right) _{i j}^{2} \end{aligned}$$
(14)

Considering that practical graphs are often sparse, an \(L_1\)-regularization is incorporated into Eq. 14 to promote sparsity. Thus, the scoring function \(Q({\varvec{W}}, {\varvec{X}})\) is defined as follows:

$$Q({\varvec{W}}, {\varvec{X}}) = \frac{1}{n}||{\varvec{X}} - {\varvec{X}}{\varvec{W}}||_F^2 + \mu ||{\varvec{W}}||_1$$

where \(\mu > 0\) is a constant coefficient. Within this framework, the problem of learning DAG structures based on \(h({\varvec{W}})\) can be formulated as the following optimization problem:

$$\begin{aligned} \min _{{\varvec{W}}\in \mathbb {W}^\alpha } {Q\left( {\varvec{W}},{\varvec{X}}\right) }\quad s.t.\quad h\left( {\varvec{W}}\right) =0 \quad \end{aligned}$$
(15)

To address the optimization problem mentioned above, we utilize the augmented Lagrangian method (ALM)[2] to transform it into the following unconstrained optimization problem:

$$\begin{aligned} \min _{{\varvec{W}}\in \mathbb {W}^\alpha }\quad \max _{\varphi \in \mathbb {R}}\quad \ell \left( {\varvec{W}},\varphi \right) \ \ \ \ \ \ \end{aligned}$$
(16)

where \(\ell \left( {\varvec{W}},\varphi \right) =Q\left( {\varvec{W}},{\varvec{X}}\right) +\frac{\sigma }{2}{h\left( {\varvec{W}}\right) }^2+\varphi h\left( {\varvec{W}}\right) \), \(\sigma > 0\) represents penalty parameter, and \(\varphi \) denotes the Lagrange multiplier. The dual ascent method is employed to iteratively solve this unconstrained optimization problem. Assuming we have the solution at the k-th iteration \({\varvec{W}}^k\) and \(\varphi ^k\), the update process is as follows:

  • Substitute \(\varphi = \varphi ^k\) into \(\ell ({\varvec{W}}, \varphi )\) and solve \(\min _{{\varvec{W}}\in \mathbb {W}^\alpha }{\ell \left( {\varvec{W}},\varphi ^k\right) }\). Then, obtain \({\varvec{W}}^{k+1}\);

  • replace \({\varvec{W}} = {\varvec{W}}^{k+1}\) into \(\ell ({\varvec{W}}, \varphi )\) and solve \(\max _{\varphi \in \mathbb {R}}{\ell \left( {\varvec{W}}^{k+1},\varphi \right) }\). Then, acquire \(\varphi ^{k+1}\). \(\varphi ^{k+1}=\varphi ^k+\sigma \cdot {\frac{\partial \ell \left( {\varvec{W}}^{k+1},\varphi \right) }{\partial \varphi }|}_{{\varvec{W}}={\varvec{W}}^{k+1},\varphi =\varphi ^k}\).

Repeated iterations of the above process are performed until convergence, resulting in an approximate optimal solution. Algorithm 1 outlines our proposed LeCaSiM algorithm, which is based on the analysis mentioned above.

Algorithm 1
figure a

LeCaSiM

Full size image

To ensure that \({h({\varvec{W}})=0}\), a strategy of gradually increasing \(\sigma \) and \(\varphi \) as penalty factors is employed during the optimization process. However, it is important to note that in the continuous optimization process, the value of \(h({\varvec{W}})\) may approach zero indefinitely without reaching exactly zero. Therefore, a precision level for the algorithm is set, and the optimization process terminates when the value of \(h({\varvec{W}})\) becomes smaller than this precision.

In practice, due to factors such as machine precision, the iterative process can only guarantee convergence to a solution near the optimal solution. However, experimental results have consistently shown that this approximate solution is already very close to the optimal solution level.

4.2 Algorithm Implementation Details

In the third step of the LeCaSiM, the parameter \(\alpha \) in \(h({\varvec{W}})\) is determined. To enforce acyclicity, \(\alpha \) must be greater than \(\rho ({\varvec{W}} \circ {\varvec{W}})\). Thus, we set \(\alpha = \rho ({\varvec{W}} \circ {\varvec{W}}) + \xi \), with \(\xi \) taking values from the set \(\{0.1, 0.5, 1, 1.5, 2\}\). Experimental results indicate that setting \(\xi \) to 1 achieves the best performance. The reason for choosing \(\xi = 1\) is as follows: during the optimization process, as \(\rho ({\varvec{W}} \circ {\varvec{W}})\) approaches 0, choosing \(\xi < 1\) leads to \(\alpha < 1\), resulting in a smaller \(\mathbb {W}^\alpha \). In this case, a smaller learning rate is required to ensure algorithm convergence, which may affect convergence stability. On the other hand, if \(\xi > 1\), it may cause the coefficients of higher-order terms to approach 0, leading to the loss of information from these terms. Similar to existing work, we employ the approximate Quasi-Newton method [32] to solve the optimization subproblem in the fourth step. In the tenth step, we apply thresholding to the candidate matrix \({\varvec{W}}\) to filter out elements with absolute values smaller than the weight threshold \(\theta \). This helps eliminate false causal associations that could induce cycles [31]. The thresholding approach ensures sparsity of the weight matrix and improves the accuracy of the algorithm by removing spurious causal edges from the graph.

5 Experiments

This section performs extensive comparative experiments to evaluate the efficiency and accuracy of the LeCaSiM algorithm in learning DAG structures.

5.1 Experimental Setup

5.1.1 Comparison Algorithms and Evaluation Metrics

In Sect. 3.2, we analyze the limitations of three acyclicity constraints proposed in existing work. Among them, \(h_{TI}({\varvec{W}})\) is found to be prone to numerical explosion during computation. To demonstrate that the proposed \(h({\varvec{W}})\) can overcome this issue, we replace the \(h({\varvec{W}})\) in the LeCaSiM with \(h_{TI}({\varvec{W}})\) to create the LeCaSiM-TI for comparison. To address the challenges of computing high-order terms in the acyclicity constraint and the problem of gradient vanishing, we also include the NOTEARS [31] algorithm based on \(h_{NT}({\varvec{W}})\) and the DAG-GNN [27] algorithm based on \(h_{DG}({\varvec{W}})\) for comparison. Additionally, to compare the performance of the matrix polynomial constraint proposed in this paper, we included the NOCURL algorithm [28] that employs the weighted gradient set.

We utilize the following four metrics [8] to evaluate the accuracy and efficiency of the algorithm:

  • Structure hamming distance (SHD): SHD calculates the standard distance between the estimated graph and the target graph using their adjacency matrices. A lower value indicates a higher similarity between the estimated and true graphs.

  • True positive rate (TPR): TPR measures the proportion of correctly identified edges in the predicted graph compared to the total number of edges in the target graph. A higher value indicates greater accuracy of the algorithm in capturing the true edges.

  • False positive rate (FPR): FPR represents the ratio of incorrectly identified edges as true edges in the predicted graph to the total number of edges missing in the target graph. A lower value indicates higher accuracy, as fewer false edges are present.

  • Runtime: This metric indicates the time required for the algorithm to execute on a computer, reflecting the convergence speed of the algorithm.

5.1.2 Parameter Settings and Environment Configuration

For the LeCaSiM algorithm, the following parameters are initialized: lagrange multiplier \(\varphi = 0\), quadratic penalty coefficient \(\sigma = 1\), \(L_1\) coefficient \(\mu = 0.1\), algorithm precision \(\tau = 10^{-6}\), weight threshold \(\theta = 0.3\), maximum number of iterations \(T = 100\).

The experimental environment in this paper was configured with the following hardware: an 8-core 16-thread AMD Ryzen 7 5800 H CPU running at a frequency of 3.20 GHz, paired with 16GB of memory.

5.2 Experimental Results and Analysis

5.2.1 Synthetic Datasets

The experimental setup in this paper follows the approach used in previous works [27, 31]. The Erdős-Rényi (ER) random graph model is employed to construct random graphs \(\mathbb {G}\) with d nodes and an anticipated number of kd edges, known as by ERk. The weights of the edges in the graph are uniformly distributed within the ranges of [\(-\)2.0, \(-\)0.5] and [0.5, 2.0]. To obtain the data matrix X, we generate 1000 samples according to the equation \({{\varvec{X}}={\varvec{XW}}+{\varvec{N}}}\). The variable matrix \({{\varvec{N}}\in \mathbb {R}^{n\times d}}\) represents the exogenous variables and is generated using one of the following distributions: Gaussian distribution (gauss), exponential distribution (exp), or Gumbel distribution (gumbel).

To ensure consistent and reproducible results, we use the same random seed for each experiment. By doing so, we generate the same \({\varvec{X}}\) every time, enabling us to evaluate the performance of different algorithms based on consistent experimental results. For each configuration, we conduct the experiment 100 times and calculate the mean of the evaluation metrics to obtain the final result.

As shown in Fig. 5, the LeCaSiM outperforms the other comparison algorithms in terms of SHD, indicating its superior accuracy in recovering the DAG structure from observed data. For example, when using ER2 random graphs and three different noise distributions, with 100 nodes (200 edges), LeCaSiM achieves an SHD of less than 10. This corresponds to a false discovery rate of approximately 5% (10/200). In comparison, the LeCaSiM-TI exhibits a higher false discovery rate of approximately 7.5%. The NOTEARS displays a significantly higher false discovery rate of 20%, while the other two algorithms have even higher rates.

Fig. 5
figure 5

The SHD (lower is better) corresponding to different algorithms regarding different random graph models (ER2, ER3) and noise distributions (gauss, exp and gumbel)

Full size image

The TPR reflects the ability of each algorithm to accurately identify true edges and learn DAG structure. The results shown in Fig. 6 demonstrate that the LeCaSiM consistently achieves the highest TPR among the four comparison algorithms in all six experimental settings. For example, in the case of ER2 random graphs, the TPR of the LeCaSiM remains consistently above 0.95 for different numbers of nodes, demonstrating that the LeCaSiM has the highest accuracy in correctly identifying true edges and is capable of learning the true DAG structure more accurately.

The FPR reflects the rate at which algorithms incorrectly identify false edges in the predicted graph. From Fig. 7, the LeCaSiM has the lowest FPR among the compared algorithms. This signifies that the LeCaSiM does not blindly learn a large number of edges in an attempt to achieve a higher TPR. Instead, it accurately learns the true edges without introducing false edges into the predicted graph. In other words, the LeCaSiM is able to identify more true edges of the target graph without increasing the number of false edges in the predicted graph. This capability allows the LeCaSiM to more accurately recover the true graph structure.

Fig. 6
figure 6

The TPR (higher is better) corresponding to different algorithms regarding different random graph models (ER2, ER3) and noise distributions (gauss, exp and gumbel)

Full size image
Fig. 7
figure 7

The FPR (lower is better) corresponding to different algorithms regarding different random graph models (ER2, ER3) and noise distributions (gauss, exp and gumbel)

Full size image
Fig. 8
figure 8

The runtime (lower is better) corresponding to different algorithms regarding different random graph models (ER2, ER3) and noise distributions (gauss, exp and gumbel)

Full size image

As shown in Fig. 4, the calculation time of \(h({\varvec{W}})\) is slightly longer compared to other constraints. However, from Fig. 8, the average runtime of the LeCaSiM is the shortest among the compared algorithms. This indicates that \(h({\varvec{W}})\) possesses certain desirable properties, such as resolving numerical explosion and vanishing gradients. These properties contribute to faster convergence of the algorithm and improve its efficiency.

For the above experiments, the performance of the algorithm is significantly better in the ER2 random graph compared to the ER3 random graph. The reason is that ER3 target graph has more edges (non-sparse graph), which adds difficulty to the optimization of the objective function with the \(L_1\)-regularization, leading to a decrease in the accuracy and efficiency of the algorithm.

Figure 9 shows that the LeCaSiM curve is positioned in the top left part of the other curves, indicating a higher TPR and a lower FPR, i.e. a higher accuracy and a lower error detection rate compared to the other algorithms.

Fig. 9
figure 9

The average FPR and TPR values plotted for the LeCaSiM and various comparison algorithms with nodes set to 10, 30, 50, 70, and 100, respectively

Full size image

In Table 3, it is evident that the LeCaSiM outperforms the other algorithms in terms of average SHD and average running time. This demonstrates that the LeCaSiM offers the highest accuracy and efficiency among the considered options.

Table 3 The average SHD values and runtimes of LeCaSiM and various comparison algorithms with nodes set to 10, 30, 50, 70 and 100, respectively (The optimal values are shown in bold)
Full size table

5.2.2 Real Dataset

Similar to previous works [27, 31], we have conducted experiments using the protein signaling networks (PSN) dataset [22], which contains 7466 samples of 11 nodes. There are 20 edges in the ground-truth graph noted by Sachs. The PSN dataset is a well-known dataset in the field of Bayesian network structure learning and has been widely used to evaluate the performance of DAG structure learning algorithms.

The proposed LeCaSiM in this paper is based on a linear model that learns the causal structure between variables, while algorithms such as DAG-GNN are based on nonlinear models to learn the causal relationship between variables. In fact, we are unsure whether the causal mechanisms between variables in the PSN dataset are linear or nonlinear. Therefore, we conduct extensive experiments for each algorithm on the PSN dataset, measuring the accuracy of each algorithm’s learning of the causal structure through a comparison of SHD and predicted edge numbers, as shown in Table 4.

The number of edges in the learned graph structure by the algorithm is referred to as the “# Predicted edges”. From Table 4, it can be observed that the predicted edge count for LeCaSiM is 17, consisting of 10 ground-truth edges, 7 erroneous edges, and 1 reverse edges. LeCaSiM achieves the lowest SHD compared to the comparison algorithms, indicating the LeCaSiM can more accurately reconstruct the true causal structure when applied to real-world datasets like the PSN dataset.

Table 4 Algorithm prediction results based on the real dataset
Full size table

6 Summary and Future Work

The problem of DAG structure learning has broad applications across various fields, including task scheduling, data flow analysis, dependency management, and more. However, the exponential growth of the DAG search space with the number of nodes poses a major challenge. Recent research has introduced a continuous acyclicity constraint function, which transforms the DAG structure learning problem into a continuous optimization problem. Motivated by this approach, this paper employs concepts from algebraic graph theory to summarize seven equivalent conditions for DAGs and compare existing acyclicity constraints. It is observed that existing methods may encounter issues such as numerical explosion or gradient vanishing during acyclicity constraint computations and optimization iterations. To address these challenges, this paper introduces M-matrices and leverages their properties to propose a novel acyclicity constraint function. By adaptively adjusting the coefficients of high-order terms using the spectral radius of candidate matrices, these issues are effectively addressed. Based on this foundation, the LeCaSiM is developed to solve the DAG structure learning problem. Comprehensive comparative experiments are conducted on both simulated and real-world datasets in this paper. The experimental results demonstrate that the proposed algorithm outperforms existing algorithms in terms of accuracy and efficiency.

While our work contributes valuable insights and advancements, there are still limitations and opportunities for further improvements. Firstly, the assumption of linear causal relationships between variables may not always hold true in practical applications. Future research should explore the incorporation of deep generative models that can capture nonlinear relationships while adhering to acyclicity constraints. Secondly, our algorithm provides an approximate solution to the unconstrained optimization problem. Further efforts should be directed towards improving the efficiency and convergence stability of the algorithm to enhance its performance in real-world scenarios. Lastly, we intend to explore the seven algebraic propositions of DAGs proposed in this paper further. There is scope for developing acyclicity constraint functions with lower computational complexity while maintaining the desired accuracy and efficiency. These potential research directions and areas for improvement can help advance the field of DAG structure learning and pave the way for more accurate and efficient algorithms in practical applications.