Hopf Bifurcation of General Fractional Delayed TdBAM Neural Networks

Abstract

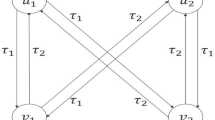
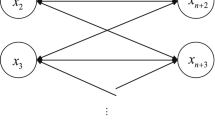
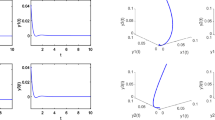
In this paper, a fractional model of a special structure of bidirectional associative memory (BAM) neural networks called tri-diagonal BAM neural networks (TdBAMNNs) is considered. The Hopf bifurcation analysis is made for the proposed fractional system in the presence of leakage and communication delays. The feasibility of the obtained theoretical results is verified by numerical simulations.

Appendix 1

Proof of Theorem 3.1:

Let $\sigma = 0$. The characteristic equation Eq. (4) can be reduced into

$$\begin{aligned} \begin{aligned} r^{2n\omega } + b_{2n-2}r^{(2n-2)\omega } + b_{2n-4}r^{(2n-4)\omega } + \dots + b_{2}r^{2\omega } + b_{0} = 0. \end{aligned} \end{aligned}$$

(14)

Substituting $r^{2\omega } = \gamma$ in Eq. (14), we have

$$\begin{aligned} \begin{aligned} \gamma ^{n} + \alpha _{n-1}\gamma ^{n-1} + \alpha _{n-2}\gamma ^{n-2} + \dots + \alpha _{2}\gamma ^{2} + \alpha _{1}\gamma + \alpha _{0} = 0, \end{aligned} \end{aligned}$$

(15)

where $\alpha _{i}$ are the coefficients of $\gamma ^{i}$ (i = 0,1,2,...,n-1).

The Routh-Hurwitz matrices for 2n-neuron FODTdBAMNNs system (2) is defined as follows.

$$\begin{aligned} \Delta _1= & {} \alpha _{n-1}, \Delta _2 = \left[ \begin{matrix} \alpha _{n-1}&{} 1 \\ \alpha _{n-3}&{} \alpha _{n-2} \end{matrix}\right] , \Delta _3 = \left[ \begin{matrix} \alpha _{n-1}&{} 1 &{} 0\\ \alpha _{n-3}&{} \alpha _{n-2}&{} \alpha _{n-1}\\ \alpha _{n-5}&{} \alpha _{n-4} &{} \alpha _{n-3} \end{matrix}\right] ,\\ \Delta _4= & {} \left[ \begin{matrix} \alpha _{n-1}&{} 1 &{} 0&{} 0\\ \alpha _{n-3}&{} \alpha _{n-2}&{} \alpha _{n-1}&{} 1\\ \alpha _{n-5}&{} \alpha _{n-4} &{} \alpha _{n-3}&{} \alpha _{n-2}\\ \alpha _{n-7}&{} \alpha _{n-6}&{} \alpha _{n-5}&{} \alpha _{n-4} \end{matrix}\right] , \Delta _5 = \left[ \begin{matrix} \alpha _{n-1}&{} 1 &{} 0&{} 0&{} 0\\ \alpha _{n-3}&{} \alpha _{n-2}&{} \alpha _{n-1}&{} 1&{} 0\\ \alpha _{n-5}&{} \alpha _{n-4} &{} \alpha _{n-3}&{} \alpha _{n-2}&{} \alpha _{n-1}\\ \alpha _{n-7}&{} \alpha _{n-6}&{} \alpha _{n-5}&{} \alpha _{n-4}&{} \alpha _{n-3}\\ \alpha _{n-9}&{} \alpha _{n-8}&{} \alpha _{n-7}&{} \alpha _{n-6}&{} \alpha _{n-5} \end{matrix}\right] ,\\ \dots \Delta _{n-1}= & {} \begin{bmatrix} \alpha _{n-1}&{} 1 &{} 0&{} 0&{} \dots &{} 0&{} 0&{} 0&{} 0\\ \alpha _{n-3}&{} \alpha _{n-2}&{} \alpha _{n-1}&{} 1&{} \dots &{} 0&{} 0&{} 0&{} 0\\ \alpha _{n-5}&{} \alpha _{n-4}&{} \alpha _{n-3}&{} \alpha _{n-2}&{} \dots &{} 0&{} 0&{} 0&{} 0\\ \alpha _{n-7}&{} \alpha _{n-6}&{} \alpha _{n-5}&{} \alpha _{n-4}&{} \dots &{} 0&{} 0&{} 0&{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \dots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0&{} 0&{} 0&{} 0&{} \dots &{} \alpha _4&{} \alpha _5&{} \alpha _6&{} \alpha _7\\ 0&{} 0&{} 0&{} 0&{} \dots &{} \alpha _2&{} \alpha _3&{} \alpha _4&{} \alpha _5\\ 0&{} 0&{} 0&{} 0&{} \dots &{} 0&{} \alpha _1&{} \alpha _2&{} \alpha _3\\ 0&{} 0&{} 0&{} 0&{} \dots &{} 0&{} 0&{} \alpha _0&{} \alpha _1 \end{bmatrix} and \, \Delta _{n} = \alpha _0. \end{aligned}$$

Let us assume $\Delta _i > 0$ $(i = 1,2,...,n)$.

Then by fractional Routh-Hurwitz conjecture [1], all the roots $\gamma _i$ of Eq. (15) have the absolute value of its argument greater than $\frac{\omega \pi }{2}$ for $i = 1,2,...,n$. So, by Lemma 2.1, we can conclude that the FODTdBAMNNs system (2) is asymptotically stable when $\sigma = 0$. Also, since Eq. (10) has no positive real roots, we can conclude that FODTdBAMNNs system (2) is asymptotically stable in the global sense for $\sigma \in \left[ 0, \infty \right)$.

This completes the validation. $\square$

Proof of Theorem 3.2:

Let $r(\sigma ) = \mu (\sigma ) + i \nu (\sigma )$ be the root of the Eq. (3) near $\sigma = \sigma _j$ satisfying $\mu (\sigma _j) = 0$ and $\nu (\sigma _j) = 0$.

Differentiate Eq. (3) with respect to $\sigma$, we obtain

$$\begin{aligned}&2n\omega r^{2n\omega -1} \dfrac{dr}{d\sigma } + b_{2n-2} \left[ (2n-2)\omega r^{(2n-2)\omega -1} e^{-2r \sigma } \dfrac{dr}{d\sigma } + r^{(2n-2)\omega } e^{-2r \sigma } \left( -2\sigma \dfrac{dr}{d\sigma } - 2r\right) \right] \\&\qquad + b_{2n-4} \left[ (2n-4)\omega r^{(2n-4)\omega -1} e^{-4r \sigma } \dfrac{dr}{d\sigma } + r^{(2n-4)\omega } e^{-4r \sigma } \left( -4\sigma \dfrac{dr}{d\sigma } - 4r\right) \right] \\&\qquad + \dots + b_{2} \left[ 2\omega r^{2\omega -1} e^{-(2n-2)r \sigma } \dfrac{dr}{d\sigma } + r^{2\omega } e^{-(2n-2)r \sigma } \left( -(2n-2)\sigma \dfrac{dr}{d\sigma } - (2n-2)r\right) \right] \\&\qquad + b_{0} e^{-2nr \sigma } \left( -2n\sigma \dfrac{dr}{d\sigma } - 2nr\right) = 0. \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{dr}{d\sigma } Q(r) - P(r) = 0, \end{aligned}$$

(16)

where

$$\begin{aligned} \begin{aligned} P(r)&= r[2b_{2n-2} r^{(2n-2)\omega } e^{-2r \sigma } + 4b_{2n-4} r^{(2n-4)\omega } e^{-4r \sigma } + 6b_{2n-6} r^{(2n-6)\omega } e^{-6r \sigma }\\&\quad + \dots + (2n-2)b_{2} r^{2\omega } e^{-(2n-2)r \sigma } + 2nb_{0} e^{-2nr \sigma }],\\ Q(r)&= 2n \omega r^{2n\omega -1} + b_{2n-2} \left[ (2n-2)\omega r^{(2n-2)\omega -1} e^{-2r \sigma } -2\sigma r^{(2n-2)\omega } e^{-2r \sigma } \right] \\&\quad + \dots + b_0 \left[ -2n\sigma e^{-2nr \sigma } \right] . \end{aligned} \end{aligned}$$

(17)

Therefore,

$$\begin{aligned} \dfrac{dr}{d\sigma } = \dfrac{P(r)}{Q(r)}. \end{aligned}$$

(18)

When $\sigma = \sigma _0$ and $\nu = \nu _0$, let $P(r) = P_1 + i P_2$ and $Q(r) = Q_1 + i Q_2$. Then, we have

$$\begin{aligned} \dfrac{dr}{d\sigma }&= \dfrac{P_1 + i P_2}{Q_1 + i Q_2} \\&= \dfrac{(P_1Q_1 - P_2Q_2) + i(P_1Q_2 + P_2Q_1)}{(Q_1)^2 + (Q_2)^2}. \end{aligned}$$

Hence by the assumption $(\mathcal {A}_2 )$, one can get

$$\begin{aligned} Re\left[ \dfrac{dr}{d\sigma } \right] _{(\sigma = \sigma _0, \nu = \nu _0)} = \dfrac{(P_1Q_1 - P_2Q_2)}{(Q_1)^2 + (Q_2)^2} \ne 0, \end{aligned}$$

where $P_1,$ $P_2,$ $Q_1$ and $Q_2$ are obtained as follows.

$$\begin{aligned} \begin{aligned} P_1&= 2b_{2n-2} \theta _0^{(2n-2)\omega +1} \cos \left( \frac{\left[ (2n-2)\omega +1\right] \pi }{2} - 2\theta _0\sigma _0\right) \\&\quad + 4b_{2n-4} \theta _0^{[(2n-4)\omega +1]} \cos \left( \frac{\left[ (2n-4)\omega +1\right] \pi }{2} - 4\theta _0\sigma _0\right) \\&\quad + \dots + 2nb_0 \theta _0 \cos \left( \frac{\pi }{2} - 2n\theta _0\sigma _0\right) ,\\ P_2&=2b_{2n-2} \theta _0^{[(2n-2)\omega +1]} \sin \left( \frac{\left[ (2n-2)\omega +1\right] \pi }{2} - 2\theta _0\sigma _0\right) \\&\quad + 4b_{2n-4} \theta _0^{[(2n-4)\omega +1]} \sin \left( \frac{\left[ (2n-4)\omega +1\right] \pi }{2} - 3\theta _0\sigma _0\right) \\&\quad + \dots + 2nb_0 \theta _0 \sin \left( \frac{\pi }{2} - 2n\theta _0\sigma _0\right) ,\\ Q_1&= 2n\omega \theta _0^{2n\omega -1} \cos \left( \frac{(2n\omega -1)\pi }{2}\right) \\&\quad + (2n-2)\omega b_{2n-2} \theta _0^{(2n-2)\omega -1} \cos \left( \frac{((2n-2)\omega -1)\pi }{2} - 2\theta _0\sigma _0\right) \\&\quad - 2\sigma _0\theta _0^{(2n-2)\omega } \cos \left( \frac{((2n-2)\omega )\pi }{2} - 2\theta _0\sigma _0\right) \\&\quad + (2n-4)\omega b_{2n-4} \theta _0^{(2n-4)\omega -1} \cos \left( \frac{((2n-4)\omega -1)\pi }{2} - 4\theta _0\sigma _0\right) \\&\quad - \sigma _0\theta _0^{(2n-4)\omega } \cos \left( \frac{((2n-4)\omega )\pi }{2} - 4\theta _0\sigma _0\right) + \dots + 2n\sigma _0b_0 \cos (2n\sigma _0\theta _0),\\ Q_2&= 2n\omega \theta _0^{2n\omega -1} \sin \left( \frac{(2n\omega -1)\pi }{2}\right) \\&\quad + (2n-2)\omega b_{2n-2} \theta _0^{(2n-2)\omega -1} \sin \left( \frac{[(2n-2)\omega -1]\pi }{2} - 2\theta _0\sigma _0\right) \\&\quad - 2b_{2n-2}\sigma _0\theta _0^{(2n-2)\omega } \sin \left( \frac{(2n-2)\omega \pi }{2} - 2\theta _0\sigma _0\right) \\&\quad + (2n-4)\omega b_{2n-4} \theta _0^{(2n-4)\omega -1} \sin \left( \frac{[(2n-4)\omega -1]\pi }{2} - 4\theta _0\sigma _0\right) \\&\quad - 4b_{2n-4}\sigma _0\theta _0^{(2n-4)\omega } \sin \left( \frac{(2n-4)\omega \pi }{2} - 4\theta _0\sigma _0\right) + \dots + 2n\sigma _0b_0\sin (2n\sigma _0\theta _0). \end{aligned} \end{aligned}$$

As Eq. (10) has at least one positive real root, we can come to the conclusion that the stability of the zero equilibrium of the FODTdBAMNNs system (2) is asymptotic in the local sense for $\sigma \in \left[ 0, \sigma _0 \right)$ and Hopf bifurcation occurs at the origin when $\sigma = \sigma _0$. $\square$