Stability and Hopf Bifurcation Analysis of A Fractional-Order BAM Neural Network with Two Delays Under Hybrid Control

Abstract

In this paper, considering that fractional-order calculus can more accurately describe memory and genetic properties, we introduce fractional integral operators into neural networks and discuss the stability and Hopf bifurcation of a fractional-order bidirectional associate memory (BAM) neural network with two delays. In addition, the hybrid controller is proposed to achieve Hopf bifurcation control of the system. By taking two time delays as the bifurcation parameters and analyzing of the corresponding characteristic equation, stability switching curves of the controllable system for two delays are obtained. The direction of the characteristic root crossing the imaginary axis in stability switching curves is determined. Sufficient criteria are sequentially given to judge the local stability and the existence of Hopf bifurcation of a fractional-order BAM neural network system. The numerical simulation results show that the hybrid controller can effectively control Hopf bifurcation of a fractional-order BAM neural network system with two delays.

1 Introduction

In order to reveal the complex dynamic properties of the biological neural network systems, researchers designed neural networks by imitating the behavioral characteristics of the biological neural networks, which can realize information reception, storage, operation and transmission. With the in-depth research of neural networks, researchers have proposed bidirectional associative memory model [1, 2], recurrent neural network model [3, 4], cellular neural network model [5] and so on. Networks research on associative memory is an important branch of neural networks. The bidirectional associative memory (BAM) neural networks proposed by B. Kosko are the most extensively applied [6]. BAM neural networks can realize bidirectional heteroassociation, which usually used to describe the ability to store or remember paired patterns through forward and backward directions. Similar to the biological neural networks, due to the limited switching speed of the neural amplifier, which causes the interaction between elements in the networks usually takes a certain amount time to achieve. So the time delay is ubiquitous in neural networks. However, the introduction of time delay often causes changes in the stability of system, such as bifurcation, periodic oscillation, chaos and other phenomena [7,8,9]. Based on this, a growing number of researchers have begun to discuss the effect of time delay on the dynamic behavior of neural networks.

In [10], Zhang et al. studied the global existence of periodic solutions to the following a simplified n-dimensional BAM neural network model with time delays

$$\begin{aligned} \left\{ \begin{aligned} {\dot{u}}_{1}(t)&=-au_{1}(t)+f_{2}(u_{2}(t-\tau _{J}))+f_{3}(u_{3}(t-\tau _{J}))+\cdots +f_{n}(u_{n}(t-\tau _{J})), \\ {\dot{u}}_{2}(t)&=-au_{2}(t)+g_{2}(u_{1}(t-\tau _{I})), \\ {\dot{u}}_{3}(t)&=-au_{3}(t)+g_{3}(u_{1}(t-\tau _{I})), \\ \vdots \\ {\dot{u}}_{n}(t)&=-au_{n}(t)+g_{n}(u_{1}(t-\tau _{I})), \end{aligned} \right. \end{aligned}$$

(1)

where the time delay from the I-layer to another J-layer is recorded as $\tau _{I}$ while the time delay from the J-layer back to the I-layer is recorded as $\tau _{J}$; There is one neuron in the I-layer and there are $n-1$ neurons in the J-layer; $a>0$ describes the internal decay rate of neuron on the I-layer and the J-layer; $u_{i}(t)(i=1,2,\ldots ,n)$ represents the state variables of neuron at time t; On the I-layer, the neurons whose states are denoted by $u_{1}(t)$ receive the inputs outputted by those neurons in the J-layer via activation functions $f_{i}$, while on the J-layer, the neurons whose associated states denoted by $u_{j}(t)(j=2,\ldots ,n)$ receive the inputs outputted by those neurons in the I-layer via activation functions $g_{j}$.

As a generalization of integer-order calculus, the research shows that fractional calculus can more accurately describe the memory properties and historical dependencies in the real world. Based on this advantage, fractional differential equations have been widely used in signal processing, system identification, rheology, materials and mechanical systems. In [11], Syed Ali et al. dealt with global Mittag-Leffler stability for impulsive delayed fractional-order BAM neural networks. Zhang et al. [12] investigated the finite-time stability for a fractional-order BAM neural network with discrete and distributed delays. In recent years, Hopf bifurcation has become one of the important research contents of fractional-order neural networks. In [13], Yan discussed the effect of leakage delay on stability and Hopf bifurcation of fractional-order complex-valued neural networks. Xu et al. [14] considered the stability and bifurcation of a six-neuron BAM neural network model with discrete delays. There are some more works on Hopf bifurcation of fractional-order neural networks that have been reported [15,16,17,18,19].

Motivated mainly by [10], we concern the stability of the following fractional-order BAM neural networks system with two time delays

$$\begin{aligned} \left\{ \begin{aligned} D^{\theta }x_{1}(t)&=-k_{1}x_{1}(t)+m_{11}f_{11}(y_{1}(t-\sigma _{1}))+m_{12}f_{12}(y_{2}(t-\sigma _{1})) \\&\quad +m_{13}f_{13}(y_{3}(t-\sigma _{1})), \\ D^{\theta }y_{1}(t)&=-k_{2}y_{1}(t)+n_{11}g_{11}(x_{1}(t-\sigma _{2})), \\ D^{\theta }y_{2}(t)&=-k_{3}y_{2}(t)+n_{21}g_{21}(x_{1}(t-\sigma _{2})), \\ D^{\theta }y_{3}(t)&=-k_{4}y_{3}(t)+n_{31}g_{31}(x_{1}(t-\sigma _{2})), \end{aligned} \right. \end{aligned}$$

(2)

where $\theta \in (0,1]$ is the fractional order, $D^{\theta }$ denotes the Caputo fractional derivative; $k_{i}>0(i=1,2,3,4)$ describes the internal decay rate of neuron; $x_{1}(t)$, $y_{j}(t)(j=1,2,3)$ represent the state variables of neuron in I-layer and J-layer at time t, respectively; $m_{1i},n_{j1}(i,j=1,2,3)$ stand for the connection weight between I-layer and J-layer; $f_{ji}(\cdot )$ and $g_{ij}(\cdot )$ denote activation function that the information of the neurons in I-layer(J-layer) input to the neurons in J-layer(I-layer) through $g_{ij}(\cdot )(f_{ji}(\cdot ))$; $\sigma _{i}\ge 0(i=1,2)$ is synaptic transmission delay. In this paper, it is assumed that the time delay of the signal from I-layer to J-layer is $\sigma _{2}$, and the time delay from J-layer feedback to I-layer is $\sigma _{1}$. The initial conditions of system (2) are $x_{1}(\xi )=\phi _{1}(\xi ),y_{1} (\xi )=\phi _{2}(\xi ),y_{2} (\xi )=\phi _{3}(\xi ),y_{3} (\xi )=\phi _{4}(\xi ),\phi _{i}(\xi ) \ge 0, i=1,2,3,4,-\sigma \le \xi \le 0$, $\sigma =max\{\sigma _{1}, \sigma _{2}\}$.

In order to get the main results of this paper, we make the following assumption:

(H1) For $i,j=1,2,3, f_{ji}(0)=g_{ij}(0)=0, \forall x\ne 0, xf_{ji}(x)>0, xg_{ij}(x)>0$.

Recently, bifurcation control has attracted the attention of many researchers from different disciplines. The study of bifurcation control can not only better grasp and change the dynamic behavior of bifurcation, but also achieve effective control of chaos and other phenomena. Since Ott et al. [20] first proposed control strategies, many effective control strategies have emerged. From the point of view of control theory, control methods are mainly divided into feedback control and non-feedback control. Common controllers include pulse controller [21], time delay feedback controller [22], and PD controller [23]. For neural networks, the time delay phenomenon generally exists in the process of information transmission, which may lead to oscillation and instability of the network, thereby destroying the original network performance. In order to improve the network security, it is particularly important to control the bifurcation of neural networks with time delays. In [24], the hybrid controller is proposed for Hopfield neural networks, which uses state feedback and parameter perturbation to control Hopf bifurcation of continuous dynamic system. The results show that the Hopf bifurcation of system without hybrid control could be delayed or eliminated by hybrid control. The hybrid control can be applied to any component of multidimensional dynamic system [25].

Considering the potential advantages of hybrid controller, the hybrid controller is introduced into system (2) to discuss the influence of controller on the stability of system in this paper. The model is as follows

$$\begin{aligned} \left\{ \begin{aligned} D^{\theta }x_{1}(t)&=-k_{1}x_{1}(t)+m_{11}f_{11}(y_{1}(t-\sigma _{1}))+m_{12}f_{12}(y_{2}(t-\sigma _{1})) \\&\quad +m_{13}f_{13}(y_{3}(t-\sigma _{1})), \\ D^{\theta }y_{1}(t)&=-k_{2}y_{1}(t)+n_{11}g_{11}(x_{1}(t-\sigma _{2})), \\ D^{\theta }y_{2}(t)&=-k_{3}y_{2}(t)+n_{21}g_{21}(x_{1}(t-\sigma _{2})), \\ D^{\theta }y_{3}(t)&=\alpha \left[ -k_{4}y_{3}(t)+n_{31}g_{31}(x_{1}(t-\sigma _{2})) \right] +\beta y_{3}(t-\sigma _{2}), \end{aligned} \right. \end{aligned}$$

(3)

where control parameters $\alpha >0$ and $\beta \in {\mathbb {R}}$.

At present, when dealing with problems with multiple delays, it is usually adopted to take one of them as the bifurcation parameter and fix the other delays to discuss the dynamic behaviors. However, fixing other delays is equivalent to not considering the practical significance of these delays, which leads to ignoring the impact of their dynamic behaviors. In [26], a integer-order system with two delays and both delays changing simultaneously is considered. The corresponding characteristic equation has the following form

$$\begin{aligned} D(\lambda ,\tau _{1},\tau _{2})=P_{0}(\lambda )+P_{1}(\lambda )e^{-\lambda \tau _{1}}+P_{2}(\lambda )e^{-\lambda \tau _{2}}+P_{3}(\lambda )e^{-\lambda (\tau _{1}+\tau _{2})}. \end{aligned}$$

(4)

By selecting two different time delays as bifurcation parameters, stability switching curves and crossing direction of the eigenvalues stability switching curves are calculated. Thus the stability and the existence of Hopf bifurcation of system are obtained. Compared to discussing the stability of system by fixing one delay and using another delay as the bifurcation parameter, the method of stability switching curves in [26] is to obtain the locally asymptotically stable region of the equilibrium in $(\tau _{1},\tau _{2})$ plane. The method of [26] is applied to discuss the stability of a heterogenous Cournot duopoly with delay dynamics [27], and study the effect of two delays on global stability of nonlinear Cournot duopoly dynamics [28]. More applications have been found [29,30,31]. With the further study, the method of stability switching curves is used to discuss the stability of fractional-order time delays systems. Li [32] and Zhu et al. [33] extended the technique of stability switching curves to the fractional-order model. Inspired by the above work, in this paper we first apply the method of stability switching curves to a fractional-order BAM neural network, and discuss the local asymptotic stability of the equilibrium and the existence of Hopf bifurcation when two time delays change simultaneously.

The main contribution of this paper are as follows:

• (i) In order to better describe the memory and genetic properties of neural networks, a new fractional-order BAM neural network with two delays is considered.

• (ii) Sufficient conditions are established to guarantee the stability and the existence of Hopf bifurcation of a fractional-order BAM neural network. It is found that time delays have important effects on the stability of system.

• (iii) A hybrid controller is introduced into a fractional-order BAM neural network system to control Hopf bifurcation successfully.

• (iv) There are few papers dealing with Hopf bifurcation of neural networks with multiple delays and time delays changing simultaneously. This paper apply the method of stability switching curves in [26] to a fractional-order system and discuss the stability of fractional-order controlled system (3).

The rest of this paper is organized as follows: In Sect. 2, we consider the local stability and the existence of Hopf bifurcation of system (2). In Sect. 3, the hybrid controller is introduced into system (3). Applying the method in [26], we derive stability switching curves and crossing direction, and analyze the existence of Hopf bifurcation of system (3). In Sect. 4, numerical simulation shows the correctness of the theoretical results. Finally, the conclusions are drawn in Sect. 5.

2 Stability and Hopf Bifurcation Analysis of System (2)

In this section, taking time delay as the bifurcation parameter, the conditions for the local stability of the equilibrium and the existence of Hopf bifurcation of system (2) are obtained.

By assumption (H1), it is easy to conclude that the equilibrium of system (2) is the origin O(0, 0, 0, 0). The linearization of system (2) at O is

$$\begin{aligned} \left\{ \begin{aligned} D^{\theta }x_{1}(t)&=-k_{1}x_{1}(t)+\phi _{11}y_{1}(t-\sigma _{1})+\phi _{12}y_{2}(t-\sigma _{1})+\phi _{13}y_{3}(t-\sigma _{1}), \\ D^{\theta }y_{1}(t)&=-k_{2}y_{1}(t)+\varphi _{11}x_{1}(t-\sigma _{2}), \\ D^{\theta }y_{2}(t)&=-k_{3}y_{2}(t)+\varphi _{21}x_{1}(t-\sigma _{2}), \\ D^{\theta }y_{3}(t)&=-k_{4}y_{3}(t)+\varphi _{31}x_{1}(t-\sigma _{2}), \end{aligned} \right. \end{aligned}$$

(5)

where $\phi _{1i}=m_{1i}f'_{1i}(0)$, $\varphi _{j1}=n_{j1}g'_{j1}(0)(i,j=1,2,3)$. By applying Laplace transformation, the characteristic equation of system (5) is

$$\begin{aligned} \begin{vmatrix} \lambda ^{\theta }+k_{1}&-\phi _{11}e^{-\lambda \sigma _{1}}&-\phi _{12}e^{-\lambda \sigma _{1}}&-\phi _{13}e^{-\lambda \sigma _{1}} \\ -\varphi _{11}e^{-\lambda \sigma _{2}}&\lambda ^{\theta }+k_{2}&0&0 \\ -\varphi _{21}e^{-\lambda \sigma _{2}}&0&\lambda ^{\theta }+k_{3}&0 \\ -\varphi _{31}e^{-\lambda \sigma _{2}}&0&0&\lambda ^{\theta }+k_{4} \end{vmatrix}=0, \end{aligned}$$

(6)

that is

$$\begin{aligned} \lambda ^{4\theta }+a_{1}\lambda ^{3\theta }+a_{2}\lambda ^{2\theta }+a_{3}\lambda ^{\theta }+a_{4}+(a_{5}\lambda ^{2\theta }+a_{6}\lambda ^{\theta }+a_{7})e^{-\lambda (\sigma _{1}+\sigma _{2})}=0, \end{aligned}$$

(7)

where

$$\begin{aligned} a_{1}&=k_{1}+k_{2}+k_{3}+k_{4}, \\ a_{2}&=k_{1}k_{2}+k_{1}k_{3}+k_{1}k_{4}+k_{2}k_{3}+k_{2}k_{4}+k_{3}k_{4}, \\ a_{3}&=k_{1}k_{2}k_{3}+k_{1}k_{2}k_{4}+k_{1}k_{3}k_{4}+k_{2}k_{3}k_{4}, \\ a_{4}&=k_{1}k_{2}k_{3}k_{4}, \\ a_{5}&=-\phi _{11}\varphi _{11}-\phi _{12}\varphi _{21}-\phi _{13}\varphi _{31}, \\ a_{6}&=-(k_{3}+k_{4})\phi _{11}\varphi _{11}-(k_{2}+k_{4})\phi _{12}\varphi _{21}-(k_{2}+k_{3})\phi _{13}\varphi _{31}, \\ a_{7}&=-k_{3}k_{4}\phi _{11}\varphi _{11}-k_{2}k_{4}\phi _{12}\varphi _{21}-k_{2}k_{3}\phi _{13}\varphi _{31}. \end{aligned}$$

The stability of the equilibrium O is discussed in two cases.

Case 1: $\sigma _{1}=\sigma _{2}=0$.

If $\sigma _{1}=\sigma _{2}=0$, Eq. (7) becomes

$$\begin{aligned} \lambda ^{4\theta }+b_{1}\lambda ^{3\theta }+b_{2}\lambda ^{2\theta }+b_{3}\lambda ^{\theta }+b_{4}=0, \end{aligned}$$

(8)

where

$$\begin{aligned} b_{1}=a_{1},\quad b_{2}=a_{2}+a_{5},\quad b_{3}=a_{3}+a_{6},\quad b_{4}=a_{4}+a_{7}. \end{aligned}$$

Lemma 1

[34] For the following fractional-order system: $D^{\theta }x(t)=Ax(t),A\in R^{n\times n}$. If all the eigenvalues $\lambda _{i}(i=1,2,\ldots ,n)$ of A satisfy $|arg(\lambda _{i}) |> \theta \pi /2$, then the equilibrium of system is locally asymptotically stable, where $\theta \in (0,1]$.

According to Lemma 1 and Routh-Hurwitz criterion, we have the following theorem.

Theorem 1

System (2) is locally asymptotically stable if and only if $D_{i}>0(i=1,2,3,4)$ hold, where $D_{i}$ is defined as follows

$$\begin{aligned} D_{1}=b_{1}, D_{2}=\begin{vmatrix} b_{1}&1\\ b_{3}&b_{2} \end{vmatrix}, D_{3}=\begin{vmatrix} b_{1}&1&0\\ b_{3}&b_{2}&b_{1}\\ 0&b_{4}&b_{3} \end{vmatrix}, D_{4}=b_{4}D_{3}>0 \end{aligned}$$

Case 2: $\sigma _{1}>0,\sigma _{2}>0.$

Let $\tau =\sigma _{1}+\sigma _{2}$, Eq. (7) becomes

$$\begin{aligned} D(\lambda ,\tau )=Q_{0}(\lambda )+Q_{1}(\lambda )e^{-\lambda \tau }=0, \end{aligned}$$

(9)

where

$$\begin{aligned} Q_{0}(\lambda )&=\lambda ^{4\theta }+a_{1}\lambda ^{3\theta }+a_{2}\lambda ^{2\theta }+a_{3}\lambda ^{\theta }+a_{4}, \\ Q_{1}(\lambda )&=a_{5}\lambda ^{2\theta }+a_{6}\lambda ^{\theta }+a_{7}. \end{aligned}$$

Assume $\lambda =\omega (\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})(\omega >0)$ is the root of the characteristic equation (9), we get

$$\begin{aligned} D(i\omega ,\tau )=Q_{0}(i\omega )+Q_{1}(i\omega )e^{-i\omega \tau }=0. \end{aligned}$$

(10)

According to Eq. (10), separating the real and imaginary parts yields, we have

$$\begin{aligned} \left\{ \begin{aligned} F_{0}+F_{1}\cos \omega \tau +G_{1}\sin \omega \tau =0, \\ G_{0}+G_{1}\cos \omega \tau -F_{1}\sin \omega \tau =0, \end{aligned} \right. \end{aligned}$$

(11)

where

$$\begin{aligned} F_{0}&=\omega ^{4\theta }\cos 2\theta \pi +a_{1}\omega ^{3\theta }\cos \frac{3\theta \pi }{2}+a_{2}\omega ^{2\theta }\cos \theta \pi +a_{3}\omega ^{\theta }\cos \frac{\theta \pi }{2}+a_{4}, \\ G_{0}&=\omega ^{4\theta }\sin 2\theta \pi +a_{1}\omega ^{3\theta }\sin \frac{3\theta \pi }{2}+a_{2}\omega ^{2\theta }\sin \theta \pi +a_{3}\omega ^{\theta }\sin \frac{\theta \pi }{2}, \\ F_{1}&=a_{5}\omega ^{2\theta }\cos \theta \pi +a_{6}\omega ^{\theta }\cos \frac{\theta \pi }{2}+a_{7}, \\ G_{1}&=a_{5}\omega ^{2\theta }\sin \theta \pi +a_{6}\omega ^{\theta }\sin \frac{\theta \pi }{2}. \end{aligned}$$

Through further calculation, we can get

$$\begin{aligned} \begin{aligned} \cos \omega \tau&=-\frac{G_{0}G_{1}+F_{0}F_{1}}{F_{1}^{2}+G_{1}^{2}}=E_{1}(\omega ), \\ \sin \omega \tau&=\frac{G_{0}F_{1}-F_{0}G_{1}}{F_{1}^{2}+ G_{1}^{2}}=E_{2}(\omega ). \end{aligned} \end{aligned}$$

(12)

From $E_{1}^{2}(\omega )+E_{2}^{2}(\omega )=1$, we have

$$\begin{aligned} \omega ^{8\theta }+e_{1}\omega ^{7\theta }+e_{2}\omega ^{6\theta }+e_{3}\omega ^{5\theta }+e_{4}\omega ^{4\theta }+e_{5}\omega ^{3\theta }+e_{6}\omega ^{2\theta }+e_{7}\omega ^{\theta }+e_{8}=0, \end{aligned}$$

(13)

where

$$\begin{aligned} e_{1}&=2a_{1}\cos \frac{\theta \pi }{2},\quad e_{2}=a_{1}^{2}+2a_{2}\cos \theta \pi ,\\ e_{3}&=2a_{3}\cos \frac{3\theta \pi }{2}+2a_{1}a_{2}\cos \frac{\theta \pi }{2},\\ e_{4}&=a_{2}^{2}+2a_{4}\cos 2\theta \pi +2a_{1}a_{3}\cos \theta \pi -a_{5}^{2},\\ e_{5}&=2a_{1}a_{4}\cos \frac{3\theta \pi }{2}+2(a_{2}a_{3}-a_{5}a_{6})\cos \frac{\theta \pi }{2},\\ e_{6}&=a_{3}^{2}-a_{6}^{2}+2(a_{2}a_{4}-a_{5}a_{7})\cos \theta \pi ,\\ e_{7}&=2(a_{3}a_{4}-a_{6}a_{7})\cos \frac{\theta \pi }{2},\\ e_{8}&=a_{4}^{2}-a_{7}^{2}. \end{aligned}$$

Let

$$\begin{aligned} \begin{aligned} G(\omega )=\omega ^{8\theta }+e_{1}\omega ^{7\theta }+e_{2}\omega ^{6\theta }+e_{3}\omega ^{5\theta }+e_{4}\omega ^{4\theta }+e_{5}\omega ^{3\theta }+e_{6}\omega ^{2\theta }+e_{7}\omega ^{\theta }+e_{8}. \end{aligned} \end{aligned}$$

If $e_{8}<0$, then $\lim \limits _{\omega \rightarrow \infty }G(\omega )=+\infty$. Thus, we can conclude that Eq. (13) has at least one positive root $\omega _{i}$. For different $\omega _{i}$, the value of $\tau _{i}$ corresponding to it can be derived from Eq. (12). According to Eq. (12), we have

$$\begin{aligned} \tau _{i}^{(k)}=\frac{1}{\omega _{i}}\left[ \arccos \left( -\frac{G_{0}G_{1}+F_{0}F_{1}}{|F_{1}^{2}+G_{1}^{2} |}\right) +2k\pi \right] ,k=0,1,2,\ldots . \end{aligned}$$

(14)

Denote

$$\begin{aligned} \tau _{0}=\tau _{i_{0}}^{(0)}=\underset{ i=1,2,\ldots }{min}\left\{ \tau _{i} ^{(0)} \right\} , \omega _{0}=\omega _{i_{0}}. \end{aligned}$$

(15)

We obtain that when $\tau =\tau _{0}$, a simple pair of purely imaginary roots of Eq. (9) exists, all roots of Eq. (9) for $\tau \in (0,\tau _{0})$ have strictly negative real parts. Let $\lambda (\tau )=\mu (\tau ) +i\omega (\tau ) (\omega >0)$ be the root of the characteristic equation (9) near $\tau =\tau _{i}^{(k)}$ satisfying $\mu (\tau _{i}^{(k)})=0, \omega (\tau _{i}^{(k)})=\omega _{i}$. Substituting $\lambda (\tau )$ into Eq. (9) and taking the derivative with respect to $\tau$, we have

$$\begin{aligned} \frac{\textrm{d} \lambda }{\textrm{d} \tau }=\frac{X(\lambda )}{Y(\lambda )}, \end{aligned}$$

where

$$\begin{aligned} X(\lambda )&=\lambda (a_{5}\lambda ^{2\theta }+a_{6}\lambda ^{\theta }+a_{7})e^{-\lambda \tau }, \\ Y(\lambda )&=4\theta \lambda ^{4\theta -1}+3\theta a_{1}\lambda ^{3\theta -1}+2\theta a_{2}\lambda ^{2\theta -1}+\theta a_{3}\lambda ^{\theta -1}\\&\quad +\left[ 2\theta a_{5}\lambda ^{2\theta -1}+ \theta a_{6}\lambda ^{\theta -1}-\tau (a_{5}\lambda ^{2\theta }+a_{6}\lambda ^{\theta }+a_{7})\right] e^{-\lambda \tau }. \end{aligned}$$

Let $X_{1},X_{2},Y_{1},Y_{2}$ be the real and imaginary parts of $X(\lambda ),Y(\lambda )$, respectively. Then, we have

$$\begin{aligned} Re\left[ \frac{\textrm{d} \lambda }{\textrm{d} \tau } \right] \bigg \vert _{\tau =\tau _{i}^{(k)}}=\frac{X_{1}Y_{1}+X_{2}Y_{2}}{Y_{1}^{2}+Y_{2}^{2}}, \end{aligned}$$

where

$$\begin{aligned} X_{1}&=a_{5}\omega _{i} ^{2\theta +1}\sin (\omega _{i} \tau _{i}^{(k)} -\theta \pi )+a_{6}\omega _{i} ^{\theta +1}\sin \left( \omega _{i} \tau _{i}^{(k)} - \frac{\theta \pi }{2}\right) +a_{7}\omega _{i}\sin \omega _{i} \tau _{i}^{(k)} , \\ X_{2}&=a_{5}\omega _{i} ^{2\theta +1}\cos (\omega _{i} \tau _{i}^{(k)} -\theta \pi )+a_{6}\omega _{i} ^{\theta +1}\cos \left( \omega _{i} \tau _{i}^{(k)} - \frac{\theta \pi }{2}\right) +a_{7}\omega _{i}\cos \omega _{i} \tau _{i}^{(k)} , \\ Y_{1}&=4\theta \omega _{i} ^{4\theta -1}\sin 2\theta \pi +3\theta a_{1}\omega _{i} ^{3\theta -1}\sin \frac{3\theta \pi }{2}-\tau _{i}^{(k)}a_{5}\omega _{i} ^{2\theta }\cos (\omega _{i} \tau _{i}^{(k)} -\theta \pi )\\&\quad +2\theta \omega _{i} ^{2\theta -1}[a_{2}\sin \theta \pi -a_{5}\sin (\omega _{i} \tau _{i}^{(k)} -\theta \pi )] -\tau _{i}^{(k)}a_{6}\omega _{i} ^{\theta }\cos \left( \omega _{i}\tau _{i}^{(k)} -\frac{\theta \pi }{2}\right) \\&\quad +\theta \omega _{i} ^{\theta -1}\left[ a_{3}\sin \frac{\theta \pi }{2}-a_{6}\sin \left( \omega _{i} \tau _{i}^{(k)} -\frac{\theta \pi }{2}\right) \right] -\tau _{i}^{(k)}a_{7}\cos \omega _{i} \tau _{i}^{(k)} , \\ Y_{2}&=-4\theta \omega _{i} ^{4\theta -1}\cos 2\theta \pi -3\theta a_{1}\omega _{i} ^{3\theta -1}\cos \frac{3\theta \pi }{2}+\tau _{i}^{(k)} a_{5}\omega _{i} ^{2\theta }\sin (\omega _{i} \tau _{i}^{(k)} -\theta \pi )\\&\quad -2\theta \omega _{i} ^{2\theta -1}[a_{2}\cos \theta \pi +a_{5}\cos (\omega _{i} \tau _{i}^{(k)} -\theta \pi )] +\tau _{i}^{(k)} a_{6}\omega _{i} ^{\theta }\sin \left( \omega _{i} \tau _{i}^{(k)} -\frac{\theta \pi }{2}\right) \\&\quad -\theta \omega _{i} ^{\theta -1}\left[ a_{3}\cos \frac{\theta \pi }{2}+a_{6}\cos \left( \omega _{i} \tau _{i}^{(k)} -\frac{\theta \pi }{2}\right) \right] +\tau _{i}^{(k)} a_{7}\sin \omega _{i} \tau _{i}^{(k)}. \end{aligned}$$

Due to $Y_{1}^{2}+Y_{2}^{2}>0$, we have

$$\begin{aligned} sign\left\{ Re\left[ \frac{\textrm{d} \lambda }{\textrm{d} \tau } \right] \bigg \vert _{\tau =\tau _{i}^{(k)}} \right\} =sign\left\{ X_{1}Y_{1}+X_{2}Y_{2} \right\} . \end{aligned}$$

(16)

If (H2) $X_{1}Y_{1}+X_{2}Y_{2}\ne 0$ holds, then the transversality condition $Re\left[ \frac{\textrm{d} \lambda }{\textrm{d} \tau } \right] \vert _{\tau =\tau ^{(k)}_{i}}\ne 0$ holds.

To sum up, the following theorem can be obtained.

Theorem 2

For system (2), assume (H1) and (H2) hold.

• (i) If $\tau \in [0,\tau _{0})$, then the equilibrium O is locally asymptotically stable;

• (ii) If $\tau >\tau _{0}$, then system (2) undergoes Hopf bifurcation at O when $\tau =\tau _{0}$.

3 Stability and Hopf Bifurcation Analysis of System (3)

In this section, we obtain the conditions of the stability and the existence of Hopf bifurcation of system (3) applying the method of stability switching curves in [26].

We note that the equilibrium of system (3) is the same as that of system (2). The linearized system (3) at equilibrium O(0, 0, 0, 0) is given by

$$\begin{aligned} \left\{ \begin{aligned} D^{\theta }x_{1}(t)&=-k_{1}x_{1}(t)+\phi _{11}y_{1}(t-\sigma _{1})+\phi _{12}y_{2}(t-\sigma _{1})\\&\quad +\phi _{13}y_{3}(t-\sigma _{1}), \\ D^{\theta }y_{1}(t)&=-k_{2}y_{1}(t)+\varphi _{11}x_{1}(t-\sigma _{2}), \\ D^{\theta }y_{2}(t)&=-k_{3}y_{2}(t)+\varphi _{21}x_{1}(t-\sigma _{2}), \\ D^{\theta }y_{3}(t)&=\alpha [-k_{4}y_{3}(t)+\varphi _{31}x_{1}(t-\sigma _{2})]+\beta y_{3}(t-\sigma _{2}). \end{aligned} \right. \end{aligned}$$

(17)

For simplicity, let $\sigma _{1}+\sigma _{2}=\tau _{1},\sigma _{2}=\tau _{2}$, then the characteristic equation of system (17) is

$$\begin{aligned} D^{*}(\lambda ,\tau _{1},\tau _{2})=P_{0}(\lambda )+P_{1}(\lambda )e^{-\lambda \tau _{1}}+P_{2}(\lambda )e^{-\lambda \tau _{2}}+P_{3}(\lambda )e^{-\lambda (\tau _{1}+\tau _{2})}=0, \end{aligned}$$

(18)

where

$$\begin{aligned} P_{0}(\lambda )&=\lambda ^{4\theta }+c_{1}\lambda ^{3\theta }+c_{2}\lambda ^{2\theta }+c_{3}\lambda ^{\theta }+c_{4}, \\ P_{1}(\lambda )&=c_{5}\lambda ^{2\theta }+c_{6}\lambda ^{\theta }+c_{7}, \\ P_{2}(\lambda )&=c_{8}\lambda ^{3\theta }+c_{9}\lambda ^{2\theta }+c_{10}\lambda ^{\theta }+c_{11}, \\ P_{3}(\lambda )&=c_{12}\lambda ^{\theta }+c_{13}, \\ c_{1}&=k_{1}+k_{2}+k_{3}+\alpha k_{4}, \\ c_{2}&=k_{1}k_{2}+k_{1}k_{3}+\alpha k_{1}k_{4}+k_{2}k_{3}+\alpha k_{2}k_{4}+\alpha k_{3}k_{4}, \\ c_{3}&=k_{1}k_{2}k_{3}+\alpha k_{1}k_{2}k_{4}+\alpha k_{1}k_{3}k_{4}+\alpha k_{2}k_{3}k_{4}, \\ c_{4}&=\alpha k_{1}k_{2}k_{3}k_{4}, \\ c_{5}&=-\phi _{11}\varphi _{11}-\phi _{12}\varphi _{21}-\alpha \phi _{13}\varphi _{31}, \\ c_{6}&=-(k_{3}+\alpha k_{4})\phi _{11}\varphi _{11}-(k_{2}+\alpha k_{4})\phi _{12}\varphi _{21}-\alpha (k_{2}+k_{3})\phi _{13}\varphi _{31}, \\ c_{7}&=-\alpha k_{3}k_{4}\phi _{11}\varphi _{11}-\alpha k_{2}k_{4}\phi _{12}\varphi _{21}-\alpha k_{2}k_{3}\phi _{13}\varphi _{31}, \\ c_{8}&=-\beta , \\ c_{9}&=-\beta (k_{1}+k_{2}+k_{3}), \\ c_{10}&=-\beta (k_{1}k_{2}+k_{1}k_{3}+k_{2}k_{3}), \\ c_{11}&=-\beta k_{1}k_{2}k_{3}, \\ c_{12}&=\beta (\phi _{11}\varphi _{11}+\phi _{12}\varphi _{21}), \\ c_{13}&=\beta (k_{3}\phi _{11}\varphi _{11}+k_{2}\phi _{12}\varphi _{21}). \end{aligned}$$

When $\tau _{1}=\tau _{2}=0$, Eq. (18) can be transformed into the following form

$$\begin{aligned} \lambda ^{4\theta }+d_{1}\lambda ^{3\theta }+d_{2}\lambda ^{2\theta }+d_{3}\lambda ^{\theta }+d_{4}=0, \end{aligned}$$

(19)

where

$$\begin{aligned} d_{1}&=c_{1}+c_{8},\quad d_{2}=c_{2}+c_{5}+c_{9},\\ d_{3}&=c_{3}+c_{6}+c_{10}+c_{12},\quad d_{4}=c_{4}+c_{7}+c_{11}+c_{13}. \end{aligned}$$

Let (H3)   $d_{4}(d_{1}d_{2}d_{3}-d_{1} ^{2}d_{4}-d_{3}^{2})>0$, according to Lemma 1 and Routh-Hurwitz criterion, we have the following theorem.

Theorem 3

For $\tau _{1}=\tau _{2}=0$, if (H1) and (H3) hold, then the zero equilibrium of system (3) is locally asymptotically stable.

3.1 Stability Switching Curves

In this subsection, when $\tau _{1}>0,\tau _{2}>0$, and $\tau _{1}\ne \tau _{2}$, the stability of system (3) is discussed using the method in [26].

In order to guarantee that Eq. (18) is the characteristic equation of system (3), the following assumptions are necessary:

• (i) Let C be the set of complex numbers. Finite number of characteristic roots on $C_{+}:=\{\lambda \in C:Re \lambda >0\}$ under the condition

  $$\begin{aligned} deg(P_{0}(\lambda ))\ge max\left\{ deg(P_{1}(\lambda )),deg(P_{2}(\lambda )),deg(P_{3}(\lambda )) \right\} . \end{aligned}$$

• (ii) Zero frequency: $\lambda =0$ is not a characteristic root for $\tau _{1}$ and $\tau _{2}$, i.e.,

  $$\begin{aligned} P_{0}(0)+P_{1}(0)+P_{2}(0)+P_{3}(0)\ne 0. \end{aligned}$$

• (iii) The polynomials $P_{0},P_{1},P_{2}$ and $P_{3}$ have no common zeros, i.e., $P_{0},P_{1},P_{2}$ and $P_{3}$ are coprime polynomials.

• (iv) $P_{k}$’s satisfy

  $$\begin{aligned} \begin{aligned} \lim \limits _{\lambda \rightarrow \infty }\bigg (\bigg |\frac{P_{1}(\lambda )}{P_{0}(\lambda )} \bigg |+\bigg |\frac{P_{2}(\lambda )}{P_{0}(\lambda )} \bigg |+\bigg |\frac{P_{3}(\lambda )}{P_{0}(\lambda )} \bigg |\bigg )<1. \end{aligned} \end{aligned}$$

Next, we verify that Eq. (18) satisfies the above assumptions $(\hbox {i})$-$(\hbox {iv})$. According to the expression of $P_{0},P_{1},P_{2}$ and $P_{3}$, $(\hbox {i})$ is satisfied. $P_{0}(0)+P_{1}(0)+P_{2}(0)+P_{3}(0)=c_{4}+c_{7}+c_{11}+c_{13}=d_{4}\ne 0$, $(\hbox {ii})$ is true. If $(\hbox {iii})$ is violated, then Eq. (18) can be written as the product of another transcendental equation satisfying $(\hbox {iii})$ and $s(\lambda )$, where $s(\lambda )$ is a common factor of $P_{n}(\lambda ) (n=0,1,2,3)$.

For $(\hbox {iv})$ holds. Since

$$\begin{aligned} \begin{aligned}&\lim \limits _{\lambda \rightarrow \infty }(|\frac{c_{5}\lambda ^{2\theta }+c_{6}\lambda ^{\theta }+c_{7}}{\lambda ^{4\theta }+c_{1}\lambda ^{3\theta }+c_{2}\lambda ^{2\theta }+c_{3}\lambda ^{\theta }+c_{4}} |+|\frac{c_{8}\lambda ^{3\theta }+c_{9}\lambda ^{2\theta }+c_{10}\lambda ^{\theta }+c_{11}}{\lambda ^{4\theta }+c_{1}\lambda ^{3\theta }+c_{2}\lambda ^{2\theta }+c_{3}\lambda ^{\theta }+c_{4}} |\\&\quad +|\frac{c_{12}\lambda ^{\theta }+c_{13}}{\lambda ^{4\theta }+c_{1}\lambda ^{3\theta }+c_{2}\lambda ^{2\theta }+c_{3}\lambda ^{\theta }+c_{4}} |)=0<1. \end{aligned} \end{aligned}$$

To obtain stability switching curves, it is necessary to find purely imaginary roots of Eq. (18). We assume that $\lambda =\omega (\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})(\omega >0)$ is a pure imaginary root of $D^{*}(\lambda ,\tau _{1},\tau _{2})=0$. Substituting it into Eq. (18), we get

$$\begin{aligned} P_{0}(i\omega )+P_{1}(i\omega )e^{-i\omega \tau _{1}}+P_{2}(i\omega )e^{-i\omega \tau _{2}}+P_{3}(i\omega )e^{-i\omega (\tau _{1}+\tau _{2})}=0. \end{aligned}$$

(20)

Because $|e^{-i\omega \tau _{2}}|=1$, we have

$$\begin{aligned} |P_{0}+P_{1}e^{-i\omega \tau _{1}}|=|P_{2}+P_{3}e^{-i\omega \tau _{1}}|, \end{aligned}$$

which is equivalent to

$$\begin{aligned} (P_{0}+P_{1}e^{-i\omega \tau _{1}})({\overline{P}}_{0}+{\overline{P}}_{1}e^{i\omega \tau _{1}})=(P_{2}+P_{3}e^{-i\omega \tau _{1}})({\overline{P}}_{2}+{\overline{P}}_{3}e^{i\omega \tau _{1}}). \end{aligned}$$

(21)

By simplifying Eq. (21), we have

$$\begin{aligned} \begin{aligned}&|P_{0}|^{2}+|P_{1}|^{2}+2Re({P}_{0}{\overline{P}}_{1})\cos (\omega \tau _{1})-2Im({P}_{0}{\overline{P}}_{1})\sin (\omega \tau _{1}) \\&\quad =|P_{2}|^{2}+|P_{3}|^{2}+2Re({P}_{2}{\overline{P}}_{3})\cos (\omega \tau _{1})-2Im({P}_{2}{\overline{P}}_{3})\sin (\omega \tau _{1}). \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} \begin{aligned} |P_{0}|^{2}+|P_{1}|^{2}-|P_{2}|^{2}-|P_{3}|^{2}=2A_{1}(\omega )\cos (\omega \tau _{1})-2B_{1}(\omega )\sin (\omega \tau _{1}), \end{aligned} \end{aligned}$$

(22)

where $P_{n}=M_{n}+iN_{n} (n=0,1,2,3)$.

$$\begin{aligned} M_{0}&=\omega ^{4\theta }\cos 2\theta \pi +c_{1}\omega ^{3\theta }\cos \frac{3\theta \pi }{2}+c_{2}\omega ^{2\theta }\cos \theta \pi +c_{3}\omega ^{\theta }\cos \frac{\theta \pi }{2}+c_{4}, \\ N_{0}&=\omega ^{4\theta }\sin 2\theta \pi +c_{1}\omega ^{3\theta }\sin \frac{3\theta \pi }{2}+c_{2}\omega ^{2\theta }\sin \theta \pi +c_{3}\omega ^{\theta }\sin \frac{\theta \pi }{2}, \\ M_{1}&=c_{5}\omega ^{2\theta }\cos \theta \pi +c_{6}\omega ^{\theta }\cos \frac{\theta \pi }{2}+c_{7}, \\ N_{1}&=c_{5}\omega ^{2\theta }\sin \theta \pi +c_{6}\omega ^{\theta }\sin \frac{\theta \pi }{2}, \\ M_{2}&=c_{8}\omega ^{3\theta }\cos \frac{3\theta \pi }{2}+c_{9}\omega ^{2\theta }\cos \theta \pi +c_{10}\omega ^{\theta }\cos \frac{\theta \pi }{2}+c_{11}, \\ N_{2}&=c_{8}\omega ^{3\theta }\sin \frac{3\theta \pi }{2}+c_{9}\omega ^{2\theta }\sin \theta \pi +c_{10}\omega ^{\theta }\sin \frac{\theta \pi }{2}, \\ M_{3}&=c_{12}\omega ^{\theta }\cos \frac{\theta \pi }{2}+c_{13}, \\ N_{3}&=c_{12}\omega ^{\theta }\sin \frac{\theta \pi }{2}, \\ A_{1}(\omega )&=Re({P}_{2}{\overline{P}}_{3})-Re({P}_{0}{\overline{P}}_{1})\\&=M_{2}M_{3}+N_{2}N_{3}-M_{0}M_{1}-N_{0}N_{1}\\&=-c_{5}\omega ^{6\theta }\cos \theta \pi +\omega ^{5\theta }\left( -c_{6}\cos \frac{3\theta \pi }{2}-c_{1}c_{5}\cos \frac{\theta \pi }{2}\right) \\&\quad +\omega ^{4\theta }[(c_{8}c_{12}-c_{1}c_{6})\cos \theta \pi -c_{7}\cos 2\theta \pi -c_{2}c_{5}]\\&\quad +\omega ^{3\theta }\left[ (c_{9}c_{12}-c_{2}c_{6}-c_{3}c_{5})\cos \frac{\theta \pi }{2}+(c_{8}c_{13}-c_{1}c_{7})\cos \frac{3\theta \pi }{2}\right] \\&\quad +\omega ^{2\theta }[(c_{9}c_{13}-c_{2}c_{7}-c_{4}c_{5})\cos \theta \pi +c_{10}c_{12}-c_{3}c_{6}]\\&\quad +\omega ^{\theta }(c_{10}c_{13}+c_{11}c_{12}-c_{3}c_{7}-c_{4}c_{6})\cos \frac{\theta \pi }{2}+c_{11}c_{13}-c_{4}c_{7}, \\ B_{1}(\omega )&=Im({P}_{2}{\overline{P}}_{3})-Im({P}_{0}{\overline{P}}_{1})\\&=N_{2}M_{3}-M_{2}N_{3}-N_{0}M_{1}+M_{0}N_{1}\\&=-c_{5}\omega ^{6\theta }\sin \theta \pi +\omega ^{5\theta }\left( -c_{6}\sin \frac{3\theta \pi }{2}-c_{1}c_{5}\sin \frac{\theta \pi }{2}\right) \\&\quad +\omega ^{4\theta }[(c_{8}c_{12}-c_{1}c_{6})\sin \theta \pi -c_{7}\sin 2\theta \pi ]\\&\quad +\omega ^{3\theta }\left[ (c_{9}c_{12}-c_{2}c_{6}+c_{3}c_{5})\sin \frac{\theta \pi }{2}+(c_{8}c_{13}-c_{1}c_{7})\sin \frac{3\theta \pi }{2}\right] \\&\quad +\omega ^{2\theta }(c_{9}c_{13}+c_{4}c_{5}-c_{2}c_{7})\sin \theta \pi \\&\quad +\omega ^{\theta }(c_{10}c_{13}+c_{4}c_{6}-c_{11}c_{12}-c_{3}c_{7})\sin \frac{\theta \pi }{2}. \end{aligned}$$

According to Eq. (22), let $\psi _{1}(\omega )=\arg \left\{ {P}_{2}{\overline{P}}_{3}-{P}_{0}{\overline{P}}_{1} \right\}$, then

$$\begin{aligned} \begin{aligned} A_{1}(\omega )&=\sqrt{A_{1}(\omega )^{2}+B_{1}(\omega )^{2}}\cos (\psi _{1}(\omega )), \\ B_{1}(\omega )&=\sqrt{A_{1}(\omega )^{2}+B_{1}(\omega )^{2}}\sin (\psi _{1}(\omega )). \end{aligned} \end{aligned}$$

Meanwhile, Eq. (22) becomes

$$\begin{aligned} \begin{aligned} |P_{0}|^{2}+|P_{1}|^{2}-|P_{2}|^{2}-|P_{3}|^{2}=2\sqrt{A_{1}(\omega )^{2}+B_{1}(\omega )^{2}}\cos (\psi _{1}(\omega )+\omega \tau _{1}). \end{aligned} \end{aligned}$$

(23)

It is obvious that the existence of $\tau _{1}$ satisfying Eq. (23) is equivalent to the following inequalities being true.

$$\begin{aligned} \begin{aligned} ||P_{0}|^{2}+|P_{1}|^{2}-|P_{2}|^{2}-|P_{3}|^{2}|\le 2\sqrt{A_{1}^{2}+B_{1}^{2}}. \end{aligned} \end{aligned}$$

(24)

Denoting

$$\begin{aligned} \begin{aligned} F(\omega )&=(|P_{0}|^{2}+|P_{1}|^{2}-|P_{2}|^{2}-|P_{3}|^{2})^{2}-4(A_{1}^{2}+B_{1}^{2}) \\&=(\omega ^{8\theta }+q_{1}\omega ^{7\theta }+q_{2}\omega ^{6\theta }+q_{3}\omega ^{5\theta }+q_{4}\omega ^{4\theta }+q_{5}\omega ^{3\theta } \\&\quad +q_{6}\omega ^{2\theta }+q_{7}\omega ^{\theta }+q_{8})^{2}-4(A_{1}^{2}+B_{1}^{2}), \end{aligned} \end{aligned}$$

(25)

where

$$\begin{aligned} q_{1}&=2c_{1}\cos \frac{\theta \pi }{2},\quad q_{2}=2c_{2}\cos \theta \pi +c_{1}^{2}-c_{8}^{2},\\ q_{3}&=2c_{3}\cos \frac{3\theta \pi }{2}+2(c_{1}c_{2}-c_{8}c_{9})\cos \frac{\theta \pi }{2}, \\ q_{4}&=2c_{4}\cos 2\theta \pi +2(c_{1}c_{3}-c_{8}c_{10})\cos \theta \pi +c_{2}^{2}+c_{5}^{2}-c_{9}^{2},\\ q_{5}&=2(c_{1}c_{4}-c_{8}c_{11})\cos \frac{3\theta \pi }{2}+2(c_{2}c_{3}+c_{5}c_{6}-c_{9}c_{10})\cos \frac{\theta \pi }{2},\\ q_{6}&=2(c_{2}c_{4}+c_{5}c_{7}-c_{9}c_{11})\cos \theta \pi +c_{3}^{2}+c_{6}^{2}-c_{10}^{2}-c_{12}^{2},\\ q_{7}&=2(c_{3}c_{4}+c_{6}c_{7}-c_{10}c_{11}-c_{12}c_{13})\cos \frac{\theta \pi }{2},\\ q_{8}&=c_{4}^{2}+c_{7}^{2}-c_{11}^{2}-c_{13}^{2}, \end{aligned}$$

and we have the equivalent from of Eq. (24)

$$\begin{aligned} \begin{aligned} F(\omega )\le 0. \end{aligned} \end{aligned}$$

(26)

Thus, there is a purely imaginary root of the characteristic equation $D^{*}(\lambda ,\tau _{1},\tau _{2})=0$ if and only if $\omega$ satisfies Eq. (26). The set of $\omega \in {\mathbb {R}}_{+}$ satisfying Eq. (26) is denoted as $\Omega ^{1}=\{\omega \vert F(\omega )\le 0\}$.

Let $\theta _{1}(\omega )=\psi _{1}+\omega \tau _{1}$, then

$$\begin{aligned} \cos (\theta _{1}(\omega ))=\frac{|P_{0}|^{2}+|P_{1}|^{2}-|P_{2}|^{2}-|P_{3}|^{2}}{2\sqrt{A_{1}^{2}+B_{1}^{2}}}, \theta _{1}\in [0,\pi ], \end{aligned}$$

and

$$\begin{aligned} \tau _{1}=\tau ^{\pm }_{1,n_{1}}(\omega )=\frac{\pm \theta _{1}(\omega )-\psi _{1}(\omega )+2n_{1}\pi }{\omega },n_{1}\in {\mathbb {Z}}. \end{aligned}$$

(27)

For any $\omega \in \Omega _{1}$, we can calculate $\tau _{1}(\omega )$ according to Eq. (27). Substituting it into Eq. (20), and we have

$$\begin{aligned} \tau _{2}=\tau ^{\pm }_{2,n_{2}}(\omega )=\frac{1}{\omega }\arg \left\{ -\frac{P_{2}+P_{3}e^{-i\omega \tau _{1}^{\pm }}}{P_{0}+P_{1}e^{-i\omega \tau _{1}^{\pm }}} \right\} +2n_{2}\pi ,n_{2}\in {\mathbb {Z}}. \end{aligned}$$

(28)

Thus stability switching curves are

$$\begin{aligned} {\mathcal {T}}:=\left\{ (\tau _{1}(\omega ),\tau _{2}(\omega ))\in {\mathbb {R}}_{+}^{2}:\omega \in \Omega ^{1}\right\} . \end{aligned}$$

(29)

Similarly, we can calculate firstly the value of $\tau _{2}$, and then get the corresponding value of $\tau _{1}$, which gives

$$\begin{aligned} \tau _{2}=\tau ^{\pm }_{2,n_{2}}(\omega )=\frac{\pm \theta _{2}(\omega )-\psi _{2}(\omega )+2n_{2}\pi }{\omega },n_{2}\in {\mathbb {Z}}, \end{aligned}$$

(30)

where

$$\begin{aligned} \begin{aligned} \cos (\theta _{2}(\omega ))&=\frac{|P_{0}|^{2}-|P_{1}|^{2}+|P_{2}|^{2}-|P_{3}|^{2}}{2\sqrt{A_{1}^{2}+B_{1}^{2}}}, \theta _{2}\in [0,\pi ], \\ \psi _{2}(\omega )&=\arg \left\{ {P}_{1}{\overline{P}}_{3}-{P}_{0}{\overline{P}}_{2} \right\} , \\ A_{2}(\omega )&=\sqrt{A_{2}(\omega )^{2}+B_{2}(\omega )^{2}}\cos (\psi _{2}(\omega )), \\ B_{2}(\omega )&=\sqrt{A_{2}(\omega )^{2}+B_{2}(\omega )^{2}}\sin (\psi _{2}(\omega )), \\ A_{2}(\omega )&=Re({P}_{1}{\overline{P}}_{3})-Re({P}_{0}{\overline{P}}_{2}), \\ B_{2}(\omega )&=Im({P}_{1}{\overline{P}}_{3})-Im({P}_{0}{\overline{P}}_{2}), \end{aligned} \end{aligned}$$

with the conditions on $\omega$

$$\begin{aligned} \vert |P_{0}|^{2}-|P_{1}|^{2}+|P_{2}|^{2}-|P_{3}|^{2}\vert \le 2\sqrt{A_{2}^{2}+B_{2}^{2}}, \end{aligned}$$

(31)

which defines a region $\Omega ^{2}$.

Compare Eqs. (24) and (31), square the two equations separately, we may find that they are equivalent. Thus,

$$\begin{aligned} \Omega :=\Omega ^{1} =\Omega ^{2}. \end{aligned}$$

Generally, $\Omega$ is called the crossing set.

3.2 Crossing Direction

To discuss the stability change of system (3), we must take into account the direction in which the solution of $D^{*}(\lambda ,\tau _{1},\tau _{2})=0$ changes as it crosses the imaginary axis.

We assume that $(\tau _{1}^{*},\tau _{2}^{*})\in {\mathcal {T}}$, then there is an $\omega ^{*}>0$ such that $\pm i\omega ^{*}$ is a pair of imaginary roots of the characteristic equation (20). If $\frac{\partial D^{*}}{\partial \lambda }(iw^{*},\tau _{1}^{*},\tau _{2}^{*})\ne 0$, a pair of conjugate complex roots $\lambda (\tau _{1},\tau _{2})=\mu (\tau _{1},\tau _{2})\pm i\omega (\tau _{1},\tau _{2})$ of Eq. (20) can be obtained in some neighborhood of $(\tau _{1}^{*},\tau _{2}^{*})$, which satisfies $\mu (\tau _{1}^{*},\tau _{2}^{*})=0$ and $\omega (\tau _{1}^{*},\tau _{2}^{*})=\omega ^{*}$. Next, we will discuss the direction of $\lambda (\tau _{1},\tau _{2})$ crossing the imaginary axis as $(\tau _{1},\tau _{2})$ deviates from a curve in ${\mathcal {T}}$. As in [35], we call the direction of the curves ${\mathcal {T}}$ corresponding to increasing $\omega \in \Omega$ as the positive direction. And the region on the right-hand(left-hand) side as we move along the positive direction of the curves ${\mathcal {T}}$ is called the region on the right (left).

Since the tangent vector of ${\mathcal {T}}$ along the positive direction is ${\varvec{h_{1}}}=(\frac{\partial \tau _{1}}{\partial \omega },\frac{\partial \tau _{2}}{\partial \omega })$, by the relationship between the tangent vector and the normal vector, the normal vector to ${\mathcal {T}}$ pointing to the right-hand side of the positive direction is ${\varvec{h_{2}}}=(\frac{\partial \tau _{2}}{\partial \omega },-\frac{\partial \tau _{1}}{\partial \omega })$. We know that as $\mu$ increases from negative to positive, a pair of correspondingly conjugated complex roots of Eq. (20) cross the imaginary axis to the right. So $(\tau _{1},\tau _{2})$ moves along the direction ${\varvec{h_{3}}}=(\frac{\partial \tau _{1}}{\partial \mu },\frac{\partial \tau _{2}}{\partial \mu })$, we can conclude that the direction of a pair of pure imaginary roots of the characteristic equation (20) is determined by the sign of the inner product of ${\varvec{h_{2}}}$ and ${\varvec{h_{3}}}$, which is

$$\begin{aligned} \delta (\omega ):={\varvec{h_{2}}}\cdot {\varvec{h_{3}}}=\left( \frac{\partial \tau _{2}}{\partial \omega },-\frac{\partial \tau _{1}}{\partial \omega }\right) \cdot \left( \frac{\partial \tau _{1}}{\partial \mu },\frac{\partial \tau _{2}}{\partial \mu }\right) =\frac{\partial \tau _{1}}{\partial \mu } \frac{\partial \tau _{2}}{\partial \omega }-\frac{\partial \tau _{2}}{\partial \mu } \frac{\partial \tau _{1}}{\partial \omega }=\begin{vmatrix} \frac{\partial \tau _{1}}{\partial \mu }&\frac{\partial \tau _{1}}{\partial \omega }\\ \frac{\partial \tau _{2}}{\partial \mu }&\frac{\partial \tau _{2}}{\partial \omega } \end{vmatrix}. \end{aligned}$$

If $\delta (\omega )>0(\delta (\omega )<0)$, the characteristic equation has roots with positive real parts on the right (left)-hand region of the curves ${\mathcal {T}}$ as we move along the positive direction of stability switching curves ${\mathcal {T}}$.

For symbolic convenience, denote $\tau _{3}=\tau _{1}+\tau _{2}$. Considering $\tau _{1}$ and $\tau _{2}$ as functions of $\lambda =\mu +i\omega$, then by the implicit function theorem

$$\begin{aligned} \begin{pmatrix} U_{1} &{} U_{2}\\ V_{1} &{} V_{2} \end{pmatrix}\begin{pmatrix} \frac{\partial \tau _{1}}{\partial \mu } &{} \frac{\partial \tau _{1}}{\partial \omega }\\ \frac{\partial \tau _{2}}{\partial \mu } &{} \frac{\partial \tau _{2}}{\partial \omega } \end{pmatrix}=\begin{pmatrix} -U_{0} &{} V_{0}\\ -V_{0}&{} -U_{0}\end{pmatrix}, \end{aligned}$$

(32)

where

$$\begin{aligned} U_{0}&=\frac{\partial ReD^{*}(\lambda ,\tau _{1},\tau _{2})}{\partial \mu }\bigg \vert _{\lambda =i\omega ^{*}}\\&=Re\left\{ P_{0}^{{}'}(i\omega ^{*} ) +\sum _{j=1}^{3}(P_{j}^{{}'}(i\omega ^{*} )-\tau _{j}^{*}P_{j}(i\omega ^{*} ))e^{-i\omega ^{*} \tau _{j}^{*}}\right\} \\&=R_{0}+(R_{1}-\tau _{1}^{*}M_{1})\cos \omega ^{*}\tau _{1}^{*}+(S_{1}-\tau _{1}^{*}N_{1})\sin \omega ^{*}\tau _{1}^{*}\\&\quad +(R_{2}-\tau _{2}^{*}M_{2})\cos \omega ^{*}\tau _{2}^{*}+(S_{2}-\tau _{2}^{*}N_{2})\sin \omega ^{*}\tau _{2}^{*} +(R_{3}-(\tau _{1}^{*}+\tau _{2}^{*})M_{3})\cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})\\&\quad +(S_{3}-(\tau _{1}^{*}+\tau _{2}^{*})N_{3})\sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})\\&=4\theta \omega ^{*4\theta -1}\sin 2\theta \pi +\omega ^{*3\theta }\left[ -\tau _{2}^{*}c_{8}\cos \left( \omega ^{*}\tau _{2}^{*}-\frac{3\theta \pi }{2}\right) \right] \\&\quad +3\theta \omega ^{*3\theta -1}\left[ c_{1}\sin \frac{3\theta \pi }{2} -c_{8}\sin \left( \omega ^{*}\tau _{2}^{*}-\frac{3\theta \pi }{2}\right) \right] \\&\quad +\omega ^{*2\theta }\left[ -\tau _{1}^{*}c_{5}\cos (\omega ^{*}\tau _{1}^{*}-\theta \pi )-\tau _{2}^{*}c_{9}\cos (\omega ^{*}\tau _{2}^{*} -\theta \pi )\right] \\&\quad +2\theta \omega ^{*2\theta -1}[c_{2}\sin \theta \pi -c_{5}\sin (\omega ^{*}\tau _{1}^{*}-\theta \pi )-c_{9}\sin (\omega ^{*}\tau _{2}^{*}-\theta \pi )]\\&\quad +\omega ^{*\theta }\left[ -\tau _{1}^{*}c_{6}\cos \left( \omega ^{*}\tau _{1}^{*}-\frac{\theta \pi }{2}\right) -\tau _{2}^{*} c_{10}\cos \bigg (\omega ^{*} \tau _{2}^{*}-\frac{\theta \pi }{2}\bigg ) \right. \\&\left. \quad -(\tau _{1}^{*}+\tau _{2}^{*})c_{12} \cos \left( \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})-\frac{\theta \pi }{2}\right) \right] +\theta \omega ^{*\theta -1}\left[ c_{3}\sin \frac{\theta \pi }{2}-c_{6}\sin \left( \omega ^{*}\tau _{1}^{*}-\frac{\theta \pi }{2}\right) \right. \\&\left. \quad -c_{10} \sin \left( \omega ^{*}\tau _{2}^{*}-\frac{\theta \pi }{2}\right) -c_{12}\sin \left( \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})-\frac{\theta \pi }{2}\right) \right] -\tau _{1}^{*}c_{7}\cos \omega ^{*}\tau _{1}^{*}\\&\quad -\tau _{2}^{*}c_{11}\cos \omega ^{*}\tau _{2}^{*}-(\tau _{1}^{*}+\tau _{2}^{*})c_{13}\cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*}), \\ V_{0}&=\frac{\partial ImD^{*}(\lambda ,\tau _{1},\tau _{2})}{\partial \mu }\bigg \vert _{\lambda =i\omega ^{*}}\\&=Im\left\{ P_{0}^{{}'}(i\omega ^{*} ) +\sum _{j=1}^{3}(P_{j}^{{}'}(i\omega ^{*} )-\tau _{j}^{*}P_{j}(i\omega ^{*}))e^{-i\omega ^{*} \tau _{j}^{*}}\right\} \\&=S_{0}+(S_{1}-\tau _{1}^{*}N_{1})\cos \omega ^{*}\tau _{1}^{*}-(R_{1}-\tau _{1}^{*}M_{1})\sin \omega ^{*}\tau _{1}^{*}\\&\quad +(S_{2}-\tau _{2}^{*}N_{2}) \cos \omega ^{*}\tau _{2}^{*}-(R_{2}-\tau _{2}^{*}M_{2})\sin \omega ^{*}\tau _{2}^{*}\\&\quad +(S_{3}-(\tau _{1}^{*}+\tau _{2}^{*})N_{3})\cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})\\&\quad -(R_{3}-(\tau _{1}^{*}+\tau _{2}^{*})M_{3})\sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})\\&=-4\theta \omega ^{*4\theta -1}\cos 2\theta \pi +\omega ^{*3\theta }\left[ \tau _{2}^{*}c_{8}\sin \left( \omega ^{*}\tau _{2}^{*}-\frac{3\theta \pi }{2}\right) \right] \\&\quad -3\theta \omega ^{*3\theta -1} \left[ c_{1}\cos \frac{3\theta \pi }{2} +c_{8}\cos \left( \omega ^{*}\tau _{2}^{*}-\frac{3\theta \pi }{2}\right) \right] \\&\quad +\omega ^{*2\theta }[\tau _{1}^{*}c_{5}\sin (\omega ^{*}\tau _{1}^{*}-\theta \pi )+\tau _{2}^{*}c_{9}\sin (\omega ^{*}\tau _{2}^{*}-\theta \pi )]\\&\quad -2\theta \omega ^{*2\theta -1}[c_{2}\cos \theta \pi +c_{5}\cos (\omega ^{*}\tau _{1}^{*}-\theta \pi )+c_{9}\cos (\omega ^{*}\tau _{2}^{*}-\theta \pi )]\\&\quad +\omega ^{*\theta }\left[ \tau _{1}^{*}c_{6}\sin \left( \omega ^{*}\tau _{1}^{*}-\frac{\theta \pi }{2}\right) +\tau _{2}^{*}c_{10}\sin \left( \omega ^{*}\tau _{2}^{*}-\frac{\theta \pi }{2}\right) \right. \\&\left. \quad +(\tau _{1}^{*}+\tau _{2}^{*})c_{12}\sin \left( \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})-\frac{\theta \pi }{2}\right) \right] \\&\quad -\theta \omega ^{*\theta -1}\left[ c_{3}\cos \frac{\theta \pi }{2}+c_{6}\cos \left( \omega ^{*}\tau _{1}^{*}-\frac{\theta \pi }{2}\right) +c_{10}\cos \left( \omega ^{*}\tau _{2}^{*}-\frac{\theta \pi }{2}\right) \right. \\&\left. \quad +c_{12}\cos \left( \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})-\frac{\theta \pi }{2}\right) \right] \\&\quad +\tau _{1}^{*}c_{7}\sin \omega ^{*}\tau _{1}^{*}+\tau _{2}^{*}c_{11}\sin \omega ^{*}\tau _{2}^{*}+(\tau _{1}^{*}+\tau _{2}^{*})c_{13}\sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*}), \end{aligned}$$

where $P_{j}^{{}'}(\lambda )\vert _{\lambda =i\omega }=R_{j}+iS_{j}, j=0,1,2,3.$

$$\begin{aligned} R_{0}&=4\theta \omega ^{4\theta -1}\sin 2\theta \pi +3\theta c_{1}\omega ^{3\theta -1}\sin \frac{3\theta \pi }{2}+2\theta c_{2}\omega ^{2\theta -1}\sin \theta \pi \\&\quad +\theta c_{3}\omega ^{\theta -1}\sin \frac{\theta \pi }{2}, \\ S_{0}&=-4\theta \omega ^{4\theta -1}\cos 2\theta \pi -3\theta c_{1}\omega ^{3\theta -1}\cos \frac{3\theta \pi }{2}-2\theta c_{2}\omega ^{2\theta -1}\cos \theta \pi \\&\quad -\theta c_{3}\omega ^{\theta -1}\cos \frac{\theta \pi }{2}, \\ R_{1}&=2\theta c_{5}\omega ^{2\theta -1}\sin \theta \pi +\theta c_{6}\omega ^{\theta -1}\sin \frac{\theta \pi }{2}, \\ S_{1}&=-2\theta c_{5}\omega ^{2\theta -1}\cos \theta \pi -\theta c_{6}\omega ^{\theta -1}\cos \frac{\theta \pi }{2}, \\ R_{2}&=3\theta c_{8}\omega ^{3\theta -1}\sin \frac{3\theta \pi }{2}+2\theta c_{9}\omega ^{2\theta -1}\sin \theta \pi +\theta c_{10}\omega ^{\theta -1}\sin \frac{\theta \pi }{2}, \\ S_{2}&=-3\theta c_{8}\omega ^{3\theta -1}\cos \frac{3\theta \pi }{2}-2\theta c_{9}\omega ^{2\theta -1}\cos \theta \pi -\theta c_{10}\omega ^{\theta -1}\cos \frac{\theta \pi }{2}, \\ R_{3}&=\theta c_{12}\omega ^{\theta -1}\sin \frac{\theta \pi }{2},\quad S_{3}=-\theta c_{12}\omega ^{\theta -1}\cos \frac{\theta \pi }{2}. \end{aligned}$$

Similarly, one can verify that

$$\begin{aligned} \begin{aligned} \frac{\partial ReD^{*}(\lambda ,\tau _{1},\tau _{2})}{\partial \omega }\bigg \vert _{\lambda =i\omega ^{*}}&=-V_{0},\\ \frac{\partial ImD^{*}(\lambda ,\tau _{1},\tau _{2})}{\partial \omega }\bigg \vert _{\lambda =i\omega ^{*}}&=U_{0}. \end{aligned} \end{aligned}$$

(33)

We also have

$$\begin{aligned} U_{1}= & {} \frac{\partial ReD^{*}(\lambda ,\tau _{1},\tau _{2})}{\partial \tau _{1}}\bigg \vert _{\lambda =i\omega ^{*}}\\= & {} \omega ^{*}[N_{1}\cos \omega ^{*}\tau _{1}^{*}-M_{1}\sin \omega ^{*}\tau _{1}^{*}+N_{3}\cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})\\{} & {} \quad -M_{3}\sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})]\\= & {} -c_{5}\omega ^{*2\theta +1}\sin (\omega ^{*}\tau _{1}^{*}-\theta \pi )-\omega ^{*\theta +1}\left[ c_{6}\sin \left( \omega ^{*}\tau _{1}^{*}-\frac{\theta \pi }{2}\right) \right. \\{} & {} \left. \quad +c_{12}\sin \left( \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})-\frac{\theta \pi }{2}\right) \right] -c_{7}\omega ^{*} \sin \omega ^{*}\tau _{1}^{*}-c_{13}\omega ^{*} \sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*}), \\ V_{1}= & {} \frac{\partial ImD^{*}(\lambda ,\tau _{1},\tau _{2})}{\partial \tau _{1}}\bigg \vert _{\lambda =i\omega ^{*}}\\= & {} -\omega ^{*}[M_{1}\cos \omega ^{*}\tau _{1}^{*}+N_{1}\sin \omega ^{*}\tau _{1}^{*}+M_{3}\cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})\\{} & {} \quad +N_{3}\sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})]\\= & {} -c_{5}\omega ^{*2\theta +1}\cos (\omega ^{*}\tau _{1}^{*}-\theta \pi )-\omega ^{*\theta +1}\left[ c_{6}\cos \left( \omega ^{*}\tau _{1}^{*}-\frac{\theta \pi }{2}\right) \right. \\{} & {} \left. \quad +c_{12}\cos \left( \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})-\frac{\theta \pi }{2}\right) \right] -c_{7}\omega ^{*} \cos \omega ^{*}\tau _{1}^{*}-c_{13}\omega ^{*} \cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*}), \\ U_{2}= & {} \frac{\partial ReD^{*}(\lambda ,\tau _{1},\tau _{2})}{\partial \tau _{2}}\bigg \vert _{\lambda =i\omega ^{*}}\\= & {} \omega ^{*}[N_{2}\cos \omega ^{*}\tau _{2}^{*}-M_{2}\sin \omega ^{*}\tau _{2}^{*}+N_{3}\cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})\\{} & {} \quad -M_{3}\sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})]\\= & {} -c_{8}\omega ^{*3\theta +1}\sin \left( \omega ^{*}\tau _{2}^{*}-\frac{3\theta \pi }{2}\right) -c_{9}\omega ^{*2\theta +1}\sin (\omega ^{*}\tau _{2}^{*}-\theta \pi )\\{} & {} \quad -\omega ^{*\theta +1}\left[ c_{10}\sin \left( \omega ^{*}\tau _{2}^{*}-\frac{\theta \pi }{2}\right) +c_{12}\sin \left( \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})-\frac{\theta \pi }{2}\right) \right] \\{} & {} \quad -c_{11}\omega \sin \omega ^{*}\tau _{2}^{*}-c_{13}\omega ^{*} \sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*}), \\ V_{2}= & {} \frac{\partial ImD^{*}(\lambda ,\tau _{1},\tau _{2})}{\partial \tau _{2}}\bigg \vert _{\lambda =i\omega ^{*}}\\= & {} -\omega ^{*}[M_{2}\cos \omega ^{*}\tau _{2}^{*}+N_{2}\sin \omega ^{*}\tau _{2}^{*}+M_{3}\cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})\\{} & {} \quad +N_{3}\sin \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})]\\= & {} -c_{8}\omega ^{*3\theta +1}\cos \left( \omega ^{*}\tau _{2}^{*}-\frac{3\theta \pi }{2}\right) -c_{9}\omega ^{*2\theta +1}\cos (\omega ^{*}\tau _{2}^{*}-\theta \pi )\\{} & {} \quad -\omega ^{*\theta +1}\left[ c_{10}\cos \left( \omega ^{*}\tau _{2}^{*}-\frac{\theta \pi }{2}\right) +c_{12}\cos \left( \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*})-\frac{\theta \pi }{2}\right) \right] \\{} & {} \quad -c_{11}\omega ^{*} \cos \omega ^{*}\tau _{2}^{*}-c_{13}\omega ^{*} \cos \omega ^{*}(\tau _{1}^{*}+\tau _{2}^{*}). \end{aligned}$$

By the implicit function theory, as long as

(H4) $det\begin{pmatrix} U_{1} &{}U_{2} \\ V_{1} &{} V_{2} \end{pmatrix}=U_{1}V_{2}-U_{2}V_{1}\ne 0,$

we have

$$\begin{aligned} \Delta (\omega ):=\begin{pmatrix} \frac{\partial \tau _{1}}{\partial \mu } &{} \frac{\partial \tau _{1}}{\partial \omega }\\ \frac{\partial \tau _{2}}{\partial \mu } &{} \frac{\partial \tau _{2}}{\partial \omega } \end{pmatrix}\bigg \vert _{\mu =0,\omega \in \Omega }=\begin{pmatrix} U_{1} &{} U_{2}\\ V_{1} &{} V_{2} \end{pmatrix}^{-1}\begin{pmatrix} -U_{0} &{} V_{0}\\ -V_{0}&{} -U_{0}\end{pmatrix}. \end{aligned}$$

(34)

Let

$$\begin{aligned} \delta (\omega )=det(\Delta (\omega ))=\begin{vmatrix} U_{1}&U_{2}\\ V_{1}&V_{2} \end{vmatrix}^{-1}\begin{vmatrix} -U_{0}&V_{0}\\ -V_{0}&-U_{0}\end{vmatrix}. \end{aligned}$$

(35)

we can give the following theorem.

Theorem 4

[36] For $(\tau _{1},\tau _{2} )=(\tau _{1}^{*},\tau _{2}^{*})\in {\mathcal {T}}$, then $D^{*}(\lambda ,\tau _{1},\tau _{2})=0$ has a pair of purely imaginary roots $\lambda =\pm i\omega ^{*}(\omega ^{*}>0)$. If $\frac{\partial D^{*}}{\partial \lambda }(i\omega ^{*},\tau _{1}^{*}, \tau _{2}^{*})\ne 0$, then there is a pair of conjugate complex roots $\lambda =\lambda (\tau _{1},\tau _{2})=\mu \pm i\omega (\omega >0)$ in some near of $(\tau _{1}^{*},\tau _{2}^{*})$, which pass through the imaginary axis at $\omega =\omega ^{*}$ and the crossing direction is determined by

$$\begin{aligned} \begin{aligned} \delta (\omega ^{*})=\pm sign(\omega ^{*2}|P_{2}\overline{P_{3}}-P_{0}\overline{P_{1}}|\sin \psi _{1}). \end{aligned} \end{aligned}$$

(36)

If $sign(\delta (\omega ^{*}))>0$, then a pair of pure imaginary roots of the characteristic equation $D^{*}(\lambda ,\tau _{1},\tau _{2})=0$ crosses the imaginary axis from the left to the right; if $sign(\delta (\omega ^{*}))<0$, the direction of crossing the imaginary axis is just the opposite.

Proof

Since

$$\begin{aligned} det\begin{pmatrix} -U_{0} &{} V_{0}\\ -V_{0} &{} -U_{0} \end{pmatrix}=U_{0}^{2}+V_{0}^{2}\ge 0, \end{aligned}$$

(37)

we have

$$\begin{aligned} sign (\delta (\omega ) )=sign\left\{ U_{1}V_{2}- U_{2}V_{1} \right\} . \end{aligned}$$

(38)

For $\frac{\partial D^{*}}{\partial \lambda }(iw^{*},\tau _{1}^{*},\tau _{2}^{*})\ne 0$, it can be deduced that either $U_{0}\ne 0$ or $V_{0}\ne 0$. For any $(\tau _{1},\tau _{2} )\in {\mathcal {T}}$, we get

$$\begin{aligned} P_{2}(i\omega )e^{i\omega (\tau _{1}-\tau _{2})}=-P_{0}(i\omega )e^{i\omega \tau _{1}}-P_{1}(i\omega )-P_{3}(i\omega )e^{-i\omega \tau _{2}}. \end{aligned}$$

(39)

So we can get that

$$\begin{aligned} \begin{aligned} U_{1}V_{2}- U_{2}V_{1}&=Im\left\{ \overline{\frac{\partial D^{*}(i\omega ,\tau _{1},\tau _{2} )}{\partial \tau _{1}}} \cdot \frac{\partial D^{*}(i\omega ,\tau _{1},\tau _{2} )}{\partial \tau _{2}}\right\} \\ \\ {}&=\omega ^{2}Im\left\{ (P_{2}\overline{P_{3}}-P_{0}\overline{P_{1}})e^{i\omega \tau _{1}^{\pm }} \right\} \\&=\omega ^{2}Im\left\{ |P_{2}\overline{P_{3}}-P_{0}\overline{P_{1}}\vert e^{i\phi _{1}}e^{i\omega \tau _{1}^{\pm }}\right\} \\&=\pm \omega ^{2} |P_{2}\overline{P_{3}}-P_{0}\overline{P_{1}}|\sin \psi _{1}, \end{aligned} \end{aligned}$$

which completes the proof. $\square$

3.3 Hopf Bifurcation

Derivating Eq. (18) on $\tau _{1}$, we can obtain that

$$\begin{aligned} \begin{aligned}&\left[ {P}'_{0}(\lambda )+{P}'_{1}(\lambda )e^{-\lambda \tau _{1}}-\tau _{1}P_{1}(\lambda )e^{-\lambda \tau _{1}} +{P}'_{2}(\lambda )e^{-\lambda \tau _{2}}-\tau _{2}P_{2}(\lambda )e^{-\lambda \tau _{2}} \right. \\&\left. \quad +{P}'_{3}(\lambda )e^{-\lambda (\tau _{1}+\tau _{2})}-(\tau _{1}+\tau _{2})P_{3}(\lambda )e^{-\lambda (\tau _{1}+\tau _{2})}\right] \frac{\textrm{d} \lambda }{\textrm{d}\tau _{1}}-\left[ \lambda P_{2}(\lambda )e^{-\lambda \tau _{2}}\right. \\&\left. \quad +\lambda P_{3} e^{-\lambda (\tau _{1}+\tau _{2})}\right] \frac{\textrm{d} \tau _{2}}{\textrm{d}\tau _{1}}-\lambda P_{1}(\lambda )e^{-\lambda \tau _{1}}-\lambda P_{3}(\lambda )e^{-\lambda (\tau _{1}+\tau _{2})}=0, \end{aligned} \end{aligned}$$

(40)

where ${P}'_{i}(\lambda )$ is the derivatives of $P_{i}(\lambda )(i=0,1,2,3)$.

According to Eq. (20), the relationship between $\tau _{1}$ and $\tau _{2}$ can be derived as follows

$$\begin{aligned} \begin{aligned} \tau _{2}(\tau _{1})=\frac{ln(-\frac{P_{2}e^{\lambda \tau _{1}}+P_{3}}{P_{0}e^{\lambda \tau _{1}}+P_{1}})}{\lambda }. \end{aligned} \end{aligned}$$

(41)

By Eqs. (40) and (41), we can get that

$$\begin{aligned} \bigg [\frac{\textrm{d} \lambda }{\textrm{d}\tau _{1}}\bigg ]^{-1}=\frac{Z}{W}+\frac{{P}'_{1}}{\lambda P_{1}}-\frac{\tau _{1}}{\lambda }, \end{aligned}$$

(42)

where

$$\begin{aligned} \begin{aligned} Z&={P}'_{0}P_1P_{3}+({P}'_{0}P_{1}P_{2}+P_{0}{P}'_{0}P_{3})e^{\lambda \tau _{1}}+P_{0}{P}'_{0}P_{2}e^{2\lambda \tau _{1}}\\&\quad +[-(\tau _{1}+2\tau _{2})P_{1}P_{2}P_{3}-(\tau _{1}+\tau _{2}){P}_{0}P_{3}^{2}+P_{1}{P}'_{2}P_{3}\\&\quad +P_{1}P_{2}{P}'_{3}+P_{0}P_{3}{P}'_{3}] e^{-\lambda \tau _{2}}+[-(\tau _{1}+2\tau _{2})P_{0}P_{2}P_{3}-(\tau _{1}+\tau _{2}){P}_{1}P_{2}^{2}\\ {}&\quad +P_{1}P_{2}{P}'_{2}+P_{0}{P}'_{2}P_{3}\\&\quad +P_{0}P_{2}{P}'_{3}]e^{\lambda (\tau _{1}-\tau _{2})}+(P_{0}P_{2}{P}'_{2}-\tau _{2}{P}_{0}P_{2}^{2})e^{\lambda (2\tau _{1}-\tau _{2})}+(P_{1}P_{3}{P}'_{3}\\&\quad -\tau _{2}{P}_{1}P_{3}^{2})e^{-\lambda (\tau _{1}+\tau _{2})}, \\ W&=\lambda (P_{0}P_{1}P_{3}+P_{1}^{2}P_{2}+P_{1}^{2}P_{3}e^{-\lambda \tau _{1}}+P_{0}P_{1}P_{2}e^{\lambda \tau _{1}}\\&\quad +2P_{1}P_{2}P_{3}e^{-\lambda \tau _{2}}+{P}_{1}P_{2}^{2} e^{\lambda (\tau _{1}-\tau _{2})}+{P}_{1}P_{3}^{2}e^{-\lambda (\tau _{1}+\tau _{2})}). \end{aligned} \end{aligned}$$

Let $Z_{1}$ and $Z_{2}$ be the real and imaginary parts of Z, respectively. $W_{1}$ and $W_{2}$ are the real and imaginary parts of W. $P_{n}=M_{n}+iN_{n} (n=0,1,2,3)$ and $P_{j}^{{}'}(\lambda )=R_{j}+iS_{j} (j=0,1,2,3)$ as previously defined. If $\lambda =\omega _{0}(\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})$ is the root of Eq. (20) and $\tau _{1}=\tau _{1}^{*}$ is a bifurcation point. Then, by calculation, the following formula can be acquire

$$\begin{aligned} Re\bigg [\frac{\textrm{d} \lambda }{\textrm{d} \tau _{1}}\bigg ]^{-1}\bigg \vert _{\omega =\omega _{0},\tau _{1}=\tau _{1}^{*}}=\frac{Z_{1}W_{1}+Z_{2}W_{2}}{W_{1}^{2}+W_{2}^{2}}+\frac{R_{1}N_{1}-S_{1}M_{1}}{\omega _{0}(M_{1}^{2}+N_{1}^{2})}, \end{aligned}$$

(43)

where

$$\begin{aligned} Z_{1}&=L_{1}\cos \omega _{0}\tau _{1}^{*}-L_{2}\sin \omega _{0}\tau _{1}^{*}+L_{3}\cos 2\omega _{0}\tau _{1}^{*}-L_{4}\sin 2\omega _{0}\tau _{1}^{*}+L_{5}\cos \omega _{0}\tau _{2}^{*}\\&\quad +L_{6}\sin \omega _{0}\tau _{2}^{*}+L_{7}\cos \omega _{0}(\tau _{1}^{*}-\tau _{2}^{*})+L_{8}\sin \omega _{0}(\tau _{1}^{*}-\tau _{2}^{*})+L_{9}, \\ Z_{2}&=L_{1}\sin \omega _{0}\tau _{1}^{*}+L_{2}\cos \omega _{0}\tau _{1}^{*}+L_{3}\sin 2\omega _{0}\tau _{1}^{*}+L_{4}\cos 2\omega _{0}\tau _{1}^{*}-L_{5}\sin \omega _{0}\tau _{2}^{*}\\&\quad +L_{6}\cos \omega _{0}\tau _{2}^{*}-L_{7}\sin \omega _{0}(\tau _{1}^{*}-\tau _{2}^{*})+L_{8}\cos \omega _{0}(\tau _{1}^{*}-\tau _{2}^{*})+L_{10}, \\ W_{1}&=-\omega _{0}(2M_{1}M_{2}N_{1}+M_{1}^{2}N_{2}-N_{1}^{2}N_{2}+M_{0}M_{3}N_{1}+M_{1}M_{3}N_{0})\\&\quad +\omega _{0}(-M_{0}M_{1}N_{2}+N_{0}N_{1}N_{2}-M_{0}M_{2}N_{1}-M_{1}M_{2}N_{0}+2M_{1}M_{3}N_{1})\cos \omega _{0}\tau _{1}^{*}\\&\quad -\omega _{0}(M_{0}M_{1}M_{2}-N_{0}N_{1}M_{2}-M_{0}N_{1}N_{2}-M_{1}N_{0}N_{2}-M_{1}^{2}M_{3}\\&\quad +M_{3}N_{1}^{2})\sin \omega _{0}\tau _{1}^{*}-2\omega _{0}(M_{2}M_{3}N_{1}+M_{1}M_{3}N_{2})\cos \omega _{0}\tau _{2}^{*}\\&\quad +2\omega _{0}(M_{1}M_{2}M_{3}-M_{3}N_{1}N_{2})\sin \omega _{0}\tau _{2}^{*}+\omega _{0}(-2M_{1}M_{2}N_{2}-M_{1}^{2}N_{1}\\&\quad +N_{1}N_{2}^{2})\cos \omega _{0}(\tau _{1}^{*}-\tau _{2}^{*})-\omega _{0}(-2M_{2}N_{1}N_{2}+M_{1}M_{2}^{2}-M_{1}N_{2}^{2})\sin \omega _{0}(\tau _{1}^{*}-\tau _{2}^{*})\\&\quad -\omega _{0}M_{3}^{2}N_{1}\cos \omega _{0}(\tau _{1}^{*}+\tau _{2}^{*})+\omega _{0}M_{1}M_{3}^{2}\sin \omega _{0}(\tau _{1}^{*}+\tau _{2}^{*}), \\ W_{2}&=\omega _{0}(-2M_{1}N_{1}N_{2}+M_{1}^{2}M_{2}-N_{1}^{2}M_{2}+M_{0}M_{1}M_{3}-M_{3}N_{0}N_{1})\\&\quad +\omega _{0}(-M_{0}M_{1}N_{2}+N_{0}N_{1}N_{2}-M_{0}M_{2}N_{1}-M_{1}M_{2}N_{0}-2M_{1}M_{3}N_{1})\sin \omega _{0}\tau _{1}^{*}\\&\quad +\omega _{0}(M_{0}M_{1}M_{2}-N_{0}N_{1}M_{2}-M_{0}N_{1}N_{2}-M_{1}N_{0}N_{2}+M_{1}^{2}M_{3}\\&\quad -M_{3}N_{1}^{2})\cos \omega _{0}\tau _{1}^{*}+2\omega _{0}(M_{2}M_{3}N_{1}+M_{1}M_{3}N_{2})\sin \omega _{0}\tau _{2}^{*}\\&\quad +2\omega _{0}(M_{1}M_{2}M_{3}-M_{3}N_{1}N_{2})\cos \omega _{0}\tau _{2}^{*}+\omega _{0}(-2M_{1}M_{2}N_{2}-M_{1}^{2}N_{1}\\&\quad +N_{1}N_{2}^{2})\sin \omega _{0}(\tau _{1}^{*}-\tau _{2}^{*})+\omega _{0}(-2M_{2}N_{1}N_{2}+M_{1}M_{2}^{2}-M_{1}N_{2}^{2})\cos \omega _{0}(\tau _{1}^{*}-\tau _{2}^{*})\\&\quad +\omega _{0}M_{3}^{2}N_{1}\sin \omega _{0}(\tau _{1}^{*}+\tau _{2}^{*})+\omega _{0}M_{1}M_{3}^{2}\cos \omega _{0}(\tau _{1}^{*}+\tau _{2}^{*}), \\ L_{1}&=R_{0}M_{1}M_{2}-R_{0}N_{1}N_{2}-S_{0}N_{1}M_{2}+S_{0}M_{1}N_{2}+R_{0}M_{0}M_{3}-R_{0}N_{0}N_{3}\\&\quad -S_{0}N_{0}M_{3}+S_{0}M_{0}N_{3}, \\ L_{2}&=R_{0}M_{1}N_{2}+R_{0}M_{1}M_{2}-S_{0}N_{1}N_{2}+S_{0}M_{1}M_{2}+R_{0}M_{0}N_{3}+R_{0}M_{0}M_{3}\\&\quad -S_{0}N_{0}N_{3}+S_{0}M_{0}M_{3}, \\ L_{3}&=R_{0}M_{0}M_{2}-R_{0}N_{0}N_{2}-S_{0}N_{0}M_{2}+S_{0}M_{0}N_{2}, \\ L_{4}&=R_{0}M_{0}N_{2}+R_{0}M_{0}M_{2}-S_{0}N_{0}N_{2}+S_{0}M_{0}M_{2}, \\ L_{5}&=-(M_{1}M_{2}M_{3}-N_{1}N_{2}M_{3}-N_{1}M_{2}N_{3}+M_{1}N_{2}N_{3})(\tau _{1}^{*}+2\tau _{2}^{*})\\&\quad -(M_{0}M_{3}^{2}-2N_{0}N_{3}M_{3}+M_{0}N_{3}^{2})(\tau _{1}^{*}+\tau _{2}^{*})\\&\quad +M_{1}R_{2}M_{3}-N_{1}S_{2}M_{3}-N_{1}R_{2}N_{3}+M_{1}S_{2}N_{3}+M_{1}M_{2}R_{3}-N_{1}M_{2}S_{3}\\&\quad -N_{1}N_{2}R_{3}+M_{1}N_{2}S_{3}+M_{0}M_{3}R_{3}-N_{0}M_{3}S_{3}-N_{0}N_{3}R_{3}-M_{0}N_{3}S_{3}, \\ L_{6}&=-(M_{1}N_{2}M_{3}+M_{1}M_{2}M_{3}-N_{1}N_{2}N_{3}+M_{1}M_{2}N_{3})(\tau _{1}^{*}+2\tau _{2}^{*})\\&\quad -(M_{0}M_{3}^{2}+2M_{0}M_{3}N_{3}-N_{0}N_{3}^{2})(\tau _{1}^{*}+\tau _{2}^{*})\\&\quad +M_{1}S_{2}M_{3}+M_{1}R_{2}M_{3}-N_{1}S_{2}N_{3}+M_{1}R_{2}N_{3}+M_{1}M_{2}S_{3}+M_{1}M_{2}R_{3}\\&\quad -N_{1}N_{2}S_{3}+M_{1}N_{2}R_{3}+M_{0}M_{3}S_{3}+M_{0}M_{3}R_{3}-N_{0}N_{3}S_{3}+M_{0}N_{3}R_{3}, \\ L_{7}&=-(M_{1}M_{2}^{2}-2N_{1}M_{2}N_{2}+M_{1}N_{2}^{2})(\tau _{1}^{*}+2\tau _{2}^{*})\\&\quad -(M_{0}M_{2}M_{3}-N_{0}M_{2}N_{3}-N_{0}N_{2}M_{3}+M_{0}N_{2}N_{3})(\tau _{1}^{*}+\tau _{2}^{*})\\&\quad +M_{1}M_{2}R_{2}-N_{1}M_{2}S_{2}-N_{1}N_{2}R_{2}+M_{1}N_{2}S_{2}+M_{0}R_{2}M_{3}-N_{0}S_{2}M_{3}\\&\quad -N_{0}R_{2}N_{3}+M_{0}S_{2}N_{3}, \\ L_{8}&=-(M_{1}M_{2}^{2}+2M_{1}M_{2}N_{2}-N_{1}N_{2}^{2})(\tau _{1}^{*}+2\tau _{2}^{*})\\&\quad -(M_{0}M_{2}N_{3}+M_{0}M_{2}M_{3}-N_{0}N_{2}N_{3}-M_{0}N_{2}M_{3})(\tau _{1}^{*}+\tau _{2}^{*})\\&\quad +M_{1}M_{2}S_{2}+M_{1}M_{2}R_{2}-N_{1}N_{2}S_{2}+M_{1}N_{2}R_{2}+M_{0}S_{2}M_{3}+M_{0}R_{2}M_{3}\\&\quad -N_{0}S_{2}N_{3}+M_{0}R_{2}N_{3}, \\ L_{9}&=M_{0}M_{2}R_{3}-N_{0}M_{2}S_{3}-N_{0}N_{2}R_{3}+M_{0}N_{2}S_{3}, \\ L_{10}&=M_{0}M_{2}S_{3}+M_{0}M_{2}R_{3}-N_{0}N_{2}S_{3}+M_{0}N_{2}R_{3}. \end{aligned}$$

Similarly, we make the following assumption

(H5) $Re[\frac{\textrm{d} \lambda }{\textrm{d} \tau _{1}}]^{-1}\vert _{\omega =\omega _{0},\tau _{1}=\tau _{1}^{*}}\ne 0.$

Based on the above analysis, the following theorem holds.

Theorem 5

Assume (H1),(H3), (H4) and (H5) hold.

• (i) If $(\tau _{1},\tau _{2})\in {\mathcal {T}}$, then system (3) has a locally asymptotically stable equilibrium O;

• (ii) If $(\tau _{1},\tau _{2})$ crosses stability switching curves ${\mathcal {T}}$, then system (3) undergoes Hopf bifurcation at O.

4 Numerical Simulation

In this section, we consider the following system:

$$\begin{aligned} \left\{ \begin{aligned} D^{\theta }x_{1}(t)&=-2.2x_{1}(t)+1.5f_{11}(y_{1}(t-\sigma _{1}))-1.5f_{12}(y_{2}(t-\sigma _{1}))\\&\quad +1.5f_{13}(y_{3}(t-\sigma _{1})), \\ D^{\theta }y_{1}(t)&=-2y_{1}(t)-1.4g_{11}(x_{1}(t-\sigma _{2})), \\ D^{\theta }y_{2}(t)&=-2y_{2}(t)+0.1g_{21}(x_{1}(t-\sigma _{2})), \\ D^{\theta }y_{3}(t)&=\alpha \left[ -2y_{3}(t)-1.5g_{31}(x_{1}(t-\sigma _{2})) \right] +\beta y_{3}(t-\sigma _{2}), \end{aligned} \right. \end{aligned}$$

(44)

where $f_{ji}(\cdot )=g_{ij}(\cdot )=\tanh (\cdot )$, $\theta =0.98$.

When $\alpha =1$, $\beta =0$, system (44) corresponds to system (2), which is discussed in two cases.

• (i) When $\sigma _{1}=\sigma _{2}=0$, by calculation, we have $D_{1}=8.2>0$, $D_{2}=191.14>0$ and $D_{3}=7621.992>0, D_{4} =271342.92>0,$ it is easy to validate that the Lemma 1 and Theorem 1 hold. Then, O is locally asymptotically stable (see Fig. 1).

• (ii) When $\sigma _{1}+\sigma _{2}=\tau \ne 0$, from the definition of $G(\omega )$, we have

  $$\begin{aligned} G(\omega )&=\omega ^{8\theta }+16.4\omega ^{7\theta }+117.56\omega ^{6\theta }+481.707\omega ^{5\theta }+1213.132\omega ^{4\theta } \\&\quad +1857.194\omega ^{3\theta }+1583.354\omega ^{2\theta }+562.677\omega ^{\theta }-14.24. \end{aligned}$$

From Eqs. (14) and (15), it can be calculated that $\omega _{0}=0.25$ and $\tau _{0}=11.59$. Then according to the Theorem 2, it can be concluded that system (44) is locally asymptotically stable when $\tau =9<\tau _{0}$ at O. System (44) exhibits Hopf bifurcation at the original equilibrium when $\tau =13>\tau _{0}$ (see Figs. 2, 3).

Fig. 1

The original equilibrium of system (44) with initial values (0.1, 0.1, 0.1, 0.1) is locally asymptotically stable when $\sigma _{1}=\sigma _{2}=0$ and $\alpha =1, \beta =0$

Fig. 2

The original equilibrium of system (44) with initial values (0.1, 0.1, 0.1, 0.1) is locally asymptotically stable when $\tau =9<\tau _{0}=11.59$ and $\alpha =1, \beta =0$

Fig. 3

System (44) with initial values (0.1, 0.1, 0.1, 0.1) undergoes Hopf bifurcation when $\tau =13>\tau _{0}=11.59$ and $\alpha =1, \beta =0$

When $\alpha \ne 0,\beta \ne 0$, system (44) corresponds to system (3). Let $\sigma _{1}+\sigma _{2}=\tau _{1},\sigma _{2}=\tau _{2}$ and $\alpha =0.2$, $\beta =-0.65$. It can be discussed in the following two cases.

$(\hbox {i})$ When $\tau _{1}=\tau _{2}=0$, we can calculate $d_{4}(d_{1}d_{2}d_{3}-d_{1} ^{2}d_{4}-d_{3}^{2} )=134.88>0$, (H3) holds. Then, O is locally asymptotically stable according to Theorem 3 (see Fig. 4).

$(\hbox {ii})$ When $\tau _{1}>0,\tau _{2}>0$ and $\tau _{1}\ne \tau _{2}$, from the definition of $F(\omega )$, we have

$$\begin{aligned} F(\omega )&=\omega ^{16\theta }+0.8292\omega ^{15\theta }+25.448\omega ^{14\theta }+17.582\omega ^{13\theta }+251.35\omega ^{12\theta } \\&\quad +139.25\omega ^{11\theta }+1183.7\omega ^{10\theta }+491.73\omega ^{9\theta }+2529.9\omega ^{8\theta }+670.14\omega ^{7\theta } \\&\quad +1252.4\omega ^{6\theta }-35.908\omega ^{5\theta }-2470.3\omega ^{4\theta }-437.16\omega ^{3\theta }-1438.1\omega ^{2\theta } \\&\quad -2.508\omega ^{\theta }+187.66. \end{aligned}$$

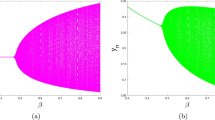
The graph of $F(\omega )$ is shown in Fig. 5 and the crossing set as $\Omega =(0.2737,0.8512)$. When $\omega \in \Omega$, according to the characteristic equation, stability switching curves are calculated (see Fig. 6).

We take points $P_{1}$, $P_{2}$ and $P_{3}$ in stability switching curves (see Fig. 6). When $(\tau _{1},\tau _{2})=(3,1)$, system (44) is locally asymptotically stable at O (see Fig. 7). System (44) occurs periodic solution when $(\tau _{1},\tau _{2})=(3,4)$ (see Fig. 8). When $(\tau _{1},\tau _{2})=(13,1)$, it is found that system (44) is still locally asymptotically stable at O as the increase of the value of $\tau _{1}$ (see Figs. 7, 9).

In order to highlight the control effect, we take different parameter values for $\alpha$ and $\beta$ to compare. Let $\beta =-0.65$ and take $\alpha =0.2,0.4$, its corresponding crossing sets are obtained as $\Omega =(0.2737,0.8512),\Omega =(0,0.9536)$, respectively. System (44) is locally asymptotically stable at O when $(\tau _{1},\tau _{2})=(3,4)$ and $\alpha =0.4$ (see Fig. 10). With the increase of $\alpha$, it can be seen from Figs. 8 and 10 that the occurrence of Hopf bifurcation of system (44) is delayed.

Similarly, fix $\alpha =1$ and let $\beta =0,-0.65$. Its corresponding crossing sets are obtained as $\Omega =(0,0.25),\Omega =(0,0.9437)$, respectively. When $\beta$ is taken as 0 and $-0.65$, system (44) changes from the periodic solution to the locally asymptotically stable. When $\alpha =1,\beta =0$, system (44) is not actually controlled and undergoes Hopf bifurcation at O (see Fig. 3). When $\alpha =1,\beta =-0.65$, system (44) is the controlled system, the equilibrium O is locally asymptotically stable (see Fig. 11). Obviously, we can get that Hopf bifurcation of system (44) without hybrid control could be delayed. The hybrid control could impact on the stability of neural network models.

Fig. 4

The original equilibrium of system (44) with initial values (0.1, 0.1, 0.1, 0.1) is locally asymptotically stable when $\tau _{1}=\tau _{2}=0$ and $\alpha =0.2, \beta =-0.65$

Fig. 5

Graph of $F(\omega )$ when $\tau _{1}>0,\tau _{2}>0$ and $\alpha =0.2, \beta =-0.65$

Fig. 6

Plot of stability switching curves when $\tau _{1}>0,\tau _{2}>0$ and $\alpha =0.2, \beta =-0.65$

Fig. 7

The original equilibrium of system (44) with initial values (0.1, 0.1, 0.1, 0.1) is locally asymptotically stable when $(\tau _{1},\tau _{2})=(3,1)$ and $\alpha =0.2, \beta =-0.65$

Fig. 8

The original equilibrium of system (44) with initial values (0.1, 0.1, 0.1, 0.1) occurs periodic solution when $(\tau _{1},\tau _{2})=(3,4)$ and $\alpha =0.2, \beta =-0.65$

Fig. 9

The original equilibrium of system (44) with initial values (0.1, 0.1, 0.1, 0.1) is locally asymptotically stable when $(\tau _{1},\tau _{2})=(13,1)$ and $\alpha =0.2, \beta =-0.65$

Fig. 10

The original equilibrium of system (44) with initial values (0.1, 0.1, 0.1, 0.1) is locally asymptotically stable when $(\tau _{1},\tau _{2})=(3,4)$ and $\alpha =0.4, \beta =-0.65$

Fig. 11

The original equilibrium of system (44) with initial values (0.1, 0.1, 0.1, 0.1) is locally asymptotically stable when $(\tau _{1},\tau _{2})=(13,1)$ and $\alpha =1, \beta =-0.65$

5 Conclusion

The research results show that multiple time delays systems can better describe the diversity and complexity of real neural networks, which makes systems have more rich dynamic characteristics. Due to the effects of memory and hereditary properties, fractional calculus can be commonly applied in BAM neural network model. In this paper, the stability and the existence of Hopf bifurcation of a fractional-order BAM neural network with two delays are considered. Hybrid feedback control of Hopf bifurcation for the model has further been investigated. By selecting two time delays as bifurcation parameters simultaneously, the method of stability switching curves is to obtain the locally asymptotically stable region of the equilibrium in $(\tau _{1},\tau _{2})$ plane. Critical value for the occurrence of Hopf bifurcation is determined. Compared with the previous work, the novelty of our work is to extend the range of the locally asymptotically stability of the equilibrium from an interval to a region in $(\tau _{1},\tau _{2})$ plane. Finally, by comparing with numerical simulation results, it is shown that the hybrid feedback control can effectively affect the occurrence of Hopf bifurcation. In addition, by selecting different control parameters, it is found that a small change of the control parameter value can affect the stability of the controlled system.