Skip to main content
SpringerLink
Log in

Hybrid modeling of multibody vehicles with partially known physics: discovering complex behaviors of tires

  • Research
  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

There are multibody systems whose physics are partially known owing to their complexity and nonlinearity. Therefore, motion equations are not utterly available to be utilized for the prediction, control, design, and monitoring of these systems. To alleviate this issue, this study aims at developing a hybrid modeling procedure to discover respective unidentified physics and, subsequently, provide a holistic governing model of the original mechanism. For approach development, a vehicle with unmodeled tires is thoroughly considered in this research work. Tires profoundly impact the dynamics of vehicles, influencing their handling, drivability, and ride comfort. Advanced chassis control systems used to improve vehicles’ safety, performance, and reliability also require knowledge of tire behavior. Nevertheless, tires are very challenging to model as they are very complex and nonlinear components. Although simplified models are often employed, they are incapable of fully capturing tire behaviors. Using neural networks, i.e., black-box models, of the tire represents a common alternative. However, these approaches do not work outside the training data distribution, and they need costly and hard-to-measure experimental data for training purposes. Thus, this research study proposes a hybrid method by combining partially known physics of vehicle dynamics and a neural network to compensate for the unknown physics of tires. The developed approach learns the tire dynamics automatically from vehicle responses without requiring costly measured tire forces but solely relying on signals from an inertial measuring unit. The suggested methodology is validated experimentally, providing accurate and stable results. The time-depending behaviors of tires during cornering are also discovered and reported. The developed model is generic and can handle either linear or nonlinear physics-based models. However, the linear tire model integrated into the hybrid procedure in this study limits the simulation to stationary trajectories and cannot address the physics of tires when a vehicle undergoes nonstationary maneuvers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Data Availability

The data and materials presented in this study are available on request from the corresponding author.

References

  1. Galvani, M.: History and future of driver assistance. IEEE Instrum. Meas. Mag. 22(1), 11–16 (2019). https://doi.org/10.1109/MIM.2019.8633345

    Article  MathSciNet  Google Scholar 

  2. Jazar, R.: Vehicle Dynamics: Theory and Application, 3rd edn. Springer, Berlin (2017)

    Book  Google Scholar 

  3. Pereira, C.L., Costa Neto, R.T., Loiola, B.R.: Cornering stiffness estimation using Levenberg–Marquardt approach. Inverse Probl. Sci. Eng. 29(12), 2207–2239 (2021). https://doi.org/10.1080/17415977.2021.1910683

    Article  MathSciNet  Google Scholar 

  4. Feng, L., Chen, W., Wu, T., Wang, H., Dai, D., Wang, D., Zhang, W.: An improved sensor system for wheel force detection with motion-force decoupling technique. Measurement 119, 205–217 (2018). https://doi.org/10.1016/j.measurement.2018.01.066

    Article  Google Scholar 

  5. Jin, X., Yin, G., Chen, N.: Advanced estimation techniques for vehicle system dynamic state: a survey. Sensors 19(19), Article ID 4289 (2019). https://doi.org/10.3390/s19194289

    Article  Google Scholar 

  6. Pacejka, H.B., Bakker, E.: The magic formula tyre model. Veh. Syst. Dyn. 21, 1–18 (1992). https://doi.org/10.1080/00423119208969994

    Article  Google Scholar 

  7. Smith, G., Blundell, M.: A new efficient free-rolling tyre-testing procedure for the parameterisation of vehicle dynamics tyre models. Proc. Inst. Mech. Eng., Part D, J. Automob. Eng., 1435–1448 (2017). https://doi.org/10.1177/0954407016675216

  8. Wang, T., Liu, Y., Ding, L., Li, J., Gao, H., Liang, Y., Sun, T.: Neural network identification of a racing car tire model. J Eng., 1–11 (2018). https://doi.org/10.1155/2018/4143794

  9. Sousa, L.C., Ayala, H.: Nonlinear tire model approximation using machine learning for efficient model predictive control. IEEE Access 10, 107549–107562 (2022). https://doi.org/10.1109/ACCESS.2022.3212420

    Article  Google Scholar 

  10. Xu, N., Askari, H., Huang, Y., Zhou, J., Khajepour, A.: Tire force estimation in intelligent tires using machine learning. IEEE Trans. Intell. Transp. Syst. 23(4), 3565–3574 (2022). https://doi.org/10.1109/TITS.2020.3038155

    Article  Google Scholar 

  11. Viehweger, M., Cyrano Vaseur, C., Aalst, S., Acosta, M., Regolin, E., Alatorre, A.: Vehicle state and tyre force estimation: demonstrations and guidelines. Veh. Syst. Dyn., 675–702 (2021). https://doi.org/10.1080/00423114.2020.1714672

  12. Kalman, R.E.: A new approach to linear filtering and prediction problems. J. Basic Eng., 35–45 (1960). https://doi.org/10.1115/1.3662552

  13. Naets, F., Aalst, S., Boulkroune, B., Ghouti, N.E., Desmet, W.: Design and experimental validation of a stable two-stage estimator for automotive sideslip angle and tire parameters. IEEE Trans. Veh. Technol. 66(1), 9727–9742 (2017). https://doi.org/10.1109/TVT.2017.2742665

    Article  Google Scholar 

  14. Doumiati, M., Victorino, A., Charara, A., Lechner, D.: Unscented Kalman filter for real-time vehicle lateral tire forces and sideslip angle estimation. IEEE Intell. Veh. Symp., 901–906 (2009). https://doi.org/10.1109/IVS.2009.5164399

  15. Acosta, M., Kanarachos, S.: Tire lateral force estimation and grip potential identification using neural networks, extended Kalman filter, and recursive least squares. Neural Comput. Appl. 30, 3445–3465 (2018). https://doi.org/10.1007/s00521-017-2932-9

    Article  Google Scholar 

  16. Nikravesh, P.: Computer-Aided Analysis of Mechanical Systems. Prentice Hall, Englewood Cliffs (1988)

    Google Scholar 

  17. Bauchau, O.A.: Flexible Multibody Dynamics. Springer, Berlin (2011)

    Book  Google Scholar 

  18. Rahnejat, H.: Multibody dynamics: historical evolution and application. J. Mech. Eng. Sci. 214, 149–173 (2000)

    Article  Google Scholar 

  19. Askari, E., Crevecoeur, G.: Evolutionary sparse data-driven discovery of multibody system dynamics. Multibody Syst. Dyn. 58, 197–226 (2023). https://doi.org/10.1007/s11044-023-09901-z

    Article  MathSciNet  Google Scholar 

  20. Kibble, T., Berkshire, W.B., Frank, H.: Classical Mechanics, 5th edn. Imperial College Press, London (2004)

    Book  Google Scholar 

  21. Askari, E., Andersen, M.S.: On the effect of friction on tibiofemoral joint kinematics. Appl. Sci. 11(16), 7516 (2021). https://doi.org/10.3390/app11167516

    Article  Google Scholar 

  22. Askari, E., Andersen, M.S.: An anatomy-based dynamic model of total knee arthroplasty. Nonlinear Dyn. 106, 3539–3555 (2021). https://doi.org/10.1007/s11071-021-06949-4

    Article  Google Scholar 

  23. De Groote, W., Kikken, E., Hostens, E., Hoecke, S.V., Guillaume Crevecoeur, G.: Neural network augmented physics models for systems with partially unknown dynamics: application to slider-Crank mechanism. IEEE/ASME Trans. Mechatron. 27(1), 103–114 (2022). https://doi.org/10.1109/TMECH.2021.3058536

    Article  Google Scholar 

  24. Haykin, S.: Neural Network, a Comprehensive Foundation, 2nd edn. Pearson Education, Upper Saddle River (1994)

    Google Scholar 

  25. Ardeh, H.A., Tupy, M., Negrut, D.: On the construction and use of surrogate models for the dynamic analysis of multibody systems. In: Volume 13: New Developments in Simulation Methods and Software for Engineering Applications; Safety Engineering, Risk Analysis and Reliability Methods; Transporta- Tion Systems, ASMEDC, vol. 13, pp. 17–26 (2009). https://doi.org/10.1115/IMECE2009-10277

    Chapter  Google Scholar 

  26. Azzam, B., Schelenz, R., Roscher, B., Baseer, A., Jacobs, G.: Development of a wind turbine gear- box virtual load sensor using multibody simulation and artificial neural networks. Forsch. Ingenieurwes./Eng. Res. 85, 241–250 (2021). https://doi.org/10.1007/s10010-021-00460-3

    Article  Google Scholar 

  27. Kahr, M., Kovács, G., Loinig, M., Brückl, H.: Condition monitoring of ball bearings based on machine learning with synthetically generated data. Sensors 22(7), 2490 (2022). https://doi.org/10.3390/s22072490

    Article  Google Scholar 

  28. Ogunmolu, O., Gu, X., Jiang, S., Gans, N.: Nonlinear systems identification using deep dynamic neural networks (2016). arXiv:1610.01439

  29. Nasr, A., Inkol, K.A., Bell, S., McPhee, J.: InverseMuscleNET: alternative machine learning solution to static optimization and inverse muscle modeling. Front. Comput. Neurosci. 15, 759489 (2021). https://doi.org/10.3389/fncom.2021.759489

    Article  Google Scholar 

  30. Ye, Y., Huang, P., Sun, Y., Shi, D.: MBSNet: a deep learning model for multibody dynamics simulation and its application to a vehicle-track system. Mech. Syst. Signal Process. 157, 107716 (2021). https://doi.org/10.1016/j.ymssp.2021.107716

    Article  Google Scholar 

  31. Mohajerin, N., Waslander, S.L.: Multistep prediction of dynamic systems with recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 30(11), 3370–3383 (2019). https://doi.org/10.1109/TNNLS.2019.2891257

    Article  Google Scholar 

  32. Raissi, M.: Deep hidden physics models: deep learning of nonlinear partial differential equations. J. Mach. Learn. Res. 19, 1–24 (2018)

    MathSciNet  Google Scholar 

  33. Schmidt, M., Lipson, H.: Distilling free-form natural laws from experimental data. Science 324(5923), 81–85 (2009). https://doi.org/10.1126/science.1165893

    Article  Google Scholar 

  34. Brunton, S.L., Proctor, J.L., Kutz, J.N.: Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. 113(15), 3932–3937 (2016). https://doi.org/10.1073/pnas.1517384113

    Article  MathSciNet  Google Scholar 

  35. Avendaño-Valencia, L.D., Abdallah, B., Chatzi, E.: Virtual fatigue diagnostics of wake-affected wind turbine via Gaussian process regression. Renew. Energy 170, 539–561 (2021). https://doi.org/10.1016/j.renene.2021.02.003

    Article  Google Scholar 

  36. Raissi, M., Perdilaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019). https://doi.org/10.1016/j.jcp.2018.10.045

    Article  MathSciNet  Google Scholar 

  37. Punjani, A., Abbeel, P.: Deep learning helicopter dynamics models. In: Proc. IEEE Int. Conf. Robot. Autom., pp. 3223–3230 (2015). https://doi.org/10.1109/ICRA.2015.7139643

    Chapter  Google Scholar 

  38. Hashemi, A., Orzechowski, G., Mikkola, A., McPhee, J.: Multibody dynamics and control using machine learning. Multibody Syst. Dyn. 58, 397–431 (2023). https://doi.org/10.1007/s11044-023-09884-x

    Article  MathSciNet  Google Scholar 

  39. Zhang, Z., Zhu, Y., Rai, R., Doermann, D.: PIMNet: physics-infuzed neural network for human motion prediction. IEEE Robot. Autom. Lett. 7(4), 8949–8955 (2022). https://doi.org/10.1109/LRA.2022.3188892

    Article  Google Scholar 

  40. Erge, O., Oort, E.: Combining physics-based and data-driven modeling in well construction: hybrid fluid dynamics modeling. J. Nat. Gas Sci. Eng. 97, 104348 (2022). https://doi.org/10.1016/j.jngse.2021.104348

    Article  Google Scholar 

  41. Rahman, M., Rasheed, A., San, O.: A hybrid analytics paradigm combining physics-based modeling and data-driven modeling to accelerate incompressible flow solvers. Fluids 3(3), 50 (2018). https://doi.org/10.3390/fluids3030050

    Article  Google Scholar 

  42. Liu, Q., Liang, J., Ma, O.: A physics-based and data-driven hybrid modeling method for accurately simulating complex contact phenomenon. Multibody Syst. Dyn. 50, 97–117 (2020). https://doi.org/10.1007/s11044-020-09746-w

    Article  MathSciNet  Google Scholar 

  43. Askari, E., et al.: Micro-CT based finite element modelling and experimental characterization of the compressive mechanical properties of 3-D zirconia scaffolds for bone tissue engineering. J. Mech. Behav. Biomed. Mater. 102, 103516 (2020). https://doi.org/10.1016/j.jmbbm.2019.103516

    Article  Google Scholar 

  44. Blakseth, S.S., Rasheed, A., Kvamsdal, T., San, O.: Combining physics-based and data-driven techniques for reliable hybrid analysis and modeling using the corrective source term approach. Appl. Soft Comput. 128, 109533 (2022). https://doi.org/10.1016/j.asoc.2022.109533

    Article  Google Scholar 

  45. Linxia, L.L., Köttig, F.: A hybrid framework combining data-driven and model-based methods for system remaining useful life prediction. Appl. Soft Comput. 44, 191–199 (2016). https://doi.org/10.1016/j.asoc.2016.03.013

    Article  Google Scholar 

  46. Zeng, Y., Song, D., Zhang, W., Zhou, B., Xie, M., Tang, X.: A new physics-based data-driven guideline for wear modelling and prediction of train wheels. Wear 456–457, 203355 (2020). https://doi.org/10.1016/j.wear.2020.203355

    Article  Google Scholar 

  47. Askari, E., Andersen, M.S.: Effect of ligament properties on nonlinear dynamics and wear prediction of knee prostheses. J. Biomech. Eng. 143, 021014 (2021). https://doi.org/10.1115/1.4048707

    Article  Google Scholar 

  48. Askari, E., Flores, P., Dabirrahmani, D., Appleyard, R.: Dynamic modeling and analysis of wear in spatial hard-on-hard couple hip replacements using multibody systems methodologies. Nonlinear Dyn. 82(1–2), 1039–1058 (2015). https://doi.org/10.1007/s11071-015-2216-9

    Article  MathSciNet  Google Scholar 

  49. Askari, E., Andersen, M.S.: A modification on velocity terms of Reynolds equation in a spherical coordinate system. Tribol. Int. 131, 15–23 (2019). https://doi.org/10.1016/j.triboint.2018.10.019

    Article  Google Scholar 

  50. Flores, P., Lankarani, H.M.: Spatial rigid-multibody systems with lubricated spherical clearance joints: modeling and simulation. Nonlinear Dyn. 60, 99–114 (2010). https://doi.org/10.1007/s11071-009-9583-z

    Article  Google Scholar 

  51. Askari, E.: Mathematical models for characterizing non-Hertzian contacts. Appl. Math. Model. 90, 432–447 (2021). https://doi.org/10.1016/j.apm.2020.08.048

    Article  MathSciNet  Google Scholar 

  52. Askari, E., Andersen, M.: A closed-form formulation for the conformal articulation of metal- on-polyethylene hip prostheses: contact mechanics and sliding distance. J. Eng. Med. 232(12), 1196–1208 (2018). https://doi.org/10.1177/0954411918810044

    Article  Google Scholar 

  53. Flores, P., Ambrósio, J., Claro, J.C.P., Lankarani, H.M.: Spatial revolute joints with clearance for dynamic analysis of multibody systems. Proc. Inst. Mech. Eng., Part K, J. Multi-Body Dyn. 220(4), 257–271 (2006). https://doi.org/10.1243/1464419JMBD70

    Article  Google Scholar 

  54. Aggarwal, C.C.: Neural Networks and Deep Learning. Springer, Berlin (2018)

    Book  Google Scholar 

  55. Moshkelgosha, E., Askari, E., Jeong, K.H., Shafiee, A.: Fluid-structure coupling of concentric double FGM shells with different lengths. Struct. Eng. Mech. 61(2), 231–244 (2017). https://doi.org/10.12989/sem.2017.61.2.231

    Article  Google Scholar 

  56. Quaghebeur, W., Nopens, I., De Baets, B.: Incorporating unmodelled dynamics into first-principles models through machine learning. IEEE Access 9, 22014–22022 (2021). https://doi.org/10.1109/ACCESS.2021.3055353

    Article  Google Scholar 

  57. Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G.S., Davis, A., Dean, J., Devin, M., Ghemawat, S., Goodfellow, I., Harp, A., Irving, G., Isard, M., Jia, Y., Jozefowicz, R., Kaiser, L., Kudlur, M., Levenberg, J., Mané, D., Monga, R., Moore, S., Murray, D., Olah, C., Schuster, M., Shlens, J., Steiner, B., Sutskever, I., Talwar, K., Tucker, P., Vanhoucke, V., Vasudevan, V., Viégas, F., Vinyals, O., Warden, P., Wattenberg, M., Wicke, M., Yu, Y., Zheng, X.: (2015). TensorFlow: Large-scale machine learning on heterogeneous systems. Software available from tensorflow.org

  58. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., et al.: Pytorch: an imperative style, high-performance 217 deep learning library. In: Proceedings of the 33rd Conference on Neural Information Processing Systems, pp. 8026–8037 (2019)

    Google Scholar 

  59. Pontryagin, L.S., Mishchenko, E., Boltyanskii, V., Gamkrelidze, R.: The Mathematical Theory of Optimal Processes. Wiley, Hoboken (1962)

    Google Scholar 

  60. Allaire, G.: A review of adjoint methods for sensitivity analysis, uncertainty quantification and optimization in numerical codes. Ing. Automob. 836, 33–36 (2015)

    Google Scholar 

  61. Giles, M., Pierce, N.: An introduction to the adjoint approach to design. Flow Turbul. Combust. 65, 393–415 (2000)

    Article  Google Scholar 

  62. Cao, Y., Li, S., Petzold, L., Serban, R.: Adjoint sensitivity analysis for differential-algebraic equations: the adjoint DAE system and its numerical solution. SIAM J. Sci. Comput. 24, 1076–1089 (2003). https://doi.org/10.1016/S0377-0427(02)00528-9

    Article  MathSciNet  Google Scholar 

  63. Sengupta, B., Friston, K.J., Penny, W.D.: Efficient gradient computation for dynamical models. NeuroImage 98, 521–527 (2014). https://doi.org/10.1016/j.neuroimage.2014.04.040

    Article  Google Scholar 

  64. Schramm, D., Hiller, M., Bardini, R.: Vehicle Dynamics: Modeling and Simulation, 2nd edn. Springer, Germany (2014)

    Book  Google Scholar 

  65. https://www.volkswagen-newsroom.com/en/electric-vehicles-3646

  66. Cho, W., Yoon, J., Yim, S., Koo, B., Yi, K.: Estimation of tire forces for application to vehicle stability control. IEEE Trans. Veh. Technol. 59(2), 638–649 (2010). https://doi.org/10.1109/TVT.2009.2034268

    Article  Google Scholar 

  67. Baffet, G., Charara, A., Lechner, D.: Estimation of vehicle sideslip, tire force and wheel cornering stiffness. Control Eng. Pract. 17, 1255–1264 (2009). https://doi.org/10.1016/j.conengprac.2009.05.005

    Article  Google Scholar 

  68. Baffet, G., Charara, A., Dherbomez, G.: An observer of tire–road forces and friction for active security vehicle systems. IEEE/ASME Trans. Mechatron. 12(6), 651–661 (2007). https://doi.org/10.1109/TMECH.2007.910099

    Article  Google Scholar 

  69. Acosta, M., Kanarachos, S., Fitzpatrick, M.: Robust virtual sensing for vehicle agile manoeuvring: a tyre-model-less approach. IEEE Trans. Veh. Technol. 67(3), 1894–1908 (2017). https://doi.org/10.1109/TVT.2017.2767942

    Article  Google Scholar 

  70. Lampe, N., Kortmann, K.P., Westerkamp, C.: Neural network based tire-road friction estimation using experimental data. IFAC-PapersOnLine 56(3), 397–402 (2023). https://doi.org/10.1016/j.ifacol.2023.12.056

    Article  Google Scholar 

  71. Viehweger, M., Vaseur, C., Aalst, S., Acosta, M., Regolin, E., Alatorre, A., Desmet, W., Naets, F., Ivanov, V., Ferrara, A., Victorino, A.: Vehicle state and tyre force estimation: demonstrations and guidelines. Int. J. Veh. Mech. Mobil. 59(5), 675–702 (2021). https://doi.org/10.1080/00423114.2020.1714672

    Article  Google Scholar 

  72. Yang, J., Chen, W., Wang, Y.: Estimate lateral tire force based on yaw moment without using tire model. Mech. Eng. 934181, 1–8 (2014). https://doi.org/10.1155/2014/934181

    Article  Google Scholar 

  73. Hrgetic, M., Deur, J., Ivanovic, V., Tseng, E.: Vehicle sideslip angle EKF estimator based on nonlinear vehicle dynamics model and stochastic tire forces modeling. SAE Int. J. Passeng. Cars - Mech. Syst. 7(1), 86–95 (2014). https://doi.org/10.4271/2014-01-0144

    Article  Google Scholar 

  74. Ray, L.R.: Nonlinear tire force estimation and road friction identification: simulation and experiments. Automatica 33(10), 1819–1833 (1997). https://doi.org/10.1016/S0005-1098(97)00093-9

    Article  MathSciNet  Google Scholar 

  75. Albinsson, A., Bruzelius, F., Jonasson, M., Jacobson, B.: Tire force estimation utilizing wheel torque measurements and validation in simulations and experiments. 12th International Symposium on Advanced Vehicle Control September 22-26 (2014)

  76. Ray, L.R.: Nonlinear state and tire force estimation for advanced vehicle control. IEEE Trans. Control Syst. Technol. 3(1), 117–124 (1995)

    Article  Google Scholar 

  77. Pacejka, H.B.: Tyre and Vehicle Dynamics, 2nd edn. Elsevier, Amsterdam (2006)

    Google Scholar 

  78. Wang, Y., Geng, K., Xu, L., Ren, Y., Dong, H., Yin, G.: Estimation of sideslip angle and tire cornering stiffness using fuzzy adaptive robust cubature Kalman filter. IEEE Trans. Syst. Man Cybern. Syst. 52(3), 1451–1462 (2022). https://doi.org/10.1109/TSMC.2020.3020562

    Article  Google Scholar 

  79. Hornik, K.: Multilayer feedforward networks are universal approximators. Neural Netw. 2, 359–366 (1989). https://doi.org/10.1016/0893-6080(89)90020-8

    Article  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the support of VLAIO (Flemish Innovation & Entrepreneurship) through the O&O project AI4Test (HBC.2022.0005).

Funding

This project is financed through the European Recovery and Resilience Facility (RRF).

figure t

Author information

Authors and Affiliations

  1. Dept. Electromechanical, Systems and Metal Engineering, Ghent University, B-9052, Ghent, Belgium

    Ehsan Askari & Guillaume Crevecoeur

  2. MIRO Core Lab, Flanders Make, 3920, Lommel, Belgium

    Ehsan Askari & Guillaume Crevecoeur

  3. Siemens Digital Industries Software, Interleuvenlaan 68, 3001, Leuven, Belgium

    Davide Gorgoretti

Authors
  1. Ehsan Askari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Davide Gorgoretti
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guillaume Crevecoeur
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

E.A. wrote and reviewed the manuscript, developed the method, validated it, wrote scripts, and D.G. wrote the manuscript and provided experiments data, and G.C. reviewed the manuscript and mentored. All authors reviewed the manuscript.

Corresponding author

Correspondence to Ehsan Askari.

Ethics declarations

Ethical approval

Not applicable.

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

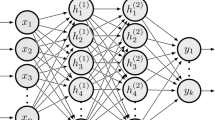
In this appendix, the formulations associated with RNN are given.

$$\begin{aligned} \begin{aligned} &V_{t}^{\left (1\right )} = w_{1} u_{t},\qquad h_{t}^{\left (1\right )} = \varphi _{1} \left ( V_{t}^{\left (1\right )} \right )\\ & V_{t}^{(2)} = w_{2} \left ( h_{t}^{\left (1\right )} + \psi _{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right ) \right ),\qquad h_{t}^{(2)} = \varphi _{2} \left ( V_{t}^{\left (2\right )} \right )\\ & V_{t}^{(3)} = w_{3} \left ( h_{t}^{\left (2\right )} + \psi _{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) \right ),\qquad y_{t} = \varphi _{3} \left ( V_{t}^{\left (3\right )} \right )\\ & S_{t}^{\left (1\right )} = h_{t}^{\left (1\right )} + \psi _{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right )\\ & S_{t}^{\left (2\right )} = h_{t}^{\left (2\right )} + \psi _{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) \end{aligned} \end{aligned}$$
(A.1)

The gradient of network output with respect to weights, computing the weight correction at each training iteration, Eq. (6), is given as follows:

$$\begin{aligned} \begin{aligned} &\frac{d z_{t}}{d w_{3}} = \dot{\varphi}_{3} \left ( V_{t}^{\left (3\right )} \right ) h_{t}^{\left (2\right )}\\ & \frac{d z_{t}}{d w_{2}} = \dot{\varphi}_{3} \left ( V_{t}^{\left (3\right )} \right ) w_{3} \dot{\varphi}_{2} \left ( V_{t}^{\left (2\right )} \right ) \left ( h_{t}^{\left (1\right )} + \psi _{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right ) \right )\\ &\phantom{\frac{d z_{t}}{d w_{2}} = }{} + \dot{\varphi}_{3} \left ( V_{t}^{\left (3\right )} \right ) w_{3} \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) w_{hh}^{\left (2\right )} \\ &\frac{d S_{t -1}^{\left (2\right )}}{d w_{2}} \frac{d z_{t}}{d w_{1}} = \dot{\varphi}_{3} \left ( V_{t}^{\left (3\right )} \right ) w_{3} \dot{\varphi}_{2} \left ( V_{t}^{\left (2\right )} \right ) w_{2} \dot{\varphi}_{1} \left ( V_{t}^{\left (1\right )} \right ) u_{t} \\ &\phantom{\frac{d S_{t -1}^{\left (2\right )}}{d w_{2}} \frac{d z_{t}}{d w_{1}} = }{}+ \dot{\varphi}_{3} \left ( V_{t}^{\left (3\right )} \right ) w_{3} \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) w_{hh}^{\left (2\right )} \frac{d S_{t -1}^{(2)}}{d w_{1}} \\ &\phantom{\frac{d S_{t -1}^{\left (2\right )}}{d w_{2}} \frac{d z_{t}}{d w_{1}} = }{}+ \dot{\varphi}_{3} \left ( V_{t}^{\left (3\right )} \right ) w_{3} \dot{\varphi}_{2} \left ( V_{t}^{\left (2\right )} \right ) w_{2} \dot{\psi}_{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right ) w_{hh}^{\left (1\right )} \frac{d S_{t -1}^{(1)}}{d w_{1}} \end{aligned} \end{aligned}$$
(A.2)

in which

$$\begin{aligned} \begin{aligned} \frac{d S_{t}^{(2)}}{d w_{2}} ={}& \dot{\varphi}_{2} \left ( V_{t}^{\left (2\right )} \right ) \left ( h_{t}^{\left (1\right )} + \psi _{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right ) \right ) + \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) w_{hh}^{\left (2\right )} \frac{d S_{t -1}^{(2)}}{d w_{2}} \\ \frac{d S_{t}^{(2)}}{d w_{1}} = {}&\dot{\varphi}_{2} \left ( V_{t}^{\left (2\right )} \right ) w_{2} \dot{\psi}_{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right ) w_{hh}^{\left (1\right )} \frac{d S_{t -1}^{(1)}}{d w_{1}} + \dot{\varphi}_{2} \left ( V_{t}^{\left (2\right )} \right ) w_{2} \dot{\varphi}_{1} \left ( V_{t}^{\left (1\right )} \right ) u_{t} \\ &{}+ \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) w_{hh}^{\left (2\right )} \frac{d S_{t -1}^{(2)}}{d w_{1}} \\ \frac{d S_{t}^{(1)}}{d w_{1}} ={}& \dot{\varphi}_{1} \left ( V_{t}^{\left (1\right )} \right ) u_{t} + \dot{\psi}_{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right ) w_{hh}^{\left (1\right )} \frac{d S_{t -1}^{(1)}}{d w_{1}} \end{aligned} \end{aligned}$$
(A.3)

The gradient of network output with respect to recurrent weights is, in turn, determined as follows:

$$\begin{aligned} \begin{aligned} \frac{d z_{t}}{d w_{hh}^{2}} ={}& \dot{\varphi}_{3} \left ( V_{t}^{\left (3\right )} \right ) w_{3} \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) S_{t -1}^{(2)}\\ &{} + \dot{\varphi}_{3} \left ( V_{t}^{\left (3\right )} \right ) w_{3} \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) w_{hh}^{\left (2\right )} \frac{d S_{t -1}^{(2)}}{d w_{hh}^{2}} \\ \frac{d z_{t}}{d w_{hh}^{1}} ={}& \dot{\varphi}_{3} \left ( V_{t}^{\left ( 3 \right )} \right ) w_{3} \dot{\varphi}_{2} \left ( V_{t}^{\left ( 2 \right )} \right ) w_{2} \dot{\psi}_{1} \left ( w_{hh}^{\left ( 1 \right )} S_{t -1}^{\left ( 1 \right )} \right ) S_{t -1}^{\left ( 1 \right )}\\ &{} + \dot{\varphi}_{3} \left ( V_{t}^{\left ( 3 \right )} \right ) w_{3} \dot{\psi}_{2} \left ( w_{hh}^{\left ( 2 \right )} S_{t -1}^{\left ( 2 \right )} \right ) w_{hh}^{\left ( 2 \right )} \frac{d S_{t -1}^{\left ( 2 \right )}}{d w_{hh}^{1}} \\ &{}+ \dot{\varphi}_{3} \left ( V_{t}^{\left ( 3 \right )} \right ) w_{3} \dot{\varphi}_{2} \left ( V_{t}^{\left ( 2 \right )} \right ) w_{2} \dot{\psi}_{1} \left ( w_{hh}^{\left ( 1 \right )} S_{t -1}^{\left ( 1 \right )} \right ) w_{hh}^{\left ( 1 \right )} \frac{d S_{t -1}^{\left ( 1 \right )}}{d w_{1}}, \end{aligned} \end{aligned}$$
(A.4)

where

$$\begin{aligned} \begin{aligned} \frac{d S_{t}^{\left (2\right )}}{d w_{hh}^{2}} ={}& \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) S_{t -1}^{\left (2\right )} + \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) w_{hh}^{\left (2\right )} \frac{d S_{t -1}^{\left (2\right )}}{d w_{hh}^{2}}\\ \frac{d S_{t}^{(2)}}{d w_{hh}^{1}} ={}& \dot{\varphi}_{2} \left ( V_{t}^{\left (2\right )} \right ) w_{2} \dot{\psi}_{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right ) w_{hh}^{\left (1\right )} \frac{d S_{t -1}^{(1)}}{d w_{hh}^{1}}\\ &{} + \dot{\varphi}_{2} \left ( V_{t}^{\left (2\right )} \right ) w_{2} \dot{\psi}_{1} \left ( w_{hh}^{\left (1\right )} S_{t -1}^{\left (1\right )} \right ) S_{t -1}^{(1)} \\ &{}+ \dot{\psi}_{2} \left ( w_{hh}^{\left (2\right )} S_{t -1}^{\left (2\right )} \right ) w_{hh}^{\left (2\right )} \frac{d S_{t -1}^{(2)}}{d w_{hh}^{1}} \\ \frac{d S_{t}^{\left ( 1 \right )}}{d w_{hh}^{1}} = {}&\dot{\psi}_{1} \left ( w_{hh}^{\left ( 1 \right )} S_{t -1}^{\left ( 1 \right )} \right ) S_{t -1}^{\left ( 1 \right )} + \dot{\psi}_{1} \left ( w_{hh}^{\left ( 1 \right )} S_{t -1}^{\left ( 1 \right )} \right ) w_{hh}^{\left ( 1 \right )} \frac{d S_{t -1}^{\left ( 1 \right )}}{d w_{hh}^{1}}. \end{aligned} \end{aligned}$$
(A.5)

Appendix B

The differentiation of the hybrid model’s output with respect to the output of the neural network for both hybrid models of S1 and S2 is given in this appendix.

The derivatives associated with the S1 hybrid model are as follows:

$$ \frac{d \mathbf{o}}{d z_{1}} = \left [ \textstyle\begin{array}{c} \left ( - \frac{1}{m} \frac{x_{3}}{v_{x}} - \frac{l_{f}}{m} \frac{x_{4}}{v_{x}} + \frac{\delta}{m} \right ) + \left ( - \frac{l_{f} x_{3}}{I_{zz}} - \frac{l_{f}^{2} x_{4}}{I_{zz}} + \frac{l_{f} v_{x}}{I_{zz}} \delta \right ) dt\\ \left ( - \frac{l_{f}}{I_{zz}} \frac{x_{3}}{v_{x}} - \frac{l_{f}^{2}}{I_{zz}} \frac{x_{4}}{v_{x}} + \frac{l_{f}}{I_{zz}} \delta \right ) dt \\ \textstyle\begin{array}{c} \left ( - \frac{l_{f}}{I_{zz}} \frac{x_{3}}{v_{x}} - \frac{l_{f}^{2}}{I_{zz}} \frac{x_{4}}{v_{x}} + \frac{l_{f}}{I_{zz}} \delta \right )\\ \left ( - \frac{1}{m} \frac{x_{3}}{v_{x}} - \frac{l_{f}}{m} \frac{x_{4}}{v_{x}} + \frac{\delta}{m} \right ) dt \end{array}\displaystyle \end{array}\displaystyle \right ] $$
(B.1)

and

$$ \frac{d \mathbf{o}}{d z_{2}} = \left [ \textstyle\begin{array}{c} \left ( - \frac{1}{m} \frac{x_{3}}{v_{x}} + \frac{l_{r}}{m} \frac{x_{4}}{v_{x}} \right ) + \left ( \frac{l_{r} x_{3}}{I_{zz}} - \frac{l_{r}^{2} x_{4}}{I_{zz}} \right ) dt \\ \left ( \frac{l_{r}}{I_{zz}} \frac{x_{3}}{v_{x}} - \frac{l_{r}^{2}}{I_{zz}} \frac{x_{4}}{v_{x}} \right ) dt \\ \textstyle\begin{array}{c} \left ( \frac{l_{r}}{I_{zz}} \frac{x_{3}}{v_{x}} - \frac{l_{r}^{2}}{I_{zz}} \frac{x_{4}}{v_{x}} \right )\\ \left ( - \frac{1}{m} \frac{x_{3}}{v_{x}} + \frac{l_{r}}{m} \frac{x_{4}}{v_{x}} \right ) dt \end{array}\displaystyle \end{array}\displaystyle \right ]. $$
(B.2)

In addition, those for S2 hybrid model can be written by

$$ \frac{d \mathbf{o}}{d z_{1}}^{T} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{\cos \delta}{m} & \frac{l_{f} \cos \delta}{I_{zz}} dt & \textstyle\begin{array}{c@{\quad}c} 0 & \frac{l_{f} \cos \delta}{I_{zz}} \end{array}\displaystyle \end{array}\displaystyle \right ] $$
(B.3)

and

$$ \frac{d \mathbf{o}}{d z_{2}}^{T} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{1}{m} & - \frac{l_{r}}{I_{zz}} dt & \textstyle\begin{array}{c@{\quad}c} 0 & - \frac{l_{r}}{I_{zz}} \end{array}\displaystyle \end{array}\displaystyle \right ]. $$
(B.4)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Askari, E., Gorgoretti, D. & Crevecoeur, G. Hybrid modeling of multibody vehicles with partially known physics: discovering complex behaviors of tires. Multibody Syst Dyn (2024). https://doi.org/10.1007/s11044-024-09983-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11044-024-09983-3

Keywords

Search

Navigation