1 Introduction

The desire for more efficiency drives the development of modern multibody systems in many application areas. This often results in increasing requirements on accuracy and/or manipulation speed of the respective system. These needs are met by improving the mechanical designs as well as the control strategies.

1.1 Background and motivation

Regarding the mechanical design, current development trends include the introduction of lightweight structures, more complex mechanisms and cable manipulators. Optimization strategies are then often used to find an optimal design of the system [1]. The aforementioned design trends often result in underactuated systems with more degrees of freedom than independent control inputs [2]. This is, for example, due to unactuated flexible modes of lightweight mechanisms. Generally, underactuation leads to challenges for the controller design, because it is not possible to control all unactuated degrees of freedom individually. Therefore, the control strategies must be adapted according to the mechanical design. While most general control-related research is performed by the control theory community, there are also many contributions by the multibody system (MBS) dynamics community. One such contribution out of the MBS community are servo-constraints used for trajectory tracking control.

1.2 Problem statement

Generally, the control of mechatronic systems is a huge field, which is tackled by the control theory community as well as the communities of the respective application examples. There exist many review papers for different aspects of this problem. However, a review analyzing the important and relevant aspects of the intersection between control theory and MBS is lacking so far.

As an efficient method for feedforward control, the framework of servo-constraints is developed by the MBS community itself. Many research papers address specific problems and individual aspects of this method. In particular, the contributions focus on either differentially flat, minimum phase or non-minimum phase systems. However, there does not exist a paper giving a comprehensive overview of the methods for all possible system types and thereby accompanying the complete process from system analysis to feedforward control design by means of servo-constraints. Moreover, there exist different mathematical formulations of the stable inversion problem in the context of servo-constraints. However, a thorough numerical comparison of the stable inversion formulations in terms of numerical efficiency and accuracy is missing so far in the literature.

1.3 Scope and contribution

The first part of this paper gives an overview about the research trends in control from a multibody dynamics perspective. This highlights the currently relevant control topics for the multibody system dynamics community. As one of the results of the literature survey, it is shown that model inversion is a crucial aspect for accurate control of complex multibody systems.

Therefore, in the remainder of the paper, the framework of servo-constraints is reviewed in more detail, since it provides an efficient method for feedforward control of general multibody systems. This approach is a very natural approach for the MBS community, since the use of constraints is an inherent feature of MBS. Thereby, the solution strategies depend on the underlying system properties. All possible system types, such as differentially flat systems, minimum phase and non-minimum phase systems are discussed in a comprehensive manner. Application examples are given for each type in order to show the versatility of the method. For this purpose, existing results are recalled for differentially flat systems (overhead crane [3]). New results are presented for minimum phase systems in terms of a three-dimensional robotic manipulator. Moreover, new numerical results are presented for a comparison of the different formulations of stable inversion for non-minimum phase systems. In total, this comprehensive overview aims to close the gap in the literature for servo-constraints by giving a broad perspective and instructions for applying servo-constraints to a general multibody system regardless of the underlying system type.

1.4 Organization of the paper

The paper is organized as follows. Control-related contributions from the multibody dynamics community are reviewed in Sect. 2. Afterwards, the focus lies on an overview of the servo-constraints framework. As a basis, the mathematical model of general multibody systems is introduced in Sect. 3. This system analysis does not only apply to feedforward control, but also gives important insights for feedback control. The framework of servo-constraints is presented in Sect. 4. In Sect. 5, the approach is detailed for differentially flat and minimum phase systems. A cable robot and a three-dimensional manipulator with one passive joint serve as application examples. In Sect. 6, solution approaches are stated for non-minimum phase systems. A manipulator with one passive joint serves as an application example. Section 7 concludes the contribution with a summary.

2 Literature survey on control approaches in multibody system dynamics

A first overview of topics that are interesting for the multibody community can be obtained by focusing on papers published in the journal Multibody System Dynamics. The increasing research activity is reflected by an increasing number of contributions in the journal that are related to control aspects, see Fig. 1. Not only the absolute number, but also the relative amount of control-related contributions has increased over the past 25 years. In the following, the literature is briefly reviewed and selected publications are summarized.

Fig. 1
figure 1

Number of control-related contributions per year in the journal of Multibody System Dynamics

Full size image

Current application examples lie in the areas of vehicle dynamics, space robotics, cable robots, parallel robots, mobile robots, and flexible multibody systems. Regarding the control concepts, feedforward and feedback strategies can be distinguished. Feedforward control is usually a control component for trajectory tracking, since the feedforward control moves the system on the prescribed trajectory. Regarding feedback control, various control strategies are applied in the context of multibody systems: optimal control, feedback linearization, robust control, and fuzzy control, to name only a few concepts. In order to give a broad overview of relevant topics, the 25 most cited contributions (20 through 99 citations as of July 2022) are categorized and summarized in the following.

2.1 Feedforward control

The most cited control-related contribution [4] in Multibody System Dynamics proposes a framework for the feedforward control of underactuated multibody systems, which have more degrees of freedom than independent control inputs. The inverse dynamics control problem is solved by introducing servo-constraints. The resulting differential algebraic equations (DAEs) are analyzed and compared to multibody systems with geometric constraints. The second most-cited contribution also deals with the feedforward control of underactuated multibody systems [5]. The inverse dynamics of a kinematically undetermined cable-suspension manipulator is computed with the help of a differentially flat system output. Further contributions deal with the feedforward control of multibody systems. The servo-constraints concept from [4] is extended in [6] to crane systems with the system dynamics directly written in partly redundant coordinates. The method of servo-constraints is compared to the classical input-output normal form approach in [7]. Moreover, an optimal design procedure is proposed to design underactuated multibody systems such that they are minimum phase systems. Methodologies for deriving the inverse dynamics of parallel robots are presented in [8, 9]. An algorithm for the real-time solution of the inverse dynamics problem of redundant manipulators is presented in [10], where the redundancy is resolved by least-squares minimization of properly chosen cost functions. In [11], the inverse dynamics of redundantly actuated parallel manipualtors is determined. Thereby, the degrees of freedom resulting from redundant actuation are used to manipulate the prestress in the manipulator in order to either eliminate prestress or to generate a desired end-effector stiffness. An inverse dynamics scheme is coupled to a PD controller in [12] with application to a manoeuvrable tether-net space robot. Thereby, the inverse dynamics is rewritten as an optimization problem. A controller for a slider–crank mechanism with joint friction and joint clearance is developed under the constraint of continuous contact within the joint clearance model in [13]. The control strategy resembles the computed torque method. A framework for solving the optimal control problem for large multibody systems using a direct approach is presented in [14]. The special structure of multibody systems in DAE form is exploited during the symbolic derivation of the necessary conditions and their Jacobian matrices. The optimal control problem for general multibody systems in DAE form is also treated in [15]. Thereby, an energy-preserving scheme is used for direct transcription of the infinitesimal optimal control problem. Examples are given for two-link and three-link manipulators.

2.2 Feedback control

For feedback control, mostly PID-type controllers, feedback linearization, and robust control have attracted attention in the multibody system dynamics community, according to the above-mentioned criteria. These are summarized in the following.

PID control

Fractional order PI and PD controllers are designed in [16] for a serial manipulator while considering the dynamics of the induction motors. The control parameters are tuned using a particle swarm optimization scheme. A cascaded control loop containing a PID and a fuzzy controller is designed in [17] in order to control an unmanned bicycle.

Feedback linearization

Feedback linearization is applied to control a space robot capturing a free-floating object in [18]. A kinematic output controller is combined with a feedback linearization scheme in [19] for the trajectory tracking problem of a car with \(n\) trailers. Thereby, experimental results are provided for a car with one trailer.

Optimal control

Nonlinear model-predictive control is applied to a wind turbine in [20]. Thereby, the controller is based on a reduced model with a defect, which estimates unmodeled dynamics using a neural network. The speed-tracking problem of a motorcycle is treated in [21] by optimal linear preview control. In [22], control of flexible multibody systems with piezoelectric sensor/actuator pairs is addressed. Thereby, classical and optimal feedback control strategies are compared for two application examples, namely a cantilever beam and a four-bar mechanism.

Robust control

Controllers are designed separately for the slow and fast subsystems of a flexible link parallel robot in [23]. A similar approach is taken in [24] for a flexible satellite moving in an orbit. Thereby, variable structure control is used for the slow subsystem and a Lyapunov-based control is applied to suppress vibrations of the fast subsystem. A robust controller based on a \(\mu \)-synthesis approach is designed in [25, 26]. In [25], it is applied to a path-following problem for a bicycle model. In [26], it is applied to reduce stick-slip vibrations in a drill-string, while considering measurement delay. A sliding mode controller is applied in [27] to a cable robot with two moving platforms that is used for open-ocean transfer of cargo. Thereby, the sea conditions are considered as a disturbance on the system.

From an application perspective, the above literature overview shows that the interest of the multibody community lies in the control of diverse application examples. Thereby, a focus on cable manipulators, parallel robots, space robots, and all types of vehicles can be identified. This trend is reflected by recent publications on vibration control of vehicles [28], nonlinear control of a parallel machine [29], and a cable manipulator [30].

From a control method perspective, the overview shows that many of the most cited contributions in the journal Multibody System Dynamics focus on feedforward control. In the framework of a two-design degree of freedom control structure shown in Fig. 2, it seems desirable to use a feedforward controller as accurate as possible in order to reduce the effort in the feedback loop. If most of the dynamics of the real system is already compensated by the feedforward controller, simple control strategies can be sufficient for accurate tracking. Accurate feedforward control is especially relevant for multibody systems undergoing large rigid body motion. Thereby, the concept of servo-constraints poses a method to compute inverse models efficiently for large nonlinear multibody systems and it is directly developed in the multibody dynamics community.

Fig. 2
figure 2

Design of a two degree of freedom control structure

Full size image

2.3 Overview of servo-constraints

The framework of servo-constraints is presented in [4, 31] in the context of multibody system dynamics. The method is directly applicable to underactuated multibody systems, which include flexible multibody systems. In the proposed approach, the equations of motion of an (underactuated) multibody system are appended by so-called servo-constraints (also called program or control constraints) in order to enforce the output to stay on a predefined desired trajectory. The resulting DAEs that describe the inverse model can have a higher differentiation index [32]. For example, this is the case for overhead cranes [3] or flexible drive trains [33]. The DAEs can be solved numerically for the feedforward control input, which moves the system on the desired trajectory. Due to the higher differentiation index, various index reduction strategies are applied in context of servo-constraints, such as Baumgarte stabilization [34, 35], minimal extension [36, 37], and projection [4]. Moreover, a reformulation as an optimization problem is proposed in [38].

The solution strategy for the inverse model DAEs depends on the underlying system class. In this context, multibody systems as general controlled nonlinear systems can be divided into three classes: differentially flat systems, minimum phase systems, and non-minimum phase systems. The inverse model of differentially flat systems is given completely algebraically [39], while the inverse model of minimum phase systems has stable dynamics behavior and the inverse model of non-minimum phase systems has unstable system behavior [40, 41]. Most literature on servo-constraints focuses on differentially flat systems, such as cranes [36, 42, 43], three-dimensional rotary cranes [37, 44], and mass–spring chains [33, 38, 45, 46]. Some literature also considers minimum phase systems, such as robotic manipulators with a few links [47, 48]. For differentially flat as well as minimum phase systems, the inverse model DAEs resulting from the servo-constraints approach can be integrated forward in time. In the literature, the servo-constraints DAEs are usually solved by the implicit Euler scheme [4, 47], but also backwards differentiation formulas are applied [45, 49]. Few papers in the literature deal with the application of servo-constraints to non-minimum phase systems, such as robotic manipulators with passive joints or flexible systems [50, 51]. Generally, a bounded solution to the inverse model problem of non-minimum phase systems can be computed in terms of stable inversion [52]. This approach is extended to the servo-constraints framework in [50, 53]. Experimental results of the concept are shown in [54, 55] for a flexible manipulator. The servo-constraints approach is presented in detail in the remainder of the paper and application examples are given for each system type.

3 Modeling and system analysis

A mathematical model forms the basis for model-based control. There exist several formulations to obtain the equations of motion of general multibody systems [56]. Here, a very general description is chosen that might be stated in redundant or generalized coordinates or a mixture of both. The considered systems have \(f\) degrees of freedom and possibly \(n_{\mathrm{c}}\) geometric constraints, e.g. describing joints or kinematic loops. This system class includes many of the above mentioned application examples, e.g., flexible multibody systems and cable robots. Fully actuated and underactuated systems are included in the description and the equations of motion arise in the very general form

$$\begin{aligned} \dot{\boldsymbol{y}} &= \boldsymbol{Z} (\boldsymbol{y}) \boldsymbol{v} \end{aligned}$$
(1)
$$\begin{aligned} \boldsymbol{M} (\boldsymbol{y},t) \, \dot{\boldsymbol{v}} + \boldsymbol{k} (\boldsymbol{y},\boldsymbol{v},t) &= \boldsymbol{q} ( \boldsymbol{y},\boldsymbol{v},t) + \boldsymbol{C} (\boldsymbol{y}, \boldsymbol{v},t)^{\mathrm{T}} \boldsymbol{\lambda } + \boldsymbol{B} ( \boldsymbol{y}) \, \boldsymbol{u} \end{aligned}$$
(2)
$$\begin{aligned} \boldsymbol{c} (\boldsymbol{y},\boldsymbol{v},t) &= \boldsymbol{0} \,. \end{aligned}$$
(3)

The system is described by either redundant or generalized coordinates \(\boldsymbol{y} \in \mathbb{R}^{n}\) and \(\boldsymbol{Z} \in \mathbb{R}^{n\times n}\) describes the kinematic relationship between positions \(\boldsymbol{y} \) and velocities \(\boldsymbol{v} \in \mathbb{R}^{n}\), \(\boldsymbol{M} \in \mathbb{R}^{n\times n}\) denotes the mass matrix, \(\boldsymbol{k} \in \mathbb{R}^{n}\) denotes the Coriolis and centrifugal forces, \(\boldsymbol{q} \in \mathbb{R}^{n}\) describes the applied forces acting on the system and \(\boldsymbol{B} \in \mathbb{R}^{n\times m}\) distributes the control input \(\boldsymbol{u} \in \mathbb{R}^{m}\) [56]. Equation (3) describes implicit constraints \(\boldsymbol{c} \in \mathbb{R}^{n_{\mathrm{c}}}\), which are enforced by the Lagrange multipliers \(\lambda \in \mathbb{R}^{n_{\mathrm{c}}}\). The Lagrange multipliers are distributed by the constraint Jacobian \(\boldsymbol{C} \in \mathbb{R}^{n_{\mathrm{c}}\times n}\). The system has \(f=n-n_{\mathrm{c}}\) degrees of freedom. When the kinematics are described by minimal coordinates, it is \(\boldsymbol{y} \in \mathbb{R}^{f}\) and \(n_{\mathrm{c}}=0\). Thus, the constraint equation (3) and reaction forces \(\boldsymbol{\lambda } \) do not occur and the equations of motion reduce to ordinary differential equations (ODEs). It is assumed that the number of system outputs equals the number of systems inputs. The system output \(z\in \mathbb{R}^{m}\) is defined as

$$\begin{aligned} \boldsymbol{z} = \boldsymbol{h} (\boldsymbol{y}) \,. \end{aligned}$$
(4)

For later reference, the first and second derivatives of the output are

$$\begin{aligned} \dot{\boldsymbol{z}} &= \frac{\partial \boldsymbol{h} (\boldsymbol{y})}{\partial \boldsymbol{y}} \boldsymbol{Z} (\boldsymbol{y}) \, \boldsymbol{v} = \boldsymbol{H} ( \boldsymbol{y}) \, \boldsymbol{v} \end{aligned}$$
(5)
$$\begin{aligned} \ddot{\boldsymbol{z}} &= \boldsymbol{H} (\boldsymbol{y})\, \dot{\boldsymbol{v}} + \dot{\boldsymbol{H}} (\boldsymbol{y}, \boldsymbol{v}) \, \boldsymbol{v} \,. \end{aligned}$$
(6)

Substituting the dynamics (2) into equation (6) shows the input-output relationship

$$\begin{aligned} \ddot{\boldsymbol{z}} &= \boldsymbol{H} \boldsymbol{M} ^{-1} \boldsymbol{B} \, \boldsymbol{u} + \boldsymbol{H} \boldsymbol{M} ^{-1} \left ( \boldsymbol{q}- \boldsymbol{k} \right ) + \dot{\boldsymbol{H}} \, \boldsymbol{v} = \boldsymbol{\alpha } \, \boldsymbol{u} + \boldsymbol{\beta } \,, \end{aligned}$$
(7)

with the coupling matrix

$$\begin{aligned} \boldsymbol{\alpha } =\boldsymbol{H} \boldsymbol{M} ^{-1} \boldsymbol{B} \,. \end{aligned}$$
(8)

In order to characterize the above model for model inversion and control design, the relative degree and the internal dynamics are of interest. For a single-input single-output (SISO) system, the relative degree \(r\) is obtained by differentiating the system output \(z\) until the input \(u\) appears. Roughly speaking, the number of taken derivatives is the relative degree \(r\) of the system [57]. In the SISO case, the coupling term in equation (8) is scalar. If \({\alpha } \neq 0\), equation (7) can be solved for the system input \(u\). Thus, the system has relative degree \(r=2\). Otherwise, the relative degree is higher and the differentiation of the output must continue until the input appears. A relative degree of \(r=2\) is common for fully actuated holonomic multibody systems and also occurs for some underactuated multibody systems. The concept of relative degree can be generalized to the multi-input multi-output (MIMO) case in a straightforward manner [40]. Then, the system with \(m\) inputs and outputs is characterized by the vector relative degree \(\boldsymbol{r} =\{r_{1}, r_{2}, \dots , r_{m}\}\) for each input-output channel if the decoupling matrix between input and output channels is regular. For example, a fully actuated robot usually has \(\boldsymbol{r} =\{2,2, \dots , 2\}\).

A derivation of the internal dynamics is here briefly outlined for SISO systems written in ODE form, with \(n_{\mathrm{c}}=0\) [40]. Deriving the internal dynamics directly for DAEs is, for example, discussed in [58, 59]. The internal dynamics can be extracted by applying a nonlinear coordinate transformation to the input-output relationship. Thereby, the new coordinates \(\bar{\boldsymbol{x}} \in \mathbb{R}^{2n}\) are chosen as the output \(z\), its first \(r-1\) derivatives and the \(2n-r\) remaining coordinates \(\boldsymbol{\eta } \). The new coordinates are collected in the vector

$$\begin{aligned} \bar{\boldsymbol{x}} = \begin{bmatrix} \bar{x}_{1} \\ \bar{x}_{2} \\ \vdots \\ \bar{x}_{r} \\ \bar{\boldsymbol{x}}_{(r+1):2n} \end{bmatrix} = \boldsymbol{\Phi } (\boldsymbol{y}, \dot{\boldsymbol{y}}, \dots , \boldsymbol{y} ^{(r-1)}) = \begin{bmatrix} z \\ \dot{z} \\ \vdots \\ z^{(r-1)} \\ \boldsymbol{\eta } \end{bmatrix} \,. \end{aligned}$$
(9)

The coordinates \(\boldsymbol{\eta } \in \mathbb{R}^{2n-r}\) describe the internal dynamics and are chosen such that the coordinate transformation \(\boldsymbol{\Phi } \) is at least locally diffeomorphic. As a rule of thumb, the unactuated coordinates are a good choice for the coordinates \(\boldsymbol{\eta } \) if the system output function \(h(\boldsymbol{y})\) contains all actuated coordinates [2, 60]. The input-output normal form in new coordinates \(\bar{\boldsymbol{x}} \) is

$$\begin{aligned} \dot{\bar{\boldsymbol{x}}} = \begin{bmatrix} \bar{x}_{2} \\ \bar{x}_{3} \\ \vdots \\ \bar{x}_{r} \\ \bar{{\alpha }}(\bar{\boldsymbol{x}}) u + \bar{{\beta }}(\bar{\boldsymbol{x}}) \\ \boldsymbol{\rho } (\bar{\boldsymbol{x}}) + \boldsymbol{\sigma } ( \bar{\boldsymbol{x}}) u \end{bmatrix} \,. \end{aligned}$$
(10)

Thereby, the terms \(\bar{{\alpha }}(\bar{\boldsymbol{x}})\) and \(\bar{{\beta }}(\bar{\boldsymbol{x}})\) are expressed in the new coordinates \(\bar{\boldsymbol{x}}\). The functions \(\boldsymbol{\rho } (\bar{\boldsymbol{x}})\) and \(\boldsymbol{\sigma } (\bar{\boldsymbol{x}})\) are given by the coordinate transformation \(\boldsymbol{\Phi } \) for a specific choice \(\boldsymbol{\eta } \). The inverse model for trajectory tracking of the desired trajectory \(z_{\mathrm{d}}(t)\) can be extracted from this input-output normal form. For this purpose, the desired trajectory \(z_{\mathrm{d}}(t)\) is substituted into equation (10), and the \(r\)th part is solved for the desired control input

$$\begin{aligned} u_{\mathrm{d}} = \dfrac{1}{\bar{{\alpha }}\left (z_{\mathrm{d}},\dot{z}_{\mathrm{d}},\dots ,z^{(r-1)}_{\mathrm{d}},\boldsymbol{\eta } \right )} \left ( {z}_{\mathrm{d}}^{(r)} - \bar{{\beta }}\left (z_{\mathrm{d}}, \dot{z}_{\mathrm{d}},\dots ,z^{(r-1)}_{\mathrm{d}},\boldsymbol{\eta } \right ) \right ) \,. \end{aligned}$$
(11)

The term \(\bar{{\alpha }}\) is nonzero by definition of the relative degree. Substituting the desired system input into the last \(2n-r\) equations of equation (10) yields the internal dynamics

$$\begin{aligned} \begin{aligned} \dot{\boldsymbol{\eta }} &= \boldsymbol{\rho } \left (z_{\mathrm{d}}, \dot{z}_{\mathrm{d}},\dots ,z^{(r-1)}_{\mathrm{d}},\boldsymbol{\eta } \right ) + \\ &~\quad \dfrac{\boldsymbol{\sigma } \left (z_{\mathrm{d}},\dot{z}_{\mathrm{d}},\dots ,z^{(r-1)}_{\mathrm{d}},\boldsymbol{\eta } \right )}{\bar{{\alpha }}\left (z_{\mathrm{d}},\dot{z}_{\mathrm{d}},\dots ,z^{(r-1)}_{\mathrm{d}},\boldsymbol{\eta } \right )} \left ( {z}_{\mathrm{d}}^{(r)} -\bar{{\beta }}\left (z_{\mathrm{d}}, \dot{z}_{\mathrm{d}},\dots ,z^{(r-1)}_{\mathrm{d}},\boldsymbol{\eta } \right ) \right ) \,, \end{aligned} \end{aligned}$$
(12)

which are driven by the desired trajectory \(z_{\mathrm{d}}(t)\). Equations (11) and (12) form the inverse model. Stability analysis of the driven internal dynamics (12) is difficult and therefore usually performed in terms of the zero dynamics [40]. Zero dynamics is derived by zeroing the output \(z(t) = 0 \) and its derivatives for all \(t\), such that

$$\begin{aligned} \dot{\boldsymbol{\eta }} = \boldsymbol{\rho } (0,0,\dots ,0, \boldsymbol{\eta }) - \dfrac{\boldsymbol{\sigma } (0,0,\dots ,0,\boldsymbol{\eta })}{\bar{{\alpha }}(0,0,\dots ,0,\boldsymbol{\eta })} \, \bar{{\beta }}(0,0,\dots ,0,\boldsymbol{\eta }) = \boldsymbol{\gamma } (\boldsymbol{\eta }) \,. \end{aligned}$$
(13)

Eigenvalue analysis of the linearized zero dynamics of the form

$$\begin{aligned} \dot{\boldsymbol{\eta }} = \left . \dfrac{\partial \boldsymbol{\gamma } (\boldsymbol{\eta }) }{\partial \boldsymbol{\eta }} \right \vert _{\boldsymbol{\eta } _{\mathrm{eq}}} \widetilde{\boldsymbol{\eta }} = \boldsymbol{A} \widetilde{\boldsymbol{\eta }} \end{aligned}$$
(14)

determines the stability around the equilibrium point \(\boldsymbol{\eta } _{\mathrm{eq}}\). Thereby, \(\widetilde{\boldsymbol{\eta }} \) denotes small variations around the equilibrium point \(\boldsymbol{\eta } _{\mathrm{eq}}\) of the zero dynamics. Systems with stable internal dynamics are called minimum phase, while systems with unstable internal dynamics are called non-minimum phase systems. In case the relative degree is \(r=2n\), the system does not have internal dynamics and is differentially flat. The described approach can be generalized to MIMO systems in a straightforward manner [2, 40].

4 General framework of servo-constraints

In the classical analytical approach, the input-output normal form provides an inverse model in terms of equations (11) and (12). However, this approach might not be applicable in a straightforward manner for complex multibody systems. For example, it might not be possible to analytically find a state transformation \(\boldsymbol{\Phi } \). Therefore, the method of servo-constraints is developed, which describes the inverse model problem in DAE form. Thereby, the so-called servo-constraints, as an extension of classical geometric constraints in multibody system dynamics are introduced

$$\begin{aligned} \boldsymbol{s}(\boldsymbol{y},t) = \boldsymbol{h} (\boldsymbol{y})- \boldsymbol{z} _{\mathrm{d}}(t) &= \boldsymbol{0}, \end{aligned}$$
(15)

which constrain the system output to the desired trajectory \(\boldsymbol{z} _{\mathrm{d}}(t)\). The servo-constraints \(\boldsymbol{s}\in \mathbb{R}^{m}\) append the system dynamics (1)–(3) to obtain the DAEs

$$\begin{aligned} \dot{\boldsymbol{y}} &= \boldsymbol{Z} (\boldsymbol{y}) \boldsymbol{v} \end{aligned}$$
(16)
$$\begin{aligned} \boldsymbol{M} (\boldsymbol{y},t) \, \dot{\boldsymbol{v}} + \boldsymbol{k} (\boldsymbol{y},\boldsymbol{v},t) &= \boldsymbol{q} ( \boldsymbol{y},\boldsymbol{v},t) + \boldsymbol{C} (\boldsymbol{y}, \boldsymbol{v},t)^{\mathrm{T}} \boldsymbol{\lambda } + \boldsymbol{B} ( \boldsymbol{y}) \, \boldsymbol{u} \end{aligned}$$
(17)
$$\begin{aligned} \boldsymbol{c} (\boldsymbol{y},\boldsymbol{v},t) &= \boldsymbol{0} \end{aligned}$$
(18)
$$\begin{aligned} \boldsymbol{s}(\boldsymbol{y},t) &= \boldsymbol{0} \,, \end{aligned}$$
(19)

which form the inverse model. Solving equations (16)–(19) yields the trajectory of all generalized coordinates \(\boldsymbol{y} \), \(\boldsymbol{v} \) and the feedforward control input \(\boldsymbol{u} _{\mathrm{ffw}}\). In case the internal dynamics (12) is unstable (non-minimum phase system), the inverse model problem (16)–(19) cannot be solved by forward integration and stable inversion must be applied.

Equations (16)–(19) have a similar structure compared to the forward dynamics (1)–(3). The Lagrange multipliers \(\boldsymbol{\lambda } \) enforce the geometric constraints \(\boldsymbol{c} \), while the system input \(\boldsymbol{u} \) enforces the servo-constraint \(\boldsymbol{s}\). While the matrix \(\boldsymbol{C} \) is the Jacobian of the geometric constraints, the input distribution \(\boldsymbol{B} \) is in general not the Jacobian of the servo-constraints. Therefore, the input does not necessarily act perpendicular to the constraint manifold. Different realizations of the servo-constraints DAEs are analyzed in [4]. They depend on the properties of the coupling term \(\boldsymbol{\alpha } \) defined in equation (8). The inverse model is in ideal realization if the input \(\boldsymbol{B} \) is orthogonal to the tangent of the constraint manifold, see Fig. 3(a). When the input includes directions in the orthogonal as well as the tangential direction, the system is in non-ideal configuration, see Fig. 3(b). Both configurations are characterized by the full-rank condition \(\text{rank}(\boldsymbol{\alpha }) = m\). If the matrix \(\boldsymbol{\alpha } \) has reduced rank, \(0<\text{rank}(\boldsymbol{\alpha })<m\), the system is in mixed orthogonal–tangential realization. For \(\text{rank}(\boldsymbol{\alpha })=0\), the inverse model is in tangential configuration, see Fig. 3(c), and no input influences the system output directly.

Fig. 3
figure 3

Configurations of the system input \(\boldsymbol{B} \) with respect to the tangent of the constraint manifold [4, 53]

Full size image

Due to these properties, the differentiation index of the DAEs (16)–(19) is larger than three for a singular matrix \(\boldsymbol{\alpha } \). Note that the computation of the differentiation index resembles the same steps as the relative degree defined above. In most cases, the differentiation index is larger by 1 than the relative degree [32]. A close relationship between both concepts is important in the context of servo-constraints. This can be seen by assuming a so-called collocated output. In this case, the input and output occur at the same point and it is \(\boldsymbol{B} = \boldsymbol{H} ^{\mathrm{T}}\). Assuming perfect tracking of the output, the collocated input-output pair can be seen as a rheonomic constraint on the dynamics. Thus, the control input corresponds to the Lagrange multipliers enforcing the rheonomic constraint and the problem has differentiation index 3. However, this is in general not true for other outputs.

5 Differentially flat and minimum phase systems

For differentially flat systems and minimum phase systems, the inverse model DAEs (16)–(19) can be integrated forward in time to obtain the feedforward control input \(\boldsymbol{u} _{ \mathrm{ffw}}\). Ideally, the solution is computed in real-time in order to implement the strategy on the real system. Then, it can be adapted to varying trajectories or varying model properties.

5.1 Numerical methods

The arising DAEs (16)–(19) can have a high differentiation index. Therefore, suitable index reduction strategies should be applied in order to simplify the numerical condition of the problem. Regarding the numerical integration, suitable DAE solvers must be chosen. Thereby, the need for a fast and exact solution must be balanced. The necessary tracking accuracy depends on the specific application and other arising disturbances, such as friction in the actuators. Since feedback control is always added in terms of the control strategy in Fig. 2, the feedback control can compensate external disturbances as well as model uncertainties and numerical errors in the model inversion.

The servo-constraints DAEs are typically solved by the implicit Euler scheme, since it yields a simple and stable implementation. For differentially flat systems, this is usually sufficient because the inverse model is an algebraic system. Therefore, the numerical damping of the implicit Euler scheme is not as relevant. However, for minimum phase systems the inverse model is a dynamic system itself. In this case, the implicit Euler scheme might damp out the dynamics and the solution must be closely monitored. Therefore, higher-order schemes such as higher-order Runge–Kutta methods or backwards differentiation formulas (BDF) are proposed in this case.

5.2 Application examples

Two application examples are given in order to demonstrate the solving process and the real-time applicability. For a cable robot, experimental results using higher-order integration schemes are given. These demonstrate the real-time capabilities of the approach. For a three-dimensional manipulator with a passive joint, simulation results demonstrate the application of servo-constraints on a complex three-dimensional system. It is shown that the implicit Euler scheme damps out the internal dynamics, while higher-order schemes result in accurate tracking and thus provide a superior feedforward control.

5.2.1 Cable robot

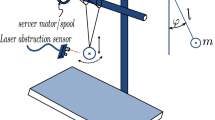
The cable-robot model represents an experimental setup at the Institute of Mechanics and Ocean Engineering at Hamburg University of Technology, see Fig. 4(a). The experimental setup consists of a trolley that can move in a range of 13 m and a load platform connected by four cables with a motion range of 9 m. In the following, the cables are operated synchronously. The multibody model has therefore \(f=3\) degrees of freedom and \(m=2\) inputs, which represent the trolley actuator and the winch actuator. The system output \(z\) is the position of the load platform. The system has a vector relative degree \(\boldsymbol{r} =\{4,2\}\). Therefore, the cable robot is differentially flat and no internal dynamics remain. Refer to [3, 53] for details on the experimental setup and the experimental results.

Fig. 4
figure 4

Experimental setup and model of the cable robot [53]

Full size image

The inverse model DAEs (16)–(19) are solved for the desired system input in real-time. For this purpose, higher-order integration schemes are implemented in the real-time environment. The 4-step BDF scheme and the Runge–Kutta Scheme Radau IIA of order 5 are compared. For the shown experimental results, the desired trajectory is chosen as a smooth transition from the initial trolley position \(x_{\mathrm{T}}=15\) m and trolley length \(L=4\) m to the final position \(x_{\mathrm{T}}=11\) m, \(L=7\) m. The desired trajectory and measurement data is shown in Fig. 5(a). It can be seen that without any external disturbances, the tracking is nearly perfect. Thereby, both integration schemes result in similar accuracy, which is sufficient for tracking. The control loop runs at a frequency of 100 Hz and the solution is computed in each time step. The computation times are measured on the experimental setup and are shown in Fig. 5(b) for the BDF scheme and in Fig. 5(c) for the Runge–Kutta scheme. It can be seen that both methods lie well below the available time of \(10^{4}\) μs, while the BDF scheme is approximately 5 times faster.

Fig. 5
figure 5

Experimental results for the cable robot with higher-order integration schemes [53, 61]

Full size image

Accurate feedforward control is normally supplemented by additional feedback control. In the following, the feedforward control is combined with a linear quadratic regulator (LQR) in accordance to the control structure shown in Fig. 2. For demonstration purposes, an initial position error of \(\Delta x_{\mathrm{T}}= 0.5\) m is introduced. The experimental results are shown in Fig. 6. The feedback controller detects the initial position error and quickly tries to minimize the error by actuating the trolley. This results in sway motion of the load platform that is reduced during the transition time and is then minimized at the final position of the trajectory. A simple feedback strategy is sufficient for this control problem, since the feedforward controller already moves the system close to the desired trajectory, such that the system can be regarded as linear in the vicinity of the desired trajectory.

Fig. 6
figure 6

Experimental results with initial position error \(\Delta x_{ \mathrm{T}}=0.5\) m

Full size image

5.2.2 Three-dimensional manipulator with one passive joint

While the cable robot is differentially flat, there exist many common multibody systems with internal dynamics, e.g., flexible systems. In this case, special care must be taken during solver selection in order to reflect the internal dynamics accurately. In the following, numerical results are shown for the three-dimensional manipulator with one passive joint shown in Fig. 7. The passive joint is a simple approximation of the first oscillation mode of a flexible link. The considered system consists of four links. The first link is in the vertical orientation. It is actuated by input \(u_{1}\) and rotates around the \(z\)-axis, denoted by the angle \(\Omega \). The second and third link are actuated by input \(u_{2}\) and \(u_{3}\), respectively, and rotate around the \(y'\)-axis denoted by the angles \({\alpha } \) and \({\beta } \), respectively. The fourth link is connected by a spring-damper combination and also rotates around the \(y'\)-axis denoted by angle \(\gamma \). The system has \(f=4\) degrees of freedom and \(m=3\) inputs. The system output is defined as the end-effector position in the inertial coordinate frame K.

Fig. 7
figure 7

Model of a three-dimensional manipulator with one passive joint [53]

Full size image

The vector relative degree of the system is \(\boldsymbol{r} =\{2,2,2\}\) and internal dynamics of dimension 2 remain. The internal dynamics can be derived analytically as shown for a planar manipulator with one passive joint in [7]. The internal dynamics is unstable for a homogeneous mass distribution of the links. The mass distribution is optimized in [7, 62] to obtain stable internal dynamics. This is realized by adding counter weights to the links. The optimized simulation parameters for minimum phase behavior are listed in Table 1.

Table 1 Optimized simulation parameters of the three-dimensional manipulator according to [2, 53, 62]
Full size table

The following model inversion results demonstrate the real-time capabilities of the servo-constraints approach in the case of internal dynamics and three-dimensional system behavior. The desired trajectory is a circular path shown in Fig. 8. The initial state vector \(\boldsymbol{y} _{0}\) is \(\boldsymbol{y} _{0}= \begin{bmatrix} \Omega _{0} & \alpha _{0} & \beta _{0} &\gamma _{0} \end{bmatrix} ^{\mathrm{T}}= \begin{bmatrix} 0^{\circ }& 10^{\circ }& 160^{\circ }& 0^{\circ }\end{bmatrix} ^{\mathrm{T}}\), which yields an initial end-effector position \(\boldsymbol{p}_{0} = \begin{bmatrix} 0.35~\mbox{m} & 0~\mbox{m} & 1~\mbox{m} \end{bmatrix} ^{\mathrm{T}}\). The inverse model DAEs (16)–(19) are solved with a 2-step BDF scheme and step size \(\Delta t=1~\mbox{ms}\). The simulation results are shown in Fig. 9. The dashed line denotes the final time of the trajectory. Regarding the system input \(\boldsymbol{u} \), oscillations are visible after the end of the trajectory, see Fig. 9(a). These oscillations compensate the motion of the internal dynamics \(\gamma \), see Fig. 9(d). The corresponding states are shown in Fig. 9(b) and the system output is shown in Fig. 9(c). The desired output trajectory is tracked perfectly and the system is at rest at the end of the trajectory. This shows that the oscillations of the internal dynamics are not observable from the output. However, an accurately computed system input is necessary to compensate the motion of the internal dynamics. Often, an implicit Euler scheme is chosen to solve the inverse model DAEs. Solving this application example with internal dynamics with the implicit Euler scheme damps out the oscillations of the internal dynamics, see Fig. 9(d). Therefore, it is not sufficient for accurate tracking and higher order integration schemes should be applied in the case of internal dynamics.

Fig. 8
figure 8

Visualization of the three-dimensional manipulator in the initial position \(\boldsymbol{y} _{0}\) and the desired trajectory \(\boldsymbol{z} _{\mathrm{d}}(t)\) [53]

Full size image
Fig. 9
figure 9

Inversion results of the three-dimensional manipulator for a circular trajectory [53], a)–c) are computed with \(k_{\mathrm{bdf}}=2\)

Full size image

The real-time capabilities of the approach are now demonstrated by solving the inverse model problem with different BDF schemes and measuring the total computation time \(t_{\mathrm{calc}}\). The bottleneck of the computation lies in solving the nonlinear equations from the BDF scheme using Newton’s method. In order to analyze the speed, different Jacobian approximations are compared. These include the precomputed analytic Jacobian \(\boldsymbol{J} _{\mathrm{ana}}\), the Jacobian \(\boldsymbol{J} _{\mathrm{broy}}\) approximated by Broyden’s method [63], and the numerical Jacobian \(\boldsymbol{J} _{\mathrm{num}}\) approximated by finite differences.

For analyzing the accuracy after computing the feedforward control input \(\boldsymbol{u} _{\mathrm{ffw}}\), it is applied to the system in a forward simulation, using the Matlab solver ode15s. The maximum tracking error between simulated output \(\boldsymbol{z} _{\mathrm{sim}}\) and the desired inverse model output \(\boldsymbol{z} _{\mathrm{d}}\) is \(e_{\mathrm{max}} = \max \,\lVert \boldsymbol{z} _{\mathrm{sim}}(t) - \boldsymbol{z} _{\mathrm{d}}(t) \rVert \). The error \(e_{\mathrm{max}}\) converges based on the given convergence order of the respective BDF scheme, see Fig. 10. The implicit Euler scheme, i.e., \(k_{\mathrm{bdf}}=1\), converges with first order and yields comparably large tracking errors due to numerical damping shown above. The other schemes yield accurate tracking, while numerical rounding errors start to influence the solutions for step sizes \(\Delta t<1~\mbox{ms}\) for \(k_{\mathrm{bdf}}=\{3,4,5\}\). In this case, the convergence in stalled and further reducing the step size will yield larger errors. For each BDF scheme, all Jacobians yield similar tracking errors respectively. However, Broyden’s method does not converge for step sizes \(\Delta t \geq 5~\mbox{ms}\) and no results are given. The computation time is shown in Fig. 10(b), where the bold horizontal line denotes the simulation time and therefore the real-time barrier. Afterwards, the real-time applicability has to be ensured by checking each time step and implementing the scheme on an experimental setup. Nevertheless, this comparison gives a good estimate of the real-time capabilities. The results show that for a given Jacobian approximation, all BDF schemes result in similar computation times. The analytical Jacobian \(\boldsymbol{J} _{\mathrm{ana}}\) yields smallest computation times and is real-time capable for \(\Delta t \geq 0.75~\mbox{ms}\). Broyden’s method is slightly slower and is real-time capable for \(\Delta t \geq 2.5~\mbox{ms}\). The numerical Jacobian \(\boldsymbol{J} _{\mathrm{num}}\) is approximately 8 times slower compared to the analytical one and is real-time capable for \(\Delta t \geq 10~\mbox{ms}\). These results demonstrate that Broyden’s method can be a convenient alternative if the analytical Jacobian is not available. Moreover, the results show that the inverse model DAEs based on servo-constraints can be real-time capable for a three-dimensional system with internal dynamics.

Fig. 10
figure 10

Simulation results for the three-dimensional manipulator [53]

Full size image

6 Non-minimum phase systems

For non-minimum phase systems, the inverse model DAEs (16)–(19) cannot be integrated forward in time. This is not only of theoretical relevance, but many typical multibody systems are non-minimum phase systems. For example, flexible manipulators are usually non-minimum phase if the end-effector is considered as an output. In this case, the stable inversion problem must be considered and is reviewed in the following.

6.1 Stable inversion formulated as boundary value problem

Stable inversion is proposed originally for ODEs describing the internal dynamics explicitly, i.e., in the form of equations (11)–(12) [52]. It is applicable in case the internal dynamics has an hyperbolic equilibrium point. In order to compute bounded desired system inputs, a boundary value problem is formulated for the explicitly given internal dynamics. The coordinates \(\boldsymbol{\eta } \) of the internal dynamics are defined to start on the unstable manifold of the equilibrium point \(\boldsymbol{\eta } _{\mathrm{eq},\mathrm{0}}\) of the internal dynamics at the beginning of the trajectory \(z_{\mathrm{d}}(t)\) and to end on the stable manifold of the equilibrium point \(\boldsymbol{\eta } _{\mathrm{eq},\mathrm{f}}\) at the end of the trajectory. The stable and unstable manifolds are locally approximated by their stable and unstable eigenspaces, respectively. The boundary conditions are then

$$\begin{aligned} \boldsymbol{B} ^{\mathrm{u}} \left ( \boldsymbol{\eta } (T_{0}) - \boldsymbol{\eta } _{\mathrm{eq},\mathrm{0}} \right ) &= \boldsymbol{0} \end{aligned}$$
(20)
$$\begin{aligned} \boldsymbol{B} ^{\mathrm{s}} \left ( \boldsymbol{\eta } (T_{f}) - \boldsymbol{\eta } _{\mathrm{eq},\mathrm{f}}\right )&= \boldsymbol{0}\,. \end{aligned}$$
(21)

Thereby, \(T_{0}\) and \(T_{f}\) denote the initial and final simulation time and the matrices \(\boldsymbol{B} ^{\mathrm{s}}\in \mathbb{R}^{n^{\mathrm{s}}\times (2n-r)}\) and \(\boldsymbol{B} ^{\mathrm{u}}\in \mathbb{R}^{n^{\mathrm{u}}\times (2n-r)}\) contain the eigenvectors of the stable and unstable eigenspaces respectively. It is shown in [50] that the stable inversion procedure can also be applied directly to the inverse model described by the DAEs (16)–(19). Respective boundary conditions are then posed in terms of the redundant coordinate vector.

Solving the boundary value problem yields a bounded, but noncausal system input \(\boldsymbol{u} _{\mathrm{ffw}}\). It consists of a pre- and postactuation phase in order to induce motion in the internal dynamics before the start of the trajectory at \(t_{0}\) and to bring the internal dynamics to rest after the end of the desired trajectory at time \(t_{f}\). In order to capture this pre- and postactuation phase, the boundary value problem is solved on the time interval \(\left [ T_{0}, T_{f} \right ]\) with \(T_{0}\leq t_{0}\) and \(T_{f}\geq t_{f}\) respectively. Deriving the boundary conditions (20)–(21) poses some difficulties in realistic and more complex problems, since the derivation of the internal dynamics (12) is not straightforward.

6.2 Stable inversion formulated as an optimization problem

In order to avoid the definition of the boundary conditions (20)–(21), a reformulation of the stable inversion problem as an optimization problem is proposed in [51, 64]. The optimization problem is defined as

$$\begin{aligned} \min _{\boldsymbol{\eta }} \, \int _{T_{0}}^{T_{f}} J( \boldsymbol{\eta },t) \, \text{d}t \,, \end{aligned}$$
(22)

subject to the internal dynamics (12). In the aforementioned references, the cost functional \(J\) is, for example, chosen as

$$\begin{aligned} J(\boldsymbol{\eta },t) = \left \| \boldsymbol{\eta }- { \boldsymbol{\eta }}_{\mathrm{eq}} \right \|_{2}^{2} \end{aligned}$$
(23)

to ensure a bounded solution. It is shown in [51] that the solution of the optimization problem (22) converges to the solution to the boundary value problem as the interval [\(T_{0} \,, T_{f}\)] goes to infinity. The optimization problem can be formulated equivalently for the servo-constraints DAEs (16)–(19), see [64].

The optimal control problem is an infinite-dimensional problem due to the cost functional (23). Direct methods or indirect methods are available for solving the optimization problem [65]. In the context of stable inversion, the optimal control problem is so far solved by direct methods, such as direct transcription [64, 66] or multiple shooting [51]. Discretizing the constraints and the cost function results in a finite-dimensional optimization problem that can be solved by optimization algorithms.

6.3 Comparison of stable inversion methods

Figure 11 shows an overview of the various approaches to the stable inversion problem. There are six different formulations of the model inversion. On the one hand, there are the inverse models based on the explicitly derived internal dynamics (12) and solved as a boundary value problem (bvp-ode), a directly solved optimization problem (opt-ode) and an indirectly solved optimization problem (idopt-ode). On the other hand, there are the inverse models based on the servo-constraints DAEs (16)–(19) and solved as a boundary value problem (bvp-dae), a directly solved optimization problem (opt-dae) and an indirectly solved optimization problem (idopt-dae).

Fig. 11
figure 11

Overview of methods to solve the stable inversion problem [53]

Full size image

For a numerical comparison, all six methods are applied to the two-link robot with one passive joint shown in Fig. 12. The angles \(\alpha \) and \(\beta \) describe the rotation of the first and second link respectively. The system input is a torque applied on the first link, while the system output \(z\) is the angle between the end-effector and the horizontal line. The system has relative degree \(r=2\) and is non-minimum phase for a homogeneous mass distribution of the two links. The coordinate \(\beta \) describes the internal dynamics. The internal dynamics are derived analytically in [47]. Here, the numerical accuracy and computation times are compared for the stable inversion methods. Thereby, the boundary value problems are solved using finite differences with Simpson discretization. The optimization problems are solved using the Matlab solver fmincon. For convergence analysis, the reference solution is computed with the Matlab solver bvp4c for the case bvp-ode and using a very small step size. The simulation parameters are chosen as \(L_{1} = L_{2} = 0.5~\mbox{m}\), \(m_{1} = m_{2} = 0.05~\mbox{kg}\), \(d = 2.5 \times 10^{-5}~\frac{\text{N}\,\text{ms}}{\text{rad}}\) and \(k = {0.5}~\frac{\text{N}\,\text{m}}{\text{rad}}\).

Fig. 12
figure 12

Model of a manipulator with one passive joint

Full size image

The desired trajectory is a smooth transition from \(z=0^{\circ}\) to \(z=30^{\circ}\), see Fig. 13(a). The phase diagram of the coordinate \(\beta \) in Fig. 13(b) shows the effect of the boundary conditions. The trajectory starts on the eigenspace \(E_{ \mathrm{f}}^{\mathrm{U}}\) approximating the unstable manifold and reaches the equilibrium in the direction of the eigenspace \(E_{\mathrm{f}}^{\mathrm{S}}\), which approximates the stable manifold.

Fig. 13
figure 13

Desired trajectory and phase-space diagram

Full size image

The convergence of the maximum error \(e_{\mathrm{max}}=\text{max}\, \vert u_{\mathrm{ref}}(t)-u_{\mathrm{d}}(t) \vert \) is shown in the upper diagram of Fig. 14. All solution approaches show a similar convergence behavior of order 4. For this application example, the solution accuracy cannot be improved for time steps below \(\Delta t=0.03~\mbox{s}\). On the other hand, there are differences in the computation times. Both direct optimization schemes opt-ode and opt-dae have larger computation times compared to the other formulations. Since the remaining four approaches have comparably computation times, it is proposed to use the simplest approach. From a practical point of view, the method bvp-dae represents the simplest approach since it does not depend on deriving the internal dynamics explicitly and no adjoint variables must be solved for.

Fig. 14
figure 14

Comparison of the stable inversion formulations for a two-link robot

Full size image

7 Conclusion

The contribution of this paper is two-fold. The first part in Sect. 2 gives an overview about the control-related literature in the journal Multibody System Dynamics during the past 25 years. It is shown that the control-related contributions have increased over the past 25 years. The most cited contributions are summarized in order to show active fields of research and to highlight the relevant control problems for the multibody community. As can be seen from the literature survey, trajectory tracking control is one major research focus. This control problem is challenging, especially for multibody systems, since multibody systems often exhibit large nonlinear motion. This explains the active research in this area.

One important aspect for the trajectory-tracking control of complex multibody systems is the design of an accurate feedforward control strategy. Therefore, the second part in Sects. 3–6 gives an overview about the method of servo-constraints, as it is a framework for feedforward control that is directly developed from the MBS community. It is an elegant way to compute an inverse model, which can be directly used as feedforward control. Servo-constraints enforce the system output to be identical to the desired trajectory. The arising DAEs have similarities to the DAEs describing the forward dynamics of general multibody systems. However, the differentiation index of the inverse model DAEs can be much higher than 3. Therefore, numerical solution strategies must be chosen with great care. Before applying servo-constraints, the system properties must be analyzed, since the solution strategy depends on the underlying system type. In order to give a comprehensive overview of the method, it is analyzed for all possible system types. For differentially flat and minimum phase systems, the servo-constraints DAEs can be integrated forward in time. The application example of an overhead crane is used to demonstrate real-time capabilities on an experimental setup. The application example of a three-dimensional robotic manipulator is used to demonstrate numerical solution properties for a complex minimum phase system. For non-minimum phase systems, a boundary value problem must be solved. In the literature, different mathematical formulations exist. Here, they are compared in a numerical study for a two-link manipulator with one passive joint. While all formulations can be solved with comparable accuracy, there are differences in the efficiency. From a practical point of view, the approach describing the inverse model as servo-constraints DAEs that are solved by a BVP represents the simplest approach since it does not depend on deriving the internal dynamics explicitly and no adjoint variables must be solved for.

With the unbroken trend for more efficiency, the development of new control strategies will continue to play an important role in future research. For feedforward control, the inverse model accuracy can be further enhanced, e.g., by adding data-driven approaches, by including multiphysics effects and by taking into account more flexible mode shapes.