On design sensitivities in the structural analysis and optimization of flexible multibody systems

Abstract

The structural analysis and optimization of flexible multibody systems become more and more popular due to the ability to efficiently compute gradients using sophisticated approaches such as the adjoint variable method and the adoption of powerful methods from static structural optimization. To drive the improvement of the optimization process, this work addresses the computation of design sensitivities for multibody systems with arbitrarily parameterized rigid and flexible bodies that are modeled using the floating frame of reference formulation. It is shown that it is useful to augment the body describing standard input data files by their design derivatives. In this way, a clear separation can be achieved between the body modeling and parameterization and the system simulation and analysis.

1 Introduction

Analysis and optimization of flexible multibody systems are important steps in the computed-aided design and dimensioning process of dynamic mechanisms. In [14, 20], typical examples from optimal control and structural optimization of flexible multibody systems are given and reviewed. In the optimization, gradient-based optimization algorithms usually work most efficiently, but they require sensitivity information of the objective and constraint functions [9].

One way to determine these gradients is by numerical differentiation. It is a simple and easy-to-implement method, but it suffers from various deficiencies. For example, the gradient can only be approximated, the perturbations of the design variables are not known a priori, and the computational effort increases proportionally with the number of design variables. However, in structural optimization, which is the focus of this work, the number of design variables is often large. For instance, the topology optimization of a flexible slider-crank mechanism presented in [13] utilizes more than 100.000 design variables. For such high numbers of design variables, numerical differentiation turns out to be prohibitively expensive.

Due to these disadvantages, semianalytical methods, such as direct differentiation and the adjoint variable method, are nowadays often preferred over numerical differentiation, despite the fact that their derivation and implementation effort is usually more demanding and significantly higher. The key idea of semianalytical methods is to derive a set of additional sensitivity equations from which the gradient can be computed. Thereby the structure of the sensitivity equations depends on the formulation of the system equations and the type of the criterion function defined.

Detailed derivations of the direct differentiation method and the adjoint variable method for the sensitivity analysis of rigid multibody systems are presented in [3–5, 12]. The methods have also been applied to flexible multibody systems. In [7], structural sensitivity analysis is performed with the direct differentiation method for a flexible slider-crank mechanism and a vehicle chassis. For the description of the flexible bodies, the floating frame of reference approach is used, whereby the body deformations are approximated with a set of eigenmodes. The application of the direct differentiation method to flexible multibody systems modeled with nonlinear finite element methods is shown, for example, in [6], where topology optimization of truss structures assembled from beams is performed. Also, both the direct differentiation and the adjoint variable method are employed for sensitivity analysis of beam structures modeled with the absolute nodal coordinate formulation; see [16].

The current work focuses on flexible multibody systems modeled with the floating frame of reference approach. It is further assumed that the material properties and the geometry of the bodies are arbitrarily parameterized by the design variables $\boldsymbol{p}\in \mathbb{R}^{h}$, which is typically the case in structural optimization [11].

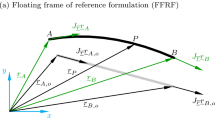
The general structure of the considered multibody system and the notation used are given in Fig. 1. It is assembled from rigid and flexible bodies, spring and damper elements, and actuators. The bodies are connected with each other and the foundation by ideal joints and bearings. Formulating the system equations in implicit descriptor form yields

$${\mathit{\varphi }}^0({\mathit{z}}_{\mathrm{I}}^0,\mathit{p})=\mathbf{0},$$

(1a)

(1b)

$$\mathit{v}:={\dot{\mathit{z}}}_{\mathrm{I}}-\mathit{Z}({\mathit{z}}_{\mathrm{I}}){\mathit{z}}_{\mathrm{II}}=\mathbf{0},$$

(1c)

(1d)

(1e)

The first two equations (1a) and (1b) are the initial conditions at position and velocity level. They are followed by the kinematic equations (1c) and the kinetic equations (1d). The latter are often denoted as equations of motion. The system equations are completed by the constraint equations (1e).

Fig. 1

Flexible multibody system

To analyze the dynamic system (1) in the time domain $t\in [ \begin{array}{c@{\ }c} t^{0}, & t^{1} \end{array} ]$ a scalar criterion function $\psi \in \mathbb{R}$ has to be defined first. If the transient system behavior is of interest, then $\psi$ is typically an integral-type function of the form

$$ \psi (\boldsymbol{p}) = \int _{t^{0}}^{t^{1}} F(t, \boldsymbol{z}_{\mathrm{I}}, \boldsymbol{z}_{\mathrm{II}}, \mbox{$\dot {\boldsymbol{z}}$}_{\mathrm{II}}, \boldsymbol{p}) { \rm d}t. $$

(2)

If the adjoint variable method is employed to compute the gradient $\nabla \psi$, then two steps are necessary. At first, a system of adjoint differential equations has to be derived. Then the gradient can be calculated using the results of the transient analysis and the adjoint analysis. For criterion functions of the form (2) and system equations of the form (1), the derivation of the adjoint system and the gradient equation is comprehensively described, for instance, in [1].

For system (1), the adjoint variables $\boldsymbol{\mu}\in \mathbb{R}^{f}$ and $\boldsymbol{\nu}\in \mathbb{R}^{f}$ can be obtained from the solution of the differential equation

$$\begin{array}{rl}{\mathit{\mu }}^1& =\mathbf{0},{\mathit{M}}^1{\mathit{\nu }}^1=\mathbf{0},\\ \dot{\mathit{\mu }}& =-{\left(\frac{\partial \mathit{v}}{\partial {\mathit{z}}_{\mathrm{I}}}\right)}^{\mathsf{T}}\mathit{\mu }+{\left(\frac{\partial \mathit{s}}{\partial {\mathit{z}}_{\mathrm{I}}}\right)}^{\mathsf{T}}(\mathit{\nu }+\mathit{\xi })+{\left(\frac{\partial \ddot{\mathit{c}}}{\partial {\mathit{z}}_{\mathrm{I}}}\right)}^{\mathsf{T}}\mathit{\gamma }-\frac{\partial F}{\partial {\mathit{z}}_{\mathrm{I}}},\\ \mathit{M}\dot{\mathit{\nu }}& =-{\left(\frac{\partial \mathit{v}}{\partial {\mathit{z}}_{\mathrm{II}}}\right)}^{\mathsf{T}}\mathit{\mu }-\dot{\mathit{M}}\mathit{\nu }+{\left(\frac{\partial \mathit{s}}{\partial {\mathit{z}}_{\mathrm{II}}}\right)}^{\mathsf{T}}(\mathit{\nu }+\mathit{\xi })+{\left(\frac{\partial \ddot{\mathit{c}}}{\partial {\mathit{z}}_{\mathrm{II}}}\right)}^{\mathsf{T}}\mathit{\gamma }-\frac{\partial F}{\partial {\mathit{z}}_{\mathrm{II}}},\end{array}$$

(3)

whereby $\boldsymbol{\xi}\in \mathbb{R}^{f}$ and $\boldsymbol{\gamma}\in \mathbb{R}^{n_{\mathrm{c}}}$ are auxiliary variables. They are necessary to take into account the accelerations and constraint equations in the adjoint analysis and can be determined from the linear equation

$$\begin{array}{r}\left[\begin{array}{cc}\mathit{M}& {\mathit{C}}^{\mathsf{T}}\\ \mathit{C}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\mathit{\xi }\\ \mathit{\gamma }\end{array}\right]=\left[\begin{array}{c}\frac{\partial F}{\partial {\dot{\mathit{z}}}_{\mathrm{II}}}\\ -\mathit{C}\mathit{\nu }\end{array}\right].\end{array}$$

(4)

After solving the adjoint system of equations (3), only the adjoint variables $\boldsymbol{\eta}^{0}\in \mathbb{R}^{f}$ and $\boldsymbol{\zeta}^{0}\in \mathbb{R}^{f}$ at the initial time $t^{0}$ remain to be determined:

$$ \begin{aligned} \left ( \dfrac {\partial \mbox{$\dot {\boldsymbol{\phi}}$}^{0}}{\partial \boldsymbol{z}_{\mathrm{II}}^{0}} \right )^{\mathsf {T}}\boldsymbol{\eta}^{0} & = \boldsymbol{M}^{0} \boldsymbol{\nu}^{0}, \\ \left ( \dfrac {\partial \boldsymbol{\phi}^{0}}{\partial \boldsymbol{z}_{\mathrm{I}}^{0}} \right )^{\mathsf {T}}\boldsymbol{\zeta}^{0} & = \boldsymbol{\mu}^{0} - \left ( \dfrac {\partial \dot {\boldsymbol{\phi}}^{0}}{\partial \boldsymbol{z}_{\mathrm{I}}^{0}} \right )^{\mathsf {T}}\boldsymbol{\eta}^{0}. \end{aligned} $$

(5)

Then the gradient can finally be computed solving

$$ \begin{aligned} \nabla \psi & = \int \limits _{t^{0}}^{t^{1}} \left [ \dfrac {\partial F}{\partial \boldsymbol{p}} - \left ( \dfrac {\partial \boldsymbol{s}}{\partial \boldsymbol{p}} \right )^{\mathsf {T}}\left ( \boldsymbol{\nu}+ \boldsymbol{\xi}\right ) - \left ( \dfrac {\partial \mbox{$\ddot {\boldsymbol{c}}$}}{\partial \boldsymbol{p}} \right )^{\mathsf {T}}\boldsymbol{\gamma}\right ]{ \rm d}t \\ & \qquad - \left ( \dfrac {\partial \boldsymbol{\phi}^{0}}{\partial \boldsymbol{p}} \right )^{\mathsf {T}}\boldsymbol{\zeta}^{0} - \left ( \dfrac {\partial \mbox{$\dot {\boldsymbol{\phi}}$}^{0}}{\partial \boldsymbol{p}} \right )^{\mathsf {T}}\boldsymbol{\eta}^{0}. \end{aligned} $$

(6)

It can be observed from the Eqs. (3)–(6) that two types of derivatives of the system equations are required in the sensitivity analysis. On the one hand, the system equations must be differentiated with respect to the position and velocity variables and, on the other hand, with respect to the design variables. The former derivatives can be determined systematically for the different multibody system formulations. The latter, which are denoted as design sensitivities throughout the paper, are, however, strongly problem-specific. Therefore setting up Eq. (6) is an individual and time-consuming process.

In the literature, symbolic algebra systems are often used to derive the sensitivity equations. For instance, the numerical examples in [4, 7] are created with MAPLE. Alternatively, it is recommended in [8] to apply automatic differentiation [10] to obtain the derivatives of the system equations with respect to the state and design variables, in particular, for complex multibody systems. A third way is presented in [22], where the state sensitivities are computed analytically and the design sensitivities by numerical differentiation.

Aside from the numerical advantages and disadvantages of the three ways, they all suffer from mixing up two fundamental problems: the derivative of body-specific properties, such as the center of gravity, with respect to the design variables, and the derivative of the system equations with respect to body-specific properties. To improve structural optimization procedures, this work aims to remove this mixing. Therefore the kinematic and kinetic equations are systematically differentiated with respect to arbitrary geometry and material parameters. Further, it is recommended to adapt the body describing object-oriented standard input data [21] and augment them by their design derivatives. In this way the modeling and parameterization of the bodies can be considered separately from the dynamic simulation and adjoint sensitivity analysis.

The rest of this paper is organized in the following way. Section 2 addresses the partial derivatives of the system equations with respect to the design variables. After a brief review of the body kinematics and kinetics, their design sensitivities are systematically derived. In Sect. 3 the standard input data are summarized, and an augmentation of the object-oriented data set is suggested to allow a general and systematic parameterization of rigid and flexible bodies. The procedure is then demonstrated in Sect. 4 using an example from the topology optimization of a flexible multibody system. Finally, Sect. 5 concludes with a brief summary and discussion.

2 Design sensitivities of system equations

To evaluate the gradient equation (6), the partial derivatives of the implicit initial conditions, of the implicit kinetic equations, and of the constraints at acceleration level with respect to the design variables are required. In the following section, these derivatives are systematically derived. At first, the marker kinematics and relative marker kinematics of flexible bodies are briefly summarized and differentiated, whereby a similar notation as in [18, 19] is used. After that, the kinetic equations are presented, and the quantities necessary for their derivatives with respect to the structural design parameters are discussed.

2.1 Marker kinematics

In the floating frame of reference formulation, the deformation of a flexible body $i$ is described with regard to a reference frame Rⁱ, which undergoes large translational and rotational motions; see Fig. 2. Thus the absolute position $\boldsymbol{\rho}^{k,i}$ of a marker $k$ at point P on the flexible body $i$ can be displayed as

$$ \boldsymbol{\rho}^{k,i} = \boldsymbol{\rho}^{i} + \boldsymbol{R}^{k,i} + \boldsymbol{u}^{k,i}, $$

(7)

where $\boldsymbol{\rho}^{i}$ is the position of the reference frame, $\boldsymbol{R}^{k,i}$ is the position of marker $k$ with respect to Rⁱ in the undeformed configuration, and $\boldsymbol{u}^{k,i}$ is the space- and time-dependent displacement due to the body deformation. It is worth noting that all vectors in Eq. (7) are represented in the reference frame Rⁱ.

Fig. 2

Kinematics of a flexible body using the floating frame of reference formulation

The absolute orientation of a frame that is fixed in P and described by the Cartesian basis $\boldsymbol{e}^{k,i}$ is represented by the rotation matrix $\boldsymbol{S}^{k,i}$, which results from two successive rotations as

$$ \boldsymbol{S}^{k,i} = \boldsymbol{S}^{i}( \boldsymbol{\beta}^{i})\boldsymbol{D}^{k, i}, \quad \boldsymbol{e}^{\mathrm{I}} = \boldsymbol{S}^{k,i} \boldsymbol{e}^{k,i}. $$

(8)

Thereby the first rotation matrix $\boldsymbol{S}^{i}$ is here parameterized by the parameters $\boldsymbol{\beta}^{i}\in \mathbb{R}^{3}$ and describes the rotation from the inertial into the reference frame, whereas $\boldsymbol{D}^{k, i}$ represents the rotation from the reference into the marker system. Provided that there is no initial rotation and assuming the deformations to be small and linear elastic, $\boldsymbol{D}^{k,i}$ can be approximated as

$$ \boldsymbol{D}^{k,i} \approx \textbf{E} + \tilde{\boldsymbol{\vartheta}}^{k,i}, $$

(9)

where $\boldsymbol{\vartheta}^{k,i} \in \mathbb{R}^{3}$ are small rotation angles, which are converted by the tilde operator $\tilde{(..)}$ into a skew-symmetric matrix as follows:

$$\widetilde{\left[\begin{array}{c}{\vartheta }_1^{k,i}\\ {\vartheta }_2^{k,i}\\ {\vartheta }_3^{k,i}\end{array}\right]}=\left[\begin{array}{ccc}0& -{\vartheta }_3^{k,i}& {\vartheta }_2^{k,i}\\ {\vartheta }_3^{k,i}& 0& -{\vartheta }_1^{k,i}\\ -{\vartheta }_2^{k,i}& {\vartheta }_1^{k,i}& 0\end{array}\right].$$

(10)

Both the elastic displacement $\boldsymbol{u}^{k,i}$ and rotation $\boldsymbol{\vartheta}^{k,i}$ depend on space and time. Using a Ritz approach, space- and time-dependency can be separated as

$$ \boldsymbol{u}^{k,i} = \boldsymbol{\Phi}^{k,i} \boldsymbol{q}^{i} \quad \text{and} \quad \boldsymbol{\vartheta}^{k,i} = \boldsymbol{\Psi}^{k,i}\boldsymbol{q}^{i}, $$

(11)

where $\boldsymbol{\Phi}^{k,i} = \boldsymbol{\Phi}^{i}( \boldsymbol{R}^{k,i})$ and $\boldsymbol{\Psi}^{k,i} = \boldsymbol{\Psi}^{i}( \boldsymbol{R}^{k,i})$ are the matrices of the shape functions defined over the entire body, and $\boldsymbol{q}^{i} \in \mathbb{R}^{n_{q}^{i}}$ are time-dependent weighting factors, which are often denoted as elastic coordinates.

The position and orientation of an arbitrary marker $k$ on the flexible body $i$ can be expressed by the position variables

$$ \boldsymbol{z}_{\mathrm{I}}^{i} = \left [ \textstyle\begin{array}{c} \boldsymbol{\rho}^{i} \\ \boldsymbol{\beta}^{i} \\ \boldsymbol{q}^{i} \end{array}\displaystyle \right ] \in \mathbb{R}^{6+n_{\mathrm{q}}^{i}}. $$

(12)

Next to the position and orientation, also the velocity and angular velocity of marker $k$ are required. Again, all kinematic quantities are represented in the body reference frame Rⁱ. For the absolute velocity and angular velocity of marker $k$ represented in Rⁱ it holds,

$$ \boldsymbol{v}^{k,i} = \boldsymbol{v}^{i} + \boldsymbol{\omega}^{i}\times \boldsymbol{r}^{k,i} + \boldsymbol{\Phi}^{k,i}\mbox{$\dot {\boldsymbol{q}}$}^{i} $$

(13)

and

$$ \boldsymbol{\omega}^{k,i} = \boldsymbol{\omega}^{i} + \boldsymbol{\Psi}^{k,i}\mbox{$\dot {\boldsymbol{q}}$}^{i}, $$

(14)

where $\boldsymbol{v}^{i}$ and $\boldsymbol{\omega}^{i}$ are the velocity and angular velocity of the reference frame Rⁱ. The velocities (13) and (14) can be written in a more compact form as

$$ \boldsymbol{v}^{k,i} = \boldsymbol{T}_{\mathrm{t}}^{k,i} \boldsymbol{z}_{\mathrm{II}}^{i} $$

(15)

and

$$ \boldsymbol{\omega}^{k,i} = \boldsymbol{T}_{\mathrm{r}}^{k,i} \boldsymbol{z}_{\mathrm{II}}^{i} $$

(16)

using the velocity coordinates

$$ \boldsymbol{z}_{\mathrm{II}}^{i} = \left [ \textstyle\begin{array}{c} \boldsymbol{v}^{i} \\ \boldsymbol{\omega}^{i} \\ \mbox{$\dot {\boldsymbol{q}}$}^{i} \end{array}\displaystyle \right ] $$

(17)

of body $i$, an auxiliary matrix for the translation

$${\mathit{T}}_{\mathrm{t}}^{k,i}({\mathit{z}}_{\mathrm{I}}^i)=\left[\begin{array}{ccc}\mathbf{\text{E}}& -{\tilde{\mathit{r}}}^{k,i}& {\mathbf{\Phi }}^{k,i}\end{array}\right],$$

(18)

and an auxiliary matrix for the rotation

$${\mathit{T}}_{\mathrm{r}}^{k,i}=\left[\begin{array}{ccc}\mathbf{0}& \mathbf{\text{E}}& {\mathbf{\Psi }}^{k,i}\end{array}\right].$$

(19)

Finally, the absolute acceleration and angular acceleration of marker $k$ represented in Rⁱ are

$$ \boldsymbol{a}^{k,i} = \mbox{$\dot {\boldsymbol{v}}$}^{i} - \tilde{\boldsymbol{r}}^{k,i} \mbox{$\dot {\boldsymbol{\omega}}$}^{i} + \boldsymbol{\Phi}^{k,i}\mbox{$\ddot {\boldsymbol{q}}$}^{i} + \tilde{\boldsymbol{\omega}}^{i} \left ( \boldsymbol{v}^{i} + 2\boldsymbol{\Phi}^{k,i} \mbox{$\dot {\boldsymbol{q}}$}^{i} + \tilde{\boldsymbol{\omega}}^{i} \boldsymbol{r}^{k,i} \right ) $$

(20)

and

$$ \boldsymbol{\alpha}^{k,i} = \mbox{$\dot {\boldsymbol{\omega}}$}^{i} + \boldsymbol{\Psi}^{k,i}\mbox{$\ddot {\boldsymbol{q}}$}^{i} + \tilde {\boldsymbol{\omega}}^{i}\left ( \boldsymbol{\omega}^{i} + \boldsymbol{\Psi}^{k,i} \mbox{$\dot {\boldsymbol{q}}$}^{i} \right ), $$

(21)

respectively. Like the velocities, they can be displayed in compact notation as

$$ \boldsymbol{a}^{k,i} = \boldsymbol{T}_{\mathrm{t}}^{k,i} \mbox{$\dot {\boldsymbol{z}}$}^{i}_{\mathrm{II}} + \boldsymbol{\zeta}^{k,i}_{\mathrm{t}} $$

(22)

and

$$ \boldsymbol{\alpha}^{k,i} = \boldsymbol{T}_{\mathrm{r}}^{k,i} \mbox{$\dot {\boldsymbol{z}}$}^{i}_{\mathrm{II}} + \boldsymbol{\zeta}^{k,i}_{\mathrm{r}}, $$

(23)

where

$$ \boldsymbol{\zeta}_{\mathrm{t}}^{k,i}(\boldsymbol{z}_{\mathrm{I}}^{i}, \boldsymbol{z}_{\mathrm{II}}^{i}) = \tilde{\boldsymbol{\omega}}^{i}\left ( \boldsymbol{v}^{i} + 2\boldsymbol{\Phi}^{k,i} \mbox{$\dot {\boldsymbol{q}}$}^{i} + \tilde{\boldsymbol{\omega}}^{i}\boldsymbol{r}^{k,i} \right ) $$

(24)

and

$$ \boldsymbol{\zeta}_{\mathrm{r}}^{k,i}(\boldsymbol{z}_{\mathrm{II}}^{i}) = \tilde{\boldsymbol{\omega}}^{i}\boldsymbol{\Psi}^{k,i} \mbox{$\dot {\boldsymbol{q}}$}^{i}. $$

(25)

2.2 Derivatives of marker kinematics

From the Eqs. (7) and (8) it can be seen that the position and orientation of marker $k$ depends both implicitly and explicitly on the design variables $\boldsymbol{p}$. On the one hand, the position variables $\boldsymbol{z}_{\mathrm{I}}^{i}$ depend implicitly via the system equations on time $t$ and the design variables $\boldsymbol{p}$. On the other hand, explicit dependencies of the position $\boldsymbol{R}^{k,i}$ in the undeformed configuration or the shape functions $\boldsymbol{\Phi}^{k,i}$ and $\boldsymbol{\Psi}^{k,i}$ can occur depending on the parameterization of the body.

To provide a systematic way to compute the partial derivatives of the system equations with respect to the design variables, the derivatives of the marker kinematics are derived first. They are required later to compute the derivatives of the constraint equations, the reaction forces, and the applied discrete forces and torques, which act at marker $k$.

Differentiating the marker position (7) and rotation (8) with respect to the $l$th component of $\boldsymbol{p}$ yields

$$ \dfrac {\partial \boldsymbol{\rho}^{k,i}}{\partial p_{l}} = \dfrac {\partial \boldsymbol{R}^{k,i}}{\partial p_{l}} + \dfrac {\partial \boldsymbol{\Phi}^{k,i}}{\partial p_{l}} \boldsymbol{q}^{i} $$

(26)

and

$$ \dfrac {\partial \boldsymbol{S}^{k,i}}{\partial p_{l}} = \boldsymbol{S}^{i} \widetilde{\left (\dfrac {\partial \boldsymbol{\Psi}^{k,i}}{\partial p_{l}}\boldsymbol{q}^{i}\right )}. $$

(27)

To compute the partial derivatives of the velocity, angular velocity, acceleration, and angular acceleration, only the partial derivatives of the auxiliary matrices $\boldsymbol{T}_{\mathrm{t}}^{k,i}$ and $\boldsymbol{T}_{\mathrm{r}}^{k,i}$ and of the auxiliary vectors $\boldsymbol{\zeta}_{\mathrm{t}}^{k,i}$ and $\boldsymbol{\zeta}_{\mathrm{r}}^{k,i}$ have to be provided. They are

$$\begin{aligned} \dfrac {\partial \boldsymbol{T}_{\mathrm{t}}^{k,i}}{\partial p_{l}} & = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \boldsymbol{0} & - \widetilde{\left ( \dfrac {\partial \boldsymbol{R}^{k,i}}{\partial p_{l}} + \dfrac {\partial \boldsymbol{\Phi}^{k,i}}{\partial p_{l}}\boldsymbol{q}^{i} \right )} & \dfrac {\partial \boldsymbol{\Phi}^{k,i}}{\partial p_{l}} \end{array}\displaystyle \right ], \end{aligned}$$

(28)

$$\begin{aligned} \dfrac {\partial \boldsymbol{T}^{k,i}_{\mathrm{r}}}{\partial p_{l}} & = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \boldsymbol{0} & \boldsymbol{0} & \dfrac {\partial \boldsymbol{\Psi}^{k,i}}{\partial p_{l}} \end{array}\displaystyle \right ], \end{aligned}$$

(29)

$$\begin{aligned} \dfrac {\partial \boldsymbol{\zeta}_{\mathrm{t}}^{k,i}}{\partial p_{l}} & = 2\tilde{\boldsymbol{\omega}}^{i} \dfrac {\partial \boldsymbol{\Phi}^{k,i}}{\partial p_{l}} \mbox{$\dot {\boldsymbol{q}}$}^{i} + \tilde{\boldsymbol{\omega}}^{i} \tilde{\boldsymbol{\omega}}^{i}\left ( \dfrac {\partial \boldsymbol{R}^{k,i}}{\partial p_{l}} + \dfrac {\partial \boldsymbol{\Phi}^{k,i}}{\partial p_{l}} \boldsymbol{q}^{i} \right ), \quad \text{and} \end{aligned}$$

(30)

$$\begin{aligned} \dfrac {\partial \boldsymbol{\zeta}_{\mathrm{r}}^{k,i}}{\partial p_{l}} & = \tilde{\boldsymbol{\omega}}^{i} \dfrac {\partial \boldsymbol{\Psi}^{k,i}}{\partial p_{l}} \mbox{$\dot {\boldsymbol{q}}$}^{i}. \end{aligned}$$

(31)

It is worth mentioning that the derivatives (28), (30), and (31) are not constant but depend on the position and velocity coordinates of body $i$.

2.3 Relative marker kinematics

Kinematic constraints lock 1 to 6 degrees of freedom between markers to model joints or bearings. Since they are of particular importance, their formulation and their derivatives are presented in the following. To this end, at first, the relative marker kinematics at joint $s$ defined between marker $k$ on body $i$ and marker $m$ on body $j$ is briefly presented; see Fig. 3. A detailed description of the relative marker kinematics can be found in [18].

Fig. 3

Relative marker kinematics at joint $s$

For readability, the upper index $(\dots )^{k,i}$ is replaced by $(\dots )^{t}$ to denote the “to” marker, and $(\dots )^{m,j}$ is replaced by $(\dots )^{f}$ for the “from” marker. Thus the absolute positions of the “to” and “from” markers are

$$ \boldsymbol{\rho}^{k,i} \equiv \boldsymbol{\rho}^{t} \quad \text{and}\quad \boldsymbol{\rho}^{m,j} \equiv \boldsymbol{\rho}^{f}. $$

(32)

The relative position $\boldsymbol{d}^{s}$ of the “from” and “to” markers represented in the “to” marker frame P^t is

$$ \boldsymbol{d}^{s} = \boldsymbol{D}^{t^{ \mathsf {T}}} \left (\boldsymbol{\rho}^{i} + \boldsymbol{R}^{t} + \boldsymbol{\Phi}^{t} \boldsymbol{q}^{i}\right ) -\boldsymbol{D}^{t^{ \mathsf {T}}}\boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j}\left (\boldsymbol{\rho}^{j} + \boldsymbol{R}^{f} + \boldsymbol{\Phi}^{f} \boldsymbol{q}^{j}\right ). $$

(33)

The relative rotation between the “from” and “to” markers is described by the rotation matrix $\boldsymbol{B}^{s}(\boldsymbol{\beta}^{s}), \boldsymbol{\beta}^{s}\in \mathbb{R}^{3}$, which can be computed by

$$ \boldsymbol{B}^{s}(\boldsymbol{\beta}^{s}) = \boldsymbol{D}^{f^{\mathsf {T}}} \boldsymbol{S}^{j^{\mathsf {T}}} \boldsymbol{S}^{i}\boldsymbol{D}^{t}, \quad \boldsymbol{e}^{f} = \boldsymbol{B}^{s}( \boldsymbol{\beta}^{s}) \boldsymbol{e}^{t}. $$

(34)

To derive the relative velocity and relative angular velocity of the “from” and “to” markers, at first, the absolute time derivative of the relative joint position $\boldsymbol{d}^{s}$ with respect to the inertial frame

$$ \dfrac{\mathrm{d}}{\mathrm{d}t}\boldsymbol{d}^{s} = \boldsymbol{V}^{s} + {^{t}}\boldsymbol{\omega}^{t} \times \boldsymbol{d}^{s}. $$

(35)

is computed. Thereby $\boldsymbol{V}^{s}$ is the relative time derivative of the relative marker position, and ${^{t}}\boldsymbol{\omega}^{t}$ is the angular velocity of the “to” marker frame represented in P^t. The latter can be obtained by transforming Eq. (16) into the “to” marker frame as

$$ {^{t}}\boldsymbol{\omega}^{t} = \boldsymbol{D}^{t^{ \mathsf {T}}} \boldsymbol{T}_{\mathrm{r}}^{t} \boldsymbol{z}_{\mathrm{II}}^{i}. $$

(36)

The absolute time derivative of the relative joint position (35) can alternatively be expressed by the absolute velocities $\boldsymbol{v}^{f}$ and $\boldsymbol{v}^{t}$ of the “from” and “to” markers. Transforming the absolute velocities into the “to” marker frame it holds,

$$ \boldsymbol{V}^{s} + {^{t}}\boldsymbol{\omega}^{t} \times \boldsymbol{d}^{s} = \boldsymbol{D}^{t^{ \mathsf {T}}}\boldsymbol{v}^{t} - \boldsymbol{D}^{t^{ \mathsf {T}}}\boldsymbol{S}^{i^{ \mathsf {T}}}\boldsymbol{S}^{j}\boldsymbol{v}^{f}. $$

(37)

Rearranging Eq. (37) for the relative joint velocity $\boldsymbol{V}^{s}$ and using the compact notation (15) for the absolute marker velocities yield

$$ \boldsymbol{V}^{s} = \boldsymbol{D}^{t^{ \mathsf {T}}}\boldsymbol{T}^{t}_{\mathrm{t}} \boldsymbol{z}^{i}_{ \rm II} - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j} \boldsymbol{T}^{f}_{\mathrm{t}} \boldsymbol{z}^{j}_{\mathrm{II}} + \tilde{\boldsymbol{d}}^{s} {^{t}} \boldsymbol{\omega}^{t}. $$

(38)

The relative angular velocity between the “from” and “to” markers represented in P^t is given by

$$ \boldsymbol{\Omega}^{s} = \boldsymbol{D}^{t^{ \mathsf {T}}}\boldsymbol{\omega}^{t} - \boldsymbol{D}^{t^{ \mathsf {T}}}\boldsymbol{S}^{i^{ \mathsf {T}}}\boldsymbol{S}^{j}\boldsymbol{\omega}^{f}, $$

(39)

which can be expressed in terms of the velocity coordinates of the “from” and “to” bodies as

$$ \boldsymbol{\Omega}^{s} = \boldsymbol{D}^{t^{ \mathsf {T}}}\boldsymbol{T}^{t}_{\mathrm{r}}\boldsymbol{z}^{i}_{ \rm II} - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j} \boldsymbol{T}^{f}_{\mathrm{r}} \boldsymbol{z}^{j}_{\mathrm{II}}. $$

(40)

In the same way as the relative velocities, the relative acceleration and angular acceleration between the “from” and “to” markers can be determined as

$$ \begin{aligned} \mbox{$\dot {\boldsymbol{V}}$}^{s} & = \boldsymbol{D}^{t^{\mathsf {T}}}\left ( \boldsymbol{T}^{t}_{\mathrm{t}} \mbox{$\dot {\boldsymbol{z}}$}^{i}_{\mathrm{II}} + \boldsymbol{\zeta}^{t}_{\mathrm{t}}\right ) + \tilde{\boldsymbol{d}}^{s} \boldsymbol{D}^{t^{ \mathsf {T}}}\left ( \boldsymbol{T}^{t}_{\mathrm{r}} \mbox{$\dot {\boldsymbol{z}}$}^{i}_{\mathrm{II}} + \boldsymbol{\zeta}^{t}_{\mathrm{r}} \right ) - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j}\left (\boldsymbol{T}^{f}_{\mathrm{t}} \mbox{$\dot {\boldsymbol{z}}$}^{j}_{\mathrm{II}} + \boldsymbol{\zeta}^{f}_{\mathrm{t}}\right ) \\ & \qquad - {^{t}}\tilde{\boldsymbol{\omega}}^{t}\left (2 \boldsymbol{V}^{s} + {^{t}}\tilde{\boldsymbol{\omega}}^{t} \boldsymbol{d}^{s}\right ) \end{aligned} $$

(41)

and

$$ \mbox{$\dot {\boldsymbol{\Omega}}$}^{s} = \boldsymbol{D}^{t^{\mathsf {T}}}\left ( \boldsymbol{T}^{t}_{\mathrm{r}} \mbox{$\dot {\boldsymbol{z}}$}_{\mathrm{II}}^{i} + \boldsymbol{\zeta}_{\mathrm{r}}^{t} \right ) - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j}\left (\boldsymbol{T}^{f}_{\mathrm{r}} \mbox{$\dot {\boldsymbol{z}}$}_{\mathrm{II}}^{j} + \boldsymbol{\zeta}_{\mathrm{r}}^{f} \right ) - {^{t}} \tilde {\boldsymbol{\omega}}^{t}\boldsymbol{\Omega}^{s}, $$

(42)

respectively.

2.4 Derivatives of relative marker kinematics

The relative marker kinematics is the basis to formulate the constraint equations. Hence their derivatives with respect to the design variables are required to compute the partial derivatives of the constraint equations with respect to $\boldsymbol{p}$. In the following, the partial derivatives of the relative marker kinematics with respect to the design variables are presented. Thereby it is assumed that the “from” body is parameterized.

The partial derivative of the relative marker position $\boldsymbol{d}^{s}$ with respect to the $l$th component of $\boldsymbol{p}$ is

$$ \dfrac {\partial \boldsymbol{d}^{s}}{\partial p_{l}} = - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j^{\mathsf {T}}} \dfrac {\partial \boldsymbol{\rho}^{f}}{\partial p_{l}}, $$

(43)

where $\partial{\boldsymbol{\rho}^{f}}/\partial{p_{l}}$ can be determined from Eq. (26). In contrast, the partial derivatives of the relative marker orientation represented by $\boldsymbol{\beta}^{s}$ cannot be directly computed. The rotation parameters $\boldsymbol{\beta}^{s}$ are only auxiliary variables, which depend on the position variables of the “from” and “to” bodies, as can be seen from Eq. (34). However, to find their derivatives with respect to the design variables $\boldsymbol{p}$, the implicit equation

$$ \boldsymbol{B}^{s}(\boldsymbol{\beta}^{s}) - \boldsymbol{D}^{f^{\mathsf {T}}}( \boldsymbol{q}^{j}, \boldsymbol{\Psi}^{f}) \boldsymbol{S}^{j^{\mathsf {T}}}( \boldsymbol{\beta}^{j})\boldsymbol{S}^{i}( \boldsymbol{\beta}^{i})\boldsymbol{D}^{t}( \boldsymbol{q}^{i}, \boldsymbol{\Psi}^{t}) = \boldsymbol{0} $$

(44)

can be rewritten in vector form as

$$ \boldsymbol{\chi}^{s}(\boldsymbol{\beta}^{s}, \boldsymbol{p}) = \boldsymbol{0}. $$

(45)

The total derivative of Eq. (45) yields

$$ \dfrac {\partial \boldsymbol{\chi}^{s}}{\partial \boldsymbol{\beta}^{s}} \Delta \boldsymbol{\beta}^{s} + \dfrac {\partial \boldsymbol{\chi}^{s}}{\partial \boldsymbol{p}} \Delta \boldsymbol{p}= \boldsymbol{0}. $$

(46)

Using either three independent equations from (46) or the pseudo-inverse $\left [ \left (\partial{\boldsymbol{\chi}^{s}}/\partial{ \boldsymbol{\beta}^{s}}\right )^{\mathsf {T}} \partial{\boldsymbol{\chi}^{s}}/\partial{ \boldsymbol{\beta}^{s}}\right ]^{-1}$, the partial derivatives of the relative orientation parameters with respect to the design variables can be determined from Eq. (46) as

$$ \dfrac{\Delta \boldsymbol{\beta}^{s}}{\Delta \boldsymbol{p}} = - \left [ \left ( \dfrac {\partial \boldsymbol{\chi}^{s}}{\partial \boldsymbol{\beta}^{s}} \right )^{\mathsf {T}} \dfrac {\partial \boldsymbol{\chi}^{s}}{\partial \boldsymbol{\beta}^{s}} \right ]^{-1}\left ( \dfrac {\partial \boldsymbol{\chi}^{s}}{\partial \boldsymbol{\beta}^{s}} \right )^{\mathsf {T}} \dfrac {\partial \boldsymbol{\chi}^{s}}{\partial \boldsymbol{p}}. $$

(47)

The partial derivatives of the relative marker velocity $\boldsymbol{V}^{s}$ and relative angular marker velocity $\boldsymbol{\Omega}^{s}$ with respect to $p_{l}$ can be computed by Eqs. (28), (29), and (43) as

$$ \dfrac {\partial \boldsymbol{V}^{s}}{\partial p_{l}} = \dfrac {\partial \tilde {\boldsymbol{d}}^{s}}{\partial p_{l}} \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{T}^{t}_{\mathrm{r}}\boldsymbol{z}^{i}_{\mathrm{II}} - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j} \dfrac {\partial \boldsymbol{T}^{f}_{\mathrm{t}}}{\partial p_{l}} \boldsymbol{z}^{j}_{\mathrm{II}} $$

(48)

and

$$ \dfrac {\partial \boldsymbol{\Omega}^{s}}{\partial p_{l}} = - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j} \dfrac {\partial \boldsymbol{T}^{f}_{\mathrm{r}}}{\partial p_{l}} \boldsymbol{z}^{j}_{\mathrm{II}}. $$

(49)

Finally, the derivatives of the relative marker acceleration $\mbox{$\dot {\boldsymbol{V}}$}^{s}$ and relative angular acceleration $\mbox{$\dot {\boldsymbol{\Omega}}$}^{s}$ with respect to the design parameters $\boldsymbol{p}$ can be determined using the derivatives of the marker kinematics (28), (29), (30), and (31) and of the relative marker kinematics (43), (48), and (49) as

$$ \begin{aligned} \dfrac {\partial \mbox{$\dot {\boldsymbol{V}}$}^{s}}{\partial p_{l}} & = \dfrac {\partial \tilde {\boldsymbol{d}}^{s}}{\partial p_{l}} \boldsymbol{D}^{t^{\mathsf {T}}}\left ( \boldsymbol{T}_{\mathrm{r}}^{t} \mbox{$\dot {\boldsymbol{z}}$}_{\mathrm{II}}^{i} + \boldsymbol{\zeta}_{\mathrm{r}}^{t} \right ) -\boldsymbol{D}^{t^{ \mathsf {T}}}\boldsymbol{S}^{i^{ \mathsf {T}}}\boldsymbol{S}^{j}\left ( \dfrac {\partial \boldsymbol{T}^{f}_{\mathrm{t}}}{\partial p_{l}} \mbox{$\dot {\boldsymbol{z}}$}^{j}_{\mathrm{II}} + \dfrac {\partial \boldsymbol{\zeta}^{f}_{\mathrm{t}}}{\partial p_{l}} \right ) \\ & \qquad -{^{t}}\tilde{\boldsymbol{\omega}}^{t}\left (2 \dfrac {\partial \boldsymbol{V}^{s}}{\partial p_{l}} + {^{t}} \tilde{\boldsymbol{\omega}}^{t} \dfrac {\partial \boldsymbol{d}^{s}}{\partial p_{l}}\right ) \end{aligned} $$

(50)

and

$$ \dfrac {\partial \mbox{$\dot {\boldsymbol{\Omega}}$}^{s}}{\partial p_{l}} = - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j}\left ( \dfrac {\partial \boldsymbol{T}^{f}_{\mathrm{r}}}{\partial p_{l}} \mbox{$\dot {\boldsymbol{z}}$}_{\mathrm{II}}^{j} + \dfrac {\partial \boldsymbol{\zeta}_{\mathrm{r}}^{f}}{\partial p_{l}} \right ) - {^{t}}\tilde {\boldsymbol{\omega}}^{t} \dfrac {\partial \boldsymbol{\Omega}^{s}}{\partial p_{l}}, $$

(51)

respectively.

2.5 Constraint equations

Using the relative marker kinematics presented in Sect. 2.3, implicit kinematical constraint equations can be formulated. For example, if all degrees of freedom are locked at joint $s$ it holds

$$ \boldsymbol{c}^{s} = \left [ \textstyle\begin{array}{c} \boldsymbol{d}^{s} \\ \boldsymbol{\beta}^{s} \end{array}\displaystyle \right ] \stackrel{!}{=} \boldsymbol{0}. $$

(52)

Differentiating Eq. (52) with respect to time $t$ yields the implicit constraint equations at velocity level for joint $s$ in terms of the relative joint coordinates

$${\dot{\mathit{c}}}^s=\left[\begin{array}{c}{\dot{\mathit{d}}}^s\\ {\dot{\mathit{\beta }}}^s\end{array}\right]=\underset{{\mathit{X}}^s}{\underbrace{\left[\begin{array}{cc}\mathbf{\text{E}}& \mathbf{0}\\ \mathbf{0}& {\mathit{X}}_{\mathrm{r}}^s({\mathit{\beta }}^s)\end{array}\right]}}\left[\begin{array}{c}{\mathit{V}}^s\\ {\mathbf{\Omega }}^s\end{array}\right]\stackrel{!}{=}\mathbf{0}.$$

(53)

It can be seen that to compute the time derivative of the rotation parameters $\mbox{$\dot {\boldsymbol{\beta}}$}^{s}$, the kinematic relation $\boldsymbol{X}_{\mathrm{r}}^{s}$ is required, which depends in turn on the rotation parameters $\boldsymbol{\beta}^{s}$; see [17].

With Eqs. (38) and (40) the relative joint velocity and angular velocity can be expressed in terms of the velocity coordinates of the “from” and “to” bodies as

$$ \left [ \textstyle\begin{array}{c} \boldsymbol{V}^{s} \\ \boldsymbol{\Omega}^{s} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c@{\quad}c} \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{T}_{\mathrm{t}}^{t} + \tilde{\boldsymbol{d}}^{s} \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{T}_{\mathrm{r}}^{t} & - \boldsymbol{D}^{{ \mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j} \boldsymbol{T}_{\mathrm{t}}^{f} \\ \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{T}^{t}_{\mathrm{r}} & - \boldsymbol{D}^{t^{ \mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}} \boldsymbol{S}^{j} \boldsymbol{T}^{f}_{\mathrm{r}} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c} \boldsymbol{z}_{\mathrm{II}}^{i} \\ \boldsymbol{z}_{\mathrm{II}}^{j} \end{array}\displaystyle \right ]. $$

(54)

Plugging Eq. (54) into Eq. (53) yields the constraints at velocity level

$$ \mbox{$\dot {\boldsymbol{c}}$}^{s} = \underbrace{ \left [\textstyle\begin{array}{c@{\quad}c} \boldsymbol{D}^{t^{\mathsf {T}}}\boldsymbol{T}_{\mathrm{t}}^{t} + \tilde{\boldsymbol{d}}^{s}\boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{T}_{\mathrm{r}}^{t} & - \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}}\boldsymbol{S}^{j} \boldsymbol{T}_{\mathrm{t}}^{f} \\ \boldsymbol{X}^{s}_{\mathrm{r}}\boldsymbol{D}^{t^{\mathsf {T}}}\boldsymbol{T}^{t}_{\mathrm{r}} & -\boldsymbol{X}^{s}_{\mathrm{r}} \boldsymbol{D}^{t^{\mathsf {T}}} \boldsymbol{S}^{i^{\mathsf {T}}}\boldsymbol{S}^{j} \boldsymbol{T}^{f}_{\mathrm{r}} \end{array}\displaystyle \right ]}_{\boldsymbol{C}^{s}} \left [ \textstyle\begin{array}{c} \boldsymbol{z}_{\mathrm{II}}^{i} \\ \boldsymbol{z}_{\mathrm{II}}^{j} \end{array}\displaystyle \right ] $$

(55)

in terms of the local Jacobian matrix $\boldsymbol{C}^{s}$ and the velocity coordinates $\boldsymbol{z}_{\mathrm{II}}^{i}$ and $\boldsymbol{z}_{\mathrm{II}}^{j}$ of the “to” and “from” bodies. Representation (55) is very useful as it shows the structure of $\boldsymbol{C}^{s}$, whose derivatives will be required in the differentiation of the reaction forces.

Differentiating the constraint equations (53) once more with respect to time $t$, the constraint equations at acceleration level are obtained as

$$ \mbox{$\ddot {\boldsymbol{c}}$}^{s} = \boldsymbol{X}^{s} \underbrace{\left [\textstyle\begin{array}{c} \mbox{$\dot {\boldsymbol{V}}$}^{s} \\ \mbox{$\dot {\boldsymbol{\Omega}}$}^{s} \end{array}\displaystyle \right ]}_{\dot {\boldsymbol{x}}_{\mathrm{II}}} + \dot {\boldsymbol{X}}^{s} \underbrace{\left [\textstyle\begin{array}{c} \boldsymbol{V}^{s} \\ \boldsymbol{\Omega}^{s} \end{array}\displaystyle \right ]}_{\boldsymbol{x}_{\mathrm{II}}} \stackrel{!}{=} \boldsymbol{0} $$

(56)

with the relative joint velocities $\boldsymbol{x}_{\mathrm{II}}$.

2.6 Derivatives of constraint equations

In this final step of the differentiation of the kinematics with respect to the design variables, the partial derivatives of the constraint equations with respect to $\boldsymbol{p}$ are given. With Eq. (43) and (47), the partial derivatives of the constraint equations at position level with respect to $p_{l}$ are simply

$$ \dfrac {\partial \boldsymbol{c}^{s}}{\partial p_{l}} = \left [ \textstyle\begin{array}{c} \dfrac {\partial \boldsymbol{d}^{s}}{\partial p_{l}} \\ \dfrac {\partial \boldsymbol{\beta}^{s}}{\partial p_{l}} \end{array}\displaystyle \right ]. $$

(57)

Derivatives (57) can be used in the evaluation of gradient (6) as part of the derivatives of the implicit initial conditions at position level $\boldsymbol{\phi}^{0}$.

To represent the partial derivatives of the constraint equations at velocity level with respect to $\boldsymbol{p}$, there are two ways. On the one hand, $\partial \mbox{$\dot {\boldsymbol{c}}$}^{s}/\partial p_{l}$ can be written in terms of the joint coordinates as

$$ \dfrac {\partial \mbox{$\dot {\boldsymbol{c}}$}^{s}}{\partial p_{l}} = \dfrac {\partial \boldsymbol{X}^{s}}{\partial p_{l}}\left [ \textstyle\begin{array}{c} \boldsymbol{V}^{s} \\ \boldsymbol{\Omega}^{s} \end{array}\displaystyle \right ] + \boldsymbol{X}^{s}\left [ \textstyle\begin{array}{c} \dfrac {\partial \boldsymbol{V}^{s}}{\partial p_{l}} \\ \dfrac {\partial \boldsymbol{\Omega}^{s}}{\partial p_{l}} \end{array}\displaystyle \right ], $$

(58)

whereby the partial derivatives of the velocity and of the angular velocity are given in Eq. (48) and (49), respectively. In Eq. (58), the partial derivatives of the kinematic matrix

$$ \dfrac {\partial \boldsymbol{X}^{s}}{\partial p_{l}} = \sum _{i=1}^{3} \dfrac {\partial \boldsymbol{X}^{s}}{\partial \beta ^{s}_{i}} \dfrac {\partial \beta ^{s}_{i}}{\partial p_{l}}. $$

(59)

are needed. They can be determined from the derivatives of $\boldsymbol{X}^{s}$ with respect to the rotation parameters $\boldsymbol{\beta}^{s}$ and the derivatives of the rotation parameters with respect to the design variables. Whereas the former depend on the choice of the rotation parameters, the latter are given by Eq. (47).

On the other hand, $\partial \mbox{$\dot {\boldsymbol{c}}$}^{s}/\partial p_{l}$ can be expressed in terms of the velocity coordinates of the “to” and “from” bodies as

$$ \dfrac {\partial \mbox{$\dot {\boldsymbol{c}}$}^{s}}{\partial p_{l}} = \dfrac {\partial \boldsymbol{C}^{s}}{\partial p_{l}} \left [ \textstyle\begin{array}{c} \boldsymbol{z}_{\mathrm{II}}^{i} \\ \boldsymbol{z}_{\mathrm{II}}^{j} \end{array}\displaystyle \right ], $$

(60)

where

$$\frac{\partial {\mathit{C}}^s}{\partial p_l}=\left[\begin{array}{cc}\frac{\partial {\tilde{\mathit{d}}}^s}{\partial p_l}{\mathit{D}}^{t^{\mathsf{T}}}{\mathit{T}}_{\mathrm{r}}^t& -{\mathit{D}}^{t^{\mathsf{T}}}{\mathit{S}}^{j^{\mathsf{T}}}{\mathit{S}}^i\frac{\partial {\mathit{T}}_{\mathrm{t}}^f}{\partial p_l}\\ \frac{\partial {\mathit{X}}_{\mathrm{r}}^s}{\partial p_l}{\mathit{D}}^{t^{\mathsf{T}}}{\mathit{T}}_{\mathrm{r}}^t& -\frac{\partial {\mathit{X}}_{\mathrm{r}}^s}{\partial p_l}{\mathit{D}}^{t^{\mathsf{T}}}{\mathit{S}}^{j^{\mathsf{T}}}{\mathit{S}}^i{\mathit{T}}_{\mathrm{r}}^f-{\mathit{X}}_{\mathrm{r}}^s{\mathit{D}}^{t^{\mathsf{T}}}{\mathit{S}}^{j^{\mathsf{T}}}{\mathit{S}}^i\frac{\partial {\mathit{T}}_{\mathrm{r}}^f}{\partial p_l}\end{array}\right].$$

(61)

Derivatives (58) or (60) can be used in the evaluation of gradient (6) as part of the derivatives of the implicit initial conditions at velocity level $\dot {\boldsymbol{\phi}}^{0}$. Moreover, the partial derivatives of the local Jacobian (61) are required for the differentiation of the reaction forces in the kinetic equations.

Finally, the derivatives of the constraint equations at the acceleration level, which are required in the solution of the adjoint problem (3) can be determined. Differentiating Eq. (56) with respect to $p_{l}$ yields

$$ \dfrac {\partial \mbox{$\ddot {\boldsymbol{c}}$}^{s}}{\partial p_{l}} = \dfrac {\partial \boldsymbol{X}^{s}}{\partial p_{l}} \dot {\boldsymbol{x}}_{\mathrm{II}}^{s} + \boldsymbol{X}^{s} \dfrac {\partial \dot {\boldsymbol{x}}_{\mathrm{II}}^{s}}{\partial p_{l}} + \dfrac {\partial \dot {\boldsymbol{X}}^{s}}{\partial p_{l}} \boldsymbol{x}_{\mathrm{II}}^{s} + \dot {\boldsymbol{X}}^{s} \dfrac {\partial \boldsymbol{x}_{\mathrm{II}}^{s}}{\partial p_{l}}. $$

(62)

The derivatives of the relative joint velocities $\boldsymbol{x}_{\mathrm{II}}$ and accelerations $\dot {\boldsymbol{x}}_{\mathrm{II}}$ are presented in Eqs. (48)–(49) and (50)–(51). Also, the derivatives of the kinematic matrix are discussed in Eq. (59). Only the derivatives $\partial{\dot {\boldsymbol{X}}^{s}}/\partial{p_{l}}$ are missing. The only submatrix of $\partial{\dot {\boldsymbol{X}}^{s}}/\partial{p_{l}}$ that does not vanish according to Eq. (53) is $\partial{\dot {\boldsymbol{X}}_{\mathrm{r}}^{s}}/\partial{p_{l}}$. It can be computed by

$$ \dfrac {\partial \dot {\boldsymbol{X}}^{s}_{\mathrm{r}}}{\partial p_{l}} = \sum _{i=1}^{3} \left ( \dfrac {\partial \dot {\boldsymbol{X}}_{\mathrm{r}}^{s}}{\partial \beta ^{s}_{i}} \dfrac {\partial \beta ^{s}_{i}}{\partial p_{l}} + \dfrac {\partial \dot {\boldsymbol{X}}_{\mathrm{r}}^{s}}{\partial \dot {\beta }^{s}_{i}} \dfrac {\partial \dot {\beta }^{s}_{i}}{\partial p_{l}}\right ), $$

(63)

whereby it is possible to obtain the partial derivatives $\partial \mbox{$\dot {\boldsymbol{\beta}}$}^{s}/\partial p_{l}$ from the derivative of the second line of Eq. (53) as

$$ \dfrac {\partial \mbox{$\dot {\boldsymbol{\beta}}$}^{s}}{\partial p_{l}} = \dfrac {\partial \boldsymbol{X}^{s}_{\mathrm{r}}}{\partial p_{l}} \boldsymbol{\Omega}^{s} + \boldsymbol{X}^{s}_{\mathrm{r}} \dfrac {\partial \boldsymbol{\Omega}^{s}}{\partial p_{l}}. $$

(64)

In Eq. (64), all quantities are known.

2.7 Kinetic equations

For the evaluation of the gradient equation (6) also the partial derivatives of the kinetic equations (1d) with respect to the design variables

$$ \dfrac {\partial \boldsymbol{s}}{\partial p_{l}} = \dfrac {\partial \boldsymbol{M}}{\partial p_{l}} \dot {\boldsymbol{z}}_{\mathrm{II}} - \dfrac {\partial \boldsymbol{C}^{\mkern -1.5mu\mathsf {T}}}{\partial p_{l}} \boldsymbol{\lambda}- \dfrac {\partial \boldsymbol{f}}{\partial p_{l}} $$

(65)

are required. The derivatives of the reaction forces $\boldsymbol{C}^{\mathsf {T}} \boldsymbol{\lambda}$ can be computed with the help of Eq. (61). For the differentiation of the global mass matrix $\partial{\boldsymbol{M}}/\partial{p_{l}}$ and the global right-hand-side vector $\partial{\boldsymbol{f}}/\partial{p_{l}}$,the local design sensitivities are needed. Therefore, in the following, the local equations of motion of a flexible body $i$ are briefly presented, and the possibility to differentiate them with respect to arbitrary structural design variables is discussed.

The local equations of motion can be derived using a principle of mechanics, such as Jourdain’s principle. It states that the virtual power of the inertias $\delta P_{\mathrm{i}}^{i}$ and of the internal forces $\delta P_{\mathrm{e}}^{i}$ equals the virtual power of the applied forces. Assuming that only body loads and $n_{\mathrm{d}}^{i}$ discrete loads act on the body it holds

$$ \begin{aligned} & \underbrace{\int \limits _{\Omega _{0}^{i}} \rho ^{i} \delta \boldsymbol{v}^{k,i^{\mathsf {T}}} \boldsymbol{a}^{k,i}\, \mathrm{d}V}_{ \delta P_{\mathrm{i}}^{i}} + \underbrace{\int \limits _{\Omega _{0}^{i}} \delta \dot{\boldsymbol{\varepsilon}}^{k,i^{\mathsf {T}}} \boldsymbol{\sigma}^{k,i}\, \mathrm{d}V}_{ \delta P_{\mathrm{e}}^{i}} \\ & \qquad = \underbrace{\int \limits _{\Omega _{0}^{i}} \rho \delta \boldsymbol{v}^{k,i^{\mathsf {T}}} \boldsymbol{b}^{i}\, \mathrm{d}V}_{ \delta P_{\mathrm{b}}^{i}} + \underbrace{\sum \limits _{k=1}^{n_{\mathrm{d}}^{i}}\left (\delta \boldsymbol{v}^{k,i^{\mathsf {T}}}\boldsymbol{f}^{k,i} + \delta \boldsymbol{\omega}^{{k,i}^{\mathsf {T}}}\boldsymbol{l}^{k,i}\right )}_{ \delta P_{\mathrm{d}}^{i}}. \end{aligned} $$

(66)

With the variation of the velocity coordinates $\delta \boldsymbol{v}^{k,i} = \boldsymbol{T}_{\mathrm{t}}^{k,i} \delta \boldsymbol{z}_{\mathrm{II}}^{i}$ and Eq. (22) for the acceleration of point P, the virtual power of the inertias yields

$$ \delta P^{i}_{\mathrm{i}} = \delta \boldsymbol{z}_{\mathrm{II}}^{i^{ \mathsf {T}}} \underbrace{\int _{\Omega _{0}^{i}} \rho ^{i} \boldsymbol{T}_{\mathrm{t}}^{k,i^{\mathsf {T}}}\boldsymbol{T}_{\mathrm{t}}^{k,i} \mathrm{d}V}_{ \boldsymbol{M}^{i}} \mbox{$\dot {\boldsymbol{z}}$}_{\mathrm{II}}^{i} + \delta \boldsymbol{z}_{\mathrm{II}}^{i^{\mathsf {T}}} \underbrace{\int _{\Omega _{0}^{i}} \rho ^{i} \boldsymbol{T}_{\mathrm{t}}^{k,i^{\mathsf {T}}} \boldsymbol{\zeta}^{k,i}_{\mathrm{t}} \mathrm{d}V}_{ \boldsymbol{h}_{\omega}^{i}}. $$

(67)

The integral in the first term represents the local mass matrix $\boldsymbol{M}^{i}$. It depends on the elastic coordinates and can be written with Eq. (18) as

$${\mathit{M}}^i={\int }_{{\mathrm{\Omega }}_0^i}{\rho }^i\left[\begin{array}{ccc}\mathbf{\text{E}}& {\tilde{\mathit{r}}}^{k,i^{\mathsf{T}}}& {\mathbf{\Phi }}^{k,i}\\ & {\tilde{\mathit{r}}}^{k,i}{\tilde{\mathit{r}}}^{k,i^{\mathsf{T}}}& {\tilde{\mathit{r}}}^i{\mathbf{\Phi }}^{k,i}\\ \text{sym.}& & {\mathbf{\Phi }}^{k,i^{\mathsf{T}}}{\mathbf{\Phi }}^{k,i}\end{array}\right]\mathrm{d}V.$$

(68)

In the second term of Eq. (67), $\boldsymbol{h}_{\omega}^{i}$ contains the inertias from the acceleration of the reference frame. In the literature, $\boldsymbol{h}_{\omega}^{i}$ is often separated into translational, rotational, and elastic parts as follows:

$$ \boldsymbol{h}^{i}_{\omega} = \left [ \textstyle\begin{array}{c} \boldsymbol{h}^{i}_{\omega , \mathrm{t}} \\ \boldsymbol{h}^{i}_{\omega , \mathrm{r}} \\ \boldsymbol{h}^{i}_{\omega , \mathrm{e}} \end{array}\displaystyle \right ]. $$

(69)

Thereby the three parts are defined as

$$\begin{aligned} \boldsymbol{h}^{i}_{\omega , \mathrm{t}} & = \tilde {\boldsymbol{\omega}}^{i} \boldsymbol{v}^{i} \int _{\Omega _{0}^{i}} \rho ^{i} \mathrm{d}V + 2 \tilde {\boldsymbol{\omega}}^{i} \int _{\Omega _{0}^{i}} \rho ^{i} \boldsymbol{\Phi}^{k,i}\mathrm{d}V \mbox{$\dot {\boldsymbol{q}}$}^{i} + \tilde {\boldsymbol{\omega}}^{i} \tilde {\boldsymbol{\omega}}^{i} \int _{\Omega _{0}^{i}} \rho ^{i} \boldsymbol{r}^{k,i} \mathrm{d}V, \end{aligned}$$

(70a)

$$\begin{aligned} \boldsymbol{h}^{i}_{\omega , \mathrm{r}} & = \int _{ \Omega _{0}^{i}} \rho ^{i} \tilde{\boldsymbol{r}}^{k,i} \mathrm{d}V \tilde {\boldsymbol{\omega}}^{i}\boldsymbol{v}^{i} + \tilde {\boldsymbol{\omega}}^{i} \int _{\Omega _{0}^{i}} \rho ^{i} \tilde{\boldsymbol{r}}^{k,i} \tilde{\boldsymbol{r}}^{k,i^{\mathsf {T}}} \mathrm{d}V \boldsymbol{\omega}^{i} + 2\int _{\Omega _{0}^{i}} \rho ^{i} \tilde{\boldsymbol{r}}^{k,i} \dot{\tilde{\boldsymbol{r}}}^{k,i^{\mathsf {T}}} { \rm d}V \boldsymbol{\omega}^{i}, \end{aligned}$$

(70b)

and

$$\begin{aligned} \boldsymbol{h}^{i}_{\omega , \mathrm{e}} & = \int _{ \Omega _{0}^{i}} \rho ^{i} \boldsymbol{\Phi}^{k,i^{ \mathsf {T}}} \mathrm{d}V \tilde {\boldsymbol{\omega}}^{i} \boldsymbol{v}^{i} + \left [ \textstyle\begin{array}{c} \boldsymbol{\omega}^{i^{\mathsf {T}}}\int \limits _{\Omega _{0}^{i}} \rho ^{i} \tilde{\boldsymbol{\Phi}}^{k,i}_{*1} \tilde{\boldsymbol{r}}^{k,i^{\mathsf {T}}} \mathrm{d}V \boldsymbol{\omega}^{i} \\ \vdots \\ \boldsymbol{\omega}^{i^{\mathsf {T}}}\int \limits _{\Omega _{0}^{i}} \rho ^{i} \tilde{\boldsymbol{\Phi}}^{k,i}_{*n_{\mathrm{q}}^{i}} \tilde{\boldsymbol{r}}^{k,i^{\mathsf {T}}} \mathrm{d}V \boldsymbol{\omega}^{i} \\ \end{array}\displaystyle \right ] \\ & \qquad + 2\int _{\Omega _{0}^{i}} \rho ^{i} \boldsymbol{\Phi}^{k,i^{\mathsf {T}}} \dot{\tilde{\boldsymbol{r}}}^{k,i^{\mathsf {T}}} { \rm d}V \boldsymbol{\omega}^{i}. \end{aligned}$$

(70c)

For the evaluation of the virtual power of inner forces $\delta P_{\mathrm{e}}^{i}$, first, the virtual distortion velocity $\delta \mbox{$\dot {\boldsymbol{\varepsilon }}$}^{k,i}$ and the stress $\boldsymbol{\sigma}^{k,i}$ in point P have to be determined. Assuming that the deformations are small and that the material behavior is linearly elastic, it holds for the distortion velocity and its variation

$$ \mbox{$\dot {\boldsymbol{\varepsilon }}$}^{k,i} = \boldsymbol{L}_{\mathrm{L}}\boldsymbol{\Phi}^{k,i} \mbox{$\dot {\boldsymbol{q}}$}^{i}, \qquad \delta \mbox{$\dot {\boldsymbol{\varepsilon }}$}^{k,i} = \boldsymbol{L}_{\mathrm{L}}\boldsymbol{\Phi}^{k,i}\delta \mbox{$\dot {\boldsymbol{q}}$}^{i} $$

(71)

and, for the stress,

$$ \boldsymbol{\sigma}^{k,i} = \boldsymbol{E}^{i} \boldsymbol{\varepsilon }^{k,i} = \boldsymbol{E}^{i} \underbrace{\boldsymbol{L}_{\mathrm{L}}\boldsymbol{\Phi}^{k,i}}_{ \boldsymbol{B}^{k,i}}\boldsymbol{q}^{i} $$

(72)

with the linear differential operator $\boldsymbol{L}_{\mathrm{L}}$, the material matrix $\boldsymbol{E}^{i}$, and the distortion matrix $\boldsymbol{B}^{k,i}$. The virtual power of the inner forces can then be written in terms of the velocity coordinates of body $i$ as

$$ \delta P_{\mathrm{e}}^{i} = \delta \boldsymbol{z}_{\mathrm{II}}^{i^{ \mathsf {T}}} \boldsymbol{h}_{\mathrm{e}}^{i} $$

(73)

with the vector $\boldsymbol{h}_{\mathrm{e}}^{i}$ of the inner forces

$$ \boldsymbol{h}_{\mathrm{e}}^{i}=\left [ \textstyle\begin{array}{c} \boldsymbol{0} \\ \boldsymbol{0} \\ \int \limits _{\Omega _{0}^{i}} \boldsymbol{B}^{k,i^{ \mathsf {T}}}\boldsymbol{E}^{k,i}\boldsymbol{B}^{k,i}\, { \rm d}V \boldsymbol{q}^{i} \end{array}\displaystyle \right ]. $$

(74)

Incorporating the virtual velocities $\delta \boldsymbol{v}^{k,i}$ and angular velocities $\delta \boldsymbol{\omega}^{k,i} = \boldsymbol{T}^{k,i}_{ \rm r}\delta \boldsymbol{z}_{\mathrm{II}}^{i}$ into the virtual power of the applied body forces and discrete loads yields

$$ \delta P^{i}_{\mathrm{b}} + \delta P^{i}_{\mathrm{d}} = \delta \boldsymbol{z}_{\mathrm{II}}^{i^{\mathsf {T}}} \underbrace{\int _{\Omega _{0}^{i}} \rho ^{i} \boldsymbol{T}_{\mathrm{t}}^{k,i^{\mathsf {T}}}\, \mathrm{d}V \boldsymbol{b}^{i}}_{ \boldsymbol{h}^{i}_{\mathrm{b}}} + \delta \boldsymbol{z}_{\mathrm{II}}^{i^{ \mathsf {T}}} \underbrace{\sum _{k=1}^{n_{\mathrm{d}}}\left (\boldsymbol{T}_{\mathrm{t}}^{{k,i}^{\mathsf {T}}}\boldsymbol{f}^{k,i} + \boldsymbol{T}_{\mathrm{r}}^{{k,i}^{\mathsf {T}}}\boldsymbol{l}^{k,i}\right )}_{ \boldsymbol{h}_{\mathrm{d}}^{i}} $$

(75)

with the body forces $\boldsymbol{h}_{\mathrm{b}}^{i}$ caused by the volume force density $\boldsymbol{b}^{i}$ and the applied load vector $\boldsymbol{h}_{\mathrm{d}}^{i}$, which contains all discrete applied forces $\boldsymbol{f}^{k,i}$ and torques $\boldsymbol{l}^{k,i}$ on the body. Whereas $\boldsymbol{h}_{\mathrm{d}}^{i}$ can be directly computed, the evaluation of $\boldsymbol{h}_{\mathrm{b}}^{i}$ requires the solution of the body integral

$$ \boldsymbol{h}_{\mathrm{b}}^{i} = \int _{\Omega _{0}^{i}} \rho ^{i} \left [ \textstyle\begin{array}{c} \textbf{E} \\ \tilde{\boldsymbol{r}}^{k,i} \\ \boldsymbol{\Phi}^{k,i^{\mathsf {T}}} \end{array}\displaystyle \right ]\,\mathrm{d}V\,\boldsymbol{b}^{i}. $$

(76)

Using the principle of the independent variation, the local equations of motion for body $i$ follow from the Eqs. (67), (73), and (75) as

$$ \boldsymbol{M}^{i}\mbox{$\dot {\boldsymbol{z}}$}_{\mathrm{II}}^{i} + \boldsymbol{h}_{\omega}^{i} + \boldsymbol{h}_{\mathrm{e}}^{i} = \boldsymbol{h}^{i}_{\mathrm{b}} + \boldsymbol{h}_{\mathrm{d}}^{i}. $$

(77)

It can be seen from this very brief derivation of the kinetic equations that for the evaluation of Eq. (77), a set of body integrals, which are not constant but dependent on the elastic coordinates has to be solved. A summary of the body integrals is given in Table 1.

Table 1 Body integrals in the local equations of motion

The body integrals play an important role in the calculation of the design sensitivities because differentiating the local equations of motion (77) with respect to the design variables, their derivatives must essentially be computed. However, since the parameterization of the flexible body is assumed to be arbitrary, it can be everything from the body domain $\Omega _{0}^{i}(\boldsymbol{p})$, the parameters of the material matrix $\boldsymbol{E}^{i}(\boldsymbol{p})$ and the shape functions $\boldsymbol{\Phi}(\boldsymbol{p})$ and $\boldsymbol{\Psi}(\boldsymbol{p})$. In most proprietary and academic multibody programs, neither the required information on the body domain, material properties, nor shape functions are available. An integrated design modeler and finite element program would be required for this task. Therefore it is suggested to provide the partial derivatives of the body integrals via a standardized data interface. There already exists a standardized data set for flexible multibody systems. These so-called standard input data and their suggested augmentation are presented in the next section.

3 Augmentation of object-oriented standard input data

The original standard input data have been proposed in [21] and pursue essentially two goals. On the one hand, they represent a general and unified dataset, which completely describes flexible bodies of multibody systems. This includes all necessary information to evaluate the marker kinematics and the body integrals. On the other hand, they are meant to accelerate the evaluation of the equations of motion. To this end, the body integrals in Table 1, most of which depend on the elastic coordinates, are expressed by Taylor series. Since the coefficient matrices of the Taylor series can be evaluated in a preprocessing step, the repeated quadrature of the body integrals during the time integration is avoided.

In [21] the standard input data are stored in an object-oriented dataset using the four classes modal, refmod, node, and taylor. A detailed list of their properties is given in Tables 2, 3, 4, 5. It can be seen that the class modal contains all properties of the flexible body. This includes general body properties, which are stored in the variable refmod. The latter is of class refmod and defines, for instance, the global properties mass or the number of elastic coordinates nelastq.

Table 2 Definition of class modal

Table 3 Definition of class refmod

Table 4 Definition of class node

Table 5 Definition of class taylor

The quantities required to describe all markers on the body and their kinematics are given in an array of objects of class node; see Table 4. In these objects, for example, the position and orientation of the markers are stored. Since these kinematic quantities depend on the elastic coordinates, they are of type taylor; see Table 5. In the class taylor the coefficient matrices of the Taylor series and their dimensions are saved. The remaining properties of the class modal are all of type taylor because they contain the coefficient matrices of the body integrals.

It is worth mentioning that the standard input data can be directly computed from finite element models without quadrature if these are assembled from continuum elements only; see [18]. In case there are additional structural elements in the finite element model, an approximate calculation is still possible.

Due to the object-oriented structure of the dataset, its augmentation is comparatively easy. All necessary changes in the class definitions are marked in gray in the tables. In fact, there are only two changes. Firstly, the property mass in class refmod is now of type taylor instead of double as in the original definition. Secondly, the taylor class has to be augmented by the property nd, which describes the number of design variables, and dM0, dM1, and dMn, which contain the partial derivatives of the coefficient matrices. By these simple changes all necessary information to compute the design sensitivities is provided. On the one hand, the design sensitivities of the marker kinematics in Eqs. (26)–(31) and the subsequent relative marker kinematics and constraints can be computed. On the other hand, the design sensitivities of the kinetic equations (65), which are based on the derivatives of the local equations of motion and hence on the derivatives of the body integrals in Table 1, can be determined.

Depending on the number of design variables, the amount of data can rise significantly. Therefore a careful examination of the influence of the derivatives of the individual coefficient matrices with respect to the overall gradient should be carried out as it has been done for large-scale topology optimization problems in [13]. In this way, it is possible to drop derivatives of body integrals with a low impact and limit the total size of the standard input data.

4 Application example: flexible slider-crank mechanism

In this section, an example from topology optimization, which closely resembles that in [1], is presented to demonstrate the practical use of the augmented standard input data in the structural analysis and optimization of multibody systems. Thereby the optimal design for a flexible crank of a slider-crank mechanism shall be found; see Fig. 4. To this end, the material properties of an underlying finite element model, from which the shape functions for the crank are obtained by modal truncation are parameterized by the so-called solid isotropic material with penalization (SIMP) approach [2]. In this method the density $\rho _{i}$ and stiffness $E_{i}$ of each finite element $i=1(1)n_{\mathrm{e}}$ are penalized by design variables $p_{i}$. The finite element model of the flexible crank is parameterized with the SIMP formulation

$$ \begin{aligned} \rho _{i} & = \textstyle\begin{cases} c p_{i}^{q}\rho _{0} & \text{for } p_{\mathrm{min}} = 0.01 \leq p_{i} < 0.1, \\ p_{i} \rho _{0} & \text{for } 0.1 \leq p_{i} \leq 1, \\ \end{cases}\displaystyle \\ E_{i} & = p_{i}^{s} E_{0}, \end{aligned} $$

(78)

where $c =10^{5}$, $q=6$, and $s = 3$. This SIMP approach works well for finite element models that are modally reduced; see [15]. The material properties and geometry of the flexible crank and the rigid body data of the piston rod are summarized in Table 6.

Fig. 4

Flexible slider-crank mechanism (left) and parameterized crank (right)

Table 6 Geometry and material parameters of slider-crank mechanism

Determining the augmented standard input data for this problem is not trivial. The following procedure is used in this work: a parameterized finite element model is established, and modal analysis is performed in the commercial finite element solver ANSYS. Then the finite element system matrices and the results of the modal analysis are imported in Matlab. In the next step the standard input data are computed as described in [18], and their derivatives are determined. It is worth noting that for the current example, all body integrals in Table 1 depend on the design variables $\boldsymbol{p}$. The type of dependency is irrelevant for the evaluation of the gradient equation. Therefore it is sufficient to extend the standard input data by the derivatives of the coefficient matrices to the design variables.

With the standard input data at hand, the transient analysis of the flexible slider-crank mechanism can be performed. The crank rotation is prescribed by the rheonomic constraint

$$ \varphi (t) = \sum _{i=0}^{7} a_{i} t^{i}, $$

(79)

whereas the polynomial coefficients $a_{i}$ satisfy the conditions

$$ \begin{aligned} t^{0}=0~\mbox{s}:\quad & \varphi = \dot{\varphi} = \ddot{\varphi} = \dddot{\varphi} = 0; \\ t^{1}=2~\mbox{s}:\quad & \varphi = 12\pi ~\mbox{rad}, \dot{\varphi} = 12\pi ~\mbox{Hz}, \ddot{\varphi} = \dddot{\varphi} = 0. \end{aligned} $$

(80)

For the system analysis, the integral compliance of the flexible crank

$$ \psi (\boldsymbol{p}) = \int _{t=0~\text{s}}^{t= 2~\text{s}} \boldsymbol{q}^{\mathsf {T}} \boldsymbol{K}\boldsymbol{q}\,\mathrm{d}t $$

(81)

is evaluated as objective function. Thereby $\boldsymbol{q}$ and $\boldsymbol{K}$ are the elastic coordinates and the modally reduced stiffness matrix of the flexible crank, respectively.

After solving the adjoint problem (3)–(4), the gradient $\nabla \psi$ can be computed according to Eq. (6) using the design sensitivities of the system equations discussed in Sect. 2. The results of the gradient computation for $p_{i} = 1$ are shown in Fig. 5. The sensitivities of the single design variables are plotted over the discretized design domain of the flexible crank. The results of the adjoint variable method are validated using the finite difference method (forward differences, perturbations $5\cdot 10^{-2}$). It turns out that both results are in good agreement.

Fig. 5

Topological gradient using the adjoint variable method

Even though the application example is chosen from topology optimization, the augmented standard input data concept can be directly transferred to any structural analysis and optimization of both rigid and flexible bodies in multibody systems.

5 Summary and conclusion

The adjoint variable method can be used to derive a set of equations for multibody systems from which the gradient of arbitrary criterion functions can be computed. In this method, among others, the partial derivatives of the system equations with respect to the design variables are required. These so-called design sensitivities are presented in detail for both the kinematical constraint equations and the equations of motion of multibody systems modeled with the floating frame of reference formulation. Thereby it has been shown that for the systematic differentiation of the constraints equations, the marker kinematics derivatives and the relative marker kinematics must be determined. When computing the partial derivatives of the kinetic equations, it turns out that the design sensitivities of the body integrals are required. Since they cannot be determined for arbitrarily parameterized rigid and flexible bodies without an integrated design modeler and finite element program, augmenting the standard input data by their derivatives has been suggested. With only minor changes in the original definition of the standard input data, it is possible to clearly separate the two tasks of modeling and parameterization of bodies and the system simulation and analysis. To demonstrate the capability of the suggested augmentation of the standard input data, the sensitivity analysis required in the topology optimization of a flexible slider-crank mechanism has been presented.