Adjoint sensitivity analysis of hybrid multibody dynamical systems

Abstract

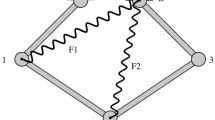
Sensitivity analysis computes the derivatives of general cost functions that depend on the system solution with respect to parameters or initial conditions. This work develops adjoint sensitivity analysis for hybrid multibody dynamic systems. The adjoint sensitivity is commonly referred to as backward propagation. Hybrid systems are characterized by trajectories that are piecewise continuous in time, with finitely-many discontinuities being caused by events such as elastic/inelastic impacts or sudden changes in constraints. The corresponding direct and adjoint sensitivity variables are also discontinuous at the time of events. The framework discussed herein uses a jump sensitivity matrix to relate the jump conditions for the direct and adjoint sensitivities before and after the time event and provides analytical jump equations for the adjoint variables. The theoretical framework for sensitivities for hybrid systems is verified on a five-bar mechanism with non-smooth contacts.

Appendices

Appendix A: Calculation of partial derivatives used in sensitivity analyses

Remark 5

The expressions ${{f}_{q}^{\text{eom}}}$, ${{f}_{v}^{\text{eom}}}$, and ${{f}_{{\rho }_{i}} ^{\text{eom}}}$ denote the partial derivatives of ${{f}^{\text{eom}}}$ with respect to the subscripted variables. The partial derivatives $\partial {{f}^{\text{eom}}}/\partial \zeta$ are obtained by differentiating ${{f}^{\text{eom}}}$ with respect to $\zeta \in \{{q},{v},{\rho }\}$:

$$ \frac{\partial {{f}^{\text{eom}}}}{\partial \zeta } =\frac{\partial (\mathsf{M}^{-1} \mathsf{F})}{\partial \zeta } = - \mathsf{M}^{-1} \mathsf{M}_{\zeta } \mathsf{M}^{-1} \mathsf{F}+ \mathsf{M}^{-1} \mathsf{F}_{\zeta }= \mathsf{M}^{-1} \bigl( \mathsf{F}_{\zeta }- \mathsf{M}_{\zeta } {{f}^{\text{eom}}} \bigr) = \mathsf{M}^{-1} ( \mathsf{F}_{\zeta }- \mathsf{M}_{\zeta } {\dot{{v}}} ). $$

(65)

Remark 6

The expressions $\tilde{{g}}_{q}$, $\tilde{{g}}_{v}$, and $\tilde{{g}}_{{\rho }_{i}}$ denote the partial derivatives of $\tilde{{g}}$ with respect to the subscripted variables. The partial derivatives $\partial \tilde{{g}}/\partial \zeta$ are obtained by differentiating (1) with respect to $\zeta \in \{{q},{v},{\rho }\}$:

$$\begin{aligned} \tilde{{g}}_{\zeta } &= g_{\zeta } + g_{\dot{{v}}} {{f}_{\zeta } ^{\text{eom}}}+ g_{\tilde{u}} \tilde{u}_{\zeta } \\ &= g_{\zeta } + g_{\dot{{v}}} {{f}_{\zeta }^{\text{eom}}}+ g_{{u}} {u}_{\zeta } + g_{{u}} u_{\dot{{v}}} {{f}_{\zeta }^{\text{eom}}}, \end{aligned}$$

(66)

which leads to

$$\begin{aligned}{} [ \tilde{{g}}_{q} {Q}_{i} + \tilde{{g}}_{v} {V}_{i} + \tilde{{g}}_{\rho _{i}} ]_{i=1,\dots ,p} ={}& \bigl[ \bigl(g_{q}+ g_{\dot{{v}}} {{f}_{q}^{\text{eom}}}+ g_{{u}} {u}_{{q}} + g_{{u}} u_{\dot{{v}}} {{f}_{q}^{\text{eom}}} \bigr)\cdot {Q}_{i} \\ & {} + \bigl(g_{v}+ g_{\dot{{v}}} {{f}_{v}^{\text{eom}}}+ g_{{u}} {u}_{{v}} + g_{{u}} u _{\dot{{v}}} {{f}_{v}^{\text{eom}}} \bigr)\cdot {V}_{i} \\ & {} + g_{{\rho }_{i}} + g_{\dot{{v}}}\cdot {{f}_{{\rho }_{i}} ^{\text{eom}}}+ g_{{u}} {u}_{{\rho }} + g_{{u}} u_{\dot{{v}}} {{f}_{{\rho }_{i}}^{\text{eom}}} \bigr]_{i=1,\dots ,p}. \end{aligned}$$

(67)

Remark 7

Similarly, the expressions $\tilde{w}_{q}$, $\tilde{w}_{v}$, and $\tilde{w}_{{\rho }_{i}}$ denote the partial derivatives of $\tilde{w}$ with respect to the subscripted variables. The partial derivatives $\partial \tilde{w}/\partial \zeta$ are obtained by differentiating $w$ with respect to $\zeta \in \{{q},{v},{\rho }\}$:

$$\begin{aligned} \tilde{w}_{\zeta } &= w_{\zeta } + w_{\dot{{v}}} {{f}_{\zeta }^{\text{eom}}}+ w_{\tilde{u}} \tilde{u}_{\zeta } \\ &= w_{\zeta } + w_{\dot{{v}}} {{f}_{\zeta }^{\text{eom}}}+ w_{{u}} {u}_{\zeta } + w_{{u}} w_{\dot{{v}}} {{f}_{\zeta }^{\text{eom}}}. \end{aligned}$$

(68)

Appendix B: Adjoint of the algebraic Lagrangian coefficient

Methods to compute the adjoint of an index-1 DAE available in the literature [3, 29, 35] use the following approach. Define the Lagrangian using the multipliers $\mu ^{Q} , \mu ^{V} , \mu ^{\Gamma }$ that correspond to the constraints posed by the index-1 DAE equations (33) as

$$ \begin{bmatrix} \mu ^{Q} \\ \mu ^{V} \\ \mu ^{\Gamma } \end{bmatrix} ^{T} \cdot \left ( \begin{bmatrix} \mathsf{I}& \mathsf{0}& \mathsf{0} \\ \mathsf{0}& {\mathsf{M}} (t,{q},{\rho } ) & {{\Phi }}_{{q}}^{\mathrm{T}} (t,{q},{\rho } ) \\ \mathsf{0}& {{\Phi }}_{{q}} (t,{q},{\rho } ) & \mathsf{0} \end{bmatrix} \cdot \begin{bmatrix} {\dot{{q}}} \\ {\dot{{v}}} \\ \mu \end{bmatrix} - \begin{bmatrix} {v} \\ {\mathsf{F}} (t,{q},{v},{\rho } ) \\ \mathsf{C} (t,{q},{v},{\rho } ) \end{bmatrix} \right ). $$

(69)

We rearrange Eq. (69) as follows:

$$\begin{aligned} &\left ( \begin{bmatrix} \mu ^{Q} \\ \mu ^{V} \\ \mu ^{\Gamma } \end{bmatrix} \cdot \begin{bmatrix} \mathsf{I}& \mathsf{0}& \mathsf{0} \\ \mathsf{0}& {\mathsf{M}} (t,{q},{\rho } ) & {{\Phi }}_{{q}}^{\mathrm{T}} (t,{q},{\rho } ) \\ \mathsf{0}& {{\Phi }}_{{q}} (t,{q},{\rho } ) & \mathsf{0} \end{bmatrix} \right ) \\&\quad \quad {}\cdot \left ( \begin{bmatrix} {\dot{{q}}} \\ {\dot{{v}}} \\ \mu \end{bmatrix} - \begin{bmatrix} \mathsf{I}& \mathsf{0}& \mathsf{0} \\ \mathsf{0}& {\mathsf{M}} (t,{q},{\rho } ) & {{\Phi }}_{{q}}^{\mathrm{T}} (t,{q},{\rho } ) \\ \mathsf{0}& {{\Phi }}_{{q}} (t,{q},{\rho } ) & \mathsf{0} \end{bmatrix} ^{-1} \cdot \begin{bmatrix} {v} \\ {\mathsf{F}} (t,{q},{v},{\rho } ) \\ \mathsf{C} (t,{q},{v},{\rho } ) \end{bmatrix} \right ) \end{aligned}$$

(70)

$$\begin{aligned} &\quad =\left ( \begin{bmatrix} \mu ^{Q} \\ \mu ^{V} \\ \mu ^{\Gamma } \end{bmatrix} ^{T} \cdot \begin{bmatrix} \mathsf{I}& \mathsf{0}& \mathsf{0} \\ \mathsf{0}& {\mathsf{M}} (t,{q},{\rho } ) & {{\Phi }}_{{q}}^{\mathrm{T}} (t,{q},{\rho } ) \\ \mathsf{0}& {{\Phi }}_{{q}} (t,{q},{\rho } ) & \mathsf{0} \end{bmatrix} \right ) \cdot \left ( \begin{bmatrix} {\dot{{q}}} \\ {\dot{{v}}} \\ \mu \end{bmatrix} - \begin{bmatrix} V \\ {{f}^{\text{DAE-}\dot{v}}} \\ {{f}^{\text{DAE-}\mu}} \end{bmatrix} \right ) \end{aligned}$$

(71)

$$\begin{aligned} &\quad = \begin{bmatrix} \lambda ^{Q} \\ \lambda ^{V} \\ \lambda ^{\Gamma } \end{bmatrix} ^{T} \cdot \left ( \begin{bmatrix} {\dot{{q}}} \\ {\dot{{v}}} \\ \mu \end{bmatrix} - \begin{bmatrix} V \\ {{f}^{\text{DAE-}\dot{v}}} \\ {{f}^{\text{DAE-}\mu}} \end{bmatrix} \right ). \end{aligned}$$

(72)

The adjoint variables $\lambda ^{Q} , \lambda ^{V} , \lambda ^{\Gamma }$ defined in this paper, and the adjoint variables $\mu ^{Q} , \mu ^{V} , \mu ^{\Gamma }$ used in the literature (69), are related by the following matrix multiplication:

$$ \begin{bmatrix} \lambda ^{Q} \\ \lambda ^{V} \\ \lambda ^{\Gamma } \end{bmatrix} = \begin{bmatrix} \mathsf{I}& \mathsf{0}& \mathsf{0} \\ \mathsf{0}& {\mathsf{M}} (t,{q},{\rho } ) & {{\Phi }}_{{q}}^{\mathrm{T}} (t,{q},{\rho } ) \\ \mathsf{0}& {{\Phi }}_{{q}} (t,{q},{\rho } ) & \mathsf{0} \end{bmatrix} \cdot \begin{bmatrix} \mu ^{Q} \\ \mu ^{V} \\ \mu ^{\Gamma } \end{bmatrix} . $$

The adjoint DAE equations and boundary conditions in the “$\mu$ formulation” [3, 29, 35] can be derived from the equations and boundary conditions in the “$\lambda$ formulation” discussed in this paper, and vice-versa.