Abstract
We have proposed a robust, secure and efficient image encryption algorithm based on chaotic maps and algebraic structure. Nowadays, the chaotic cryptosystems gained more attention due to their efficiency, the assurance of robustness and high sensitivity corresponding to initial conditions. In literature, there are many encryption algorithms that can simply guarantees security while the schemes based on chaotic systems only promises the uncertainty, both of them can not encounter the needs of current scenario. To tackle this issue, this article proposed an image encryption algorithm based on Lorenz chaotic system and primitive irreducible polynomial substitution box. First, we have proposed 16 different S-boxes based on projective general linear group and 16 primitive irreducible polynomials of Galois field of order 256, and then utilized these S-boxes with combination of chaotic map in image encryption scheme. Three chaotic sequences can be produced by the disturbed of Lorenz chaotic system corresponding to variables x, y and z. We have constructed a new pseudo random chaotic sequence ki based on x, y and z. The plain image is encrypted by the use of chaotic sequence ki and XOR operation to get a ciphered image. To show the strength of presented image encryption, some renowned analyses are performed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Substitution box (S-box) is one of the fundamental constitute of symmetric key algorithms which implement substitution. Substitution boxes are building blocks of symmetric cryptosystems. The substitution tables (S-boxes) play a vital role in the encryption algorithms in order to meet the definition of a perfect security. Sometime big structures like S-box slowdown the processing of the encryption in a scenario where big data processing is required, the main reason is the complexity of that system and this kind of negative effect reduce the utility of that encryption algorithm in practical communication. In literature, there are many chaotic schemes that are using one or multiple (S-boxes) to get more security, there is no doubt that when one will use S-box the confusion creating ability of that algorithm between ciphertext and secret key will improve but it will definitely slow down the speed of encryption [6, 9, 10, 13, 18, 23, 24, 27, 29, 33,34,35,36, 39,40,41]. In this paper, we have proposed an image encryption algorithm that is based on chaotic maps and S-boxes. First, we have proposed a novel 16 different S-boxes based on 16 different primitive irreducible polynomials of Galois field of order 256 and project general linear group, then we used proposed S-boxes in image encryption. The proposed work is to construct a secure and efficient image encryption scheme based on straightforward and little complex steps, by chaotic Lorenz system.
1.1 Related work
Last decade is considered as a remarkable era for secure communication and image processing. In wireless communication, protection of digital data such as text, sound, image and video has more importance because multimedia kind of stuff has taken hold on many important fields like electronic commerce, banking industry, law enforcement agencies requirements and personal data. The performance of old cryptosystems for image is poor in encryption of bulk sized data [44, 45]. To tackle this problem, new schemes based on chaos for image encryption have been developed.
In [3, 17], Amigo et al., and Jakimoski, has shown a link between secure communication and chaos theory. They said chaotic maps could achieve some basic requirements of secure communication such as randomness, robustness and sensitivity to initial conditions. In [2, 28], Ott and Alvarez has observed that values breaded by chaotic maps can be regained based on initial conditions but extremely erratic, and this kind of behavior is valuable for cryptosystems. Based on these properties, some cryptographers has proposed novel cryptosystems in [11, 31]. Pseudorandom number generator based on chaotic maps is one of the emerging field nowadays and can be utilized in different cryptosystems to get more security [30]. In [21], the virtual analysis of Advanced Encryption Standard (AES), Data Encryption Standard (DES) and 3DES are presented. The scrutiny of AES is explained considering the high throughput, area efficiency and elevated performance [20, 46]. It is presented that AES is as authorized Advance Encryption standard (AES) and it is well apt for hardware exercise. Moreover, the work described how to minimize the power dissipation and how to map the S-box into prototype chip. Further, the work highlighted the secure components of S-box which is using XOR operations instead of polynomial multiplication still there is a limitation of complex look up tables that were used in the creation of S-box. In [14], the cryptanalysis of previously published cryptosystem is presented. The already previously published cryptosystem was based on the on iterating chaotic map. It is shown in [14] that this previously published cryptosystem is weak and can easily be broken. To strengthen it, [14] proposed novel improvements to the proposed chaotic cryptosystem.
The rest of paper is arranged as follows: Some basic definitions of mathematical background for cryptography and details of chaotic map are given in Section 2. The detailed description of proposed image encryption algorithm is given Section 3. Section 4 depicts the results of simulation and different analyses. The conclusion of whole scheme is given in Section 5.
2 Basic definitions
In this section, the structural units of proposed image encryption technique are briefly discussed. First, an introduction to the Galois field and its primitive irreducible polynomials is presented followed with the basics of Projective General Linear Group. Secondly, the comprehensive description of chaotic Lorenz map is discussed in this section.
2.1 Galois field and its primitive irreducible polynomials
From the knowledge of Galois field, we can say that if p is a non-zero element of a Principle Ideal Domain (PID) R, then \(\frac {R}{p}\) will be a field if p is irreducible. Therefore, for a prime p and q = pn, we can denote the finite field of order q as GF(q) = GF(pn). The polynomial extension R[x] of intergral domanin R is also intergral domain, therefore, in case of polynomial extension \(\mathbf {R}[x]/\left \langle p(x)\right \rangle \) will be a field structure when p(x) is primitive irreducible polynomial, where \(\left \langle p(x)\right \rangle \) is a maximal ideal.
Where m(x) is monic primitive irreducible polynomial of degree n in Galois field GF(pn). The example of above formula is as follows:
The elements of GF(28) can be represented by a polynomial of degree 8 and \(\left \langle m(x)\right \rangle \) is the maximal ideal generated by monic irreducible polynomial, when the degree of polynomial will exceed from 7 this maximal ideal will absorb it. Now, the question is how many different irreducible polynomials are there corresponding to any Galosi field GF(pn). The formula to find all irreducible polynomials is as follows:
By using above formula, it can be seen in Table 1, that there are 30 irreducible polynomials for GF(28). But for the construction of Galosi field which can generate its non-zero elements we need primitive irreducible polynomials. In Table 1, we have shown that out of 30 irreducible polynomials 16 are primitive irreducible. We have used Rabin’s test to find 30 irreducible polynomials, Rabin’s test is as follows:
Theorem 1
Let p1,p2,...,pk be all the prime divisors of n, and denoted ni = n/pi, for 1 ≤ i ≤ k. A polynomial f ∈Fq[x] of defree n is irreducible in \(\mathbf {F}_{q}[x] \Leftrightarrow gcd(f, x^{q^{n_{i}}}-x mod f)=1\) for 1 ≤ i ≤ k, and f divides \(x^{q^{n}}-x\).
A primitive polynomial is a polynomial that generates all elements of an extension field from a base field. Primitive polynomials are also irreducible polynomials. For any prime or prime power q and any positive integer n, there exists a primitive polynomial of degree n over GF(q). There are
primitive polynomials over GF(q), where ϕ(n) is the totient function.
Theorem 2
A polynomial of degree n over the finite field GF(2) is primitive if it has polynomial order 2n − 1.
Theorem 1, gave us 30 irreducible polynomial of Table 1. Now, the question is how to get 16 primitive irreducible polynomials from 30 irreducible polynomials. To explain this procedure, we have considered an example of GF(24).
There are two primitive irreducible polynomials for GF(24). The process to check whether an irreducible polynomial is primitive irreducible or not is shown in the example and counter example below.
Let f(x) = x4 + x3 + 1 is an irreducible polynomial. suppose α is the root of f(x). If α is the root of f(x) then we have
Because the coefficients of polynomial are in GF(2), that is why − 1 = + 1.
Where 2α3 = 0 due to GF(2).
It can be seen in above example that we are getting α15 = 1, and the order of GF(24) is 16, it means f(x) = x4 + x3 + 1 is a primitive polynomial because it is generating all non-zero elements of GF(24). Where α the root of primitive polynomial is known as primitive element, in other words, because GF is also a cyclic group so α is the generator. All irreducible polynomials are not primitive, to show this fact a counter example is as follows:
Let \(f^{\prime }(x)= x^{4}+x^{2}+1\) is an irreducible polynomial. suppose β is the root of f(x). If β is the root of \(f^{\prime }(x)\) then we have
Because the coefficients of polynomial are in GF(2), that is why − 1 = + 1.
It can be seen that \(f^{\prime }(x)= x^{4}+x^{2}+1\) is irreducible but not primitive, because it is not generating all non-zero elements of GF(24). Similarly, in Table 1, we have got all primitive irreducible polynomials form irreducible polynomials.
2.2 Projective General Linear group (PGL)
The Projective General Linear Group (PGL) can be defined as the group acting on \(\stackrel {-}{F}=\textbf {GF}(p^{n})\bigcup \left \{\infty \right \}\) is the group of all transformations and is denoted by PGL(2,GF(pn)). With the standard understanding about \(\infty \), PGL(2,GF(pn)) is the set of all linear fractional transformations (LFT) of \(\stackrel {-}{F}=\textbf {GF}(p^{n})\bigcup \left \{\infty \right \}\),
Linear fractional transformation g(z) is shortly denoted by LFT. We study a special class of maps
A LFT of PGL(2,GF(28)) ×GF(28) is a map of the form \(g(z)=\frac {az+b}{cz+d},\) a,b,c,d ∈GF(28) and ad − bc≠ 0
Transformation is depending on the invertible 2 × 2 matrix \(\begin {pmatrix} a & b\\ c & d \end {pmatrix}\)
2.3 Chaotic Lorenz system
The idea to define the chaotic dynamics with the help of chaotic maps is a big breakthrough in the filed of dynamical systems. In the atmosphere, the mathematical modelling of the air flow was first presented by E. Lorenz [10, 23]. The system of chaotic differential equation is given as
Where the intervals for variables x,y and z are given − 60 ≤ x ≤ 60, − 60 ≤ y ≤ 60, − 60 ≤ z ≤ 60. For chaotic behavior, the values for parameters a,b, and c are a = 10, b = 28 and c = 8/3 respectively.
3 Primitive irreducible polynomial S-boxes
Now from the above linear transforamtion, we have;
Where pi(x), i = 1,2,3,...,16 are set of primitive irreducible polynomials of Table 1 for GF(28). Therefore, we have 16 different fi, where i = 1,2,3,...16 to construct 16 different S-boxes with fixed a,b,c,d ∈ GF(28). The order of \(PGL\left (2,GF(2^{8})\right )\) is 16776960, therefore one can construct huge number of S-boxes by changing a,b,c,d ∈ GF(28). In this section, we have given an example for the construction of one S-box based on a = 32,b = 22,c = 11,d = 8 ∈ GF(28) and p1(x) = x8 + x4 + x3 + x2 + 1. In polynomial form, a = x5,b = x4 + x2 + x,c = x3 + x + 1,d = x3. Here it must be noted that the sign ′ +′ indicates XOR operation.
For z = 0
Where μ239 = μ4 + μ2 + μ, μ3 = x3 based on p1(x) = x8 + x4 + x3 + x2 + 1, corresponding to different primitive polynomials pi(x) of GF(28) these values of μ power will be different.
For z = 1
Where μ249 = μ5 + μ4 + μ2 + μ, μ25 = μ + 1 based on p1(x) = x8 + x4 + x3 + x2 + 1
For z = 2
Where μ219 = μ6 + μ4 + μ2 + μ, μ76 = μ4 + μ3 + μ2 + μ based on p1(x) = x8 + x4 + x3 + x2 + 1. Similarly, for z = 3,4,5,...,255 all the elements can be constructed corresponding to primitive irreducible polynomial p1(x) = x8 + x4 + x3 + x2 + 1. All elements of p1(x) S-box are shown in Table 2.
3.1 Analysis for evaluating the strength of S-box
In the analysis section, we shall determine the cryptographic strength of the propose S-box with some suitable measures. To find the S-box with fitting confusion creating strength many standard evaluating analysis are presented in literature such as Non-linearity, Bit independent criterion (BIC), Strict avalanche criterion (SAC), Linear approximation probability (LP) and Differential approximation probability (DP). We shall also use these criteria to test the security of proposed S-box.
To measure the good properties of S-box benchmark criteria are presented in literature like bijectivity, differential approximation probability (DP), strict avalanche criterion (SAC), bit independence criterion (BIC), nonlinearity, and linear probability (LP). We carry out the security analysis of the proposed S-box of example given in Table 2 using these well known criteria.
-
1.
Bijectivity: [16, 22] If the linear sum of the Boolean function fi of each component of the designed n × n S-box is 2n− 1, then f is a bijection. Mathematically, we can write as
$$ wt(a_{1}f_{1}+a_{2}f_{2}+...+a_{n} f_{n}). $$(34)where ai ∈ 0,1, (a1,a2,...,an)≠(0,0,...,0), wt() denotes the Hamming weight. In effect, an inverse is important specifically in a substitution netwrok, therefore S-box should be bijective.
-
2.
Nonlinearity: The nonlinearity of an S-box can be tested by the following formula:
$$ N_{f}=2^{-n}\left( 1-max_{\omega \in GF(2^{n})}\left|2^{-n}\sum\limits_{x\in GF(2^{n})} (-1)^{f(x)\oplus x.\omega}\right|\right), $$(35)where ω ∈ GF(28).
-
3.
Strict avalanche criterion: This analysis depicts information that while one bit of eight lengths input byte of plaintext modifies, will yield a 0.5 probability of the outcomes changes in byte of 8 bits balanced for entries.
-
4.
Bit independent criterion: For two Boolean function fj, fk, one can test the independence criterion of a substitution box by validating if, for any two output bits of the S-box, fj ⊕ fk (j≠k) fulfills the SAC and nonlinearity.
-
5.
XOR table and differential invariant: XOR table of substitution box basically depends on the calculation of \(\rho _{L}(a,b)= \left \{ x\in GF(2^{8}): L(x)\oplus L(a\oplus x)= M\right \}\) ∀a,b ∈ GF(28). The differential invariant ρL(a,b) is found as follows:
\(\rho _{L}(a,b) =\underbrace {\max \limits }_{a,b \in GF(2^{8}), a \neq 0}\left |\left \{ x\in GF(2^{8}): L(x)\oplus L(a\oplus x)= M\right \}\right |\).
Table 3 presents the results of above discussed analysis for our proposed S-boxes with different Primitive polynomial of GF(28).
4 Proposed algorithm for image encryption cryptosystem
In order to encrypt the digital information, we need to design a pseudorandom sequence generator to transform the real solves of chaotic Lorenz system to a digital sequence. The details are represented as follows. From the above system, we can get three real sequences denoted as x, y and z. In order to achieve to a better randomness, we cut off the first N values of the real sequences. Here we set N = 100 and denote the three real sequences as \(\left \{x_{i} \right \},\left \{y_{i}\right \},\left \{z_{i}\right \}\), where i = 1,2,3,...,m × n, where m × n is the size of plain image. The tth value of the sequences of x, y, and z are defined as xt, yt and zt. A disturbing procession is added to avoid the appearance of the periodic absolutely. That is, change the value of x and y with an interval of 10000:
First, we discard the integral part of the real sequences for all of x, y and z:
Where floor(x) denotes the maximum integer that is smaller than x. Second, develop a new chaotic sequence as following:
At last, we get the modified chaotic sequence ki, the beauty of proposed chaotic sequence is that it has the flavor of three xi,yi and zi chaotic sequences of chaotic Lorenz system. During experiment we have changed the length of ki according to the size of plain image m × n by discarding some of its values from the end.
In order to get an improved image encryption scheme, we have changed the position of plaintext image pixels by randomness of ki. The proposed scheme consists of two phases, first phase starts from equation 4 and ends at equation 8. The basic purpose of first phase is to changed the pixel positions of image. The second phase consists of equation (9), (10) and (11) and in this process we are attaining pixel value change based on XOR operation to get a fully encrypted image. Let us suppose that the plain image is I with m rows and n columns. For the sake of convince, we have changed the image I to a one dimensional vector, say I1(1 : m ×n).
where p = 1,2,3,...,m and q = 1,2,3,...,n. Now, the chaotic sequence ki, will change the vector I1 to I2 with the help of following procedure.
where i = 1,2,3,...,m × n. Define a new sequence with elements from GF(28) based on ki as follows.
After getting l(i) sequence of random decimal numbers from GF(28). We will XOR l(i) with I2(i) to get the final vector I3(i). Reshape I5(i) in the form of m × n matrix to get the first level ciphered image as shown in equation (11).
As a last step for the proposed algorithm, we have applied the substitution step. We can define the process of substitution in following steps:
-
1.
Consider the pixelof the image in the form of binary byte i.e., 8 binary bits. We divide this set into four LSBs (Least significant bits) and Most significant bits (MSBs).
-
2.
In the next step, the MSBs and LSBs having 4 bits each are converted into decimal values. Conventionally, the pixel value which has to be replaced by S-box value is selected with the help of decimal value of LSBs and MSBs. The column of S-box is selected by the decimal value of LSBs whereas the row of S-box is carefully chosen by decimal value of MSBs.
-
3.
One by one all the pixel values are substituted with the values of S-box.
-
4.
In this case, as there are number of S-boxes so each pixel of the image is replaced by single S-box, second pixel value is replaced by another S-box and this procedure will continue till last pixel value.
-
5.
For the selection of S-box out of 256 S-boxes with whom the original value will be replaced is done with the help of x, y, z trajectories of Lorenz map. The proposed algorithm in the form of a flowchart is shown in Fig. 1.
5 Simulation results and statistical analysis
For simulation results, we take an image of cameraman having size 256 × 256. Table 4 represents the initial values of the chaotic maps which are used as secret keys. The plain image and histogram of cameraman are depicted in Fig. 2a and c. Figure 2a undergoes the process of encryption through our proposed encryption scheme and the encrypted image is given in Fig. 2b. The strong visual results of encrypted image indicate the quality of encryption algorithm. Furthermore, the histogram of encrypted image in Fig. 2d also confirms the strength of our scheme. On the other hand, the proposed image encryption scheme is applied on gray scale image having gray value of 124. The gray scale image is given in Fig. 3a and b represents the encrypted image of the gray scale image. Moreover, Fig. 3c and d depicts the histogram images of plaintext image and encrypted image respectively. The results of encryption are satisfactory regardless of high autocorrelation in the plain image. Similarly, the histogram of the encrypted gray scale image shows strength of our proposed technique.
5.1 Statistical analysis
The statistical analyses are used to evaluate the strength of proposed image encryption technique. In this work, we have employed different statistical analyses to determine the standard of our proposed image encryption technique. In addition to this, the results of proposed technique are being compared with the results of well-known image encryption techniques. The description of these analyses is given in the following subsections.
5.1.1 Correlation
The correlation of an image is given as [5, 26]:
where (i,j) corresponds to image pixels positions, (ρ(i,j)) is pixel value at (ith) row and (jth) column of image, μ is the variance, φ is the standard deviation. The correlation analysis determines the similarity between two neighbor image pixels over the whole image having range between [− 1 1] with 1 showing the perfect correlation.
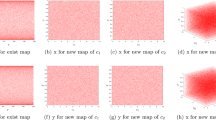
Figure 4a shows the distribution of horizontally adjacent pixels of cameraman image and Fig. 4b shows the distribution of horizontally adjacent pixels of encrypted cameraman image. The distribution of vertical adjacent pixels in ciphered cameraman image will act similar as they respond in horizontal adjacent pixels.
5.1.2 Entropy
The entropy of an image is given as [5, 26]:
where i,j corresponds to image pixels positions, ρ(i,j) is pixel value at ith row and jth column of image and pr(ρ(i,j)) is the probability of image pixel. Entropy shows the randomness of image having range between [0 8] for an image having 256 gray scales. A greater value of entropy shows the greater amount of randomness.
5.1.3 Contrast
The contrast of an image is given as [5, 26]:
where i,j corresponds to image pixels positions, ρ(i,j) is pixel value at ith row and jth column of image. The contrast analysis of the image enables the viewer to vividly identify the objects in texture of an image. The contrast values ranges from [0 (size(Image) − 1)2]. The contrast value of a constant image is 0. The greater value of the contrast shows greater variation in image pixels.
5.1.4 Homogeneity
In [5, 26], the homogeneity of image is defined as:
where the location of image pixels is given by i,j. In this analysis, the closeness of gray level cooccurrence matric (GLCM) diagonal and GLCM is calculated. The interval for homogeneity is [0 1].
5.1.5 Energy
The energy of an image can be defined as [5, 26]:
where i,j depicts the position of image pixels. The above equation interprets the energy analysis as the summation of square of all elements in GLCM. The value of energy lies in the interval [0 1] and the constant image has maximum energy value of 1. Table 5 shows the value of energy analysis and also the comparison with other existing techniques. This comparison indicates the quality of our proposed scheme.
6 Security analysis
It is mandatory to compute the security analyses to assess the strength of any cryptosystem. In this section, we assessed the security of our scheme with the help of certain security analyses like key space, key sensitivity, avalanche analysis, noise resistant analysis and cryptanalysis. The comparison of the outcomes of these analyses with the security analyses of other schemes exemplify the strength of our proposed technique. Following sections describe the security analyses in detail.
6.1 Key space and key sensitivity
For any cryptographic system, the total number of secret keys which are used to encrypt the data are named as key space and it has its importance as far as security of whole scheme is concerned. In this work, the secret keys are the initial conditions of three different chaotic maps. The secret key has average range of 1020 and we have used three different secret keys so the total number of different keys can be given as 1020×3 = 1060. A recent personal computer will require over 1010 years to go through all possible blends of this huge keyspace.
One of the features of the quality cryptosystem is there sensitivity to a tiny change in secret keys. For instance, the change in secret key during decoding process will give altogether a different decoded image. This mechanism is named as key sensitivity. Our proposed encryption technique is sensitive to even a minor change in the initial conditions. To prove this claim, we will change the secret keys and show the pictorial results. By using secret keys as mentioned in Table 2, we have encrypted the cameraman image as given in Fig. 2a. Considering four different cases of changing initial secret keys we have following results.
-
Case I: If the initial secret key k1 is slightly changed i.e., k1 = a = 10 to \(k_{1}^{\prime } = a = 10.0000000001\) then it is observed that the decryption process does not get the required results. Figure 5a depicts the decryption of plain-image with key \(k_{1}^{\prime }\). In this process, the remaining two keys were remained the same.
-
Case II: For the second case, the key k2 is changed from its original value i.e., k2 = b = 28 to \(k_{2}^{\prime } = b = 28.0000000001\) and again with this slight change in one key, the decryption image does not resemble to the original plaintext image and hence prove our claim of key sensitivity. The decryption is given in Fig. 5b.
-
Case III: The initial secret key k3 is slightly changed while keeping the remaining keys same. A change of 0.0000000001 in k3 i.e k3 = c = 8/3 to \(k_{3}^{\prime } = c = 8/3 + 0.0000000001\) provides a different original image as given in Fig. 5c.
-
Case IV: For the last case, the key k4 is changed like k1 = a = 10 to \(k_{1}^{\prime } = a = 9.99999999999\) and the decrypted image is given in Fig. 5d.
In all four cases, even a slight change in the initial secret key could not obtain the original image and hence prove our claim of key sensitivity for proposed algorithm.
Key sensitivity analysis a First secret key is changed from k1 = a = 10 to \(k_{1}^{\prime } = a = 10.0000000001\) b Second secret key is k2 = b = 28 to \(k_{2}^{\prime } = b = 28.0000000001\) c Third secret key is changed from k3 = c = 8/3 to \(k_{3}^{\prime } = c = 8/3 + 0.0000000001\) d Fourth secret key is changed from k1 = a = 10 to \(k_{1}^{\prime } = a = 9.99999999999\)
6.2 Avalanche analysis
In block ciphers, the effect of avalanche mentions one of the properties of strong cryptographic algorithms. If a single input bit change effect the half number of output bits, then it is an apparent avalanche effect. Researchers prefer unified average change intensity (UACI) and number of pixel change rate (NPCR) to measure the effect of avalanche criteria. The detailed description of this effect is provide in [43] as:
Where the two ciphered digital images C1 and C2 are attained by changing the single bit of plain image. Moreover, the height and width of cipher images are given by N and M respectively. We can define the D(i,j) as
By adjusting the single pixel of plaintext image, the rate of change of pixel quantity of encrypted image is measured by number of pixel change rate (NPCR) analysis. Moreover, the normal power of contrast between plain and encrypted images is calculated by unified average change intensity analysis (UACI). The calculated minimum value for NPCR must be 50percent. In our work, three different plain images of Lena, baboon and cameraman have been through NPCR and UACI analyses. For each image, the position of bit is firstly changed around first pixel then around middle pixel and finally around the last pixel. Table 6 depicts the outcomes of NPCR and UACI for all cases of three images. In this Table, the value of NPCR remains greater than 99 percent and value of UACI is greater than 33 percent. These results indicate the strong avalanche effects. In addition to this, a comparison has been established between avalanche values of proposed scheme and AES
By using NPCR and UACI analyses, the key sensitivity of proposed scheme is also evaluated. In first case, two same keys with difference of only 1 bit are used to calculate the difference between two encrypted images. For the second case, the difference of one bit between two keys would remain the same but we calculated the difference between encrypted and decrypted images. Table 6 gives the results of both cases along with comparison with AES. The results of Table 6 show the required avalanche effect.
6.3 Noise resistant analysis
The noise resistant encryption algorithm depicts the strength of any cryptosystem. Any transmitted data may get effected by channel (irrespective of wired or wireless channel) noise or deliberately added noise. It is observed that it is hard to decipher the abandoned cipher image even the portion of the image is affected. Few methods like error detection and correction have been used to counter these situations but at the cost of computational complexity. For successful transmission and decryption of cipher data, the error detection and correction are required before both the steps. So, ultimately it increases the complexity of the system. In this proposed technique, the addition of noise does not become the hurdle to decipher image correctly with some minor changes. To verify this claim, a series of experiments regarding successful deciphering have been done with noise addition in the cipher images. Figure 6a and b represent the plain image and encrypted images respectively. This encryption is done with the help of secret keys of Table 4. For noise resistance test, the 10,000 pixels of encrypted image are either cropped or made corrupted with white pixels as shown in Fig. 6c. The deciphering of this image is given in Fig. 6d. Clearly, this pictorial representation indicates the successful decryption with minor changes. To prove this claim for other images, the cameraman image is encrypted with the secret keys of Table 4. The plain image with noise and its encryption is given in Fig. 6e and f respectively. Now, again we removed first 10, 000 pixels either with the help of cropping or by corrupting the image. Interestingly, the decryption is successful with minor changes and as shown in Fig. 6g and h.
a A test image, b encryption of test image using secret keys. c Adding noise in the cipher image by changing first 10,000 pixels either by cropping or corrupting the file by using the white pixels. d Deciphered image. e The cameraman noisy image, f encryption of cameraman image using secret keys. g Adding noise in the cipher image by changing first 10,000 pixels either by cropping or corrupting the file by using the white pixels. After decryption, h Deciphered image
On the other hand, there is a difference between the deciphering of plain text and digital image. For noisy cipher text, the deciphering of the text gives a whole new text. There are many examples in which the major concern is to recognize the face of the person and object irrespective of quality of decipher images. For this reason, the deciphering of encrypted images having added noise is major breakthrough.
6.4 Cryptanalysis
To evaluate the strength of proposed scheme against different malicious attacks, following attacks are considered to evaluate the proposed cryptosystem.
6.4.1 Linear cryptanalysis
Linear approximation probability is used to analyze the imbalance of an event. The maximum value of imbalance of the event can also be obtained with the help of this analysis. In this analysis, two masks Γx and Γy, are applied to parity of both input and output bits, respectively. In [25], it is defined as:
where all the inputs values are contained by set X and total number of this set are 2n. As we have used 8 different S-boxes and the average maximum value of LP is LPmax = 2− 4.21 and having distinct 256 S-boxes the maximum LP is given as \(LP_{\max \limits }^{4r} = 2^{-4.21 \times 256} = 2^{-1077}\). By seeing the outcomes of LP, it is almost impossible for an invader to differentiate our proposed cipher with the help of random permutation and hence, the proposed algorithm will show resistance for countering linear cryptanalysis.
6.4.2 Differential cryptanalysis
One of the precise goals for assurance of uniform mapping, the input differential extraordinarily supervises the differential at output end. These features certify the probability of uniform mapping for every input bit i. The main purpose of approximation probability is to calculate differential uniformity of S-box. In [8] it is given as:
where the input and output differentials are given by Δx and Δy respectively. For S-boxes, the maximum average value of DP is \(DP_{\max \limits } = 2^{-4.05}\). Here, the number of active S-boxes is exactly 256 i.e., \(DP_{\max \limits }^{4r} = 2^{-4.05 \times 256} = 2^{-1036}\). By seeing this outcome, it is confirmed that proposed scheme has the ability to resist against malicious differential cryptanalysis.
Moreover, we have done the security analysis of the proposed substitution box and compared with the state-of-art recent works. Table 7 shows the comparative results strict avalanche criterion, bit independent criterion, BIC for SAC, linear approximation probability, and differential approximation probability of proposed and other S-boxes demonstrating the superiority of our proposed S-Box.
6.5 Computational time
The other requirement for the encryption algorithm is the computational complexity, which is required to be as minimum as possible for the effective and efficient implementation of encryption algorithm over the different platforms. We have computed the time required for the proposed encryption algorithm considering 12 rounds and a data block size of 20 MB. We have compared the computational time of the proposed algorithm and compared with the state-of-art recent works. Table 8 shows the comparative results of computational time of proposed and other works demonstrating the superiority of our proposed work. The time is computed on a desktop machine using MATLAB software on Windows 10 with i5 processor and 8GB RAM.
7 Conclusion
In this paper, combination of proposed S-boxes and chaotic maps is used for image encryption algorithm. This scheme consists of two phases. In the first phase, substitution is performed by using multiple S-boxes instead a single S-box. The application of several S-boxes not only provide Additional security but also utilizes less round of encryption. The initial values of Lorenz chaotic map help to operate each round of encryption. In addition to this, permutation is performed in the second phase. The resistance of proposed encryption scheme is depicted through simulation and security analyses results. The outcomes of cryptanalysis also confirm the robustness of our proposed scheme. This work also motivates researchers to add different changes like increasing number of S-boxes and encryption rounds by keeping standard of encryption and computational complexity.
References
Ahmad J, Hwang SO (2015) Chaos-based diffusion for highly autocorrelated data in encryption algorithms. Nonlinear Dynamics 82(4):1839–1850
Alvarez G, Li S (2006) Some basic cryptographic requirements for chaos-based cryptosystems. Int J Bifurcation Chaos 16(08):2129–51
Amigo JM, Kocarev L, Szczepanski J (2007) Theory and practice of chaotic cryptography. Phys Lett Section A 366(3):211–16. https://doi.org/10.1016/j.physleta.2007.02.021
Anees A, Siddiqui AM, Ahmed F (2014) Chaotic substitution for highly autocorrelated data in encryption algorithm. Commun Nonlinear Sci Numer Simul 19(9):3106–3118
Anees A, Siddiqui AM, Ahmed J, Hussain I (2014) A technique for digital steganography using chaotic maps. Nonlinear Dynamics 75(4):807–816
Bakhache B, Ghazal JM, El Assad S (2014) Improvement of the security of zigbee by a new chaotic algorithm. IEEE Syst J 8(4):1021–30. https://doi.org/10.1109/JSYST.2013.2246011
Belazi M, E-Latif AAA, Belghith S (2017) Khan efficient cryptosystem approaches: S-boxes and permutation-substitution-based encryption. Wirel Pers Commun 87(1):337–361
Biham E, Shamir A (1993) Differential cryptanalysis of the data encryption standard. Springer
Çavuşoğlu U, Akgül A, Kaçar S, Pehlivan İ, Zengin A (2016) A novel chaos-based encryption algorithm over TCP data packet for secure communication. Secur Commun Netw 9(22):5968–74
Chen G, Mao Y, Chui CK (2004) A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fractals 21(3):749–61. https://doi.org/10.1016/j.chaos.2003.12.022
Cicek S, Uyaroğlu Y, Pehlivan I (2013) Simulation and circuit implementation of sprott case h chaotic system and its synchronization application for secure communication systems. J Circuits Syst Comput 22(04):1350022
Daemen J, Rijmen V (2002) The design of Rijndael: AES - The advanced encryption standard. Springer
Dillak RY (2013) Digital color image encryption using RC4 stream cipher and chaotic logistic map Information Technology and Electrical Engineering (ICITEE), 2013 International Conference on
Farah MAB, Kachouri A, Samet M (2011) Improvement of cryptosystem based on iterating chaotic map. Commun Nonlinear Sci Numer Simul 16 (6):2543–2553
Guesmi R, Farah MAB (2021) A new efficient medical image cipher based on hybrid chaotic map and DNA code. Multimed Tools Appl 80:1925–1944
Hussain I (2013) A projective general linear group based algorithm for the construction of substitution box for block ciphers. Neural Computing & Applications 22:1085–1093
Jakimoski G, Kocarev L (2001) Chaos and cryptography: block encryption ciphers based on chaotic maps. IEEE Trans Circuits Syst I 48(2):163–9. https://doi.org/10.1109/81.904880
Jolfaei A, Mirghadri A (2011) Image encryption using chaos and block cipher. Comput Inf Sci 4(1):172–85. www.ccsenet.org/cis
Khan M, Shah T, Batool SI (2016) Construction of S-box based on chaotic Boolean functions and its application in image encryption. Neural Comput and Applic 27(3):667–685
Kohli R, KKumar M (2013) Optimized on system analysis using AES and X-tea. IJARCSSE 3(2). ISSN 2277-128X
Kohli R, Sharma D, Baliyan MK (2012) S-Box design analysis and parameter variation in AES algorithm. Int J Comput Appl 60(2)
Li S, Mou X, Cai Y (2001) Pseudo-random bit generator based on couple chaotic systems and its applications in stream-cipher cryptography. Proceedings, Lecture Notes in Computer Science 2247:316–329
Liu H, Kadir A, Niu Y (2014) Chaos-based color image block encryption scheme using S-box. AEU - Int J Electr Commun 68(7):676–86. https://doi.org/10.1016/j.aeue.2014.02.002
Liu Y, Tian S, Hu W, Xing C (2012) Design and statistical analysis of a new chaotic block cipher for wireless sensor networks. Commun Nonlinear Sci Numer Simul 17(8):3267–78. https://doi.org/10.1016/j.cnsns.2011.11.040
Matsui M (1994) Linear cryptanalysis of the data encryption standard. In: Eurocrypt’93, LNCS, vol 765. Springer, pp 386–397
Morioka S (2002) An optimized S-box circuit architecture for low power AES design. Workshop on cryptographic hardware and embedded systems, CHES.02. In: LNCS, vol 2523, pp 172–186
Noura H, El Assad S, Vladeanu C (2010) Design of a fast and robust chaos-based crypto-system for image encryption. In: 2010 8th international conference on communications, COMM 2010, pp 423–6. https://doi.org/10.1109/ICCOMM.2010.5509114
Ott E (1979) Chaos in dynamical systems. Second edition
Ozkaynak F, Yavuz S (2013) Designing chaotic S-boxes based on time-delay chaotic system. Nonlinear Dyn 74(3):551–7. https://doi.org/10.1007/s11071-013-0987-4
Pareschi F, Setti G, Rovatti R (2010) Implementation and testing of high-Speed CMOS true random number generators based on chaotic systems. IEEE Trans Circuits Syst I 57(12):3124–37. https://doi.org/10.1109/TCSI.2010.2052515
Pehlivan I, Wei Z (2012) Analysis, nonlinear control, and chaos generator circuit of another strange chaotic system. Turk J Electr Eng Comput Sci 20 (SUPPL.2):1229–39. https://doi.org/10.3906/elk-1103-14
Pisarchika AN, Zaninb M (2008) Image encryption with chaotically coupled chaotic maps. Physica D: Nonlinear Phenomena 237(20):2638–2648
Rhouma R, Solak E, Belghith S (2010) Cryptanalysis of a new substitution-diffusionbased image cipher. Commun Nonlinear Sci Numer Simul 15(7):1887–92. https://doi.org/10.1016/j.cnsns.2009.07.007
Solak E, Çokal C, Yildiz OT, BIYIKOG LU T (2010) Cryptanalysis of Fridrich chaotic image encryption. Int J Bifurcation Chaos 20(05):1405–13
Tang G, Liao X (2005) A method for designing dynamical S-boxes based on discretized chaotic map. Chaos Solitons Fractals 23(5):1901–9. https://doi.org/10.1016/j.chaos.2004.07.033
Tang G, Liao X, Chen Y (2005) A novel method for designing S-boxes based on chaotic maps. Chaos Solitons Fractals 23(2):413–19. https://doi.org/10.1016/j.chaos.2004.04.023, http://www.sciencedirect.com/science/article/pii/S0960077904002474
Ullah SS, Shah T (2017) Jamal A novel construction of substitution box using a combination of chaotic maps with improved chaotic range. Nonlinear Dynamics 88(4):2757–2769
Wang X, Teng L, Qin X (2012) A novel colour image encryption algorithm based on chaos. Signal Process 92(4):1101–1108
Wang Y, Wong K-W, Liao X, Chen G (2011) A new chaos-based fast image encryption algorithm. Appl Soft Comput 11 (1):514–22. https://doi.org/10.1016/j.asoc.2009.12.011
Wang Y, Wong KW, Liao X, Xiang T (2009a) A block cipher with dynamic S-boxes based on tent map. Commun Nonlinear Sci Numer Simul 14(7):3089–99. https://doi.org/10.1016/j.cnsns.2008.12.005
Wang Y, Xie Q, Wu Y, Du B (2009b) A software for S-box performance analysis and test. In: Proceedings - 2009 International conference on electronic commerce and business intelligence, ECBI 2009, p 125–8. https://doi.org/10.1109/ECBI.2009.15
Wang X-Y, Yang L, Liu R, Kadir A (2010) A chaotic image encryption algorithm based on perceptron model. Nonlinear Dynamics 62(3):615–621
Wu Y, Noonan JP, Agaian S (2010) NPCR and UACI randomness tests for image encryption. Cyber Journals: Multidisciplinary journals in science and technology, Journal of selected areas in telecommunications, pp 31–38
Yang D, Liao X, Wang Y, Yang H, Wei P (2009) A novel chaotic block cryptosystem based on iterating map with output-feedback. Chaos Solitons Fractals 41(1):505–10. https://doi.org/10.1016/j.chaos.2008.02.017
Yang H, Wong K -W, Liao X, Zhang W, Wei P (2010) A fast image encryption and authentication scheme based on chaotic maps. Commun Nonlinear Sci Numer Simul 15(11):3507–17. https://doi.org/10.1016/j.cnsns.2010.01.004
Zhang Y (2013) Encryption speed improvement on an improvement over an image encryption method based on total shuffling. In: Proceedings of 2013 International conference on sensor network security technology and privacy communication system, Nangang, China
Funding
Open access funding provided by the Qatar National Library.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Al-Maadeed, T.A., Hussain, I., Anees, A. et al. A image encryption algorithm based on chaotic Lorenz system and novel primitive polynomial S-boxes. Multimed Tools Appl 80, 24801–24822 (2021). https://doi.org/10.1007/s11042-021-10695-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-021-10695-5