Mean-field behavior of Nearest-Neighbor Oriented Percolation on the BCC Lattice Above 8 + 1 Dimensions

Abstract

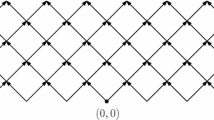
In this paper, we consider nearest-neighbor oriented percolation with independent Bernoulli bond-occupation probability on the d-dimensional body-centered cubic (BCC) lattice ${\mathbb {L}^d}$ and the set of non-negative integers ${{\mathbb {Z}}_+}$. Thanks to the orderly structure of the BCC lattice, we prove that the infrared bound holds on ${\mathbb {L}^d} \times {{\mathbb {Z}}_+}$ in all dimensions $d\ge 9$. As opposed to ordinary percolation, we have to deal with complex numbers due to asymmetry induced by time-orientation, which makes it hard to bound the bootstrap functions in the lace-expansion analysis. By investigating the Fourier–Laplace transform of the random-walk Green function and the two-point function, we derive the key properties to obtain the upper bounds and resolve a problematic issue in Nguyen and Yang’s bound. The issue is caused by the fact that the Fourier transform of the random-walk transition probability can take the value $-1$.

Appendices

Appendix A: Random Walk Quantities on the BCC Lattice

In this section, we show the expressions of the upper bounds on (1.2) to compute their numerical values. We use Stirling’s formula due to the property (1.1) of the BCC lattice, which helps us to obtain highly-precise estimates. Recall (1.1). Note that

$$\begin{aligned} D^{\mathbin {*}2n}(o) = \left( \left( {\begin{array}{c}2n\\ n\end{array}}\right) \frac{1}{2^{2n}}\right) ^d \le \left( \frac{1}{\sqrt{\pi n}}\right) ^d, \end{aligned}$$

(A.1)

for $n\in {\mathbb {N}}$. Now, fix a sufficiently large number N. For $\nu \in {\mathbb {N}}$, (A.1) and the bounds given by the integral test for convergence imply that

$$\begin{aligned} \varepsilon _1^{(\nu )}&= \sum _{n=\nu }^{\infty } D^{\mathbin {*}2n}(o) \le \sum _{n=\nu }^{\nu + N - 1} D^{\mathbin {*}2n}(o) + \sum _{n=\nu + N}^{\infty } \frac{1}{(\pi n)^{d/2}}\\&\le \sum _{n=0}^{N - 1} D^{\mathbin {*}2 (n + \nu )}(o) + \frac{1}{\pi ^{d/2} (\nu + N)^{d/2}} + \frac{1}{\pi ^{d/2}} \int \limits _{\nu + N}^{\infty } s^{-d/2} {\textrm{d}s}\\&\le \sum _{n=0}^{N - 1} D^{\mathbin {*}2 (n + \nu )}(o) + \frac{1}{\pi ^{d/2} (\nu + N)^{d/2}} + \frac{2}{\pi ^{d/2} \left( d - 2\right) } \left( \nu + N\right) ^{(2 - d)/2}. \end{aligned}$$

Moreover,

$$\begin{aligned} \varepsilon _2^{(\nu )}&= \sum _{n=\nu }^{\infty } \left( n - \nu + 1\right) D^{\mathbin {*}2n}(o)\\&\le \sum _{n=\nu }^{\nu + N - 1} \left( n - \nu + 1\right) D^{\mathbin {*}2n}(o) + \sum _{n=\nu + N}^{\infty } \left( n - \nu + 1\right) \frac{1}{(\pi n)^{d/2}}\\&\le \sum _{n=0}^{N - 1} \left( n + 1\right) D^{\mathbin {*}2 (n + \nu )}(o) + \frac{1}{\pi ^{d/2} (\nu + N)^{d/2 - 1}}\\&\quad + \frac{1}{\pi ^{d/2}} \int \limits _{\nu + N}^{\infty } s^{1 - d/2} {\textrm{d}s} - \frac{\nu - 1}{\pi ^{d/2}} \int \limits _{\nu + N}^{\infty } s^{-d/2} {\textrm{d}s}\\&\le \sum _{n=0}^{N - 1} \left( n + 1\right) D^{\mathbin {*}2 (n + \nu )}(o) + \frac{1}{\pi ^{d/2} (\nu + N)^{(d - 2)/2}}\\&\quad + \frac{2}{\pi ^{d/2} \left( d - 4\right) } \left( \nu + N\right) ^{(4 - d)/2} - \frac{2 \left( \nu - 1\right) }{\pi ^{d/2} \left( d - 2\right) } \left( \nu + N\right) ^{(2 - d)/2}. \end{aligned}$$

When $N=500$, we obtain numerical values in Table 1 by directly computing these expressions.

Table 1 Numerical values of random-walk quantities on the BCC lattice

Proof of Lemma 2.3

In this section, we prove Lemma 2.3. It is the result of Lemma 6.1 below. In this lemma, we first divide percolation events by cases, which are based on the fact of whether or not double connections are collapsed and where a path intersects a double connection. Next, these observations yield a lot of disjoint events such as $\lbrace \varvec{x} \rightarrow \varvec{y}\rbrace \circ \lbrace \varvec{u} \rightarrow \varvec{v}\rbrace$, where $\circ$ denotes that the left and right events must occur disjointly. Then, by the BK inequality [38], we bound the probability of such events in terms of the product of the two-point functions, e.g.,

$$\begin{aligned} {\mathbb {P}}_p\bigl (\lbrace \varvec{x} \rightarrow \varvec{y}\rbrace \circ \lbrace \varvec{u} \rightarrow \varvec{v}\rbrace \bigr ) \le {\mathbb {P}}_p(\varvec{x} \rightarrow \varvec{y}) {\mathbb {P}}_p(\varvec{u} \rightarrow \varvec{v}) = \varphi _p(\varvec{y} - \varvec{x}) \varphi _p(\varvec{v} - \varvec{u}). \end{aligned}$$

Such a product is represented by a diagram like (2.6). Also, the method to obtain Lemma 2.3 from Lemma 6.1 is based on decomposing diagrams by the inequality

$$\begin{aligned} \left\Vert f g \right\Vert _1 :=\sum _{\varvec{x}\in {\mathbb {L}^d} \times {{\mathbb {Z}}_+}} f(\varvec{x}) g(\varvec{x}) \le \left\Vert f \right\Vert _\infty \left\Vert g \right\Vert _1, \end{aligned}$$

(B.1)

where f and g are functions depending on a sum of a product of the two-point functions.

Lemma 6.1

For ${\varvec{x}\in {\mathbb {L}^d} \times {{\mathbb {Z}}_+}}$ and $N\ge 2$,

(B.2)

(B.3)

(B.4)

Proof of (B.2) in Lemma 6.1

This proof is inspired by [39, Sect. 3.1]. First, we rewrite the event in $\pi _p^{(0)}(\varvec{x})$. To do so, we introduce an ordering among bonds as follows. Let ${{\mathscr {B}}((x, t)) = \{((x, t), (y, t+1)) \in ({\mathbb {L}^d} \times {{\mathbb {Z}}_+})^2 \mid x - y \in {\mathscr {N}}^d\}}$ for ${(x, t) \in {\mathbb {L}^d} \times {{\mathbb {Z}}_+}}$, which is the set of directed bonds whose bottoms are (x, t). We can order the elements in ${\mathscr {B}}((x, t))$ because it is a finite set. For a pair of bonds $\varvec{b}_1$ and $\varvec{b}_2$, we write $\varvec{b}_1 \prec \varvec{b}_2$ if $\varvec{b}_1$ is smaller than $\varvec{b}_2$ in that ordering. Then, we obtain

$$\begin{aligned} \pi _p^{(0)}(\varvec{x})&= {\mathbb {P}}_p(\varvec{o} \Rightarrow \varvec{x} \ne \varvec{o}) \nonumber \\&= {} {\mathbb {P}}_p\left( \bigsqcup _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} \Big ({\{\varvec{o} \rightarrow x\} \circ \{\varvec{b} \rightarrow {x}\}} \cap \{{\forall \varvec{b}'\prec \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}\}}\Big )\right) \nonumber \\&= {} {\mathbb {P}}_p\left( \bigsqcup _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} \Big ({\{\varvec{o} \rightarrow {x}\} \circ \{\varvec{b} \rightarrow {x}\}} \cap \{{\forall \varvec{b}'\succ \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}\}}\Big )\right) \nonumber \\&= {} \frac{1}{2} \sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} \Bigl ({\mathbb {P}}_p\left( {\lbrace \varvec{o} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{x}\rbrace } \cap \lbrace \forall \varvec{b}'\prec \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}\rbrace \right) \nonumber \\&\quad + {\mathbb {P}}_p\left( \big \{{\lbrace \varvec{o} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{x}\rbrace }\big \} \cap \lbrace \forall \varvec{b}'\succ \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}\rbrace \right) \Bigr ). \end{aligned}$$

(B.5)

Next, we rewrite the event in $\pi _p^{(1)}(\varvec{x})$. By definition, we can easily see that

$$\begin{aligned} E\left( \varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{y})\right) \subset \{{y} \rightarrow {x}\} \circ \{{b} \rightarrow {x}\}. \end{aligned}$$

(B.6)

By splitting the event $\lbrace \varvec{o} \Rightarrow \underline{\varvec{b}}\rbrace$ into two events based on whether $\underline{\varvec{b}}$ equals $\varvec{o}$ or not,

$$\begin{aligned} \pi _p^{(1)}(\varvec{x})&= {} \sum _{\varvec{b}} {\mathbb {P}}_p\left( \{\varvec{o} \Rightarrow \underline{\varvec{b}}\} \cap E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) \nonumber \\&= {} \sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} {\mathbb {P}}_p \left( E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) + \sum _{\varvec{b}} {\mathbb {P}}_p \left( {\{\varvec{o} \Rightarrow \underline{\varvec{b}} \ne \varvec{o}}\} \cap E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) \nonumber \\&= {} \sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} \biggl ( {\mathbb {P}}_p\big (\{\varvec{o} \rightarrow \varvec{x}\} \circ \{\varvec{b} \rightarrow \varvec{x}\}\big ) \nonumber \\&\quad - {\mathbb {P}}_p \left( {\lbrace \varvec{o} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{x}\rbrace } \setminus E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) \biggr ) \nonumber \\&\quad + \sum _{\varvec{b}} {\mathbb {P}}_p \left( \lbrace \varvec{o} \Rightarrow \underline{\varvec{b}} \ne \varvec{o}\rbrace \cap E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) . \end{aligned}$$

(B.7)

Since both

$$\begin{aligned} \lbrace \forall \varvec{b}'\prec \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}\rbrace \sqcup \lbrace \exists \varvec{b}''\prec \varvec{b}, \varvec{b}'' \rightarrow \varvec{x}\rbrace \end{aligned}$$

and

$$\begin{aligned} \{\forall \varvec{b}'\succ \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}\} \sqcup \{\exists \varvec{b}''\succ \varvec{b}, \varvec{b}'' \rightarrow \varvec{x}\} \end{aligned}$$

are the whole event, respectively,

$$\begin{aligned}&{\mathbb {P}}_p\big (\{\varvec{o} \rightarrow \varvec{x}\} \circ \{\varvec{b} \rightarrow \varvec{x}\}\big )\\&\quad = {} \underbrace{\mathbb {P}_p \left( \{{\{\varvec{o} \rightarrow \varvec{x}\} \circ \{\varvec{b} \rightarrow \varvec{x}\}\}} \cap { \{\forall \varvec{b}'\prec \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}\} \cap \{\forall \varvec{b}''\succ \varvec{b}, \varvec{b}'' \not \rightarrow \varvec{x}\} }\right) }_{=0}\\&\qquad + {\mathbb {P}}_p \left( {{\{\{{\varvec{o}} \rightarrow \varvec{x}}\} \circ \{{\varvec{b} \rightarrow \varvec{x}}}\}\} \cap {\{\{ {\forall \varvec{b}'\prec \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}}\}\} \cap \{{\exists \varvec{b}''\succ \varvec{b}, \varvec{b}'' \rightarrow \varvec{x}}\}\} }\right) \\&\qquad + {\mathbb {P}}_p \left( {\{\{{{\varvec{o}} \rightarrow \varvec{x}}\} \circ \{{|\varvec{b}} \rightarrow {x}\}}\} \cap { \{\{\forall | {\varvec{b}}'\succ {\varvec{b}}, {\varvec{b}}' \not \rightarrow \varvec{x}\} \cap {\exists \varvec{b}''\prec \varvec{b}, \varvec{b}'' \rightarrow \varvec{x}}\}\} }\right) \\&\qquad + {\mathbb {P}}_p \left( {{\{\{\varvec{o} \rightarrow \varvec{x}}\} \circ \{{\varvec{b} \rightarrow \varvec{x}}}\}\} \cap {\{\{ {\forall \varvec{b}'\prec \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}}\}\} \cap \{{\exists \varvec{b}''\succ {\varvec{b}}, {\varvec{b}}'' \rightarrow \varvec{x}}\}\} }\right) \\&\quad = {} {\mathbb {P}}_p \left( {\{\{{\varvec{o} \rightarrow \varvec{x}}\} \circ \{\{{{\varvec{b}} \rightarrow \varvec{x}}}\}\} \cap \{{\forall \varvec{b}'\prec \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}\}}\right) \\&\qquad + {\mathbb {P}}_p \left( {\{\{{\varvec{o} \rightarrow \varvec{x}}\} \circ {\{{\varvec{b}} \rightarrow \varvec{x}}} \cap {\forall \varvec{b}'\succ \varvec{b}, \varvec{b}' \not \rightarrow \varvec{x}}\right) \}\\&\qquad + {\mathbb {P}}_p \left( {\lbrace \{\varvec{o} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{x}\rbrace } \cap { \lbrace \exists \varvec{b}'\prec \varvec{b}, \varvec{b}' \rightarrow \varvec{x}\rbrace \cap \lbrace \exists \varvec{b}''\succ \varvec{b}, \varvec{b}'' \rightarrow \varvec{x}\rbrace }\right) . \end{aligned}$$

By (B.5), taking the sum of the above over $\varvec{b} \in {\mathscr {B}}(\varvec{o})$ yields

$$\begin{aligned}{} & {} \sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} {\mathbb {P}}_p \big (\lbrace \varvec{o} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{x}\rbrace \big ) = 2 {\mathbb {P}}_p \left( \varvec{o} \Rightarrow \varvec{x} \ne \varvec{o}\right) \nonumber \\{} & {} \quad + \sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} {\mathbb {P}}_p { {\lbrace \varvec{o} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{x}\rbrace } \cap { \lbrace \exists \varvec{b}'\prec \varvec{b}, \varvec{b}' \rightarrow \varvec{x}\rbrace \cap \lbrace \exists \varvec{b}''\succ \varvec{b}, \varvec{b}'' \rightarrow \varvec{x}\rbrace } }.\nonumber \\ \end{aligned}$$

(B.8)

Substituting (B.8) into (B.7) and subtracting (B.5), we obtain

$$\begin{aligned}{} & {} \pi _p^{(1)}(\varvec{x}) - \pi _p^{(0)}(\varvec{x}) = \underbrace{{\mathbb {P}}_p(\varvec{o} \Rightarrow \varvec{x} \ne \varvec{o})}_{\mathrm {(a)}}\nonumber \\{} & {} \quad + \underbrace{\sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} {\mathbb {P}}_p \left( {\lbrace \varvec{o} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{x}\rbrace } \cap { \lbrace \exists \varvec{b}'\prec \varvec{b}, \varvec{b}' \rightarrow \varvec{x}\rbrace \cap \lbrace \exists \varvec{b}''\succ \varvec{b}, \varvec{b}'' \rightarrow \varvec{x}\rbrace } \right) }_{\mathrm {(b)}}\nonumber \\{} & {} \quad - \underbrace{\sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} {\mathbb {P}}_p \left( {\{\{{\varvec{o} \rightarrow \varvec{x}}\} \circ \{{{\varvec{b}} \rightarrow \varvec{x}\}\}}} \setminus E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) }_{\mathrm {(c)}}\nonumber \\{} & {} \quad + \underbrace{\sum _{{b}} {\mathbb {P}}_p \left( {\lbrace {\varvec{o}} \Rightarrow \underline{\varvec{b}}\} \ne {\varvec{o}}\rbrace } \cap E({\varvec{b}}, {\varvec{x}}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) }_{\mathrm {(d)}}. \end{aligned}$$

(B.9)

Finally, we show how (B.9) leads to the upper bound (B.2). In the following, we repeatedly use the trivial inequality

$$\begin{aligned} \varphi _p(\varvec{x}) \varvec{\mathbb {1}}_{\{o \ne x\}} \le \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{x}) \end{aligned}$$

(B.10)

and the fact that, if there are two disjoint connections, then their lengths are at least two for oriented percolation. By Boole’s and the BK inequalities, (a) in (B.9) is bounded above as

$$ \begin{aligned}&{\mathbb {P}}_p(\varvec{o} \Rightarrow \varvec{x} \ne \varvec{o})\\&\quad ={\mathbb {P}}_p\Biggl (\bigcup _{\begin{array}{c} \varvec{b}_1, \varvec{b}_2\in {\mathscr {B}}(\varvec{o})\\ (\varvec{b}_1 \prec \varvec{b}_2) \end{array}} \bigcup _{\begin{array}{c} \varvec{b}_1'\in {\mathscr {B}}(\overline{\varvec{b}}_1),\\ \varvec{b}_2'\in {\mathscr {B}}(\overline{\varvec{b}}_2) \end{array}}\\&\qquad \Big \{\lbrace \varvec{b}_1\text { is occupied} \mathrel { \& } \varvec{b}_1'\rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b}_2\text { is occupied} \mathrel { \& } \varvec{b}_2'\rightarrow \varvec{x}\rbrace \Big \}\Biggr )\\&\quad \le \sum _{\begin{array}{c} \varvec{b}_1, \varvec{b}_2\in {\mathscr {B}}(\varvec{o})\\ (\varvec{b}_1 \prec \varvec{b}_2) \end{array}} \sum _{\begin{array}{c} \varvec{b}_1'\in {\mathscr {B}}(\overline{\varvec{b}}_1),\\ \varvec{b}_2'\in {\mathscr {B}}(\overline{\varvec{b}}_2) \end{array}} q_p(\varvec{b}_1) q_p(\varvec{b}_1') \varphi _p(\varvec{x} - \overline{\varvec{b}}_1') \cdot q_p(\varvec{b}_2) q_p(\varvec{b}_2') \varphi _p(\varvec{x} - \overline{\varvec{b}}_2')\\&\quad \le \frac{1}{2} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{x})^2, \end{aligned}$$

which corresponds to the 1st term in (B.2). The factor 1/2 in the last line is due to ignoring the ordering. To bound (b) in (B.9), we note that, for $\varvec{b}\in {\mathscr {B}}(\varvec{o})$,

$$\begin{aligned}{} & {} {\{\{{\varvec{o} \rightarrow \varvec{x}}\} \circ \{{{\varvec{b}} \rightarrow \varvec{x}}}\}\} \cap { \{{\exists {\varvec{b}}'\prec \varvec{b}, \varvec{b}' \rightarrow \varvec{x}}\} \cap \{{\exists \varvec{b}''\succ {\varvec{b}}, \varvec{b}'' \rightarrow \varvec{x}}}\}\}\\{} & {} \subset \bigcup _{\varvec{b}', \varvec{b}'' \in {\mathscr {B}}(\varvec{o})} \bigcup _{\varvec{y}} { \{\{{\varvec{b} \rightarrow \varvec{y} \rightarrow \varvec{x}}\} \circ \{{\varvec{b}' \rightarrow \varvec{x}}\} \circ \{{{\varvec{b}}'' \rightarrow \varvec{y}} }\}\}. \end{aligned}$$

By Boole’s and the BK inequalities, we have

$$\begin{aligned}{} & {} \sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})} {\mathbb {P}}_p \left( {\{\{{\varvec{o} \rightarrow \varvec{x}}\} \circ \{{{\varvec{b}} \rightarrow \varvec{x}}}\} \cap { \{\{{\exists {\varvec{b}}'\prec \varvec{b}, \varvec{b}' \rightarrow \varvec{x}}\} \cap \{{\exists {\varvec{b}}''\succ \varvec{b}, \varvec{b}'' \rightarrow \varvec{x}} }\right) \}\}\\{} & {} \qquad \qquad \le \sum _{\varvec{y}} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{y})^2 \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{x}) \varphi _p(\varvec{x} - \varvec{y}), \end{aligned}$$

which corresponds to the 2nd term in (B.2). To bound (c) in (B.9), we note that, for $\varvec{b}\in {\mathscr {B}}(\varvec{o})$,

$$\begin{aligned}&{\lbrace {\varvec{o}} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{x}\rbrace } \setminus E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o})) \nonumber \\&\quad \subset {} \bigcup _{\varvec{y}} \bigcup _{\varvec{b}'} \Bigl \{ \{ \lbrace {\varvec{o}} \rightarrow \varvec{y} \rightarrow \varvec{x}\rbrace \circ \lbrace {\varvec{b}} \rightarrow \varvec{b}' \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{y} \rightarrow \underline{\varvec{b}}'\rbrace \} \nonumber \\&\qquad \sqcup \{ {{{\varvec{o}} \rightarrow \varvec{b}' \rightarrow \varvec{x}}\} \circ \{ {{\varvec{b}} \rightarrow \varvec{y} \rightarrow \underline{\varvec{b}}'}\} \circ \lbrace \varvec{y} \rightarrow \varvec{x}\rbrace } \Bigr \} \nonumber \\&\quad ={}\bigcup _{\varvec{b}'} { \lbrace \varvec{o} \rightarrow \varvec{x}\rbrace \circ \lbrace {\varvec{o}} \rightarrow \underline{\varvec{b}}'\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{b}' \rightarrow \varvec{x}\rbrace } \nonumber \\&\qquad \sqcup \bigcup _{\varvec{b}'} { \lbrace \varvec{o} \rightarrow \underline{\varvec{b}}' \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{b}' \rightarrow \varvec{x}\rbrace } \nonumber \\&\qquad \sqcup \bigcup _{\varvec{b}'} \bigcup _{\varvec{y} \ne \varvec{o}, \underline{\varvec{b}}'} { \lbrace \varvec{o} \rightarrow \varvec{y} \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{b}' \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{y} \rightarrow \underline{\varvec{b}}'\rbrace } \nonumber \\&\qquad \sqcup \bigcup _{\varvec{b}'} { \lbrace \varvec{o} \rightarrow \varvec{b}' \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \underline{\varvec{b}}'\rbrace \circ \lbrace \underline{\varvec{b}}' \rightarrow \varvec{x}\rbrace } \nonumber \\&\qquad \sqcup \bigcup _{\varvec{b}'} \bigcup _{\varvec{y} \ne \underline{\varvec{b}}'} { \lbrace \varvec{o} \rightarrow \varvec{b}' \rightarrow \varvec{x}\rbrace \circ \lbrace \varvec{b} \rightarrow \varvec{y} \rightarrow \underline{\varvec{b}}'\rbrace \circ \lbrace \varvec{y} \rightarrow \varvec{x}\rbrace }. \end{aligned}$$

(B.11)

By Boole’s and the BK inequalities, we have

$$\begin{aligned}&\sum _{\varvec{b} \in {\mathscr {B}}(\varvec{o})}{\mathbb {P}}_p\left( \{ {{\varvec{o} \rightarrow \varvec{x}}\} \circ \lbrace {\varvec{b}} \rightarrow \varvec{x}\rbrace } \setminus E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) \\&\quad \le {} \sum _{\varvec{u}} \left( q_p^{\mathbin {\star }3} \mathbin {\star }\varphi _p\right) (\varvec{x}) \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{u})^2 \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{u})\\&\quad \quad + \sum _{\varvec{u}} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{u})^2 \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{u})^2\\&\quad \quad + \sum _{\varvec{u}, \varvec{y}} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{u}) \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{y}) \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{u} - \varvec{y})\\&\qquad \quad \times \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{u}) \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{y})\\&\quad + \sum _{\varvec{u}} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{u})^2 \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{u})^2\\&\quad + \sum _{\varvec{u}, \varvec{y}} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{u}) \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{y}) \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{u} - \varvec{y})\\&\qquad \times \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{y}) \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{u}). \end{aligned}$$

Each term in the above upper bound corresponds to contributions of the 3rd term, the 4th term, the 5th term, the 4th term and the 6th term in (B.2), respectively. To bound (d) in (B.9), we apply (B.6) and split the below event into two events based on where the branching point is assigned:

$$\begin{aligned}{} & {} {\{ \varvec{o} \Rightarrow \varvec{u} \ne \varvec{o}}\} \cap \lbrace \varvec{o} \rightarrow \varvec{x}\rbrace \subset {\lbrace \varvec{o} \Rightarrow \varvec{u} \ne \varvec{o}\rbrace \circ \lbrace \varvec{o} \rightarrow \varvec{x}\rbrace }\nonumber \\{} & {} \quad \cup \bigcup _{\begin{array}{c} \varvec{y} \ne {o}\\ ({\mathfrak {t}}(\varvec{y}) \le {\mathfrak {t}}(\varvec{u})) \end{array}} {\lbrace \varvec{o} \rightarrow \varvec{u}\rbrace \circ \lbrace \varvec{o} \rightarrow \varvec{y} \rightarrow \varvec{u}\rbrace \circ \lbrace \varvec{y} \rightarrow \varvec{x}\rbrace }. \end{aligned}$$

(B.12)

Then, we obtain

(B.13)

Applying the BK [38] inequality and the same method for (a) to the right-most in the above, and paying attention to the disjointness of the connections, we arrive at

$$\begin{aligned}&\sum _{\varvec{b}} {\mathbb {P}}_p\left( \lbrace \varvec{o} \Rightarrow \underline{\varvec{b}} \ne \varvec{o}\rbrace \cap E(\varvec{b}, \varvec{x}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{o}))\right) \\&\quad \le {} \frac{1}{2} \sum _{\varvec{u}} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{u})^2 \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{u}) \left( q_p^{\mathbin {\star }3} \mathbin {\star }\varphi _p\right) (\varvec{x})\\&\qquad + \sum _{\varvec{u}} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{u})^2 \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{u})^2\\&\qquad + \sum _{\varvec{u}, \varvec{y}} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{u}) \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{y}) \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{u} - \varvec{y})\\&\qquad \times \left( q_p \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{u}) \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (\varvec{x} - \varvec{y}). \end{aligned}$$

Each term in the above upper bound corresponds to contributions of the 3rd term, the 4th term and the 5th term in (B.2), respectively. Combining the upper bounds on (a)–(d) completes the proof of (B.2). $\square$

Proof of (B.3) in Lemma 6.1

It is not hard to prove the upper bound by using (B.6), (B.11) and (B.14), so that we omit it. $\square$

Proof of (B.4) in Lemma 6.1

By definition,

$$\begin{aligned}{} & {} E(\varvec{b}, \varvec{u}; \tilde{{\mathcal {C}}}^{\varvec{b}}(\varvec{v})) \cap \lbrace \overline{\varvec{b}} \rightarrow \varvec{x}\rbrace \nonumber \\{} & {} \quad \subset \bigcup _{\begin{array}{c} \varvec{y}\\ ({\mathfrak {t}}(\underline{\varvec{b}}) < {\mathfrak {t}}(\varvec{y}) \le {\mathfrak {t}}(\varvec{u})) \end{array}} \Bigl \{ \lbrace {\varvec{b} \rightarrow \varvec{u}}\rbrace \circ \lbrace \varvec{v} \rightarrow \varvec{y} \rightarrow \varvec{u}\rbrace \circ \lbrace \varvec{y} \rightarrow \varvec{x}\rbrace \nonumber \\{} & {} \qquad \cup \lbrace {\varvec{b} \rightarrow \varvec{y} \rightarrow \varvec{u}}\rbrace \circ \{ {\varvec{v} \rightarrow \varvec{u}}\} \circ \lbrace \varvec{y} \rightarrow \varvec{x}\rbrace \Bigr \}. \end{aligned}$$

(B.14)

Paying attention to the disjointness of connections and the magnitude relationship between times, we obtain

By applying (B.14) to the above repeatedly,

$$\begin{aligned} \pi _p^{(N)}(\varvec{x}){} & {} \le \sum _{\varvec{v}_1}\sum _{\begin{array}{c} \{\varvec{y}_i\}_{i=2}^{N}, \{\varvec{u}_i\}_{i=1}^{N}\\ (\forall i:{\mathfrak {t}}(\varvec{u}_{i-1}) < {\mathfrak {t}}(\varvec{y}_i) \le {\mathfrak {t}}(\varvec{u}_i)) \end{array}}\\{} & {} \quad \Bigl ( {\mathbb {P}}_p\big (\lbrace \varvec{o} \Rightarrow \varvec{u}_1\rbrace \cap \lbrace (\varvec{u}_1, \varvec{v}_1) \rightarrow \varvec{u}_2\rbrace \circ \lbrace \varvec{o} \rightarrow \varvec{y}_2\rbrace \big )\\{} & {} \qquad +{\mathbb {P}}_p\big (\lbrace \varvec{o} \Rightarrow \varvec{u}_1\rbrace \cap \lbrace (\varvec{u}_1, \varvec{v}_1) \rightarrow \varvec{y}_2\rbrace \circ \lbrace \varvec{o} \rightarrow \varvec{u}_2\rbrace \big ) \Bigr )\\{} & {} \qquad \times \left( \prod _{j=2}^{N-1} \Xi (\varvec{y}_j, \varvec{u}_j; \varvec{y}_{j+1}, \varvec{u}_{j+1})\right) \frac{1}{2} \Xi (\varvec{y}_N, \varvec{u}_N; \varvec{x}, \varvec{x}). \end{aligned}$$

Finally, using Boole’s and the BK [38] inequality, and applying a similar method to (B.2), we arrive in (B.4). $\square$

Multiplying the diagrammatic bounds in Lemma 6.1 by the factors $m^t$, t or $1 - \cos k\cdot x$, and taking the sum of them, we obtain Lemma 2.3. The upper bounds (2.13)–(2.9) also require a telescopic inequality for the cosine function. Since its proof is quite the same as the literature, we omit it.

Lemma 6.2

([12, Lemma 2.13] or [21, Lemma 7.3]) Let $J\ge 1$ and $t_j\in {\mathbb {R}}$ for $j=1, \dots , J$. Then,

$$\begin{aligned} 0 \le 1 - \cos \sum _{j=1}^{J}t_j \le J \sum _{j=1}^{J}\left( 1 - \cos t_j\right) . \end{aligned}$$

(B.15)

Sketch proof of Lemma 2.3

We only deal with three examples of the bounds on the sum of a diagram multiplied by the factors $m^t$, t or $1 - \cos k\cdot x$ because one can easily calculate the other bounds on the analogy of such examples. The following proof is almost identical to the proof of [17, Lemma 5.3].

First, we consider the bounds (2.7)–(2.9). By the translation-invariance, for example,

which corresponds to the last term in the right hand side in (2.7). In the second equality, we have used the translation invariance.

Next, we consider the bounds (2.10)–(2.12). Note that

$$\begin{aligned}{} & {} \left( q_p \mathbin {\star }\varphi _p\right) (x, t) t \le \left( q_p \mathbin {\star }\varphi _p^{\mathbin {\star }2}\right) (x, t),\\{} & {} \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p\right) (x, t) t \le \left( q_p^{\mathbin {\star }2} \mathbin {\star }\varphi _p^{\mathbin {\star }2}\right) (x, t) + \left( q_p \mathbin {\star }\varphi _p^{\mathbin {\star }2}\right) (x, t). \end{aligned}$$

By using the above inequalities, for example,

which corresponds to the 5th term in the right hand side in (2.11).

Finally, we consider (2.13)–(2.15). By Lemma 6.2, for example,

which corresponds to the last term on the right hand side in (2.14). $\square$