On the Essential Spectrum of Schrödinger Operators on Trees

Abstract

It is known that the essential spectrum of a Schrödinger operator H on $\ell ^{2}\left (\mathbb {N}\right )$ is equal to the union of the spectra of right limits of H. The natural generalization of this relation to $\mathbb {Z}^{n}$ is known to hold as well. In this paper we generalize the notion of right limits to general infinite connected graphs and construct examples of graphs for which the essential spectrum of the Laplacian is strictly bigger than the union of the spectra of its right limits. As these right limits are trees, this result is complemented by the fact that the equality still holds for general bounded operators on regular trees. We prove this and characterize the essential spectrum in the spherically symmetric case.

Appendices

Appendix A: Calculating the spectrum of $A_{\tilde T}$

Proof of Lemma 4.1

The tree $\widetilde {T}=\widetilde {T}_{d}$ is composed of a d-regular tree $T=T_{d}$ connected at a point $0\in T$ to the first point $1\in \mathbb {N}$ in a line. Thus $A_{\widetilde {T}}$ is a finite rank perturbation of $A_{T}\oplus A_{\mathbb {N}}$, and so

$$\sigma_{\text{ess}}\left( A_{\widetilde{T}}\right)=\sigma_{\text{ess}}\left( A_{T}\right)\cup\sigma_{\text{ess}}\left( A_{\mathbb{N}}\right)=\sigma_{\text{ess}}\left( A_{T}\right)=[-2\sqrt{d-1},2\sqrt{d-1}]. $$

Therefore $d\notin \sigma _{\text {ess}}\left (A_{\widetilde {T}}\right )$. We want to exclude the possibility that $d \in \sigma \left (A_{\widetilde {T}} \right )$ $\setminus \sigma _{\text {ess}}\left (A_{\widetilde {T}} \right )$.

Using Dirac’s bra-ket notation, define $A_{0}=A_{\widetilde {T}}-\left |\delta _{0}\right \rangle \left \langle \delta _{1}\right |-\left |\delta _{1}\right \rangle \left \langle \delta _{0}\right |$ and $R\left (z\right )=\left (A_{\widetilde {T}}-z\right )^{-1}$, $R_{0}\left (z\right )=\left (A_{0}-z\right )^{-1}$. Recall the resolvent identity (we omit the dependence on z),

$$ R_{0}-R=R_{0}\left( A_{\widetilde{T}}-A_{0}\right)R=R_{0}\left( \left|\delta_{0}\right\rangle \left\langle \delta_{1}\right|+\left|\delta_{1}\right\rangle \left\langle \delta_{0}\right|\right)R. $$

(6.2)

Multiplying by $\delta _{0}$ on both sides we have

$$m_{T}(z)-m(z)=m_{T}(z)\left\langle \delta_{1}\right|R(z)\left|\delta_{0}\right\rangle, $$

where

$$m_{T}\left( z\right)=\left\langle \delta_{0}\right|R_{0}\left( z\right)\left|\delta_{0}\right\rangle $$

$$m_{\mathbb{N}}\left( z\right)=\left\langle \delta_{1}\right|R_{0}\left( z\right)\left|\delta_{1}\right\rangle $$

$$m\left( z\right)=\left\langle \delta_{0}\right|R\left( z\right)\left|\delta_{0}\right\rangle . $$

Additionally, by multiplying the identity (6.2) by $\delta _{1}$ on the left and by $\delta _{0}$ on the right we have

$$0-\left\langle \delta_{1}\right|R(z)\left|\delta_{0}\right\rangle =m_{\mathbb{N}}(z)m(z). $$

Combining we get,

$$m_{T}(z)-m(z)=m_{T}(z)\left( -m_{\mathbb{N}}(z)m(z)\right), $$

which implies

$$ m(z)=\frac{m_{T}(z)}{1-m_{T}(z)m_{\mathbb{N}}(z)}. $$

(6.3)

Now, if $\lambda \in \sigma \left (A_{\widetilde {T}}\right )\Big \backslash \sigma _{\text {ess}}\left (A_{\tilde {T}}\right )$, then $\lim _{\varepsilon \to 0}\text {Im}\left (m\left (\lambda +i\varepsilon \right )\right )\neq 0$. We will consider this expression for $\lambda =d$. It follows from (6.3) that

$$\text{Im}\left( m\right)=\frac{\text{Im}\left( m_{T}\left( 1+\overline{m_{T}m_{\mathbb{N}}}\right)\right)}{\left|1-m_{T}m_{\mathbb{N}}\right|^{2}}=\frac{\text{Im}\left( m_{T}\right)-\left|m_{T}\right|^{2}\text{Im}\left( m_{\mathbb{N}}\right)}{\left|1-m_{T}m_{\mathbb{N}}\right|^{2}}. $$

It is known (see, e.g., [28]) that

$$m_{\mathbb{N}}\left( z\right)=\frac{-z+\sqrt{z^{2}-4}}{2} $$

$$m_{T}\left( z\right)=\frac{-2\left( d-1\right)}{\left( d-2\right)z+d\sqrt{z^{2}-4\left( d-1\right)}}. $$

Thus

$$\lim_{\varepsilon\to0}\text{Im}\left( m_{T}\left( d+i\varepsilon\right)\right)=\lim_{\varepsilon\to0}\text{Im}\left( m_{\mathbb{N}}\left( d+i\varepsilon\right)\right)= 0. $$

Additionally the denominator of $\text {Im}\left (m\right )$ satisfies,

$$\begin{array}{@{}rcl@{}} 1-m_{T}\left( d+i0\right)m_{\mathbb{N}}\left( d+i0\right)&=&1-\left( d-1\right)\frac{d-\sqrt{d^{2}-4}}{\left( d-2\right)d+d\sqrt{d^{2}-4\left( d-1\right)}}=\\ &&1-\frac{\left( d-1\right)\left( d-\sqrt{d^{2}-4}\right)}{2d\left( d-2\right)} \neq 0, \end{array} $$

since the number $\sqrt {d^{2}-4}$ is irrational for every $2<d\in \mathbb {N}$ (d² − 4 is not a perfect square). Thus

$$ \lim_{\varepsilon\to0}\left|1-m_{T}\left( d+i\varepsilon\right)m_{\mathbb{N}}\left( d+i\varepsilon\right)\right|^{2}>0, $$

and we get

$$\lim_{\varepsilon\to0}\text{Im}\left( m\left( d+i\varepsilon\right)\right)= 0. $$

This implies that $d\notin \sigma \left (A_{\widetilde {T}}\right )\Big \backslash \sigma _{\text {ess}}\left (A_{\widetilde {T}}\right )$, and we can conclude that $d\notin \sigma \left (A_{\widetilde {T}}\right )$. □

Remark

As mentioned in 4.2, actually $\sigma \left (A_{\widetilde {T}}\right )=\sigma \left (A_{T}\right )$. The inclusion $\sigma \left (A_{T}\right )\subseteq \sigma \left (A_{\widetilde {T}}\right )$ is clear. Additionally, it is not hard, but is a bit cumbersome to see that for any $\lambda \notin \sigma \left (A_{T}\right )$ the expression $1-m_{T}\left (\lambda \right )m_{\mathbb {N}}\left (\lambda \right )$ is nonzero, and thus in this case also $\lambda \notin \sigma \left (A_{\widetilde {T}}\right )$.

Appendix B: Proof of Theorem 5

We begin by discussing some properties of $\mathcal {R}$-limits of regular trees. Let H be a Jacobi matrix on a d-regular tree T (with $d>2$) with root vertex $O\in T$. Let $\left \{H^{\prime },T^{\prime },v_{0}^{\prime }\right \}$ be an $\mathcal {R}$-limit of H along a path to infinity ${\left \{v_{j}\right \}_{j = 0}^{\infty }\subset V\left (T\right )}$. Since a regular tree is homogeneous, any $\mathcal {R}$-limit of H is defined on the same regular tree. Thus $T^{\prime }$ is another copy of the d-regular tree, which, for convenience, we take to be distinct from T.

Definition 8.1

Given an isometry between trees $f:T\to T^{\prime }$, denote by $I_{f}:\ell ^{2}\left (T\right )\to \ell ^{2}\left (T^{\prime }\right )$ the isometry operator: $\left (I_{f}\psi \right )\left (v\right )=\psi \left (f\left (v\right )\right )$.

Definition 8.2

For any vertex $u\in T$, $R>0$, denote by $P_{u,R}$ the projection operator onto $\ell ^{2}\left (B_{R}\left (u\right )\right )$. Further, for any operator X on $\ell ^{2}\left (T\right )$, let $X_{u,R}=P_{u,R}XP_{u,R}$.

Proposition 8.3

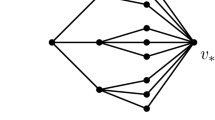
Let H be a Jacobi matrix on a d-regular tree T, and assume $\left \{H^{\prime },T^{\prime },v_{0}^{\prime }\right \}$ is an $\mathcal {R}$ -limit of H along a path to infinity $\left \{v_{j}\right \}_{j = 0}^{\infty }$ . Then there exists a subsequence of vertices $\left \{u_{j}\right \}_{j = 1}^{\infty }\subseteq \left \{v_{j}\right \}_{j = 0}^{\infty }$ and a sequence of tree isometries $\left \{f_{j}:T\to T^{\prime }\right \}_{j = 1}^{\infty }$ , with $f_{j}\left (u_{j}\right )=v_{0}^{\prime }$ (see Fig. 2 ) satisfying, for every $R>0$ ,

$$ \left\Vert I_{f_{j}}H_{u_{j},R}I_{f_{j}}^{-1}-H^{\prime}_{v_{0}^{\prime},R}\right\Vert \underset{j\to\infty}{\longrightarrow}0. $$

(6.4)

Fig. 2

The isometries f_j between T and $T^{\prime }$

Moreover, if $H^{\prime }$ is a Jacobi matrix on $T^{\prime }$ and there exist sequences $\left \{u_{j}\right \}_{j = 1}^{\infty }$, and $\left \{f_{j}\right \}_{j = 1}^{\infty }$ as above, s.t. (6.4) is satisfied for any $R>0$, then $\left \{H^{\prime },T^{\prime },v_{0}^{\prime }\right \}$ is an $\mathcal {R}$-limit of H along the path $\left \{v_{j}\right \}_{j = 0}^{\infty }$.

Proof

Assume the $\mathcal {R}$-limit $H^{\prime }$ is obtained along the subsequence $\left \{v_{n_{j}}\right \}_{j = 1}^{\infty }$ (as in Definition 2.2), and define $u_{j}=v_{n_{j}}$. Note that for any $j\in \mathbb {N}$ the coherent isomorphisms sequence $\left \{\mathcal {I}^{(j)}_{k} \right \}_{k = 1}^{\infty }$ can be extended to an isomorphism $\mathcal {I}_{j}:\ell ^{2}\left (T\right )\to \ell ^{2}\left (\mathbb {N}\right )$, that agrees on balls around $u_{j}$ with $\mathcal {I}^{(j)}_{k}$. Similarly, the sequence $\mathcal {I^{\prime }}_{k}$ can be extended to an isomorphism $\mathcal {I^{\prime }}:\ell ^{2}\left (T^{\prime }\right )\to \ell ^{2}\left (\mathbb {N}\right )$. Now we can define $I_{f_{j}}$ (and $f_{j}$) by $I_{f_{j}}={\mathcal {I^{\prime }}^{-1}\mathcal {I}_{j}}$. The convergence (6.4) then follows directly from (2.1).

In the other direction, assume $\left \{u_{j}\right \}$ is a sequence of vertices and $\left \{f_{j}\right \}_{j = 1}^{\infty }$ is a sequence of tree isometries as above. By compactness there is a path to infinity, $\left \{v_{j}\right \}_{j = 1}^{\infty }$, which contains a subsequence $\left \{u_{j}^{\prime }\right \}_{j = 1}^{\infty }\subseteq \left \{u_{j}\right \}_{j = 1}^{\infty }$, i.e. $u_{j}^{\prime }=v_{n_{j}}$, for a corresponding sequence $\left \{n_{j}\right \}\subseteq \mathbb {N}$. Let $\left \{\mathcal {I^{\prime }}_{k}\right \}_{k = 1}^{\infty }$ be any sequence of coherent isomorphisms of $T^{\prime }$ around $v_{0}^{\prime }$. We can now define for any $j\in \mathbb {N}$ a coherent sequence of isomorphisms $\left \{\mathcal {I}^{(j)}_{k}\right \}_{k = 1}^{\infty }$ of T around $u_{j}^{\prime }$ by

$$\mathcal{I}^{(j)}_{k}=\mathcal{I^{\prime}}_{k} \mathcal{I}_{f_{j}}|_{B_{k}\left( u_{j}^{\prime}\right)}. $$

The convergence (2.1) follows directly from (6.4). □

As we show next, it is possible to choose the isometries $\left \{f_{j}\right \}$ s.t. the path from $u_{j}$ to $v_{0}$ is always mapped to the same sequence of vertices in $T^{\prime }$ from $v_{0}^{\prime }$ to infinity.

Definition 8.4

Denote by $N\left (u\right )$ the set of neighbors of the vertex u. Additionally, assuming $u\neq v_{0}$, denote by $A\left (u\right )=A^{1}(u)=A_{v_{0}}\left (u\right )$ the vertex ${w\in N(u)}$ on the (shortest) path from $v_{0}$ to u. For $n\in \mathbb {N}$, let $A^{n}(v)=A\left (A^{n-1}\left (v \right )\right )$.

Proposition 8.5

Let $\left \{T,v_{0}\right \}$ and $\left \{T^{\prime },v_{0}^{\prime }\right \}$ be two copies of the d-regular tree, assume $\left \{v_{j}\right \}_{j = 0}^{\infty }$ is a path to infinity in T, $\left \{w_{j}\right \}_{j = 1}^{\infty }\subseteq \left \{v_{j}\right \}_{j = 0}^{\infty }$ is a subsequence, and $\left \{g_{j}:T\to T^{\prime }\right \}_{j = 1}^{\infty }$ is a sequence of tree isometries, with $g_{j}\left (w_{j}\right )=v_{0}^{\prime }$. Then there exist a subsequence of vertices $\left \{u_{j}\right \}_{j = 1}^{\infty }\subseteq \left \{w_{j}\right \}_{j = 1}^{\infty }$, a corresponding subsequence of tree isometries $\left \{f_{j}\right \}_{j = 1}^{\infty }\subseteq \left \{g_{j}\right \}_{j = 1}^{\infty }$, and a path to infinity ${\left \{v_{k}^{\prime }\right \}_{k = 0}^{\infty }\subset V\left (T^{\prime }\right )}$, s.t.

$$ \forall n\in\mathbb{N},\ f_{j}\left( A^{n}\left( u_{j}\right)\right)=v_{n}^{\prime}, $$

(6.5)

for any $j\in \mathbb {N}$ s.t. $\left |u_{j}\right |>n$.

Proof

By compactness, the sequence $\left \{ f_{j}\left (A\left (w_{j}\right )\right )\right \}_{j = 1}^{\infty }\subset T^{\prime }$ contains a vertex ${v\in N(v_{0}^{\prime })}$ an infinite number of times, denote it by $v_{1}^{\prime }=v$ and restrict to this sebsequence. Continue further inductively to define the path to infinity $\{v_{k}^{\prime }\}_{k = 0}^{\infty }$. Finally take the diagonal over the resulting subsequences of vertices $\subseteq \left \{w_{j}\right \}_{j = 1}^{\infty }$ and tree isometries $\subseteq \left \{g_{j}\right \}_{j = 1}^{\infty }$ to define the subsequence $\left \{u_{j}\right \}_{j = 1}^{\infty }$ and the subsequence $\left \{f_{j}\right \}_{j = 1}^{\infty }$. □

We refer to the sequence $\{v_{k}^{\prime }\}_{j = 0}^{\infty }$ from Proposition 8.5 as an ancestors sequence.

Corollary 8.6

Let H be a Jacobi matrix on a d-regular tree T, and assume $\left \{H^{\prime },T^{\prime },v_{0}^{\prime }\right \}$ is an $\mathcal {R}$ -limit of H along a path to infinity ${\left \{v_{j}\right \}_{j = 0}^{\infty }}$ . Then there exists a subsequence of vertices $\left \{u_{j}\right \}_{j = 1}^{\infty }\subseteq \left \{v_{j}\right \}_{j = 0}^{\infty }$ , a sequence of tree isometries $\left \{f_{j}\right \}_{j = 1}^{\infty }$ as in Proposition 8.3, and an ancestors sequence ${\left \{v_{k}^{\prime }\right \}_{k = 0}^{\infty }\subset V\left (T^{\prime }\right )}$ , s.t. ( 6.4 ) and ( 6.5 ) are satisfied.

As the term ‘ancestors’ suggests, an ancestors sequence defines a natural direction on $T^{\prime }$ that we want to think of as a direction ‘toward the past’ (or toward the tree T). Considering $v_{k + 1}^{\prime }$ as an ancestor of $v_{k}^{\prime }$, we obtain a partial order relation on the tree comparing ancestors and their ‘descendants’. Explicitly, given an ancestors sequence $\left \{ v_{k}^{\prime }\right \}_{k = 0}^{\infty }$ in $T^{\prime }$, and $k \in \mathbb {N} \cup \{0\}$, the subtree ${\Gamma }_{v_{k}^{\prime }}$ is the connected component containing $v_{k}^{\prime }$ in the graph obtained from $T^{\prime }$ by removing the edge $(v_{k + 1}^{\prime }, v_{k}^{\prime })$. For any $v \in {\Gamma }_{v_{k}^{\prime }}$ such that $v \neq v_{k}^{\prime }$ we write $v_{k}^{\prime }>_{D} v$ (thus ${\Gamma }_{v_{k}^{\prime }}$ is the tree of ‘descendants’ of $v_{k}^{\prime }$, together with the ancestor $v_{k}^{\prime }$). Moreover, if $v \in {\Gamma }_{v_{k}^{\prime }}$ for some k, let ${\Gamma }_{v}$ be the connected component containing v in the graph obtained from ${\Gamma }_{v_{k}^{\prime }}$ by removing the edge on the unique shortest path between v and $v_{k}^{\prime }$. ${\Gamma }_{v}$ is the tree of descendants of v and we write v > _Du for any $u \in {\Gamma }_{v}$ with $u\neq v$. The tree structure implies that this is well defined (i.e. ${\Gamma }_{v}$ does not depend on k and the definitions coincide for $v = v_{k}^{\prime }$) so that we get a partial order relation on $T^{\prime }$.

With this notation in place, we are finally ready for the

Proof of Theorem 5

Let $J^{(r)}$ be a right limit of $J=S_{1}$ along a sequence $\left \{ l_{i}\right \}_{i = 1}^{\infty }\subseteq \mathbb {N}$, i.e.

$$ \left\Vert J_{l_{i},R}-J_{0,R}^{\left( r\right)}\right\Vert \underset{i\to\infty}{\longrightarrow}0, $$

(6.6)

for any $R>0$. We claim that we can find a corresponding $\mathcal {R}$-limit $\left \{L,T^{\prime },v_{0}\right \}$ of H, s.t. $\sigma \left (J^{\left (r\right )}\right )\subseteq \sigma \left (L\right )$. Indeed, for $i\in \mathbb {N}$ take some $u_{i}\in T$ s.t. $\text {\text {dist}}\left (u_{i},v_{0}\right )=l_{i}$, and take any isomorphism of trees $f_{i}:T\to T^{\prime }$ s.t. $f_{i}\left (u_{i}\right )=v_{0}^{\prime }$. Moreover, by Proposition 8.5 and restricting to a subsequence if necessary, we can assume the existence of an ancestors sequence $\left \{ v_{j}^{\prime }\right \}_{j = 0}^{\infty }$ s.t. (6.5) is satisfied. For any $j\in \mathbb {N}$ define a Jacobi matrix $L^{\left (j\right )}$ on $\ell ^{2}\left ({\Gamma }_{v_{j}^{\prime }}\right )$, with diagonal terms:

$$\left( L^{\left( j\right)}\right)_{x,x}=\left( J^{\left( r\right)}\right)_{\left|x\right|-j,\left|x\right|-j}, $$

and off diagonal terms

$$\left( L^{\left( j\right)}\right)_{x,y}=\frac{1}{\sqrt{d-1}}\left( J^{\left( r\right)}\right)_{\left|x\right|-j,\left|y\right|-j}, $$

where for $x\in {\Gamma }_{v_{j}^{\prime }}$, $\left |x\right |=\text {dist}\left (x,v_{j}^{\prime }\right )$. Note that $L^{\left (j\right )}$ is spherically symmetric around $v_{j}^{\prime }$, and that the sequence $\left \{L^{\left (j\right )}\right \}_{j = 1}^{\infty }$ satisfies $L^{(j)}|_{{\Gamma }_{v^{\prime }_{j}}}=L^{(k)}|_{{\Gamma }_{v^{\prime }_{j}}}$ for $k\geq j$ (see Fig. 3).

Thus, we may define L on $\ell ^{2}\left (T^{\prime }\right )$ by $L|_{{\Gamma }_{v^{\prime }_{j}}}=L^{\left (j\right )}$. This defines an operator on $\ell ^{2}\left (T^{\prime }\right )$ since $\cup _{j = 1}^{\infty } {\Gamma }_{v_{j}^{\prime }}=T^{\prime }$. The sequence $\left \{L^{\left (j\right )}\right \}_{j = 1}^{\infty }$ converges strongly to L: indeed, for any $\varepsilon >0$ and $g\in \ell ^{2}\left (T^{\prime }\right )$ we can find $R>0$ s.t. $\left \Vert g|_{T^{\prime }\backslash B_{R}\left (v_{0}^{\prime }\right )}\right \Vert <\varepsilon$, and thus for any $j>R + 1$,

$$\left\Vert \left( L-L^{\left( j\right)}\right)g\right\Vert <\left\Vert L\right\Vert \left\Vert g|_{T^{\prime}\backslash B_{R}\left( v_{0}^{\prime}\right)}\right\Vert <\left\Vert L\right\Vert \varepsilon. $$

Fig. 3

The subtrees ${\Gamma }_{v^{\prime }_{j}}$, and the diagonal terms of L, $(J)_{k}\equiv \left (J^{(r)}\right )_{k,k}$

Next notice that by the spherical decomposition (and the symmetry) there exists for any $i\in \mathbb {N}$ a map $n_{i}(x):B_{R}\left (u_{i}\right )\to \mathbb {N}\cap [1,2R + 1]$, s.t. for $x,y\in B_{R}\left (u_{i}\right )$

$$ \left( H_{u_{i},R}\right)_{x,y}=\left\{ \begin{array}{cc} \left( J_{l_{i},R}\right)_{n_{i}(x),n_{i}(y)} & \mathrm{if } x=y \\ \frac{1}{\sqrt{d-1}}\left( J_{l_{i},R}\right)_{n_{i}(x),n_{i}(y)} & \mathrm{if } x\neq y \end{array} \right.. $$

Similarly, each term $\left (L_{v_{0}^{\prime },R}\right )_{x,y}$ corresponds to a term $\left (J^{(r)}_{0,R}\right )_{\widetilde {n}(x),\widetilde {n}(y)}$ (note that $L_{v_{0}^{\prime },R}$ is spherically symmetric around $v_{R}^{\prime }$, but not around $v_{0}^{\prime }$). Moreover, by the construction of L, the maps $\widetilde {n}$ and $n_{i}$ are related by $\widetilde {n}\left (f_{i}(x)\right )=n_{i}(x)$ (for $i\in \mathbb {N},\ x\in B_{R}\left (u_{i}\right )$). It follows, using (6.6), that for any $R\in \mathbb {N}$

$$\left\Vert I_{f_{i}}H_{u_{i},R}I_{f_{i}}^{-1} - L_{v_{0}^{\prime},R}\right\Vert<d^{R}\left\Vert J_{l_{i},R}-J_{0,R}^{(r)}\right\Vert\underset{i\to\infty}\longrightarrow 0. $$

Thus by Proposition 8.3, L is an $\mathcal {R}$-limit of H.

The spherical decomposition of $L^{\left (j\right )}$ produces a direct sum of half-line Jacobi matrices,

$$ L^{\left( j\right)}\cong\bigoplus\limits_{i = 0}^{\infty}\left( \oplus L_{i}^{\left( j\right)}\right), $$

(6.7)

Now, from each approximate eigenfunction of $J^{\left (r\right )}$ we can produce approximate eigenfunctions of $L_{i}^{\left (j\right )}$ above, for any $j-i$ large enough: assume g is an approximate eigenfunction of $J^{\left (r\right )}$, satisfying $\left \Vert J^{\left (r\right )}g-\lambda g\right \Vert <\varepsilon$, since $\| g \|_{2}= 1$ we can take N large enough s.t. $\left \Vert g|_{\mathbb {Z}\backslash \left (-N,N\right )}\right \Vert <\varepsilon$. For any $m\in \mathbb {Z}$ define $h_{m}\in \ell ^{2}\left (\mathbb {N}\right )$ by

$$h_{m}(n)=\left\{\begin{array}{ll} g(n-m-1) & \left|n-m\right|<N\\ 0 & \left|n-m\right|\geq N \end{array}\right., $$

then for any $j,i\in \mathbb {N}$ s.t. $j-i>N$,

$$\left( L_{i}^{\left( j\right)}h_{j-i}\right)\left( k\right)=\left( J^{\left( r\right)}g|_{[-N,N]}\right)\left( k-j+i-1\right), $$

for every $k\in \mathbb {N}\cap \left (-N-j+i-1,N-j+i-1\right )$. Thus,

$$\begin{array}{@{}rcl@{}} \left\Vert L_{i}^{\left( j\right)}h_{j-i}-\lambda h_{j-i}\right\Vert & \leq & \left\Vert J^{\left( r\right)}g|_{[-N,N]}-\lambda g|_{[-N,N]}\right\Vert +\varepsilon \end{array} $$

$$\leq\left\Vert J^{\left( r\right)}g-\lambda g\right\Vert +\left( \left\Vert J^{\left( r\right)}\right\Vert +\left|\lambda\right|\right)\left\Vert g|_{\mathbb{Z}\backslash[-N,N]}\right\Vert +\varepsilon<C\cdot\varepsilon. $$

By the unitary equivalence (6.7), an approximate eigenfuction of some $L_{i}^{\left (j\right )}$ will correspond to an approximate eigenfunction of $L^{\left (j\right )}$, with the same eigenvalue. Moreover, since the infinite matrix $L^{(j)}_{i}$ depends only on $j-i$, the same function is an approximate eigenfunction of $L^{(j)}$ for any j large enough. Thus, using the strong convergence $L^{(j)}\to L$ we get an approximate eigenfunction of L. Therefore $\sigma \left (J^{(r)}\right )\subseteq \sigma \left (L\right )$.

We now turn to the second case indicated in Proposition 6.2, and assume $J_{\left (s\right )}$ is a strong limit of the sequence $\left \{ J_{k}\right \}_{k = 1}^{\infty }$. Any such $J_{\left (s\right )}$ will appear as the restriction to the half line $\ell ^{2}\left (\mathbb {N}\right )$ of some right limit $J^{\left (r\right )}$ which corresponds, as above, to an $\mathcal {R}$-limit, L. Thus $J_{(s)}$ is contained in the set of matrices $\left \{ L_{i}^{\left (j\right )}\right \}_{i,j = 0}^{\infty }$ above. Thus, again, any approximate eigenfunction of $J_{\left (s\right )}$ corresponds to an approximate eigenfunction of some $L_{i}^{\left (j\right )}$, and thus also of L. Hence $\sigma \left (J_{(s)}\right )\subseteq \sigma \left (L\right )$. □