Skip to main content
SpringerLink
Log in

Generalization of a Nonlinear Maxwell-Type Viscoelastoplastic Model and Simulation of Creep and Recovery Curves

  • Published:
Mechanics of Composite Materials Aims and scope

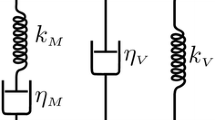
A generalization of the physically nonlinear Maxwell-type constitutive equation with two material functions for non-aging rheonomic materials, whose general properties and area of application have been studied analytically in previous articles, was suggested. To extend the set of basic rheological phenomena simulated, a third strain component expressed as the Boltzmann–Volterra linear integral operator governed by an arbitrary creep function was added. For generality and convenience of managing the constitutive equation and its fitting to various materials and lists of effects simulated, a weight factor (degree of nonlinearity) was introduced into the constitutive relation, which enabled to combine the primary physically nonlinear Maxwell-type model with the linear viscoelasticity equation in arbitrary proportion to construct a hybrid model and to regulate the prominence of different phenomena described by the two constitutive equations. A general expression for creep and recovery curves produced by the constitutive equation proposed was derived and analyzed. The general properties of creep and recovery curves were studied assuming three material functions are arbitrary. New properties were established, which enabled the generalized model to adjust the form of creep and recovery curves and to simulate additional effects (in comparison with the primary Maxwell-type model) observed in creep and recovery tests of various materials at different stress levels.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.

Similar content being viewed by others

References

  1. A. V. Khokhlov, “Two-sided estimates for the relaxation function of the linear theory of heredity via the relaxation curves during the ramp-strain and the methodology of identification,” Mech. Solids, 53, No. 3, 307-328 (2018). DOI: https://doi.org/10.3103/S0025654418070105

    Article  Google Scholar 

  2. A. V. Khokhlov, “Analysis of properties of ramp stress relaxation curves produced by the Rabotnov non-linear hereditary theory,” Mech. Compos. Mater., 54, No. 4, 473-486 (2018). DOI: https://doi.org/10.1007/s11029-018-9757-1

    Article  CAS  Google Scholar 

  3. A. V. Khokhlov, “Properties of the set of strain diagrams produced by Rabotnov nonlinear equation for rheonomous materials,” Mech. Solids, 54, No. 3, 384-399 (2019). DOI: https://doi.org/10.3103/S002565441902002X

    Article  Google Scholar 

  4. A. V. Khokhlov, “Long-term strength curves generated by the nonlinear Maxwell-type model for viscoelastoplastic materials and the linear damage rule under step loading,” J. Samara State Tech. Univ., Ser. Phys. & Math. Sci., 20, No. 3, 524-543 (2016). doi: https://doi.org/10.14498/vsgtu1512

  5. A. V. Khokhlov, “The nonlinear Maxwell-type model for viscoelastoplastic materials: simulation of temperature influence on creep, relaxation and strain-stress curves,” J. Samara State Tech. Univ., Ser. Phys. & Math. Sci., 21, No. 1, 160-179 (2017). doi:https://doi.org/10.14498/vsgtu1524

  6. A. V. Khokhlov, “A nonlinear Maxwell-type model for rheonomic materials: stability under symmetric cyclic loadings,” Moscow Univ. Mech. Bull., 73, No. 2, 39-42 (2018). doi:https://doi.org/10.3103/S0027133018020036

    Article  Google Scholar 

  7. A. V. Khokhlov, “Applicability indicators and identification techniques for a nonlinear Maxwell-type elasto-viscoplastic model using multi-step creep curves,” Vestn. Mosk. Gos. Tekh. Univ. im. N. E. Baumana, Estestv. Nauki [Herald of the Bauman Moscow State Tech. Univ., Nat. Sci.] No. 6, 92-112 (2018). doi: https://doi.org/10.18698/1812-3368-2018-6-92-112

  8. A. V. Khokhlov, “Applicability indicators and identification techniques for a nonlinear Maxwell-type elastoviscoplastic model using loading-unloading curves,” Mech. Compos. Mater., 55, No. 2, 195-210 (2019). doi:https://doi.org/10.1007/s11029-019-09809-w

    Article  CAS  Google Scholar 

  9. A. V. Khokhlov, “Possibility to describe the alternating and nonmonotonic time dependence of Poisson’s ratio during creep using a nonlinear Maxwell-type viscoelastoplasticity model,” Russ. Metallurgy (Metally), No.10, 956-963 (2019). doi:https://doi.org/10.1134/S0036029519100136

  10. A. V. Khokhlov, O. N. Stolyarov, A. V. Shaporev, “Loading-unloading-recovery curves for polyester yarns and identification of the nonlinear Maxwell-type viscoelastoplastic model,” Mech. Compos. Mater., 59, No. 1, 129-146 (2023). doi: https://doi.org/10.1007/s11029-023-10086-x

    Article  CAS  Google Scholar 

  11. Yu. N. Rabotnov, Creep of Structural Elements [in Russian], M., Nauka (1966).

  12. I. I. Bugakov, Creep of Polymeric Materials [in Russian], M., Nauka (1973).

  13. N. N. Malinin, Calculations for the Creep of Elements of Machine-Building Structures [in Russian], M., Mashinostroenie (1981).

  14. D. A. Gokhfeld and O. S. Sadakov, Plasticity and Creep of Structural Elements Under Repeated Loading [in Russian], M., Mashinostroenie (1984).

  15. A. F. Nikitenko, Creep and Long-Term Strength of Metallic Materials [in Russian], Novosibirsk, NGASU (1997).

    Google Scholar 

  16. J. Betten, Creep Mechanics, Berlin, Heidelberg, Springer-Verlag (2008).

    Google Scholar 

  17. A. M. Lokoshchenko, Creep and Long-Term Strength of Metals [in Russian], M., Fizmatlit (2016).

  18. R. S. Lakes, Viscoelastic Materials, Cambridge Univ. Press (2009).

    Book  Google Scholar 

  19. J. S. Bergstrom, Mechanics of Solid Polymers. Theory and Computational Modeling, Elsevier, William Andrew (2015).

  20. G. V. Vinogradov and A. Ya. Malkin, Rheology of Polymers [in Russian], M., Khimiya (1977).

  21. R. G. Larson, Constitutive Equations for Polymer Melts and Solutions, Butterworth, Boston (1988).

    Google Scholar 

  22. R. K. Gupta, Polymer and Composite Rheology, N.Y., Marcel Dekker (2000).

    Book  Google Scholar 

  23. A. Y. Malkin and A. I. Isayev, Rheology: Conceptions, Methods, Applications (2nd Ed.), Toronto, Chem. Tec. Publishing (2012).

    Google Scholar 

  24. H. F. Brinson and L. C. Brinson, Polymer Engineering Science and Viscoelasticity, Springer Science and Business Media (2008).

  25. A. E. Kalinnikov and A. V. Vakhrushev, “On the creep of materials with different resistance to tension and compression at variable stresses,” Mech. Compos. Mater., No. 3, 400-405 (1982).

  26. A. Fatemi and L. Yang, “Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials,” Int. J. Fatigue, 20, No. 1, 9-34 (1998).

    Article  CAS  Google Scholar 

  27. A. Launay, M. H. Maitournam, Y. Marco, I. Raoult, and F. Szmytka, “Cyclic behavior of short glass fiber reinforced polyamide: Experimental study and constitutive equations,” Int. J. Plasticity, 27, 1267-1293 (2011).

    Article  CAS  Google Scholar 

  28. M. K. Darabi, R. K. A. Al-Rub, E. A. Masad, C.-W. Huang, and D. N. Little, “A modified viscoplastic model to predict the permanent strain of asphaltic materials under cyclic-compression loading at high temperatures,” Int. J. Plasticity, 35, 100-134 (2012).

    Article  Google Scholar 

  29. H. Takagi, M. Dao, and M. Fujiwara, “Prediction of the constitutive equation for uniaxial creep of a power-law material through instrumented microindentation testing and modeling,” Materials Transactions, 55, No. 2, 275-284 (2014).

    Article  CAS  Google Scholar 

  30. N. Q. Chinh and P. Szommer, “Mathematical description of indentation creep and its application for the determination of strain rate sensitivity,” Mater. Sci. and Eng., A, 611, 333-336 (2014).

  31. D. S. Petukhov and I. E. Keller, “Dual problems of plane creeping flows of a power-law incompressible medium,” Vestn. Samara Gos. Tekhn. Univ. Ser. Fiz.-Mat. Nauki, 20, No. 3, 496-507 (2016).

  32. O. A. Kaibyshev, Superplasticity of Industrial Alloys [in Russian], M., Metallurgia (1984).

  33. T. G. Nieh, J. Wadsworth, and O. D. Sherby, Superplasticity in Metals and Ceramics, Cambridge Univ. Press (1997).

    Book  Google Scholar 

  34. K. A. Padmanabhan, R. A. Vasin, and F. U. Enikeev, Superplastic Flow: Phenomenology and Mechanics, Berlin, Heidelberg, Springer-Verlag (2001).

    Book  Google Scholar 

  35. V. M. Segal, I. J. Beyerlein, C. N., Tome, V. N. Chuvil’deev, and V. I. Kopylov, Fundamentals and Engineering of Severe Plastic Deformation, N.Y., Nova Science Pub. Inc. (2010).

  36. A. P. Zhilayev and A. I. Pshenichnyuk, Superplasticity and Grain Boundaries in Ultrafine-Grained Materials, Cambridge Intern. Sci. Publ. (2010).

    Google Scholar 

  37. Y. Cao, “Determination of the creep exponent of a power-law creep solid using indentation tests,” Mech. Time Dependent Mater., 11, 159-172 (2007).

    Article  Google Scholar 

  38. M. Megahed, A. R. S. Ponter, and C. J. Morrison, “An experimental and theoretical investigation into the creep properties of a simple structure of 316 stainless steel,” Int. J. Mech. Sci., 26, No. 3, 149-164 (1984).

    Article  Google Scholar 

  39. F. U. Enikeev, “Experimental evaluation of the velocity sensitivity of a superplastic material with a highly inhomogeneous stress-strain state,” Zavodskaya Lab., Mater. Diagn., 73, No. 10, 44-50 (2007).

  40. A. V. Mikhaylovskaya, A. A. Kishchik, A. D. Kotov, et al., “Precipitation behavior and high strain rate superplasticity in a novel fine-grained aluminum based alloy,” Mater. Sci. Eng. A, 760, 37-46 (2019).

    Article  CAS  Google Scholar 

  41. M. E. Eglit, A. E. Yakubenko, and Yu.S. Zaiko, “Mathematical modeling of slope flows taking into account the non-Newtonian properties of a moving medium,” Trudy V. A. Steklov Matemat. Inst. RAS, 300, 229-239 (2018).

    Google Scholar 

  42. V. P. Radchenko and D. V. Shapievsky, “Mathematical model of creep of a micro-inhomogeneous nonlinear elastic material,” PMTF, 49, No. 3, 157-163 (2008).

    Google Scholar 

  43. K. Naumenko, H. Altenbach, and Y. Gorash, “creep analysis with a stress range dependent constitutive model.,” Arch. Appl. Mech., 79, 619-630 (2009).

    Article  Google Scholar 

  44. L. Y. Lu, G. L. Lin, and M. H. Shih, “An experimental study on a generalized Maxwell model for nonlinear viscoelastic dampers used in seismic isolation.,” Eng. Struct., 34, No. 1, 111-123 (2012).

    Article  Google Scholar 

  45. M. D. Monsia, “A simplified nonlinear generalized maxwell model for predicting the time dependent behavior of viscoelastic materials,” World J. Mech., No. 1, 158-167 (2011). doi:https://doi.org/10.4236/wjm.2011.13021

  46. A. M. Stolin and A. V. Khokhlov, “Nonlinear model of shear flow of thixotropic viscoelastic-plastic continua, taking into account the evolution of the structure, and its analysis,” Moscow Univ. Mech. Bull., 77, No.5, 127-135 (2022). DOI: https://doi.org/10.3103/s0027133022050065

    Article  Google Scholar 

  47. V. A. Gorodtsov and A. I. Leonov, “On kinematics, nonequilibrium thermodynamics and rheological relations in the nonlinear theory of viscoelasticity,” PMM, 32, No. 1, 70-94 (1968).

    Google Scholar 

  48. A. I. Leonov, E. Ch. Lipkina, E. D. Paskhin, and A. N. Prokunin, “Theoretical and experimental investigations of shearing in elastic polymer liquids,” Rheol. Acta, 15, No. 7/8, 411-426 (1976).

    Article  CAS  Google Scholar 

  49. V. A. Palmov, “Rheological models in nonlinear mechanics of deformable bodies,” Adv. in Mech., 3, No. 3, 75-115 (1980).

    Google Scholar 

  50. A. N. Prokunin, “On nonlinear constitutive relations of Maxwellian type for describing the motion of polymer liquids,” PMM, 48, No. 6, 957-965 (1984).

    Google Scholar 

  51. A. I. Leonov and A. N. Prokunin, Nonlinear Phenomena in Flows of Viscoelastic Polymer Fluids, London, Chapman and Hall (1994).

    Book  Google Scholar 

  52. A. I. Leonov, “Constitutive equations for viscoelastic liquids: Formulation, analysis and comparison with data,” Rheology Series, 8, 519-575 (1999).

    Article  CAS  Google Scholar 

  53. A. V. Khokhlov, “Analysis of creep curves produced by the linear viscoelasticity theory under cyclic stepwise loadings,” J. Samara State Tech. Univ., Ser. Phys. Math. Sci., 21. No. 2, 326-361 (2017). doi:https://doi.org/10.14498/vsgtu1533

Download references

Author information

Authors and Affiliations

  1. Lomonosov Moscow State University, Institute of Mechanics, Moscow, Russia

    A. V. Khokhlov

  2. North-Eastern Federal University, Laboratory of “Polymer composites for the North”, Yakutsk, Russia

    A. V. Khokhlov

Authors
  1. A. V. Khokhlov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. V. Khokhlov.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khokhlov, A.V. Generalization of a Nonlinear Maxwell-Type Viscoelastoplastic Model and Simulation of Creep and Recovery Curves. Mech Compos Mater 59, 441–454 (2023). https://doi.org/10.1007/s11029-023-10107-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-023-10107-9

Keywords

Search

Navigation