Analytical Solution of the Bending Problem for Rectangular Orthotropic Plates with a Variable in-Plane Stiffness

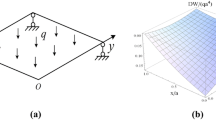
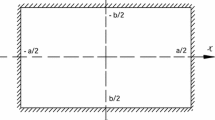
The analytical solution of the bending problem for a clamped rectangular plate with a variable in-plane stiffness is found by using the method of superposition. The flexural rigidity of the plate varies across its width according to an exponential function. First, the analytical solution for a simply supported rectangular plate with a variable in-plane stiffness is obtained, and then the bending problem for the plate clamped at its four edges is solved analytically by the superposition of one simply supported plate under the transverse load and two simply supported plates under pure bending. The influence of the variable in-plane stiffness, aspect ratio, and different boundary conditions on the deflection and bending moment is studied by numerical examples. The analytical solution presented here may be helpful for the design of rectangular plates with a variable in-plane stiffness.

Appendix A

The expressions of Φ_i (y), i = 1,2,3,4 .

1) r₁, r₂, r₃, and r₄ are real;

$$ {\displaystyle \begin{array}{c}{r}_1\ne {r}_2\ne {r}_3\ne {r}_4\\ {}{\varPhi}_1(y)={e}^{r_1y},{\varPhi}_2(y)={e}^{r_2y},{\varPhi}_3(y)={e}^{r_3y},{\varPhi}_4(y)={e}^{r_4y};\end{array}} $$

(A1a)

$$ {\displaystyle \begin{array}{c}{r}_1\ne {r}_2,{r}_3\ne {r}_1,\mathrm{and}\;{r}_4\ne {r}_1,\\ {}{\varPhi}_1(y)={e}^{r_1y},{\varPhi}_2(y)=y{e}^{r_1y},{\varPhi}_3(y)={e}^{r_3y},{\varPhi}_4(y)={e}^{r_4y};\end{array}} $$

(A1b)

$$ {\displaystyle \begin{array}{c}{r}_1={r}_2={r}_3\ne {r}_4,\\ {}{\varPhi}_1(y)={e}^{r_1y},{\varPhi}_2(y)=y{e}^{r_1y},{\varPhi}_3(y)={y}^2\;{e}^{r_3y},{\varPhi}_4(y)={e}^{r_4y};\end{array}} $$

(A1c)

$$ {\displaystyle \begin{array}{c}{r}_1={r}_2={r}_3={r}_4,\\ {}{\varPhi}_1(y)={e}^{r_1y},{\varPhi}_2(y)=y{e}^{r_1y},{\varPhi}_3(y)={y}^2\;{e}^{r_1y},{\varPhi}_4(y)={y}^3\;{e}^{r_1y}\end{array}}. $$

(A1d)

2) P(r) = (r − r₁)(r − r₂)(r² + 2α₁r + α₀); r₁, and r₂ are real and ${\alpha}_1^2-{\alpha}_0<0:$

$$ {\displaystyle \begin{array}{c}\kern8em {r}_1\ne {r}_2,\\ {}\kern1em {\varPhi}_1(y)={e}^{r_1y},\kern7em {\varPhi}_2(y)={e}^{r_2y},\\ {}{\varPhi}_3(y)={e}^{-{\alpha}_1y}\cos \left(\mu y\right),\kern2em {\varPhi}_4(y)={e}^{-{\alpha}_1y}\sin \left(\mu y\right);\end{array}} $$

(A2a)

$$ {\displaystyle \begin{array}{c}\kern8em {r}_1={r}_2,\\ {}\kern1em {\varPhi}_1(y)={e}^{r_1y},\kern7em {\varPhi}_2(y)=y{e}^{r_1y},\\ {}{\varPhi}_3(y)={e}^{-{\alpha}_1y}\cos \left(\mu y\right),\kern2em {\varPhi}_4(y)={e}^{-{\alpha}_1y}\sin \left(\mu y\right),\end{array}} $$

(A2b)

where

$$ \mu =\sqrt{\alpha_0-{\alpha}_1^2}. $$

3) $P(r)=\left({r}^2+2{\alpha}_1r+{\alpha}_0\right)\left({r}^2+2{\beta}_1r+{\beta}_0\right),\kern0.5em {\alpha}_1^2-{\alpha}_0<0,$ and ${\beta}_1^2-{\beta}_0<0,\kern0.5em {\left({\alpha}_1-{\beta}_1\right)}^2+{\left({\alpha}_0-{\beta}_0\right)}^2\ne 0,$

$$ {\displaystyle \begin{array}{cc}{\varPhi}_1(y)={e}^{-{\alpha}_1y}\cos \left(\mu y\right),& {\varPhi}_2(y)={e}^{-{\alpha}_1y}\sin \left(\mu y\right),\\ {}{\varPhi}_3(y)={e}^{-{\beta}_1y}\cos \left(\lambda y\right),& {\varPhi}_4(y)={e}^{-{\beta}_1y}\sin \left(\lambda y\right);\end{array}} $$

(A3a)

$$ {\displaystyle \begin{array}{c}\kern5em {\alpha}_1={\beta}_1,\mathrm{and}\;{\alpha}_0={\beta}_0,\\ {}{\varPhi}_1(y)={e}^{-{\alpha}_1y}\cos \left(\mu y\right),\kern1em {\varPhi}_2(y)=y{e}^{-{\alpha}_1y}\cos \left(\mu y\right),\\ {}{\varPhi}_3(y)={e}^{-{\alpha}_1y}\sin \left(\mu y\right),\kern1em {\varPhi}_4(y)=y{e}^{-{\alpha}_1y}\sin \left(\mu y\right),\end{array}} $$

(A3b)

where $\mu =\sqrt{\alpha_0-{\alpha}_1^2},$ and $\lambda =\sqrt{\beta_0-{\beta}_1^2}.$