Skip to main content
SpringerLink
Log in

Numerical Simulation of the Process of Loss of Stability of Composite Cylindrical Shells Under Combined Quasi-Static and Dynamic Actions

  • Published:
Mechanics of Composite Materials Aims and scope

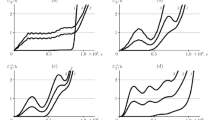
Based on the applied theory of shells, an energy-consistent resolving system of equations is constructed, and a complex numerical method is developed which, within in the framework of an explicit variational-difference scheme, makes it possible to solve both quasi-static and dynamic problems of nonlinear nonaxisymmetric deformation and buckling of composite cylindrical shells. The quasi-static loading mode is simulated by setting an internal pressure in the form of a linearly increasing function reaching a steady-state value during three periods of vibration of a composite cylindrical shell at the lower form. The critical buckling load is determined by the characteristic kink on the maximum deflection–loading amplitude curve. The reliability of the method developed is substantiated by comparing calculation results with experimental data. The characteristic forms and critical buckling loads of GRP cylindrical shells as functions of the level of preloading by a quasi-static internal pressure and of the subsequent dynamic loading by an external pressure are analyzed for various reinforcement patterns in a wide range of loading rate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.

Similar content being viewed by others

References

  1. L. I. Manevich, G. V. Mikhailov, I. D. Pavlenko, and E. F. Prokopalo, “Research on the stability of shells at a joint action of static and dynamic loads,” Prikl. Mekh., XIII, No. 1, 27-32 (1977).

  2. V. N. Baskakov A. I. Kostoglotov, and L. A. Shvetsova, “Investigation of the dynamic stability of smooth cylindrical shells,” Probl. Prochn. No. 5, 31-33 (1982).

  3. V. V. Bendyukov and V.V. Deryushev, “Dynamic short-wave instability of thin-walled cylindrical shells at the local action of an external pressure pulse,” Probl. Prochn., No. 4, 36-43 (1995).

  4. E. D. Skurlatov, “An experimental study on the behaviour of cylindrical shells at dynamic loadings,” Probl. Prochn., No. 9, 79-83 (1972).

  5. A. I. Kostoglotov, V. V. Bendyukov, V. V. Deryushev, and L. A. Shevtsov, “ Investigation of the process of loss of stability of smooth thin-walled cylindrical shells at the local action of a radiation pulse,” Probl. Prochn., No. 5, 56-62 (2004).

  6. V. M. Dubrovin and T. A. Butina, “Modeling the dynamic stability of a cylindrical shell at the action of an axial compressing load,” Matemat. Model. Chisl. Metodi, No. 6, 46-57 (2015).

  7. A. A. Kolomoets and A. S. Modin, “Nonlinear dynamics of a preliminary loaded imperfect cylindrical shell at the action of a nonuniform external pressure,” Vest. Saratov. Gos. Tekhn. Univ., No. 80, 7-12 (2015).

  8. A. E. Bogdanovich and E. G. Feldmane, “Calculation of the supporting capacity of cylindrical shells under dynamic loading,” Mech. Compos. Mater., No. 3, 334-340 (1980).

  9. A. E. Bogdanovich and E. G. Feldmane, “Strength and axisymmetric deformation of laminate cylindrical shells under axial impact,” Mech. Compos. Mater., No. 4, 449-456 (1982).

  10. A. E. Bogdanovich, Nonlinear Problems of the Dynamics of Cylindrical Composite Shells [in Russian], Riga, Zinatne (1987).

  11. I. V. Victorova and P. E. Tovstik, “Some problems of the stability of anisotropic cylindrical shells,” Tr. XIII Mezhdunar. Konf. “Sovr. Probl. Mekh. Sploshn. Sredy”, Rostov-on-Don, 57-62 (2009).

  12. E. L. Jansen, “Dynamic stability problems of anisotropic cylindrical shells via a simplified analysis,” Nonlinear Dynamics, 39, 349-367 (2005).

    Article  Google Scholar 

  13. C. Bisagni, “Dynamic buckling of fiber composite shells under impulsive axial compression,” Thin-Walled Struct., 43, 499-514 (2005).

    Article  Google Scholar 

  14. T. Rahman, E. L. Jansen, and Z. Gürdal, “Dynamic buckling analysis of composite cylindrical shells using a finite element based perturbation method,” Nonlinear Dynamics, 66, No. 3, 389-401 (2011).

    Article  Google Scholar 

  15. L. A. Shapovalov, “Consideration of transverse compression in equations of the nonlinear dynamics of shells,” Izv. RAN, Mekh. Tverd. Tela, No. 3. 156-168 (1997).

  16. A. K. Malmeister, V. P. Tamuzh, and G. A. Teters, Strength of Polymer and Composite Materials [in Russian], Riga, Zinatne (1980).

  17. N. A., Abrosimov and V. G. Bazhenov, “Nonlinear Problems of Dynamics of Composite Structures [in Russian], Nizhni Novgorod, Izd NNGU (2002).

  18. V. V. Vasil’yev, Mechanics of Structures from Composite Materials [in Russian], M, Mashinostroenie (1988).

  19. N. A. Abrosimov, A. V. Elesin, and S. A. Pirogov, “A numerical analysis of nonaxisymmetric strains and progressive destruction of layered composite cylindrical shells in pulsed loading,” Probl. Prochn. Plastich., 77, No. 1, 23-32 (2015).

    Google Scholar 

Download references

Acknowledgement

This work was performed at a financial support of the Federal program “Investigations and elaborations in the priority development directions of the scientific tehnological complex of Russia on years 2014-2020,” according to agreement NO. 14.578.21.0246 (unique identifier RFMEFI 57817X0246) and RFFI (grants Nos. 16-08-01124 and 18-08-01234).

Author information

Authors and Affiliations

  1. N. I. Lobachevsky Scientific Research Institute of Mechanics of the National Research Nizhni Novgorod State University, Nizhni Novgorod, Russia

    N. A. Abrosimov, A. V. Elesin & L. A. Igumnov

Authors
  1. N. A. Abrosimov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. V. Elesin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. L. A. Igumnov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. A. Abrosimov.

Additional information

Translated from Mekhanika Kompozitnykh Materialov, Vol. 55, No. 1, pp. 61-76, January-February, 2019.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abrosimov, N.A., Elesin, A.V. & Igumnov, L.A. Numerical Simulation of the Process of Loss of Stability of Composite Cylindrical Shells Under Combined Quasi-Static and Dynamic Actions. Mech Compos Mater 55, 41–52 (2019). https://doi.org/10.1007/s11029-019-09790-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-019-09790-4

Keywords

Search

Navigation