Skip to main content
SpringerLink
Log in

A Simple Finite Element with Five Degrees of Freedom Based on Reddy’s Third-Order Shear Deformation Theory

  • Published:
Mechanics of Composite Materials Aims and scope

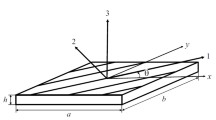
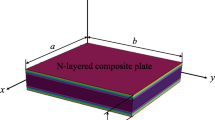
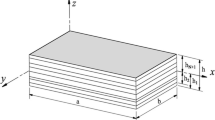
A simple four-node isoparametric finite element with five degrees of freedom, based on Reddy’s third-order shear deformation theory, is elaborated and used in a model for analizing the bending of laminated plates. The results obtained are compared with solutions given by the three-dimensional elasticity and other theories.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. S. K. Gill, M. Gupta, and P. Satsangi, “Prediction of cutting forces in machining of unidirectional glass-fiber-reinforced plastic composites,” Frontiers of Mechanical Engineering, 8, No. 2. 187-200 (2013).

  2. A. Mouritz et al., “Review of advanced composite structures for naval ships and submarines,” Compos. Struct., 53, No. 1, 21-42 (2001).

    Article  Google Scholar 

  3. A. Tati and A. Abibsi, “Un element fini pour la flexion et le flambage des plaques minces stratifiees en materiaux composites,” Revue Des Composites Et Des Materiaux Avances, 17, No. 3, 279–296 (2007).

  4. Y. Zhang and C. Yang, “Recent developments in finite element analysis for laminated composite plates,” Compos. Struct., 88, No. 1, 147-157 (2009).

    Article  Google Scholar 

  5. R. Mindlin, “Influence of rotary inertia and shear in flexural motions of isotropic elastic plates,” J. Appl. Mech., 18, 31-38 (1951).

    Google Scholar 

  6. J. M. Whitney and A. W. Leissa, “Analysis of heterogeneous anisotropic plates,” J. Appl. Mech., 36, No. 2, 261-266 (1969).

    Article  Google Scholar 

  7. J. N. Reddy, Energy and Variational Methods in Applied Mechanics, N. Y., John Wiley, 1984.

    Google Scholar 

  8. E. Reissner, “The effect of transverse shear deformations on the bending of elastic plates,” J. Appl. Mech., 12, A69-A77 (1945).

    Google Scholar 

  9. E. Reissner, “A consistent treatment of transverse shear deformations in laminated anisotropic plates,” AIAA J., 10, No. 5, 716-718 (1972).

    Article  Google Scholar 

  10. J. M. Whitney, “The effect of transverse shear deformation on the bending of laminated plates,” J. Compos. Mater., 3, No. 3, 534-547 (1969).

  11. J. N. Reddy, Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, CRC Press, Boca Raton, FL, Second Edition, 2004.

  12. R. Christensen K. Lo, and E. Wu, “A high-order theory of plate deformation part 1: homogeneous plates,” J. Appl. Mech., 44, No. 7, 663-668 (1977).

    Google Scholar 

  13. S. Mau, “A refined laminated plate theory,” J. Appl. Mech., 40, No. 2, 606-607 (1973).

    Article  Google Scholar 

  14. C.-T. Sun, “Theory of laminated plates,” J. Appl. Mech., 38, No. 1, 231-238 (1971).

    Article  Google Scholar 

  15. J. Whitney and C. Sun, “A higher order theory for extensional motion of laminated composites,” J. of Sound and Vibration, 30, No. 1, 85-97 (1973).

    Article  Google Scholar 

  16. J. N. Reddy, “A refined nonlinear theory of plates with transverse shear deformation,” Int. J. of Solids and Structures, 20, No. 9, 881-896 (1984).

    Article  Google Scholar 

  17. J. N. Reddy, “A simple higher-order theory for laminated composite plates,” J. Appl. Mech., 51, No. 4, 745-752 (1984).

    Article  Google Scholar 

  18. N. N. Khoa and T. I. Thinh, “Finite element analysis of laminated composite plates using high order shear deformation theory,” Vietnam J. of Mechanics, 29, No. 1, 47-57 (2008).

    Google Scholar 

  19. J. L. Batoz and M. B. Tahar, “Evaluation of a new quadrilateral thin plate bending element,” Int. J. for Numerical Methods in Engineering, 18, No. 11, 1655-1677 (1982).

    Article  Google Scholar 

  20. C. H. Thai et al., “Analysis of laminated composite plates using higher-order shear deformation plate theory and nodebased smoothed discrete shear gap method,” Appl. Mathematical Modelling, 36, No. 11, 5657-5677 (2012).

    Article  Google Scholar 

  21. H. Fukunaga, N. Hu, and G. Ren, “FEM modeling of adaptive composite structures using a reduced higher-order plate theory via penalty functions,” Int. J. of Solids and Structures, 38, No. 48,. 8735-8752 (2001).

    Article  Google Scholar 

  22. A. H. Sheikh and A. Chakrabarti, “A new plate bending element based on higher-order shear deformation theory for the analysis of composite plates,” Finite Elements in Analysis and Design, 39, No. 9, 883-903 (2003).

  23. T. Kant and B. Pandya, “A simple finite element formulation of a higher-order theory for unsymmetrically laminated composite plates,” Compos. Struct., 9, No. 3, 215-246 (1988).

    Article  Google Scholar 

  24. L. V. Tran, C. H. Thai, and H. Nguyen-Xuan, “An isogeometric finite element formulation for thermal buckling analysis of functionally graded plates,” Finite Elements in Analysis and Design, 73, 65-76 (2013).

    Article  Google Scholar 

  25. A. J. Ferreira, MATLAB codes for finite element analysis: solids and structures, 157, Springer, 2008,.

  26. J. V. Kouri, Improved Finite Element Analysis of Thick Laminated Composite Plates by the Predictor Corrector Technique and Approximation of C (1) Continuity with a New Least Squares Element, DTIC Document, 1991.

  27. J. Reddy, E. Barbero, and J. Teply, “A plate bending element based on a generalized laminate plate theory,” Int. J. for Numerical Methods in Engineering, 28, No. 10, 2275-2292 (1989).

    Article  Google Scholar 

  28. N. Pagano, “Exact solutions for rectangular bidirectional composites and sandwich plates,” J. Compos. Mater., 4, No. 1, 20-34 (1970).

    Google Scholar 

  29. Z. Wu, R. Chen, and W. Chen, “Refined laminated composite plate element based on global–local higher-order shear deformation theory,” Compos. Struct., 70, No. 2, 135-152 (2005).

    Article  Google Scholar 

  30. N. Pagano and H. J. Hatfield, “Elastic behavior of multilayered bidirectional composites,” AIAA J., 10, No. 7, 931-933 (1972).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire de Génie Energétique et Matériaux (LGEM), Université de Biskra, B.P. 145, Biskra, 07000, Algeria

    K. Belkaid

  2. Laboratory of Metallic and Semiconducting Materials, Université de Biskra, B.P. 145 RP, 07000, Biskra, Algeria

    A. Tati & R. Boumaraf

Authors
  1. K. Belkaid
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Tati
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. Boumaraf
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. Belkaid.

Additional information

Russiam translation published in Mekhanika Kompozitnykh Materialov, Vol. 52, No. 2, pp. 367-384, March-April, 2016.

Appendix

Appendix

The matrix of the first-order derivative can be presented as

$$ \left\{\begin{array}{c}\hfill \frac{\partial }{\partial \xi}\hfill \\ {}\hfill \frac{\partial }{\partial \eta}\hfill \end{array}\right\}=\left[\begin{array}{cc}\hfill \frac{\partial x}{\partial \xi}\hfill & \hfill \frac{\partial y}{\partial \xi}\hfill \\ {}\hfill \frac{\partial x}{\partial \eta}\hfill & \hfill \frac{\partial y}{\partial \eta}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill \frac{\partial }{\partial x}\hfill \\ {}\hfill \frac{\partial }{\partial y}\hfill \end{array}\right\}\iff \left\{\begin{array}{c}\hfill \frac{\partial }{\partial \xi}\hfill \\ {}\hfill \frac{\partial }{\partial \eta}\hfill \end{array}\right\}=\left[J\right]\left\{\begin{array}{c}\hfill \frac{\partial }{\partial x}\hfill \\ {}\hfill \frac{\partial }{\partial y}\hfill \end{array}\right\}\Rightarrow \left\{\begin{array}{c}\hfill \frac{\partial }{\partial x}\hfill \\ {}\hfill \frac{\partial }{\partial y}\hfill \end{array}\right\}={\left[J\right]}^{-1}\left\{\begin{array}{c}\hfill \frac{\partial }{\partial \xi}\hfill \\ {}\hfill \frac{\partial }{\partial \eta}\hfill \end{array}\right\}. $$

To obtain the second-order derivatives, the chain rule is successively applied to these relations, resulting in

$$ \begin{array}{c}\hfill \left\{\begin{array}{l}\frac{\partial^2}{\partial {\xi}^2}=\frac{\partial }{\partial x}.\frac{\partial^2x}{\partial {\xi}^2}+\frac{\partial }{\partial y}.\frac{\partial^2y}{\partial {\xi}^2}+\frac{\partial^2}{\partial {x}^2}{\left(\frac{\partial x}{\partial \xi}\right)}^2+\frac{\partial^2}{\partial {y}^2}{\left(\frac{\partial y}{\partial \xi}\right)}^2+2\frac{\partial^2}{\partial x\partial y}.\frac{\partial x}{\partial \xi }.\frac{\partial y}{\partial \xi },\hfill \\ {}\frac{\partial^2}{\partial {\eta}^2}=\frac{\partial }{\partial x}.\frac{\partial^2x}{\partial {\eta}^2}+\frac{\partial }{\partial y}.\frac{\partial^2y}{\partial {\eta}^2}+\frac{\partial^2}{\partial {x}^2}{\left(\frac{\partial x}{\partial \eta}\right)}^2+\frac{\partial^2}{\partial {y}^2}{\left(\frac{\partial y}{\partial \eta}\right)}^2+2\frac{\partial^2}{\partial x\partial y}.\frac{\partial x}{\partial \eta }.\frac{\partial y}{\partial \eta },\hfill \\ {}\frac{\partial^2}{\partial \xi \partial \eta }=\frac{\partial }{\partial x}.\frac{\partial^2x}{\partial \xi \partial \eta }+\frac{\partial }{\partial y}.\frac{\partial^2y}{\partial \xi \partial \eta }+\frac{\partial^2}{\partial {x}^2}.\frac{\partial x}{\partial \xi }.\frac{\partial x}{\partial \eta }+\frac{\partial^2}{\partial {y}^2}.\frac{\partial y}{\partial \xi }.\frac{\partial y}{\partial \eta }+\frac{\partial^2}{\partial x\partial y}\left(\frac{\partial x}{\partial \eta }.\frac{\partial y}{\partial \xi }+\frac{\partial x}{\partial \xi }.\frac{\partial y}{\partial \eta}\right),\hfill \end{array}\right.\hfill \\ {}\hfill \left\{\begin{array}{l}\frac{\partial^2}{\partial {\xi}^2}-\frac{\partial }{\partial x}.\frac{\partial^2x}{\partial {\xi}^2}-\frac{\partial }{\partial y}.\frac{\partial^2y}{\partial {\xi}^2}=\frac{\partial^2}{\partial {x}^2}{\left(\frac{\partial x}{\partial \xi}\right)}^2+\frac{\partial^2}{\partial {y}^2}{\left(\frac{\partial y}{\partial \xi}\right)}^2+2\frac{\partial^2}{\partial x\partial y}.\frac{\partial x}{\partial \xi }.\frac{\partial y}{\partial \xi },\hfill \\ {}\frac{\partial^2}{\partial {\eta}^2}-\frac{\partial }{\partial x}.\frac{\partial^2x}{\partial {\eta}^2}-\frac{\partial }{\partial y}.\frac{\partial^2y}{\partial {\eta}^2}=\frac{\partial^2}{\partial {x}^2}{\left(\frac{\partial x}{\partial \eta}\right)}^2+\frac{\partial^2}{\partial {y}^2}{\left(\frac{\partial y}{\partial \eta}\right)}^2+2\frac{\partial^2}{\partial x\partial y}.\frac{\partial x}{\partial \eta }.\frac{\partial y}{\partial \eta },\hfill \\ {}\frac{\partial }{\partial \xi \partial \eta }-\frac{\partial }{\partial x}.\frac{\partial^2x}{\partial \xi \partial \eta }-\frac{\partial }{\partial y}.\frac{\partial^2y}{\partial \xi \partial \eta }=\frac{\partial^2}{\partial {x}^2}.\frac{\partial x}{\partial \xi }.\frac{\partial x}{\partial \eta }+\frac{\partial^2}{\partial {y}^2}.\frac{\partial y}{\partial \eta }+\frac{\partial^2}{\partial x\partial y}\left(\frac{\partial x}{\partial \eta }.\frac{\partial y}{\partial \xi }+\frac{\partial x}{\partial \xi }.\frac{\partial y}{\partial \eta}\right),\hfill \end{array}\right.\hfill \\ {}\hfill \left\{\begin{array}{l}\frac{\partial^2}{\partial {\xi}^2}\hfill \\ {}\frac{\partial^2}{\partial {\eta}^2}\hfill \\ {}\frac{\partial^2}{\partial \xi \partial \eta}\hfill \end{array}\right\}-\frac{1}{ \det \left[J\right]}\left[\begin{array}{l}\frac{\partial^2x}{\partial {\xi}^2}\kern1em \frac{\partial^2y}{\partial {\xi}^2}\hfill \\ {}\frac{\partial^2x}{\partial {\eta}^2}\kern1em \frac{\partial^2y}{\partial {\eta}^2}\hfill \\ {}\frac{\partial^2x}{\partial \xi \partial \eta}\kern0.5em \frac{\partial^2y}{\partial \xi \partial \eta}\hfill \end{array}\right]\left[\begin{array}{l}\frac{\partial y}{\partial \eta}\kern1em -\frac{\partial y}{\partial \xi}\hfill \\ {}-\frac{\partial x}{\partial \eta}\kern1em \frac{\partial x}{\partial \xi}\hfill \end{array}\right]\left\{\begin{array}{l}\frac{\partial }{\partial \xi}\hfill \\ {}\frac{\partial }{\partial \eta}\hfill \end{array}\right\}==\left[\begin{array}{l}{\left(\frac{\partial x}{\partial \xi}\right)}^2\kern1em {\left(\frac{\partial y}{\partial \xi}\right)}^2\kern4em 2\frac{\partial x}{\partial \xi }.\frac{\partial y}{\partial \xi}\hfill \\ {}{\left(\frac{\partial x}{\partial \eta}\right)}^2\kern1em {\left(\frac{\partial y}{\partial \eta}\right)}^2\kern4em 2\frac{\partial x}{\partial \eta }.\frac{\partial y}{\partial \eta}\hfill \\ {}\frac{\partial x}{\partial \xi }.\frac{\partial x}{\partial \eta}\kern1em \frac{\partial y}{\partial \xi }.\frac{\partial y}{\partial \eta}\kern1em \left(\frac{\partial x}{\partial \xi }.\frac{\partial y}{\partial \eta }+\frac{\partial x}{\partial \eta }.\frac{\partial y}{\partial \xi}\right)\hfill \end{array}\right]\left\{\begin{array}{l}\frac{\partial^2}{\partial {x}^2}\hfill \\ {}\frac{\partial^2}{\partial {y}^2}\hfill \\ {}\frac{\partial^2}{\partial x\partial y}\hfill \end{array}\right\},\hfill \\ {}\hfill \left\{\begin{array}{l}\frac{\partial^2}{\partial {x}^2}\hfill \\ {}\frac{\partial^2}{\partial {y}^2}\hfill \\ {}\frac{\partial^2}{\partial x\partial y}\hfill \end{array}\right\}={\left[{J}^B\right]}^{-1}\left[\left\{\begin{array}{l}\frac{\partial^2}{\partial {\xi}^2}\hfill \\ {}\frac{\partial^2}{\partial {\eta}^2}\hfill \\ {}\frac{\partial^2}{\partial \xi \partial \eta}\hfill \end{array}\right\}-\frac{1}{ \det \left[J\right]}\left[\begin{array}{l}\frac{\partial^2x}{\partial {\xi}^2}\kern1em -\frac{\partial^2y}{\partial {\xi}^2}\hfill \\ {}\frac{\partial^2x}{\partial {\eta}^2}\kern1em \frac{\partial^2y}{\partial {\eta}^2}\hfill \\ {}\frac{\partial^2x}{\partial \xi \partial \eta}\kern1em \frac{\partial^2y}{\partial \xi \partial \eta}\hfill \end{array}\right]\left[\begin{array}{l}\frac{\partial y}{\partial \eta}\kern1em -\frac{\partial y}{\partial \xi}\hfill \\ {}-\frac{\partial x}{\partial \eta}\kern1em \frac{\partial x}{\partial \xi}\hfill \end{array}\right]\left\{\begin{array}{l}\frac{\partial }{\partial \xi}\hfill \\ {}\frac{\partial }{\partial \eta}\hfill \end{array}\right\}\right].\hfill \end{array} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Belkaid, K., Tati, A. & Boumaraf, R. A Simple Finite Element with Five Degrees of Freedom Based on Reddy’s Third-Order Shear Deformation Theory. Mech Compos Mater 52, 257–270 (2016). https://doi.org/10.1007/s11029-016-9578-z

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-016-9578-z

Keywords

Search

Navigation