1 Introduction

The stiffness tailoring capability of variable stiffness (VS) composite laminates enlarges the design space of thin-walled structures used in several structural engineering applications [1,2,3]. In recent years, several researchers have shown a considerable improvement in the buckling behaviour of VS structures compared to that of their constant stiffness (CS) counterparts [4, 5] made with unidirectional composite laminates. Furthermore, it has been shown that VS thin-walled structures have an enhanced load-carrying capacity in postbuckling behaviour that can be exploited to reduce their weight further and lead to appealing, lightweight solutions where weight is a major design driver [6]. Recently, Liguori et al. [7, 8] showed the potential of VS composite laminates also in civil engineering applications by optimising the geometrically nonlinear response of short-length bridge girders made with glass fibre composite laminates, leading to more sustainable design solutions than those made with traditional unidirectional composite laminates.

However, for all the abovementioned applications made with VS composites, the computational cost from the incremental-iterative procedure to study nonlinear problems and the mesh required for accurately modelling the fibre angle variations typical of VS laminates can be computationally expansive, mainly when a large number of results is needed as for optimisation problems.

An effective way to reduce the computational cost of those problems is by reducing the number of discrete variables describing them. An appealing way to reduce the number of discrete variables is achieved through isogeometric formulations, which exploit both the high continuity of interpolation functions and highly performing Finite Elements (FE) [9]. In this regard, Liguori et al. [10] developed an isogeometric framework for the optimal design of VS shells undergoing large deformations that uses a fast multimodal Koiter algorithm. Koiter’s method represents an alternative solution approach to path-following analyses, being based on the construction of a reduced order model which is usually a function of only few tens of variables [11]. Additionally, Koiter’s method allows to take into account the effect that geometrical imperfections have on the initial postbuckling response within a single analysis, thereby allowing for imperfection sensitivity analyses and postbuckling optimisation problems to be solved with efficiency and robustness [6, 10].

In light of these premises, this work aims to extend a high-performance, recently developed mixed shell element to study the geometrically nonlinear response of VS composite laminate structures. The element’s name is MISS-4C, the acronym for mixed, isostatic, self-equilibrated stress for composite laminates. The element is formulated for linear-elastic problems. Then, a corotational formulation is used within a Koiter asymptotic algorithm to obtain the buckling and initial post-buckling behaviour of VS structures as originally developed in [11,12,13,14]. MISS-4C is derived from the Hellinger–Reissner fnctional. As such, both its stress and displacement fields are primary unknowns. Then, for the stress interpolation of symmetric composite laminates, MISS-4C uses a linear elastic closed-form solution. Furthermore, the stress fields a priori satisfy both the equilibrium equations when bulk loads are null and compatibility equations, as with the hybrid-Trefftz method [15,16,17]. The element has a quadrilateral flat geometry with 24 kinematical Degrees of Freedom (DoFs) considered at its four vertices (i.e. six per vertex). More precisely, each node has three translations and three rotations, including drilling. The element is isostatic [18, 19] and, as such, uses the lowest possible number of stress parameters. The First-order Shear Deformation Theory (FSDT) is used to obtain the terms of the elastic matrix. Finally, MISS-4C is implemented within a Koiter multimodal algorithm to efficiently obtain the elastic initial postbuckling behaviour of VS thin-walled structures.

In this work, the performance of MISS-4C is first assessed through the buckling and post-buckling analysis of carbon fibre VS composite laminate plates subjected to compressive stresses. In particular, results obtained with MISS-4C are compared with those obtained with the MISS4 element, which was initially developed by Madeo et al. [19, 20] for the linear elastic analysis of isotropic shell structures and later extended to composite laminated VS structures by Zucco et al. [21]. Subsequently, the potential of using MISS-4C within a Koiter multimodal algorithm is shown by optimising the response of an actual structural application. In particular, a multi-objective optimisation of a short-length bridge girder made with glass fibre VS composite laminates is conducted to enhance its linear static, buckling and post-buckling response.

The manuscript is structured as follows. Section 2 introduces the mixed functional from which MISS-4C is derived and the linear element model. Section 3 presents the element field interpolations and its corotational formulation. Section 4 recalls the main steps of the initial pos-buckling analysis when using a Koiter multimodal algorithm. Numerical results are presented and commented on in Sect. 5. Finally, conclusions are drawn in Sect. 6.

2 Hellinger–Reissner functional and linear FE model

2.1 Mixed functional

Consider the Hellinger–Reissner functional

$$\begin{aligned} {\Pi }_{HR}[\varvec{t}, \varvec{d}]={\Phi }[\varvec{t}, \varvec{d}] - \mathcal {W}[\varvec{d}], \end{aligned}$$
(1)

where \({\Phi }[\varvec{t}, \varvec{d}]\) is the mixed strain energy defined as a function of the stress resultants, \(\varvec{t}\), and the generalised displacements, \(\varvec{d}\), while \(\mathcal {W}[\varvec{d}]\) is the work done by the external loads.

For flat shells, the mixed strain energy is

$$\begin{aligned} {\Phi }[\varvec{t}, \varvec{d}]={\Phi }_d[\varvec{t}, \varvec{d}] -{\Phi }_c [\varvec{t}], \end{aligned}$$
(2)

where \({\Phi }_d[\varvec{t}, \varvec{d}]\) is the strain work while \({\Phi }_c[\varvec{t}]\) is the complementary strain energy that are respectively

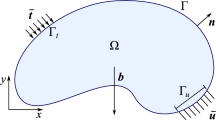
$$\begin{aligned} {\Phi }_d[\varvec{t}, \varvec{d}] = \int \nolimits _{\Omega }\left( \varvec{t}^T\varvec{e}[\varvec{d}]\right) \textrm{d}A \quad ,\quad {\Phi }_c[\varvec{t}]= \frac{1}{2}\,\int \nolimits _{\Omega }\left( \varvec{t}^T\varvec{C}^{-1}\varvec{t}\right) \textrm{d}A, \end{aligned}$$
(3)

with \(\Omega\) the two-dimensional structural domain. Introducing a Cartesian reference system \(\{\zeta _1, \zeta _2, \zeta _3\}\) with \(\zeta _3\)-axis aligned along the thickness direction, the constitutive matrix \(\varvec{C}\), for a composite laminate with n layers, when using FSDT [22], is

$$\begin{aligned} \varvec{C}= \begin{bmatrix} \varvec{C}_{m} &{} \varvec{C}_{mb} &{} {\cdot } \\ \varvec{C}_{mb}^T &{} \varvec{C}_{b} &{} {\cdot } \\ {\cdot } &{} {\cdot } &{} \varvec{C}_{s} \\ \end{bmatrix} \end{aligned}$$
(4)

where

$$\begin{aligned} \left. \begin{aligned} \varvec{C}_m&= \sum _{j=1}^{n} (\zeta _{3(j)}-\zeta _{3(j-1)})\varvec{C}_m^{(j)} ,\\ \varvec{C}_{mb}&= \frac{1}{2}\,\sum _{j=1}^{n} (\zeta _{3(j)}^2-\zeta _{3(j-1)}^2)\varvec{C}_m^{(j)} \\ \varvec{C}_{b}&= \frac{1}{3}\,\sum _{j=1}^{n} (\zeta _{3(j)}^3-\zeta _{3(j-1)}^3)\varvec{C}_m^{(j)} ,\\ \varvec{C}_{s}&= \varvec{\kappa }\odot \sum _{j=1}^{n} (\zeta _{3(j)}-\zeta _{3(j-1)})\varvec{C}_s^{(j)} \end{aligned} \right. \end{aligned}$$
(5)

with \(\zeta _{3(j)}\) and \(\zeta _{3(j-1)}\) are the top and bottom coordinates of the j-th lamina, respectively. The subscripts m, b and s indicate membrane, bending and shear quantities, respectively. Therfore, the terms within \(\varvec{C}\) are the lamina constitutive matrices referring to the in-plane, \(\varvec{C}_{m}\), out-of-plane, \(\varvec{C}_{b}\), and transverse shear stress/strain, \(\varvec{C}_{s}\), respectively. Then, \(\varvec{\kappa }\) is a \([2 \times 2]\) matrix that collects the shear factors [11] and the symbol \(\odot\) indicates the component product that allows multiplying \(\varvec{C}_{s}\) by different values of the shear correction factor. It is worth noting that for VS composite laminates, \(\varvec{C}\) varies through \(\Omega\) . However, for the sake of simplicity, the dependence of \(\varvec{C}\) on \(\Omega\) is omitted in the expressions.

The vectors \(\varvec{t}\) and \(\varvec{d}\) collect the stress resultants and generalised displacements as

$$\begin{aligned} \quad \varvec{t}= \begin{bmatrix} \varvec{t}_m\\ \varvec{t}_f\\ \end{bmatrix} \quad ,\quad \varvec{d}=\begin{bmatrix} \varvec{d}_m \\ \varvec{d}_f \\ \end{bmatrix}, \end{aligned}$$
(6)

where the f indicates the flexural quantities. Subsequently, the compatibility equations are obtained as \(\varvec{e}[\varvec{d}]=\varvec{Q}\varvec{d}\), where \(\varvec{Q}\) is the differential operator.

The external work \(\mathcal {W}[\varvec{d}]\) of a structure subjected to bulk loads \(\bar{\varvec{q}}\) and tractions \(\bar{\textbf{f}}\) is

$$\begin{aligned} \mathcal {W} = \int _{\Omega }\varvec{d}^T\bar{\varvec{q}}\,\textrm{d}A + \int _{\Gamma } \varvec{d}^T\bar{\textbf{f}} \, \textrm{d}s. \end{aligned}$$
(7)

where \(\Gamma\) is the contour of \(\Omega\).

If \(\varvec{t}\) satisfies the equilibrium equations when \(\bar{\varvec{q}}\) are null, then

$$\begin{aligned} \varvec{Q}_m^T\varvec{t}_m = \textbf{0} \quad , \quad \varvec{Q}^T_b\varvec{t}_b-\hat{\varvec{I}}\varvec{t}_s=\textbf{0} \quad , \quad \varvec{Q}_s^T\varvec{t}_s = \textbf{0}, \end{aligned}$$
(8)

where \(\varvec{t}_b\) and \(\varvec{t}_s\) are the bending and shear components within \(\varvec{t}_f\) while \(\varvec{Q}_m\), \(\varvec{Q}_s\), \(\varvec{Q}_b\), \(\hat{\varvec{I}}\) are differential operators defined as

$$\begin{aligned} \varvec{Q}_m= & {} \begin{bmatrix} \partial /\partial \zeta _1 &{} \cdot \\ \cdot &{} \partial /\partial \zeta _2 \\ \partial /\partial \zeta _2 &{} \partial /\partial \zeta _1 \\ \end{bmatrix}, \quad \varvec{Q}_s = \begin{bmatrix} \partial /\partial \zeta _1 \\ \partial /\partial \zeta _2 \\ \end{bmatrix}, \nonumber \\ \varvec{Q}_b= & {} \begin{bmatrix} \cdot &{} - \partial /\partial \zeta _1\\ \partial /\partial \zeta _2 &{} \cdot \\ \partial /\partial \zeta _1 &{} -\partial /\partial \zeta _2 \\ \end{bmatrix}, \,\hat{\varvec{I}} = \begin{bmatrix} \cdot &{} 1\\ -1 &{} \cdot \\ \end{bmatrix}, \end{aligned}$$
(9)

from which it holds that

$$\begin{aligned} \int _{\Omega } \varvec{t}^T\varvec{Q}\varvec{d}\, \textrm{d}A = \int _{\Gamma } \varvec{t}^T\varvec{N}\varvec{d}\, \textrm{d}s. \end{aligned}$$
(10)

In Eq. 10, \(\varvec{N}\) is the matrix collecting the components of the unit outward normal to the contour defined as in [23]. If \(\varvec{t}\) also satisfies the compatibility equations, then it represents a possible solution \(\varvec{d}_t\) of the elastic displacement field as

$$\begin{aligned} \varvec{t}= \varvec{C}\varvec{Q}\varvec{d}_t \end{aligned}$$
(11)

leading to the following identity

$$\begin{aligned} \int _{\Omega } \varvec{t}^T\varvec{C}^{-1} \varvec{t}\textrm{d}A=\int _{\Gamma } \varvec{t}^T\varvec{N}\varvec{d}_t \, \textrm{d}s. \end{aligned}$$
(12)

Finally, considering Eqs. (10) and (12), the mixed strain energy is efficiently calculated through integration along the element contour, \(\Gamma\).

2.2 Field interpolations

The displacement and stress fields of the generic element, e, are approximated separately. The interpolation of the stress resultants is

$$\begin{aligned} \varvec{t}= {\varvec{\mathcal {T}}}\varvec{\beta }_e ,\quad \begin{bmatrix} \varvec{t}_m \\ \varvec{t}_f \\ \end{bmatrix}= \begin{bmatrix} {\varvec{\mathcal {T}}}_m &{} \cdot \\ \cdot &{} {\varvec{\mathcal {T}}}_f \\ \end{bmatrix} \begin{bmatrix} \varvec{\beta }_{me} \\ \varvec{\beta }_{fe} \\ \end{bmatrix}, \end{aligned}$$
(13)

where \({\varvec{\mathcal {T}}}\) is the interpolation matrix collecting the stress modes assumed for the membrane and the flexural generalised stresses respectively indicated with \({\varvec{\mathcal {T}}}_m\) and \({\varvec{\mathcal {T}}}_f\). Whereas the vectors \(\varvec{\beta }_{me}\) and \(\varvec{\beta }_{fe}\) collect the interpolation parameters for the membrane and flexural stress fields, respectively.

Similarly to Eq. 13, the displacement field interpolation is

$$\begin{aligned} \varvec{d}= {\varvec{\mathcal {D}}}\varvec{d}_e ,\quad \begin{bmatrix} \varvec{d}_m \\ \varvec{d}_f \\ \end{bmatrix}= \begin{bmatrix} {\varvec{\mathcal {D}}}_{m} &{} \cdot \\ \cdot &{} {\varvec{\mathcal {D}}}_{f}\\ \end{bmatrix} \begin{bmatrix} \varvec{d}_{me}\\ \varvec{d}_{fe}\\ \end{bmatrix}, \end{aligned}$$
(14)

where \({\varvec{\mathcal {D}}}\) collects the interpolation functions. More precisely, \({\varvec{\mathcal {D}}}_{m}\) collects the shape functions for the in-plane displacements while \({\varvec{\mathcal {D}}}_{f}\) collects those for the out-of-plane displacements. Then, the vector \(\varvec{d}_e\) collects the displacement interpolation parameters.

Subsequently, by substituting Eqs. (13) and (14) into (2) and integrating over \(\Omega _e\), it is possible to calculate the mixed strain energy of the element as

$$\begin{aligned}{} & {} {\Phi }_e[\varvec{\beta }_e,\varvec{d}_e] = \varvec{\beta }_e^T {\varvec{\mathcal {Q}}}_e \varvec{d}_e - \frac{1}{2}\, \varvec{\beta }_e^T {\varvec{\mathcal {F}}}_e \varvec{\beta }_e , \nonumber \\{} & {} \quad \quad \left\{ \begin{aligned} {\varvec{\mathcal {Q}}}_e&= \int _{\Omega _e} {\varvec{\mathcal {T}}}^T\varvec{Q}\,{\varvec{\mathcal {D}}}\textrm{d}A\\ {\varvec{\mathcal {F}}}_e&= \int _{\Omega _e} {\varvec{\mathcal {T}}}^T\varvec{C}^{-1}{\varvec{\mathcal {T}}}\textrm{d}A\\ \end{aligned} \right. , \end{aligned}$$
(15)

where \({\varvec{\mathcal {Q}}}_e\) is the compatibility matrix of the generic element, while \({\varvec{\mathcal {F}}}_e\) is its compliance matrix.

Similarly, the element force vector \(\varvec{f}_e\) is evaluated from the expression of the external work \(\mathcal {W}\).

If \(\varvec{t}\) satisfies the equilibrium equations when the bulk loads are null, then the compatibility matrix in Eq. (15) is evaluated through an integration along the element contour as

$$\begin{aligned} {\varvec{\mathcal {Q}}}_e = \int _{\Gamma _e} {\varvec{\mathcal {T}}}^T\varvec{N}{\varvec{\mathcal {D}}}\,ds. \end{aligned}$$
(16)

Furthermore, if \(\varvec{t}\) also satisfies the internal compatibility equations, the compliance matrix in Eq. (15) is evaluated through an integration along along the element contour as

$$\begin{aligned} {\varvec{\mathcal {F}}}_e = \int _{\Gamma _e} {\varvec{\mathcal {T}}}^T\varvec{N}{\varvec{\mathcal {D}}}_t\,ds, \end{aligned}$$
(17)

where \({\varvec{\mathcal {D}}}_t\) is a matrix collecting the shape functions for the elastic displacements \(\varvec{d}_t\) (see Eq. (12)) expressed in terms of the stress interpolation parameters \(\varvec{t}_e\) as

$$\begin{aligned} \varvec{d}_t={\varvec{\mathcal {D}}}_t \varvec{t}_e ,\quad \begin{bmatrix} \varvec{d}_{tm} \\ \varvec{d}_{tf} \\ \end{bmatrix}= \begin{bmatrix} {\varvec{\mathcal {D}}}_{tm} &{} \cdot \\ \cdot &{} {\varvec{\mathcal {D}}}_{tf}\\ \end{bmatrix} \begin{bmatrix} \varvec{\beta }_{me}\\ \varvec{\beta }_{fe}\\ \end{bmatrix}. \end{aligned}$$
(18)

3 MISS-4C linear and corotational formulations

3.1 Generalised stress field interpolation

The generalised stress fields are defined in the rotated local Cartesian reference system \(\{\zeta _1,\,\zeta _2, \,\zeta _3\}\). An interpolation of the generalised stress fields is employed to satisfy the compatibility equations and equilibrium equations when the bulk loads are null. In total, 18 static parameters, \(n_\beta\), are used, namely, nine parameters for interpolating the membrane generalised stress field and nine parameters to interpolate the flexural generalised stress field.

3.1.1 Assumed membrane stress field

The membrane stress field interpolation is defined through a polynomial shape of the elastic in-plane displacement solution \(\varvec{d}_{tm}\) as

$$\begin{aligned} \varvec{d}_{tm} = \bar{{\varvec{\mathcal {T}}}}_{m} \bar{\varvec{\beta }}_{me} \quad , \quad \bar{{\varvec{\mathcal {T}}}}_m = \left[ \begin{array}{ccc} \bar{{\varvec{\mathcal {T}}}}_{mu} &{} \cdot \\ \cdot &{} \bar{{\varvec{\mathcal {T}}}}_{mu}\\ \end{array} \right] , \end{aligned}$$
(19)

where \(\bar{{\varvec{\mathcal {T}}}}_{mu}\) collects the shape functions as

$$\begin{aligned} \bar{{\varvec{\mathcal {T}}}}_{mu} = \left[ \begin{array}{ccccccccccccc} 1 &{} \zeta _1 &{} \zeta _2 &{} \zeta _1^2 &{} \zeta _1\zeta _2 &{} \zeta _2^2 &{} \dots &{} \zeta _1^4 &{} \zeta _1^3 \zeta _2&{} \zeta _1^2 \zeta _2^2 &{} \zeta _1 \zeta _2^3 &{} \zeta _2^4 \\ \end{array} \right] \end{aligned}$$
(20)

while \(\bar{\varvec{\beta }}_{me}\) is a \([30 \times 1]\) vector collecting the interpolation parameters.

The generalised membrane stresses for symmetric composite laminates obtained by applying the compatibility and constitutive equations to Eq. (19) are

$$\begin{aligned} \varvec{t}_m = \varvec{C}_m \varvec{Q}_m \bar{{\varvec{\mathcal {T}}}}_{m} \bar{\varvec{\beta }}_{me}, \end{aligned}$$
(21)

which can be rewritten by superimposing the equilibrium through Eqs. (8). Subsequently, a hierarchical selection of nine independent polynomials is conducted as in [24], obtaining

$$\begin{aligned} \varvec{d}_{tm} = {{\varvec{\mathcal {T}}}_{f}} \varvec{\beta }_{me}. \end{aligned}$$
(22)

The in-plane elastic displacement solution \(\varvec{d}_{tm}\) is expressed as a function of the static parameters \(\varvec{\beta }_{me}\) as

$$\begin{aligned} \varvec{d}_{tm} = {\varvec{\mathcal {D}}}_{tm} \varvec{\beta }_{me}. \end{aligned}$$
(23)

The explicit expressions of \({\varvec{\mathcal {T}}}_{m}\) and \({\varvec{\mathcal {D}}}_{tm}\) can be found in [24]. Note that the assumed membrane stresses correspond to an Airy solution [25]

3.1.2 Assumed flexural stress field

The flexural stress field interpolation is defined through a polynomial shape of the elastic out-of-plane displacement solution \(\varvec{d}_{tf}\) as

$$\begin{aligned} \varvec{d}_{tf} = \bar{{\varvec{\mathcal {T}}}}_f \bar{\varvec{\beta }}_{fe} \quad ,\quad \bar{{\varvec{\mathcal {T}}}}_f = \left[ \begin{array}{ccc} \bar{{\varvec{\mathcal {T}}}}_{fu} &{} \cdot &{} \cdot \\ \cdot &{} \bar{{\varvec{\mathcal {T}}}}_{f\varphi } &{} \cdot \\ \cdot &{} \cdot &{} \bar{{\varvec{\mathcal {T}}}}_{f\varphi }\\ \end{array} \right] , \end{aligned}$$
(24)

where

$$\begin{aligned} \begin{aligned} \bar{{\varvec{\mathcal {T}}}}_{fu}&= \left[ \begin{array}{ccccccccccccc} 1 &{} \zeta _1 &{} \zeta _2 &{} \zeta _1^2 &{} \zeta _1\zeta _2 &{} \zeta _2^2 &{} \cdots &{} \zeta _1^5 &{} \zeta _1^4 \zeta _2&{} \zeta _1^3 \zeta _2^2 &{} \zeta _1^2 \zeta _2^3 &{} \zeta _1 \zeta _2^4 &{}\zeta _2^5 \\ \end{array} \right] ,\\ \bar{{\varvec{\mathcal {T}}}}_{f\varphi }&= \left[ \begin{array}{cccccccccccc} 1 &{} \zeta _1 &{} \zeta _2 &{} \zeta _1^2 &{} \zeta _1\zeta _2 &{} \zeta _2^2 &{} \cdots &{} \zeta _1^4 &{} \zeta _1^3 \zeta _2 &{} \zeta _1^2 \zeta _2^2 &{} \zeta _1 \zeta _2^3 &{} \zeta _2^4 \\ \end{array} \right] \\ \end{aligned} \end{aligned}$$
(25)

while \(\bar{\varvec{\beta }}_{fe}\) is a \([51 \times 1]\) vector. Then, the following generalised flexural stresses are obtained for a symmetric composite laminate by applying the compatibility and constitutive equations to Eq. (24)

$$\begin{aligned} \varvec{t}_f = \varvec{C}_f\varvec{Q}_f \bar{{\varvec{\mathcal {T}}}}_f \bar{\varvec{\beta }}_{fe}, \end{aligned}$$
(26)

which can be rewritten by superimposing the equilibrium through Eqs. (8). Subsequently, a hierarchical selection of nine independent polynomials is conducted as in [24]

$$\begin{aligned} {\varvec{d}_{tf}} = {\varvec{\mathcal {T}}}_{f} \varvec{\beta }_{fe}. \end{aligned}$$
(27)

The out-of-plane elastic displacement solution \(\varvec{d}_{tf}\) is expressed as a function of the static parameters \(\varvec{\beta }_{fe}\) as

$$\begin{aligned} \varvec{d}_{tf} = {\varvec{\mathcal {D}}}_{tf} \varvec{\beta }_{fe}. \end{aligned}$$
(28)

The explicit expression of \({\varvec{\mathcal {T}}}_{f}\) and \({\varvec{\mathcal {D}}}_{tf}\) can be found in [24]. It is worth observing that the assumed membrane stress corresponds to a Trefftz solution [26].

3.2 Generalised displacement field interpolation

A total of 24 nodal parameters are used to interpolate the displacement field \(\varvec{d}\), namely 12 translations and 12 rotations. The vector \(\varvec{d}_e\) collects those parameters. Then, considering the assumed stress field, the interpolation of the displacement field is described along the element contour. In particular, for a generic side \(\Gamma _k\) of the element contour, the vectors \(\varvec{d}_{ie} = [d_{i1},\,d_{i2},\,d_{i3},\,\varphi _{i1},\,\varphi _{i2},\,\varphi _{i3}]^T\) and \(\varvec{d}_{je} = [d_{j1},\,d_{j2},\,d_{j3},\,\varphi _{j1},\,\varphi _{j2},\,\varphi _{j3}]^T\) collect the displacements at its end nodes \(i,\,j\), respectively.

3.3 Assumed in-plane displacements

Along the element’s generic side \(\Gamma _k\), the in-plane displacements are assumed as the sum of three contributions

$$\begin{aligned} \varvec{d}_{km}=\, & {} \varvec{d}_{km}^{(l)}+\varvec{d}_{km}^{(q)}+\varvec{d}_{km}^{(c)} \quad ,\nonumber \\{} & {} \left\{ \begin{aligned} \varvec{d}_{km}^{(l)}&= \frac{1}{2}[(1 -\zeta )\,\varvec{d}_ {i} + (1 + \zeta )\,\varvec{d}_{j}]\\ \varvec{d}_{km}^{(q)}&= \frac{\ell _{k}}{8} \, (1-\zeta ^2) (\varphi _{jz}-\varphi _{iz})\,\varvec{n}_k\\ \varvec{d}_{km}^{(c)}&= \frac{1}{4} \, \ell _{k}(\zeta -\zeta ^3) \varvec{n}_k \,\alpha _c\\ \end{aligned} \right. \end{aligned}$$
(29)

In this expression, \(\zeta\) is the one-dimensional abscissa \(-1\le \zeta \le 1\) along \(\Gamma _k\), \(\ell _k\) and \(\varvec{n}_k\) are the length and the normal vector to the side k-th, respectively. Then, the vectors \(\varvec{d}_i\) and \(\varvec{d}_j\) collect the nodal displacements as

$$\begin{aligned} \varvec{d}_i = [d_{i1},\,d_{i2}]^T \; , \quad \varvec{d}_j = [d_{j1},\,d_{j2}]^T. \end{aligned}$$
(30)

The contribution \(\varvec{d}_{km}^{(q)}\) is evaluated through the Allman’s kinematic approach [19] while \(\varvec{d}_{km}^{(c)}\) is a cubic expansion for the normal component of the side displacement proportional to the average distortional drilling nodal rotation

$$\begin{aligned} \alpha _c = \frac{1}{4} \sum _{i=1}^4\varphi _{i3} - \varphi _{e3}, \end{aligned}$$
(31)

where the expression of each term is given in [24]. This cubic contribution corresponds to an incompatible mode introduced to avoid rank defectiveness, as discussed in [19].

3.4 Assumed out-of-plane displacements

The out-of-plane displacement, \(d_{k3}\), along \(\Gamma _k\) is assumed as the sum of three contributions, namely

$$\begin{aligned} d_{k3} = d_{k3}^{(l)}+ d_{k3}^{(q)} + d_{k3}^{(c)} \quad ,\quad \left\{ \begin{aligned} d_{k3}^{(l)}&= \frac{1}{2}\left[ (1-\zeta )d_{i3} + (1+\zeta )d_{j3} \right] \\ d_{k3}^{(q)}&= \frac{\ell _k}{8}\,(1-\zeta ^2)(\varvec{\varphi }_{ki}-\varvec{\varphi }_{kj})^T\varvec{n}_k\\ d_{k3}^{(c)}&= -\dfrac{\ell _k}{4}\left( \zeta ^3 - \zeta \right) \varphi _{en}\\ \end{aligned} \right. \end{aligned}$$
(32)

where

$$\begin{aligned} \varvec{\varphi }_{ki}= & {} [\varphi _{i1}, \varphi _{i2}]^T \quad , \quad \varvec{\varphi }_{kj}= [\varphi _{j1}, \varphi _{j2}]^T \quad , \quad \nonumber \\ \varphi _{en}= & {} \frac{1}{8}\sum _{k=1}^{4} \left( \varvec{\varphi }_{kj} - \varvec{\varphi }_{ki} \right) ^T \varvec{n}_k -\frac{\varphi _{e1}+\varphi _{e2}}{2} \end{aligned}$$
(33)

and

$$\begin{aligned} \varphi _{e1}= \frac{d_{43}- d_{13}}{2 \ell _4} +\frac{d_{33}- d_{23}}{2 \ell _2} \quad , \quad \varphi _{e2}= \frac{d_{43}- d_{33}}{2 \ell _3} +\frac{d_{13}- d_{23}}{2 \ell _1} \end{aligned}$$
(34)

Similarly to the cubic term in Eq. (29), \(d_{k3}^{(c)}\) is an incompatible mode introduced to avoid rank defectiveness and depends on the difference between each side’s normal rotation and the element’s rigid rotation.

The normal rotation \(\varphi _{kn}\) along \(\Gamma _k\) is assumed to be the sum of a linear and a quadratic contribution

$$\begin{aligned} \varphi _{kn} = \varphi _{kn}^{(l)}+ \varphi _{kn}^{(q)} \quad ,\quad \left\{ \begin{aligned} \varphi _{kn}^{(l)}&= \frac{1}{2}\left[ (1-\zeta )\varphi _{in} + (1+\zeta )\varphi _{jn} \right] \\ \varphi _{kn}^{(q)}&= 2\, d_{{kz}_{,\zeta }}^{(c)}/\ell _k\\ \end{aligned} \right. , \end{aligned}$$
(35)

while the tangential rotation \(\varphi _{kt}\) is assumed to be linear,

$$\begin{aligned} \varphi _{kt} = \frac{1}{2}\left[ (1-\zeta )\varphi _{it} + (1+\zeta )\varphi _{jt} \right] . \end{aligned}$$
(36)

3.5 Geometrically nonlinear FE mixed energy

A corotational approach [27,28,29,30] is employed to use the linear version of MISS-4C presented above to conduct geometrically nonlinear static analyses [12, 31]. First, the FE mixed energy Eq. (15) is expressed in terms of kinematic parameters \(\bar{\varvec{d}}_e\) referred to the corotational frame that filters the average rigid body motion of the element,

$$\begin{aligned} \Phi _e[\varvec{\beta }_e,\varvec{d}_e] = \varvec{t}_e^T {\varvec{\mathcal {Q}}}_e \bar{\varvec{d}}_e - \frac{1}{2}\varvec{\beta }_e^T {\varvec{\mathcal {F}}}_e \varvec{\beta }_e. \end{aligned}$$
(37)

Then, introducing the geometrically nonlinear relationship

$$\begin{aligned} \bar{\varvec{d}}_e = \varvec{\varrho }_e[\varvec{d}_e] \end{aligned}$$
(38)

between the corotational kinematic parameters \(\bar{\varvec{d}}_e\) and those referred to the global fixed frame, \(\varvec{d}_e\), the nonlinear expression of the mixed energy for the element becomes

$$\begin{aligned} \Phi _e[\varvec{\beta }_e,\varvec{d}_e] = \varvec{t}_e^T {\varvec{\mathcal {Q}}}_e \varvec{\varrho }_e[\varvec{d}_e] - \frac{1}{2}\varvec{\beta }_e^T {\varvec{\mathcal {F}}}_e \varvec{\beta }_e. \end{aligned}$$
(39)

The explicit expression of \(\varvec{\varrho }_e\) is a function of the translation \(\varvec{c}\) and rotation \(\varvec{R}\) that define the corotational frame. Moreover, that expression contains the geometrically nonlinear transformations between displacements and rotations in the corotational frame and those in the global fixed frame. The details on how \(\varvec{\varrho }_e\) is evaluated in this work can be found in [24]. Subsequently, the mixed energy of each FE can be expressed as a function of the unknown vector

$$\begin{aligned} \varvec{u}_e = \left\{ \varvec{\beta }_e,\,\varvec{d}_e \right\} ^T \end{aligned}$$
(40)

which collects the stress and displacement parameters of the single element. The vector \(\varvec{u}_e\) can be related to the global configuration vector \(\varvec{u}\) through the FE assemblage operator \({\varvec{\mathcal {A}}}_e\)

$$\begin{aligned} \varvec{u}_e = {\varvec{\mathcal {A}}}_e \varvec{u}. \end{aligned}$$
(41)

Finally, the derivatives of Eqs. (39), (41) with respect to \(\varvec{u}\) are evaluated until the fourth order as needed by the Koiter asymptotic analysis described in the next Section.

4 Reduced order model for initial postbuckling analysis

This Section recalls the main steps of the Koiter multi-modal algorithm, originally proposed by Casciaro [32]. Further aspects making that approach a robust tool for the initial postbuckling analysis of thin-walled structures can be found in [6, 9, 10, 33,34,35,36].

For a structural system, its equilibrium condition is expressed as

$$\begin{aligned} \delta \varvec{u}^T(\varvec{s}[\varvec{u}]-\lambda \hat{\varvec{p}}) = 0 \quad \quad \forall \delta \varvec{u}, \end{aligned}$$
(42)

which is a nonlinear problem where \(\lambda\) is the load amplification factor, \(\varvec{s}[\varvec{u}]\) is the structural response, \(\hat{\varvec{p}}\) is the reference load vector and \(\delta \varvec{u}\) a variation of the configuration vector \(\varvec{u}\). The main tenet of Koiter’s method is approximating the initial postbuckling behaviour by constructing a reduced system of equilibrium equations whose number of unknowns is \(m+1\), where m is the number of buckling modes used in the analysis. The reduced order model is usually constructed based on a few modes (i.e., a few tens), making it an efficient alternative to path-following algorithms. In this regard, Zucco and Weaver [37] investigated how the buckling modes contribute to the nonlinear solution and identified a strategy to further reduce the computational cost of Koiter’s analysis by taking into account the initial degree of symmetry of the structural problem under consideration. The following steps summarise the algorithm.

  1. 1.

    Initially, the structure’s pre-critical behaviour is evaluated as

    $$\begin{aligned} \varvec{u}^f = \varvec{u}_0+\lambda \varvec{\hat{u}}\end{aligned}$$
    (43)

    where \(\varvec{u}_0\) is an initial known configuration, while \(\varvec{\hat{u}}\) represents the initial linear elastic response calculated from

    $$\begin{aligned} \varvec{K}[\varvec{u}_0]\,\varvec{\hat{u}}= \varvec{\hat{p}}\end{aligned}$$
    (44)

    where \(\varvec{K}\) is the stiffness matrix and \(\varvec{K}[\varvec{u}_0]\) its evaluation at the initial configuration.

  2. 2.

    A multi-modal buckling problem is solved to obtain m buckling loads \(\lambda _i\), \(i=1 \dots m\) and their corresponding modes \(\varvec{\dot{v}}_i\) along \(\varvec{u}^f\). Hence, the buckling problem

    $$\begin{aligned} \varvec{K}[\varvec{u}_0+\lambda _i \varvec{\hat{u}}]\, \varvec{\dot{v}}_i = \textbf{0} \end{aligned}$$
    (45)

    is solved for \(\lambda _i\) and \(\varvec{\dot{v}}_i\). Then, the buckling modes are normalised using the following orthogonality condition

    $$\begin{aligned} \Phi '''_b\hat{\varvec{u}}\dot{\varvec{v}}_i\dot{\varvec{v}}_j=0\quad ,\quad \forall i,j=1\dots m \end{aligned}$$
    (46)

    where \(\Phi '''_b\) is the third Fr\(\grave{\text {e}}\)chet derivative evaluated at \(\lambda _b\) which is an appropriate reference value among the m buckling loads (e.g. the smallest \(\lambda _i\) or their mean value).

  3. 3.

    Subsequently, the quadratic corrections belonging to \({{\mathcal {W}}} = \{ \varvec{w}: \varvec{w}\bot \varvec{\dot{v}}_i\,,\; i=1 \dots m\}\), which is a space orthogonal to that of the buckling modes are evaluated as

    $$\begin{aligned} \varvec{w}\bot \varvec{\dot{v}}_i \;\Leftrightarrow \; \Phi '''_b\hat{\varvec{u}}\dot{\varvec{v}}_i \varvec{w}=0. \end{aligned}$$
    (47)

    introducing \(\xi _0 = (\lambda -\lambda _b)\) and \(\varvec{\dot{v}}_0 = \varvec{\hat{u}}\), the equilibrium path is asymptotically approximated through an expansion in terms of mode amplitudes \(\xi _j\) as

    $$\begin{aligned} \varvec{u}[\lambda , \xi _k] = \varvec{u}_0+\lambda _b \varvec{\hat{u}}+ \sum _{i=0}^m \xi _i \varvec{\dot{v}}_i + \frac{1}{2}\sum _{i,j=0}^m \xi _i \xi _j \varvec{w}_{ij}. \end{aligned}$$
    (48)

    In Eq. 48, \(\varvec{w}_{ij} \in {\mathcal {W}}\) are quadratic corrections introduced to satisfy the projection of the equilibrium equation onto \({{\mathcal {W}}}\), obtained by the linear orthogonal equations

    $$\begin{aligned} \delta \varvec{w}^T(\varvec{K}[\varvec{u}_0+\lambda _b \varvec{\hat{u}}] \varvec{w}_{ij} + \varvec{p}_{ij})=0 \;,\;\;\forall \varvec{w}\in \mathcal {W} \end{aligned}$$
    (49)

    where vectors \(\varvec{p}_{ij}\) are defined as a function of the buckling modes \(\varvec{\dot{v}}_i\, , \;i=0 \dots m\), and energy equivalence \(\delta \varvec{w}^T \varvec{p}_{ij} = \Phi _b''' \delta \varvec{w}\, \dot{\varvec{v}}_j\dot{\varvec{v}}_j\).

  4. 4.

    The energy terms

    $$\begin{aligned} \left. \begin{aligned} \mathcal {C}_{ik}&= \Phi ''_b \varvec{w}_{00} \varvec{w}_{ik},\\ \mathcal {A}_{ijk}&=\Phi '''_b \dot{\varvec{v}}_i \dot{\varvec{v}}_j \dot{\varvec{v}}_k, \\ \mathcal {B}_{ijhk}&=\Phi ''''_b \dot{\varvec{v}}_i \dot{\varvec{v}}_j\dot{\varvec{v}}_h\dot{\varvec{v}}_k - \Phi ''_b (\varvec{w}_{ij} \varvec{w}_{hk} + \varvec{w}_{ih} \varvec{w}_{jk}+ \varvec{w}_{ik}\varvec{w}_{jh})\\ \end{aligned} \right. \end{aligned}$$
    (50)

    are evaluated for \(i,j = 0 \dots m\), \(k = 1 \dots m\).

  5. 5.

    The equilibrium path is recovered by solving the nonlinear algebraic system

    $$\begin{aligned}{} & {} \frac{1}{2}\sum _{i,j=0}^m \xi _i\xi _j \mathcal {A}_{ijk} +\frac{1}{6}\sum _{i,j,h=0}^m \xi _i\xi _j\xi _h \mathcal {B}_{ijhk} +\mu _k[\lambda ]\nonumber \\{} & {} \qquad -\lambda _b\left( \lambda -\frac{1}{2}\lambda _b\right) \sum _{i=0}^m \xi _i \mathcal {C}_{ik} = 0 \;,\;\;k=1 \ldots m \end{aligned}$$
    (51)

    of m equations with \(m+1\) unknowns \(\xi _0, \dots , \xi _m\), where

    $$\begin{aligned} \mu _k[\lambda ] = \frac{1}{2}\lambda _b\left( \lambda -\frac{1}{2}\lambda _b\right) \Phi _b'''\hat{\varvec{u}}^2 \dot{\varvec{v}}_k +\frac{1}{6}\lambda _b^2(\lambda _b-3\lambda )\Phi ''''_b\hat{\varvec{u}}^3 \dot{\varvec{v}}_k \end{aligned}$$
    (52)

    are the implicit imperfection factors obtained from the 4th order expansion of the unbalanced work along the fundamental path.

Finally, previous work showed the Koiter multi-modal algorithm’s efficiency in assessing the imperfection sensitivity of thin-walled structures [33, 35]. In fact, the effect of different geometrical \(\tilde{\varvec{u}}\) and load \(\tilde{\varvec{p}}\) imperfections to their load carrying capacity can be studied by simply changing the magnitude of the imperfection factors \(\mu _k[\lambda ]\) in Eq. (51). Therefore, the effect of a large number of imperfections (i.e. thousands) means only solving the same system as many times as the number of imperfections considered where each time \(\mu _k[\lambda ]\) has a different value mimicking the effect of a different imperfection.

5 Numerical results

This Section first describes the VS laminates in more detail, providing a linear function with which the fibre angles vary over a generic laminate’s layer. Then, it presents the numerical results. In particular, the first test regards the initial post-buckling analysis of a carbon fibre VS plate under compressive stresses where the performance of MISS-4C is compared with with that of another mixed element in the literature. Finally, the efficiency of the MISS-4C element, when implemented within a multi-modal Koiter algorithm, is shown through a multi-objective optimisation of the structural response of a glass fibre VS composite laminate girder of a short-length bridge [7].

5.1 Variable stiffness laminates

Unlike traditional composite laminates with straight fibre orientations, VS laminates have fibre angles varying over the structure with a predefined expression. In 1993, Gürdal and Olmedo [38] proposed a linear variation of the fibre angles in VS structures, which is commonly used for its simplicity nowadays. In particular, considering a plane layer of a composite laminate, the fibre angle linear variation is

$$\begin{aligned} \vartheta [\eta ] = \varphi + \left( \dfrac{T_1 - T_0}{a} \right) |\eta | + T_0 \end{aligned}$$
(53)

where \(\eta\) is an abscissa measured along a direction rotated of \(\varphi\), as shown in Fig. 1. Then, \(T_0\) and \(T_1\) are the fibre angles at the point when \(\eta =0\) and \(\eta = \pm a\), respectively, and measured with respect to \(\varphi\). Commonly, the notation \([\varphi <T_0|T_1>]\) with the values of \(\varphi\), \(T_0\), and \(T_1\) indicates a composite layer with a linear fibre variation.

Fig. 1
figure 1

Fibre trajectory over a flat surface described by Eq. 53

Full size image

It is worth mentioning that current trends in VS structures showed that nonlinear variations of the fibre angles provide larger design spaces than those with linear variations, leading to further possibilities for exploiting the VS technology [10]. However, independent of whether it is linear or nonlinear, the fibre angle variation must be bound by manufacturing constraints depending on the manufacturing process to ensure good manufacturing quality of the structure. Interesting insights on that aspect can be found in [39, 40].

5.2 Carbon fibre VS composite laminate plate

Firstly, the performance of the MISS-4C element is tested for the linear static and geometrically nonlinear static analysis of a VS composite plate. In particular, a carbon fibre VS composite plate square, as shown in Fig. 2, is considered. The plate length, \(\ell\), equals 508 mm, while the thickness of each of its lamina is \(t_l=1.172\cdot 10^{-4}\) mm. The plate is simply supported at its contour, as shown in Fig. 2, and in-plane constraints are applied to avoid rigid body motions. Along its vertical sides, the plate is subjected to a uniformly distributed compressive load \(q_1=1\) \(\textrm{N}/\textrm{mm}^2\). Moreover, a uniformly distributed surface load \(q_3 = 10^{-8}\) \(\textrm{N}/\textrm{mm}^2\) acts on its surface.

Fig. 2
figure 2

VS composite laminate plate: geometry, loading and boundary conditions, and initial mesh

Full size image
Table 1 VS composite laminate plate: material properties
Full size table

The material properties are shown in Table 1, where direction 1 is aligned with the fibre angle. Then, the fibre angle variation of each layer is described by Eq. 53, and the stacking sequence is \([\pm 0<0|45>]_{2S}\).

First, the performance of MISS-4C in obtaining the linear buckling solution of the plate is investigated when using a regular mesh, as shown on the right-end-side of Fig. 2. Two meshes are considered, namely mesh 2 with \(4 \times 4\) elements and mesh 6 with \(64 \times 64\) elements. For those meshes, Table 2 compares the four lowest buckling loads obtained using MISS-4C with those evaluated through MISS-4. Although results shown in Table 2 converge to the same values, it is worth noting how MISS-4C provides more accurate solutions than MISS4 when using coarse meshes as also shown in Fig. 3 displaying the buckling modes corresponding to the four lowest buckling loads obtained with MISS-4C.

Table 2 VS composite laminate plate: four lowest buckling loads obtained with different levels of mesh refinement, normalised on 2.4288
Full size table
Fig. 3
figure 3

VS composite laminate plate: buckling modes corresponding to the four lowest buckling loads

Full size image

Subsequently, the accuracy of MISS-4C in obtaining the initial postbuckling response of the VS composite laminate plate when using Koiter’s analysis is assessed. For both MISS-4C and MISS-4, Fig. 4 shows the equilibrium paths evaluated at the plate centroid when using only the lowest buckling mode in Koiter’s analysis.

It is worth noting that the performance of the MISS-4 element is documented in the literature for linear elastic, buckling and post-buckling problems [11, 21, 41] showing higher accuracy and convergence rates than displacement-based shell elements in Abaqus. Therefore, in this work, comparisons between results obtained with the MISS-4C element are only made with those obtained with the MISS-4 element.

Fig. 4
figure 4

VS composite laminate plate: equilibrium path for different levels of mesh refinement. The load factor \(\lambda\) is normalised by the lowest buckling load \(\lambda _1\), whose value is shown in Table 2

Full size image

5.3 Glass fibre VS composite laminate girder

As shown in Fig. 5, a short-length bridge made with glass fibre composite laminates is considered. The girder’s cross-section geometry is the same as that designed by Strongwell in Bristol in the late 1990s [42] used to erect composite bridges with spans of up to 18 m. The dimensions of the girder’s cross-section are shown in Fig. 6.

This work assumes that the girder has a length \(L=10\) m and is made entirely with glass fibre laminates whose properties are shown in Table 3. Then, each girder’s vertical web is made with VS laminates. In particular, for each vertical web, the steering direction coincides with the \(\zeta _2-\)axis as shown in Fig. 7 and the fibre angle variation is described by Eq. 53. Therefore, for each layer of the girder’s vertical webs, the fibre angle is \(T_1\) when \(\zeta _2=0\) and \(\zeta _2=L\) while it equals \(T_0\) when \(\zeta _2=L/2\). Finally, considering Eq. 53, the abscissa \(\eta\) in Fig. 7 coincides with the local reference axis \(e_1\) whose origin is at the web centroid.

Table 3 VS composite laminate girder: material properties expressed in GPa
Full size table
Fig. 5
figure 5

VS composite laminate girder: short-length bridge and a detail of one of its girders [42]

Full size image
Fig. 6
figure 6

VS composite laminate girder: dimensions of the girder’s cross-section from [42]. All the lengths are expressed in mm

Full size image
Fig. 7
figure 7

VS composite laminate girder: plane view of a single layer of the girder’s vertical web with a linear variation of its fibre angles described by Eq. 53

Full size image

Figure 8 shows the loading and boundary conditions of the girder. In particular, the bottom panel is simply supported at its ends while a constant surface load \(q_3\) acts on the top panel.

Fig. 8
figure 8

VS composite laminate girder: boundary and loading conditions

Full size image

A multi-objective optimisation of the VS girder is conducted to show the performance of the MISS-4C element within a Kolter multi-modal algorithm. The optimisation regards only the fibre angle trajectories in the vertical webs of the girder whose stacking sequence is

$$\begin{aligned} {[}0\pm \langle \vartheta _2|\vartheta _1 \rangle / 0\pm \langle \vartheta _4|\vartheta _3 \rangle ]_{S}, \end{aligned}$$
(54)

which has eight layers controlled by four variables \(\vartheta _i\), \(i=1,\dots ,4\), whereas the horizontal panels are made with CS panels whose fibre angles align with the girder’s longitudinal direction (stacking sequence \([0]_6\)). The dimensions of the cross-section are kept constant (Fig. 6). This choice relies on the purpose of showing the potential advantages of VS laminates to improve the girder’s structural performance by tailoring the fibre orientations of its layups without changing the girder’s mass, as well as showing the efficiency of a Koiter multi-modal algorithm to obtain the initial postbuckling behaviour of the structure under consideration. In this case, the Koiter multi-modal algorithm uses the first lowest eight buckling modes, namely \(m=8\) in Eq. 51, to obtain the girder’s initial postbuckling response.

Three objective functions are selected, namely the deflection at point A, \(d_3^A\), located at the centroid of the bottom panel, the lowest linearised buckling load, \(\lambda _1\), and the limit load, \(\lambda _c\). The limit load represents an indicator of the girder’s actual load-carrying capacity, which is affected by an unstable postbuckling response, as shown in Fig. 9. The girder’s unstable behaviour is explained by the interaction between the first (flexural) and the third (local) buckling modes, as it is observed from the equilibrium paths as a function of the Koiter mode amplifiers \(\xi _i\) obtained from Eq. 51 and shown on the right-hand side of Fig. 9.

Fig. 9
figure 9

VS composite laminate girder: for the VS girder with \(\varvec{\vartheta }=[0,0,0,0]\), on the left-end-side equilibrium path as a function of the vertical deflection measured at the centroid of the bottom panel; on the right-end-side equilibrium paths as a function of the Koiter mode amplifiers \(\xi _i\) obtained from Eq. 51

Full size image

For comparison, the optimisation is also conducted for the same girder with CS laminates, for which a parametric stacking sequence similar to the VS case is adopted, namely

$$\begin{aligned} {[}\pm \vartheta _1/\pm \vartheta _2]_{S}. \end{aligned}$$
(55)

In this case, the number of parameters is two. Both the parametric stacking sequences used to optimise the VS and CS layups are balanced and symmetric.

Hence, for both cases, the multi-objective optimisation problem reads as

$$\begin{aligned} \begin{aligned}&\underset{{\varvec{\vartheta }}}{\text {minimise}}{} & {} \left[ d_3^A[\varvec{\vartheta }], \quad -\lambda _1[\varvec{\vartheta }], \quad -\lambda _c[\varvec{\vartheta }]\right] \\&\text {subject to}{} & {} -90^\circ \le \vartheta _i \le 90^\circ , \quad i=1\dots nv\\ \end{aligned} \end{aligned}$$
(56)

where nv is the number of optimisation variables collected in \(\varvec{\vartheta } = [\vartheta _1\dots ,\vartheta _{nv}]\). The limit load \(\lambda _c[\varvec{\vartheta }]\) is efficiently evaluated through a geometrically nonlinear analysis using the multi-modal Koiter’s algorithm.

The optimisation functions are nonlinear and nonconvex [6]. The solutions of the problem in Eq. (56) are named non-inferior solution points for which an improvement in one objective requires a degradation in the other. The locus of non-inferior solutions is usually named Pareto front [43]. The Pareto front is obtained using a variant of the genetic algorithm NSGA-II [43], implemented in Matlab [44]. The parameters used for solving the optimisation problem are given in Table 4. The sensitivity of the Pareto front to this setting has been tested by modifying those parameters and running the optimisation problem multiple times.

Table 4 VS composite laminate girder: genetic algorithm parameters
Full size table

With the aim of testing more in-deep the performance of MISS-4C, a convergence study is first conducted. The initial mesh, denoted as mesh-0 and composed by 192 FEs, is represented in Fig. 10. Finer meshes are obtained by h-refinement and are denoted as mesh-h, being h the number of refinements. Results in terms of deflection of point A and of the eight lowest buckling loads are given in Table 5, considering the stacking sequence \([0\pm \langle 0|90 \rangle / 0\pm \langle 0|45 \rangle ]_{S}\). It can be observed how the linear displacement and the first buckling load are well predicted even using coarse meshes. Conversely, the other buckling modes require a finer mesh to be correctly estimated. This different behaviour is due to the fact that these buckling loads are associated with local buckling modes constituted by small dimples located near the beam’s end. The buckling modes’ shapes are represented in Fig. 11.

The convergence properties of MISS-4C for VS structures are illustrated by the results given in Fig. 12. The convergence graphs give, in a double logarithmic scale, the square root of the degrees of freedom (\(\sqrt{DOFs}\)) of mesh-h and the relative error \(\mathcal {E}_d\) evaluated as

$$\begin{aligned} \mathcal {E}_d = \dfrac{\Vert (d_h-d_{ref})\Vert }{d_{ref}} \end{aligned}$$

where \(d_h\) is a pointwise displacement or a buckling load evaluated for mesh-h, while \(d_{ref}\) is the reference value, obtained by performing a numerical solution with a very fine mesh. Figure 12 shows, in particular, the convergence for the linear deflection at point A and the three lowest buckling loads. It can be observed how in all cases the convergence rate is \(h^2\), where, as usual, the exponent is the slope of the convergence curve. This result highlights the good performance of MISS-4C in capturing the geometrically nonlinear behaviour of VS structures, even in presence of complex buckling modes.

Fig. 10
figure 10

VS composite laminate girder: mesh-0

Full size image
Table 5 VS composite laminate girder: linear elastic solution and first eight buckling loads for different meshes, stacking sequence \([0\pm \langle 0|90 \rangle / 0\pm \langle 0|45 \rangle ]_{S}\)
Full size table
Fig. 11
figure 11

VS composite laminate girder: buckling modes corresponding to the eight lowest buckling loads evaluated using mesh-2

Full size image
Fig. 12
figure 12

VS composite laminate girder: convergence of the linear elastic solution and of the first three buckling loads for the stacking sequence \([0\pm \langle 0|90 \rangle / 0\pm \langle 0|45 \rangle ]_{S}\)

Full size image

A total of two optimisation problems are solved, one when the girder web is made with VS laminates and another for the same girder web with CS laminates. The obtained Pareto fronts are shown in Fig. 13, where the linear deflections and the buckling loads are normalised with respect to the corresponding results obtained for the quasi-isotopic (QI) baseline. In all cases, it is observed that the solutions of the CS configurations represent sub-optimal cases for the Pareto front of the girders with VS webs. The girders with VS laminates exhibit better structural performance than their corresponding CS laminate counterparts. Furthermore, it is worth noting that the QI girder solution is a sub-optimal case of both the VS and CS configurations. Plane views of the Pareto front obtained for the VS laminates are shown in Fig. 14.

For the VS case, the Pareto front is approximately vertical, meaning it is possible to improve the buckling load largely without significantly increasing the linear elastic deflection. This suggests that it is possible to set a deflection limit and, through the Pareto front, select the VS layup that gives the largest buckling load.

The results obtained for the VS laminates present some differences with respect to those obtained for the CS laminates. In particular, the Pareto front for the CS laminates indicates that if one wants to maximise the girder’s buckling load, a substantial increase of its linear deflection is required.

Finally, it is worth observing in Fig. 14 that an increase in the buckling load does not always lead to an increase in the limit load. In particular, the maximum limit load is not reached in the Pareto point having the maximum linearised buckling load, and conversely, a maximisation of the buckling load leads to a limit load decrease. This highlights the importance of adopting a fully geometrically nonlinear analysis for robust optimisation of structures with unstable postbuckling behaviour.

Fig. 13
figure 13

VS composite laminate girder: Pareto front obtained by solving the multi-objective optimisation for VS and CS laminates

Full size image
Fig. 14
figure 14

VS composite laminate girder: different plane views of the Pareto front obtained by solving the multi-objective optimisation for VS laminates

Full size image

6 Conclusion

A Hellinger–Reissner shell finite element has been presented for studying the geometrically nonlinear response of variable stiffness (VS) composite laminate structures. The element has a quadrilateral flat geometry and four nodes with six degrees of freedom per node. For symmetric composite laminates, the assumed stress fields a priori satisfy the equilibrium equations when the bulk loads are null and the compatibility equations. As a result, the element’s kinematic has been assumed only along its contour. Meanwhile, its operators are obtained through an analytical integration along its contour. Then, a corotational kinematic is employed to use the element’s linear formulation for studying geometrically nonlinear problems, which, in this work, are solved through an efficient multi-modal Koiter algorithm.

For a standard benchmark, comparisons with the MISS-4 finite element, whose accuracy and robustness are already known in the literature, showed good performance for the MISS-4C element and higher accuracy when using coarse meshes. Finally, due to its robustness and efficiency when implemented within a Koiter multi-modal approach, MISS-4C has been used to optimise a short-length bridge girder made with glass fibre VS composite laminates. In particular, multi-objective optimisation has been conducted to select the orientations of the VS layups that maximise the girder’s buckling load and limit load, and minimise its deflection. Results have shown that the girders made with VS composite laminates have a better structural performance than their traditional straight fibre counterparts, highlighting the importance of design tools that use robust and effective numerical approaches.