Nonlinear response of a planar repetitive space truss with joints based on multi-harmonic equivalent model

Abstract

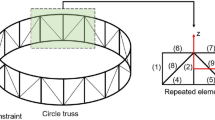
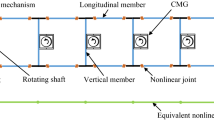
This paper presents a nonlinear response of a planar repetitive space truss with polynomial-nonlinear joints based on a multi-harmonic equivalent continuum beam model. The nonlinear joints are modeled as the multi-harmonic dynamic stiffness matrix with eccentricity. To overcome the limitation of classical equivalent method based on energy, a high-order displacement equivalent modeling method is proposed, where the micro-rotation is included to improve the accuracy and avoid the pseudo inverse of matrix. Furthermore, in the experiment, a novel suspension device used to support the space truss structure is designed, which not only offsets the gravity but allows the truss to bend and twist freely on the granite table. A bending sweeping test was conducted to obtain the nonlinear frequency response of bending and bending-torsion coupling of the space truss. The results show the similar nonlinear characteristic  between the nonlinearity of joints and the repetitive truss. During the vibration test, the coupled torsional vibration of planar repetitive truss has a larger amplitude at the bending resonance frequencies, rather than at the torsion resonance frequencies, indicating a nonlinear bending-torsion coupling feature.

Appendices

Appendix A

1.1 Multi-harmonic describing function method

Let $y(t)$ and $\dot{y}(t)$ be the relative joint deformation and its derivative with respect to time $t$, $f_s (t)$ and $f_d (t)$ the stiffness and damping force of nonlinear joint in the time domain. Assuming that $f_s (t)$ and $f_d (t)$ are the polynomial function of $y(t)$ and $\dot{y}(t)$, respectively. For convenience of expression, the time t will be omitted in what follows. To deal with nonlinearity, the multi-harmonic describing function method (MHDFM) proposed by Ferreira and Ewins [36] will be introduced and extended to obtain a new hybrid element.

If the motion of system is periodic, the nonlinear force and displacement of joint, in truncated Fourier coefficients up to $N_H$ harmonics, can be written

$$f_s (y) \approx \sum_{k = - N_H }^{N_H } {F_k^s {\text{e}}^{ik\omega t} } ,f_d (\dot{y}) \approx \sum_{k = - N_H }^{N_H } {F_k^d {\text{e}}^{ik\omega t} }$$

(A.1)

$$y \approx y^{[N_H ]} = \sum_{k = - N_H }^{N_H } {Y_k {\text{e}}^{ik\omega t} } ,\dot{y} \approx \dot{y}^{[N_H ]} = \sum_{k = - N_H }^{N_H } {ik\omega Y_k {\text{e}}^{ik\omega t} }$$

(A.2)

where $F_k^s$, $F_k^d$ and $Y_k$ are the $k$-th Fourier coefficient of $f_s$, $f_d$ and $y$. Since no additional information is contained in the conjugated complex parts, equation (A.1) can be simplified as

$$f_s (y) \approx \sum_{k = 0}^{N_H } {F_k^s {\text{e}}^{ik\omega t} } ,f_d (\dot{y}) \approx \sum_{k = 0}^{N_H } {F_k^d {\text{e}}^{ik\omega t} }$$

(A.3)

Note that $F_k^s$ and $F_k^d$ can be expressed in the analytical form.

$$F_k^s = \sum_{i = 0}^{N_H } {G_{ki} Y_i } ,F_k^d = \sum_{i = 0}^{N_H } {D_{ki} Y_i }$$

(A.4)

where $G_{ki}$ and $D_{ki}$, the element of matrix ${\bf{G}}$ and ${\bf{D}}$, are given by

$$G_{ki} = {{(F_k^s (y^{[N_H ]} ) - F_k^s (y^{[N_H - 1]} ))} / {Y_i }},D_{ki} = {{(F_k^d (\dot{y}^{[N_H ]} ) - F_k^d (\dot{y}^{[N_H - 1]} ))} / {Y_i }}$$

(A.5)

and $y^{[i]}$ denotes the periodic signal of the joint deformation including k harmonics.

According to Eq. (A.4), the multi-harmonic dynamic stiffness matrix Δ of the nonlinear joint can be obtained as

$$\Delta (Y_{1} ,Y_{2} ,...,Y_{{N_{H} }} ;\omega ) = G(Y_{1} ,Y_{2} ,...,Y_{{N_{H} }} ) + D(Y_{1} ,Y_{2} ,...,Y_{{N_{H} }} ;\omega )$$

(A.6)

and the constitutive equation of the three-dimension nonlinear joint in the frequency domain reads

$${\bf{F}}_c = {\bf{S}}_c {\bf{Y}}_c$$

(A.7)

where ${\bf{F}}_c$ is the multi-harmonic vector consisting of the internal forces and moments of the joint along three directions of the local coordinate system, ${\bf{Y}}_c$ is the multi-harmonic vector made up of the corresponding deformation of the joint, and ${\bf{S}}_c$ is assembled by the matrix Δ.

Appendix B

2.1 Constitutive equation of hybrid beam element

The Euler beam equation with the material damping ratio $\eta$ and the linear viscous damping $c_v$ can be written as

$$\rho A\frac{\partial^2 w}{{\partial t^2 }} + c_v \frac{\partial w}{{\partial t}} + EI(\frac{\partial^4 w}{{\partial x^4 }} + \eta \frac{\partial^5 w}{{\partial^4 x\partial t}}) = 0$$

(B.1)

where $E$,$I$,$\rho$,$A$ and $L$ are Young’s modulus, the second-moment inertia of cross section, mass density, the area of the cross-section, and length of beam, respectively. The wavenumbers for pure bending $k_F$ and torsion $k_T$ arrive at

$$k_F = [{{(\omega^2 \rho A - ic_v \omega )} / {(EI + iEI\eta \omega )}}]^{1 / 4} ,k_T = [{{(\omega^2 \rho I_p - ic_v \omega )} / {(GI_p + iGI_p \eta \omega }})]^{1 / 2}$$

(B.2)

Then the spectral element matrix of Euler beam [37] is obtained

$${\bf{F}}_B = {\bf{S}}_B (\omega ){\bf{U}}_B$$

(B.3)

where ${\bf{F}}_B$ and ${\bf{U}}_B$ are the nodal force and displacement of two beam nodes in Fourier coefficients.

Consider the two nonlinear joints at the both ends of the Euler beam, Eq. (A.7) becomes

$${\bf{F}}_C = {\bf{S}}_C ({\bf{Y}}_c ,\omega ){\bf{Y}},{\bf{S}}_C = {\text{diag}}({\bf{S}}_{Ac} ,{\bf{S}}_{Bc} )$$

(B.4)

where ${\bf{F}}_C$ and ${\bf{Y}}$ are the multi-harmonic vectors of internal force and relative displacement of two joints, respectively. ${\bf{S}}_{Ac}$ and ${\bf{S}}_{Bc}$ denote the ${\bf{S}}_c$ of two joints A and B.

Let ${\bf{U}}_{nd}$($nd \in${$Ae$,$Ac$,$Ab$,$Bb$,$Bc$,$Be$}) represent the multi-harmonic displacement vector of node $nd$. If the connection blocks are assumed to be rigid, the joint displacement ${\bf{Y}} = [{\bf{U}}_{Ac}^{\text{T}} - {\bf{U}}_{Ab}^{\text{T}} ,{\bf{U}}_{Bc}^{\text{T}} - {\bf{U}}_{Bb}^{\text{T}} ]^{\text{T}}$ can be written as

$${\bf{Y}} = ({\bf{I}} + {\bf{E}})^{\text{T}} {\bf{U}}_E - {\bf{U}}_B$$

(B.5)

where ${\bf{U}}_B = [{\bf{U}}_{Ab}^{\text{T}} ,{\bf{U}}_{Bb}^{\text{T}} ]^{\text{T}}$, ${\bf{U}}_E = [{\bf{U}}_{Ae}^{\text{T}} ,{\bf{U}}_{Be}^{\text{T}} ]^{\text{T}}$ and ${\bf{E}}$ denotes the transformation matrix from ${\bf{U}}_C = [{\bf{U}}_{Ac}^{\text{T}} ,{\bf{U}}_{Bc}^{\text{T}} ]^{\text{T}}$ to ${\bf{U}}_E$ considering the length of connection blocks

$${\bf{U}}_C = ({\bf{I}} + {\bf{E}}^{\text{T}} ){\bf{U}}_E$$

(B.6)

The deformation compatibility equation can be found by considering the condition of displacement equivalence, namely

$${\bf{Y}} = ({\bf{I}} + {\bf{E}}^{\text{T}} ){\bf{U}}_E - ({\bf{S}}_B + {\bf{S}}_C )^{ - 1} {\bf{S}}_C ({\bf{I}} + {\bf{E}}^{\text{T}} ){\bf{U}}_E$$

(B.7)

where

$${\bf{E}} = \left[ {\begin{array}{*{20}c} {{\bf{E}}_A } & {\bf{0}} \\ {\bf{0}} & {{\bf{E}}_B } \\ \end{array} } \right],{\bf{E}}_A = \left[ {\begin{array}{*{20}c} {{\bf{E}}_{A1} } & {\bf{0}} \\ {\bf{0}} & {{\bf{E}}_{A1} } \\ \end{array} } \right],{\bf{E}}_{A1} = \left[ {\begin{array}{*{20}c} {\bf{0}} & {\bf{0}} & {\bf{0}} \\ {\bf{e}} & {\bf{0}} & {\bf{0}} \\ {\bf{0}} & {\bf{0}} & {\bf{0}} \\ \end{array} } \right],{\bf{E}}_A = - {\bf{E}}_B$$

(B.8)

with ${\bf{0}}$ being the zero matrix and ${\bf{e}}$ the diagonal matrix with the element e denoting the length (or eccentricity) of connection blocks. The relation between the relative displacement of joints and the node displacement of the hybrid beam element are described as follows

$${\bf{U}}_C = ({\bf{I}} + {\bf{E}}^{\text{T}} ){\bf{U}}_E$$

(B.9)

Consequently, the constitutive equation of joint-beam-joint shown in Fig. 1b can be assembled by Eqs. (B.3) and (B.4) to the following form

$$\left[ {\begin{array}{*{20}c} {{\bf{F}}_C } \\ {{\bf{F}}_B } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\bf{S}}_C } & { - {\bf{S}}_C } \\ { - {\bf{S}}_C } & {{\bf{S}}_C + {\bf{S}}_B } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\bf{U}}_C } \\ {{\bf{U}}_B } \\ \end{array} } \right]$$

(B.10)

The condensed constitutive equation can be expressed by the dynamic condensation

$${\bf{F}}_C = [{\bf{S}}_C - {\bf{S}}_C ({\bf{S}}_B + {\bf{S}}_C )^{ - 1} {\bf{S}}_C ]{\bf{U}}_C$$

(B.11)

Taking the mass and length of the connection blocks into account, one can derive the force-balance equation considering the beam-joint element with two rigid connection blocks, i.e.,

$${\bf{F}}_C = ({\bf{I}} - {\bf{E}}){\bf{F}}_E + {\bf{M}}_E {\bf{U}}_E$$

(B.12)

where ${\bf{M}}_E$ stands for the mass and moment of inertia of the connection blocks.

Combining the Eqs. (B.9), (B.11) and (B.12) yields the following constitutive matrix of hybrid beam element

$${\bf{D}}_{hybrid} = ({\bf{I}} + {\bf{E}})[ - {\bf{M}}_E + {\bf{S}}_C - {\bf{S}}_C ({\bf{S}}_C + {\bf{S}}_B )^{ - 1} {\bf{S}}_C ]({\bf{I}} + {\bf{E}}^{\text{T}} )$$

(B.13)