1 Introduction

Nowadays, the increasing diffusion of micro- and nanotechnologies has recently generated the need of mathematical models capable of providing reliable simulations of the mechanics of micro- and nanostructures. The classical continuum mechanics theory cannot be used to model size effects at small scales, due to its inherent scale-independent behavior. On the other hand, other strategies to simulate micro- and nanomechanics, such as molecular dynamics, are computationally expensive and sometimes even prohibitive. For these reasons, in the last decades non-local models have known a considerable interest in the field of micro- and nanomechanics. From the pioneering works of Mindlin [1] and Eringen [2] many non-local approaches have been proposed with the purpose of capturing different aspects of small scale mechanics such as wave dispersion, stiffening and/or softening effects.

Non-local models are subdivided into two main classes [3]: strong or integral non-local models, characterized by constitutive relationships or governing equations that involve integrals of some state variables (strain, displacement, stress) and weak or gradient non-local models, obtained as generalization of classical local constitutive laws enriched by additional higher-order terms.

The idea of formulating a constitutive law in integral form dates back to 1972 [2] with the purpose of predicting waves dispersion phenomena not provided by classical continuum theory. This approach, often labeled as strain driven model, has also been effective in modeling other phenomena such as screw dislocation [4]. Nevertheless, in presence of bounded domains this approach provides paradoxical results, such as violation of the static equilibrium [5,6,7]. For this reason, many modifications to the original Eringen model or alternative formulations have been proposed, such as local/non-local mixture models [8, 10,11,12], strain difference models [13,14,15], the peridynamic model [16], the mechanically based [17,18,19,20,21,22] and, more recently, the stress driven model [7, 23]. All these approaches belong to the class of strong non-locality and are not affected by the inconsistency of the original Eringen model. Further, each approach has some advantage, such as the capability of providing analytical solution [7, 23, 24], the possibility to be justified on a physical basis [16, 17] or the possibility to define an associated finite element formulation [13, 19, 25, 26]. Gradient models [27,28,29,30,31,32,33,34,35,36,37,38,39] have also been proposed in order to study non-local phenomena. Some interesting results have been obtained in literature with these models. However, differently from the integral formulations, only local operators are involved in the mathematical description of these models, therefore defined as weak non-local models. For this reason strong non-local models appears more attractive for the simulation of non-local effects.

Recently, some studies have proposed generalizations of existing non-local models that involve the presence of fractional-order operators in the non-local constitutive equation [40]. Indeed, fractional order derivatives and integrals are by definition non-local operators and appear suitable in modeling non-local phenomena [41, 42]. This strategy has been proposed both for integral models [43,44,45,46] and for gradient models [47, 48], not only in non-local elasticity but also in non-local fluid mechanics [49,50,51]. Recently, it has been shown that a proper definition of a fractional non-local model is capable of modeling both stiffening and softening non-local effects [52], typical of integral and gradient models, respectively.

In this paper, the fractional calculus approach to non-local elasticity is adopted with two main purposes. First, the adoption of power-law attenuation function leads to truly strong non-local models, i.e. integral non-local models which inversion leads again to integral non-local models. Conversely, strong integral non-local models with exponential Helmholtz kernel leads to gradient models with additional boundary conditions (BC), characterized by the presence of local differential operators only. Second, it is shown that with a proper arrangement of the power-law attenuation functions, the main integral non-local models, i.e. the strain driven, the stress driven and the peridynamic models, are equivalent each other. With this result, the main limitations of each of these approaches is overcome.

The paper is organized as follows. In Sect. 2, the basic definitions of fractional operators are introduced. Section 3 describes the main integral approaches and their gradient counterparts obtained by adopting exponential kernel. In Sect. 4, the equivalence between strong non-local models with power-law attenutation functions is demonstrated. In Sect. 5 the main results and future developments are briefly discussed.

2 Preliminaries on fractional calculus

In this section some basic concepts and definitions of fractional order operators are introduced.

The left sided and right sided Riemann-Liouville (RL) fractional integrals of order \(\alpha \in {\mathcal {R}}^+\) of a function f(x) are defined as

$$\begin{aligned}&(_aI_x^\alpha f)(x)=\frac{1}{\Gamma (\alpha )}\int _a^x (x-\xi )^{\alpha -1}f(\xi )d\xi , \end{aligned}$$
(1a)
$$\begin{aligned}&(_xI_b^\alpha f)(x)=\frac{1}{\Gamma (\alpha )}\int _t^b (\xi -x)^{\alpha -1}f(\xi )d\xi , \end{aligned}$$
(1b)

where \(\Gamma (\cdot )\) is the Euler Gamma function. Conversely, the right sided and left sided RL fractional derivatives of order \(\alpha \) are defined as

$$\begin{aligned}&\left( _aD_x^\alpha f\right) (x)=\frac{1}{\Gamma (n-\alpha )}\frac{d^n}{dx^n}\int _a^x \frac{f(\xi )}{(x-\xi )^{\alpha -n+1}}d\xi \end{aligned}$$
(2a)
$$\begin{aligned}&\left( _xD_b^\alpha f\right) (x)=\frac{(-1)^n}{\Gamma (n-\alpha )}\frac{d^n}{dx^n}\int _x^b \frac{f(\xi )}{(\xi -x)^{\alpha -n+1}}d\xi \end{aligned}$$
(2b)

where \(n-1<\alpha <n\). Notice that the definitions given in Eqs. (1) and (2) are suitable also for \(a\rightarrow -\infty \) and \(b\rightarrow \infty \).

Integration and differentiation of fractional order may be performed also in unbounded domains. To this regard Riesz fractional integrals and derivative are defined as

$$\begin{aligned}&\begin{aligned} \left( ^RI^\alpha f\right) (x)&=\frac{1}{2\nu _c(\alpha )}\int _{-\infty }^\infty \frac{f(\xi )}{|x-\xi |^{1-\alpha }}d\xi \\&=\frac{1}{2\cos \left( \alpha \pi /2\right) }\left[ \left( _{-\infty }I_x^\alpha f\right) (x) + \left( _xI_\infty ^\alpha f\right) (x) \right] \end{aligned}\end{aligned}$$
(3a)
$$\begin{aligned}&\begin{aligned} \left( ^RD^\alpha f\right) (x)&=\frac{1}{2\nu _c(-\alpha )}\int _{-\infty }^\infty \frac{f(\xi )-f(x)}{|x-\xi |^{\alpha +1}}d\xi \\&=\frac{1}{2\cos \left( \alpha \pi /2\right) }\left[ \left( _{-\infty }D_x^\alpha f\right) (x) + \left( _xD_{\infty }^\alpha f\right) (x) \right] \end{aligned} \end{aligned}$$
(3b)

where \(\nu _c(\alpha )=\Gamma (\alpha )\cos (\alpha \pi /2)\). It is noteworthy that Riesz fractional operators may be expressed in terms of RL operators, as revealed by the definitions in Eqs. (3).

For the developments of the next sections, a useful definition is the Caputo fractional derivative, in its right sided and left sided formulations

$$\begin{aligned}&\left( _a^CD_x^\alpha f\right) (x)=\frac{1}{\Gamma (n-\alpha )}\int _a^x \frac{f^{(n)}(\xi )}{(x-\xi )^{\alpha -n+1}}d\xi \end{aligned}$$
(4a)
$$\begin{aligned}&\left( _x^CD_b^\alpha f\right) (x)=\frac{(-1)^n}{\Gamma (n-\alpha )}\int _x^b \frac{f^{(n)}(\xi )}{(\xi -x)^{\alpha -n+1}}d\xi \end{aligned}$$
(4b)

provided that f(x) is differentiable up to n-order. Remarkably, the Caputo fractional derivatives in Eqs. (4) may be obtained from the RL fractional derivatives by means of the following relationships

$$\begin{aligned}&\left( _a^CD_x^\alpha f\right) (x)=\left[ _aD_x^\alpha \left( f(x)-\sum _{k=0}^{n-1}\frac{f^{(k)}(a)}{k!}(x-a)^k\right) \right] \end{aligned}$$
(5a)
$$\begin{aligned}&\left( _x^CD_b^\alpha f\right) (x)=\left[ _xD_b^\alpha \left( f(x)-\sum _{k=0}^{n-1}\frac{f^{(k)}(b)}{k!}(b-x)^k\right) \right] \end{aligned}$$
(5b)

Correspondingly, the RL fractional derivatives can be obtained from the Caputo derivatives as follows

$$\begin{aligned}&\left( _aD_x^\alpha f\right) (x)=\left( _a^CD_x^\alpha f\right) (x)+\sum _{k=0}^{n-1}\frac{f^{(k)}(a)}{\Gamma (1+k-\alpha )}(x-a)^{k-\alpha } \end{aligned}$$
(6a)
$$\begin{aligned}&\left( _xD_b^\alpha f\right) (x)=\left( _x^CD_b^\alpha f\right) (x)+\sum _{k=0}^{n-1}(-1)^k\frac{f^{(k)}(b)}{\Gamma (1+k-\alpha )}(b-x)^{k-\alpha } \end{aligned}$$
(6b)

More details about the definitions and the properties introduced in this section may be found in [41, 42].

3 Existing non-local approaches

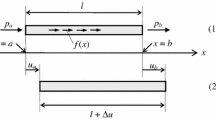
In this section the main existing integral non-local models are introduced. The main strengths and weakness are highlighted for the strain driven, stress driven and for the peridynamic model and mixture models are also briefly discussed. The non-local models are introduced with reference to the model of a rod, but the concepts highlighted in the following are valid also for beam models.

3.1 Strain driven models

The first and most celebrated integral non-local formulation is due to Eringen [2, 4] and was initially introduced to solve wave dispersion problems in unbounded domains. It assumes that the stress \({\varvec{\sigma }}\) at a point \({\varvec{x}}\) of a non-local body \({\mathcal {B}}\) is given by a convolution between the elastic strain field \({\varvec{\varepsilon }}\) and a scalar positive kernel g. That is,

$$\begin{aligned} {\varvec{\sigma }}({\varvec{x}})=\int _{\mathcal {B}}g({\varvec{x}},{\varvec{\xi }}){\varvec{E}}({\varvec{\xi }}){\varvec{\varepsilon }}({\varvec{\xi }})d{\varvec{\xi }} \end{aligned}$$
(7)

where \({\varvec{E}}\) is the elastic stiffness tensor and \({\varvec{x}}\), \({\varvec{\xi }}\) are position vectors. Since in the constitutive Eq. (7) the stress field is obtained from the strain field, the Eringen model is often labeled as strain driven. By particularizing the integral law in Eq. (7) to an infinite rod, an integral non-local constitutive relation between the axial force N and the axial strain \(\varepsilon \) is obtained. That is,

$$\begin{aligned} N (x)= \int _{-\infty }^{\infty } g(x-\xi )k_a(\xi )\varepsilon (\xi )d\xi \end{aligned}$$
(8)

where the beam axis coincides with the x-axis and \(k_a(x)\) is the elastic axial stiffness. The model in Eq. (8) is capable of capturing wave dispersion phenomena in unbounded domain that can not be explained in the theory of local elastic continuum. The kernel g is the attenuation function that can be selected among exponential, Gaussian or power-law type functions and must satisfy the properties of symmetry, positivity and limit impulsivity. A frequent choice is the bi-exponential Helmholtz function defined as follows

$$\begin{aligned} g(x)=\frac{1}{2 L_c}\exp \left( {-\frac{|x|}{L_c}}\right) \end{aligned}$$
(9)

where \(L_c\) is a characteristic length governing the spatial decaying of the attenuation function. Notice that for \(L_c\rightarrow 0\) the attenuation function in Eq. (9) reverts to the Dirac’s delta function (impulsivity property) and Eq. (7) reverts to the Hooke law. With the choice of the attenuation function in Eq. (9) and assuming a constant axial stiffness \(k_a=E A\), being E the Young modulus and A the cross section area of the rod, a differential formulation equivalent to Eq. (8) is found by inverting the constitutive law (8) in the Fourier domain:

$$\begin{aligned} \varepsilon (x)=\frac{1}{EA}\left[ N(x)-L_c^2 N^{(2)}(x)\right] \end{aligned}$$
(10)

Interestingly, the formulation of Eq. (8), belonging to the class of so-called strong non-local formulations, is equivalent to an ordinary differential constitutive law and hence belonging to the class of weak non-local models. This is quite surprisingly, since the mathematical structure of Eq. (8) describes a mechanics involving long-range interaction, while in Eq. (10) only local operators (second order derivative) related to local interactions are present.

Further, by considering a limited domain \(0\leqslant x\leqslant L\) in Eq. (8), simple mathematical manipulations still lead to Eq. (10) with the following constitutive boundary conditions (BC):

$$\begin{aligned} \left\{ \begin{aligned}&N^{(1)}(0)=\frac{1}{L_c}N (0)\\&N^{(1)}(L)=-\frac{1}{L_c}N (L) \end{aligned}\right. \end{aligned}$$
(11)

where the signs in Eq. (11) are consequence of the fact that the first derivative of the attenuation function is an odd function [7]. Eqs. (11) are clearly in contrast with the static boundary conditions of most structural schemes. Also from the integral formulation it is possible to prove that inserting the equilibrated stress in Eq. (8) particularized in the bounded domain \(0\leqslant x\leqslant L\), the Fredholm equation admits no solution in terms of elastic strain [7]. Therefore, the incompatibility between the equilibrium requirements and the constitutive non-local law reveals that applying the strain-driven model to bounded domains leads to ill-posed mechanical problems.

3.2 Stress driven models

An efficient strategy to overcome the limits of Eringen’s formulation in presence of bounded domains has been developed in Refs. [7, 23]. It consists in an integral non-local constitutive law, the stress-driven model, obtained by formally swapping the roles of stress and strain fields in the strain driven model of Eq. (7). The formulation belongs to the class of strong non-local models. According to the stress driven formulation, the elastic strain field at a point \({\varvec{x}}\) of the continuous body \({\mathcal {B}}\) is given by the convolution integral between the local elastic strain field \({\varvec{\varepsilon }}\) and the attenuation function \(\Phi _\lambda \). That is,

$$\begin{aligned} {\varvec{\varepsilon }}({\varvec{x}})=\int _{\mathcal {B}}g({\varvec{x}},{\varvec{\xi }}){\varvec{C}}({\varvec{\xi }}){\varvec{\sigma }}({\varvec{\xi }})d{\varvec{\xi }} \end{aligned}$$
(12)

where \({\varvec{C}}\) is the elastic compliance \({\varvec{C}}={\varvec{E}}^{-1}\).

Applied to a 1-D domain, such as a rod, the stress-driven model gives

$$\begin{aligned} \varepsilon (x)=\int _{-\infty }^{\infty } g(x-\xi )\frac{N (\xi )}{k_a(\xi )}d\xi \end{aligned}$$
(13)

Similarly to the Eringen model, by assuming the bi-exponential attenuation function of Eq. (9), for \(L_c\rightarrow 0\) Eq. (12) reverts the Hooke law. An equivalent differential formulation may be found by inverting the constitutive law in Eq. (13), with the choice of the attenuation function (9), in the Fourier domain. That is,

$$\begin{aligned} N(x)=EA \left[ \varepsilon (x)-L_c^2\varepsilon ^{(2)}(x)\right] \end{aligned}$$
(14)

If the rod is limited in the domain \(0\leqslant x\leqslant L\), simple mathematical manipulations of Eq. (13) still lead to Eq. (14) with the following constitutive BCs

$$\begin{aligned} \left\{ \begin{aligned}&\varepsilon ^{(1)}(0)=\frac{1}{L_c}\varepsilon (0)\\&\varepsilon ^{(1)}(L)=-\frac{1}{L_c}\varepsilon (L) \end{aligned}\right. \end{aligned}$$
(15)

Unlike BCs in Eq. (11) related to the strain driven model, those in Eq. (15) are not in contrast with the equilibrium of the rod, hence the stress driven model leads to well posed problems providing exact solutions capable of describing the actual behavior of micro- and nano-structures, both in static and dynamical problem. However, similarly to the Eringen model, the inverse constitutive law of the stress driven integral formulation involves only local differential operators, capable of capturing a mechanics with local interactions only.

3.3 Peridynamic models

The peridynamic model was firstly introduced by Silling [16]. According to this model, each couples of volume elements in an elastic body mutually exchanges forces proportional to their volumes, their relative displacements and an attenuation function depending on their distance. Contact forces characterizing the classical Cauchy continuum are not included. With this approach, the non-local force in \({\varvec{x}}\), due to the relative motion with the volume element in \({\varvec{\xi }}\), is written as:

$$\begin{aligned} d{\varvec{f}}\left( {\varvec{x,\xi }}\right) ={\tilde{E}}\left[ {\varvec{u}}({\varvec{\xi }}) - {\varvec{u}}({\varvec{x}})\right] {\varvec{G}}\left( {\varvec{x,\xi }}\right) dV({\varvec{x}})dV({\varvec{\xi }}) \end{aligned}$$
(16)

where \({\tilde{E}}\) is the non-local modulus and \({\varvec{G}}\left( {\varvec{x,\xi }}\right) =g\left( {\varvec{x,\xi }}\right) {\varvec{J}}({\varvec{x}},{\varvec{\xi }})\) being \({\varvec{J}}({\varvec{x}},{\varvec{\xi }})\) the Jacobi directional tensor containing the components of the unit vectors associated with the direction \({\varvec{x}}-{\varvec{\xi }}\), that is the direction of the non-local force \(d{\varvec{f}}\left( {\varvec{x,\xi }}\right) \). The resultant of non-local forces on the volume element in \({\varvec{x}}\) is evaluated by integrating Eq. (16) over the domain \({\mathcal {B}}\) of the body:

$$\begin{aligned} d{\varvec{f}}\left( {\varvec{x}}\right) =dV({\varvec{x}}){\tilde{E}}\int _{\mathcal {B}}\left[ {\varvec{u}}({\varvec{\xi }}) - {\varvec{u}}({\varvec{x}})\right] {\varvec{G}}\left( {\varvec{x,\xi }}\right) dV({\varvec{\xi }}) \end{aligned}$$
(17)

It follows that the static equilibrium of the generic volume element in \({\varvec{x}}\) is written as

$$\begin{aligned} {\tilde{E}}\int _{\mathcal {B}}\left[ {\varvec{u}}({\varvec{\xi }}) - {\varvec{u}}({\varvec{x}})\right] {\varvec{G}}\left( {\varvec{x,\xi }}\right) dV({\varvec{\xi }})=-{\varvec{b}}({\varvec{x}}) \end{aligned}$$
(18)

being \({\varvec{b}}({\varvec{x}})\) the external volume force field per unit volume. The model in Eq. (18) belongs to class of integral or strong non-local models. Since non-local forces depend of the displacement field, the peridynamic model is considered a displacement based non-local model. The main advantage of this model is its mechanical representation since the non-local interactions in Eq. (16) may be interpreted by the approach described in [17, 19]. In order to substantiate this statement, consider a non-local peridynamic unbounded rod with cross section area A. Due to the relative motion \(u(\xi ) - u(x)\), an axial force \(df_x\left( x,\xi \right) \) is applied to the volume element \(dV(x)=Adx\):

$$\begin{aligned} df_x\left( x,\xi \right) ={\tilde{E}}A^2\left[ u(\xi ) - u(x)\right] g\left( x-\xi \right) dx d\xi \end{aligned}$$
(19)

and a force \(df_x\left( \xi ,x\right) =-df_x\left( x,\xi \right) \) is applied to the volume element \(dV(\xi )=Ad\xi \). From a mechanical point view, the force in Eq. (19) mutually exerted between the volume elements in x and in \(\xi \) can be modeled as an elastic interaction due to the presence of a long-range spring connecting the two volumes dV(x) and \(dV(\xi )\), as depicted in Fig. 1. To the long-range spring is associated a non-local distance-dependent stiffness \(k_{nl}(x-\xi )={\tilde{E}}A^2g(x-\xi )dxd\xi \).

Fig. 1
figure 1

Mechanical representation of the non-local interaction between two volume elements of the rod

Full size image

Considering Eq. (19) the equilibrium equation of the generic volume element dV(x) of an unbounded rod may be written as

$$\begin{aligned} {\tilde{E}}A^2\int _{-\infty }^{\infty }\left[ u(\xi ) - u(x)\right] g\left( x-\xi \right) d\xi =-b(x) \end{aligned}$$
(20)

being u the axial displacement and b(x) the axial force per unit length.

The peridynamic model has been proven powerful in solving elastic problems in presence of discontinuity of the domain and it is suitable for the modeling of non-local elastic phenomena. However, since no contact forces are taken into account in the peridynamic formulation, the classical notion of Cauchy stress is not contemplated in this theory. Further, in presence of bounded domain non-local BCs, cumbersome to handle, appears. By assuming the attenuation function in Eq. (9) and considering the unbounded rod introduced before, inversion of the equilibrium equation Eq. (20) in the Fourier domain leads to an ordinary differential equation. That is,

$$\begin{aligned} {\tilde{E}}A^2L_c^2u^{(2)}(x)=-b(x)+L_c^2b^{(2)}(x) \end{aligned}$$
(21)

Analogously to the case of strain driven and stress driven models, a strong non-local formulation with the peridynamic approach (Eq. (20)) is equivalent to a weak non-local formulation (Eq. (21)). It is noticed that Eq. (21) is of the same order of the classical differential equation of a local elastic rod. If a rod with finite length L is considered, by means of some manipulations the integral model again corresponds to a differential equation given as:

$$\begin{aligned} {{\tilde{E}}A^2L_c^2}\left[ \gamma (x)u^{(2)}(x)+2\gamma ^{(1)}(x)u^{(1)}(x)\right] =-b(x)+L_c^2b^{(2)}(x) \end{aligned}$$
(22)

where

$$\begin{aligned} \gamma (x)=\int _0^L g(x,\xi ) d\xi \end{aligned}$$
(23)

with the following constitutive BCs

$$\begin{aligned} \left\{ \begin{aligned}&u^{(1)}(0)=\frac{b(0)-L_cb^{(1)}(0)}{{\tilde{E}}A^2L_c \gamma (0)}\\&u^{(1)}(L)=-\frac{b(L)+L_cb^{(1)}(L)}{{\tilde{E}}A^2L_c \gamma (L)} \end{aligned}\right. \end{aligned}$$
(24)

Notice that as the boundaries of the integral in Eq. (23) go to \(\pm \infty \), \(\gamma (x)\rightarrow 1\) and \(\gamma ^{(1)}(x)\rightarrow 0\), and Eq. (22) reverts to Eq. (21).

3.4 Mixture models

The formulations described in the previous Sections may be further enriched by considering both non-local interactions, as modeled in the different approaches, and contact forces between volume elements as in the classical Cauchy continuum. These model are labeled as mixture models since they involve both local and non-local contributions in the definition of the governing equations.

For an unbounded non-local strain driven rod, such a strategy may result in the adoption of the following constitutive equation

$$\begin{aligned} N (x)=\beta E A\varepsilon (x)+(1-\beta )\int _{-\infty }^{\infty } g(x-\xi )k_a(\xi )\varepsilon (\xi )d\xi \end{aligned}$$
(25)

where \(0\leqslant \beta \leqslant 1\) weight the amount of local and non-local contributions. The model in Eq. (25) overcome the drawbacks related to constitutive BCs of the pure strain driven model and has been adopted in several studies [5, 8,9,10, 13,14,15, 23]. However both for unbounded and bounded domains, the constitutive Eq. (25) is equivalent to an ordinary differential equation with additional constitutive BCs, as already observed for the pure strain driven model in Sect. 3.1. The equivalent differential formulation and the associated constitutive BCs are not reported here for brevity, see [59] for more details. Therefore, while the mathematical structure of the direct constitutive law in Eq. (25) is a proper representation of a mechanics involving long range elastic interaction, the equivalent differential equation involves only local operators that do not appear capable of describing the presence of non-local actions.

Similarly, a mixture model may be formulated also by assuming the non-local forces are modeled with the stress driven approach. For an unbounded rod, the stress driven mixture model may be written as

$$\begin{aligned} \varepsilon (x)=\beta \frac{\sigma (x)}{E}+(1-\beta )\int _{-\infty }^{\infty } g(x-\xi )\frac{N (\xi )}{k_a(\xi )}d\xi )\varepsilon (\xi )d\xi \end{aligned}$$
(26)

With the same approach, the peridynamic model may be enriched with contact forces, resulting in the so-called mechanically-based non-local model, following the approach widely studied in several papers [17, 19,20,21,22]. For an unbounded non-local mechanically-based rod model, the governing equation reads

$$\begin{aligned} \beta EA u^{(2)}(x)+(1-\beta ){\tilde{E}}A^2\int _{-\infty }^{\infty }\left[ u(\xi ) - u(x)\right] g\left( x-\xi \right) d\xi =-b(x) \end{aligned}$$
(27)

The advantage of the model in Eq. (27) is that when formulated for bounded domains the non-local contributions to BCs are negligible in comparison with local BCS. It follows that the same BCs valid for problems involving classical local elastic continua still hold for the mechanically based non-local model. However, also in this case the strong non-local formulation is equivalent to a differential equation involving only local differential operators (see [59] for more details).

4 Unified formulation with power-law attenuation function

In the previous section the main integral non-local models have been introduced and discussed in the particular case of bi-exponential attenuation function, that is the most common choice in many theoretical study involving integral non-local models. It has been shown that all the considered integral non-local models can be reduced to differential non-local models, with additional constitutive boundary conditions, when the attenuation function is selected as the bi-exponential one in Eq. (9). From a mechanical point of view, the correspondence between a strong non-local model and a weak non-local model is not desirable, since it suggests that the integral non-local model may not be really considered as strong non-local models. On the other hand, this undesirable feature of integral non-local models appears to be related to the particular choice of the attenuation function g. In order to substantiate this statement, the case of integral non-local models is compared with the problem of viscoelasticity that can be interpreted as non-locality in time and has some analogy with non-local elasticity.

4.1 Analogy between non-locality and viscoelasticity (non-locality in time).

In linear viscoelasticity external actions on a viscoelastic materials produce effects delayed in time. In this light, viscoelastic materials are considered materials with memory, in the sense that past external input on the viscoelastic material has still consequences at the actual time. Based on this observation, viscoelasticity may be interpreted as a sort of non-locality in the time domain.

Fig. 2
figure 2

Maxwell (a) and KV (b) viscoelastic models

Full size image

The first viscoelastic models were formulated by combining the features of purely elastic solid and of purely viscous fluids [53], resulting in the well known Maxwell (series spring-dashpot) and Kelvin-Voigt (KV) (parallel spring-dashpot) models (see Fig. 2). The differential governing equation of these models are given as follows:

$$\begin{aligned}&{\dot{\sigma }}(t)+\sigma (t)/\tau _0=E{\dot{\varepsilon }}(t) \end{aligned}$$
(28a)
$$\begin{aligned}&{\dot{\varepsilon }}(t)+\varepsilon (t)/\tau _0=\sigma (t)/\eta \end{aligned}$$
(28b)

being E the spring stiffness, \(\eta \) the dashpot viscosity and \(\tau _0=E/\eta \) is the so-called characteristic time. Linear viscoelastic materials in time domain are commonly characterized by the creep and relaxation functions. The creep function J(t) describes the increasing behavior of the strain when a constant stress is applied, while the relaxation function R(t) provides the decreasing behavior of the stress due to an applied constant strain. As an example, the relaxation function for the Maxwell model is easily evaluated from Eq. (28a) by assuming \(\varepsilon (t)=U(t)\), being U(t) the unit step function:

$$\begin{aligned} R(t)=E\exp \left( -\frac{t}{\tau _0}\right) \end{aligned}$$
(29)

while the creep function for the KV model is found from Eq. (28b) by assuming \(\sigma (t)=U(t)\):

$$\begin{aligned} J(t)=\left( 1-\exp \left( -\frac{t}{\tau _0}\right) \right) /E \end{aligned}$$
(30)

In the theory of linear viscoelasticity the Boltzmann superposition principle is assumed valid. Accordingly, the response in terms of stress (strain) history due to an applied strain (stress) can be evaluated by means of a convolution integral, where the relaxation (creep) function is the kernel:

$$\begin{aligned}&\sigma (t)=\int _0^t R(t-\tau ){\dot{\varepsilon }}(\tau )d\tau \end{aligned}$$
(31a)
$$\begin{aligned}&\varepsilon (t)=\int _0^t J(t-\tau ){\dot{\sigma }}(\tau )d\tau \end{aligned}$$
(31b)

Similarly to the case of non-local elasticity, Eq. (31a) is a strain driven Boltzmann equation while Eq. (31b) is its stress driven counterpart.

If the creep and relaxation function in Eqs. (29) and (30) are assumed in Eq. (31a) and Eq. (31b), respectively, these integral formulations are equivalent to the differential formulation in Eqs. (28). Although the mathematical form of Eqs. (31) suggests long memory of the materials, the equivalent differential equations in Eqs. (28) appear only suitable to describe memory effects in short time scales. Further, the parameter \(\tau _0\) governs the time necessary for the creep function and for the relaxation function to reach a constant value. In other words, it is a measure of the length of the memory of the material. In the analogy between viscoelasticity and non-local elasticity, the parameter \(\tau _0\) has a role analogous of that of the parameter \(L_c\).

Although simple model as the Maxwell and the KV exhibit memory effects qualitatively similar to those of real materials, several studies have been devoted to the development of viscoelastic models able of capturing the real behavior of viscoelastic materials (see e.g. [53] and related references). In the field of classical viscoelasticity, the memory capability has been improved by defining more complex viscoelastic models, constituted by different arrangements of springs and dashpots as Standard Linear Solid (SLS) models and other [41]. As the number of springs and dashpots increases, the number of exponential function in the creep and relaxation functions, each with a different characteristic time, increases as well, producing models capable of capturing more pronounced viscoelastic effects. Correspondingly, the maximum order of (time) derivatives in the associated differential equation increases. To the limit, this strategy has lead to the formulation of viscoelastic models such as the Kelvin Voigt and Maxwell chains [53] or hierarchical models of Schiessel and Blumen [55] and of Heymans and Bauwens [54]. Thank to the high number of time scale in the creep and relaxation functions, these models are characterized by very long memory, but are also difficult to calibrate due to the high number of mechanical parameters. On the other hand, from the observation that creep and relaxation of real materials are well fitted by power-law function of real order instead of exponential, the fractional order viscoelastic models, typically featuring power-law creep and relaxation functions, have become very popular in the last decades. The introduction of power-law creep and relaxation functions in Eq. (31) naturally leads to integro-differential operator of real order, namely fractional derivatives and integrals. Indeed, it is not a case if fractional models have been proved to be equivalent to hierarchical arrangements of infinite springs and dashpots [54,55,56]. It follows that the fractional models are more powerful in reproducing the real behavior of viscoelastic materials because the power-law creep and relaxation functions feature a very high number, or even infinite, of time scales [57, 58]. Further, inversion of a fractional viscoelastic constitutive laws always results in mathematical law involving fractional order operator, that are non-local by definition, instead of local differential operators. Specifically, if we assume the following kernel functions

$$\begin{aligned}&R(t)=\frac{E_\beta t^{-\beta }}{\Gamma (1-\beta )} \end{aligned}$$
(32a)
$$\begin{aligned}&J(t)=\frac{ t^{\beta }}{E_\beta \Gamma (1+\beta )} \end{aligned}$$
(32b)

in the Boltzmann integrals (31) we obtain fractional constitutive laws. That is,

$$\begin{aligned}&\sigma (t)=E_\beta \left( _0^CD_t^\beta \varepsilon \right) (t) \end{aligned}$$
(33a)
$$\begin{aligned}&\varepsilon (t)=\frac{1}{E_\beta } \left( _0I_t^\beta \sigma \right) (t) \end{aligned}$$
(33b)

where \(E_\beta \) is a viscoelastic modulus with anomalous dimension and \(0\leqslant \beta \leqslant 1\). Eqs. (32) is the only case where the Boltzmann strain driven and stress driven relations are related each other by a simple differentiation/integration operation. On the basis of the analogy between non-local elasticity and viscoelasticity, the concepts discussed with regard to viscoelasticity may be useful also in the field of non-local elasticity. It is clear that integral non-local models reverts to differential models with weak non-locality due to choice of kernels characterized by a single length scale. From these observations, a possible strategy to formulate proper strong non-local models may be to imitate the fractional viscoelasticity approach, as shown in the next section.

4.2 Integral non-local models with power-law kernel—unbounded domain

With the purpose of defining non-local models featuring strong non-locality properties in both the direct and the inverse formulation, power-law attenuation function may be assumed. This is not a novelty, since in the recent literature different works considering power-law attenuation function exist. A common result of this choice is that the governing equation of the non-local problem is governed by fractional integro-differential operators [43, 44]. However in the following, some interesting relationship are found.

Consider a unbounded rod with cross section area A and non-local modulus \({\tilde{E}}_{\alpha }\). If the non-local behavior of the bar is modeled with the peridynamic approach, the governing equation of the bar is that in Eq. (20). Following the fractional approach in viscoelasticity, a power-law attenuation kernel is selected. Since the attenuation function must satisfy symmetry, positivity and limit impulsivity, the power-law attenuation function is arranged as follows:

$$\begin{aligned} g(x)=\frac{|x|^{-1-\alpha }}{2\nu _c(\alpha )} \end{aligned}$$
(34)

with \(1<\alpha \leqslant 2\). By inserting Eq. (34) into Eq. (20) the following governing equation is obtained:

$$\begin{aligned} {\tilde{E}}_{\alpha }A^2 \left( ^RD^\alpha u\right) (x)=-b(x) \end{aligned}$$
(35)

where \(\left( ^RD^\alpha u\right) (x)\) is the Riesz fractional derivative introduced in Eq. (3b). The model in Eq. (35) has a clear mechanical interpretation and, given the specific form assumed for the power-law attenuation function, as \(\alpha \rightarrow 2\) it reverts to classical governing equation of local rod. Indeed, the Riesz derivative reverts to second order derivative as \(\alpha \rightarrow 2\). Further, the presence of the Riesz fractional derivative allows to easily define the inverse of the relationship in Eq. (35). To this aim, notice that the inverse of the Riesz fractional derivative of order \(\alpha \) is the Riesz fractional integral of order \(\alpha \) introduced in Eq. (3a). It follows that, given the external axial force per unit length b(x), the response in terms of displacements for the model in Eq. (35), is found as

$$\begin{aligned} u(x)=-\frac{\left( ^RI^\alpha b\right) (x)}{{\tilde{E}}_\alpha A^2} \end{aligned}$$
(36)

Remarkably, inversion of the strong non-local formulation in Eq. (35) leads to the strong formulation in Eq. (36). This is quite different from what it has been shown in Section 3.3 where the peridynamic model with exponential attenuation function has been found to be equivalent to weak non-local model. The governing Eq. (36) describes a mechanics in which the displacement at a given location x depends of the volume forces distribution in the whole domain of the body, mirroring the mechanics associated with Eq. (35). Specifically, the kernel of the Riesz integral in Eq. (36) is of order \(\alpha -1>0\). It follows that the displacement at a given location x is more influenced by volume forces applied far from x than those applied in location close to x. However, since the model in Eq. (36) is found by exact inversion of the power peridynamic model (35), the increasing behavior of the kernel in Eq. (36) is in agreement with the mechanics described in Fig. 1.

The adoption of power-law attenuation function produce other very interesting results. Consider the strain driven model in Eq. (8). With the assumption of the following power-law kernel

$$\begin{aligned} g(x)=\frac{|x|^{1-\alpha }}{2\nu _c(\alpha )}, \end{aligned}$$
(37)

with \(1<\alpha \leqslant 2\), the integral in Eq. (8) reverts to the Riesz integral of order \(2-\alpha \) and the strain driven model may be written as

$$\begin{aligned} N(x)=E_\alpha A \left( ^RI^{2-\alpha } \varepsilon \right) (x) \end{aligned}$$
(38)

being \(E_\alpha \) the anomalous Young modulus. Unlike the strain driven model with exponential attenuation function, inversion of the model in Eq. (38) leads to an integral non-local model in the form

$$\begin{aligned} \varepsilon (x)=\frac{1}{E_\alpha A} \left( ^RD^{2-\alpha } N\right) (x) \end{aligned}$$
(39)

Interestingly, the formulation in Eq. (39) can be interpreted as the stress driven model in Eq. (13) with the following attenuation function

$$\begin{aligned} g(x)=\frac{|x|^{\alpha -3}}{2\nu _c(-\alpha )} \end{aligned}$$
(40)

Remarkably, not only the inverse of a non-local integral model with power-law kernel is still an integral non-local model, but also with this choice the strain driven and the stress driven models are one the inverse of the other. Notice that since \(1<\alpha \leqslant 2\) the order of fractional integral in Eq. (38) and the fractional derivative in Eq. (39) are of order \(0\leqslant 2-\alpha <1\). Further, as \(\alpha \rightarrow 2\) both the power-law strain driven model in Eq. (38) and the power-law stress driven model in Eq. (39) reverts to the Hooke law of elasticity. In agreement with exponential kernel strain driven and stress driven models, the attenuation functions in Eq. (37) and in Eq. (40) are both decreasing. Indeed, in Eq. (37) \(-1\leqslant 1-\alpha <0\) and in Eq. (40) \(-2<\alpha -3\leqslant -1\).

The choice of the orders of the power-law kernels in Eq. (37) and Eq. (40) is not casual because generates some more interesting relationship between integral non-local models. To this regard, consider the power-law strain driven model in Eq. (38). The Riesz integral of order \(2-\alpha \) may be written as a summation of left and right RL integrals (see Eq. (3a)), that is

$$\begin{aligned} N(x)=\frac{E_\alpha A}{2\cos (\alpha \pi /2)} \left[ \left( _{-\infty }I_x^{2-\alpha } \varepsilon \right) (x) + \left( _xI_\infty ^{2-\alpha } \varepsilon \right) (x) \right] \end{aligned}$$
(41)

Since \(\varepsilon (x)=u^{(1)}(x)\), the RL fractional integrals of order \(2-\alpha \) coalesces with the Caputo fractional derivatives of order \(\alpha -1\) as in the following

$$\begin{aligned} \begin{aligned} \left( _{-\infty }I_x^{2-\alpha } \varepsilon \right) (x)&=\frac{1}{\Gamma (2-\alpha )}\int _{-\infty }^x (x-\xi )^{1-\alpha }\varepsilon (\xi )d\xi \\&=\frac{1}{\Gamma (2-\alpha )}\int _{-\infty }^x \frac{u^{(1)}(\xi )}{(x-\xi )^{\alpha -1}}d\xi =\left( _{-\infty }^CD_x^{\alpha -1}u\right) (x) \end{aligned} \end{aligned}$$
(42)

for the left sided fractional operator, but analogous relationship holds for the right sided definitions. In view of Eq. (6a) and considering that for \(x\rightarrow -\infty : u(x)=0\) the following relationship holds

$$\begin{aligned} \left( ^C_{-\infty }D_x^{\alpha -1}u\right) (x)=\left( _{-\infty }D_x^{\alpha -1}u\right) (x) \end{aligned}$$
(43)

and analogous relationship is valid between the right sided Caputo derivative of order \(\alpha -1\) and the right sided RL derivative of order \(\alpha -1\). It follows that, remembering Eq. (3b), Eq. (38) may be written as

$$\begin{aligned} N(x)=E_\alpha A\left( ^RD^{\alpha -1}u(x)\right) \end{aligned}$$
(44)
Fig. 3
figure 3

Equilibrium of a rod element

Full size image

The Riesz integral of order \(2-\alpha \) of the strain is then equivalent to Riesz derivative of order \(\alpha -1\) of the displacement. At this point, consider the equilibrium equation of a rod element as in Fig. 3

$$\begin{aligned} N^{(1)}(x)=-b(x) \end{aligned}$$
(45)

Combination of Eq. (44) with Eq. (45) leads to the following governing equation

$$\begin{aligned} E_\alpha A \left( ^RD^\alpha u\right) (x)=-b(x) \end{aligned}$$
(46)

If we assume that \({\tilde{E}}_{\alpha }=E_\alpha /A\), then Eq. (46) coalesces with Eq. (35) related to the power-law peridynamic model. Some remarkable consequences descend from this finding:

  • The choice of power-law attenuation functions ensures that the non-local models considered in this paper are characterized by strong non-locality in both integral and differential form. Indeed, as in viscoelasticity power-law time kernels are able to represents long memory effects, in non-locality power-law space kernels are able to simulate long-range interactions.

  • If the power-law attenuation functions of each strong non-local model considered in this study are properly chosen, the strain driven, the stress driven and peridynamic model for an unbounded rod are all equivalent to each other.

  • Due to the equivalence of the power-law peridynamic model with the strain driven and stress driven models with proper selected power-law kernels, the mechanics associated with the peridynamic model can be associated also with the strain driven and stress driven models.

  • The power-law peridynamic model can be obtained starting from the power-law stress driven model and considering standard equilibrium equations as in Eq. (45). It follows that the axiomatic definition of Cauchy stress is preserved for the power-law peridynamic model.

  • The peridynamic model is defined directly in terms of equilibrium equation and in general the associated constitutive law, namely the stress-strain relationship, is not available. For the specific case of the power-law attenuation function, instead, the constitutive law associated with the peridynamic model is constituted by the power-law strain driven model in Eq. (38) or, equivalently, the power-law stress driven model in Eq. (39).

Therefore, the adoption of power-law strong non-local models appears to be a suitable strategy for the definition of an universally recognized formulation of non-local mechanics. However, this is actually at the theoretical stage since some limitations arise when the proposed strategy is applied to bounded domains. Indeed, for bounded domains, the equivalences described in Sect. 2 between Riesz fractional operators and the sum of left sided and right sided RL or Caputo operators do not hold anymore. Also, the Riesz fractional derivative in bounded domain is not the inverse of the Riesz fractional integral in the same bounded domain. These drawbacks have partially faced up in [44], where a fractional order strong non-local models has coherently formulated for bounded domains. Indeed, the Riesz fractional derivative in bounded domain may be written in terms of the sum of left sided and right sided Marchaud fractional derivatives [42], defined as the sum of a convolution integral with power-law kernel and a non-integral term. However, in order to give a suitable mechanical interpretation to the additional non-integral terms, long-range springs between boundaries and between boundaries and volume elements have been introduced. While long-range springs connecting volume elements may be qualitatively associated to intermolecular interactions, long-range springs involving boundaries have not a clear physical correspondence. Moreover, this approach [44] does not allow to find for bounded domains the relationship found in the present study between different existing strong non-local approaches. In order to overcome these drawbacks in the future other theoretical developments are needed, as well as accurate experimental observations capable of validating power-law non-local models.

5 Conclusions and discussions

A mechanically consistent non-local formulation based on fractional operators has been presented in this paper. The proposed strong non-local model has been derived from a peridynamic physical scheme where long-range interactions are taken into account. Following this approach the stress-strain relation is ruled by a Fredholm integral equation where the kernel is an attenuation function. This function rules how long-range interactions decay in the non-local continuum. It has been shown that if the long range forces decay proportional to a specific space-dependent power-law function the stress-strain relation is ruled by fractional differential or integral operator. Specifically, in the proposed non-local formulation for unbounded domain the stress is proportional to the Riesz fractional integral of the strain while the strain is proportional to the Riesz fractional derivative of the stress. Both the involved operators are convolution integrals and the selected power-law kernel assures strong non-local interactions. By the proposed unified non-local stress-strain relation based on the fractional operators it has been proven that non-local stress driven and non-local strain driven models are fully consistent each another as it happens in fractional viscoelasticity. As in fact in the latter case the stress history is related to the strain history (strain driven) by the Caputo’s fractional derivative while the strain history is related to the stress history (stress driven) by the inverse operator, namely the RL fractional integral. Exactly the same thing happens in non-local elasticity by assuming that the long range interactions are power-law and also in this case stress driven and strain driven are ruled by inverse operators each another giving a physically consistent model. Some concluding remarks and useful outcomes have been derived and discussed considering the unbounded non-local rod.