Multimodal vibration suppression of nonlinear Euler–Bernoulli beam by multiple time-delayed vibration absorbers

Abstract

For a nonlinear beam under broadband excitations, the multimodal nonlinear resonance phenomena will be induced. To suppress the multimodal nonlinear resonances, the multiple time-delayed vibration absorbers (TDVAs) are introduced. The optimal time-delayed parameters of the TDVAs are determined by the proposed multimodal equal-peak principle consisting of three design criteria. In the proposed three criteria, the stability criterion ensures the stability of the equilibrium state for the system; the extremes equal criterion figures out the time-delayed parameters to realize the equal resonance peaks around each concerned mode; the minimum peak criterion can obtain the optimal time-delayed parameters for the minimum resonance peaks. The results show that the TDVAs designed by the proposed multimodal equal-peak principle consisting of three criteria could simultaneously suppress the resonance peaks of the beam around multiple modes to the equal and minimum values. Besides, the equal resonance peaks are much lower than the absorbers without time-delayed feedback under the same mass constraint. The proposed TDVAs and the multimodal equal-peak principle have wide application prospects in suppressing the multimodal vibrations for nonlinear continuous systems with broad frequency band and large amplitudes excitation in the fields of civil engineering and aerospace.

Appendices

Appendix A

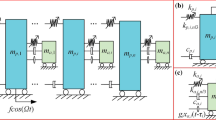
The Galerkin truncation is adopted to discretize the partial differential equation Eq. (1), the deflection of the beam can be represented by a finite sum as

$$w\left( {s,t} \right) \approx \sum\limits_{{p = 1}}^{P} {\phi _{p} \left( s \right)q_{p} \left( t \right)} ,$$

(20)

where $P$ is the number of modes retained. $q_{p} \left( t \right)$ and $\phi _{p} \left( s \right)$ are the pth generalized coordinate and mode shape function. For hinged-hinged supported beam, the mode shape function is given as follow

$$\phi _{p} \left( s \right) = \sqrt 2 \sin \left( {\frac{{p\pi s}}{l}} \right).$$

(21)

The mode shape function satisfies the orthogonality conditions as

$$\int_{0}^{l} {\rho A\phi _{{p_{1} }} \left( s \right)\phi _{{p_{2} }} \left( s \right)ds} = \left\{ \begin{gathered} \rho Al,\qquad p_{1} = p_{2} , \hfill \\ 0,\qquad\quad p_{1} \ne p_{2} . \hfill \\ \end{gathered} \right.$$

(22)

Assuming the beam is subjected to the harmonic concentrated excitation with amplitude $f$ and frequency $\Omega$

$$F_{e} = f\cos \left( {{\Omega }t} \right).$$

(23)

Substituting Eq. (20) into Eq. (1), multiplying both sides by the mode function $\phi _{p} \left( s \right)$, then integrating the result along the length of the beam l, one can obtain $P + N$ Galerkin-reduced equations

$$\begin{gathered} M_{p} \ddot{q}_{p} + C_{p} \dot{q}_{p} + K_{p} q_{p} - \int_{0}^{l} {\left\{ {\frac{{EA}}{{2l}}\left[ {\int_{0}^{l} {\left( {\sum\limits_{{p = 1}}^{P} {\phi ^{\prime}_{p} \left( s \right)q_{p} } } \right)^{2} ds} } \right]\sum\limits_{{p = 1}}^{P} {\phi ^{\prime\prime}_{p} \left( s \right)q_{p} } } \right\}\phi _{p} \left( s \right)ds} \hfill \\ + \sum\limits_{{i = 1}}^{P} {m_{i} \ddot{v}_{i} \left( t \right)\phi _{p} \left( {s_{i} } \right)} = F_{p} ,{\text{ }}p = 1,2,...,P, \hfill \\ m_{i} \ddot{v}_{i} + k_{i} \left[ {v_{i} - \sum\limits_{{p = 1}}^{P} {\phi _{p} \left( {s_{i} } \right)q_{p} } } \right] + c_{i} \left[ {\dot{v}_{i} - \sum\limits_{{p = 1}}^{P} {\phi _{p} \left( {s_{i} } \right)\dot{q}_{p} } } \right] - g_{i} v_{i} \left( {t - \tau _{i} } \right) = 0,{\text{ }}i = 1,2,...,N, \hfill \\ \end{gathered}$$

(24)

where the pth modal mass, damping, stiffness and force are

$$\begin{gathered} M_{p} = \int_{0}^{l} {\rho A\phi _{p}^{2} \left( s \right)ds} , \hfill \\ C_{p} = \int_{0}^{l} {c\phi _{p}^{2} \left( s \right)ds} , \hfill \\ K_{p} = \int_{0}^{l} {EI\left[ {\phi ^{\prime\prime}_{p} \left( s \right)} \right]^{2} ds} = \int_{0}^{l} {EI\phi _{p} ''''\left( s \right)\phi _{p} \left( s \right)ds} , \hfill \\ F_{p} = f\cos \left( {\Omega t} \right)\phi _{p} \left( {s_{f} } \right). \hfill \\ \end{gathered}$$

(25)

Introducing the dimensionless transform parameters as.

$\bar{t} = \bar{\omega }_{1} t = \sqrt {\frac{{K_{1} }}{{M_{1} }}} t$,$\bar{x}_{p} = \frac{{q_{p} K_{1} }}{f}$,$\bar{y}_{i} = \frac{{v_{i} K_{1} }}{f}$,$\bar{\omega }_{p} = \sqrt {\frac{{K_{p} }}{{M_{p} }}} = \sqrt {\frac{{K_{p} }}{{M_{1} }}}$,$\bar{\eta }_{i} = \sqrt {\frac{{k_{i} }}{{m_{i} }}}$,$\bar{\zeta }_{p} = \frac{{C_{p} }}{{2\sqrt {M_{1} K_{1} } }}$,$\bar{\gamma }_{i} = \frac{{c_{i} }}{{2\sqrt {m_{i} k_{i} } }}$,$\bar{\lambda }_{p} = \frac{{\bar{\omega }_{p} }}{{\bar{\omega }_{1} }}$,$\bar{\beta }_{i} = \frac{{\bar{\eta }_{i} }}{{\bar{\omega }_{1} }}$,$\bar{\mu }_{i} = \frac{{m_{i} }}{{M_{1} }}$,$\bar{\tau }_{i} = \omega _{1} \tau _{i}$,$\bar{\Omega } = \frac{\Omega }{{\omega _{1} }}$,$\bar{g}_{i} = \frac{{g_{i} }}{{\bar{\mu }_{i} K_{i} }}$,

substituting the above dimensionless parameters into Eq. (24), then dropping the bar of the dimensionless symbols $\bar{t}$, $\bar{x}_{p}$, $\bar{y}_{i}$, $\bar{\omega }_{p}$, $\bar{\eta }_{i}$, $\bar{\zeta }_{p}$, $\bar{\gamma }_{i}$, $\bar{\lambda }_{p}$, $\bar{\beta }_{i}$, $\bar{\mu }_{i}$, $\bar{\tau }_{i}$, $\bar{\Omega }$ and $\bar{g}_{i}$ for convenience, we can derive Eq. (2).

For $P = 2$, $N = 2$ in the case from Sect. 3.1 to Sect. 3.3, the matrix and vector of Eq. (4) are

$${\mathbf{M}} = \left[ {\begin{array}{*{20}c} 1 & 0 & {\mu _{1} \phi _{1} \left( {s_{1} } \right)} & {\mu _{2} \phi _{1} \left( {s_{2} } \right)} \\ 0 & 1 & {\mu _{1} \phi _{2} \left( {s_{1} } \right)} & {\mu _{2} \phi _{2} \left( {s_{2} } \right)} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],$$

(26)

$${\mathbf{C}} = \left[ {\begin{array}{*{20}c} {2\zeta _{1} } & 0 & 0 & 0 \\ 0 & {2\zeta _{2} } & 0 & 0 \\ { - 2\beta _{1} \gamma _{1} \phi _{1} \left( {s_{1} } \right)} & { - 2\beta _{1} \gamma _{1} \phi _{2} \left( {s_{1} } \right)} & {2\beta _{1} \gamma _{1} } & 0 \\ { - 2\beta _{2} \gamma _{2} \phi _{1} \left( {s_{2} } \right)} & { - 2\beta _{2} \gamma _{2} \phi _{2} \left( {s_{2} } \right)} & 0 & {2\beta _{2} \gamma _{2} } \\ \end{array} } \right],$$

(27)

$${\mathbf{K}} = \left[ {\begin{array}{*{20}c} {\lambda _{1}^{2} } & 0 & 0 & 0 \\ 0 & {\lambda _{2}^{2} } & 0 & 0 \\ { - \beta _{1}^{2} \phi _{1} \left( {s_{1} } \right)} & { - \beta _{1}^{2} \phi _{2} \left( {s_{1} } \right)} & {\beta _{1}^{2} } & 0 \\ { - \beta _{2}^{2} \phi _{1} \left( {s_{2} } \right)} & { - \beta _{2}^{2} \phi _{2} \left( {s_{2} } \right)} & 0 & {\beta _{2}^{2} } \\ \end{array} } \right],$$

(28)

$${\mathbf{F}}_{n} = \left[ {\begin{array}{*{20}c} {f_{{nl,1}} } & {f_{{nl,2}} } & 0 & 0 \\ \end{array} } \right]^{{\text{T}}} ,$$

(29)

$${\mathbf{X}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {y_{1} } & {y_{2} } \\ \end{array} } \right]^{{\text{T}}} ,$$

(30)

$$F = \left[ {\begin{array}{*{20}c} {\phi _{1} \left( {s_{f} } \right)\cos \left( {\Omega t} \right)} & {\phi _{2} \left( {s_{f} } \right)\cos \left( {\Omega t} \right)} & 0 & 0 \\ \end{array} } \right]^{{\text{T}}} .$$

(31)

The last matrix on the left side of Eq. (11) is

$${\mathbf{\bar{G}}}_{\tau } \left( {{\mathbf{p}}_{\tau } } \right) = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & { - g_{1} \lambda _{1}^{2} {\text{e}}^{{ - s\tau _{1} }} } & 0 \\ 0 & 0 & 0 & { - g_{2} \lambda _{2}^{2} {\text{e}}^{{ - s\tau _{2} }} } \\ \end{array} } \right).$$

(32)

Appendix B

The Averaging Method is adopted to derive the approximate steady-state harmonic response of Eq. (2). The approximate solution is assumed as

$$\begin{gathered} \left\{ \begin{gathered} x_{p} = A_{{p,1}} \cos \left( {\Omega t} \right) + A_{{p,2}} \sin \left( {\Omega t} \right) \hfill \\ \dot{x}_{p} = - A_{{p,1}} \Omega \sin \left( {\Omega t} \right) + A_{{p,2}} \Omega \cos \left( {\Omega t} \right) \hfill \\ \end{gathered} \right.,\,\quad p = 1,2...,P, \hfill \\ \left\{ \begin{gathered} y_{i} = B_{{i,1}} \cos \left( {\Omega t} \right) + B_{{i,2}} \sin \left( {\Omega t} \right) \hfill \\ \dot{y}_{i} = - B_{{i,1}} \Omega \sin \left( {\Omega t} \right) + B_{{i,2}} \Omega \cos \left( {\Omega t} \right) \hfill \\ \end{gathered} \right.,\qquad i = 1,2...,N, \hfill \\ \end{gathered}$$

(33)

where $A_{{p,1}}$, $A_{{p,2}}$, $B_{{i,1}}$, $B_{{i,{\text{2}}}}$ are slow-varying functions of $t$. Substituting Eq. (33)into Eq. (2), reducing the trigonometric function and dropping the higher-order harmonic terms, then equating the coefficients of sine and cosine terms to zero, one can derive the amplitude modulation equations

$${\mathbf{v^{\prime}}} = \Gamma \left( {{\mathbf{v}},{\Omega },{\mathbf{p}},{\mathbf{p}}_{\tau } } \right),$$

(34)

where ${\mathbf{v}} = \left\{ {A_{{p,1}} ,A_{{p,2}} ,B_{{i,1}} ,B_{{i,2}} } \right\}^{{\text{T}}}$, ${\mathbf{p}}_{\tau } = \left\{ {g_{i} ,\tau _{i} } \right\}$, $p = 1,2...,P$, $i = 1,2...,N$. The response of the system can be obtained by solving the equation

$$\Gamma \left( {{\mathbf{v}},\Omega ,{\mathbf{p}},{\mathbf{p}}_{\tau } } \right) = 0.$$

(35)

The non-dimensional frequency response curve (FRC) of the beam at the location point $s_{c}$ is

$$a\left( {s_{c} } \right) = \sqrt {\left( {\sum\limits_{{p = 1}}^{P} {A_{{p,1}} \phi _{p} \left( {s_{c} } \right)} } \right)^{2} + \left( {\sum\limits_{{p = 1}}^{P} {A_{{p,2}} \phi _{p} \left( {s_{c} } \right)} } \right)^{2} } .$$

(36)

The stability of the steady-state solution is determined by the corresponding eigenvalues of the Jacobian matrix. The Jacobian matrix of Eq. (34) for the response coefficients ${\mathbf{v}}$, time-delayed parameters ${\mathbf{p}}_{\tau } = \left\{ {g_{i} ,\tau _{i} } \right\},i = 1,...,N$ at the resonance frequencies $\Omega$ is

$${\mathbf{J}}= \frac{{\partial \Gamma }}{{\partial {\mathbf{v}}}} = {\mathbf{J}}\left( {{\mathbf{v}},\Omega ,{\mathbf{p}} ,{\mathbf{p}}_{\tau }} \right).$$

(37)

Appendix C

Fig. 11

The incremental-iteration procedure of the multimodal equal-peak principle for multimodal vibration suppression

Figure 11 shows the procedure of realizing the multimodal equal-peak principle for nonlinear multimodal vibration suppression. In Fig. 11, ${\mathbf{p}}_{0}$ is structural parameters of LTVAs designed by the generalized fixed-points theory as Eqs. (7)and (9), ${\mathbf{p}}$ is structural parameters of TDVAs that may be different from ${\mathbf{p}}_{0}$ due to some designable requirements in practical, ${\mathbf{p}}_{\tau }$ is the time-delayed parameters of the TDVAs, ${\mathbf{R}}$ is the harmonic coefficients at all the resonance frequencies, $P$ is the modes retained for the nonlinear beam and $N$ is the number of the TDVAs with $N \le P$. By applying the procedure as Fig. 11, the optimal ${\mathbf{p}}_{\tau }$ with the minimum peaks around the concerned modes are obtained for the structural parameters of the TDVA p with increasing force amplitudes $f$. The main steps of the procedure are shown as follows:

Step 0: Start the optimization procedure.

Step 1: For $f = 0$, the beam degenerates into a linear one, the LTVAs with the structural parameters determined by Eqs. (7)and (9), the initial time-delayed parameters ${\mathbf{p}}_{\tau } = 0$, can suppress the peaks for the first two modes to the equal values (see Fig. 3a for details). For the case from Sect. 3.1 to 3.3, the structural parameters of the LTVAs are

$${\mathbf{p}}_{0} = \left\{ {\beta _{1}^{0} ,\beta _{2}^{0} ,\gamma _{1}^{0} ,\gamma _{2}^{0} ,f} \right\} = \left\{ {0.9813,3.9962,0.0838,0.019,0} \right\}.$$

(38)

The vector in Eq. (38) are selected as the initial structural parameters of TDVAs. The initial responses at all the resonance frequencies are determined by analyzing the degenerated linear system, as

$${\mathbf{R}}= \left\{ {{\mathbf{v}}_{1}^{0} ,\Omega _{1}^{0} ,{\mathbf{v}}_{2}^{0} ,\Omega _{2}^{0} ,{\mathbf{v}}_{3}^{0} ,\Omega _{3}^{0} ,{\mathbf{v}}_{4}^{0} ,\Omega _{4}^{0} } \right\},$$

(39)

where ${\mathbf{v}}_{i}^{0}$, $i = 1,2,3,4$ is the vector of harmonic coefficients at the resonance frequency $\Omega _{i}^{0}$,$i = 1,2,3,4$ for the degenerated linear system. The values of the symbols in Eq. (39) are

$$\Omega _{1}^{0} = 0.942472,\Omega _{2}^{0} = 1.0399,\Omega _{3}^{0} = 3.95392,\Omega _{4}^{0} = 4.04211,$$

(40)

$$\begin{gathered} {\mathbf{v}}_{1}^{0} = \left\{ {2.55104,3.63826, - 0.0549022,0.000147676, - 12.2292,33.4645,2.61703,3.85413} \right\}, \hfill \\ {\mathbf{v}}_{2}^{0} = \left\{ { - 1.84668,3.99843, - 0.0558216,0.000204213, - 19.0512, - 22.2499,2.06857,4.28766} \right\}, \hfill \\ {\mathbf{v}}_{3}^{0} = \left\{ { - 0.0479816,0.0356316, - 1.20162, - 2.03108,0.0019377, - 0.00640033,35.144, - 68.9216} \right\}, \hfill \\ {\mathbf{v}}_{4}^{0} = \left\{ { - 0.04907, - 0.0308489,1.09542, - 2.00446,0.00620877, - 0.000535353,39.8503,60.1105} \right\}. \hfill \\ \end{gathered}$$

(41)

In this case, the structural parameters of TDVAs are

$${\mathbf{p}} = \left\{ {\beta _{1} ,\beta _{2} ,\gamma _{1} ,\gamma _{2} ,f} \right\} = \left\{ {1.5\beta _{1}^{0} ,1.5\beta _{2}^{0} ,0.3\gamma _{1}^{0} ,0.3\gamma _{2}^{0} ,0\sim10^{5} } \right\}.$$

(42)

The structural parameters of TDVA should be updated from ${\mathbf{p}}_{0}$ to ${\mathbf{p}}$ in $k_{t}$ steps, each augmentation is $~{\mathbf{\Delta p}} = {{\left( {{\mathbf{p}} - {\mathbf{p}}_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{{\rm {p}}}} - {\mathbf{{\rm {p}}}}_{0} } \right)} {k_{t} }}} \right. \kern-\nulldelimiterspace} {k_{t} }}$. The elements $\beta _{1}$, $\beta _{2}$, $\gamma _{1}$, $\gamma _{2}$, $f$ are sequentially updated. It should be noted that every update step of the parameters from ${\mathbf{p}}_{0}$ to ${\mathbf{p}}$ may lead to the divergence of the two peaks around each mode (see Fig. 4 for details). The introduced time-delayed parameters ${\mathbf{p}}_{\tau } = \left\{ {g_{i} ,\tau _{i} } \right\},i = 1,...,N$ are calculated in Step 2 to retune the resonance peaks equally and minimum.

Step 2: In the kth update process of structural parameters, ${\mathbf{p}}_{k} = {\mathbf{p}}_{{k - 1}} + {\mathbf{\Delta p}}$, where the subscript k indicates the kth iteration. Update the optimal time-delayed parameters ${\mathbf{p}}_{\tau }$, the responses at resonance frequencies ${\mathbf{R}}$ for suppressing the peaks around all the modes concerned as follows:

Step 2.1: Update ${\mathbf{p}}_{\tau }$ for suppressing the peaks around the ith mode.

Fix $\tau _{j}$ for $j \ne i$, update other parameters in ${\mathbf{p}}_{\tau }$ by Eq. (14), the resonance peaks around the first mode are tuned equally by the extremes equal condition Eq. (18) and suppressed to the minimum values by the minimum peak condition Eq. (19). Meanwhile, the stability of the equilibrium state should be ensured by the stability condition Eq. (12). The optimal ${\mathbf{p}}_{\tau }$ and corresponding ${\mathbf{R}}$ are selected as the initial values for suppressing the resonance peaks around the next mode.

Step 2.2: Repeat Step 2.1 for other concerned modes, update ${\mathbf{p}}_{\tau }$ and ${\mathbf{R}}$, then obtain the optimal ${\mathbf{p}}_{\tau }$ for suppressing the peaks around all modes concerned.

Step 3: At the end of kth loop, the structural parameters of TDVAs ${\mathbf{p}}_{k}$, the force amplitudes $f$, corresponding optimal time-delayed parameters ${\mathbf{p}}_{\tau }$ are selected as the initial values of (k + 1)th loop and then repeat Step 2.

Step 4: End the loop if $k = k_{t}$ and obtain the structural parameters of TDVAs ${\mathbf{p}}$, the optimal time-delayed parameters ${\mathbf{p}}_{\tau }$, harmonic coefficients at all resonance frequencies ${\mathbf{R}}$ with various force amplitudes $f$.