Skip to main content
SpringerLink
Log in

Prediction of exit profile distortion in forward extrusion process using Riemann mapping theorem and upper bound method

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

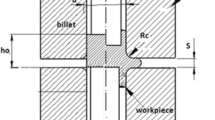
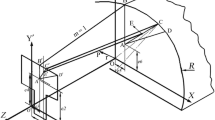
One of the substantial topics in the forward extrusion process is using theoretical methods to predict the exit profile distortion due to the non-symmetry of sections or the off-centricity of die cavity. In this paper, a new approach based on the Riemann mapping theorem and upper bound method is developed to obtain the velocity field and the strain distribution. Then, the strain distribution is determined for the die with off-centered square sections. Afterwards, the exit profile curvature is calculated using an approach based on elastic–plastic bending of beams. Theoretical results are compared to the results yielded through experimental and finite element simulation and validated. Subsequently, the effect of various parameters such as relative die length and friction factor is examined on the amount of the exit profile distortion. The results show that the obtained theory can be used to predict the strain distribution and the exit profile distortion in addition to the process pressure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Abbreviations

Bz, Dz :

Arbitrary curve boundary and its area

Bw, Dw :

Unite circle boundary and its area

E:

Elastic modulus

J:

Total power consumption

K:

Strength coefficient

Kxz, Kyz :

Exit profile curvature in XZ and YZ planes

L:

Die length

L/R:

Relative die length

M(u,q,t):

Function defining the velocity in the z direction

Pave :

Average extrusion pressure

R:

Radius of the billet

T:

Time

Wi :

Power due to internal deformation

Wx :

Power due to exit surface of velocity discontinuities

We :

Power due to entry surface of velocity discontinuities

Wf :

Power due to die–material interface friction

a:

Half of the square length

e1, e2 :

Off-centric positions in x and y directions

f(z):

Mapping power series

f, g, h:

Functions of u, q, and t, which representing position of control points in Cartesian coordinates

m:

Frictional factor

n:

Strain hardening exponent

u, q, t:

Dimensionless Parameters changing between 0 and 1

ye :

Distance of the yield point to the neutral axis

\(\varepsilon_{e}\) :

Strain at the yield point

\({\dot{\upvarepsilon }}_{\text{ij }}\) :

Components of strain rate

\(\varepsilon_{\text{x}}\), \(\varepsilon_{\text{y}}\), \(\varepsilon_{\text{z}}\) :

Strain components

\(\vartheta\) :

Poisson ratio

\(\rho\) :

Density

\(\rho_{{f,{\text{xz}}}}\), \(\rho_{{f,{\text{yz}}}}\) :

Final radius of profile curvature

References

  1. Yang DY, Lee CH (1978) Analysis of three-dimensional extrusion of sections through curved dies by conformal transformation. Int J Mech Sci 20(9):541–552. https://doi.org/10.1016/0020-7403(78)90012-7

    Article  MathSciNet  Google Scholar 

  2. Yang DY, Lange K (1984) Analysis of hydrofilm extrusion of three-dimensional shapes from round billets. Int J Mech Sci 26(1):1–19. https://doi.org/10.1016/0020-7403(84)90037-7

    Article  Google Scholar 

  3. Boer C, Schneider W, Eliasson B, Avitzur B (1980) An upper bound approach for the direct drawing of square section rod from round bar. In: Proceedings of the twentieth international machine tool design and research conference, Springer, pp 149–156. https://doi.org/10.1007/978-1-349-05172-4_17

  4. Gunasekera J, Hoshino S, Brown R (1980) Extrusion of non-circular sections through shaped dies. CIRP Ann 29(1):141–145. https://doi.org/10.1016/S0007-8506(07)61310-9

    Article  Google Scholar 

  5. Chitkara N, Abrinia K (1990) A generalised upper bound solution for three-dimensional extrusion of shaped sections using Cad-Cam bilinear surface dies. In: Proceedings of the twenty-eighth international, Springer, pp. 417–424. https://doi.org/10.1007/978-1-349-10890-9_57

  6. Celik K, Chitkara N (2000) Application of an upper bound method to off-centric extrusion of square sections, analysis and experiments. Int J Mech Sci 42(2):321–345. https://doi.org/10.1016/S0020-7403(98)00131-3

    Article  MATH  Google Scholar 

  7. Qi HY, Wang SX, Zhu HJ (2006) Similar extrusion and mapping optimization of die cavity modeling for special-shaped products. Trans Nonferrous Met Soc China 16(3):587–592. https://doi.org/10.1016/S1003-6326(06)60103-9

    Article  Google Scholar 

  8. Hongyuan Q, Keshan C, Wanhua S, Hengjun Z (2007) Vertical curve analysis of extruding die cavity and conformal mapping. J Rare Earths 25:375–378. https://doi.org/10.1016/S1002-0721(07)60509-2

    Article  Google Scholar 

  9. Ajiboye J, Adeyemi M (2007) Upper bound analysis for extrusion at various die land lengths and shaped profiles. Int J Mech Sci 49(3):335–351. https://doi.org/10.1016/j.ijmecsci.2006.08.017

    Article  Google Scholar 

  10. Assempour A, Hassannejadasl A (2009) Minimization of the exit profile curvature in non-symmetric T-shaped sections in the extrusion process. Mater Des 30(4):1350–1355. https://doi.org/10.1016/j.matdes.2008.06.038

    Article  Google Scholar 

  11. Abrinia K, Davarzani H (2012) A universal formulation for the extrusion of sections with no axis of symmetry. J Mater Process Technol 212(6):1355–1366. https://doi.org/10.1016/j.jmatprotec.2012.01.015

    Article  Google Scholar 

  12. Gordon W, Van Tyne C, Moon Y (2012) Minimizing distortion during extrusion using adaptable dies. Int J Mech Sci 62(1):1–17. https://doi.org/10.1016/j.ijmecsci.2012.05.006

    Article  Google Scholar 

  13. Gordon W, Van Tyne C, Moon Y (2013) Adaptable dies to minimize distortion in non-axisymmetric extrusions. Int J Mech Sci 77:65–81. https://doi.org/10.1016/j.ijmecsci.2013.09.008

    Article  Google Scholar 

  14. Abrinia K, Ghorbani M (2012) Theoretical and experimental analyses for the forward extrusion of nonsymmetric sections. Mater Manuf Processes 27(4):420–429. https://doi.org/10.1080/10426914.2011.577869

    Article  Google Scholar 

  15. Karami K, Abrinia K (2014) An analytical formulation as an alternative to FEM software giving strain and stress distributions for the three-dimensional solution of extrusion problems. Int J Adv Manuf Technol 71(1–4):653–665. https://doi.org/10.1007/s00170-013-5500-1%20

    Article  Google Scholar 

  16. Abrinia K, Farahmand P, Parchami-Sarghin M (2014) Formulation of a new generalized kinematically admissible velocity field with a variable axial component for the forward extrusion of shaped sections. Int J Adv Manuf Technol 70(5–8):1427–1435. https://doi.org/10.1007/s00170-013-5365-3

    Article  Google Scholar 

  17. Das R, Sarmah A, Lakshmi D, Sood A (2014) A finite element analysis on the effect of location of holes, die pockets and extrusion speed in multi-hole extrusion process. Proc Eng 97:1247–1253. https://doi.org/10.1016/j.proeng.2014.12.403

    Article  Google Scholar 

  18. Onlaghi SN, Assempour A (2015) On the minimization of the exit profile curvature in extrusion through multi-hole dies: a methodology and some verifications. Meccanica 50(5):1249–1261. https://doi.org/10.1007/s11012-014-0080-1

    Article  MathSciNet  Google Scholar 

  19. Tabatabaei SA, Abrinia K, Tabatabaei SM, Shahabadi M, Besharati MK (2015) Analytical modeling of the extrusion process using the electrostatics concept. Mech Mater 88:87–102. https://doi.org/10.1016/j.mechmat.2015.03.007

    Article  Google Scholar 

  20. Parghazeh A, Haghighat H (2016) Prediction of central bursting defects in rod extrusion process with upper bound analysis method. Trans Nonferrous Met Soc China 26(11):2892–2899. https://doi.org/10.1016/S1003-6326(16)64418-7

    Article  Google Scholar 

  21. Zhou W, Lin J, Dean TA, Wang L (2018) Feasibility studies of a novel extrusion process for curved profiles: experimentation and modelling. Int J Mach Tools Manuf 126:27–43. https://doi.org/10.1016/j.ijmachtools.2017.12.001

    Article  Google Scholar 

  22. Sheikhpour M (2012) Forward extrusion bearing design using upper bound. Dissertation, University of Tehran. https://thesis2.ut.ac.ir/thesisinfo/ThesisPdf15PagesFiles/2013-12/261316-15Page-.pdf

  23. Louhghalam A, Igusa T, Park C, Choi S, Kim K (2011) Analysis of stress concentrations in plates with rectangular openings by a combined conformal mapping–finite element approach. Int J Solids Struct 48(13):1991–2004. https://doi.org/10.1016/j.ijsolstr.2011.03.005

    Article  Google Scholar 

  24. Liang NW, Lai CH, Hsu CY, Chiang YC, Chang CC, Chen SL (2014) A conformal-mapping method for predicting the thermal properties of U-shaped borehole heat-exchangers. Geothermics 50:66–75. https://doi.org/10.1016/j.geothermics.2013.08.006

    Article  Google Scholar 

  25. Sahraei S (2018) Computation of plane potential flow past multi-element airfoils using conformal mapping, Dissertation, Wichita State University. https://soar.wichita.edu/bitstream/handle/10057/15424/d18021_Sahraei.pdf?sequence=1&isAllowed=y

  26. Planche T, Jung PM, Saminathan S, Baartman R, Basso MJ (2019) Conformal mapping approach to dipole shim design. Nucl Instrum Methods Phys Res Sect A 925:101–105. https://doi.org/10.1016/j.nima.2019.01.038

    Article  ADS  Google Scholar 

  27. Schinzinger R, Laura PA (2003) Conformal mapping: methods and applications. Courier Corporation, Mineola

    MATH  Google Scholar 

  28. El Megharbel A, El Nasser G, El Domiaty A (2008) Bending of tube and section made of strain-hardening materials. J Mater Process Technol 203(1–3):372–380. https://doi.org/10.1016/j.jmatprotec.2007.10.078

    Article  Google Scholar 

Download references

Funding

This study was funded by Babol Noshirvani University of Technology (grant number BNUT/370203/97).

Author information

Authors and Affiliations

  1. Advanced Materials Forming Research Center, Babol Noshirvani University of Technology, P.O.B. 484, Babol, Iran

    Majid Sheikhpour, Seyed Jamal Hosseinipour & Mohammad Javad Mirnia

Authors
  1. Majid Sheikhpour
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Seyed Jamal Hosseinipour
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammad Javad Mirnia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seyed Jamal Hosseinipour.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sheikhpour, M., Hosseinipour, S.J. & Mirnia, M.J. Prediction of exit profile distortion in forward extrusion process using Riemann mapping theorem and upper bound method. Meccanica 55, 1099–1118 (2020). https://doi.org/10.1007/s11012-020-01141-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-020-01141-1

Keywords

Search

Navigation