Double frictional receding contact problem for an orthotropic layer loaded by normal and tangential forces

Abstract

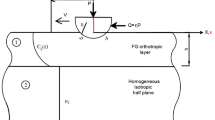
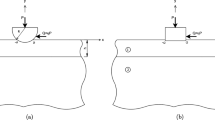
With the increasing research in the field of contact mechanics, different types of contact models have been investigated by many researchers by employing various complex material models. To ascertain the orthotropy effect and modeling parameters on a receding contact model, the double frictional receding contact problem for an orthotropic bilayer loaded by a cylindrical punch is taken into account in this study. Assuming plane strain sliding conditions, the governing equations are found analytically using Fourier integral transformation technique. Then, the resulting singular integral equations are solved numerically using an iterative method. The weight function describing the asymptotic behavior of the stresses are investigated in detail and powers of the stress singularities are provided. To control the trustworthiness and correctness of the analytical formulation and to compare the resulting stress distributions and contact boundaries, a numerically efficient finite element method was employed using augmented Lagrange contact algorithm. The aim of this paper is to investigate the orthotropy effect, modeling parameters and coefficients of friction on the surface and interface stresses, surface and interface contact boundaries, powers of stress singularities, weight function and to provide highly parametric benchmark results for tribological community in designing wear resistant systems.

Appendices

Appendix 1

Expressions for $C_{11}$, $C_{13}$, $C_{33}$ and $C_{55}$ appearing in Eq. (5)

$$\begin{aligned}&{{C}_{11}}=\frac{{{E}_{xx}}(-1+{{\nu }_{yz}}{{\nu }_{zy}})}{\varDelta } \end{aligned}$$

(30a)

$$\begin{aligned}&{{C}_{13}}=-\frac{{{E}_{xx}}({{\nu }_{zx}}+{{\nu }_{yx}}{{\nu }_{zy}})}{\varDelta } \end{aligned}$$

(30b)

$$\begin{aligned}&{{C}_{33}}=-\frac{{{E}_{zz}}(-1+{{\nu }_{xy}}{{\nu }_{yx}})}{\varDelta } \end{aligned}$$

(30c)

$$\begin{aligned}&{{C}_{55}}={{G}_{xz}} \end{aligned}$$

(30d)

where

$$\begin{aligned}&\varDelta =-1+{{\nu }_{xy}}({{\nu }_{yx}}+{{\nu }_{yz}}{{\nu }_{zx}})+{{\nu }_{yz}}{{\nu }_{zy}}+{{\nu }_{xz}}({{\nu }_{zx}}+{{\nu }_{yx}}{{\nu }_{zy}}) \end{aligned}$$

(31)

$$\begin{aligned}&{{\nu }_{yx}}={{\nu }_{xy}}\frac{{{E}_{yy}}}{{{E}_{xx}}}, {{\nu }_{zx}}={{\nu }_{xz}}\frac{{{E}_{zz}}}{{{E}_{xx}}}, {{\nu }_{zy}}={{\nu }_{yz}}\frac{{{E}_{zz}}}{{{E}_{yy}}} \end{aligned}$$

(32)

Appendix 2

Expressions for ${{k}_{11}}({{x}_{1}},{{t}_{1}})$, ${{k}_{12}}({{x}_{1}},{{t}_{2}})$, ${{k}_{21}}({{x}_{2}},{{t}_{1}})$, ${{k}_{22}}({{x}_{2}},{{t}_{2}})$ appearing in Eq. (17),

$$\begin{aligned}&{{k}_{11}}({{x}_{1}},{{t}_{1}})=\int \limits _{0}^{\infty }{\frac{I\ {{M}_{11}}(\xi )-{{\varphi }_{1}}}{{{\varphi }_{1}}}}\sin \xi ({{t}_{1}}-{{x}_{1}})d\xi \nonumber \\&\quad +{{\eta }_{1}}\int \limits _{0}^{\infty }{\frac{\ {{N}_{11}}(\xi )-{{\varphi }_{2}}}{{{\varphi }_{1}}}}\cos \xi ({{t}_{1}}-{{x}_{1}})d\xi \end{aligned}$$

(33)

$$\begin{aligned}&{{k}_{12}}({{x}_{1}},{{t}_{2}})=\int \limits _{0}^{\infty }{\frac{I\ {{M}_{12}}(\xi )}{{{\varphi }_{1}}}}\sin \xi ({{t}_{2}}-{{x}_{1}})d\xi \nonumber \\&\quad +{{\eta }_{1}}\int \limits _{0}^{\infty }{\frac{\ {{N}_{12}}(\xi )}{{{\varphi }_{1}}}}\cos \xi ({{t}_{2}}-{{x}_{1}})d\xi \end{aligned}$$

(34)

where

$$\begin{aligned}&{{M}_{11}}(\xi )=\sum \limits _{j=1}^{4}{\xi {{k}_{j}}A_{j}^{p1}}, {{N}_{11}}(\xi )=\sum \limits _{j=1}^{4}{\xi {{k}_{j}}A_{j}^{q1}},\nonumber \\&{{M}_{12}}(\xi )=\frac{{{C}_{66}}}{{{\mu }_{2}}}\sum \limits _{j=1}^{4}{\xi {{k}_{j}}A_{j}^{p2}}, {{N}_{12}}(\xi )=\frac{{{C}_{66}}}{{{\mu }_{2}}}\sum \limits _{j=1}^{4}{\xi {{k}_{j}}A_{j}^{q2}} \end{aligned}$$

(35)

$$\begin{aligned}&{{k}_{21}}({{x}_{2}},{{t}_{1}})=\int \limits _{0}^{\infty }{\frac{I\ {{M}_{21}}(\xi )}{{{\varphi }_{3}}}}\sin \xi ({{t}_{1}}-{{x}_{2}})d\xi \nonumber \\&\quad +{{\eta }_{2}}\int \limits _{0}^{\infty }{\frac{\ {{N}_{21}}(\xi )}{{{\varphi }_{3}}}}\cos \xi ({{t}_{1}}-{{x}_{2}})d\xi \end{aligned}$$

(36)

$$\begin{aligned}&{{k}_{22}}({{x}_{2}},{{t}_{2}})=\int \limits _{0}^{\infty }{\frac{I\ {{M}_{22}}(\xi )-{{\varphi }_{3}}}{{{\varphi }_{3}}}}\sin \xi ({{t}_{2}}-{{x}_{2}})d\xi \nonumber \\&\quad +{{\eta }_{2}}\int \limits _{0}^{\infty }{\frac{\ {{N}_{22}}(\xi )-{{\varphi }_{4}}}{{{\varphi }_{3}}}}\cos \xi ({{t}_{2}}-{{x}_{2}})d\xi \end{aligned}$$

(37)

where

$$\begin{aligned}&{{M}_{21}}(\xi )=\sum \limits _{j=1}^{4}{-\xi ({{k}_{j}}{{e}^{-\xi {{n}_{j}}{{h}_{1}}}}A_{j}^{p1}})\nonumber \\&\quad -\xi \left( B_{1}^{p1}{{e}^{-\xi {{h}_{1}}}}+B_{2}^{p1}\left( -{{h}_{1}}-\frac{{{\kappa }_{2}}}{\xi }\right) {{e}^{-\xi {{h}_{1}}}}\nonumber \right. \\&\quad \left. -B_{3}^{p1}{{e}^{\xi {{h}_{1}}}}-B_{4}^{p1}\left( -{{h}_{1}}+\frac{{{\kappa }_{2}}}{\xi }\right) {{e}^{\xi {{h}_{1}}}}\right) \end{aligned}$$

(38a)

$$\begin{aligned}&{{M}_{22}}(\xi )=\frac{{{C}_{66}}}{{{\mu }_{2}}}\sum \limits _{j=1}^{4}{-\xi ({{k}_{j}}{{e}^{-\xi {{n}_{j}}{{h}_{1}}}}A_{j}^{p2}})\nonumber \\&\quad -\xi \left( B_{1}^{p2}{{e}^{-\xi {{h}_{1}}}}\nonumber \right. \\&\quad \left. +B_{2}^{p2}\left( -{{h}_{1}}-\frac{{{\kappa }_{2}}}{\xi }\right) {{e}^{-\xi {{h}_{1}}}}\nonumber \right. \\&\quad \left. -B_{3}^{p2}{{e}^{\xi {{h}_{1}}}}-B_{4}^{p2}\left( -{{h}_{1}}+\frac{{{\kappa }_{2}}}{\xi }\right) {{e}^{\xi {{h}_{1}}}}\right) \end{aligned}$$

(38b)

$$\begin{aligned}&{{N}_{22}}(\xi )=\frac{{{C}_{66}}}{{{\mu }_{2}}}\sum \limits _{j=1}^{4}{-\xi ({{k}_{j}}{{e}^{-\xi {{n}_{j}}{{h}_{1}}}}A_{j}^{q2}})\nonumber \\&\quad -\xi \left( B_{1}^{q2}{{e}^{-\xi {{h}_{1}}}}+B_{2}^{q2}\left( -{{h}_{1}}-\frac{{{\kappa }_{2}}}{\xi }\right) {{e}^{-\xi {{h}_{1}}}}\nonumber \right. \\&\quad \left. -B_{3}^{q2}{{e}^{\xi {{h}_{1}}}}-B_{4}^{q2}\left( -{{h}_{1}}+\frac{{{\kappa }_{2}}}{\xi }\right) {{e}^{\xi {{h}_{1}}}}\right) \end{aligned}$$

(38c)

Expressions for $a_{j}$ and $b_{i}$ appearing in Eq. 18,

$$\begin{aligned}&{{a}_{1}}=\frac{\sqrt{{{C}_{11}}}}{\sqrt{2{{C}_{55}}}\left( C_{13}^{2}-{{C}_{11}}{{C}_{33}} \right) } \end{aligned}$$

(39a)

$$\begin{aligned}&{{a}_{2}}=-C_{13}^{2}+{{C}_{11}}{{C}_{33}}-2{{C}_{13}}{{C}_{55}} \end{aligned}$$

(39b)

$$\begin{aligned}&{{a}_{3}}=(C_{13}^{2}-{{C}_{11}}{{C}_{33}})\left( -{{C}_{11}}{{C}_{33}}+{{({{C}_{13}}+2{{C}_{55}})}^{2}} \right) \end{aligned}$$

(39c)

$$\begin{aligned}&{{a}_{4}}=\frac{1}{{{C}_{13}}+\sqrt{{{C}_{11}}{{C}_{33}}}} \end{aligned}$$

(39d)

$$\begin{aligned}&{{b}_{1}}=\frac{\kappa +1}{4\mu _2 }, {{b}_{2}}=\frac{1-\kappa }{4\mu _2 } \end{aligned}$$

(39e)