On Properties and Applications of Gaussian Subordinated Lévy Fields

Abstract

We consider Gaussian subordinated Lévy fields (GSLFs) that arise by subordinating Lévy processes with positive transformations of Gaussian random fields on some spatial domain. The resulting random fields are distributionally flexible and have in general discontinuous sample paths. Theoretical investigations of the random fields include pointwise distributions, possible approximations and their covariance function. As an application, a random elliptic PDE is considered, where the constructed random fields occur in the diffusion coefficient. Further, we present various numerical examples to illustrate our theoretical findings.

1 Introduction

Ample applications that are modeled stochastically require stochastic processes or random fields, which allow for discontinuities or possess higher distributional flexibility than the standard Gaussian model (see for example Hosseini (2017), Schoutens (2003) and Zhang and Kang (2004)). In case of a one-dimensional parameter domain, where the parameter often represents time, Lévy processes are widely used since they have in general discontinuous paths and allow for modeling of non-Gaussian behavior (see Ki (2013), Applebaum (2009) and Schoutens (2003)). For higher-dimensional parameter domains, some extensions of the Gaussian model have been proposed in the literature: The authors of Ernst et al. (2021) consider (smoothed) Lévy noise fields with high distributional flexibility and continuous realizations as coefficient of a PDE. Another generalization of the standard Gaussian model are hierarchical Gaussian random fields (see, for example, Cui et al. (2022) and the references therein). However, even though the constructed fields are more flexible than standard Gaussian random fields, they usually have continuous paths. This might be unnatural in some applications, like groundwater flow modeling in fractured porous media. In Li et al. (2016), the authors consider a spatially discontinuous random field model in the diffusion coefficient of a general elliptic PDE to model two-phase random media. In this reference, the piecewise constant diffusion coefficient is discontinuous along an interface, which divides the domain into two subdomains. In Barth and Stein (2018b), the authors propose a general random field model which allows for spatial discontinuities with flexible jump geometries and an arbitrary number of jump domains. However, in its general form, it not easy to investigate theoretical properties of the random field itself. In the context of Bayesian inversion, the level set approach combined with Gaussian random fields is often used as a discontinuous random field model (see, e.g. Iglesias et al. (2016), Dunbar et al. (2020) and Dunlop et al. (2017)). The distributional flexibility of the resulting model is, however, again restricted since the stochasticity is governed by the Gaussian field. Another extension of the Gaussian model has been investigated in the recent paper Merkle and Barth (2022b). The construction is motivated by the subordinated Brownian motion, which is a Brownian motion time-changed by a Lévy subordinator (i.e. a non-decreasing Lévy process). As a generalization, the authors consider Gaussian random fields on a higher-dimensional parameter domain subordinated by several independent Lévy subordinators. The constructed random fields allow for spatial jumps and display great distributional flexibility. However, the jump geometry is restricted in the sense that the jump interfaces are always rectangular and, hence, these fields are not invariant under rotation, which could be a major drawback in applications.

In this paper, we investigate another specific class of discontinuous random fields: the Gaussian subordinated Lévy fields (GSLFs). Motivated by the subordination of standard Lévy processes, the GSLF is constructed by subordination of a general real-valued Lévy process by a transformation of a Gaussian random field. The resulting fields allow for spatial discontinuities, are distributionally flexible and relatively easy to simulate. In contrast to the aforementioned subordinated Gaussian random field (see Merkle and Barth (2022b)), the GSLF allows for very flexible geometries of the jump domains and a more direct jump modeling via the underlying Lévy process (see Sect. 3). We prove a formula for the pointwise characteristic function, the covariance structure and present possible approximations of the GSLF. These results are of great importance for applications of the fields. Besides a theoretical investigation, we present numerical examples and introduce a possible application of the GSLF in the diffusion coefficient of an elliptic model equation. Such a problem arises, for instance, in models for subsurface/groundwater flow in heterogeneous/porous media (see Barth and Stein (2018b), Dagan et al. (1991), Naff et al. (1998) and the references therein).

The rest of the paper is structured as follows: In Sect. 2 we shortly introduce Lévy processes and Gaussian random fields, which are crucial for the definition of the GSLF in Sect. 3. The pointwise distribution of the random fields are investigated in Sect. 4, where we derive a formula for its (pointwise) characteristic function. Section 5 deals with numerical approximations of the GSLF, including an investigation of the approximation error and the pointwise distribution of the approximated fields. Our theoretical investigations are concluded in Sect. 6, where we derive a formula for the covariance function. In Sect. 7, we present various numerical examples which validate and illustrate the theoretical findings of the previous sections. Section 8 concludes the paper and highlights the application of the GSLF in the context of random elliptic PDEs, exploring theoretical as well as numerical aspects.

2 Preliminaries

In the following section, we give a short introduction to Lévy processes and Gaussian random fields following Merkle and Barth (2022b) since they are crucial elements for the construction of the Gaussian subordinated Lévy field. For more details we refer the reader to Adler and Taylor (2007); Ki (2013); Applebaum (2009). Throughout the paper, we assume that $(\Omega ,\mathcal {F},\mathbb {P})$ is a complete probability space.

2.1 Lévy Processes

We consider a Borel-measurable index set $\mathcal {T}\subseteq \mathbb {R}_+:=[0,+\infty )$. A stochastic process $\ell =(\ell (t),~t\in \mathcal {T})$ on $\mathcal {T}$ is a family of random variables on the probability space $(\Omega ,\mathcal {F},\mathbb {P})$ and $\ell$ is called Lévy process if $\ell (0)=0$ $\mathbb {P}-a.s.$, $\ell$ has independent and stationary increments and $\ell$ is stochastically continuous. The well known Lévy-Khinchin formula yields a parametrization of the class of Lévy processes by the so called Lévy triplet $(\gamma ,b,\nu )$.

Theorem 1

(Lévy-Khinchin formula, see (Applebaum 2009, Th. 1.3.3 and p. 29) Let $\ell$ be a real-valued Lévy process on $\mathcal {T}\subseteq \mathbb {R}_+:=[0,+\infty )$. There exist parameters $\gamma \in \mathbb {R}$, $b\in \mathbb {R}_+$ and a measure $\nu$ on $\mathbb {R}$ such that the characteristic function $\phi _{\ell (t)}$ of the Lévy process $\ell$ admits the representation

$$\begin{aligned} \phi _{\ell (t)}(\xi ) := \mathbb {E}(\exp (i\xi \ell (t))) = \exp (t\psi (\xi )),~\xi \in \mathbb {R}, \end{aligned}$$

for $t\in \mathcal {T}$. Here, $\psi$ denotes the characteristic exponent of $\ell$ which is given by

$$\begin{aligned} \psi (\xi ) = i\gamma \xi - \frac{b}{2}\xi ^2 + \int _{\mathbb {R}\setminus \{0\}}e^{i\xi y}-1-i\xi y\mathbbm {1}_{\{\vert y\vert \le 1\}}(y)\nu (dy),~\xi \in \mathbb {R}. \end{aligned}$$

Further, the measure $\nu$ satisfies

$$\begin{aligned} \int _\mathbb {R} \min (y^2,1) \,\nu (dy)<\infty , \end{aligned}$$

and is called Lévy measure and $(\gamma ,b,\nu )$ is called Lévy triplet.

2.2 Gaussian Random Fields

A random field defined over the Borel set $\mathcal {D}\subset \mathbb {R}^d$ is a family of real-valued random variables on the probability space $(\Omega ,\mathcal {F},\mathbb {P})$ parametrized by $\underline{x}\in \mathcal {D}$. The Gaussian random field defines an important example.

Definition 1

(see (Adler and Taylor 2007, Sc. 1.2)) A random field $(W(\underline{x}),\,\underline{x}\!\in \!\mathcal {D})$ on a d-dimensional domain $\mathcal {D}\subset \mathbb {R}^d$ is said to be a Gaussian random field (GRF) if, for any $\underline{x}^{(1)},$$\dots ,\!\underline{x}^{(n)} \!\in \! \mathcal {D}$ with $n\!\in \! \mathbb {N}$, the n-dimensional random variable $(W(\underline{x}^{(1)}),\dots ,W(\underline{x}^{(n)}))$ follows a multivariate Gaussian distribution. In this case, we define the mean function $\mu _W(\underline{x}^{(i)})$$:=\mathbb {E}(W(\underline{x}^{(i)}))$ and the covariance function $q_W(\underline{x}^{(i)},\underline{x}^{(j)}):=\mathbb {E}((W(\underline{x}^{(i)})-\mu _W(\underline{x}^{(i)}))(W(\underline{x}^{(j)})-\mu _W(\underline{x}^{(j)})))$, for $\underline{x}^{(i)},~\underline{x}^{(j)}\in \mathcal {D}$. The GRF W is called centered, if $\mu _W(\underline{x})=0$ for all $\underline{x}\in \mathcal {D}$.

Note that every GRF is determined uniquely by its mean and covariance function. The GRFs considered in this paper are assumed to be mean-square continuous, which is a common assumption (cf. Adler and Taylor (2007)). We denote by $Q:L^2(\mathcal {D})\rightarrow L^2(\mathcal {D})$ the covariance operator of W which is defined by

$$\begin{aligned} Q(\psi )(\underline{x})=\int _{\mathcal {D}}q_W(\underline{x},\underline{y})\psi (\underline{y})d\underline{y} \text {, for } \underline{x}\in \mathcal {D}, \end{aligned}$$

for $\psi \in L^2(\mathcal {D})$. Here, $L^2(\mathcal {D})$ denotes the Lebesgue space of all square integrable functions over $\mathcal {D}$ (see, for example, Adams and Fournier (2003)). If $\mathcal {D}$ is compact, it is well known that there exists a decreasing sequence $(\lambda _i,~i\in \mathbb {N})$ of real eigenvalues of Q with corresponding eigenfunctions $(e_i,~i\in \mathbb {N})\subset L^2(\mathcal {D})$ which form an orthonormal basis of $L^2(\mathcal {D})$ (see (Adler and Taylor 2007, Section 3.2) and (Werner 2011, Theorem VI.3.2 and Chapter II.3)). A GRF W is called stationary if the mean function $\mu _W$ is constant and the covariance function $q_W(\underline{x}^{(1)},\underline{x}^{(2)})$ only depends on the difference $\underline{x}^{(1)}-\underline{x}^{(2)}$ of the values $\underline{x}^{(1)},~\underline{x}^{(2)}\in \mathcal {D}$ and a stationary GRF W is called isotropic if the covariance function $q_W(\underline{x}^{(1)},\underline{x}^{(2)})$ only depends on the Euclidean length $\Vert \underline{x}^{(1)}-\underline{x}^{(2)}\Vert _2$ of the difference of the values $\underline{x}^{(1)},~\underline{x}^{(2)}\in \mathcal {D}$ (see Adler and Taylor (2007), p. 102 and p. 115).

Example 1

The Matérn-GRFs are a class of continuous GRFs which are commonly used in applications. For a certain smoothness parameter $\nu > 1/2$, correlation parameter $r>0$ and variance $\sigma ^2>0$, the Matérn-$\nu$ covariance function is defined by $q_M(\underline{x},\underline{y})=\rho _M(\Vert \underline{x}-\underline{y}\Vert _2)$, for $(\underline{x},\underline{y})\in \mathbb {R}_+^d\times \mathbb {R}_+^d$, with

$$\begin{aligned} \rho _M(s) = \sigma ^2 \frac{2^{1-\nu }}{\Gamma (\nu )}\Big (\frac{2s\sqrt{\nu }}{r}\Big )^\nu K_\nu \Big (\frac{2s\sqrt{\nu }}{r}\Big ), \text { for }s\ge 0. \end{aligned}$$

Here, $\Gamma (\cdot )$ is the Gamma function and $K_\nu (\cdot )$ is the modified Bessel function of the second kind (see (Graham et al. 2015, Section 2.2 and Proposition 1)). A Matérn-$\nu$ GRF is a centered GRF with covariance function $q_M$.

3 The Gaussian Subordinated Lévy Field

In this section, we define Gaussian subordinated Lévy fields. The construction of these fields is motivated by the subordination of standard Lévy processes: If $\ell$ denotes a Lévy process and S denotes a Lévy subordinator (i.e. a non-decreasing Lévy process), which is independent of $\ell$, the time-changed process

$$\begin{aligned} t\mapsto \ell (S(t)),~t\ge 0, \end{aligned}$$

is called subordinated Lévy process. It can be shown that this process is again a Lévy process (cf. (Applebaum 2009, Theorem 1.3.25)).

In order to construct the GSLF we consider a domain $\mathcal {D}\subset \mathbb {R}^d$ with $1\le d\in \mathbb {N}$. Let $\ell =(\ell (t),~t\ge 0)$ be a Lévy process, $W:\Omega \times \mathcal {D}\rightarrow \mathbb {R}$ be an $\mathcal {F}\otimes \mathcal {B}(\mathcal {D})$-$\mathcal {B}(\mathbb {R})$-measurable GRF which is independent of $\ell$ and $F:\mathbb {R}\rightarrow \mathbb {R_+}$ be a measurable, non-negative function. The Gaussian subordinated Lévy field is defined by

$$\begin{aligned} L(\underline{x}) = \ell (F(W(\underline{x}))), \text { for } \underline{x}\in \mathcal {D}. \end{aligned}$$

Note that assuming the GRF W to have continuous paths is sufficient to ensure joint measurability (see (Aliprantis and Border 2006, Lemma 4.51)). Since the Lévy process $\ell$ is in general discontinuous, the GSLF L has in general discontinuous paths. This is demonstrated in Fig. 1, which shows samples of the GSLF.

Fig. 1

Sample of a Matérn$-$1.5-GRF-subordinated Poisson process

Remark 1

Discontinuous random fields often serve as prior model to solve inverse problems with a Bayesian approach as an alternative to the standard Gaussian prior (see e.g. Iglesias et al. (2016); Hosseini (2017)). In these situations, the prior model is often set to be a Gaussian(-related) level-set function. One way to construct such a prior model is as follows:

$$\begin{aligned} u(\underline{x}) = \sum _{i=1}^n u_i\mathbbm {1}_{D_i}(\underline{x}),~\underline{x}\in \mathcal {D}, \end{aligned}$$

where $n\in \mathbb {N}$, $(u_i,~i=1,\dots ,n)\subset {\mathbb {R}}$ are fixed and

$$\begin{aligned} D_i=\{\underline{x}\in \mathcal {D} ~\vert ~c_{i-1}\le W(\underline{x})< c_i\}, \end{aligned}$$

with fixed levels $(c_i,~i=1,\dots ,n)\subset \mathbb {R}$ and a GRF W (see e.g. Dunlop et al. (2017); Dunbar et al. (2020)). The GSLF, as defined above, may be interpreted as a generalization of the Gaussian level-set function.

Remark 2

The GSLF is measurable: A Lévy process $\ell :\Omega \times \mathbb {R}_+\rightarrow \mathbb {R}$ has càdlàg paths and, hence, is $\mathcal {F}\otimes \mathcal {B}(\mathbb {R}_+)-\mathcal {B}(\mathbb {R})$-measurable (see (Protter 2004, Chapter 1, Theorem 30) and (Sato 2013, Chapter 6)). Further, since F and W are measurable by assumption, the mapping

$$\begin{aligned} (\omega ,\underline{x})\mapsto F(W(\omega ,\underline{x})), ~(\omega ,\underline{x})\in \Omega \times \mathcal {D}, \end{aligned}$$

is $\mathcal {F}\otimes \mathcal {B}(\mathcal {D})-\mathcal {B}(\mathbb {R}_+)$-measurable. It follows now by (Aliprantis and Border 2006, Lemma 4.49), that the mapping

$$\begin{aligned} (\omega ,\underline{x})\mapsto (\omega ,F(W(\omega ,\underline{x}))),~(\omega ,\underline{x})\in \Omega \times \mathcal {D}, \end{aligned}$$

is $\mathcal {F}\otimes \mathcal {B}(\mathcal {D})-\mathcal {F}\otimes \mathcal {B}(\mathbb {R}_+)$-measurable. Therefore, the GSLF

$$\begin{aligned} (\omega ,\underline{x})\mapsto \ell (\omega ,F(W(\omega ,\underline{x}))),~(\omega ,\underline{x})\in \Omega \times \mathcal {D}, \end{aligned}$$

is $\mathcal {F}\otimes \mathcal {B}(\mathcal {D})-\mathcal {B}(\mathbb {R})$-measurable (cf. (Aliprantis and Border 2006, Lemma 4.22)).

4 The Pointwise Characteristic Function of a GSLF

In the following section we derive a formula for the pointwise characteristic function of the GSLF, which determines the pointwise distribution entirely. Such a formula is especially valuable in applications, where distributions of a random field have to be fitted to data observed from real world phenomena. We start with a technical lemma on the computation of expectations of functionals of the GSLF.

Lemma 1

Let $\ell =(\ell (t),~t\ge 0)$ be a stochastic process with a.s. càdlàg paths and $W_+$ be a real-valued, non-negative random variable which is stochastically independent of $\ell$. Further, let $g:\mathbb {R}\rightarrow \mathbb {R}$ be a continuous function. It holds

$$\begin{aligned} \mathbb {E}(g(\ell (W_+))) = \mathbb {E}(m(W_+)), \end{aligned}$$

with $m(z):= \mathbb {E}(g(\ell (z)))$ for $z\in \mathbb {R}_+$.

Proof

The proof follows by the same arguments as the proof of (Merkle and Barth 2022b, Lemma 4.1). $\square$

Remark 3

Note that Lemma 1 also holds for complex-valued, continuous and bounded functions $g:\mathbb {R}\rightarrow \mathbb {C}$. Further, we emphasize that Lemma 1 also holds for an $\mathbb {R}_+^d$-valued random variable $W_+$ and a random field $(\ell (\underline{t}),~\underline{t}\in \mathbb {R}_+^d)$, independent of $W_+$, which is a.s. càdlàg in each variable, i.e. for $\mathbb {P}$-almost all $\omega \in \Omega$, it holds

$$\begin{aligned} \underset{n\rightarrow \infty }{lim}\ \ell (t_1^{(n)},\dots ,t_d^{(n)}) = \ell (t_1,\dots ,t_d), \end{aligned}$$

for $t_j^{(n)} \searrow t_j$, for $n\rightarrow \infty$, $j=1,\dots ,d$, and any $\underline{t}=(t_1,\dots ,t_d)\in \mathbb {R}_+^d$.

With Lemma 1 at hand, we are able to derive a formula for the pointwise characteristic function of the GSLF. This formula is of great importance for practical applications giving access to the pointwise distributional properties of the field.

Corollary 1

Let $\ell =(\ell (t),~t\ge 0)$ be a Lévy process with Lévy triplet $(\gamma ,b,\nu )$ and $W=(W (\underline{x}),~\underline{x} \in \mathcal {D})$ be an independent GRF with pointwise mean $\mu _W(\underline{x})=\mathbb {E}(W(\underline{x}))$ and variance $\sigma _W(\underline{x})^2:=Var(W(\underline{x}))$ for $\underline{x} \in \mathcal {D}$. Further, let $F:\mathbb {R}\rightarrow \mathbb {R}_+$ be measurable. It holds

$$\begin{aligned} \phi _{\ell (F(W(\underline{x})))}(\xi )&=\mathbb {E}\Big (\exp (i\xi \,\ell (F(W(\underline{x}))))\Big ) \\&=\frac{1}{\sqrt{2\pi \sigma _W(\underline{x})^2}}\int _\mathbb {R}exp\Big ( F(y)\psi (\xi )- \frac{(y-\mu _W(\underline{x}))^2}{2\sigma _W(\underline{x})^2}\Big ) dy, \end{aligned}$$

for $\underline{x}\in \mathcal {D}$, where $\psi$ denotes the characteristic exponent of $\ell$ defined by

$$\begin{aligned} \psi (\xi ) = i\gamma \xi - \frac{b}{2}\xi ^2 + \int _{\mathbb {R}\setminus \{0\}}e^{i\xi y}-1-i\xi y\mathbbm {1}_{\{\vert y\vert \le 1\}}(y)\nu (dy),~\xi \in \mathbb {R}. \end{aligned}$$

Proof

We consider a fixed $\underline{x}\in \mathcal {D}$ and use Lemma 1 with $g(\cdot )\!:=\! \exp (i\xi \cdot )$ and $W_+:=F$$(W(\underline{x}))$ to calculate

$$\begin{aligned} \mathbb {E}\Big (\exp (i\xi \,\ell (F(W(\underline{x}))))\Big ) = \mathbb {E}(g(\ell (W_+)) = \mathbb {E}(m(W_+)) = \mathbb {E}(m(F(W(\underline{x})))), \end{aligned}$$

where m is defined through

$$\begin{aligned} m(z) = \mathbb {E}(\exp (i\xi \ell (z)) = \exp (z\,\psi (\xi )),~z\in \mathbb {R}_+, \end{aligned}$$

by the Lévy-Khinchin formula (see Theorem 1). Hence, we obtain

$$\begin{aligned} \mathbb {E}\Big (\exp (i\xi \,\ell (F(W(\underline{x}))))\Big )&= \mathbb {E}\Big (\exp (F(W(\underline{x}))\psi (\xi ))\Big )\\&=\frac{1}{\sqrt{2\pi \sigma _W(\underline{x})^2}}\int _\mathbb {R}exp\Big ( F(y)\psi (\xi )- \frac{(y-\mu _W(\underline{x}))^2}{2\sigma _W(\underline{x})^2}\Big ) dy. \end{aligned}$$

$\square$

5 Approximation of the Fields

The GSLF may in general not be simulated exactly since in most situations it is not possible to draw exact samples of the corresponding GRF and the Lévy process. For applications of the GSLF, it is therefore of great interest how these fields may be approximated and how the corresponding approximation error may be quantified. In this section we answer both questions. We prove an approximation result for the GSLF where we approximate the GRF and the Lévy process separately. To be more precise, we approximate the Lévy processes using a piecewise constant càdlàg approximation on a discrete grid (see e.g. Barth and Stein (2018a) and the remainder of the current section). The GRF may be approximated by a truncated Karhuen-Loève-expansion or using values of the GRF simulated on a discrete grid, e.g. via Circulant Embedding (see, e.g. Barth and Stein (2018b); Abdulle et al. (2013); Teckentrup et al. (2013) resp. Graham et al. (2018a, 2018b)). Naturally, we have to start with some assumptions on the regularity of the GRF and the approximability of the Lévy process. For simplicity, we consider centered GRFs in this subsection.

Assumption 1

Let W be a zero-mean GRF on the compact domain $\mathcal {D}$. We denote by $q_W:\mathcal {D}\times \mathcal {D}\rightarrow \mathbb {R}$ the corresponding covariance function and by $((\lambda _i,e_i),~i\in \mathbb {N})$ the eigenpairs associated to the corresponding covariance operator Q (see Sect. 2.2).

• i We assume that the eigenfunctions are continuously differentiable and there exist positive constants $\alpha , ~\beta , ~C_e, ~C_\lambda >0$ such that for any $i\in \mathbb {N}$ it holds

  $$\begin{aligned} \Vert e_i\Vert _{L^\infty (\mathcal {D})}\le C_e,\Vert \nabla e_i\Vert _{L^\infty (\mathcal {D})}\le C_e i^\alpha ,~ \sum _{i=1}^ \infty \lambda _ii^\beta \le C_\lambda < + \infty . \end{aligned}$$

• ii $F:\mathbb {R}\rightarrow \mathbb {R}_+$ is Lipschitz continuous and globally bounded by $C_F>0$, i.e. $F(x)<C_F,$ $x\in \mathbb {R}$.

• iii $\ell$ is a Lévy process on $[0,C_F]$ with Lévy triplet $(\gamma ,b,\nu )$ which is independent of W. Further, we assume there exists a constant $\eta >1$ and càdlàg approximations $\ell ^{(\varepsilon _\ell )}$ of this process such that for every $s\in [1,\eta )$ it holds

  $$\begin{aligned} \mathbb {E}(\vert \ell (t)-\ell ^{(\varepsilon _\ell )}(t)\vert ^s)\le C_\ell \varepsilon _\ell ,~ t\in [0,C_F), \end{aligned}$$

  (1)

  for $\varepsilon _\ell >0$ and

  $$\begin{aligned} \mathbb {E}(\vert \ell (t)\vert ^s)\le C_{\ell }t^\delta ,~ t\in [0,C_F), \end{aligned}$$

  (2)

  with $\delta \in (0,1]$ and a constant $C_\ell >0$ which may depend on s but is independent of t and $\varepsilon _\ell$.

We continue with a remark on Assumption 1.

Remark 4

Assumtion 1 i is natural for GRFs and guarantees certain regularity properties for the paths of the GRF (see e.g. Barth and Stein (2018b); Merkle and Barth (2022c); Charrier (2011)). Equation (1) ensures that we can approximate the Lévy subordinators in an $L^s$-sense. This can be achieved under appropriate assumptions on the tails of the distribution of the Lévy processes, see (Barth and Stein 2018a, Assumption 3.6, Assumption 3.7, Theorem 3.21) and (Merkle and Barth 2022c, Section 7). There are several results in the direction of condition (2). For example, in Luschgy and Pagès (2008) and Deng and Schilling (2015), the authors formulate general assumptions on the Lévy measure which guarantee Eq. (2) and similar properties. Further, in Luschgy and Pagès (2008) the authors explicitly derive the rate $\delta$ in Eq. (2) for several Lévy processes. In (Brockwell and Schlemm 2013, Proposition 2.3), an exact polynomial time-dependence of the absolute moments of a Lévy process under the assumption that the absolute moment of the Lévy process exists up to a certain order was proven. In order to illustrate (2), we present a short numerical example: for three different Lévy processes, we estimate $\mathbb {E}(\vert \ell (t)\vert ^s)$ for $t=2^i$ with $i\in \{1,0,-1,\dots ,-16\}$ using $10^7$ samples of the process $\ell$ and different values for the exponent $s\ge 1$. The results are shown in Fig. 2, where the estimated moments $\mathbb {E}(\vert \ell (t)\vert ^s)$ are plotted against the time parameter t. The results clearly indicate that $\mathbb {E}(\vert \ell (t)\vert ^s) = \mathcal {O}(t)$, $t\rightarrow 0$ which implies (2) with $\delta =1$ in the considered examples.

Fig. 2

Estimated s-moment for different Lévy processes and different values of s. Top: Gamma(2,4)-process, middle: Poisson(5)-process, bottom: NIG(2,1,1)-process

We close this subsection with a remark on a possible way to construct approximations of Lévy processes.

Remark 5

One way to construct a càdlàg approximation $\ell ^{(\varepsilon _\ell )}\approx \ell$ is a piecewise constant extension of the values of the process on a discrete grid: assume $\{t_i,\! i\!=\!0\dots ,N_\ell \}$, with $t_0=0$ and $t_{N_\ell }=C_F$ is a grid on $[0,C_F]$ with $\vert t_{i+1}-t_i\vert =t_{i+1}-t_i=\varepsilon _\ell >0$ for $i=0,\dots ,{N_\ell }-1$ and $\{\ell (t_i),~i=0,\dots ,{N_\ell }\}$ are the values of the process $\ell$ on this grid. We define

$$\begin{aligned} \ell ^{(\varepsilon _\ell )} (t) = \sum _{i=1}^{N_\ell } \mathbbm {1}_{[t_{i-1},t_i)} (t) \,\ell (t_{i-1}),~t\in [0,C_F). \end{aligned}$$

Such a construction yields an admissible approximation in the sense of Assumption 1 iii for many Lévy processes (see e.g. (Merkle and Barth 2022c, Section 7) for the case of Poisson and Gamma processes). Note that the values of the process on the grid may be simulated easily for many Lévy processes using the independent and stationary increment property.

5.1 Approximation of the GRF

In this subsection, we shortly introduce two possible approaches to approximate the GRF W. In the following and for the rest of the section, we consider $\mathcal {D}=[0,D]^d$. Assumption 1 allows conclusions to be drawn on the spatial regularity of the GRF W. The next lemma on the approximation of the GRF W follows from the regularity properties of W (see Merkle and Barth 2022c, Lemma 4.4) and Charrier (2011)).

Lemma 2

Let $G^{(\varepsilon _W)}=\{(x_{i^{(1)}},\dots ,x_{i^{(d)}})\vert ~{i^{(1)}},\dots , {i^{(d)}}=0,\dots ,M_{\varepsilon _W}\}$ be a grid on $\mathcal {D}$ where $(x_i,~i=0,\dots ,M_{\varepsilon _W})$ is an equidistant grid on [0, D] with maximum step size $\varepsilon _W$. Further, let $W^{(\varepsilon _W)}$ be an approximation of the GRF W on the discrete grids $G^{(\varepsilon _W)}$ which is constructed by point evaluation of the random field W on the grid and multilinear interpolation between the grid points. Under Assumption 1 i, it holds for $n\in [1,+\infty )$:

$$\begin{aligned} \Vert W-W^{(\varepsilon _W)}\Vert _{L^n(\Omega ;L^\infty (\mathcal {D}))}&\le C(D,n,d)\varepsilon _W^\gamma \end{aligned}$$

for $\gamma < \min (1,\beta /(2\alpha ))$, where $\beta$ and $\alpha$ are the parameters from Assumption 1 i.

It follows by the Karhunen-Loève-Theorem (see e.g. (Adler and Taylor 2007, Section 3.2)) that the GRF W admits the representation

$$\begin{aligned} W(\underline{x}) = \sum _{i=1}^\infty \sqrt{\lambda _i} Z_i e_i(\underline{x}),~\underline{x}\in \mathcal {D}, \end{aligned}$$

with i.i.d. $\mathcal {N}(0,1)$-distributed random variables $(Z_i,~i\in \mathbb {N})$ and the sum converges in the mean-square sense, uniformly in $\underline{x}\in \mathcal {D}$. The Karhunen-Loève expansion (KLE) motivates another approach to approximate the GRF W: For a fixed cut-off index $N\in \mathbb {N}$, we define the approximation $W^{N}$ by

$$\begin{aligned} W^{N}(\underline{x}) = \sum _{i=1}^{N} \sqrt{\lambda _i} Z_i e_i(\underline{x}),~\underline{x}\in \mathcal {D}. \end{aligned}$$

(3)

Under Assumption 1 we can quantify the corresponding approximation error (cf. (Barth and Stein 2018b, Theorem 3.8)).

Lemma 3

Let Assumption 1 i hold. Then, it holds for any $N\in \mathbb {N}$ and $n\in [1,+\infty )$:

$$\begin{aligned} \Vert W-W^N\Vert _{L^n(\Omega ;L^\infty (\mathcal {D}))}&\le C(D,n,d)N^{-\frac{\beta }{2}}. \end{aligned}$$

Proof

It follows by (Barth and Stein 2018b, Theorem 3.8) that

$$\begin{aligned} \Vert W-W^N\Vert _{L^n(\Omega ;L^\infty (\mathcal {D}))}^2\le C(D,n,d) \sum _{i=N+1}^\infty \lambda _i, \end{aligned}$$

for all $N\in \mathbb {N}$. We use Assumption 1 i to compute

$$\begin{aligned} \sum _{i=N+1}^\infty \lambda _i = \sum _{i=N+1}^\infty \lambda _i i^{\beta } i^{-\beta }\le N^{-\beta }\sum _{i=N+1}^\infty \lambda _i i^{\beta }\le C_\lambda N^{-\beta }, \end{aligned}$$

which finishes the proof.$\square$

In the following, we denote by $W^N$ an approximation of the GRF of W. The notation is clear if we approximate the GRF by the truncated KLE. If we approximate W by sampling on a discrete grid (cf. Lemma 2), then we use $\varepsilon _W = 1/N$ and abuse notation to write $W^N = W^{(1/N)}$. Regardless of the choice between these two approaches, we thus obtain an approximation $W^N\approx W$ with

$$\begin{aligned} \Vert W-W^N\Vert _{L^n(\Omega ;L^\infty (\mathcal {D}))}&\le C(D,n,d)R(N), \end{aligned}$$

(4)

for $N\in \mathbb {N}$ and $n\in [1,+\infty )$, where $R(N)=N^{-\gamma }$ if we approximate the GRF by discrete sampling and $R(N)=N^{-\frac{\beta }{2}}$ if we approximate it by the KLE approach.

5.2 Approximation of the GSLF

We are now able to quantify the approximation error for the GSLF where both components, the Lévy process and the GRF, are approximated.

Theorem 2

Let Assumption 1 hold and assume an approximation $W^N\approx W$ of the GRF is given, as introduced in Sect. 5.1. For a given real number $1\le p<\eta$ and a globally Lipschitz continuous function $g:\mathbb {R}\rightarrow \mathbb {R}$, it holds

$$\begin{aligned} \Vert g(\ell ^{(\varepsilon _\ell )}(F(W^N))) - g(\ell (F(W)))\Vert _{L^p(\Omega ;L^p(\mathcal {D}))}\le C( \varepsilon _\ell ^{\frac{1}{p}} + R(N)^\frac{\delta }{p} ), \end{aligned}$$

for $N\in \mathbb {N}$ and $\varepsilon _\ell >0$, where $\delta$ is the positive constant from (2).

Proof

We calculate using Fubini’s theorem and the triangle inequality

$$\begin{aligned}&\Vert g(\ell ^{(\varepsilon _\ell )}(F(W^N))) - g(\ell (F(W)))\Vert _{L^p(\Omega ;L^p(\mathcal {D}))}\\&\le \Vert g(\ell ^{(\varepsilon _\ell )}(F(W^N))) - g(\ell (F(W^N)))\Vert _{L^p(\Omega \times \mathcal {D})} \\&~~~ + \Vert g(\ell (F(W^N))) - g(\ell (F(W)))\Vert _{L^p(\Omega \times \mathcal {D})}\\&=:I_1+I_2 \end{aligned}$$

Further, we use the Lipschitz continuity of g together with Lemma 1 to obtain for any $\underline{x}\in \mathcal {D}$

$$\begin{aligned}&\mathbb {E}(\vert g(\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x})))) - g(\ell (F(W^N(\underline{x}))))\vert ^p) \\&\le C_g\mathbb {E}(\vert \ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x}))) - \ell (F(W^N(\underline{x})))\vert ^p) = \mathbb {E}(m(F(W^N(\underline{x}))) \end{aligned}$$

with

$$\begin{aligned} m(z) = \mathbb {E}(\vert \ell (z)-\ell ^{(\varepsilon _\ell )}(z)\vert ^p)\le C_\ell \varepsilon _\ell \end{aligned}$$

for $z\in [0,C_F)$ by Assumption 1 iii. Therefore, we obtain

$$\begin{aligned} \mathbb {E}(\vert g(\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x})))) - g(\ell (F(W^N(\underline{x}))))\vert ^p)\le C_\ell \varepsilon _\ell , \end{aligned}$$

for all $\underline{x}\in \mathcal {D}$ and, hence,

$$\begin{aligned} I_1^p&= \int _\mathcal {D}\mathbb {E}(\vert g(\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x})))) - g(\ell (F(W^N(\underline{x})))) \vert ^p)d\underline{x}\\&\le D^d C_\ell \varepsilon _\ell . \end{aligned}$$

For the second summand we calculate using Lemma 1 and Remark 3 with $\tilde{\ell }(t_1,t_2)$ $:=\ell (t_1)-\ell (t_2)$ and $\tilde{W}_+:=(F(W(\underline{x})),F(W^N(\underline{x})))$

$$\begin{aligned} \mathbb {E}(\vert \ell (F(W(\underline{x}))) - \ell (F(W^N(\underline{x})))\vert ^p) = \mathbb {E}(\tilde{m}(F(W(\underline{x})),F(W^N(\underline{x})))), \end{aligned}$$

with

$$\begin{aligned} \tilde{m}(t_1,t_2) = \mathbb {E}(\vert \ell (t_1)-\ell (t_2)\vert ^p),~t_1,t_2\in [0,C_F). \end{aligned}$$

For $C_F> t_1\ge t_2\ge 0$, the stationarity of $\ell$ together with Assumption 1 iii yields

$$\begin{aligned} \tilde{m}(t_1,t_2)= \mathbb {E}(\vert \ell (t_1-t_2)\vert ^p) \le C_\ell \vert t_1-t_2\vert ^\delta . \end{aligned}$$

Further, for $0\le t_1\le t_2< C_F$ we have

$$\begin{aligned} \tilde{m}(t_1,t_2)= \mathbb {E}(\vert \ell (t_2)-\ell (t_1)\vert ^p)=\mathbb {E}(\vert \ell (t_2-t_1)\vert ^p) \le C_\ell \vert t_2-t_1\vert ^\delta . \end{aligned}$$

Overall, we obtain for any $\omega \in \Omega$ the pathwise estimate

$$\begin{aligned} \tilde{m}(F(W(\underline{x})),F(W^N(\underline{x})))&\le C_\ell \vert F(W(\underline{x})) - F(W^N(\underline{x}))\vert ^\delta , \end{aligned}$$

for any $\underline{x}\in \mathcal {D}$. We apply Hölder’s inequality and Eq. (4) to obtain

$$\begin{aligned} \mathbb {E}(\vert \ell (F(W(\underline{x}))) - \ell (F(W^N(\underline{x})))\vert ^p)&= \mathbb {E}(\tilde{m}(F(W(\underline{x})),F(W^N(\underline{x})))),\\&\le C_\ell \mathbb {E}(\vert F(W(\underline{x})) - F(W^N(\underline{x}))\vert ^\delta )\\&\le C_\ell \mathbb {E}(\vert F(W(\underline{x})) - F(W^N(\underline{x}))\vert )^\delta \\&\le C_\ell C_F\mathbb {E}(\vert W(\underline{x}) - W^N(\underline{x})\vert )^\delta \\&\le C_\ell C_F C(D,d)^\delta R(N)^{\delta }, \end{aligned}$$

for any $\underline{x}\in \mathcal {D}$. Finally, we use the Lipschitz contnuity of g to obtain:

$$\begin{aligned} I_2^p&= \int _\mathcal {D}\mathbb {E}(\vert g(\ell (F(W^N(\underline{x})))) - g(\ell (F(W(\underline{x})))) \vert ^p)d\underline{x}\\&\le C(C_\ell ,D,d,\delta ,C_F,C_g)R(N)^{\delta }. \end{aligned}$$

Overall, we end up with

$$\begin{aligned} \Vert g(\ell ^{(\varepsilon _\ell )}(F(W^N)))&- g(\ell (F(W)))\Vert _{L^p(\Omega ;L^p(\mathcal {D}))}\\ {}&\le C(C_\ell ,D,d,\delta ,C_F,C_g,p)(\varepsilon _\ell ^{\frac{1}{p}} + R(N)^{\frac{\delta }{p}}). \end{aligned}$$

$\square$

5.3 The Pointwise Distribution of the Approximated GSLF

In Sect. 4 we investigated the pointwise distribution of a GSLF and derived a formula for its pointwise characteristic function. In Sect. 5, we demonstrated how approximations of the Lévy process $\ell$ and the underlying GRF W may be used to approximate the GSLF and quantified the approximation error. This is of great importance especially in applications, since it is in general not possible to simulate the GRF or the Lévy process on their continuous parameter domains. The question arises how such an approximation affects the pointwise distribution of the field. For this purpose, we prove in the following a formula for the pointwise charateristic function of the approximated GSLF.

Corollary 2

We consider a GSLF with Lévy process $\ell$ and an independent GRF W. Let $\ell ^{(\varepsilon _\ell )}\approx \ell$ be a càdlàg approximation of the Lévy process and $W^N\approx W$ be an approximation of the GRF, where we assume that the mean $\mu _W$ of the GRF W is known and does not need to be approximated. For $\underline{x}\in \mathcal {D}$, the pointwise characteristic function of the approximated GSLF is given by

$$\begin{aligned} \phi _{\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x})))}(\xi ) =\mathbb {E}\Big (\exp (i\xi \ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x}))))\Big )=\mathbb {E}(\rho _{\ell ^{(\varepsilon _\ell )}}(F(W^N(\underline{x})),\xi )), \end{aligned}$$

for $\xi \in \mathbb {R}$, where

$$\begin{aligned} \rho _{\ell ^{(\varepsilon _\ell )}}(t,\xi ) = \mathbb {E}(\exp (i\xi \ell ^{(\varepsilon _\ell )}(t))), \end{aligned}$$

denotes the pointwise characteristic function of $\ell ^{(\varepsilon _\ell )}$. Further, consider the discrete grid $\{t_i,~i=0,\dots ,N_\ell \}$ with $t_0=0$, $t_{N_\ell }=C_F$ and $\vert t_{i+1}-t_i\vert =\varepsilon _\ell$, for $i=0,\dots ,N_\ell -1$.

If the Lévy process is approximated according to Remark 5 and the GRF is approximated with the truncated KLE, that is

$$\begin{aligned} W^N(\underline{x}) =\mu _W(\underline{x})+ \sum _{i=1}^N \sqrt{\lambda _i} Z_i e_i(\underline{x}) \approx \mu _W(\underline{x}) + \sum _{i=1}^\infty \sqrt{\lambda _i} Z_i e_i(\underline{x})=W(\underline{x}), \end{aligned}$$

for $\underline{x}\in \mathcal {D}$ with some $N\in \mathbb {N}$, i.i.d. standard normal random variables $(Z_i,~i\in \mathbb {N})$ and eigenbasis $((\lambda _i,e_i),~i\in \mathbb {N})$ corresponding to the covariance operator Q of W (cf. Section 5.1) and $F(\cdot )<C_F$, we obtain

$$\begin{aligned} \phi _{\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x})))}(\xi )&= \frac{1}{\sqrt{2\pi \sigma _{W,N}^2 (\underline{x})}}\int _\mathbb {R}exp\Big (t_{\lfloor F(y)/\varepsilon _\ell \rfloor } \psi (\xi ) - \frac{(y - \mu _W(\underline{x}))^2}{2\sigma _{W,N}^2(\underline{x})}\Big )dy, \end{aligned}$$

for $\xi \in \mathbb {R}$. Here, $\sigma _{W,N}^2$ is the variance function of the approximation $W^N$, which is given by

$$\begin{aligned} \sigma _{W,N}^2(\underline{x}) := Var(W^N(\underline{x})) = \mathbb {E}\Big (\sum _{i=1}^N \sqrt{\lambda _i} Z_i e_i(\underline{x})\Big )^2 = \sum _{i=1}^N \lambda _i e_i^2(\underline{x}),~\underline{x}\in \mathcal {D}. \end{aligned}$$

The function $\psi$ denotes the characteristic exponent of $\ell$ defined by

$$\begin{aligned} \psi (\xi ) = i\gamma \xi - \frac{b}{2}\xi ^2 + \int _{\mathbb {R}\setminus \{0\}}e^{i\xi y}-1-i\xi y\mathbbm {1}_{\{\vert y\vert \le 1\}}(y)\nu (dy), \end{aligned}$$

and, for any positive real number x, we denote by $\lfloor x \rfloor$ the largest integer smaller or equal than x.

Proof

As in the proof of Corollary 1, we use Lemma 1 to calculate

$$\begin{aligned} \phi _{\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x})))}(\xi )&= \mathbb {E}\Big (\exp (i\xi \ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x}))))\Big ) \\&=\mathbb {E}(\rho _{\ell ^{(\varepsilon _\ell )}}(F(W^N(\underline{x})),\xi )),~\xi \in \mathbb {R}. \end{aligned}$$

In the next step, we compute the charateristic function of the approximation $\ell ^{(\varepsilon _\ell )}$ of the Lévy process constructed as described in Remark 5. We use the independence and stationarity of the increments of the Lévy process to obtain

$$\begin{aligned} \ell ^{(\varepsilon _\ell )} (t)&= \sum _{i=1}^{N_\ell } \mathbbm {1}_{[t_{i-1},t_i)} (t) \ell (t_{i-1})= \sum _{i=1}^{N_\ell } \mathbbm {1}_{[t_{i-1},t_i)} (t) \sum _{j=1}^{i-1}\ell (t_j)-\ell (t_{j-1}) {\mathop {=}\limits ^{\mathcal {D}}} \sum _{k=1}^{\lfloor t/\varepsilon _\ell \rfloor }\ell _k^{\varepsilon _\ell }, \end{aligned}$$

where $(\ell _k^{\varepsilon _\ell },~k\in \mathbb {N})$ are i.i.d. random variables following the distribution of $\ell (\varepsilon _\ell )$ and we denote by ${\mathop {=}\limits ^{\mathcal {D}}}$ equivalence of the corresponding probability distributions. The convolution theorem (see e.g. (Klenke 2013, Lemma 15.11)) yields the representation

$$\begin{aligned} \phi _{\ell ^{(\varepsilon _\ell )}(t)}(\xi )&= \prod _{k=1}^{\lfloor t/\varepsilon _\ell \rfloor } \mathbb {E}(\exp (i\xi \ell _k^{(\varepsilon _\ell )})) = \prod _{k=1}^{\lfloor t/\varepsilon _\ell \rfloor } \exp (\varepsilon _\ell \psi (\xi )) = \exp (\lfloor t/\varepsilon _\ell \rfloor \varepsilon _\ell \psi (\xi ))\\&= \exp (t_{\lfloor t/\varepsilon _\ell \rfloor } \psi (\xi )), \end{aligned}$$

for $t\in [0,C_F)$ and $\xi \in \mathbb {R}$. Therefore, we obtain

$$\begin{aligned} \phi _{\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x})))}(\xi )&= \mathbb {E}(\exp (t_{\lfloor F(W^N(\underline{x}))/\varepsilon _\ell \rfloor } \psi (\xi ))),~\xi \in \mathbb {R}. \end{aligned}$$

The second formula for the characteristic function of the approximated field now follows from the fact that $W^N(\underline{x})\sim \mathcal {N}(\mu _W(\underline{x}),\sigma _{W,N}^2(\underline{x}))$.$\square$

6 The Covariance Structure of GSLFs

In many modeling applications one aims to use a random field model that mimics a specific covariance structure which is, for example, obtained from empirical data. In such a situation it is useful to have access to the theoretical covariance function of the random fields used in the model. Therefore, we derive a formula for the covariance function of the GSLF in the following section.

Lemma 4

Assume W is a GRF and $\ell$ is an independent Lévy process with existing first and second moment. We deonte by $\mu _W$, $\sigma _W^2$ and $q_W$, the mean, variance and covariance function of W and by $\mu _\ell (t)=\mathbb {E}(\ell (t))$, $\mu _\ell ^{(2)}(t):=\mathbb {E}(\ell (t)^2)$ the functions for the first second moment of the Lévy process $\ell$. For $\underline{x}\ne \underline{x}'\in \mathcal {D}$, the covariance function of the GSLF L is given by

$$\begin{aligned} q_L(\underline{x},\underline{x}')&=\int _{\mathbb {R}^2} c_\ell (F(u),F(v))f_{(W(\underline{x}),W(\underline{x}'))}(u,v)d(u,v) \\&~-\int _\mathbb {R}\mu _\ell (F(u))f_{W(\underline{x})}(u)du\int _\mathbb {R}\mu _\ell (F(v))f_{W(\underline{x}')}(v)dv, \end{aligned}$$

where we define

$$\begin{aligned} f_{W(\underline{x})}(u)&:=\frac{exp\Big (-\frac{(u-\mu _W(\underline{x}))^2}{2\sigma _W^2(\underline{x})}\Big )}{\sqrt{2\pi \sigma _W^2(\underline{x})}},\\ \Sigma _W(\underline{x},\underline{x}')&:=\begin{bmatrix} \sigma _W^2(\underline{x}) &{} q_W(\underline{x},\underline{x}') \\ q_W(\underline{x},\underline{x}') &{} \sigma _W^2(\underline{x}') \end{bmatrix} ,\\ c_\ell (u,v)&:= \mu _\ell (\vert u-v\vert )\mu _\ell (u\wedge v) + \mu _\ell ^{(2)}(u\wedge v),\\ f_{(W(\underline{x}),W(\underline{x}'))}(u,v) :=&\frac{exp\Big (-\frac{1}{2}\begin{pmatrix}u-\mu _W(\underline{x})\\ v-\mu _W(\underline{x}')\end{pmatrix}^T\Sigma _W(\underline{x},\underline{x}')^{-1}\begin{pmatrix}u-\mu _W(\underline{x})\\ v-\mu _W(\underline{x}')\end{pmatrix}\Big )}{\sqrt{(2\pi )^2\big (\sigma _W^2(\underline{x})\sigma _W^2(\underline{x}') - q_W^2(\underline{x},\underline{x}')\big )}}, \end{aligned}$$

for $u,v\in \mathbb {R}$ with $u\wedge v:=\min (u,v)$. For $\underline{x} = \underline{x}'\in \mathcal {D}$, the pointwise variance is given by

$$\begin{aligned} \sigma _L^2(\underline{x}) = q_L(\underline{x},\underline{x}) = \int _\mathbb {R}\mu _\ell ^{(2)}(F(u))f_{W(\underline{x})}(u)du - \Big (\int _\mathbb {R}\mu _\ell (F(u))f_{W(\underline{x})}(u)du \Big )^2. \end{aligned}$$

Proof

We compute using Lemma 1, for $\underline{x}\in \mathcal {D}$

$$\begin{aligned} \mu _L(\underline{x}):=\mathbb {E}(L(\underline{x})) = \mathbb {E}\Big (\ell (F(W(\underline{x})))\Big ) = \mathbb {E}\Big (\mu _\ell (F(W(\underline{x}))))\Big ). \end{aligned}$$

Further, we calculate for $\underline{x},\underline{x}'\in \mathcal {D}$

$$\begin{aligned} q_L(\underline{x},\underline{x}')&=\mathbb {E}\Big ((L(\underline{x}) - \mu _L(\underline{x}))(L(\underline{x}') - \mu _L(\underline{x}'))\Big )\\&= \mathbb {E}(L(\underline{x})L(\underline{x}')) - \mu _L(\underline{x})\mu _L(\underline{x}'). \end{aligned}$$

Next, we consider $0\le t_1\le t_2$ and use the fact that $\ell$ has stationary and independent increments to compute

$$\begin{aligned} \mathbb {E}(\ell (t_1)\ell (t_2)) = \mathbb {E}\big ((\ell (t_2)-\ell (t_1))\ell (t_1)\big ) + \mathbb {E}(\ell (t_1)^2) = \mu _\ell (t_2-t_1)\mu _\ell (t_1) + \mu _\ell ^{(2)}(t_1). \end{aligned}$$

Similarly, we obtain for $0\le t_2\le t_1$

$$\begin{aligned} \mathbb {E}(\ell (t_1)\ell (t_2)) = \mathbb {E}\big ((\ell (t_1)-\ell (t_2))\ell (t_2)\big ) + \mathbb {E}(\ell (t_2)^2) = \mu _\ell (t_1-t_2)\mu _\ell (t_2) + \mu _\ell ^{(2)}(t_2), \end{aligned}$$

and, hence, it holds for general $t_1,t_2\ge 0$:

$$\begin{aligned} c_\ell (t_1,t_2):=\mathbb {E}(\ell (t_1)\ell (t_2)) = \mu _\ell (\vert t_1-t_2\vert )\mu _\ell (t_1 \wedge t_2) + \mu _\ell ^{(2)}(t_1\wedge t_2). \end{aligned}$$

Another application of Lemma 1 and Remark 3 yields

$$\begin{aligned} \mathbb {E}(L(\underline{x})L(\underline{x}')) = \mathbb {E}(\ell (F(W(\underline{x})))\ell (F(W(\underline{x}')))) = \mathbb {E}(c_\ell (F(W(\underline{x})),F(W(\underline{x}')))). \end{aligned}$$

Putting these results together, we end up with

$$\begin{aligned} q_L(\underline{x},\underline{x}')&= \mathbb {E}(L(\underline{x})L(\underline{x}')) - \mu _L(\underline{x})\mu _L(\underline{x}')\\&= \mathbb {E}(c_\ell (F(W(\underline{x})),F(W(\underline{x}')))) - \mathbb {E}(\mu _\ell (F(W(\underline{x}))))\mathbb {E}(\mu _\ell (F(W(\underline{x'})))), \end{aligned}$$

for $\underline{x},~\underline{x}'\in \mathcal {D}$. The assertion now follows from the fact that $W(\underline{x})\sim \mathcal {N}(\mu _W(\underline{x}),\sigma _W^2(\underline{x}))$ and $(W(\underline{x}),W(\underline{x}'))^T\sim \mathcal {N}_2((\mu _W(\underline{x}),\mu _W(\underline{x}'))^T, \Sigma _W(\underline{x},\underline{x}'))$, for $\underline{x}\ne \underline{x}'\in \mathcal {D}$, together with $c_\ell (t,t) = \mu _\ell ^{(2)}(t)$ for $t\ge 0$.$\square$

7 Numerical Examples

In this section, we present numerical experiments on the theoretical results presented in the previous sections. The aim is to investigate the results of existing numerical methods and to illustrate the theoretical properties of the GSLF which have been proven in the previous sections, e.g. the pointwise distribution of the approximated fields or the quality of this approximation (see Theorem 2). Further, the presented numerical experiments and methods may also be useful for fitting the GSLF to existing data in various applications.

7.1 Pointwise Characteristic Function

Corollary 1 gives access to the pointwise characteristic function of the GSLF $L(\underline{x})\!=\!\ell$$(F(W(\underline{x})))$, $\underline{x}\in \mathcal {D}$, with a Lévy process $\ell$ and a GRF W, which is independent of $\ell$. Using the characteristic function and the Fourier inversion (FI) method (see Gil-Pelaez (1951)) we may compute the pointwise density function of the GSLF. Note that in both of these steps, the application of Corollary 1 and of the Fourier inversion theorem, numerical integration is necessary which may be inaccurate or computationally expensive. In this subsection, we choose specific Lévy processes together with a GRF and compare the computed density function of the corresponding GSLF with the histogram of samples of the simulated field. To be precise, we choose a Matérn$-$1.5-GRF, a Gamma process, set $F=\vert \cdot \vert +1$ and consider the GSLF $L(\underline{x})=\ell (F(W(\underline{x}))$ on $\mathcal {D}=[0,1]^2$. The distributions and the corresponding density functions are presented in Fig. 3. In line with our expectations, the FI approach perfectly matches the true distribution of the field at (1, 1).

Fig. 3

$10^5$ samples of the GSLF evaluated at (1, 1) and the corresponding density functions approximated via FI. Left: Gamma(3,10)-process and a Matérn GRF with $\sigma =2$. Right: Gamma(2,4)-process with Matérn GRF with $\sigma =1.5$

7.2 Pointwise Distribution of Approximated Fields

In Sect. 7.1 we presented a numerical example regarding the pointwise distribution of the GSLF. In the following, we aim to provide a numerical experiment in order to visualize the distributional effect of sampling from an approximation of the GSLF (cf. Section 5.3). For a specific choice of the Lévy process $\ell$, the transformation function F and the GRF W, we use Corollary 2 and the FI method to compute the pointwise distribution of the approximated field $\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x}))) \approx \ell (F(W(\underline{x})))$ for different approximation parameters $\varepsilon _\ell$ (resp. N) of the Lévy process (resp. the GRF). The computed densities are then compared with samples of the approximated field. We set $\mathcal {D}=[0,1]^2$ and consider the evaluation point $\underline{x}=(0.4,0.6)$. The GRF W is given by the KLE $W=\sum _{k=1}^\infty \sqrt{\lambda _k} e_k(x,y)Z_k$, where the eigenbasis is given by

$$\begin{aligned} e_k(x,y)=2\, sin\left( \pi kx\right) sin\left( \pi ky\right) ,~\lambda _k=10(k^2\pi ^2+0.1^2)^{-\nu }, \end{aligned}$$

with $\nu \!\!=\!\!0.6$ (see (Fasshauer and Mccourt 2015, Appendix A)). Further, we set $F(x)\!\!=\!\!1$$+\min (\vert x\vert ,30)$ and choose $\ell$ to be a Gamma(3,10)-process. The threshold 30 in the definition of F is large enough to have no effect in our numerical example since the absolute value of W does not exceed 30 in all considered samples. We use piecewise constant approximations $\ell ^{(\varepsilon _\ell )}$ of the Lévy process $\ell$ on an equidistant grid with stepsize $\varepsilon _\ell >0$ (see Remark 5) and approximate the GRF W by the truncated KLE with varying truncation indices N. To be more precise, we choose 6 different approximation levels for these two approximation parameters, as described in Table 1.

Table 1 Discretization parameters for the approximation of the GSLF

For each discretization level, we compute the characteristic function using Corollary 2, approximate the density function via FI and compare it with $10^5$ samples of the approximated field evaluated at the point (0.4, 0.6). The results are given in Fig. 4.

Fig. 4

Approximated pointwise densities (FI) of the GSLF on the different discretization levels together with samples of the corresponding approximated GSLF

As expected from Sect. 7.1, we see that the densities of the pointwise distribution of the approximated GSLF, which are approximated by FI, fit the actual samples of the approximated field accurately. In order to get a better impression of the influence of the approximation on the different levels, Fig. 5 shows the densities of the evaluated approximated GSLF on the different levels, together with the density of the exact field. We see how the densities of the approximted GSLF converge to the density of the exact field for $\varepsilon _\ell \rightarrow 0$ and $N \rightarrow \infty$. The results also show that the effect of the approximation of the GSLF should not be underestimated: on the lower levels, we obtain comparatively large deviations of the pointwise densities from the density of the exact field, which should be taken into account in applications. Obviously, the effect of the approximation depends heavily on the specific choice of the Lévy process and the underlying GRF.

Fig. 5

Approximated pointwise densities (FI) of the GSLF on the different discretization levels together with the pointwise density of the actual GSLF

7.3 Numerical Approximation of the GSLF

In Sect. 5, we considered approximations $\ell ^{(\varepsilon _\ell )}\approx \ell$ of the Lévy process and $W^N\approx W$ of the GRF and derived an error bound on the corresponding approximation $\ell ^{(\varepsilon _\ell )}(F(W^N(\underline{x})))\approx \ell$$(F(W(\underline{x})))$ (see Theorem 2). In fact, under Assumption 1, if we choose the approximation parameter N of the GRF W such that $R(N) \sim \varepsilon _\ell ^{1/\delta }$ with R(N) from Eq. (4), we obtain an overall approximation error which is dominated by $\varepsilon _\ell ^{1/p}$:

$$\begin{aligned} \Vert \ell ^{(\varepsilon _\ell )}(F(W^N)) - \ell (F(W))\Vert _{L^p(\Omega ;L^p(\mathcal {D}))} = \mathcal {O}(\varepsilon _\ell ^{1/p}),~\varepsilon _\ell \rightarrow 0. \end{aligned}$$

In this section, we present numerical experiments to showcase this approximation result.

We set $F(x)=\min (\vert x\vert ,30)$ and consider the domain $\mathcal {D}=[0,1]^2$. Let

$$\begin{aligned} W(x,y)=\sum _{k=1}^\infty \sqrt{\lambda _k} e_k(x,y)Z_k, \end{aligned}$$

be a GRF with corresponding eigenbasis

$$\begin{aligned} e_k(x,y)=2 sin\left( \pi kx\right) sin\left( \pi ky\right) ,~\lambda _k=100\,(k^2\pi ^2+0.2^2)^{-\nu }, ~\nu >0.5. \end{aligned}$$

(5)

With this choice, Assumption 1 i is satisfied with $\alpha = 1$ and $0<\beta < 2\nu -1$, since

$$\begin{aligned} \sum _{k=1}^\infty \lambda _k k^\beta \le C\sum _{k=1}^\infty k^{\beta -2\nu }<\infty , \end{aligned}$$

where we used that $\lambda _k\le C k^{-2\nu }$ for $k\in \mathbb {N}$. Hence, we obtain by Lemma 3

$$\begin{aligned} \Vert W-W^N\Vert _{L^n(\Omega ;L^\infty (\mathcal {D}))}\le C(D,n)N^{-\frac{\beta }{2}}, \end{aligned}$$

for $0<\beta <2\nu -1$, i.e. $R(N)= N^{-\frac{\beta }{2}}$ in Eq. (4) and Theorem 2. In our experiments, we choose the Lévy subordinator $\ell$ to be a Poisson or Gamma process. Approximations $\ell ^{(\varepsilon _\ell )}\approx \ell$ of these processes satisfying Assumption 1 iii may be obtained by piecewise constant extensions of values of the process on a grid with stepsize $\varepsilon _\ell$ (see Remark 5). For these processes, we obtain $\delta =1$ in (2) (see Remarks 4 and 5). Overall, Theorem 2 yields the error bound

$$\begin{aligned} \Vert \ell ^{(\varepsilon _\ell )}(F(W^N)) - \ell (F(W))\Vert _{L^p(\Omega ;L^p(\mathcal {D}))} = C(\varepsilon _\ell ^\frac{1}{p} + N^{-\frac{\beta }{2p}}), \end{aligned}$$

for $0<\beta <2\nu -1$. Hence, in order to equilibrate the error contributions from the GRF approximation and the approximation of the Lévy process, one should choose the cut-off index N of the KLE approximation of the GRF W according to

$$\begin{aligned} N \simeq \varepsilon _\ell ^{-\frac{2}{2\nu -1}}, \end{aligned}$$

(6)

which then implies

$$\begin{aligned} \Vert \ell ^{(\varepsilon _\ell )}(F(W^N)) - \ell (F(W))\Vert _{L^p(\Omega ;L^p(\mathcal {D}))} \le C\varepsilon _\ell ^\frac{1}{p}. \end{aligned}$$

(7)

In our experiments, we set the approximation parameters of the Lévy process to be $\varepsilon _\ell = 2^{-k}$, for $k=2,\dots ,10$ and the cut-off indices of the GRF are choosen according to (6). In order to verify (7), we draw 150 samples of the random variable

$$\begin{aligned} \ell ^{(\varepsilon _\ell )}(F(W^N)) - \ell (F(W)), \end{aligned}$$

for the described approximation parameters to estimate the corresponding $L^p$ norm of the approximation error for $p \in \{1,2,2.5,3,3.3\}$ which is expected to behave as $\mathcal {O}(\varepsilon _\ell ^{1/p})$.

In our first example, we set $\ell$ to be a Poisson(8)-process and $\nu =2.5$ in Eq. (5). For each sample, we compute a reference field by taking 150 summands in the KLE of the GRF W and use an exact sample of a Poisson process computed by the Uniform Method (see (Schoutens 2003, Section 8.1.2)). The resulting estimates for the $L^p$ approximation error are plotted against $\varepsilon _\ell$ for $p\in \{1,2,2.5,3.3\}$, which is illustrated in the Fig. 6.

Fig. 6

Estimated $L^p$ approximation errors against the discretization parameter $\varepsilon _\ell$ for different values of p using a Poisson(8)-process (top) and overview for $p = {1},~{2},~{2.5},~{3},~{3.3}$ (bottom)

As expected, the approximated $L^p$ errors converge asymptotically with rate $\varepsilon _\ell ^{1/p}$ for the considered moments p. The bottom plot of Fig. 6 shows an overview of the $L^p$ approximation errors for different values of p and illustrates that the $L^p$-errors indeed converge with different rates.

In our second numerical example, we set $\ell$ to be a Gamma(2,4)-process. Further, we set $\nu =2$ in Eq. (5). The approximations $\ell ^{(\varepsilon _\ell )}\approx l$ of the Lévy process on the different levels are again computed by piecewise constant extensions of values of the process on an equidistant grid with stepsize $\varepsilon _\ell$. Aiming to verify Eq. (7), we use 150 samples to estimate the $L^p$ approximation error, for $p \in \{1,2,2.5,3,3.3\}$. In order to compute a sufficiently accurate reference field in each sample, we use 500 summands in the KLE approximation of the GRF W and the Gamma process is computed on a reference grid with stepsize $\varepsilon _\ell =2^{-13}$. The convergence of the estimated $L^p$ error plotted against the discretization parameter $\varepsilon _\ell$ is visualized in Fig. 7, which shows the expected behaviour of the estimated $L^p$ error for the considered moments p. As in the previous experiment, we provide a plot with all estimated $L^p$ errors in one figure (see bottom plot in Fig. 7), which again confirms that the $L^p$-error of the approximation converge in $\varepsilon _\ell$ with rate 1/p for the considered values of p.

Fig. 7

Estimated $L^p$ approximation errors against the discretization parameter $\varepsilon _\ell$ for different values of p using a Gamma(2,4)-process (top) and overview for $p = {1},~{2},~{2.5},~{3},~{3.3}$ (bottom)

7.4 Empirical Estimation of the Covariance of the GSLF

Lemma 4 gives access to the covariance function of the GSLF. This is of interest in applications, since it is often required that a random field mimics a specific covariance structure which is determined by (real world) data. In this example, we choose specific GSLFs and spatial points to compute the corresponding covariance using Lemma 4 and compare it with empirically estimated covariances using samples of the GSLF. We choose $\mathcal {D}=[0,2]^2$ and estimate the covariance with a single level Monte Carlo estimator using a growing number of samples of the field L evaluated at the two considered points $\underline{x},~\underline{x}'\in \mathcal {D}$. If M denotes the number of samples used in this estimation and $E_M(\underline{x},\underline{x}')$ denotes the Monte Carlo estimation of the covariance, the convergence rate of the corresponding RMSE for a growing number of samples is $-1/2$, i.e.

$$\begin{aligned} RMSE := \Vert q_L(\underline{x},\underline{x}')-E_M(\underline{x},\underline{x}')\Vert _{L^2(\Omega )} = \mathcal {O}(1/\sqrt{M}),~M\rightarrow \infty . \end{aligned}$$

Fig. 8

Convergence of RMSE of empirical covariance $q_L(\underline{x},\underline{x}')$; left: $\ell$ is a Gamma(4,1.5)-process, $r=1$, $\sigma ^2 = 4$, $\underline{x} = (0.2,1.5)$, $\underline{x}' = (0.9,0.8)$, $q_L(\underline{x},\underline{x}') \approx 3.0265$; right: $\ell$ is a Gamma(5,6)-process, $r=1.2$, $\sigma ^2 = 1.5^2$, $\underline{x} = (0.9,1.2)$, $\underline{x}' = (1.6,0.5)$, $q_L(\underline{x},\underline{x}') \approx 0.236$

In our experiments, we use Poisson and Gamma processes and W is set to be a centered GRF with squared exponential covariance function, i.e.

$$\begin{aligned} q_W(\underline{x},\underline{x}') = \sigma ^2 \exp (-\Vert \underline{x}-\underline{x}'\Vert _2^2/r^2),~\underline{x},~\underline{x}'\in \mathcal {D}, \end{aligned}$$

with pointwise variance $\sigma ^2>0$, correlation length $r>0$ and $F=\vert \cdot \vert$. In our first experiment we choose $\ell$ to be a Gamma process with varying parameters. The RMSE is estimated for a growing number of samples M and 100 independent MC runs. The results are shown in Fig. 8. As expected, the approximated RMSE convergences with order $\mathcal {O}(1/\sqrt{M})$ for both experiments.

In our second example we set $\ell$ to be a Poisson process. The results are shown in Fig. 9.

Fig. 9

Convergence of RMSE of empirical covariance $q_L(\underline{x},\underline{x}')$; left: $\ell$ is a Poisson(8)-process, $r=0.5$, $\sigma ^2 = 1.5^2$, $\underline{x}=(0.5,0.8)$, $\underline{x}' = (0.6,1.5)$, $q_L(\underline{x},\underline{x}') \approx 6.4807$; right: $\ell$ is a Poisson(3)-process, $r=1$, $\sigma ^2 = 1$, $\underline{x}=(1.2,0.6)$, $\underline{x}' = (0.9,1.7)$, $q_L(\underline{x},\underline{x}') \approx 1.6485$

As in the previous example, we see a convergence rate of order $\mathcal {O}(1/\sqrt{M})$ of the MC estimator for the covariance in each experiment. For small sample numbers, the error values for the estimation of the covariances might seem quite high: for example, in the left plot of Fig. 9, using $M=100$ samples, we obtain an approximated RMSE which is approximately two times the exact value of the covariance. This seems to large at first glance. However, one has to keep in mind that the RMSE is bounded by $std(L(\underline{x})\cdot L(\underline{x}'))/\sqrt{M}$ and the standard deviation of the product of the evaluated field may become quite large. In fact, in the left hand side of Fig. 9 we obtain $std(L(\underline{x})\cdot L(\underline{x}'))\approx 138,46$ which fits well to the observed results, being approximately $10 = \sqrt{100}$ times the approximated RMSE for $M=100$ samples. In practice, it is therefore important to keep in mind that the estimation of the covariance based on existing data might require a large number of observations.

8 GSLFs in Elliptic PDEs

In the previous sections, we considered theoretical properties of the GSLF and presented numerical examples to validate and visualize these results. In the last section of this paper we present an application of the GSLF as coefficient of a general elliptic PDE. Such an equation might be used, for example, to model subsurface/groundwater flow in heterogeneous or fractured media. In this situation, the media is often modeled by a random field to take into account uncertainties. In order to obtain a realistic model, the random field has to fulfill certain requirements. In the following, we discuss some of these requirements in more detail and explain why the GSLF yields an appropriate model for the described application, especially compared to commonly used alternative random field models. Distributional flexibility and rotational invariance are essential statistical properties for random fields used to describe subsurface/groundwater flow (cf. Hosseini (2017) and Sanchez-Vila et al. (2006)), which are both satisfied by the GSLF. Further, in order to model material fractures, the random field has to be able to exhibit spatially discontinuous realizations. The GSLF allows for discontinuous realizations and, in addition, displays great geometrical flexibility in the jump domains, which allows the consideration of a wide variety of different fractured material. From a numerical point of view, the existence of efficient sampling techniques is important since otherwise simulations of the random PDE might become computationally unfeasible, especially if sampling-based approaches are considered to approximate the random PDE solution (cf. Merkle and Barth (2022a)). By construction, sampling of the GSLF reduces to sampling a Lévy process on a one-dimensional parameter domain and sampling a GRF, which results in moderate sampling effort for most configurations of the GSLF.

Alternative random field models which can be used in the context of subsurface/ground-water flow in heterogeneous or fractured materials often have the disadvantage of not satisfying at least one of the above mentioned requirements. For example, the standard (log-)Gaussian model suffers from very limited distributional flexibility and path continuity. Generalizations, like hierarchical Gaussian random fields (see Cui et al. (2022)), display higher distributional flexibility. However, these random fields also have continuous realizations. A discontinuous random field model in the context of an elliptic PDE has been considered in Merkle and Barth (2022c). These fields are spatially discontinuous and distributionally flexible but not rotationally invariant. Another random field model for the mentioned application are mixed moving average fields driven by a Lévy field (see Curato et al. (2023), Jónsdóttir et al. (2013) and Surgailis et al. (1993)). Depending on their specific configuration, these random fields display very flexible distributional properties. However, simulation and approximation of Lévy-driven mixed moving average fields might become difficult or at least computationally expensive in many situations and, to the best of the authors’ knowledge, an approximation theory in the sense of Sect. 5 is not available. In summary, it can be concluded that the GSLF possesses important properties, which are required for random fields used in the context of subsurface/groundwater flow and not satisfied by other commonly used random fields. This motivates the consideration and investigation of a general elliptic PDE where the GSLF occurs in the diffusion coefficient. We introduce the considered elliptic PDE in Sect. 8.1 following Merkle and Barth (2022a), Merkle and Barth (2022c) and Barth and Stein (2018b). Spatial discretization methods are discussed in Sect. 8.2 and we conclude this section with numerical experiments in Sect. 8.3.

8.1 Problem Formulation and Existence of Solutions

Let $\mathcal {D}\subset \mathbb {R}^2$ be a bounded, connected Lipschitz domain.¹ Define $H:=L^2(\mathcal {D})$ and consider the elliptic PDE

$$\begin{aligned} -\nabla \cdot (a(\omega ,\underline{x})\nabla u(\omega ,\underline{x}))=f(\omega ,\underline{x}) \text { in }\Omega \times \mathcal {D}, \end{aligned}$$

(8)

where we impose the boundary conditions

$$\begin{aligned} u(\omega ,\underline{x})&=0 \text { on } \Omega \times \Gamma _1,\end{aligned}$$

(9)

$$\begin{aligned} a(\omega ,\underline{x}) \overrightarrow{n}\cdot \nabla u(\omega ,\underline{x})&=g(\omega ,\underline{x}) \text { on } \Omega \times \Gamma _2. \end{aligned}$$

(10)

Here, we split the boundary $\partial \mathcal {D}=\Gamma _1\overset{.}{\cup }\Gamma _2$ in two one-dimensional manifolds $\Gamma _1,~\Gamma _2$ and assume that $\Gamma _1$ is of positive measure and that the exterior normal derivative $\overrightarrow{n}\cdot \nabla v$ on $\Gamma _2$ is well-defined for every $v\in C^1(\overline{\mathcal {D}})$, where $\overrightarrow{n}$ is the outward unit normal vector to $\Gamma _2$. The mappings $f:\Omega \times \mathcal {D}\rightarrow \mathbb {R}$ and $g:\Omega \times \Gamma _2\rightarrow \mathbb {R}$ a measurable functions and $a:\Omega \times \mathcal {D}\rightarrow \mathbb {R}$ is defined by

$$\begin{aligned} \begin{aligned} a:\Omega \times \mathcal {D}&\rightarrow (0,+\infty ), \\ (\omega ,x,y)&\mapsto \overline{a}(x,y) + \Phi _1(W_1(x,y)) + \Phi _2(\ell (F(W_2(x,y)))), \end{aligned} \end{aligned}$$

(11)

where

• $\overline{a}:\mathcal {D}\rightarrow (0,+\infty )$ is deterministic, continuous and there exist finite constants $\overline{a}_+,\overline{a}_->0$ with $\overline{a}_-\le \overline{a}(x,y)\le \overline{a}_+$ for $(x,y)\in \mathcal {D}$.

• $\Phi _1,~\Phi _2:\mathbb {R}\rightarrow [0,+\infty )$ are continuous.

• $F:\mathbb {R}\rightarrow \mathbb {R}_+$ is Lipschitz continuous and globally bounded by $C_F>0$, i.e. $F(x)<C_F, ~x\in \mathbb {R}$.

• $W_1$ and $W_2$ are zero-mean GRFs on $\overline{\mathcal {D}}$ with $\mathbb {P}-a.s.$ continuous paths.

• $\ell$ is a Lévy process on $[0,C_F]$.

Note that we consider the case of a homogeneous Dirichlet boundary condition on $\Gamma _1$ in the theoretical analysis to simplify notation. Non-homogeneous Dirichlet boundary conditions could also be considered, since such a problem can always be formulated as a version of (8)–(10) with modified source term and Neumann data (see also (Barth and Stein 2018b, Remark 2.1)).

Next, we shortly introduce the pathwise weak solution of problem (8)–(10) following Merkle and Barth (2022c) and Merkle and Barth (2022a). We denote by $H^1(\mathcal {D})$ the Sobolev space and by T the trace operator $T:H^1(\mathcal {D})\rightarrow H^{\frac{1}{2}}(\partial \mathcal {D})$ where $Tv=v\vert _{\partial \mathcal {D}}$ for $v\in C^\infty (\overline{\mathcal {D}})$ (see Ding (1996)). Further, we introduce the solution space $V\subset H^1(\mathcal {D})$ by $V:=\{v\in H^1(\mathcal {D})~\vert ~Tv\vert _{\Gamma _1}=0\}$, where we take over the standard Sobolev norm, i.e. $\Vert \cdot \Vert _V:=\Vert \cdot \Vert _{H^1(\mathcal {D})}$. We identify H with its dual space $H'$ and work on the Gelfand triplet $V\subset H\simeq H'\subset V'$. Multiplying the left hand side of Eq. (8) by a test function $v\in V$ and integrating by parts (see e.g. (Valli 2020, Section 6.3)) we obtain the following pathwise weak formulation of the problem: For fixed $\omega \in \Omega$ and given mappings $f(\omega ,\cdot )\in V'$ and $g(\omega ,\cdot )\in H^{-\frac{1}{2}}(\Gamma _2)$, find $u(\omega ,\cdot )\in V$ such that

$$\begin{aligned} B_{a(\omega )}(u(\omega ,\cdot ),v) = F_\omega (v) \end{aligned}$$

(12)

for all $v\in V$. The function $u(\omega ,\cdot )$ is then called pathwise weak solution to problem (8)–(10) and the bilinear form $B_{a(\omega )}$ and the linear operator $F_\omega$ are defined by

$$\begin{aligned} B_{a(\omega )}:V\times V\rightarrow \mathbb {R}, ~(u,v)\mapsto \int _{\mathcal {D}}a(\omega ,\underline{x})\nabla u(\underline{x})\cdot \nabla v(\underline{x})d\underline{x}, \end{aligned}$$

and

$$\begin{aligned} F_\omega :V\rightarrow \mathbb {R}, ~v\mapsto \int _\mathcal {D}f(\omega ,\underline{x})v(\underline{x})d\underline{x} + \int _{\Gamma _2}g(\omega ,\underline{x})[Tv](\underline{x})d\underline{x}, \end{aligned}$$

where the integrals in $F_\omega$ are understood as the duality pairings:

$$\begin{aligned} \int _\mathcal {D}f(\omega ,\underline{x})v(\underline{x})d\underline{x}&= {}_{V'}{\langle }f(\omega ,\cdot ),v\rangle _V \text { and }\\ \int _{\Gamma _2}g(\omega ,\underline{x})[Tv](\underline{x})d\underline{x}&= {}_{H^{-\frac{1}{2}}(\Gamma _2)}{\langle }g(\omega ,\cdot ),Tv\rangle _{H^\frac{1}{2}(\Gamma _2)}, \end{aligned}$$

for $v\in V$.

Remark 6

Note that any real-valued, càdlàg function $f:[a,b]\rightarrow \mathbb {R}$ on a compact interval [a, b], with $a<b$, is bounded. Otherwise, one could find a sequence $(x_n,~n\in \mathbb {N})\subset [a,b]$ such that $\vert f(x_n)\vert >n$ for all $n\in \mathbb {N}$. In this case, since [a, b] is compact, there exists a subsequence $(x_{n_k},~k\in \mathbb {N})\subset [a,b]$ with a limit in [a, b], i.e. $x_{n_k}\rightarrow x^*\in [a,b]$ for $k\rightarrow \infty$. Since f is right-continuous in $x^*$ and $lim_{x\nearrow x^*}f(x)$ exists, f is bounded in a neighborhood of $x^*$, i.e. there exists $\delta ,C>0$ such that $\vert f(x)\vert \le C$ for $x\in [a,b]$ with $\vert x-x^*\vert <\delta$, which contradicts the fact that $\vert f(x_{n_k})\vert >n_k$ since $\vert x_{n_k}-x^*\vert <\delta$ and $n_k>C$ both hold for k large enough.

The diffusion coefficient a is jointly measurable by construction (see Remark 2) and, for any fixed $\omega \in \Omega$, it holds $a(\omega ,x,y)\ge \overline{a}_->0$ for all $(x,y)\in \mathcal {D}$ and

$$\begin{aligned} a(\omega ,x,y) \le \overline{a}_+ + \underset{(x,y)\in \overline{\mathcal {D}}}{sup}\Phi _1(W_1(\omega ,x,y)) + \underset{z\in [0,C_F]}{sup}\Phi _2(\ell (\omega ,z)) < +\infty , \end{aligned}$$

for all $(x,y)\!\in \!\mathcal {D}$, where the finiteness follows by the continuity of $\Phi _1,\,\Phi _2,\,W_1$ and Remark 6.

It follows by a pathwise application of the Lax-Milgram lemma that the elliptic model problem (8)–(10) with the diffusion coefficient a has a unique, measurable pathwise weak solution.

Theorem 3

(see Merkle and Barth 2022c, Theorem 3.7, Remark 2.4) and (Barth and Stein 2018b, Theorem 2.5)) Let $f\in L^q(\Omega ;H),$ $g\in L^q(\Omega ;L^2(\Gamma _2))$ for some $q\in [1,+\infty )$. There exists a unique pathwise weak solution $u(\omega ,\cdot )\in V$ to problem (8)–(10) with diffusion coefficient (11) for $\mathbb {P}$-almost every $\omega \in \Omega$. Furthermore, $u\in L^r(\Omega ;V)$ for all $r\in [1,q)$ and

$$\begin{aligned} \Vert u\Vert _{L^r(\Omega ;V)}\le C(\overline{a}_-,\mathcal {D})(\Vert f\Vert _{L^q(\Omega ;H)} + \Vert g\Vert _{L^q(\Omega ;L^2(\Gamma _2))}), \end{aligned}$$

where $C(\overline{a}_-,\mathcal {D})>0$ is a constant depending only on the indicated parameters.

8.2 Spatial Discretization of the Elliptic PDE

In the following, we briefly describe numerical methods to approximate the pathwise solution to the random elliptic PDE. Our goal is to approximate the weak solution u to problem (8)–(10) with diffusion coefficient a given by Eq. (11). Therefore, for almost all $\omega \in \Omega$, we aim to approximate the function $u(\omega ,\cdot )\in V$ such that

$$\begin{aligned} \begin{aligned} B_{a(\omega )} (u(\omega ,\cdot ), v)&:=\int _{\mathcal {D}}a(\omega ,\underline{x})\nabla u(\omega ,\underline{x})\cdot \nabla v(\underline{x})d\underline{x} \\&=\int _\mathcal {D}f(\omega ,\underline{x})v(\underline{x})d\underline{x} + \int _{\Gamma _2} g(\omega ,\underline{x})[Tv](\underline{x})d\underline{x}=:F_\omega (v), \end{aligned} \end{aligned}$$

(13)

for every $v\in V$. We compute an approximation of the solution using a standard Galerkin approach with linear basis functions. Therefore, assume a sequence of finite-element subspaces is given, which is denoted by $\mathcal {V}=(V_k,~k\in \mathbb {N}_0)$, where $V_k\subset V$ are subspaces with growing dimension $\dim (V_k)=d_k$. We denote by $(h_k,~k\in \mathbb {N}_0)$ the corresponding refinement sizes with $h_k \rightarrow 0$, for $k\rightarrow \infty$. Let $k\in \mathbb {N}_0$ be fixed and denote by $\{v_1^{(k)},\dots ,v_{d_k}^{(k)}\}$ a basis of $V_k$. The (pathwise) discrete version of problem (13) reads: Find $u_k(\omega ,\cdot )\in V_k$ such that

$$\begin{aligned} B_{a(\omega )}(u_k(\omega ,\cdot ),v_i^{(k)})=F_\omega (v_i^{(k)}) \text { for all } i=1,\dots ,d_k. \end{aligned}$$

If we expand the solution $u_k(\omega ,\cdot )$ with respect to the basis $\{v_1^{(k)},\dots ,v_{d_k}^{(k)}\}$, we end up with the representation

$$\begin{aligned} u_k(\omega ,\cdot )=\sum _{i=1}^{d_k} c_iv_i^{(k)}, \end{aligned}$$

where the coefficient vector ${\textbf {c}}=(c_1,\dots ,c_{d_k})^T\in \mathbb {R}^{d_k}$ is determined by the linear system of equations

$$\begin{aligned} {\textbf {B}}(\omega ){\textbf {c}}={\textbf {F}}(\omega ), \end{aligned}$$

with stochastic stiffness matrix ${\textbf {B}}(\omega )_{i,j}=B_{a(\omega )}(v_i^{(k)},v_j^{(k)})$ and load vector $\textbf{F}(\omega )_i=F_\omega (v_i^{(k)})$ for $i,j=1,\dots ,d_k$.

8.2.1 Standard Linear Finite Elements

Let $(\mathcal {K}_k,~k\in \mathbb {N}_0)$ be a sequence of admissible triangulations of the domain $\mathcal {D}$ (cf. (Hackbusch 2017, Definition 8.36)) and denote by $\theta _k>0$ the minimum interior angle of all triangles in $\mathcal {K}_k$, where we assume $\theta _k\ge \theta >0$ for a positive constant $\theta$. For $k \in \mathbb {N}_0$, we denote by $h_k:=\underset{K\in \mathcal {K}_k}{\max }\, diam(K)$ the maximum diameter of the triangulation $\mathcal {K}_k$ and define the finite dimensional subspaces by $V_k:=\{v\in V~\vert ~v\vert _K\in \mathcal {P}_1,~K\in \mathcal {K}_k\}$, where $\mathcal {P}_1$ denotes the space of all polynomials up to degree one. If we assume that there exists a positive regularity parameter $\kappa _a>0$ such that for $\mathbb {P}-$almost all $\omega \in \Omega$ it holds $u(\omega ,\cdot )\in H^{1+\kappa _a}(\mathcal {D})$ and $\Vert u\Vert _{L^2(\Omega ;H^{1+\kappa _a}(\mathcal {D}))}\le C_u$ for some constant $C_u>\infty$, we immediately obtain the following bound by Céa’s lemma (see (Barth and Stein 2018b, Section 4), (Hackbusch 2017, Chapter 8))

$$\begin{aligned} \Vert u-u_k\Vert _{L^2(\Omega ;V)}\le C\, h_k^{\min (\kappa _a,1)}, \end{aligned}$$

(14)

for some constant C which does not depend on $h_k$. For general deterministic elliptic interface problems, one obtains a discretization error of order $\kappa _a < 1$ and, hence, one cannot expect the full order of convergence $\kappa _a=1$ in general for standard triangulations of the domain (see Babuška (1970) and Barth and Stein (2018b)). Therefore, we present one possible approach to enhance the performance of the FE method for the considered elliptic PDE in Sect. 8.2.2. We point out that it is not possible to derive optimal rates $\kappa _a>0$ such that (14) holds for our general random diffusion coefficient (see also Merkle and Barth (2022c), Barth and Stein (2018b)). However, we investigate the existence of such a constant numerically in Sect. 8.3. We close this subsection with a remark on the practical simulation of the GRFs $W_1,~W_2$ and the Lévy process $\ell$ in the diffusion coefficient (11).

Remark 7

It is in general not possible to draw exact samples of the Lévy process and the GRFs in the diffusion coefficient (11). In practice, one has to use appropriate approximations $\ell ^{(\varepsilon _\ell )}\approx l$ of the Lévy process and $W_1^{N}\approx W_1,~W_2^{N}\approx W_2$ of the GRFs with approximation parameters $\varepsilon _\ell >0$ and $N\in \mathbb {N}$, as introduced in Sect. 5. In the context of FE approximations of the PDE (8)–(10) with diffusion coefficient (11), the question arises, how to choose these approximation parameters in practice, given a specific choice of the FE approximation parameter $h_k$ in (14). Obviously, the choice of $\varepsilon _\ell$ and N should depend on the FE parameter $h_k$, since a higher resolution of the FE approximation will be worthless if the approximation of the diffusion coefficient is poor.

In Merkle and Barth (2022c), the authors considered the PDE (8)–(10) with a different diffusion coefficient a. The coefficient considered in the mentioned paper also incorporates GRFs and Lévy processes, which in turn have to be approximated in practice, leading to an approximation $\tilde{a}\approx a$. The authors derived a rule on the choice of the approximation parameters, such that the error contributions from the approximation of the diffusion coefficient and the FE discretization are equilibrated (see (Merkle and Barth 2022c, Section 7)). We want to emphasize that this result is essentially based on the quantification of the approximation error $\tilde{a}-a$ of the corresponding diffusion coefficient in an $L^p(\Omega ,L^p(\mathcal {D}))$-norm, for some $p\ge 1$ (see (Merkle and Barth 2022c, Theorem 4.8 and Theorem 5.11)). In Theorem 2, we derived an error bound on the approximation error of the GSLF in the $L^p(\Omega ,L^p(\mathcal {D}))$-norm under Assumption 1. A corresponding error bound on the approximation of the diffusion coefficient defined in (11) immediately follows under mild assumptions on $\Phi _1$ and $\Phi _2$. Therefore, following exactly the same arguments as in Merkle and Barth (2022c) together with Theorem 2, we obtain the following rule for the practical choice of the approximation parameters $\varepsilon _\ell$ and N such that the overall error contributions from the approximation of the GRFs, the Lévy process and the FE discretization are equilibrated and the error is dominated by the FE refinement parameter $h_k$: For $k\in \mathbb {N}$, choose $\varepsilon _\ell$ and N such that

$$\begin{aligned} \varepsilon _\ell \simeq h_k^{2\kappa _a}\text { and } R(N) \simeq h_k^{\frac{2\kappa _a}{\delta }}. \end{aligned}$$

For example, if we approximate the GRF by the KLE approach (see Sect. 5.1), one should choose the cut-off index such that $N\simeq h_k^{-\frac{4\kappa _a}{\beta \delta }}$ with $\beta$ from Assumption 1 i.

8.2.2 Adaptive Finite Elements

One common way to improve the FE method for elliptic PDEs with discontinuous diffusion coefficients is to use triangulations which are adapted to the jump discontinuities in the sense that the spatial jumps lie on edges of elements of the triangulation (see for example Barth and Stein (2018b) and Merkle and Barth (2022c) and the references therein). In the cited papers, the jump locations are known and the jump geometries allow for an (almost) exact alignment of the triangulation to the interfaces due to their specific geometrical properties. This is, however, not the case for the diffusion coefficient considered in the current paper, where the spatial jump positions are not known explicitly, nor is it possible to align the triangulation exactly in the described sense due to the complex jump geometries.

Another possible approach to improve the FE method are adaptive Finite Elements (see e.g. Ainsworth and Oden (1997) and Grätsch and Bathe (2005) and the references therein). The idea is to identify triangles with a high contribution to the overall error of the FE approximation, which are then refined. For a given FE approximation $u_k \in V_k \subset V$ of the solution $u\in V$, the discretization error $u-u_k$ is estimated in terms of the approximated solution $u_k$ and no information about the true solution u is needed. This may be achieved by the use of the Galerkin orthogonality and partial integration. For a given triangulation $\mathcal {T} = \{K,~K\subset \mathcal {D} \}$ with corresponding FE approximation $u_k$, the approximation error of the FE approximation to the considered elliptic problem (8)–(10) may be estimated by

$$\begin{aligned} err_\mathcal {T}(u_k, a, f,g) = \left( \sum _{K\in \mathcal {T}} err_\mathcal {T}(u_k,a,f,g,K)\right) ^{\frac{1}{2}}. \end{aligned}$$

Here, $err_\mathcal {T}(u_k,a,f,g,K)$ corresponds the error contribution of the approximation on the element $K\in \mathcal {T}$, which may be approximated by

$$\begin{aligned} \begin{aligned} err_{\mathcal {T}}&(u_k, a, f,g, K) = h_K^2\Vert f\Vert _{L^2(K)}^2 + \sum _{e\in \partial K \cap \Gamma _2} h_e \Vert g-\overrightarrow{n}_K\cdot a\,\nabla u_k{\big \vert _K}\Vert _{L^2(e)}^2 \\&+\sum _{e\in \partial K\setminus (\Gamma _2\cup \Gamma _1)} h_e\Vert \overrightarrow{n}_K\cdot a\,\nabla u_k{\big \vert _K}+ \overrightarrow{n}_{J(K,e)}\cdot a\,\nabla u_k{\big \vert _{J(K,e)}}\Vert _{L^2(e)}^2, \end{aligned} \end{aligned}$$

(15)

where we denote by $e\in \partial K$ an edge of the triangle $K\in \mathcal {T}$ and ${J(K,e)}\in \mathcal {T}$ is the unique triangle which is the direct neighbor of the triangle K along the edge e. Further, $h_K$ is the diameter of the triangle K and $h_e$ is the length of the edge e (see Grätsch and Bathe (2005) and Bernardi and Verfürth (2000)). The triangle-based estimated error obtained by Eq. (15) allows for an identification of the triangles with the largest contribution to the overall error. One common local mesh refinement strategy is to start with an initial triangulation, compute the error contribution of each triangle according to Eq. (15) and refine all triangles which have an approximated error contribution which is at least $50\%$ of the error contribution with the largest approximated error (see, e.g., (Verfürth 1994, Section 5)).

Example 2

Consider the PDE problem (8)–(10) with homogeneous Dirichlet boundary conditions on $\mathcal {D}=(0,1)^2$ and $f\equiv 10$. The diffusion coefficient a as defined in Eq. (11) is given by

$$\begin{aligned} a(x,y) = 0.1 + \ell (min\{\vert W_1(x,y)\vert ,30\}), \end{aligned}$$

where $\ell$ is a Poisson(2)-process and $W_1$ is a centered GRF with squared exponential covariance function. In order to illustrate the adaptive mesh generation decribed above, we consider 3 samples of the diffusion coefficient and compute the adaptive meshes, where we use an initial mesh with FE refinement parameter $h=0.025$ and refine all triangles which have an estimated error contribution exceeding $50\%$ of the largest estimated error.

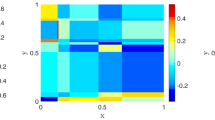
Figure 10 shows the three samples of the diffusion coefficient and the corresponding adaptive triangulations. This example illustrates how the element-wise a-posteriori estimation of the error according to Eq. (15) enables an identification of the triangles with a high error contribution, which results in a higher mesh resolution near the discontinuities.

8.3 Numerical Experiments for the Random Elliptic PDE

Fig. 10

Samples of the diffusion coefficient a (top) and adaptive triangulations (bottom)

In this section, we present numerical examples for the experimental investigation of the existence of a positive parameter $\kappa _a>0$ such that Eq. (14) holds. Further, in the presented examples, we compare the performance of a standard FE discretization with the FE approach using the local refinement strategy described in Sect. 8.2.2. We consider the domain $\mathcal {D}=(0,1)^2$ and set $f\equiv 10$, $\overline{a}\equiv 0.1$, $\Phi _1 = 0.1\,\exp (\cdot )$, $\Phi _2=\vert \cdot \vert$, $F = \min (\vert \cdot \vert , 30)$ in Eq. (11). $W_1$ and $W_2$ are centered GRFs with squared exponential covariance function (see Sect. 7.4), where we set $\sigma =0.5$ and $r=1$. We use the circulant embedding method (see cf. Graham et al. (2018a) and Graham et al. (2018b)) to draw samples of the GRFs $W_1,~W_2$ on an equidistant grid with stepsize $h_W=1/200 = 0.005$ and obtain evaluations everywhere on the domain by multilinear interpolation. Due to the high spatial regularity of $W_1$ and $W_2$ and the high correlation length, this stepsize is fine enough to ensure that the approximation error of the GRFs $W_1,~W_2$ is negligible. The Lévy process $\ell$ is set to be a Poisson process with intensity parameter $\lambda >0$, which will be specified later. It follows that $\ell (t)-\ell (s)\sim Poiss(\lambda (t-s))$ for $0\le s\le t$ and we draw samples from the Poisson process by the Uniform Method (see (Schoutens 2003, Section 8.1.2)).

The goal of our numerical experiments is to approximate the strong error: We set $h_k=0.25 \cdot 2^{-(k-1)}$, for $k=1,\dots , 8$ and approximate the left hand side of Eq. (14) by

Fig. 11

Samples of the diffusion coefficient with $\lambda =2$ and corresponding FE solution to the elliptic PDE with homogeneous Dirichlet boundary conditions

$$\begin{aligned} RMSE^2 := \Vert u-u_k\Vert _{L^2(\Omega ;V)}^2 \approx \frac{1}{M}\sum _{i=1}^M \Vert u_{ref}^{(i)}-u_k^{(i)}\Vert _V^2, \end{aligned}$$

(16)

for $k = 1,\dots ,5$, where $(u_{ref}^{(i)}-u_k^{(i)}, ~i=1,\dots ,M)$ are i.i.d. copies of the random variable $u_{ref}-u_k$ and $M\in \mathbb {N}$. We use a reference grid on $\mathcal {D}$ with $801\times 801$ grid points for interpolation and prolongation and take $u_{ref}:=u_{8}$ as the pathwise reference solution. The RMSE is estimated for the standard FE method and for the FE method with adaptive refinement as described in Sect. 8.2.2. In order to obtain comparable approximations on each FE level, we compute the adaptive meshes as follows: for $k\in \{1,\dots ,5\}$, we denote by $n_k$ the number of triangles in the non-adaptive triangulation with FE mesh refinement parameter $h_k$. The (sample-dependent) adaptive mesh on level k is obtained by performing the local refinement procedure described in Sect. 8.2.2 until the number of triangles in the adaptive mesh exceeds $n_k$. The resulting mesh is then used to compute the adaptive FE approximation on level k.

Fig. 12

Convergence of the (standard and adaptive) FE method (left) and degrees-of-freedom to error plot (right) where $\ell$ is a Poisson(2)-process and we impose homogeneous Dirichlet boundary conditions

8.3.1 Homogeneous Dirichlet Boundary Conditions

In our first experiment, we choose homogeneous Dirichlet boundary contitions on $\partial \mathcal {D}$ and set $\lambda =2$. Figure 11 shows samples of the diffusion coefficient and the corresponding PDE solutions approximated by the FE method.

We use $M=150$ samples so approximate the RMSE according to Eq. (16) with the non-adaptive and the adaptive FE approach. Figure 12 shows the approximated RMSE plotted against the inverse FE refinement parameter. For the adaptive FE approximations, the sample-dependent mesh refinement parameters on each discretization level are averaged over all 150 samples. We see a convergence with rate $\approx 0.65$ for the standard FE method, which is in line with our expectations (see Sect. 8.2). Further, we observe that the adaptive refinement strategy yields an improved convergence rate of $\approx 0.85$ and a smaller estimated RMSE on the considered levels.

Fig. 13

Samples of the diffusion coefficient with $\lambda =3$ and corresponding FE solution to the elliptic PDE with mixed Dirichlet-Neumann boundary conditions

The right hand side of Fig. 12 shows the estimated RMSE plotted against the degrees of freedom of the linear FE-system on each discretization level. For the adaptive FE method, the degrees of freedom are averaged over all samples. After a pre-asymptotic behaviour on the first and second level, we see that the adaptive FE method performs more efficient in terms of the degrees of freedom: the adaptive FE method achieves a certain RMSE with less degrees of freedom compared to the standard FE method.

8.3.2 Mixed Dirichlet-Neumann Boundary Conditions

In the second numerical example, we use mixed Dirichlet-Neumann boundary conditions: we split the domain boundary $\partial \mathcal {D}$ by $\Gamma _1=\{0,1\}\times [0,1]$ and $\Gamma _2=(0,1)\times \{0,1\}$ and impose the following pathwise boundary conditions

$$\begin{aligned} u(\omega ,\cdot )={\left\{ \begin{array}{ll} 0.1 &{} ~on~ \{0\}\times [0,1] \\ 0.3 &{}~on~\{1\}\times [0,1] \end{array}\right. } \text { and } a\overrightarrow{n}\cdot \nabla u=0 \text { on } \Gamma _2, \end{aligned}$$

for $\omega \in \Omega$. Further, we set $\lambda =3$, which results in a higher number of jumps in the diffusion coefficient. Figure 13 shows samples of the diffusion coefficient and the corresponding PDE solutions approximated by the FE method.

As in the first experiment, we use $M=150$ samples to approximate the RMSE according to (14) with the standard FE approach and the adaptive approach. The approximated values are plotted against the inverse FE refinement parameter. The results are presented in Fig. 14, which shows a convergence rate of $\approx 0.6$ for the standard FE approach, which is slightly smaller than the observed convergence rate of $\approx 0.65$ in the first numerical example, where we imposed homogeneous Dirichlet boundary conditions and considered a Poisson process with intensity parameter $\lambda = 2$, leading to a smaller expected number of jumps in the diffusion coefficient. Further, Fig. 14 shows a convergence rate of $\approx 0.85$ for the adaptive FE approach and smaller magnitudes of the RMSE compared to the standard FE method. The right plot of Fig. 14 reveals the higher efficiency of the adaptive FE method compared to the standard approach in the sense that the number of degrees of freedom, which are necessary to achieve a certain error, is significantly smaller compared to the standard FE approach. Further, we see that the performance difference of the standard and the adaptive FE method is larger compared to the first example due to the higher number of expected jumps in the diffusion coefficient, which renders the adaptive local refinement strategy even more suitable for this problem. Overall, the results are in line with our expectations.

Fig. 14

Convergence of the (standard and adaptive) FE method (left) and degrees-of-freedom to error plot (right) where $\ell$ is a Poisson(3)-process and we impose mixed Dirichlet-Neumann boundary conditions

Fig. 15

Convergence of the (standard and adaptive) FE method (left) and degrees-of-freedom to error plot (right) where $\ell$ is a Poisson(4)-process, we impose mixed Dirichlet-Neumann boundary conditions and use a high-contrast diffusion coefficient

8.3.3 Mixed Dirichlet-Neumann Boundary Conditions and Jump- Accentuated Coefficients

In our last experiment we consider mixed Dirichlet-Neumann boundary conditions as in the previous section. The diffusion coefficient is set to be

$$\begin{aligned} a(x,y) = 0.01 + 0.01\,\exp (W_1(x,y)) + 30\,\ell (F(W_2(x,y)), \end{aligned}$$

for $(x,y)\in \mathcal {D}$, where $\ell$ is a Poisson(4)-process. This leads to a jump-accentuated coefficient with high contrast. We take $M=500$ samples to estimate the RMSE for the standard FE method and the adaptive approach according to (16). The results are presented in Fig. 15.

We obtain a convergence rate of $\approx 0.55$ for the standard FE approach and $\approx 0.8$ for the adaptive FE method, which is slightly slower than the observed rates in the previous experiment. This is in line with our expectations since we have an increased jump intensity in the underlying Poisson process and larger jump heights in the diffusion coefficient, both having a negative influence on the convergence rate of the FE method (see also Merkle and Barth (2022c); Barth and Stein (2018b); Petzoldt (2001)). Figure 15 also reveals, as expected, that the magnitude of the RMSE is significantly smaller in the adaptive FE approach. The right plot of Fig. 15 demonstrates that the adaptive refinement strategy is able to achieve a certain error with significantly less degrees of freedom in the corresponding linear FE system, than the standard FE approach.