Abstract
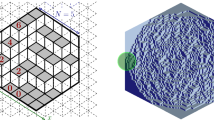
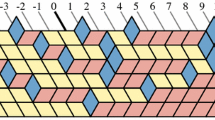
We study lozenge tilings of a domain with partially free boundary. In particular, we consider a trapezoidal domain (half-hexagon), s.t. the horizontal lozenges on the long side can intersect it anywhere to protrude halfway across. We show that the positions of the horizontal lozenges near the opposite flat vertical boundary have the same joint distribution as the eigenvalues from a Gaussian Unitary Ensemble (the GUE-corners/minors process). We also prove the existence of a limit shape of the height function, which is also a vertically symmetric plane partition. Both behaviors are shown to coincide with those of the corresponding doubled fixed boundary hexagonal domain. We also consider domains where the different sides converge to \({\infty}\) at different rates and recover again the GUE-corners process near the boundary.
Similar content being viewed by others
References
Baryshnikov Y.: GUEs and queues. Probab. Theory Relat. Fields 119(2), 256–274 (2001)
Billinglsey, P.: Probability and measure, 3rd edn. Wiley, New York (1995)
Borodin, A., Bufetov A., Olshanski G.: Limit shapes for growing extreme characters of \({U(\infty)}\) . arXiv:1311.5697
Borodin A., Corwin I., Gorin V.: Stochastic six-vertex model (2014, preprint). arXiv:1407.6729
Bufetov A., Gorin V.: Representations of classical Lie groups and quantized free convolution. arXiv:1311.5780
Ciucu M., Krattenthaler C.: The interaction of a gap with a free boundary in a two dimensional dimer system. Commun. Math. Phys 302, 253–289 (2011)
Cohn, H., Kenyon, R., Propp, J.: A variational principle for domino tilings. J. Am. Math. Soc. 14(2), 297–346 (2001) arXiv:math/0008220
Cohn, H., Larsen, M., Propp, J.: The shape of a typical boxed plane partition. N. Y. J. Math 4, 137–165 (1998) arXiv:math/9801059
Di Francesco Ph., Reshetikhin N.: Asymptotic shapes with free boundaries. Commun. Math. Phys 309(1), 87–121 (2012)
Forrester P., Nordenstam E.: The anti-symmetric GUE minors process. Mosc. Math. J. 9(4), 749–774 (2009)
Fulton, W., Harris, J.: Representation Theory: A First Course. Springer-Verlag, Berlin (1991)
Gorin, V., Panova, G.: Asymptotics of symmetric polynomials with applications to statistical mechanics and representation theory. Ann. Probab. (to appear) (2014)
Johansson K., Nordenstam E.: Eigenvalues of GUE minors. Electron J. Probab. 11(50), 1342–1371 (2006)
Kenyon, R.: Lectures on dimers. IAS/Park City Mathematical Series, vol. 16: Statistical Mechanics, AMS (2009) arXiv:0910.3129
Kenyon, R., Okounkov, A.: Limit shapes and Burgers equation. Acta Math. 199(2), 263–302 (2007) arXiv:math-ph/0507007
Kenyon, R., Okounkov, A., Sheffield, S.: Dimers and amoebae. Ann. Math. (2) 163(3), 1019–1056 (2006)
Krattenthaler C.: Identities for classical group characters of nearly rectangular shape. J. Algebra 209(1), 1–64 (1998)
Macdonald, I.G.: Symmetric functions and Hall polynomials, 2nd edn. Oxford University Press, Oxford (1999)
Mehta, M.L.: Random matrices. Academic Press, Series: Pure and Applied Mathematics (2004)
Nordenstam, E.: Interlaced particles in tilings and random matrices. Doctoral thesis, KTH (2009)
Nordenstam, E., Young, B.: Domino shuffling on Novak half-hexagons and Aztec half-diamonds. Electron. J. Comb. 18 (2011) arXiv:1103.5054
Novak J.: On the central limit theorem for lozenge tilings of sawtooth domains (preprint)
Yu A., Okounkov N., Reshetikhin Y.: The birth of a random matrix. Mosc. Math. J. 6(3), 553–566 (2006)
Petrov, L.: Asymptotics of random Lozenge tilings via Gelfand–Tsetlin schemes. Probab. Theory Relat. Fields (2013) arXiv:1202.3901
Proctor R.: Bruhat lattices, plane partition generating functions, and minuscule representations. Eur. J. Comb. 5(4), 331–350 (1984)
Sagan, B.E.: The ubiquitous Young tableau. Invariant theory and tableaux (Minneapolis, MN, 1988), IMA Vol. Math. Appl., 19, pp. 262–298. Springer, New York (1990)
Sheffield, S.: Random Surfaces: Large Deviations Principles and Gradient Gibbs Measure Classifications. PhD Thesis, Standford Univ. (2003)
Stanley, R.P.: Enumerative combinatorics, vol. 2. Cambridge Studies in Advanced Mathematics, vol. 62. Cambridge University Press, Cambridge (1999)
Weyl, H.: The Classical Groups: Their Invariants and Representations. Princeton University Press, Princeton (1939)
Zhelobenko, D.P.: Compact Lie Groups and their Representations. Nauka, Moscow (1970) (Russian); English translation: Transl. Math. Monographs 40, A. M. S., Providence, RI, 1973
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Panova, G. Lozenge Tilings with Free Boundaries. Lett Math Phys 105, 1551–1586 (2015). https://doi.org/10.1007/s11005-015-0794-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-015-0794-6