Resource Model Updating For Compositional Geometallurgical Variables

Abstract

In the field of mineral resources extraction, one main challenge is to meet production targets in terms of geometallurgical properties. These properties influence the processing of the ore and are often represented in resource modeling by coregionalized variables with a complex relationship between them. Valuable data are available about geometalurgical properties and their interaction with the beneficiation process given sensor technologies during production monitoring. The aim of this research is to update resource models as new observations become available. A popular method for updating is the ensemble Kalman filter. This method relies on Gaussian assumptions and uses a set of realizations of the simulated models to derive sample covariances that can propagate the uncertainty between real observations and simulated ones. Hence, the relationship among variables has a compositional nature, such that updating these models while keeping the compositional constraints is a practical requirement in order to improve the accuracy of the updated models. This paper presents an updating framework for compositional data based on ensemble Kalman filter which allows us to work with compositions that are transformed into a multivariate Gaussian space by log-ratio transformation and flow anamorphosis. This flow anamorphosis, transforms the distribution of the variables to joint normality while reasonably keeping the dependencies between components. Furthermore, the positiveness of those variables, after updating the simulated models, is satisfied. The method is implemented in a bauxite deposit, demonstrating the performance of the proposed approach.

1 Introduction

Predictive geometallurgy is a challenging topic in the mining industry. This discipline aims at providing quantitative approaches to forecast and optimize all steps of the mineral value chain from exploration to different processing circuits (Tolosana-Delgado and van den Boogaart 2018). In doing so, geometallurgy considers all ore properties that will have an influence on the process to obtain a final metal product, not just a grade. Thus, modeling geometallurgical variables involves the highly multivariate settings of the problem with complex relationships between geometallurgical variables (Boisvert et al. 2013). Understanding the spatial distribution of the geometallurgical variables is key for the efficiency of mine planning production scheduling and operation control (Benndorf and Dimitrakopoulos 2018). During grade control, a large number of samples are obtained. An opportunity to decrease the uncertainty related to the resource model knowledge is to assimilate these monitoring data into the model. In that regard, Benndorf (2015) has proposed to use a closed-loop reconciliation system that nearly continuously generates updates of the model in real-time. This method provides up-to-date information for decision-makers in mine planning and operation control. Based on ensemble Kalman filter (EnKF), some univariate approaches of this updating method have been documented and successfully implemented in an operational framework in recent years (Benndorf 2015; Yüksel et al. 2017; Wambeke and Benndorf 2017).

Stewart (2016) generally distinguishes between primary and secondary properties of the ore, the former being uniquely related to the ore while the latter depends on its processing. This contribution focuses on primary geometallurgical variables. The most commonly used primary geometallurgical properties involve characteristics of the elements (as proportions), minerals (as modal mineralogies), texture, hardness, fragmentation, among others (Rossi et al. 2014; Tolosana-Delgado and van den Boogaart 2018). Many of these variables, such as geochemical data, modal mineralogy or mineral association, can be expressed in ppm, percentage, etc. This contribution focuses on geometallurgical variables of a compositional nature such as geochemical compositions. These variables are formed by vectors of positive components (Pawlowsky-Glahn and Buccianti 2011) and are often mutually linked through complex multivariate relationships such as non-linearities and heteroscedasticities (Nathan and Scobell 2012; Hosseini and Asghari 2019). This compromises the traditional geostatistical analysis, since a separate Normal Score transformation of each variable would not yield a multivariate Gaussian distribution (Hosseini and Asghari 2019). These variables are measured with sensor-based techniques that allow online monitoring, providing a large amount of data with low accuracy in the absolute abundances of the measured components. EnKF methods combine the simulated model, as prior information, and observation monitored by sensors to update the realizations of the simulated model. Meanwhile, in classical application environments of EnKF observations are obtained repeatedly in the same position, in mining, every new observation is obtained at a different location. However, the application of this method to resource model updating in a multivariate setting in particular, is a challenging issue. In this contribution, several challenges are identified and addressed. First, the proposed method has to provide a reasonable result when the support (the volume of reference) of the simulated model and the observations differ. The support problem is well known in mining (Wackernagel 2003). This consists of anticipating, before production, what the proportion of the profitable SMUs will be based on initial exploration data, so that a decision can be taken about wether to start extraction. Observations are usually obtained by bulk sampling the volume of each SMU after the blasting operation are used to update the grade-control model that might be represented at point support. This issue has been extensively documented within the inverse problem literature (Hansen et al. 2006) or in geostatistics (Wackernagel 2003). It is important to remark that the deposit is not a dynamic system that changes over time, it is, instead, our knowledge about it what evolves.

The second challenge is that the variables considered here are compositional. Working with compositions within the EnKF framework breaks the linear analysis assumptions in Gaussian settings: zero probabilities should be assigned to negative values since physical observations of a non-negative variable will not be negative (Amezcua and Van Leeuwen 2014). This positiveness is reflected in the support (domain) of the distribution over zero since it is not able to take negative values. However, after updating the variables, one might see negative values breaking the consistency of the constrained data (as compositional data). For that reason, these transformations are of crucial importance. This issue is discussed at length and referenced in Amezcua and Van Leeuwen (2014).

EnKF is not applicable for the estimation of discontinuous functions or non-negative states (Chen and Snyder 2007; Simon and Bertino 2009). The nature of the observation error is seldom additive. Indeed, this error tends to be multiplicative according to Amezcua and Van Leeuwen (2014). Some authors (Bertino et al. 2002; Simon and Bertino 2009; Simon et al. 2012) have proposed to map the positive variables into a Gaussian space by a non-linear change of variables named anamorphosis. Janjić et al. (2014) have proposed to work with logarithms only to update the model in consistency with Gaussian assumptions. In that study, a positive error is added to the state variable to allow computing the logarithm transformation when these are zero. Simon et al. (2012) have proposed to work in a hyperspherical coordinate system to ensure the constant sum of components, arguing that the log-ratio transformation may produce problems when one of the components is zero.

For large-scale settings, the compositions can significantly change from one region to another. Here, it is assumed that all the components analysed are present in the whole area of study. The first step (Aitchison 1984; Pawlowsky-Glahn et al. 2015) to solve compositional data problems in geostatistics is to transform the data by means of log-ratio transformations (alr, clr or ilr). This removes the sum constraint and avoids spurious correlation problems (Pearson 1897; Pawlowsky-Glahn et al. 2015). Then one can apply standard techniques to the scores, for example model variograms, in order to perform a co-Kriging or co-simulation. After obtaining the spatially interpolated model, a transformation to the original composition is needed to interpret the results of this study. This contribution makes use of this general approach. However, EnKF is optimal for Gaussian assumptions, and the non-Gaussianity of the variables makes its use suboptimal (Carrassi et al. 2018). Many methods for simulation and co-simulation of random fields are derived from the framework of Gaussian processes. Nevertheless, the assumption of Gaussianity is seldom acceptable in multivariate regionalized compositional data. Several techniques have been proposed for mapping variables into a Gaussian space. Univariate Gaussian anamorphosis or Normal Score transformations are commonly used (Verly 1984; Ziegel et al. 1998; Simon and Bertino 2009; Chiles et al. 2000; Amezcua and Van Leeuwen 2014; Zhou et al. 2012). However, only the marginal distributions of the variables are transformed to normality, independently from each other. This does not guarantee that the joint distributions become multivariate Gaussian normal (Zhou et al. 2011; Carrassi et al. 2018). Recently, two approaches to transform data into a multivariate Gaussian space have been proposed: the Projection Pursuit Multivariate Transform (Barnett et al. 2014; Nathan and Scobell 2012) and flow anamorphosis (van den Boogaart et al. 2017; Mueller et al. 2017). These methods have never been combined with EnKF.

This contribution presents a new assimilation framework for compositional data. This study accounts for the problems of positivity preservation and the sum to one constraint after updating the model by working with log-ratios of the components and flow anamorphosis (Tolosana-Delgado and van den Boogaart 2018). In this way, multi-Gaussianity of observations and model variables are achieved. At the same time, the framework allows one to naturally work with multiplicative error observation models and capture the relative nature of many modern online sensors.

The framework introduced in this paper was applied to a real case study from a bauxite deposit in the Caribbean. The bulk sampling process was simulated a selecting defined SMUs and perturbing these with observation errors. The complex relationship of the variables was co-simulated. Practical considerations of the transformations and EnKF when working with real data are demonstrated in this way. This paper is subdivided into several sections. Section 2 reviews the mathematical foundations of the method. Section 3 explains the updating algorithm that has been developed. Section 4 explores the application to a real test case study is described. Section 5 presents conclusions. For completeness, some theoretical developments associated are reported in Appendix 1.

2 Mathematical Foundation

2.1 Fundamental Concepts of Compositional Data

Compositional data quantitatively describe the relative weight, importance or contribution of some parts of a whole. The sample space of compositional data is the simplex,

$$\begin{aligned} S ^D = \left\{ \mathbf{s } \in {\mathbb {R}}^D \quad | \quad \text {s}_i > 0, \quad \sum _{i=1}^{D} \text {s}_i = {\mathsf {k}}\right\} \text {,} \end{aligned}$$

(1)

where ${\mathsf {k}}$ is the closure constraint constant. The purpose of compositional data analysis is to capture the relative information conveyed by data through a log-ratio transformation. Several transformations can be found in literature: additive log-ratio (alr) (Aitchison 1984), centered log-ratio (Jones and Aitchison 1987), isometric log-ratio (Egozcue et al. 2003), and others proposed by Jones and Aitchison (1987). The scores of some of these transformations are related to each other through linear relations (Aitchison 1984; Egozcue et al. 2003). In Appendix 1 it is proven that, under these circumstances, all invertible log-ratio transformations provide equivalent results. Hence, in this paper, the alr will be used. This transformation consists of applying the logarithm to the relation between each component and a chosen component as denominator, for instance the last one

$$\begin{aligned} \begin{array}{ll} &{}\mathrm {alr}:{\mathbb {S}}^D \rightarrow {\mathbb {R}}^{D-1} \\ &{}\mathbf{s } \mapsto \mathbf{x } = \left( \ln \frac{\text {s}_1}{\text {s}_D}, \ln \frac{\text {s}_2}{\text {s}_D}, \cdots , \ln \frac{\text {s}_{D-1}}{\text {s}_D}\right) \end{array} \text {,} \end{aligned}$$

(2)

where the inverse transformation is

$$\begin{aligned} \begin{array}{ll} &{}\mathrm {alr}^{-1}:{\mathbb {R}}^{D-1} \rightarrow {\mathbb {S}}^D \\ &{}\mathbf{x } \mapsto \mathbf{s } = {\mathcal {C}}[\exp (\text {x}_1),\dots ,\exp (\text {x}_{D-1}),1 ] \end{array} \text {,} \end{aligned}$$

(3)

The closure operator is here denoted as ${\mathcal {C}}$. It scales its argument to ensure that the result satisfies the constant sum constraint (Pawlowsky-Glahn et al. 2015). Moreover, $\mathbf{S }=[S_1,S_2,\dots ,S_D]$ denotes a random composition and the alr transformation $\mathbf{X } = {{\,\mathrm{\mathrm {alr}}\,}}(\mathbf{S })$.

2.2 Flow Anamorphosis

Constructing the right flow anamorphosis transformation is of special importance in mineral resource estimation since different data sets are treated during the run of the mine (Mariz et al. 2019). These are obtained by different sampling methods and sensor devices. Moreover, the measurement times and the key variables measured might differ between data sets. These variations are reflected in the quality of each data set and show differences in the statistics. Real data usually show bias, specially in the production data with respect to the exploration data. This bias should be considered when the transformation is computed. Furthermore, Amezcua and Van Leeuwen (2014) proposed different ways to apply the univariate Gaussian anamorphosis: independent transformations for state variables and observations, or joint state variable and observation transformations. Since this study is performed by a twin experiment where the production data is simulated by mapping from a ground truth model, the observations domain and the state vector are assumed to be the same. Therefore, two transformations are taken into account in the current study: for a grid point support ${\varvec{\phi }}_\mathbf{u }$ and for a SMU support ${\varvec{\phi }}_\mathbf{v }$.

In order to implement the EnKF, the log-ratio transformed compositions are further transformed into a Gaussian space. In the field of data assimilation it is common to apply such a transformation to normality prior to the data analysis, often via a univariate anamorphosis (Simon and Bertino 2009). However, this approach is inappropriate for compositional data because the resulting scores do not necessarily show joint multi-Gaussianity, nor do they reproduce the original dependence relationships between variables. The flow anamorphosis transforms data by means of a smooth deformation of the underlying space transporting the probability mass from a kernel density estimate of the original distribution to a multivariate standard Gaussian distribution (Mueller et al. 2017). The flow anamorphosis is a truly multivariate Gaussian anamorphosis and presents invariance under affine transformations, hence it provides a Normal Score transformation that guarantees that the results do not depend on the choice of log ratio transformation (Mueller et al. 2017). The transformation is non-linear and its deformation is controlled by the original bandwidth of the kernel estimation (van den Boogaart et al. 2017; Mueller et al. 2017). In this contribution, $\mathbf{Z }$ is used to denote the Gaussian transformed data, $\mathbf{Z }=\phi (\mathbf{X })$. Hence, if X is a random alr transformed composition, then Z will be a Gaussian random vector.

2.3 Compositional Random Function

The initial model is assumed to be a regionalized vector-valued random function $\mathbf{Z }(\mathbf{u })$ indexed by $\mathbf{u } \in {\mathbb {R}}^3$, a spatial location on a three-dimensional Euclidean space. At each location, the random field has $(D-1)$-components $\mathbf{Z }(\mathbf{u }) = [Z_1(\mathbf{u }), \dots , Z_{\text {D-1}}(\mathbf{u })]$. Intrinsic stationarity of the random function $\mathbf{Z }(\mathbf{u })$ is assumed. This implies that the expected increment of the vector random function between two different locations ($\mathbf{u }_1$ and $\mathbf{u }_2$) is zero and its variance does not depend on the exact locations being considered, but on their lag distance $\mathbf{h }=\mathbf{u }_1 - \mathbf{u }_2$

$$\begin{aligned} {{\,\mathrm{{\mathbb {E}}}\,}}[\mathbf{Z }(\mathbf{u }_1) -\mathbf{Z }(\mathbf{u }_2)]&= 0 \text {,} \end{aligned}$$

(4)

$$\begin{aligned} \text {Var}[\mathbf{Z }(\mathbf{u }_1) - \mathbf{Z }(\mathbf{u }_2)]&= {\varvec{\Gamma }}_{\mathbf{Z }}(\mathbf{h })\text {.} \end{aligned}$$

(5)

${\varvec{\Gamma }}_{\mathbf{Z }}(\mathbf{h })$ represents a matrix valued variogram

$$\begin{aligned} {\varvec{\Gamma }}_{\mathbf{Z }}(\mathbf{h })&= \frac{1}{2}{{\,\mathrm{{\mathbb {E}}}\,}}[(\mathbf{Z }(\mathbf{u}+h ) - \mathbf{Z }(\mathbf{u }))(\mathbf{Z }(\mathbf{u}+h ) - \mathbf{Z }(\mathbf{u }))^T] \text {,} \end{aligned}$$

(6)

to be estimated as usual in geostatistics (Wackernagel 2003; Pawlowsky-Glahn et al. 2015). The empirical variogram values are modelled through a linear model of coregionalization (LMC) to ensure the conditional negative-definiteness of the system (Wackernagel 2003) as

$$\begin{aligned} {\varvec{\Gamma }}_{\mathbf{Z }}(\mathbf{h }) = \sum _{u=0}^{s}\mathbf{B }_u{\varvec{\gamma }}_u(\mathbf{h })\text {,} \end{aligned}$$

(7)

with $\gamma _u$ a variogram model with unit sill and {$\mathbf{B }_u\} \in {\mathbb {R}}^{D-1\times D-1}$ symmetric positive semi-definite matrices for each u, being $\mathbf{B } = \sum _{u=0}^{s} \mathbf{B }_u$. These matrices describe the correlation structure of a multivariate spatial process at different spatial scales given by the ranges of the variogram models $\gamma _u$ attached to them (Rondon 2012). Unsampled locations are co-simulated with the proposed fitted model using any appropriate geostatistical simulation technique, such as sequential Gaussian simulation (Carr 2003).

2.4 The Support Effect in Compositions

In this contribution two different supports were considered for production: point and SMU supports. The first one is a fine scale support matching the data support, for example, chip samples, channel sampling, boreholes or sensor excitation volumes over the mine face. The grade-control model is specified on this fine-scaled grid and used to improve the estimation of relatively small volumes of the deposit. The second support matches the SMU, which roughly coincides with the ore volume typically blasted. The grade control model is updated based on the observations made over this SMU volume.

In this study, the grade control model is simulated in two different grids. The fine scale model is given in a domain with locations that are indexed by $\mathbf{u }=\{\mathbf{u }_1, \mathbf{u }_2,\dots ,\mathbf{u }_n\}$. The model simulated at SMU support is obtained by re-blocking through averaging the cell grids contained in each unit. The model is indexed by the SMU locations $\mathbf{v }=\{\mathbf{v }_1, \mathbf{v }_2,\dots ,\mathbf{v }_m\}$.

The function that re-blocks the cell grids contained by each block is

$$\begin{aligned} \psi _{\mathbf{v }}(\mathbf{v }) = \mathbf{S }(\mathbf{v }) = \int _{\mathbf{v }} \mathbf{S }(\mathbf{u }')d\mathbf{u }' \approx \frac{1}{\#\mathbf{u }(\mathbf{v })} \sum _{\mathbf{u }'_i \in \mathbf{u }(\mathbf{v })} \mathbf{S }(\mathbf{u }'_i) ,\, \end{aligned}$$

(8)

where $\mathbf{u }'$ represents each $\mathbf{u }$ point that discretizes the analyzed SMU $\mathbf{v }$ and $\#\mathbf{u }(\mathbf{v })$ is the total number of grid cells within the block v.

This re-blocking function shows a non-linear behaviour when applied as part of the composite functions Eqs. (12) and (13). This will be discussed later.

It is important to remark that Eq. (8) follows the assumption that both mass and volume of the block have a linear relationship, avoiding to compute the integral with the density (Tolosana-Delgado et al. 2014). This has been assumed due to the lack of data (e.g., permeability) available for the experiment.

3 Model Updating

3.1 Ensemble Filter Update

The updating method proposed here for a static system is the EnKF (Evensen 1994; Burgers et al. 1998; Kalman 1960). This method sequentially estimates the space time system state and its uncertainty by means of a collection of realizations of the state variables or ensemble. The average of the ensemble is taken as the estimate of the true state, while the variance of the ensembles represents the uncertainty related to that estimate.

A system that does not evolve on time but is regularly sampled at different times (or locations) is represented by a set of ensembles reproducing the desired Gaussian random function $\mathbf{Z }(\mathbf{u },t)$. The sample location relates to time and space, as each point can only be sampled once. The observations are on SMU support and these are reconciled into a grade control model defined by a point support. The simulated random field of the system is represented by $\mathbf{Z }_t \in {\mathbb {R}}^{n\cdot (D-1) \times r}$, where r is the number of realizations and n the number of cell grids in the simulated model. This matrix is updated based on information gathered up to a time t. Columns $\mathbf{z }_{t}^i$ of $\mathbf{Z }_{t}$ are r ensemble members represented as

$$\begin{aligned} \mathbf{z }_{t}^i&= [ \mathbf{z }_{t,1}^i, \mathbf{z }_{t,2}^i, \dots , \mathbf{z }_{t,D-1}^i ],&\quad i = 1,\dots ,r \text {, where} \end{aligned}$$

(9)

$$\begin{aligned} \mathbf{z }_{t,j}^i&= [ \text {z}_{t,j}^i(\mathbf{u }_1),\dots , \text {z}_{t,j}^i(\mathbf{u }_n)],&\quad j = 1,\dots ,D-1 \text {,.} \end{aligned}$$

(10)

Here the state vector $\mathbf{z }_{t}^i \in {\mathbb {R}}^{n\cdot (D-1)}$ represents the ith realization of the $D-1$ variables gridded into n cell grids located by $\mathbf{u }$.

Thus, the updating step (also known as analysis step) that conditions the state variable to the observed data gives

$$\begin{aligned} \mathbf{Z }_{t+1} = \mathbf{Z }_{t} + \mathbf{W }_{t+1}(\mathbf{Y }_{t+1} - {\mathcal {A}}_{t+1, \mathbf{v }}(\mathbf{Z }_{t})) \text {,} \end{aligned}$$

(11)

with ${\mathcal {A}}_{t+1,\mathbf{v }}(\mathbf{Z }_{t})$ the observation operator that approximates the forward simulator and $\mathbf{Y }_{t+1} \in {\mathbb {R}}^{D-1\times r}$ the matrix of observations. The matrix $\mathbf{W }_{t+1}\in {\mathbb {R}}^{n\cdot (D-1)\times (D-1)}$ denotes the Kalman gain operator that is applied to each ensemble member. The updating step for a time invariant system is optimal under conditions of (i) Gaussianity in the non-updated model (prior ensemble), (ii) linearity of the observation operator and observations and (iii) Gaussianity in the additive observation error. When these conditions are not satisfied, the application of the EnKF in the analysis step is sub-optimal, but can still be satisfactory in a non-linear, non-Gaussian and high dimensional setting (Wikle and Berliner 2007; Amezcua and Van Leeuwen 2014; Carrassi et al. 2018). In the current study, the observation operator is non-linear since it is a combination of additive up-scaling, log-ratio calculations and flow anamorphosis. Moreover, the updating operation has to satisfy the Gaussianity of the prior ensemble. Thus, the application of the EnKF in the present study operates on sub-optimal conditions.

Fig. 1

Flow-chart describing the strategy followed for the data assimilation process control simulated model updating

3.2 Implementation Strategy

Figure 1 shows a flow-chart of the approach followed in this study. The initial information is given by vector $\mathbf{s }_0(\mathbf{u }_{{\varvec{\alpha }}})$. This vector is indexed by the set of locations $\mathbf{u }_\alpha$ on a point support. The ${{\,\mathrm{\mathrm {alr}}\,}}$ transformation is applied to transform the data into the log-ratio space as $\mathbf{x }_0(\mathbf{u }_{{\varvec{\alpha }}})$. This set of vectors used to compute a flow anamorphosis transformation ${\varvec{\phi }}_\mathbf{u }$ for data indexed in the point support $\mathbf{u }$ giving as a result the new Gaussian vector $\mathbf{z }_0(\mathbf{u }_{\varvec{\alpha }})$. This is coregionalized as explained in Sect. 2.3. The Gaussian vector is used as conditional information to simulate a model at point-support $\mathbf{u }$.

The ${\varvec{\phi }}_\mathbf{u }$ and the ${{\,\mathrm{\mathrm {alr}}\,}}$ transformations are used to back-transform the point-support Gaussian data into the compositional scale. Then, a re-blocking of the multiple grids is performed in order to obtain a SMU model $\mathbf{S }_0(\mathbf{v })$ for each realization. The SMUs obtained from this simulation are used to compute the transformation ${\varvec{\phi }}_\mathbf{v }$ at SMU support that transforms each SMU value into a Gaussian space of the model $\mathbf{Z }_0(\mathbf{v })$. Amezcua and Van Leeuwen (2014) propose different ways to apply the Gaussian anarmophosis: independent transformations for state variables and observations, or joint state variable and observation transformations. In this study, the sample space of the observations and the state variable at SMU (volume) support are the same. Therefore, the same transformation ${\varvec{\phi }}_\mathbf{v }$ is applied to them.

First, the vectors of observations $\mathbf{d }\in {\mathbb {R}}^{d}$ are transformed into the Gaussian space by applying the composite function $(\psi _{\mathbf{v }} \circ {{\,\mathrm{\mathrm {alr}}\,}})$. This is replicated r times to produce the perturbed observations matrix $\mathbf{Y }_{t+1} \in {\mathbb {R}}^{(D-1)\times r}$

$$\begin{aligned} \mathbf{Y }_{t+1} = (\phi _{\mathbf{v }} \circ {{\,\mathrm{\mathrm {alr}}\,}})(\mathbf{d }_{t+1})\mathbf{1 }_{D-1\times r} + \mathbf{E }_{t+1}; \qquad \mathbf{E }_{t+1} \sim {\mathcal {N}}(0,\, \mathbf{C }_{t+1,\text {vv}})\,. \end{aligned}$$

(12)

Here the matrix $\mathbf{E }_{t+1}\in {\mathbb {R}}^{(D-1)\times r}$ shows the observation error as an additive random error term and $\mathbf{C }_{t+1,\text {vv}}$ the error covariance of the observations at time $t+1$. This represents the time independent instrumental error of the observing devices. These observations are transformed before adding the error and each realization is back transformed at each time before the next propagation step (Carrassi et al. 2018). The change of support function $\psi _{\mathbf{v }}$ is implemented over the cell grids in point support contained in the SMU at the original components and back transformed as

$$\begin{aligned} {\mathcal {A}}_{t+1,\mathbf{v }}(\mathbf{Z }_t)= (\phi _{\mathbf{v }} \circ {{\,\mathrm{\mathrm {alr}}\,}}\circ \psi _{\mathbf{v }} \circ {{\,\mathrm{\mathrm {alr}}\,}}^{-1} \circ \phi _{\mathbf{u }}^{-1} )(\mathbf{Z }_t (\mathbf{u }(\mathbf{v }))) ,\, \end{aligned}$$

(13)

where ${\mathcal {A}}_{t+1,\mathbf{v }}: {\mathbb {R}}^{(D-1) \times n'} \rightarrow {\mathbb {R}}^{D-1}$. Thus, the observation operator happens to be a function of state variables at the nodes of the grid that fall within the SMU $\mathbf{v }$ being observed in a time t. It depends essentially on the mine scheduling. As indicated by the observations, this observation operator is also a non-linear function. This study is simplified to the observation of one SMU at a time. Nevertheless, this can be easily extended to multiple SMUs observed simultaneously. In this case, assumptions about the sensor precision, measurement volumes, update intervals and blending ratios should be made following Wambeke and Benndorf (2017, (2018). The classical Kalman filter implements the Kalman gain matrix $\mathbf{W }_{t+1}$ as

$$\begin{aligned} \mathbf{W }_{t+1} = \mathbf{C }_{t,\text {zz}}\mathbf{A }_{t+1}^T(\mathbf{A }_{t+1}\mathbf{C }_{t,\text {zz}}\mathbf{A }_{t+1}^T + \mathbf{C }_{t+1,\text {vv}})^{-1} \,, \end{aligned}$$

(14)

where $\mathbf{A }_{t+1}\in {\mathbb {R}}^{n\cdot (D-1)\times D-1}$ is a linear operator. The superscript T refers to the transpose matrix and $\mathbf{C }_{t+1,\text {zz}}\in {\mathbb {R}}^{n\cdot (D-1)\times n\cdot (D-1)}$ is the error covariance matrix of the state variables. Formulating Kalman gain matrix for a general observation operator requires the linearisation of the $\text {A}_{t+1}$ term into the already defined ${\mathcal {A}}_{t+1,\mathbf{v }}$. However, the main idea behind EnKF is to use the information of multiple realizations to derive the covariance of the Kalman gain. Equation (14) is computed replacing the ensemble covariances by moment estimates of these quantities

$$\begin{aligned} \mathbf{C }_{t,\text {zz}}\mathbf{A }_{t+1}^T&\equiv \frac{1}{r-1}\big (\mathbf{Z }_t -\overline{\mathbf{Z }_t}\big ) \big ( {\mathcal {A}}_{t+1,\mathbf{v }}(\mathbf{Z }_{t}) - \overline{\mathbf{M }_{t}} \big )^T \,, \end{aligned}$$

(15a)

$$\begin{aligned} \mathbf{A }_{t+1}\mathbf{C }_{t,\text {zz}}\mathbf{A }_{t+1}^T + \mathbf{C }_{t+1,\text {vv}}&\equiv \frac{1}{r-1} \big ( \mathbf{L }_{t} - \overline{\mathbf{L }_{t}} \big ) \big ( \mathbf{L }_{t} - \overline{\mathbf{L }_{t}} \big )^T \,, \end{aligned}$$

(15b)

where bars denote ensemble averages

$$\begin{aligned} \overline{\mathbf{Z }_{t}}&= \Big (\frac{1}{r} \sum _{i=1}^{r}\mathbf{z }_{t}^i \Big )\mathbf{1 }^T_{n\cdot (D-1)} ,\, \end{aligned}$$

(16a)

$$\begin{aligned} \overline{\mathbf{L }_{t}}&= \Big (\frac{1}{r} \sum _{i=1}^{r} {\mathcal {A}}_{t+1,\mathbf{v }}(\mathbf{z }_{t}^i) + \mathbf{e }_{t+1}^i \Big )\mathbf{1 }^T_{n\cdot (D-1)} ,\, \end{aligned}$$

(16b)

$$\begin{aligned} \overline{\mathbf{M }_{t}}&= \Big (\frac{1}{r} \sum _{i=1}^{r} {\mathcal {A}}_{t+1,\mathbf{v }}(\mathbf{z }_{t}^i)\Big )\mathbf{1 }^T_{n\cdot (D-1)} \,. \end{aligned}$$

(16c)

Note that Eqs. (16a)–(16c) involve outer products, resulting in matrices and not scalar products. Here, $\mathbf{e }^i$ is the ith column vector of matrix $\mathbf{E }_{t+1}$ and

$$\begin{aligned} \mathbf{L }_{t} = {\mathcal {A}}_{t+1,\mathbf{v }}(\mathbf{Z }_{t})+ \mathbf{E }_{t+1} \,. \end{aligned}$$

(17)

This Monte-Carlo approach of the EnKF updates all the members of the ensemble in the analysis step. In order to provide appropriate sample estimators, the number of realizations (r) should be larger than the number of observations (Carrassi et al. 2018). Moreover, the initial realizations of the grade control model at a time $t=0$ should provide an appropriate representation of the deposit studied since the sample estimators will depend on this initial set of realizations. It is important to notice that EnKF approximates the non-linearities existing between the background model and the observations. In this way, Eq. (15a) estimates the covariance between point and SMU support through the realizations of the grade-control model at point support and the knowledge of the observations at a time step t for a SMU support. Moreover, Eq. (15b) considers the error in the measurements of the devices employed to perform the observation measurement. When this error is not considered, the Kalman gain can be identified by the co-Kriging weights (Vargas-Guzmán and Yeh 1999; Chiles et al. 2000; Dubrule 2018; Kumar and Srinivasan 2019).

3.3 Validation Strategy

In this section, the methodology proposed has been validated producing an individual realization $\mathbf{s }^*(\mathbf{v })$, not included in the EnKF ensemble calculations, to represent the ground truth. Following a log-ratio analysis to assess the accuracy of the assimilated compositions, the squared Aitchison’s distance between each realization and the ground truth vector with the real compositions are used as measures of the lack of fit

$$\begin{aligned} d^2_a(\mathbf{S }(\mathbf{v }),\mathbf{s }^*(\mathbf{v })) = \frac{1}{r} \sum _{i=1}^{r}\sum _{d=1}^{D} \Big (\log \frac{\text {s}^i_d(\mathbf{v })}{\mathbf{g }(\mathbf{s }^i(\mathbf{v }))} - \log \frac{\text {s}_d^*(\mathbf{v })}{\mathbf{g }(\mathbf{s }^*(\mathbf{v }))}\Big )^2, \quad i = 1,\dots ,r ,\, \end{aligned}$$

(18)

where $\mathbf{s }^*(\mathbf{u })$ is the true value of the modelled deposit. Then, $g(\mathbf{s }^i(\mathbf{v }))$ and $g(\mathbf{s}* (\mathbf{v }))$ are the geometric mean of each original composition for each realization and each SMU. Egozcue et al. (2018) related the squared Aitchison distance with the sample variance matrix of simple log-ratios between parts of a certain composition.

Since this study aims to assimilate constrained data as a vector of compositions, it is important to provide a measure between the updated and non-updated models. The Aitchison distance average over ensembles provides an appropriate measure of the updated model’s accuracy since this distance is doubly relative, it considers the relations among not any variables, but also among observations. The Aitchison distance can be interpreted as a measurement of both central tendency and dispersion with respect to the ground truth.

4 Application

4.1 Case Study Description

The deposit used in this study is a bauxite formation located in the Caribbean. The study location is one particular panel selected from 50 kt of ore. The components of interest are oxide minerals, such as g.Al$_2$O$_3$ (gibbsite), b.Al$_2$O$_3$ (bohemite), SiO$_2$, P$_2$O$_5$, Fe$_2$O$_3$ and the rest.

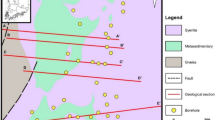
A total of 306 boreholes are drilled by an average sampling mesh of 15 by 15 m$^2$ spacing. Figure 2 shows a three-dimensional spatial representation of the boreholes used in this study. These are sampled at 1,501 intervals providing information of the six components of interest. This information corresponds to variable $\mathbf{s }_0(\mathbf{u }_{\varvec{\alpha }})$ in Fig. 1. The variable is transformed to Gaussian space by alr and the flow anamorphosis ($\mathbf{z }_0(\mathbf{u }_{\varvec{\alpha }})$). Figure 3 shows the histograms of the data in their original state and after applying the flow anamorphosis transformation (${\varvec{\phi }}_\mathbf{u }$). The number of components is reduced one when the log-ratio is applied. After applying flow anamorphosis, the variables do not physically represent the initial components anymore, as they are non-linear mixtures of the original variables.

Fig. 2

Map of the bore-holes used as initial information from the bauxite deposit

Fig. 3

Histograms of the initial compositions (blue) and the Gaussian transformed data (green)

Table 1 Descriptive analysis given by the mean, minimumn, maximum and standard deviation values and (co)variances of the initial data

Table 2 Descriptive analysis given by the mean, standard deviation and (co)variances of the transformed data

Table 1 summarizes the descriptive values of the original data. All variables are positive and their sum is 100 %. The right side of Table 1 shows the covariance between variables. On the other hand, Table 2 provides descriptive statistics of the Gaussian transformed data. These show a standard deviation close to 0.9. This parameter depends on the value of the kernels for the flow anamorphosis transformation.

Figure 4 illustrates the bivariate scatter plots of some variables and their associated distributions through the Gaussian kernel density estimated. The three panels in the upper part of Fig. 4 are scatter plots of the original data. These show that the variables do not follow a bivariate Gaussian marginal distribution. The three panels in the lower part of Fig. 4 are scatter plots of the variables after being transformed by flow anamorphosis. In contrast, to the upper scatter plots, these represent a multivariate Gaussian marginal distribution.

Fig. 4

Scatterplots of the initial data and after applying flow anamorphosis

4.2 Updating Process

After transforming the data into a Gaussian multivariate space, a three-dimensional model of the area of 120 m $\times$ 45 m $\times$ 33 m is simulated. This is conditionally simulated to the initial information producing 201 realizations. A panel of 60 m $\times$ 30 m $\times$ 3 m is selected to show the results of the experiment. One of these realizations is taken as ground truth in order to test the methodology in a fully known environment. In this way, the realization is known to be in the same support (domain) as the simulated model and a join transformation (${\varvec{\phi }}_\mathbf{v }$) for the observations and the simulated model are performed (Amezcua and Van Leeuwen 2014). However, taken as a ground truth one realizations simulated has the major drawback that this does not fully represent the reality. Therefore, this can be inappropriately narrow under model misspecification. This decision is made to simplify the problem and compute a transformation based on a compositional random field of the same grid support as the observations made.

Each SMU is set with a dimension of 3 m $\times$ 3 m $\times$ 3 m. A total of 40 SMUs are assimilated in the whole panel. Figure 5 is a representation of the grid support map of the six original non-updated compositions. The first two pannels correspond to the values of g.Al$_2$O$_3$ and SiO$_2$, the next two to P$_2$O$_5$ and b.Al$_2$O$_3$ and the last two to Fe$_2$O$_3$ and the rest. The rectangle in the middle of each map is the area where the 40 assimilated SMU are located. The extraction strategy is defined from west to east along each drift and from south to north through drifts. The update is implemented by observing the ground truth of the compositions. These are represented in Fig. 6 a SMU support. Figure 7 illustrates a SMU support map that is obtained after assimilating 10 SMUs (time $t=10$) of the first drift. This last SMU assimilated is represented by a black bold square within the assimilation rectangle. A localization function is implemented to exponentially decrease the correlations with distance in this spatial system (Carrassi et al. 2018). This function has a value one in 15 m a radio range from the center of the SMU that is being updated. Further than this range, the grids are weighted by a sigmoid function that happens to be the complement of the Gaussian cumulative distribution function with 0.6 standard deviation and 0 mean.

Fig. 5

Maps of the mean of the realizations of the original composition in the point support. g.Al$_2$O$_3$ (upper right), b.Al$_2$O$_3$ (upper left), SiO$_2$ (mid right), P$_2$O$_5$ (mid left), Fe$_2$O$_3$ (lower right) and rest (lower left). The black square correspond to the area of extraction

Fig. 6

Maps of the ground truth compositions at SMU support

This function is calculated by the cumulative distribution function (cdf) as $1-cdf$ of a normal distribution with 15 m as mean and standard deviation 0.6. This works as a re-weighting function with domain [0, 1]. The standard deviation is related to the abrupt change of the slope in the transition area between updated and non-updated cell grid, where areas further than this 15 m range are assumed to get negligible updating.

Fig. 7

Maps of the mean of the realizations of the original composition in the SMU-support. The simulated model is updated after observing ten SMUs (black small square)

Fig. 8

Histograms of the realizations of the 14th SMUs assimilated in the Gaussian transformed space. The blue histogram represents the non-updated model. The pink histograms represents the updated model at different times

Fig. 9

Ternary diagrams of the ensembles for the 14th SMU non-updated (blue), updated (pink) and the observation (beige) at times 11, 12, 13 and 14 (from first to last row)

Fig. 10

Kernels densities of the ensembles. Non updated (left), updated by a 9 m further SMU (mid), updated by a 6 m further SMU (right). Beige point is again the observation

The sensor error chosen in this study has zero mean and 0.1 standard deviation. The reported parameter defines the measurement error on a scale of a single SMU. The influence of this parameter on the overall performance of the algorithm has been addressed by Wambeke and Benndorf (2018). In this paper, only this error has been considered to test the proposed framework. After updating, the ensembles decrease the spread of the distribution, representing the uncertainty of the model. Moreover, the set of realizations move closer to the real value of the considered SMU. This effect is shown in Fig. 8, representing the histograms at different updating times. Each column represents a different variable (V1, V3 and V4) in the Gaussian space. The blue dashed line represents the ground truth value, also in the Gaussian space. Histograms in blue colour illustrate the realizations at updating time $t=0$ for the SMU that will be assimilated at $t=14$. For the pink histograms, the first three panels at the top of Fig. 8 represent the realizations for the SMU that will be observed at time $t=14$ after being updated at time $t=11$. The three pink histograms at the second row report the values at $t=12$ the SMU planned to be extracted at time $t=14$. In the third row, the ensembles are represented at time $t=13$ and the three bottom panels represent it at time $t=14$ (after assimilating). Accordingly, as the SMU is updated by closer neighbouring observations, the uncertainty about its values is reduced. Thus, when the model is updated at time $t=11$ and the SMU evaluated is the one that will be updated at time $t=14$ it means that the update is made upon information that is 9 m away (from the each SMU center). Following this argument, the rest of the ensembles represent information from 6 m, 3 m and 0 m respectively. It is interesting to observe how the variance decrements are reflected in the original compositions. The variance of the distribution of the ensembles updates decreases when the updated SMU is closer to the observation. As well, the mean value of the distribution is closer to the observed value. While this is observed for each component independently at Figs. 8, 9 shows ternary diagrams of the ensemble of the compositions when these are updated from SMU located at same distances. The point in beige represents the observation. The points in blue are the ensemble representation of the initial data. The points in pink represent the updated ensemble at different distances. The first row of ternary represents again 9 m distance updated ensembles. The second row represents 6 m distance, the third row 3 m distance, and the last row the updated ensemble at distance 0. The colour of the points represent the kernel density estimation for the set of points (realizations). These plots are interpreted as the joint behaviour of the updated ensemble of components with respect to the original ensemble. Coinciding with the results in Fig. 8, the variance of the distribution represented in each ternary diagram by the ensembles also decreases in a joint behaviour while keeping the sum constraint property. Figure 10 shows kernel density estimates for the SMU that are assimilated at time $t=14$ while this is updated at different times. The mode tends to move to the observed value while keeping the sum constraint of the components constant and the positivity of all the variables. Equation (18) is implemented for all the assimilated SMUs in order to provide a quantification of the reduced variance of the compositions. Table 3 shows the results obtained as an average of all the squared Aitchison distances for all the SMUs (of the panel). The uncertainty, in terms of squared Aitchison distance, is reduced by 42.7 % on average for all the assimilated panels between the non-assimilated model and evaluating neighbouring updated SMUs (i.e., evaluate SMUs at 9 m distance represents three SMUs apart).

Table 3 Average of the squared Aitchison distances between ensembles and the ground truth

5 Conclusions

The proposed methodology is an efficient method to update variables jointly with the presence of complex dependencies between themselves as non-linearities, heteroscedasticities and compositional constrains. The method combines the ease of modeling by compositional functions as chain transformations (additive log-ratios and flow anamorphosis) with different supports between the underlying models that represent reality and the observations obtained. The positiveness constrain of the variables is satisfied during the updating process by transforming these with log-ratio transformations and flow anamorphosis. The uncertainty of the assimilated variables is reduced while the relationship between variables are satisfied to the compositional constrains. The proposed methodology is applied to a bauxite deposit in the Caribbean. A ground truth model and a set of realizations as simulation of the compositional random field is simulated based on information obtained in a drill hole campaign.

The question still remains whether a proper transformation is achieved when the domain and the support of the real observations and the data that compute the transformation are not the same. Further research should address this problem and look at the influence of the spatial decorrelation of the variables by the Flow Anamorphosis and other methods such as Maximum-minimum Autocorrelation Factors (MAF) in the assimilation process.

Appendix: Invariance to the Choice of Log-ratio Representation.

In case one does want to use the framework proposed without using flow anamorphosis, it is important to show that the system is invariant to the different transformations available. Jones and Aitchison (1987) showed the relationship between alr and clr and Egozcue et al. (2003) showed the relation between ilr and clr. These are related by linear transformations. For the case of the alr there are D different transformations. These reduce the multivariate random vector into $D-1$ dimension. To simplify the case, the model represented by Eq. (11) is assumed to be one realization in its vector form as

$$\begin{aligned} \mathbf{z }_{t+1}^i = \mathbf{z }_{t}^i + \mathbf{W }_{t+1}(\mathbf{y }_{t+1}^i - {\mathcal {A}}_{t+1, \mathbf{v }}(\mathbf{z }_{t}^i) ) \quad \forall \quad i = 1,\dots ,r .\, \end{aligned}$$

(19)

Two different alr representations are considered

$$\begin{aligned}&\text {Representation 1:} \qquad \mathrm {alr}_1(\mathbf{s })= \mathbf{z }_1 = \left( \ln \frac{\text {z}_2}{\text {z}_1}, \ln \frac{\text {z}_3}{\text {z}_1}, \cdots , \ln \frac{\text {z}_{\text {D}-1}}{\text {z}_1}\right) ,\, \end{aligned}$$

(20a)

$$\begin{aligned}&\text {Representation 2:} \qquad \mathrm {alr}_2(\mathbf{s })= \mathbf{z }_2 = \left( \ln \frac{\text {z}_1}{\text {z}_2}, \ln \frac{\text {z}_3}{\text {z}_2}, \cdots , \ln \frac{\text {z}_{\text {D}-1}}{\text {z}_2}\right) ,\, \end{aligned}$$

(20b)

related with

$$\begin{aligned} \text {M}_{12}{{\,\mathrm{\mathrm {alr}}\,}}_1 = {{\,\mathrm{\mathrm {alr}}\,}}_2 ,\, \end{aligned}$$

(21)

where matrix $\text {M}_{12}$ is an invertible matrix that defines the change between representation 1 and 2. The transformation of the covariance is

$$\begin{aligned} \text {M}_{12} \mathrm {alr}_1(\mathbf{s }(\mathbf{x })) = \text {M}_{12} \mathbf{z }_1(\mathbf{x })&= \mathrm {alr}_2(\mathbf{s }(\mathbf{x })) = \mathbf{z }_2(\mathbf{x }) ,\, \end{aligned}$$

(22a)

$$\begin{aligned} \mathbf{C }_{t,\text {zz},1}&= \text {M}_{12}\mathbf{C }_{t,\text {zz,2}}\text {M}_{12}^t ,\, \end{aligned}$$

(22b)

extending this to the Kalman gain matrix as

$$\begin{aligned} \mathbf{W }_{t+1\text {, 2}}&= \text {M}_{12}\mathbf{C }_{t,\text {zd},1}\text {M}_{12}^t (\text {M}_{12}\mathbf{C }_{t,\text {dd},1}\text {M}_{12}^t)^{-1} \end{aligned}$$

(23a)

$$\begin{aligned}&= \text {M}_{12}\mathbf{C }_{t,\text {zd},1}\text {M}_{12}^t (\text {M}_{12}^t)^{-1}\mathbf{C }^{-1}_{t,\text {dd},1}\text {M}_{12}^{-1} \end{aligned}$$

(23b)

$$\begin{aligned}&= \text {M}_{12}\mathbf{C }_{t,\text {zd},1}\mathbf{C }^{-1}_{t,\text {dd},1}\text {M}_{12}^{-1}.\, \end{aligned}$$

(23c)

The Kalman filter is expressed as

$$\begin{aligned} \text {M}_{12} \mathbf{z }_{t+1, 1}&= \text {M}_{12} (\mathbf{z }_{t, 1} + \mathbf{W }_{t+1, 1}(\mathbf{d }_{t+1, 1} - {\mathcal {A}}_{t+1, \mathbf{v }}(\mathbf{z }_{t, 1}))) ,\, \end{aligned}$$

(24a)

$$\begin{aligned} \text {M}_{12} \mathbf{z }_{t+1, 1}&= \text {M}_{12}\mathbf{z }_{t, 1} + \text {M}_{12}\mathbf{W }_{t+1, 1}(\mathbf{d }_{t+1, 1} - {\mathcal {A}}_{t+1, \mathbf{v }}(\mathbf{z }_{t, 1})) ,\, \end{aligned}$$

(24b)

$$\begin{aligned} \text {M}_{12} \mathbf{z }_{t+1, 1}&= \text {M}_{12}\mathbf{z }_{t, 1} + \text {M}_{12}\mathbf{C }_{t,\text {zd},2}\mathbf{C }^{-1}_{t,\text {dd},2}\text {M}_{12}^{-1}\text {M}_{12}(\mathbf{d }_{t+1, 1} - {\mathcal {A}}_{t+1, \mathbf{v }}(\mathbf{z }_{t, 1})) ,\, \end{aligned}$$

(24c)

$$\begin{aligned} \mathbf{z }_{t+1, 2}&= \mathbf{z }_{t, 2} + \mathbf{C }_{t,\text {zd},2}\mathbf{C }^{-1}_{t,\text {dd},2}(\mathbf{d }_{t+1, 2} - {\mathcal {A}}_{t+1, \mathbf{v }}(\mathbf{z }_{t, 2})) .\, \end{aligned}$$

(24d)

$$\begin{aligned} \mathbf{z }_{t+1, 2}&= \mathbf{z }_{t, 2 } + \mathbf{W }_{t+1, 2}(\mathbf{d }_{t+1, 2} - {\mathcal {A}}_{t+1, \mathbf{v }}(\mathbf{z }_{t, 2})). \end{aligned}$$

(24e)

Therefore, Eq. (19) is invariant to any full-rank linear transformation such as those in Eqs. (24a) and (24b). As a consequence, the method is invariant under the choice of log-ratio transformation. This is extended to the set of realizations defined by Eq. (11).