Second order stress gradient plasticity with an application to thin foil bending

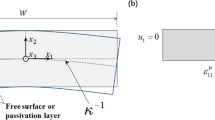
Abstract

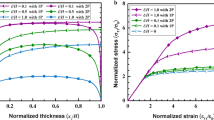
The continuum theory of dislocations is applied to formulate the problem of a double ended dislocation pileup under quadratic applied stress. Accordingly, a second order stress gradient plasticity model is presented to address the contribution of the first and the second stress gradients in the effect interpretation. The model is employed to predict the initial strengthening and subsequent hardening in curved and straight thin foils under pure bending within the continuum framework. It is shown that the so-called stress gradient plasticity model that ignores the second stress gradient may not give sound interpretations of the size effects. The plastic response of thin foils is affected by both the first and second stress gradients, yet their interaction strongly depends upon the length scale parameter. The larger the length scale parameter, the quadratic term contribution would be important and the predictions of the first and second order models deviate significantly from each other.

Appendices

Appendix 1: Details for the evaluation of integral in Eq. (1)

The solution of Eq. (1) can be derived analytically by several approaches including the general theory of Hilbert transform (Liu et al. 2013), theory of functions of complex variables (Muskhelishvili 1953) and the real-variable proof through the trigonometric functions (Bilby and Eshelby 1968). It is found that all methods result in the same expression for the dislocation density function as

$$ n\left( x \right) = \frac{1}{{Ab\pi^{2} }}\frac{1}{{\sqrt {\left( {\frac{{L_{\text{obs}} }}{2}} \right)^{2} - x^{2} } }}\int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {\frac{{ g\left( {x^{{\prime }} } \right)dx^{{\prime }} }}{{\left( {x - x^{{\prime }} } \right)}} + \frac{E}{{\sqrt {\left( {\frac{{L_{\text{obs}} }}{2}} \right)^{2} - x^{2} } }},} $$

(16)

with

$$ g\left( {x^{{\prime }} } \right) = \tau \left( {x^{{\prime }} } \right)\sqrt {\left( {\frac{{L_{\text{obs}} }}{2}} \right)^{2} - x^{{{\prime }2}} } , $$

(17)

and

$$ E = \frac{1}{\pi }\int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {n\left( {x^{{\prime }} } \right)dx^{{\prime }} .} $$

(18)

The applied stress is assumed as Eq. (2). For a pure dislocation pileup, the total number of dislocations in the pileup must be zero, i.e. $N = \int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {n(x)dx = 0}$; hence, we have E = 0. The integral in Eq. (16) can be performed by converting it to a contour integral in the complex plane, following the fundamental work of Friedman and Chrzan (1998). Integrating over $\left( { - \frac{{L_{\text{obs}} }}{2} ,\frac{{L_{\text{obs}} }}{2}} \right)$ is equal to half the integral over C ₁ as shown in Fig. 9. Since C ₁ is a closed contour, it can be deformed into the contour C ₂ which is an infinite circle as sketched in Fig. 9. Hence,

$$ \int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {\frac{{ g\left( {x^{{\prime }} } \right)dx^{{\prime }} }}{{\left( {x - x^{\prime} } \right)}} = \frac{1}{2}\mathop {\oint }\limits_{{C_{2} }}^{{}} h\left( z \right)dz,} $$

(19)

where

$$ h\left( z \right) = \frac{{ - \tau_{0} \left( {1 + \chi z + \xi z^{2} } \right)}}{{Ab\pi^{2} {\text{i}}\left( {1 - \frac{x}{z}} \right)}}\sqrt {1 - \left( {\frac{{L_{\text{obs}} /2}}{z}} \right)^{2} } . $$

(20)

Fig. 9

Integrating over $\left( { - \frac{{L_{\text{obs}} }}{2} ,\frac{{L_{\text{obs}} }}{2}} \right)$ is equivalent to half the integral over the contour C ₂

To evaluate the integral, we use the following Maclaurin series to simplify the integrand in Eq. (19),

$$ \begin{array}{*{20}c} {\sqrt {1 - u} = 1 - \frac{1}{2}u - \frac{1}{8}u^{2} - \frac{1}{16}u^{3} \ldots ,} \\ {\frac{1}{1 - u} = 1 + u + u^{2} + u^{3} + \ldots .} \\ \end{array} $$

(21)

Therefore, Eq. (20) becomes

$$ h\left( z \right) = \frac{{ - \tau_{0} }}{{Ab\pi^{2} {\text{i}}}}\left( {1 + \chi z + \xi z^{2} } \right)\left( {1 + \frac{x}{z} + \left( {\frac{x}{z}} \right)^{2} + \left( {\frac{x}{z}} \right)^{3} + \ldots } \right)\left( {1 - \frac{1}{2}\frac{{L_{\text{obs}} /2}}{z} - \frac{1}{8}\left( {\frac{{L_{\text{obs}} /2}}{z}} \right)^{2} - \frac{1}{16}\left( {\frac{{L_{\text{obs}} /2}}{z}} \right)^{3} + \ldots } \right)\left( {1 + \frac{1}{2}\frac{{L_{\text{obs}} /2}}{z} - \frac{1}{8}\left( {\frac{{L_{\text{obs}} /2}}{z}} \right)^{2} + \frac{1}{16}\left( {\frac{{L_{\text{obs}} /2}}{z}} \right)^{3} \ldots } \right). $$

(22)

Note that, the integral of h(z) over a closed contour equals the coefficient of 1/z in its expansion multiplied by $( - 2\pi {\text{i}})$. Therefore, the integral in Eq. (19) becomes

$$ \int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {\frac{{ g\left( {x^{\prime}} \right)dx^{\prime}}}{{\left( {x^{\prime} - x} \right)}} = \frac{{ - \tau_{0} }}{{2Ab\pi^{2} {\text{i}}}}\left[ {\left( {x^{2} - \frac{1}{2}\left( {L_{\text{obs}} /2} \right)^{2} } \right)\chi + \left( {x^{3} - \frac{x}{2}\left( {L_{\text{obs}} /2} \right)^{2} } \right)\xi + x} \right]\left( { - 2\pi {\text{i}}} \right).} $$

(23)

Substitution of Eq. (23) into Eq. (16) yields

$$ n\left( x \right) = \frac{B}{{\sqrt {\left( {\frac{{L_{\text{obs}} }}{2}} \right)^{2} - x^{2} } }}, $$

(24)

with

$$ B = \frac{{\tau_{0} }}{Ab\pi }\left[ {\left( {\chi + \xi x} \right)\left( {x^{2} - \frac{{L_{\text{obs}}^{2} }}{8}} \right) + x} \right]. $$

(25)

Appendix 2: Calculation of the force on the leading dislocation

As mentioned in Sect. 2, two methods can be applied with apparent success to calculate the force on the leading dislocation in the pileup configuration. A direct calculation through a limit formula derived by Bilby and Eshelby (1968) and a physically-based energy release method introduced in Hirth and Lothe (1982). For the cases of constant, $\tau \left( x \right) = \tau_{0} ,$ linear, $\tau (x) = \tau_{0} \chi x,$ and quadratic, $\tau \left( x \right) = \tau_{0} \xi x^{2} ,$ stress distributions, we achieve the same expression for the force with both methods. However, for their combination i.e. $\tau (x) = \tau_{0} \left( {1 + \chi x + \xi x^{2} } \right),$ the resulting expressions for the force calculated by two methods are found to be different.

Following Bilby and Eshelby (1968), the resulting expression for the forces at the left and the right tips are

$$ \begin{aligned} F\left( { - \frac{{L_{\text{obs}} }}{2}} \right) = - \frac{1}{2}b\left( {Ab} \right)\pi^{2} \mathop {\lim }\limits_{{x \to - L_{\text{obs}} /2}} \left( {x + \frac{{L_{\text{obs}} }}{2}} \right)\left( {n\left( x \right)} \right)^{2} , \hfill \\ F\left( { + \frac{{L_{\text{obs}} }}{2}} \right) = - \frac{1}{2}b\left( {Ab} \right)\pi^{2} \mathop {\lim }\limits_{{x \to - L_{\text{obs}} /2}} \left( {x - \frac{{L_{\text{obs}} }}{2}} \right)\left( {n\left( x \right)} \right)^{2} . \hfill \\ \end{aligned} $$

(26)

The force at the right tip is obtained by substitution of Eq. (3) into Eq. (26) as

$$ F\left( {\frac{{L_{\text{obs}} }}{2}} \right) = \frac{{\tau_{0}^{2} L_{\text{obs}} }}{8A}\left\{ {\left( {\chi + \frac{{L_{\text{obs}} }}{2}\xi } \right)\frac{{L_{\text{obs}} }}{4} + 1} \right\}^{2} = \frac{{\tau_{0}^{2} }}{A}\left\{ {\frac{{L_{\text{obs}} }}{8} + \frac{{L_{\text{obs}}^{3} }}{{2^{7} }}\chi^{2} + \frac{{L_{\text{obs}}^{5} }}{{2^{9} }}\xi^{2} + \frac{{L_{\text{obs}}^{3} }}{{2^{5} }}\xi + \frac{{L_{\text{obs}}^{4} }}{{2^{7} }}\chi \xi + \frac{{L_{\text{obs}}^{2} }}{{2^{4} }}\chi } \right\}. $$

(27)

Alternatively, we can use an approach formulated in Hirth and Lothe (1982) to calculate this force. Thus, the energy released in forming the pileup is given by

$$ W = \int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {\sigma d\varepsilon } = \int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {\tau_{0} \left( {1 + \chi x + \xi x^{2} } \right) bxn\left( x \right)dx.} $$

(28)

Substituting Eq. (3) into Eq. (28) yields

$$ W = \int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {\tau_{0} \left( {1 + \chi x + \xi x^{2} } \right) bx\frac{{\tau_{0} \left[ {\left( {\chi + x\xi } \right)\left( {x^{2} - \frac{1}{2}\left( {L_{\text{obs}} /2} \right)^{2} } \right) + x} \right]}}{{Ab\pi \sqrt {\left( {L_{\text{obs}} /2} \right)^{2} - x^{2} } }}dx.} $$

(29)

To simplify the integral, we could change the integral variable as $x = \frac{{L_{\text{obs}} }}{2}\cos\beta$. Equation (29) then becomes

$$ W = \frac{{\tau_{0}^{2} }}{A\pi }\int_{{ - L_{\text{obs}} /2}}^{{L_{\text{obs}} /2}} {\left( {1 + \chi L_{\text{obs}} /2\cos\beta + \xi \left( {L_{\text{obs}} /2} \right)^{2} \cos^{2} \beta } \right) b\left( {L_{\text{obs}} /2} \right)^{2} \cos\beta \left[ {\left( {\chi + L_{\text{obs}} /2\cos\beta \xi } \right)L_{\text{obs}} /2\left( {\cos^{2} \beta - \frac{1}{2}} \right) + \cos\beta } \right]d\beta , } $$

(30)

which is evaluated as¹

$$ W = - \frac{{\tau_{0}^{2} }}{A}\left\{ {\frac{{L_{\text{obs}}^{2} }}{8} + \frac{{L_{\text{obs}}^{4} }}{{2^{7} }}\chi^{2} + \frac{{L_{\text{obs}}^{6} }}{{2^{9} }}\xi^{2} + \frac{{L_{\text{obs}}^{4} }}{{2^{5} }}\xi + 0.5747 \times 10^{ - 11} L_{\text{obs}}^{5} \chi \xi + 0.3448 \times 10^{ - 10} L_{\text{obs}}^{3} \chi } \right\}. $$

(31)

Hence, the force per unit length on the leading dislocation is calculated as the rate of energy relaxation of the crystal during the advancing of pile up, i.e.

$$ F = \frac{\partial W}{2\partial L} = \frac{{\tau_{0}^{2} }}{A}\left\{ {\frac{{L_{\text{obs}} }}{8} + \frac{{L_{\text{obs}}^{3} }}{{2^{7} }}\chi^{2} + \frac{{L_{\text{obs}}^{5} }}{{2^{9} }}\xi^{2} + \frac{{L_{\text{obs}}^{3} }}{{2^{5} }}\xi + 0.5747 \times 10^{ - 11} L_{\text{obs}}^{4} \chi \xi + 0.3448 \times 10^{ - 10} L_{\text{obs}}^{2} \chi } \right\}. $$

(32)

By comparing Eqs. (27) and (32), we conclude that the physically-based energy release method underestimates the interaction between the first and second stress gradient, i.e. $\frac{{L_{\text{obs}}^{4} }}{{2^{7} }}\chi \xi$, and also the interaction between first stress gradient and constant stress, i.e. $\frac{{L_{\text{obs}}^{2} }}{{2^{4} }}\chi$. It is thus emphasized that the resulting expression for the force on the leading dislocation in Eq. (27) cannot be obtained via a combination of this force for the constant, linear and quadratic stress cases.

For the force at the left tip, a similar procedure would apply which is not detailed here. However, the resulting expression is

$$ F\left( { - \frac{{L_{\text{obs}} }}{2}} \right) = \frac{{ - \tau_{0}^{2} L_{\text{obs}} }}{8A}\left\{ {\left( {\chi - \frac{{L_{\text{obs}} }}{2}\xi } \right)\frac{{L_{\text{obs}} }}{4} - 1} \right\}^{2} = \frac{{ - \tau_{0}^{2} }}{A}\left\{ {\frac{{L_{\text{obs}} }}{8} + \frac{{L_{\text{obs}}^{3} }}{{2^{7} }}\chi^{2} + \frac{{L_{\text{obs}}^{5} }}{{2^{9} }}\xi^{2} + \frac{{L_{\text{obs}}^{3} }}{{2^{5} }}\xi - \frac{{L_{\text{obs}}^{4} }}{{2^{7} }}\chi \xi - \frac{{L_{\text{obs}}^{2} }}{{2^{4} }}\chi } \right\}. $$

(33)

Appendix 3: Numerical integration of governing equations in bending analysis

In this section, a numerical method based on the semi-implicit backward Euler integration scheme (Belytschko et al. 2000) is described to analyze the thin foil bending with the SσGP model. It is worth noting that the stress gradients are averaged over the length scale and attribution of these parameters into the fully implicit numerical method is quite complicated. Therefore, the stress gradients are assumed unchanged in each increment and the remaining parameters are obtained through the Newton–Raphson procedure.

The governing Eqs. (10) and (11) are reduced to solve the following non-linear algebraic equations

$$ a = - \sigma_{11}^{{\left( {t + \Delta t} \right)}} + \sigma_{11}^{\left( t \right)} + 4G \frac{{ - \dot{\theta }}}{\theta }\frac{{x_{2} }}{{R - x_{2} }}\Delta t\left( {1 - \left( {\frac{\sqrt 3 }{2}\frac{{\left| {\sigma_{11}^{{\left( {t + \Delta t} \right)}} } \right|}}{{\sigma_{Y}^{\prime} f\left( {\bar{\varepsilon }_{k}^{{p\left( {t + \Delta t} \right)}} } \right)}}} \right)^{m} } \right), $$

(34)

$$ b = - \bar{\varepsilon }^{{p\left( {t + \Delta t} \right)}} + \bar{\varepsilon }^{p\left( t \right)} + \frac{2}{\sqrt 3 }\left| {\frac{{\dot{\theta }}}{\theta }\frac{{x_{2} }}{{R - x_{2} }}} \right| \Delta t\left( {\frac{\sqrt 3 }{2}\frac{{\left| {\sigma_{11}^{{\left( {t + \Delta t} \right)}} } \right|}}{{\sigma_{Y}^{{\prime }} f\left( {\bar{\varepsilon }_{k}^{{p\left( {t + \Delta t} \right)}} } \right)}}} \right)^{m} , $$

(35)

which can be linearized as (Belytschko et al. 2000)

$$ a_{k + 1} = a_{k} - \Delta \sigma_{11k}^{{\left( {t + \Delta t} \right)}} + 4G \frac{ - \Delta \theta }{\theta }\frac{{x_{2} }}{{R - x_{2} }}\left( { - A} \right), $$

(36)

$$ b_{k + 1} = b_{k} - \Delta \bar{\varepsilon }_{k}^{{p\left( {t + \Delta t} \right)}} + \frac{2}{\sqrt 3 } \left| {\frac{\Delta \theta }{\theta }\frac{{x_{2} }}{{R - x_{2} }}} \right| \left( A \right), $$

(37)

where $k$ denotes the iteration number, and

$$ A = m\left( {\frac{\sqrt 3 }{2}\frac{{\left| { \sigma_{11k}^{{\left( {t + \Delta t} \right)}} } \right|}}{{\sigma_{Y}^{{\prime }} f\left( {\bar{\varepsilon }_{k}^{{p\left( {t + \Delta t} \right)}} } \right)}}} \right)^{m - 1} \left\{ {\frac{\sqrt 3 }{2}\frac{{\left| { \sigma_{11k}^{{\left( {t + \Delta t} \right)}} } \right|/ \sigma_{11k}^{{\left( {t + \Delta t} \right)}} }}{{\sigma_{Y}^{{\prime }} f\left( {\bar{\varepsilon }_{k}^{{p\left( {t + \Delta t} \right)}} } \right)}} \Delta \sigma_{11k}^{{\left( {t + \Delta t} \right)}} + \frac{\sqrt 3 }{2}\frac{{ - \left| { \sigma_{11k}^{{\left( {t + \Delta t} \right)}} } \right|\sigma_{Y}^{{\prime }} \left( {\frac{df}{{d\bar{\varepsilon }^{p} }}} \right)_{k}^{{\left( {t + \Delta t} \right)}} }}{{\left( {\sigma_{Y}^{{\prime }} f\left( {\bar{\varepsilon }_{k}^{{p\left( {t + \Delta t} \right)}} } \right)} \right)^{2} }} \Delta \bar{\varepsilon }_{k}^{{p\left( {t + \Delta t} \right)}} } \right\}. $$

(38)

Hence, following set of equations can be solved for stress and plastic strain increments

$$ 0 = \left\{ {\begin{array}{*{20}c} {a_{k} } \\ {b_{k} } \\ \end{array} } \right\} + \left[ J \right]_{k} \left\{ {\begin{array}{*{20}c} {\Delta \sigma_{11} } \\ {\Delta \bar{\varepsilon }^{p} } \\ \end{array} } \right\}_{k} . $$

(39)

Then, the effective plastic strain and stress are updated according to the incremental values as well as the solution at the last increment. This process is continued until the convergence is achieved to within a sufficient tolerance. It is noted that the governing Eqs. (14) and (15) for the straight foil can be solved in a similar manner by replacing $\frac{ - \Delta \theta }{\theta }$ with $\Delta \kappa$ and $\frac{{x_{2} }}{{R - x_{2} }}$ with x ₂ in above equations.