An encoding approach for stable change point detection

Abstract

Without imposing prior distributional knowledge underlying multivariate time series of interest, we propose a nonparametric change-point detection approach to estimate the number of change points and their locations along the temporal axis. We develop a structural subsampling procedure such that the observations are encoded into multiple sequences of Bernoulli variables. A maximum likelihood approach in conjunction with a newly developed searching algorithm is implemented to detect change points on each Bernoulli process separately. Then, aggregation statistics are proposed to collectively synthesize change-point results from all individual univariate time series into consistent and stable location estimations. We also study a weighting strategy to measure the degree of relevance for different subsampled groups. Simulation studies are conducted and shown that the proposed change-point methodology for multivariate time series has favorable performance comparing with currently available state-of-the-art nonparametric methods under various settings with different degrees of complexity. Real data analyses are finally performed on categorical, ordinal, and continuous time series taken from fields of genetics, climate, and finance.

1 Introduction

Physical, biological, and social dynamic complex systems found in real-world and in many sciences manifest transitions from a phase to another. That is, phase-transitional non-stationarity is natural and essential. Upon describing such a complex system via non-stationary time series of any dimensions, abrupt distributional changes are ubiquitous patterns of great interest for such phase-transitions, at least fundamentally.

Change points as temporal locations of such occurrences and their multiplicity are key parts of deterministic structures of the time series under study. Nowadays, change-point analysis has well recognized in statistics literature and beyond as an essential scientific methodology that aims to detect change points on the time-ordered observations and then partition the whole time series into homogeneously distributional segments. Change-point analysis can be traced back to 1950 s (Page, 1954; Chernoff & Zacks, 1964; Kander & Zacks, 1966). So far, it has been playing a crucial role in diverse fields including bioinformatics (Picard et al., 2005; Muggeo & Adelfio, 2011), behavioural science (Rosenfield et al., 2010; Hoover et al., 2012), neuroimage (Bosc et al., 2003), climate science (Robbins et al., 2011), finance (Talih & Hengartner, 2005), and speech recognition (Malladi et al., 2013).

In general, such an analysis can be conducted under either parametric or nonparametric settings. Parametric approaches rely heavily upon assumptions of underlying distributions belonging to a known family. Likelihood or penalized likelihood functions are generally involved (Yao, 1988; Chen & Gupta, 1997; Bai & Perron, 2003). In contrast, nonparametric approaches make very few assumptions regarding stochasticity underlying the time series. The likelihood principle is not directly applicable. Nonetheless, such approaches fit well in a wider variety of applications. Such an advantageous feature has popularity and a vast amount of research attention in the past decade.

In fact, the likelihood principle is still applicable under a rather mild independence assumption that, at least, approximately endorses some distributional characters upon observed or computed recurrent events occurring along with the time series. For instance, Kawahara & Sugiyama (2011) and Liu et al. (2013) attempted to estimate the likelihood ratio using KL divergence; Chen & Zhang (2015) proposed a graph-based approach and applied it in multivariate non-Euclidean data. Zou et al. (2014) developed an empirical likelihood approach to discover an unknown number of change-points via BIC. Haynes et al. (2017) extended the empirical likelihood approach and introduced a nonparametric invariant of the Pruned Exact Linear Time (PELT) (Killick et al., 2012) to improve computational efficiency. Matteson and James (2014) present a U-statistic to quantify the difference between the characteristic functions of two segments. Lung-Yut-Fong et al. (2015) generalized Mann–Whitney rank-based statistic to multivariate settings. Arlot et al. (2019) improved the kernel-based method by Harchaoui and Cappe (2007) with a generalized model-selection penalty.

However, most of the existing nonparametric research focused on the single change-point problem and the extension of multiple change point detection is achieved via dynamic programming (Harchaoui & Cappe, 2007; Lung-Yut-Fong et al., 2015; Arlot et al., 2019) or bisection procedure (Vostrikova, 1981; Olshen & Venkatraman, 2004; Matteson & James, 2014). It is still scarce in the literature to efficiently discover multiple change points under multivariate settings, especially when the covariance structure changes in chronological order.

In the paper, a new nonparametric approach is proposed to detect multiple distributional changes. Our developments are anchored on independent time-ordered observations. The basic idea is to systematically select a subset of the data points at each iteration, with which we encode the continuous observations into a sequence of Bernoulli variables. The number of change points & their locations are estimated by aggregating all the dynamic information discovered from the collection of Bernoulli processes. Instead of working on the unknown distribution directly, the proposed approach takes advantage of dividing the problem into several easier tasks, so that the maximum likelihood approach can be applied to analyze the Bernoulli processes, respectively. We demonstrate that this divide-and-conquer framework is sensitive to detect any underlying distributions and can be implemented in conjunction with other parametric approaches.

Another important extension of the aggregation technique is the stability change-point detection. Such a stability selection introduced by Meinshausen and Buhlmann (2010) was designed to improve the performance of variable selection and provide control for false discoveries. We demonstrate that the idea of aggregating results by applying a procedure to subsamples of the data can be well implemented under our framework. One can aggregate the estimation from the Bernoulli sequences, and select the estimated change-point locations with votes beyond a predetermined threshold. To our limited knowledge, this could be the first method in the change-point literature that holds both asymptotic property and finite-sample control of false discoveries.

The paper is organized as follows. In Sect. 2, the paper introduces an efficient algorithm for detecting multiple change points within a change-in-parameter Bernoulli sequence. The algorithm forms the basis of the proposed approach for handling change point detection in univariate time series. Building upon the algorithm introduced in Sect. 2, Sect. 3 presents the main divide-and-conquer framework to encode continuous observations into Bernoulli processes and estimate the locations of change points in the multivariate setting. Section 4 discusses the application of the stability detection technique within the proposed change point framework. In Sect. 5, the paper presents a weighting strategy to measure the relevance of results from different sample sets in practical implementation. Numerical experiments are shown in Sect. 6 to compare with other state-of-the-art nonparametric approaches. Real data applications including categorical and continuous data in univariate and multivariate settings are reported in Sect. 7. We note that the proposed approach can be easily generalized to multivariate categorical or ordinal time series data, though we mainly focus on continuous data under the multivariate setting in this paper.

The main contributions of this paper can be summarized as follows: This paper

• (1) Proposes a novel approach for detecting change points in time series data that does not rely on any specific underlying distributions;

• (2) Extends the Hierarchical Feature Selection (HFS) from single change-point detection to scenarios with multiple change points for Bernoulli processes.

• (3) Introduces a stability detection technique that enhances the accuracy of change point estimation and provides finite-sample error control for false discoveries.

• (4) Conducts numerical experiments to compare the proposed approach with other well-known nonparametric methods and applies the proposed method to real data from various fields.

2 Related work

2.1 Nonparametric change point analysis

The statistical literature on nonparametric changepoint analysis is comparably limited. However, there have been valuable steps towards developing nonparametric approaches. In the context of univariate data, Zou et al. (2014) developed an empirical likelihood-based estimator with consistency guarantees. Haynes et al. (2017) extended the empirical likelihood function and explored a non-parametric variant of PELT to enhance computational efficiency. Pein et al. (2017) proposed the Heterogeneous Multiscale Change Point Estimator to detect changes in mean and variance. Vanegas et al. (2022) focused on analyzing serial data with an underlying quantile function consisting of constant segments. Padilla et al. (2021) developed a change point detector by measuring the magnitude of the distribution changes using the Kolmogorov-Smirnov statistic.

In the context of multivariate nonparametric settings, Lung-Yut-Fong et al. (2015) proposed a test statistic that generalized the Mann-Whitney Wilcoxon two-sample test to multivariate settings. Matteson and James (2014) presented a U-statistic to quantify the difference between the characteristic functions of two segments and demonstrated its consistent estimations of the changepoints. In the context of multivariate nonparametric settings, Arlot et al. (2019) conducted a penalized kernel least squares estimator and derived a non-asymptotic oracle inequality. Cabrieto et al. (2018) performed kernel changepoint detection and compared pairwise similarities between running statistics computed via the Gaussian kernel. Padilla et al. (2022) studied the multivariate changepoint problem when the underlying distributions are piecewise constant with Lipschitz densities.

2.2 Multiple change points detection

The technique of single change point detection can be applied recursively to generalize to the detection of multiple changes. For example, Binary Segmentation (Scott & Knott, 2022) and its variants, such as Wild Binary Segmentation (Fryzlewicz, 2014), narrowest over threshold (Baranowski et al., 2019), and Seeded Binary Segmentation (Kovács et al., 2023), offer a greedy approach to search different intervals and determine the best split points. Another general approach is the dynamic programming approach, such as Segment Neighbourhood Search (Auger & Lawrence, 1989), used to search for multiple change points. Alternatively, the pruned dynamic programming (Rigaill, 2015) is employed to prune a set of change point candidates, and a similar idea can also be found in the screening step in Zou et al. (2014). Additionally, Pruned Exact Linear Time (PELT) (Killick et al., 2012) achieves linear computational complexity but at the sacrifice of statistical consistency. Unlike Binary Segmentation approaches that locally fit subsets of samples, our proposed method takes a different approach. It focuses on exploring the binary emerging pattern of each sample subset, which is obtained through clustering. By using voting to aggregate change point candidates, our method efficiently searches for multiple change points over the Bernoulli sequences. This dynamic programming extension of the Hierarchical Feature Selection (HFS) (Hsieh et al., 2012) provides a computationally effective solution for change point detection, allowing us to accurately identify multiple change points in multivariate time series without an exhaustive search.

3 Sequence of Bernoulli variables

3.1 Background

Consider a sequence of 0–1 independent Bernoulli variables $\{E_t\}_{t=1}^N$. Suppose that k change points are embedded within the sequence at locations $0 = \tau ^*_0< \tau ^*_1<...< \tau ^*_k < \tau ^*_{k+1}=N$, so the observations are partitioned into $k+1$ segments. Observations within segments are identically distributed but observations between adjacent segments are not. Specially, $E_t {\mathop {\sim }\limits ^{iid}} Bern(p_i)$ for $E_t \in \{E_{\tau ^*_{i}+1},\ldots ,E_{\tau ^*_{i+1}}\}$, for $i=0,\ldots ,k$. Now, given the number of change points k, one task of change point detection is to estimate the k locations. In the most general case, both number of change points and their locations need to be estimated.

Change point analysis in a Bernoulli-variable sequence was well studied when $k=1$. Hinkley and Hinkley (1970) provided asymptotic distributions of likelihood ratio statistics for testing the existence of a change point. Pettitt (1980) introduced CUSUM statistics and showed its asymptotical equivalence to the maximum likelihood estimator. Miller and Siegmund (1982) investigated maximally selected chi-square statistics for two-sample comparison in a form of $2 \times 2$ table. Later on, Halpern (1999) advocated a statistic based on the minimum value of Fisher’s Exact Test. Tatti (2019) demonstrated that the process of identifying the optimal change-point split can be accelerated in logarithmic time. When $k>1$, Fu and Curnow (1990) firstly attempted to search for optimal change points such that the likelihood function is maximized. However, it still lacks a computationally efficient algorithm especially when k is large.

In this section, we present a new algorithm to address the problem of performing multiple change points detection within a Bernoulli-variable sequence. The idea is motivated by Hierachical Feature Selection (HFS) (Hsieh et al., 2012) which was designed to detect a shift pattern between low- and high-volatility phases under financial time series. By tracking the recurrence of 1’s in a Bernoulli sequence, our algorithm is able to partition observations into disjoint segments with different emergence intensities. Thus, the number and location of change points can be estimated based on the resultant segmentation. It is noted that the searching procedure is conducted in a fashion of dynamic programming, so the time complexity keeps relatively feasible.

3.2 Multiple change points searching algorithm

For simplicity of computation, we only consider the situation in which change point locates at the emergence position of 1’s. Suppose that the number of 1’s in the ith segment is $M_i$, so the total number of 1’s is $M=\sum _{i=1}^{k+1} M_i$ and the total number of 0’s is $N-M$. By further supposing that the recurrent time can be 0 if two 1’s appear consecutively, and $R_1=0$ if $E_1=1$, and $R_{M+1}=0$ if $E_N=1$, the Bernoulli-variable sequence can be represent by a sequence of recurrent time between consecutive 1’s, denoted as $\{R_t\}_{t=1}^{M+1}$. Especially, there are $M_i+1$ recurrent times in the ith segment where $R_t \sim Geom(p_i)$. The task then becomes to search for the change points within the recurrent-time sequence.

The searching procedure is done by iteratively taking off the smallest number $R_{min}$ from the rest $R_t$’s and merge the time points within $R_{min}$. For example, if $R_{min}$ is the recurrent time between j and $j'$, we merge the locations from $(j+1)$ to $j'$ as a time window, denoted as $w_{j\rightarrow j'}$. Here, it is supposed that $E_j=1$, $E_{j'}=1$, and $E_t=0$ for $t \in (j,j')$. In the next step, if the smallest $R_t$ is taken from the recurrent time between $j'$ and $j''$, a new time window is recorded as from $(j'+1)$ to $j''$, named $w_{(j'+1)\rightarrow j''}$. We can further combine the two consecutive time windows $w_{(j+1)\rightarrow j'}$ and $w_{(j'+1)\rightarrow j''}$ into $w_{(j+1)\rightarrow j''}$. Indeed, we merge time locations between a pair of nearest 1’s at each step and update the recorded time windows according to their connectivity. It turns out that the recorded time windows contain recurrent time with relatively smaller values, which corresponds to a period with high frequency of 1’s. Hence, the boundaries of the time windows can be extracted as potential change point locations that partition the observations into segments with low and high Bernoulli parameters.

So far, the algorithm works very similarly to the hierarchical clustering with a single-linkage, by agglomerating two closest single 1’s or two location groups from bottom to top. However, it is well known that this greedy algorithm does not guarantee global optimization. Our remedy is to set a tuning parameter $C^*$ to control the minimal length of the recorded segments. Additionally, we count the number of $R_t$ absorbed within each recorded time window. Continuing with the above example, the count of recurrent time in window $w_{(j+1)\rightarrow j'}$ and $w_{(j+1)\rightarrow j''}$ is denoted as $C_{(j+1)\rightarrow j'}=1$ and $C_{(j+1)\rightarrow j''}=2$, respectively. The recorded time window, for example, $w_{.\rightarrow ..}$ can be regarded as a high-intensity segment only if its count $C_{.\rightarrow ..}$ is greater than the threshold $C^*$. Now, hierarchical clustering with a single-linkage is just a special case when $C^*=0$. Another most extreme case is when $C^*=M$, so there is no period having a count number above $C^*$, thus no change point exists. Without any prior knowledge about the minimal length of the segments, we run over all the choice of $C^*$ starting from 0 to M to generate all possible segmentation. The optimum is the one that fit the Bernoulli or Geometric observations best.

Suppose the observations are partitioned into $\tilde{k}+1$ segments via $\tilde{k}$ time window boundaries or change points $\tilde{\tau }_1,\ldots ,\tilde{\tau }_{\tilde{k}}$. The Bernoulli parameter $\tilde{p}_i$ between $\tilde{\tau }_{i-1}$ and $\tilde{\tau }_{i}$ can be estimated by MLE $\hat{\tilde{p}}_i=\frac{\{ \#~\text {of}~1's~\in ~(\tilde{\tau }_{i-1},\tilde{\tau }_i)\}}{\tilde{\tau }_i-\tilde{\tau }_{i-1}}$. To measure the goodness-of-fit, model selection is done by maximizing log-likelihood function within each segment, while penalizing the number of change points and related estimation parameters. The penalized likelihood or loss function can be written by,

$$\begin{aligned} L(\tilde{\tau }_1,\ldots ,\tilde{\tau }_{\tilde{k}}) = -2 \sum _{i=1}^{\tilde{k}+1} \sum _{t \in (\tilde{\tau }_{i-1},\tilde{\tau }_i)}[{E_t}log\hat{\tilde{p}}_i + {(1-E_t)}log(1-\hat{\tilde{p}}_i)] + \phi (N)Q_{\tilde{k}} \end{aligned}$$

(1)

where $Q_k$ is the total number parameters; $\phi (N)$ is the penalty coefficient; $\phi (N)=2$ for AIC and $\phi (N)=log(N)$ for BIC.

Suppose that W(.) is a mapping that records the corresponding time window of $R_t$. For example, $W(R_t)=w_{(j+1)\rightarrow j'}$ where $R_t$ is the recurrent time between j and $j'$. Denote window length $\vert w \vert$ as the count of recurrent time within a window w, for example, $\vert W(R_t) \vert =C_{(j+1)\rightarrow j'}$. It is marked that the segmentation and the loss function can be updated based on the results in the last step. After applying a big loop cycling through $C^*$ from 0 to M, the total time complexity now becomes $O(M^2)$. As a result, an optimal window set is returned, so the change points locations are estimated based on the window boundaries. The multiple change-point searching algorithm is fully described in Algorithm 1.

4 MCP for multivariate time series

A large part of change point detection literature deals with continuous observation. In this section, we firstly proposed an encoding approach to categorize continuous time series into multiple Bernoulli sequences, and then analyze change points embedded within the multivariate process. The idea of categorizing real-value observations aims to extract more relevant information and filter out noise. It is claimed that the proposed approach is sensitive to encode any underlying distributions and is easily generalized to either categorical or continuous observations.

4.1 Encoding continuous time series

In the analysis of single stock returns, Hsieh et al. (2012) utilized a pair of thresholds to mark absolutely large stock returns as 1 and 0 otherwise, then revealed the volatility pattern behind the resultant 0–1 sequence. The encoding process is written as

$$\begin{aligned} E_t = {\left\{ \begin{array}{ll} 1 &{} \quad X_t\le \alpha , \,\, X_t\ge \beta \\ 0 &{} \quad \text {Otherwise} \end{array}\right. } \end{aligned}$$

(2)

where $\{E_t\}_t$ is an excursion process after marking a sequence of stock returns. Later, Wang and Hsieh (2021) proposed an encoding method to explore the local dependence of observations when $X_t \in {\mathbb {R}}^p$. Following up the idea, we firstly partition ${\mathbb {R}}^p$ space into V disjoint subarea, denoted as $B^{(v)}$ for $v=1,2,\ldots ,V$, then transform the continuous observations $\{X_t\}_{t=1}^{N}$ into V Bernoulli sequences or a V-dimensional multinominal process $\{(E_t^{(1)}, E_t^{(2)},\ldots , E_t^{(V)})\}_{t=1}^{N}$, such that

$$\begin{aligned} E_t^{(j)} = {\left\{ \begin{array}{ll} 1 &{} \quad X_t\in B^{(j)}\\ 0 &{} \quad \text {Otherwise} \end{array}\right. } \end{aligned}$$

(3)

Here, subarea $B^{(j)}$ plays an important role in reserving the change-point pattern into a Bernoulli process. Denote the Bernoulli parameter in the ith segments of $\{E_t^{(j)}\}$ as $p_{i}^{(j)}$. So,

$$\begin{aligned} p_{i}^{(j)}=\int _{B^{(j)}} dF_{i} \end{aligned}$$

(4)

where $F_{i}$ corresponds to the CDF of $\{X_t\}_t$ in the ith time segments. There is actually a tradeoff between the size and the total number of the subareas. Larger number of subareas with smaller size can discover the distributional difference more precisely but sacrifice statistical power due to the reduced sample size. In the following subsections, we would assume that V is fixed and $B^{(j)}$’s are predetermined. Besides, the degree of relevance should be measured given a $B^{(j)}$. Especially, it is easier to detect the change point in between the ith and $i+1$th segments if $p_{i}^{(j)}$ is far apart from $p_{i+1}^{(j)}$, and vice versa. We leave the practical issues in implementing the encoding procedure in Sect. 5.

4.2 Single change point detection

Starting with the simplest setting, let’s assume that there exists a single change point at $\tau ^*$. Specifically, $\{X_t\}_{t=1}^{\tau ^{*}} {\mathop {\sim }\limits ^{iid}} F_1$ and $\{X_t\}_{t=\tau ^{*}+1}^{N} {\mathop {\sim }\limits ^{iid}} F_2$ where $F_1$ and $F_2$ are two unknown CDFs. The goal is to test the homogeneity between the two sample sets. Following the encoding procedure above, we obtain a multinomial process $\{(E_t^{(1)}, E_t^{(2)},\ldots , E_t^{(V)})^{'}\}_{t=1}^{N}$ where $\{E_t^{(j)}\}_{t=1}^{\tau ^{*}} \sim Bern(p^{(j)}_{1,\tau ^{*}})$ and $\{E_t^{(j)}\}_{t=\tau ^{*}+1}^{N} \sim Bern(p^{(j)}_{2,\tau ^{*}})$.

Robbins et al. (2011) extent the multivariate CUSUM statistics with uncorrelated components to the multinomial settings and derived its asymptotic distributions under the null hypothesis. The estimators of Bernoulli parameters at a hypothesized time location $\tau$ is defined by

$$\begin{aligned} {\hat{p}}^{(j)}_{1,\tau } = {\sum _{t=1}^{\tau } \mathbbm {1}\{E_t^{(j)}=1\}}/{\tau } \end{aligned}$$

(5)

and

$$\begin{aligned} {\hat{p}}^{(j)}_{2,\tau } = {\sum _{t=\tau +1}^{N} \mathbbm {1}\{E_t^{(j)}=1\}}/{(N-\tau )} \end{aligned}$$

(6)

for $j=1,2,\ldots ,V$. Then, a chi-square statistic proposed by Robbins et al. (2011) is written as,

$$\begin{aligned} \chi _{\tau }^2 = \sum _{j=1}^{V} \frac{(\sum _{t=1}^{\tau }\mathbbm {1}\{E^{(j)}_t=1\} -{\hat{p}}^{(j)}_{1,\tau })^2}{{\hat{p}}^{(j)}_{1,\tau }} +\frac{(\sum _{t=\tau +1}^{N}\mathbbm {1}\{E^{(j)}_t=1\} -{\hat{p}}^{(j)}_{2,\tau })^2}{{\hat{p}}^{(j)}_{2,\tau }} \end{aligned}$$

Moreover, if there exists no change point under the null hypothesis, the maximally selected chi-square statistics $\chi _{{\hat{\tau }}}^2$ converges to a Brownian motion asymptotically.

4.3 Multiple change points detection

Now, we consider multiple change point detection when the number of change points k is known. Suppose the change point locations are $0 = \tau ^*_0< \tau ^*_1<...< \tau ^*_k < \tau ^*_{k+1} = N$. Specifically, $\{X_t\}_{t=\tau ^*_i}^{\tau ^*_{i+1}} {\mathop {\sim }\limits ^{iid}} F_i$ for $i=0,1,\ldots ,k$, and consecutive CDFs $F_i$ and $F_{i+1}$ are different. A naive method to search for $O(N^k)$ possible change point locations is computationally intractable. Bisection procedure as in Vostrikova (1981) and Olshen and Venkatraman (2004), dynamic programming in Harchaoui and Cappe (2007), or the one we proposed in Sect. 2 can work for the purpose. It is claimed that the proposed algorithm outperforms others in searching for the global optima but only adapts to a single-dimensional Bernoulli-variable sequence.

A divide-and-concur approach is proposed as a remedy to the multivariate problem. Denote $\{E_t^{(j)}\}_{t=1}^{N}$ as the jth Bernoulli process after encoding the observations via $B^{(j)}$, and $p^{(j)}_{i}$ as the true parameters of $E_t^{(j)}$ defined by (4). We firstly apply Algorithm 1 to estimate the change point locations within $\{E^{(j)}_t\}$, for $j=1,2,\ldots ,V$, respectively. Suppose the estimated change point locations in the jth sequence are $0= {\hat{\tau }}^{(j)}_0< {\hat{\tau }}^{(j)}_1< {\hat{\tau }}^{(j)}_2<...< {\hat{\tau }}^{(j)}_{{\hat{k}}^{(j)}} < {\hat{\tau }}^{(j)}_{{\hat{k}}^{(j)}+1} = N$. So, the observations are partitioned into ${\hat{k}}^{(j)}+1$ homogeneous segments. Note that the number of change points ${\hat{k}}^{(j)}$ does not necessarily equal k. The estimation should depend on the subarea by which we encode the observations and the loss function in (1). After that, a vector of length N is generated to record the estimated Bernoulli parameter, denoted as $\{{\hat{r}}^{(j)}_t\}_{t=1}^N$. Let ${\hat{p}}^{(j)}_{i}$ be the estimated parameter when t is between ${\hat{\tau }}^{(j)}_{i-1}$ and ${\hat{\tau }}^{(j)}_{i}$, so

$$\begin{aligned} {\hat{p}}^{(j)}_{i} = \frac{\sum _{t={\hat{\tau }}^{(j)}_i+1}^{{\hat{\tau }}^{(j)}_{i+1}} \mathbbm {1}\{E_t^{(j)}=1\}}{{\hat{\tau }}^{(j)}_{i+1}-{\hat{\tau }}^{(j)}_{i}} \end{aligned}$$

for $i=0,1,\ldots ,{\hat{k}}^{(j)}$ and $j=1,2,\ldots ,V$. Thus, there are ${\hat{\tau }}^{(j)}_{i}-{\hat{\tau }}^{(j)}_{i-1}$ duplicates of ${\hat{p}}^{(j)}_{i}$ in $\{{\hat{r}}^{(j)}_t\}_{t=1}^N$, especially, ${\hat{r}}^{(j)}_t={\hat{p}}^{(j)}_{i}$, for $t \in ({\hat{\tau }}^{(j)}_{i-1},{\hat{\tau }}^{(j)}_{i}]$. Repeating the above procedure through the V sequences, we can eventually obtain a sequence of V-dimensional estimated parameters, denoted as $\{{\hat{r}}_t\}_t=\{({\hat{r}}^{(1)}_t, {\hat{r}}^{(2)}_t,\ldots , {\hat{r}}^{(V)}_t)^{'}\}_t$.

Generated by encoding observations from subarea $B^{(j)}$, the Bernoulli-variable sequence $E^{(j)}_t$ can partially reserve the distributional changes from the raw observations. Indeed, some ${\hat{r}}^{(j)}_t$’s reflect the dynamic pattern, while others or at least some subsequences of ${\hat{r}}^{(j)}_t$ may work as irrelevant noise, for example, when $\int _{B^{(j)}} dF_{i} \cong \int _{B^{(j)}} dF_{i+1}$. An aggregation statistic is further present to combine all pieces of information from $j=1,2,\ldots ,V$, and weighting each $\{E_t^{(j)}\}_{t=1}^{N}$ according to its degree of relevance. In this section, we would treat every sequence equally for theoretical proof. The weighting procedure is described in Sect. 5.

Different from the CUSUM statistics, here the within-group variance in $\{{\hat{r}}_t\}_t$ is considered. Given k hypothesized change point locations $\tau _1,\tau _2,\ldots ,\tau _k$, the statistic is written as,

$$\begin{aligned} {\hat{G}}(\tau _1,\tau _2,\ldots ,\tau _k):= \sum _{i=0}^{k} \sum _{t=\tau _i+1}^{\tau _{i+1}} \frac{\Vert {\hat{r}}_t - {\bar{r}}_{i}\Vert ^2}{\tau _{i+1}-\tau _i} \end{aligned}$$

(7)

where ${\bar{r}}_{i}={\sum _{t=\tau _i+1}^{\tau _{i+1}}{\hat{r}}_t}/{(\tau _{i+1}-\tau _i)}$ for $i=0,1,\ldots ,k$. Change point locations are then estimated as the ones that minimize the within-group variance, so

$$\begin{aligned} {\hat{\tau }}_1,{\hat{\tau }}_2,\ldots ,{\hat{\tau }}_k = \mathop {{\textrm{argmin}}}\limits _{\tau _1,\tau _2,\ldots ,\tau _k} {\hat{G}}(\tau _1,\tau _2,\ldots ,\tau _k) \end{aligned}$$

(8)

It is shown in the next section that consistency holds for the statistic when N goes into infinity. Moreover, it is computationally easier to search for multiple change point locations when $k>1$.

We firstly stack the estimated parameters $\{{\hat{r}}_t\}_{t=1}^{N}$ in a $N \times V$design matrix denoted as ${\mathcal {M}}$, in other words,

$$\begin{aligned} {\mathcal {M}}_{N \times V}=[{\mathcal {M}}(t,j)]_{t,j}=[{\hat{r}}_t^{(j)}]_{t,j}~~ \textit{for}~t=1,\ldots ,N;~j=1,\ldots ,V \end{aligned}$$

A time-order-kept agglomerate hierarchical clustering algorithm is applied upon ${\mathcal {M}}$ to cluster time locations (rows) with comparable V-dimensional covariables. The classical hierarchical clustering algorithm is modified so that only consecutive time points or groups are agglomerated at each iteration, so the original time order is kept. A Wald’s type of linkage is applied for the purpose of minimizing the within-group variance. The agglomeration algorithm terminates when $k+1$ consecutive time point clusters get returned, so k change point locations are estimated correspondingly.

4.4 Consistency

We present the consistency of the estimated change point locations obtained from our statistics. It shows that if a part of the likelihood-based estimators from Bernoulli sequences are consistent, then the estimators derived by the aggregation statistic in (7) can converge to the true change point locations asymptotically. We firstly demonstrate the consistency property for the single change point case and then do the same in the multiple change points setting.

Suppose the true change point location is $\tau ^*$, so $\{E_t^{(j)}\}_{t=1}^{\tau ^*} \sim Bern(p^{(j)}_{1,\tau ^*})$ and $\{E_t^{(j)}\}_{t=\tau ^{*}+1}^{N} \sim Bern(p^{(j)}_{2,\tau ^*})$. By definition,

$$\begin{aligned} {\hat{r}}^{(j)}_t = {\left\{ \begin{array}{ll} {\hat{p}}^{(j)}_{1,{\hat{\tau }}^{(j)}}, &{} \quad t \in [1,{\hat{\tau }}^{(j)}]\\ {\hat{p}}^{(j)}_{2,{\hat{\tau }}^{(j)}}, &{} \quad t \in ({\hat{\tau }}^{(j)},N] \end{array}\right. } \end{aligned}$$

(9)

where ${\hat{\tau }}^{(j)}$ is the estimated change point locations in $\{E^{(j)}_t\}_t$. To prove the consistency, it is typical to assume that the sizes of the two half time sequence cut by $\tau ^*$ go into infinity as $N \rightarrow \infty$, and the proportion of the first half converges to a constant $\gamma ^* \in (0,1)$, a.k.a. $\tau ^*/N \rightarrow \gamma ^* \, (N \rightarrow \infty )$. The within-group variance of (7) at any proportion cut $\gamma$ can be written as,

$$\begin{aligned} {\hat{G}}(\gamma )= \frac{\sum _{t=1}^{\lfloor N\gamma \rfloor }\Vert {\hat{r}}_t - {\bar{r}}_{1}\Vert ^2}{\lfloor N\gamma \rfloor } + \frac{\sum _{t=\lfloor N\gamma \rfloor +1}^{N}\Vert {\hat{r}}_t - {\bar{r}}_{2}\Vert ^2}{N-\lfloor N\gamma \rfloor } \end{aligned}$$

(10)

where ${\bar{r}}_{1}=\frac{\sum _{t=1}^{\lfloor N\gamma \rfloor } {\hat{r}}_t}{\lfloor N\gamma \rfloor }$ and ${\bar{r}}_{2}=\frac{\sum _{t=\lfloor N\gamma \rfloor +1}^{N} {\hat{r}}_t}{N-\lfloor N\gamma \rfloor }$. The estimated change point location now becomes

$$\begin{aligned} {\hat{\tau }} = \mathop {{\textrm{argmin}}}\limits _{\tau }~{\hat{G}}(\tau /N) \end{aligned}$$

(11)

in the finite-sample situation.

The theorem below shows that if some of the estimators ${\hat{\tau }}^{(j)}$ are consistent, then ${\hat{\tau }}$ converges to $\tau ^*$ asymptotically. Suppose that there exist at least one encoded Bernoulli sequence such that $p_{1,\tau ^*}^{(j)} \ne p_{2,\tau ^*}^{(j)}$. Without loss of the generalization, we suppose that a change point exists in $\{E_t^{(j)}\}_t$ for $j=1,2,\ldots ,u$, and no change point exists for $j=(u+1),\ldots ,V$ where $1 \le u \le V$.

Theorem 1

Assume that if $p_{1,\tau ^*}^{(j)} \ne p_{2,\tau ^*}^{(j)}$, then ${\hat{\tau }}^{(j)}/N$ converges to $\gamma ^*$ asymptotically; otherwise, ${\hat{\tau }}^{(j)}/N$ converges to 0 or 1 meaning that no change point exists in $\{E_t^{(j)}\}_t$. Then, for any $\epsilon >0$,

$$\begin{aligned} P(|{\hat{\tau }}/N-\gamma ^* |< \epsilon ) \rightarrow 1 \end{aligned}$$

as $N \rightarrow \infty$.

Theorem 1 assumes that ${\hat{\tau }}^{(j)}$ is a consistent estimator if a change point exists in $\{E^{(j)}_t\}_t$. So long as $u \ge 1$, the distributional discrepancy can be captured by ${\hat{\tau }}$. For a Bernoulli-variable sequence, the change point analysis is relatively easier. One can test the existence of a single change point and plug in a consistent estimator if the null is rejected.

In a more general case of multiple change points detection, suppose that observations are independent and distributed from $k+1$ distributions $\{F_i\}_{i=0}^k$. Let $\tau ^*_i/N \rightarrow \gamma ^*_i$ as $N\rightarrow \infty$, and $0=\gamma ^*_0<\gamma ^*_1<...<\gamma ^*_{k}<\gamma ^*_{k+1}=1$. Since $\{E^{(j)}_t\}_t$ may only reserve partial information of the distributional discrepancy, the number of change points in $\{E^{(j)}_t\}_t$ could be smaller than k and varies for different j. By further assuming the existence of consistent estimator in the Bernoulli-variable sequence, the theorem below shows that the consistency still holds when the number of change point $k>1$.

Theorem 2

Define that $C_i = \{j: {\hat{\tau }}^{(j)}_i/N \rightarrow \gamma _i^{*}~as~N\rightarrow \infty \}$. Suppose that the following assumptions hold,

• A1 $\vert C_i \vert \ge 1$ and ${\hat{\tau }}^{(j)}_i$ is none if $j \in \{1,\ldots ,V\}/C_i$

• A1 $\zeta _i + \zeta _{i+1}< \tau ^*_{i+1} - \tau ^*_i$ where $\zeta _i = \max _{j \in C_i} \vert {\hat{\tau }}^{(j)}_i-\tau ^{*}_i \vert$, for $i=1,\ldots ,k$

Then, for any $\epsilon >0$,

$$\begin{aligned} P(\max _{i=1,\ldots ,k} \vert {\hat{\tau }}_i/N-\gamma ^{*}_i\vert < \epsilon )\rightarrow 1 \end{aligned}$$

as $N \rightarrow \infty$.

Theorem 2 requires that the change point estimator is consistent if it exists, and there exists at least one estimator over the V Bernoulli sequences pertaining to a true change point. With such a strong assumption, it actually transforms the change point detection for unknown underlying distributions into the analysis of Bernoulli-variable sequence. The task becomes easier since an explicit likelihood function exists without further assuming any family of distributions. So, parametric approaches can get involved and fitted well under the framework. In practice, the searching algorithm advocated in Sect. 2 is employed to detect the change points for each Bernoulli process. Another advantages by applying the encoding-and-aggregation algorithm is that the error rate of change point detection can get controlled theoretically, which is present in the next section.

5 Stability change point analysis

Finally, it comes to the most general case that the number of change points and their locations are unknown. The current approaches can be divided into two types: model selection and multi-stage testing. A searching algorithm is usually applied in conjunction with a model selection procedure to explore a possible number of change points from 1 to a large number. Multi-stage testing is conducted to insert an additional change point at each stage and test the existence of the change point. However, the estimation results are not stable to the objective function or to the significance level in multi-stage testing. None of the approaches above provides a control for the discovery error of change point detection.

5.1 The stability detection method

In this section, we borrow the idea of stability variable selection and propose a robust change point detection framework, named stability detection. Stability selection was firstly advocated by Meinshausen and Buhlmann (2010) to enhance the robustness and control the false discovery rate of variable selection. By iteratively selecting half of the samples to feed into a base model, the relevant variables are ultimately discovered based on the votes aggregated over all the variable selection results. Later, Beinrucker et al. (2016) extent the stability selection by sampling disjoint subsets of samples.

Similar to the strategy of subsampling, we select a pre-determined subset of samples in $B^{(j)}$ to generate a Bernoulli sequence, and then estimate the number and locations of change points under the encoded Bernoulli sequences, respectively. By treating each time location as a variable, the stability selection framework is employed here to aggregate the estimated change points over $B^{(j)}$ for $j=1,2,\ldots ,V$. The successive change points are the ones with votes or selected probability above a predetermined threshold. However, it could be unrealistic to break down the chronological order and treat each time point separate from others. The points around the true change point locations could also be considered as acceptable results.

Denote that ${\mathcal {S}}^{(j)}$ is a set of change points detected based on Bernoulli sequence $\{E^{(j)}_t\}_t$, and $p^{(j)}(t)$ is the probability that a time location t is selected, i.e. $p^{(j)}(t)=P(t \in {\mathcal {S}}^{(j)})$. After aggregating all the change points sets ${\mathcal {S}}^{(j)}$ for $j=1,2,\ldots ,V$, the probability of selection for location t is defined by

$$\begin{aligned} \Pi ^V(t)=\frac{\sum _{j=1}^V \mathbbm {1}\{t \in {\mathcal {S}}^{(j)}\}}{V} \end{aligned}$$

(12)

The valid change points are ultimately detected if the probability $\Pi ^V(t)$ is above a threshold $\pi \in (0,1)$,

$$\begin{aligned} {\mathcal {S}}^{V}_{\pi }=\{t: \Pi ^V(t) \ge \pi \} \end{aligned}$$

(13)

5.2 Error control

To evaluate the false discovery rate, we need to define the noisy time points that we should exclude from the admissible set. Especially, we suppose that time locations around the true change point $\tau ^*$ are admissible change points and locations far away from $\tau ^*$ are noise. Define ${\mathcal {A}}=\{t: t\in (\tau _i^* -w_{\mathcal {A}},\tau _i^* +w_{\mathcal {A}}),~i=1,2,...\}$ as a set of admissible change points including true change points and their close neighbors. Here, $w_{\mathcal {A}}$ is an admissible window width and it can change over i. Similarly, define ${\mathcal {N}}=\{t: t \notin (\tau _i^* -w_{\mathcal {N}},\tau _i^* +w_{\mathcal {N}}),~i=1,2,...\}$ as a set of noisy time points which is outside from the neighbors of the true change points where $w_{\mathcal {N}}$ is a noisy window width. Note the window width $w_{\mathcal {A}}$ can be narrower than $w_{\mathcal {N}}$ such that ${\mathcal {A}} \subset {\mathcal {N}}^C$.

Theorem 3

Suppose that the following assumptions hold for $w_{\mathcal {A}}$ and $w_{\mathcal {N}}$,

• A1 $\sum _{j=1}^V p^{(j)}(t)/V$ are identical for any $t \in {\mathcal {N}}$

• A2 $\sum _{j=1}^V p^{(j)}(t)/V$ are identical for any $t \in {\mathcal {A}}$

Under the assumption A1 and A2, denote $p^{V}_{{\mathcal {N}}} = \sum _{j=1}^V p^{(j)}(t)/V$ for $t \in {\mathcal {N}}$ and $p^{V}_{{\mathcal {A}}} = \sum _{j=1}^V p^{(j)}(t)/V$ for $t \in {\mathcal {A}}$. Let $\pi \in (0,1)$ be the selection threshold.

For any $0< \xi < 1/p^{V}_{{\mathcal {N}}} -1$, if $\pi > (1+\xi )p^{V}_{{\mathcal {N}}}$ we have

$$\begin{aligned} \frac{E[\vert {\mathcal {S}}^{V}_{\pi } \cap {\mathcal {N}}\vert ]}{\vert {\mathcal {N}}\vert } \le \frac{1-(1+\xi )p^{V}_{{\mathcal {N}}}}{\pi -(1+\xi )p^{V}_{{\mathcal {N}}}}~exp\left( - \frac{\xi ^2 V}{\xi +2} p^{V}_{{\mathcal {N}}}\right) \end{aligned}$$

(14)

For any $0< \xi < 1$, if $\pi < (1-\xi )p^{V}_{{\mathcal {A}}}$ we have

$$\begin{aligned} \frac{E[\vert ({\mathcal {S}}^{V}_{\pi })^C \cap {\mathcal {A}}\vert ]}{\vert {\mathcal {A}}\vert } \le \frac{(1-\xi )p^{V}_{{\mathcal {A}}}}{(1-\xi )p^{V}_{{\mathcal {A}}}-\pi }~exp\left( - \frac{\xi ^2 V}{\xi +2} p^{V}_{{\mathcal {A}}}\right) \end{aligned}$$

(15)

Here, we assume that the noisy locations have the same expected probability to be selected, and so do the admissible locations. Under these assumptions, the theorem above is shown to bound the expectation of false positive rate or false negative rate of change point detection, depending on the choice of threshold $\pi$.

While the bound of false positive rate or false negative rate decays with V, it fails to choose the number of iterations as large as possible since a larger V would reduce the sample size at each iteration. In order to control the false discovery rate from both sides, one should increase the signal-selection rate $p^{V}_{{\mathcal {A}}}$ and decrease the noise-selection rate $p^{V}_{{\mathcal {N}}}$. It is ideal to set threshold in between, $(1+\xi )p^{V}_{{\mathcal {N}}}< \pi < (1-\xi )p^{V}_{{\mathcal {A}}}$. Recall the definition of the selection set ${\mathcal {S}}^{(j)}:=\{{\hat{\tau }}^{(j)}_i,~i=1,\ldots ,{\hat{k}}^{(j)}\}$ where ${\hat{\tau }}^{(j)}_i$ is the ith estimator of the jth Bernoulli sequence. $p^{V}_{{\mathcal {A}}}$ can be simplified by $\sum _{j=1}^V P({\hat{\tau }}^{(j)}_i \in (\tau _i^* -w_{\mathcal {A}},\tau _i^* +w_{\mathcal {A}}))/V$. Thus, with a fixed width of $w_{\mathcal {A}}$, a good estimator ${\hat{\tau }}^{(j)}_i$ is favored in the sense that it is close the true change point location with high probability.

Another way to increase $p^{V}_{{\mathcal {A}}}$ is to sightly expand the selection set ${\mathcal {S}}^{(j)}$, that is to say, selecting the estimators and their neighbors. So, ${\mathcal {S}}^{(j)}=\{t: t \in neig({\hat{\tau }}^{(j)}_i),~i=1,\ldots ,{\hat{k}}^{(j)}\}$. A wider neighbor set neig() tend to comprise more admissible change points but endure the risk of involving more noise. In the analysis of a Bernoulli sequence, it is supposed in Sect. 2 that a change point is located exactly at the position of 1’s. A conservative way in expanding the selection set is to also contain the 0’s locations between the last and the next 1’s.

6 Subsampling and weighting strategy

From an application perspective, there are still two real problems to be addressed. Firstly, how to generate a series of subarea $\{B^{(j)}\}_{j=1,\ldots ,V}$ in the encoding phase. Secondly, how to weighting the contribution for each encoded Bernoulli sequence $\{E_t^{(j)}\}_t$ based on its degree of relevance. A follow-up question is that how to measure the goodness-of-fit for each $\{E_t^{(j)}\}_t$ and weighting their contributions accordingly. In this section, we resolve both problems via a subsampling weighting technique.

To address the first one, a natural way is to apply clustering analysis to obtain V disjoint clusters as $\{B^{(j)}\}$. But it raises another problem related to how to choose a certain number of clusters and the second question becomes even hard due to the unbalanced cluster size. Model selection criterion in (1) can be reused to measure the goodness-of-fit if the cluster sizes are balanced. To ensure robustness and efficiency, we attempt to generate a larger number of clusters but with fixed cluster size, so overlappings are expected. Our numerical experiments show that the result is not sensitive to the choice of V. We advocate that $V=50$ is large enough and subsampling proportion can be fixed at $M/N=0.1$, so a sample is selected 5 times on average.

Denote ${\mathbb {X}}=[X_1, X_2,\ldots , X_N]^{'}$ as a $N \times p$ matrix recording the time series $\{X_t\}_{t=1}^N$ where $X_t \in {\mathbb {R}}^p$. The subsampling algorithm is described as follows. We firstly apply K-Means upon ${\mathbb {X}}$ to get V cluster centroids. Then, cycle through each centroid to search for its M nearest neighbors in ${\mathbb {X}}$. We mark the M samples as 1 and the other $N-M$ as 0 at each iteration, so V Bernoulli sequences are encoded. If without confusion, let’s denote the M marked samples in the jth step as $B^{(j)}$.

Since the degree of relevance is inversely proportional to the model selection criterion values or loss in (1), one can consider a mapping function ${\mathcal {F}}: {\mathbb {R}}\mapsto {\mathbb {R}}$ to scale the quantity,

$$\begin{aligned} {\mathcal {F}}(x)=1-\frac{x-\min (x)}{\max (x)-\min (x)} \end{aligned}$$

so, the weight $w^{(j)}$ measuring the importance of jth Bernoulli sequence is defined by,

$$\begin{aligned} w^{(j)} = \frac{{\mathcal {F}}(L^{(j)})}{\sum _{j=1}^V {\mathcal {F}}(L^{(j)})} \end{aligned}$$

(16)

where $L^{(j)} = L({\hat{\tau }}^{(j)}_1,{\hat{\tau }}^{(j)}_2,...)$ is the loss of the jth sequence. Thus, a $N \times V$ weighted design matrix ${\mathcal {M}}^{weighted}$ is fed into the time-order-kept hierarchical clustering algorithm mentioned in Sect. 3.3,

$$\begin{aligned} {\mathcal {M}}^{weighted}={\mathcal {M}}_{N \times V} \times diag(w^{(1)},\ldots ,w^{(V)}) \end{aligned}$$

(17)

Another weighting technique is based on the iterative weighting algorithm proposed in Wang and Hsieh (2021). In a simple case that only one change point exists in a Bernoulli sequence, it is complicated or even impossible to detect the parameter change if the Bernoulli parameters are too close. Indeed, one can qualify the goodness-of-fit via the difference between $p^{(j)}_{1,\tau ^*}$ and $p^{(j)}_{2,\tau ^*}$ or the estimated delta $\vert {\hat{p}}^{(j)}_{1,{\hat{\tau }}}-{\hat{p}}^{(j)}_{2,{\hat{\tau }}}\vert$ in practice. The estimated delta can be further approximated by the proportion of two recovered segments in $B^{(j)}$. The more purity of $B^{(j)}$, the better $E_t^{(j)}$ can be fitted. It enlightens us to measure the Shannon entropy in $B^{(j)}$ as an approximation when $k>1$.

Denote the weight of the jth sequence at the current step as $w_c^{(j)}$ and the entropy of set $B^{(j)}$ at the current step as $H_c(B^{(j)})$. We iteratively apply clustering algorithm upon the weighted matrix in (17) and update the the entropy $H_c(B^{(j)})$ based on the recovered segments in the last step. So, the weight in the next step can be updated by

$$\begin{aligned} w_{c+1}^{(j)} = 0.5~w_{c}^{(j)} + 0.5~ \frac{{\mathcal {F}}(H_c(B^{(j)}))}{\sum _{j=1}^V {\mathcal {F}}(H_c(B^{(j)}))} \end{aligned}$$

(18)

until convergence. Here, 0.5 is set to smooth the learning curve and to make the sum of weights equal 1.

7 Numerical experiment

In this section, we conduct simulation experiments to evaluate the performance of our model on various univariate and multivariate distributions with both known and unknown numbers of change points.

When the number of change points k is known, we implement the time-order-kept hierarchical clustering algorithm with the proposed weighting techniques from Eqs. (16) and (18). To distinguish between the two weighting techniques, we refer to (16) as “Simp Weight” and (18) as “Iter Weight”. When k is unknown, the stability detection is implemented by aggregating the estimated change points over the Bernoulli sequences via weighted voting. We compare the performance of our approaches with other nonparametric methods such as Multiscale Quantile Segmentation (MQS) by Vanegas et al. (2022), nonparametric PELT (np PELT) by Haynes et al. (2017), and Narrowest-Over-Threshold (NOT) by Baranowski et al. (2019), specifically in the univariate settings. For both univariate and multivariate scenarios, we also evaluate the performance of E-Divisive by Matteson and James (2014), Kernel Multiple Change Point (KernelMCP) by Arlot et al. (2019), and MultiRank by Lung-Yut-Fong et al. (2015).

Our method was implemented with $V=50$, cluster proportion $M/N=0.1$, and $\phi (N)=2$ (AIC) for the iterative weighting. In the iterative process, we set the iteration number to $R=150$ and used a stop criterion that stops the iterations when the weights do not change for 10 consecutive steps. For comparison, we implemented MQS and nonparametric PELT using the official R packages mqs and changepoint.np, respectively, with their tuning parameters set to the default values. NOT was implemented using the not package with a prefixed contrast function chosen to best fit the simulation scenario. E-Divisive was implemented using the ecp package with the tuning parameter $\alpha =1$ and $R=499$ as advocated by the authors. KernelMCP was implemented using the Python package named Chapydette with the default settings, including a Gaussian kernel with Euclidean distance, a bandwidth of 0.1, and $\alpha =2$. For MultiRank, we used the R codes provided in the supplementary file of Matteson and James (2014).

To compare the performance of change point detection result, we calculate the Adjusted Rand Index (ARI) (Hubert & Arabie, 1985) between the recovered segments and the true segments. Rand Index (RI) (Rand, 1971) was originally used to measure the similarity between two data clustering results. Suppose that $A=\{A_1, A_2,\ldots , A_a\}$ and $B=\{B_1, B_2,\ldots , B_b\}$ are two different partitions for a sequence of observations of length N with cluster number a and b, respectively. Let u be the number of pairs of observations that are in the same subset in both A and B, and v be the number of pairs of observations that are in different subsets in both A and B. The Rand Index (RI) is then defined by

$$\begin{aligned} RI = \frac{u + v}{N(N-1)/2} \end{aligned}$$

(19)

The Rand Index measures the number of agreements between A and B over the total pairs of observations. In the context of segmentation detection, we can consider A as the ground truth segmentation and B as the predicted one. The Rand Index represents the accuracy of the algorithm’s decisions. To account for chance grouping, the Adjusted Rand Index (ARI) is commonly used. It corrects the Rand Index by comparing it with a baseline that represents the expected similarity of all pairwise comparisons. An ARI value of 1 indicates a perfect result, while negative or 0 values imply that the recovered segment is significantly different from the underlying segment.

7.1 Known number of change points

In the simulation study, we generated univariate distributions with different variance or tailedness. Three segments were sequentially generated with distributions ${\mathcal {N}}(0,1)$, ${\mathcal {G}}$, and ${\mathcal {N}}(0,1)$, respectively. For changes in variance, ${\mathcal {G}} \sim {\mathcal {N}}(0,\sigma ^2)$; for changes in tailedness, ${\mathcal {G}} \sim t_{df}(0,1)$. The segments were unbalanced with time lengths n, 2n, and n, respectively, where n varied at $n=100, 200, 300$, while the proportion of the three segments remained the same.

Table 1 ARI values in univariate student-t setting

We measured the accuracy of change point detection using the Adjusted Rand Index (ARI) values for our methods, E-Divisive, KernelMCP, and MultiRank, given the number of change points. In the setting of Gaussian distribution with variance changes, E-Divisive performed the best as shown in Table 6 in the Appendix. The overall performance was worse in the setting of changes in tailedness (see Table 1), but our iterative weighting approach performed slightly better than others. KernelMCP performed well when ${\mathcal {G}}$ was Gaussian distributed but failed otherwise, indicating sensitivity to the choice of kernel. As a nonparametric approach designed particularly for changes in mean, MultiRank consistently failed in the simulation settings.

In the next part of the numerical experiment, we generated multivariate observations with distributions from ${\mathcal {N}}_d(0,I)$, ${\mathcal {N}}_d(0,\Sigma )$, and ${\mathcal {N}}_d(0,I)$, respectively. The observations were simulated in dimensions $d=2, 3, 5, 10$. Two types of covariance matrices, $\Sigma _1$ and $\Sigma _2$, were used for the generation. $\Sigma _1$ was set with diagonal elements of 1 and off-diagonal elements of $\rho$; $\Sigma _2$ was set with diagonal elements of 1 and $\pm 1$ for off-diagonal elements of $\rho$. Since KernelMCP is not easily adaptive when the dimension is higher, we only compared the performance of our method with that of E-Divisive as a baseline in Table 2. A full comparison between our method and KernelMCP in binormal settings is available in Table 7 in the Appendix.

The results show that the two weighting techniques are comparable in identifying the change point locations in the case of $\Sigma _1$. In the more complicated case of $\Sigma _2$, the iterative weighting performs the best among the methods compared.

Table 2 ARI values in d-dim Gaussian setting

7.2 Unknown number of change points

In our simulation study, we addressed the scenario where the number of change points is unknown. Unlike manually selecting different values of the predetermined number of change points k, our proposed stability detection approach estimates the probability of selecting each time stamp directly. By searching for the local maxima time stamps with probabilities above a threshold, we can effectively estimate the change point locations without exhaustive searching or predefined candidate values of k. This is achieved by encoding the continuous observations into V Bernoulli sequences, resulting in V voting sets, and computing the probability of selection for each time stamp as a weighted sum of the voting results using the simple weighting technique (16).

The simulation involved generating observations with a time axis containing a total of $k=6$ change points. Each segment had a fixed length of data points (=100), and adjacent segments followed different distributions, denoted as $\{{\mathcal {N}}, {\mathcal {G}},{\mathcal {N}}, {\mathcal {G}},{\mathcal {N}}, {\mathcal {G}},{\mathcal {N}}\}~ \text{where}~ {\mathcal {N}} \sim {\mathcal {N}}(0,1) ~\text{and}~ {\mathcal {G}} \sim m + t_{df}(0,1)$. We evaluated our approach using the Adjusted Rand Index (ARI) and the absolute error of the estimated number of change points ($|{\hat{k}} - k|$) as metrics. In addition to our proposed approach, we compared our results with six other nonparametric change point detection methods: nonparametric PELT, MQS, NOT, E-Divisive, Multirank, and KernelCPA. The mean and standard deviation of the evaluation results are presented in Table 3.

Table 3 Univariate simulation setting when the number of change point are unknown

Our proposed method exhibits robustness and outperforms other nonparametric approaches in various simulation settings. It accurately estimates both the number and location of change points, even in challenging scenarios with small changes in mean and variance. The nonparametric PELT performs exceptionally well in cases of abrupt changes in mean or variance, highlighting its capability to capture significant distribution changes.

In the multivariate setting, we conducted an experiment with observations generated from a d-dimensional normal distribution with 6 change points. The segments with indices [1,100], [201,300], [401,500], and [601,700] followed the distribution ${\mathcal {N}}_d(0, I)$, while the remaining observations had changes in either the mean or the covariance matrix. Specifically, the mean was set as ${\mathcal {N}}_d(m {\textbf{1}}, \Sigma )$, where ${\textbf{1}}$ is a d-dimensional vector with all elements equal to 1, and $\Sigma$ had diagonal elements equal to 1 and off-diagonal elements equal to $\rho$.

Table 4 Multivariate simulation setting when the number of change point are unknown

To evaluate the performance of different change point detection methods, including E-Divisive, MultiRank, KernelMCP, and our proposed method, we measured their accuracy in detecting the change point locations. The results are presented in Table 4, where each column represents a different dimension (ranging from 2 to 10). E-Divisive performed best in detecting change points with only mean changes, while KernelMCP showed promising results for lower dimensions but struggled when the dimension exceeded 5. In cases of changes in the covariance matrix, the other methods failed to detect the change points, whereas our proposed method consistently demonstrated good performance. This highlights the robustness of our approach in handling various settings of distributional changes.

7.3 Ablation study of the number of clusters

In the ablation study, we explored the influence of varying the number of clusters V on the performance of our proposed method in segmenting the dimensional space. To assess the performance, we used the Adjusted Rand Index (ARI) as a measure. In the scenario where there were changes in covariance, we found that the ARI was not significantly affected by the number of clusters as shown in Table 5. However, slightly improved results were obtained when V was set to 50 or greater. Based on these findings, we chose to use $V=50$ as the parameter for practical implementation of our method.

Table 5 Number of clusters

7.4 Consistency as sample size increases

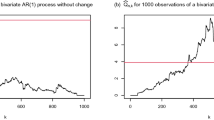
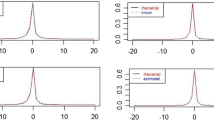
As the sample size N increases in the 6-change-point simulation scenario, we observe that the probability of selection curve becomes more pronounced with prominent spikes. The local maxima in the curve align more closely with the ground truth change points, indicating improved accuracy in estimating the change point locations. This trend is consistently observed, as shown in Fig. 1. Moreover, the Adjusted Rand Index (ARI) metric, which measures the similarity between the estimated change points and the ground truth, increases from 0.75 in (A) to 0.88 in (C) as the sample size N increases. This demonstrates that our proposed method achieves consistently higher accuracy with larger sample sizes.

Fig. 1

Simulation setting: covariance $\Sigma$ changes with $\rho =0.7$ and $d=2$. Probability of selection curve with sample size (A) $N=200 \times 7$; (B) $N=300 \times 7$; (C) $N=400 \times 7$

7.5 Penalty coefficient study

We generate observations independently from three binormal distributions: ${\mathcal {N}}_2(0,I)$, ${\mathcal {N}}_2(0,[[1,0.7],[0.7,1]] )$, and ${\mathcal {N}}_2(0,I)$, with sample sizes of 300, 600, and 300, respectively. In the change point analysis, we employ a model selection criterion with a penalty coefficient $\phi (N)$, where $\phi (N)$ varies from 2, corresponding to AIC, to log(N), corresponding to BIC. The time axis is divided into evenly-sized, disjoint time bins, and the probability of selection is computed based on the accumulated votes within each time bin.

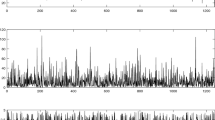
The results indicate that the selected time bins have relatively high probabilities regardless of the choice of penalty term. These selected time bins, marked in Fig. 2, include the first and second bins (320, 360) and (360, 400), which are close to the first change point located at 300, as well as the third and fourth bins (280, 320) and (880, 920), which cover the true change point locations. The visualization of detection results is shown in Fig. 6 in the Appendix. The two prominent spikes in the plots indicate that the number of change points is 2. By applying a threshold of 0.1, we can identify two consecutive time windows that cover the true change point locations.

Fig. 2

Probability of selection with different penalty coefficient $\phi (N)$; different time bins are plotted in different curves

7.6 Time complexity analysis

In the univariate setting, the Pruned Exact Linear Time (PELT) algorithm has been successful in reducing the computational cost of change detection to O(N) under certain assumptions. However, in the multivariate setting, the time complexity of change detection has traditionally been on the order of $O(KN^2)$, where K is the maximum number of change points. The proposed approach in this paper addresses this limitation by leveraging the encoding of observations into multiple Bernoulli sequences. The voting results from these Bernoulli sequences are then aggregated to obtain the final change point estimations. Importantly, this aggregation can be efficiently performed in parallel using modern parallel programming techniques. As a result, the time complexity can be reduced to $O(N^2)$, making the approach scalable and efficient in scenarios with a high number of change points.

8 Real data application

8.1 Genome data

CpG dinucleotide clusters or ‘CpG islands’ are genome subsequences with a relatively high number of CG dinucleotides (a cytosine followed by a guanine). They are observed close to transcription start sites (Sxonov et al., 2006) and play a crucial role in gene expression regulation and cell differentiation (Bird, 2002). There were developed many computational tools for CpG island identification. A sliding window is typically employed to scan the genome sequence to figure out CpG islands based on some filtering criteria. However, the criteria are set with subjective choice (G$+$c proportion, observation versus expectation ratio, etc) and it has evolved over time. It commonly happens that different CpG island finders would provide various results.

In this section, we implement our change point detection approach in the categorical nucleotide sequence. It is demonstrated that the proposed algorithm is able to detect an abrupt change in C-G patterns, and the estimated change point locations may help researchers to identify potential CpG islands. A contig (accession number $\text{NT\_000874.1}$) on human chromosome 19 was taken as an example for CpG island searching. The dataset is available on the website of National Center for Biotechnology Information(NCBI).

Denote the genome sequence as $\{X_t\}_{t=1}^N$ with $X_t \in \{A,G,T,C\}$. In the encoding phase, a 0–1 sequence $\{E_t\}_t$ is generated such that $E_t=1$ if $X_{t}=C \& X_{t+1}=G$ and $E_t=0$ otherwise, for $t=1,\ldots ,N-1$. Algorithm 1 is implemented to search for multiple change points in the Bernoulli sequence. Results from a CpG island searching software CpGIE (Wang & Leung, 2004) are shown as a benchmark for comparison. Criteria advocated by the authors are employed in the usage of CpGIE (length $\ge 500$ bp, G $+$ C content $\ge 50\%$ and CpG O/E ratio $\ge 0.60$). Note that our algorithm does not need any tuning parameter. The result in Fig. 3 shows that there is a high proportion of overlapping segments between ours and CpGIE’s. Our approach can also find extra genome subsequence with a higher number of C-Gs which are misspecified by CpGIE.

Fig. 3

Encoded DNA sequence-CG dinucleotides patterns; the CpG islands discovered by CpGIE are marked by angle brackets; the estimated change point locations are marked by vertical bars

8.2 Hurricane data

It was widely recognized that the global temperature has risen due to anthropogenic factors, such as increased carbon dioxide emissions and other human activities. According to NOAA’s 2020 global climate report, the annual temperature has increased globally at an average rate of 0.14 degrees Fahrenheit per decade since 1880 and over twice that rate (0.32 degrees Fahrenheit) since 1981. It was argued by climatologists that the warmer sea surface leads to an increasing number of stronger tropical cyclones (Emanuell, 2005; Saunders & Lee, 2008). However, Landsea et al. (2010) believes that the warmer sear surface increases only weak cyclones which are short and even hard to be detected. In this section, we studied the number of cyclones between 1851 and 2019. We are interested to detect potential change points embedded within the tropical cyclone history.

The dataset HURDAT2 recording the activities of cyclones in the Atlantic basin is available on the website of National Oceanic Center(NHC). NHC tracked the intensity of each tropical cyclone per 6 h every day (at 0, 6, 12, and 18). The intensity level is categorized based on wind strength in knots, such as hurricane (intensity greater than 64 knots), tropical storm (intensity between 34 and 63 knots), and tropical depression (intensity less than 34 knots). Different from Robbins et al. (2011) in categorizing cyclones, we summarize the number of time units for which a category is observed, so the count is at most $4\times 31$ in a month. The monthly frequency of tropical storm-level and higher-level cyclones is reported in Fig. 4A. If we apply 5 change points which is detected by the local maxima of stability detection in Fig. 4B, the time range is then partitioned based on the variation of storm count. Figure 4A shows that storms are more active in the 1880 s, 1960 s and after 2000. Though the global temperature trends to go upward since 1980, the storms are relatively sparse between 1980 and 2000. Thus, our analysis result challenges the original supposition that higher temperatures would increase the number of hurricanes.

Fig. 4

A monthly hurricane counts in Atlantic basin from year 1851 to 2019; estimated change points are plotted in vertical lines. B probability of selection for all the time points; local maximas are plotted in vertical lines

8.3 Financial data

Lastly, the proposed approach is applied to detect the abrupt time-varying dependence within bivariate stock log returns. CTSH and IBM are chosen as representative of IT Consulting subcategories of S &P500 based on Global Industrial Classification Standard(GICS). The first and last hours in the transaction time are filtered out (so it is from 10am to 4pm), and the hourly price returns are calculated in the business days of the year 2006. A constant is added to the returns of CTSH for a better visualization in Fig. 5(A). It was noted that the lagged correlation statistics are not significant based on the sample autocorrelation function of stock returns. Conditional heteroskedasticity can be studied by a more complicated time series model, like GARCH, but it is out of our concentration.

We encode the bivariate time series and apply stability detection techniques. Figure 5B shows that there exist 3 or 4 change points within the returns. The top3 change point locations with the highest probability are marked by vertical lines in Fig. 5A. It shows that the returns are partitioned into segments with different volatility levels. If we further look into the scatterplot between CTSH and IBM under different time partitions (left, middle, right segments) in Fig. 7 in the Appendix, both returns in the middle phase are relatively high, and their correlation is much stronger.

Fig. 5

A hourly index returns of CTSH and IBM in 2006; top3 change points with the highest probability of selection are plotted in vertical lines. B probability of selection for all time points

9 Conclusion

In this paper, we have presented a robust and efficient solution for change point detection in time series data without requiring strong distributional assumptions. It involves encoding continuous observations into Bernoulli processes and utilizing aggregation techniques to estimate the number and locations of change points. Our approach is applicable to both univariate and multivariate settings, and it can handle scenarios with known or unknown numbers of change points.

The theoretical analysis of our method demonstrates that it holds both asymptotic properties and finite-sample error control, ensuring its reliability and accuracy in practical applications. The numerical experiments conducted on simulated data have shown that our approach outperforms existing nonparametric methods, especially in situations with complex distributional changes. Furthermore, the real-world data analyses on various types of time series, including continuous, categorical, and ordinal data, have further confirmed the versatility and effectiveness of our method.

We acknowledge that the subsampling strategy based on K-means clustering may make the results less interpretable. In the future, we aim to explore alternative sampling strategies to enhance the interpretability of the results. For instance, in the univariate scenario, instead of relying solely on K-means clustering, we can consider modifying the encoding process by applying quantile thresholds to identify extreme observations, as discussed in Wang and Hsieh (2022). Moreover, we plan to investigate other encoding techniques that are more tailored to specific data characteristics. For multivariate data, alternative clustering algorithms or dimensionality reduction techniques may be explored to improve the efficiency and interpretability of the encoding process.

Appendices

Appendix A: Proof of theorem in 3.4

Proof of Theorem 1

Let ${\hat{\gamma }}^{(j)}={\hat{\tau }}^{(j)}/N$. For any $\gamma \in (0,1)$, rewrite

$$\begin{aligned} {\hat{G}}(\gamma )= \sum _{j=1}^V g({\hat{\gamma }}^{(j)},\gamma ) ({\hat{p}}_{1,{\hat{\tau }}^{(j)}}^{(j)}-{\hat{p}}_{2,{\hat{\tau }}^{(j)}}^{(j)})^2 \end{aligned}$$

where

$$\begin{aligned} g({\hat{\gamma }}^{(j)},\gamma )= \frac{{\hat{\gamma }}^{(j)}}{\gamma }\left( 1-\frac{{\hat{\gamma }}^{(j)}}{\gamma }\right) \mathbbm {1} \{\gamma \ge {\hat{\gamma }}^{(j)}\} + \frac{1-{\hat{\gamma }}^{(j)}}{1-\gamma }\left( 1-\frac{1-{\hat{\gamma }}^{(j)}}{1-\gamma }\right) \mathbbm {1} \{\gamma <{\hat{\gamma }}^{(j)}\} \end{aligned}$$

For $j=1,\ldots ,u$, with the consistency of ${\hat{\tau }}^{(j)}$, we can have

$$\begin{aligned} g({\hat{\gamma }}^{(j)},\gamma ) ({\hat{p}}_{1,{\hat{\tau }}^{(j)}}^{(j)}-{\hat{p}}_{2,{\hat{\tau }}^{(j)}}^{(j)})^2 \rightarrow g(\gamma ^*,\gamma )(p_{1,\tau ^*}^{(j)}-p_{2,\tau ^*}^{(j)})^2 \end{aligned}$$

While for $j=(u+1),\ldots ,V$, it shows

$$\begin{aligned} g({\hat{\gamma }}^{(j)},\gamma ) ({\hat{p}}_{1,{\hat{\tau }}^{(j)}}^{(j)}-{\hat{p}}_{2,{\hat{\tau }}^{(j)}}^{(j)})^2 \rightarrow 0 \end{aligned}$$

since $g(0,\gamma )=g(1,\gamma )=0$. Therefore,

$$\begin{aligned} {\hat{G}}(\gamma ) \rightarrow \sum _{j=1}^u g(\gamma ^*,\gamma )(p_{1,\tau ^*}^{(j)}-p_{2,\tau ^*}^{(j)})^2 = g(\gamma ^*,\gamma ) \Vert p^u_{1,\tau ^*}-p^u_{2,\tau ^*}\Vert ^2= G(\gamma ) \end{aligned}$$

as $N \rightarrow \infty$, uniformly in $\gamma$. Let ${\hat{\gamma }}={\hat{\tau }}/N$. It follows that

$$\begin{aligned} {\hat{G}}({\hat{\gamma }}) < {\hat{G}}(\gamma ^*) \end{aligned}$$

Additionally, the minimum value of $g(\gamma ^*,\gamma )$ is attained when $\gamma =\gamma ^*$. For any $\epsilon >0$, there exists $\eta >0$, such that $G(\gamma )-G(\gamma ^*)>\eta$, for all $\gamma$ with $|\gamma -\gamma ^* |\ge \epsilon$. Therefore,

$$\begin{aligned} \begin{aligned} P(\vert {\hat{\gamma }}-\gamma ^* \vert>\epsilon )&\le P(G({\hat{\gamma }})-G(\gamma ^*)>\eta ) \\&= P(G({\hat{\gamma }})-{\hat{G}}({\hat{\gamma }}) +{\hat{G}}({\hat{\gamma }})-G(\gamma ^*)>\eta )\\&\le P(G({\hat{\gamma }})-{\hat{G}}({\hat{\gamma }}) +{\hat{G}}(\gamma ^*)-G(\gamma ^*)>\eta )\\&\le P( \vert G({\hat{\gamma }})-{\hat{G}}({\hat{\gamma }}) \vert> \eta /2) + P(\vert {\hat{G}}(\gamma ^*)-G(\gamma ^*) \vert > \eta /2) \rightarrow 0 \end{aligned} \end{aligned}$$

as N goes into infinity. $\square$

Proof of Theorem 2

Denote $\tau _i^*=N\gamma _i^*$. Consider a group of change point locations that $\tilde{\tau }_i=\tau _i^*+\zeta _i$, for $i=1,2,\ldots ,k$. By the definition of $\zeta _i$, it follows that

$$\begin{aligned} \begin{aligned} {\hat{G}}(\tilde{\tau }_1,\ldots ,\tilde{\tau }_k)&\le \sum _{i=0}^{k-1} \sum _{j\in C_{i+1}}\frac{2\vert {\hat{\tau }}^{(j)}_i-\tau ^{*}_i\vert }{\tau ^{*}_{i+1}-\tau ^{*}_i} \left( 1-\frac{2\vert {\hat{\tau }}^{(j)}_i-\tau ^{*}_i\vert }{\tau ^{*}_{i+1} -\tau ^{*}_i})({\hat{p}}^{(j)}_{i+1}-{\hat{p}}^{(j)}_{i}\right) ^2\\&\le \sum _{i=0}^{k-1} \vert C_{i+1} \vert \frac{2\zeta _i/N}{\gamma ^{*}_{i+1}-\gamma ^{*}_i} \left( 1-\frac{2\zeta _i/N}{\gamma ^{*}_{i+1}-\gamma ^{*}_i}\right) \end{aligned} \end{aligned}$$

Then, denote $\Theta = \{(\tau _1,\ldots ,\tau _k): \max _{i=1,\ldots ,k} \vert \tau _i/N-\gamma ^{*}_i \vert \le \epsilon \}$. It shows that, for any $\epsilon >0$,

$$\begin{aligned} P(\max _{i=1,\ldots ,k} \vert {\hat{\tau }}_i/N-\gamma ^*_i \vert \ge \epsilon ) \le P(G({\hat{\tau }}_1,\ldots ,{\hat{\tau }}_k) \le \min _{(\tau _1,\ldots ,\tau _k) \in \Theta } G(\tau _1,\ldots ,\tau _k)) \end{aligned}$$

(*)

Moreover, since $\zeta _i$ is consistent to 0, uniformly in i, by the assumption. So,

$$\begin{aligned} P(\max _{i=1,\ldots ,k}\zeta _i > \epsilon ) \rightarrow 0 \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} (*) \quad&\le P(G({\hat{\tau }}_1,\ldots ,{\hat{\tau }}_k) \le \min _{(\tau _1,\ldots ,\tau _k) \in \Theta } G(\tau _1,\ldots ,\tau _k \vert \max _{i}\zeta _i< \epsilon )P(\max _{i}\zeta _i < \epsilon ) \\&\quad + P(G({\hat{\tau }}_1,\ldots ,{\hat{\tau }}_k) \le \min _{(\tau _1,\ldots ,\tau _k) \in \Theta } G(\tau _1,\ldots ,\tau _k \vert \max _{i}\zeta _i \ge \epsilon )P(\max _{i}\zeta _i \ge \epsilon )\\&\le P(G({\hat{\tau }}_1,\ldots ,{\hat{\tau }}_k) \le G(\tilde{\tau }_1,\ldots ,\tilde{\tau }_k)) + P(\max _{i}\zeta _i \ge \epsilon ) \\&\rightarrow P(G({\hat{\tau }}_1,\ldots ,{\hat{\tau }}_k) \le 0) + 0 = 0 \end{aligned} \end{aligned}$$

as N goes into infinity. $\square$

Appendix B: Proof of theorem in 4.2

Proof of Theorem 3

For any $0< \xi < V/\sum _{j=1}^V p^{(j)}(t) -1$, denote $\pi _{{\mathcal {N}}} = (1+\xi )\sum _{j=1}^V p^{(j)}(t)/V$, so that $\pi _{{\mathcal {N}}} \in (0,1)$.

It is easy to show that $\Pi ^V(t) \le (1-\pi _{{\mathcal {N}}})\mathbbm {1}\{\Pi ^V(t) \ge \pi _{{\mathcal {N}}}\} + \pi _{{\mathcal {N}}}$ for a fix $t \in \{1,2,\ldots ,N\}$. Thus,

$$\begin{aligned} \begin{aligned} P(\Pi ^V(t) \ge \pi )&\le P((1-\pi _{{\mathcal {N}}})\mathbbm {1}\{\Pi ^V(t) \ge \pi _{{\mathcal {N}}}\} + \pi _{{\mathcal {N}}} \ge \pi )\\&= P\left( \mathbbm {1}\{\Pi ^V(t) \ge \pi _{{\mathcal {N}}}\} \ge \frac{\pi - \pi _{{\mathcal {N}}}}{1 - \pi _{{\mathcal {N}}}}\right) \\&\le \frac{1 - \pi _{{\mathcal {N}}}}{\pi - \pi _{{\mathcal {N}}}} P(\Pi ^V(t) \ge \pi _{{\mathcal {N}}})\\&= \frac{1 - \pi _{{\mathcal {N}}}}{\pi - \pi _{{\mathcal {N}}}} P\left( \sum _{j=1}^V \mathbbm {1}\{t \in {\mathcal {S}}^{(j)}\} \ge (1+\xi )\sum _{j=1}^V p^{(j)}(t)\right) \end{aligned} \end{aligned}$$

The last inequality holds based on Markov’s inequality and the condition that $\pi >\pi _{{\mathcal {N}}}$.

Moreover, $\mathbbm {1}\{t \in {\mathcal {S}}^{(j)}\}$ are independent for $j=1,2,\ldots ,V$. It holds because that we select disjoint samples to make up $\{E^{(j)}_t\}_t$ so for a fixed time t, its selection does not reply on the iteration index j. The resultant probability can be further bounded via Chernoff upper bound,

$$\begin{aligned} \begin{aligned} P(\sum _{j=1}^V \mathbbm {1}\{t \in {\mathcal {S}}^{(j)}\} \ge (1+\xi )\sum _{j=1}^V p^{(j)}(t)) \le exp\left( -\frac{\xi ^2}{\xi +2} \sum _{j=1}^V p^{(j)}(t)\right) \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \frac{E[\vert {\mathcal {S}}^{V}_{\pi } \cap {\mathcal {N}}\vert ]}{\vert {\mathcal {N}}\vert }&= \frac{\sum _{t \in {\mathcal {N}}} P(\Pi ^V(t) \ge \pi )}{\vert {\mathcal {N}}\vert }\\&\le \sum _{t \in {\mathcal {N}}} \frac{1 - \pi _{{\mathcal {N}}}}{\pi - \pi _{{\mathcal {N}}}}~exp\left( -\frac{\xi ^2}{\xi +2} \sum _{j=1}^V p^{(j)}(t)\right) ~/~\vert {\mathcal {N}}\vert \end{aligned} \end{aligned}$$

By further assuming identical $\sum _{j=1}^V p^{(j)}(t)$ for $t \in {\mathcal {N}}$, we can cancel ${\mathcal {N}}$ for both numerator and denominator, so the inequality (14) is obtained. Inequality (15) can be proved similarly via the lower bound of Chernoff’s. $\square$

Appendix C: Tables and figures

See Tables 6, 7 and Figures 6, 7.

Table 6 ARI values in univariate Gaussian setting

Table 7 ARI values in 2-dim Gaussian setting

Fig. 6

A probability of selection with $\phi (N)=2$ as AIC; B probability of selection with $\phi (N)=log(N)$ as BIC. True change point locations are plotted in vertical lines

Fig. 7

Scatterplot of returns of CTSH versus IBM; A observations on the left segment; B observations on the middle segment; C observations on the right segment