1 Introduction

Drug discovery (DD) is a process that consists in the identification of a new candidate drug that could be therapeutically useful in treating a pathological condition. An important step in the DD process is the development of quantitative structure-activity relationships (QSAR) models. These models allow understanding which structural properties of the tested molecules can be quantitatively correlated to the associated bioactivity, in order to eventually design more potent molecules as lead compounds to be developed as clinical candidates.

Because of the complexity of this task, researchers have shown interest in the use of deep learning (DL) methods in DD, as they can provide accurate predictions while making the overall process less expensive and time-consuming. Moreover, several DL models are able to equal or also exceed the results of previously existing methods for drug discovery based on machine learning or classical QSAR (Lenselink et al., 2017). In particular, graph neural networks (GNNs) (Scarselli et al., 2009b) are widely used in DD (Wieder et al., 2020) because they exploit molecular graph representations, without requiring to represent molecules in other machine-readable formats, and make structure interpretation easier. Their ability to outperform traditional machine learning methods in the prediction of several molecular properties, such as hydrophobicity (Shang et al., 2021; Wang et al., 2019) and toxicity (Withnall et al., 2020; Xu et al., 2017) is mostly owed to their approximation capabilities (Scarselli et al., 2009a). Despite these promising results, it is in general difficult to understand the reasoning which leads to the models’ output predictions.

This problem is addressed by explainable AI (XAI), which focuses on the development of interpretable AI systems. This crucial aspect needs to be investigated to bring machine learning closer to other scientific disciplines and increase the models’ reliability. In general, explainability methods for GNNs are categorized as instance-based or model-based (Yuan et al., 2020). While the former provides example-specific explanations by identifying input features that are important for the output predictions, the latter tries to capture high-level insights into GNNs functioning. In this work, we focus on instance-level explanations. Many of the recently developed XAI approaches for GNNs propose post-hoc solutions, i.e., they provide explanations for already trained models. These methods often come from the generalization of techniques for convolutional neural networks (CNNs) (Pope et al., 2019; Schwarzenberg et al., 2019; Schnake et al., 2022), such as class activation mapping (Zhou et al., 2016), gradient-weighted class activation mapping (Selvaraju et al., 2019), and excitation backpropagation (Zhang et al., 2017). However, there is not much prior work on self-interpretable GNNs (Dai & Wang, 2021; Gui et al., 2022; Ragno et al., 2022), and in particular concept-based explanations for GNNs represent an unexplored research path.

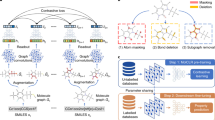
In this work, we propose an adaptation of a widely used XAI approach for CNNs, called concept whitening (CW) (Chen et al., 2020), to graph data, in order to develop self-interpretable QSAR models for DD. In particular, we focus on spatial convolutional GNNs (Conv-GNNs) (Kipf & Welling, 2017), which can be seen as the CNNs’ counterpart in the graph domain. Basically, CW consists of a module that can be added to a CNN to align the axes of the latent space with known concepts of interest. Its main application is in image recognition tasks, where Chen et al. (2020) show that CW increases the networks’ interpretability while maintaining the same performance. Our idea is to use molecular descriptors as concepts in the CW module, in order to predict a specific molecular property. In this way, CW can benefit the task of QSAR by identifying how each concept contributes to the output prediction and consequently how a given property in a certain part of the molecule mostly contributes to modulating its biological behavior. To this aim, we analyze the importance of the concepts in each of the CW layers. As well as showing how inserting CW layers affects the models’ performances, we also compare the results obtained using three different architectures: spatial Conv-GNNs (GCNs) (Kipf & Welling, 2017), graph attention networks (GATs) Veličković (2018), and graph isomorphism networks (GINs) (Xu et al., 2019). Moreover, as Chen et al. (2020) substitute CW layers to the batch normalization (BatchNorm) layers (Ioffe & Szegedy, 2015) of a pre-trained model, we additionally test whether using different types of normalization in the black-boxes then leads to higher performances after their substitution with CW layers. Specifically, we compare the results obtained using BatchNorm (Ioffe & Szegedy, 2015), instance normalization (InstanceNorm) (Ulyanov et al., 2016), layer normalization (LayerNorm) (Ba et al., 2016) and graph normalization (GraphNorm) (Cai et al., 2021), respectively. We also introduce two new activation modes to be used within the CW layers in GNNs, which leverage top-k pooling (Knyazev et al., 2019). We perform experiments using several benchmark datasets from MoleculeNet (Wu et al., 2018). Finally, to understand which structural properties of the molecules are the most relevant for a given concept, we use the post-hoc explainability method GNNExplainer (Ying et al., 2019) on the concepts’ activations.

In summary, the specific contributions of our work are the following:

  • Adaptation of CW to Conv-GNNs, in order to obtain concept-based explanations for this type of networks, and analysis of the performances obtained using different architectures;

  • Definition of two novel activation modes leveraging top-k pooling;

  • Design of a way of interpreting QSAR models, by understanding which concepts, i.e., which properties of interest, mostly contribute to a specific type of activity of a given molecule and to which part of the molecules themselves to directly drive the chemical modifications.

  • Comparisons between the performances obtained after the addition of the CW layers when using different types of normalization in the black-box models.

The code of this project is available at the following link https://github.com/KRLGroup/Molecular-CW and it is implemented in the www.3d-qsar.com portal (Ragno, 2019).

2 Related work

2.1 Graph neural networks

Graph neural networks (GNNs) (Scarselli et al., 2009b) represent a particular type of neural network developed to operate on graph-structured data. As highlighted by Scarselli et al. (2009a), GNNs can approximate up to any degree of precision any function preserving the unfolding equivalence, and most useful maps on graphs belong to this class of functions. Thanks to their approximation properties and due to the large availability of graph data coming from different scientific areas, GNNs are popular and used to solve several tasks in a wide variety of applications (Zhou et al., 2020).

GNNs core building blocks are the message passing layers, which are responsible for combining the node and edge information into the node embeddings. This is done by iteratively aggregating the information of each node with its neighbors’ one, thus obtaining a new embedding that is used to update the representation of each node. Overall, GNNs can be divided in convolutional (Conv-GNNs) and recurrent. In this work, we just focus on the former. Conv-GNNs are in turn categorized in spectral (Bruna et al., 2014; Defferrard et al., 2016) and spatial (Kipf & Welling, 2017). In this work, we focus on spatial Conv-GNNs, and more specifically on the graph convolutional network proposed by Kipf and Welling (2017), to which we refer as GCN, and on graph attention networks (GATs) Veličković (2018), and graph isomorphism networks (GINs) (Xu et al., 2019), which differ in the aggregate and update functions. GCNs are characterized by the propagation rule, first proposed by Kipf and Welling (2017), that expresses the spatial convolution for a node. Differently from GCNs, where all neighboring nodes are assumed to contribute equally to the update of a given node i, GATs (Veličković, 2018) exploit graph attentional layers to produce attention scores that represent the importance of the features of each neighboring node j to node i. Finally, Xu et al. (2019) design GIN to maximize the representational power. In fact, they show that the proposed network has the same discriminative power as the Weisfeiler–Lehman graph isomorphism test, which is used to evaluate the non-isomorphicity of two graphs. In GIN, node embeddings are aggregated through a sum operator, with the neighboring nodes contributing equally to the update of the central node. However, the latter is weighted by a learnable parameter \(\epsilon\), and a multi-layer perceptron (MLP) is added after the aggregation of the neighbors’ features has been performed.

2.2 GNNs in drug discovery

DL methods and, in particular, GNN-based methods are promising for addressing several tasks in DD (Kim et al., 2021).

Many works use such approaches to predict drug-target interactions, in order to identify lead compounds with a higher potency starting from hit compounds. For instance, Gilmer et al. (2017) specifically develop message passing neural networks (MPNNs) to achieve state-of-the-art performance on molecular property prediction. Similarly, Hamilton et al. (2017) propose GraphSAGE, a novel framework that generates node embeddings by aggregating information from local neighborhoods, and demonstrate its ability to generalize to unseen graphs in protein-protein interaction prediction. In particular, the use of GCNs, GATs and GINs in this work is motivated by their success in the prediction of different molecular properties (Wieder et al., 2020), such as toxicity (Chen et al., 2021; Hu et al., 2020; Peng et al., 2020; Wieder et al., 2020), hydrophobicity, blood-brain barrier permeability (Hu et al., 2020), and solvation free energy (Hu et al., 2020; Wang et al., 2019).

Another important application of GNNs in DD is the prediction of drug side effects (Bongini et al., 2022), which are generally caused by complex biological processes related to many factors, including drug structure and protein-protein interactions. Similarly, GNNs are used to predict polypharmacy effects (Deac et al., 2019; Zitnik et al., 2018) arising from the combined use of different drugs. The use of DL models is crucial in this case, as it allows drugs screening before the clinical trials and potentially leads to the identification of undesired effects that could still be unknown when the drug is on the market.

Finally, GNNs are widely used in de novo drug design in order to generate novel molecules with desired properties (Bongini et al., 2021; Li et al., 2018; Lim et al., 2019).

2.3 Drug discovery with XAI

In general, XAI methods can be categorized into post-hoc approaches, which produce explanations for trained neural networks by looking at their outputs and parameters, and self-explaining approaches, which consist in defining inherently interpretable models (Jiménez-Luna et al., 2020).

Feature attribution methods are post-hoc explanation approaches that determine the relevance of every input feature for the final prediction and they have been widely used in DD. For example, McCloskey et al. (2019) employ gradient-based attribution (Sundararajan et al., 2017) to detect fragment pharmacophores relevant for ligand binding. However, the study also shows that the models can still learn spurious correlations. Pope et al. (2019) adapt gradient-based feature attribution, more specifically gradient-weighted class activation mapping (Selvaraju et al., 2019) and excitation backpropagation (Zhang et al., 2017), to identify relevant functional groups in adverse effect predictions. Ishida et al. (2019) use gradient-based feature attribution methods, such as integrated gradients (Sundararajan et al., 2017), together with GCNs for retrosynthetic reaction predictions and identify the atoms involved in each reaction step. Additionally, (Rodríguez-Pérez & Bajorath, 2019, 2020) use Shapley additive explanations (SHAP) (Lundberg & Lee, 2017) to interpret relevant features for compound potency and multitarget activity prediction. Among the post-hoc approaches specifically developed for GNNs, GNNExplainer (Ying et al., 2019) learns soft masks for edges and nodes features to find the crucial subgraphs and features to explain the predictions. Tested on a dataset for the classification of the molecules’ mutagenic effect on Salmonella typhimurium (Debnath et al., 1992), GNNExplainer is able to identify several known mutagenic functional groups as relevant.

Since post-hoc explanations are not directly linked to the decision flow of GNNs, they can be biased and misrepresent the true explanations (Dai & Wang, 2021). For this reason, some studies focus on the development of self-explaining models. For instance, Dai and Wang (2021) propose a new framework to achieve explainable node classification by finding the K-nearest labeled nodes for each unlabeled node. While most current methods aim at explaining graph nodes, edges, or features, Gui et al. (2022) identify and exploit the most important message flows to provide explanations. None of these methods has ever been adopted in DD.

Finally, in the context of CNNs, there are several works studying how a predefined concept influences the internal representation of the hidden units of the networks. For instance, Kim et al. (2018) have introduced a method, called testing with concept activation vectors, that uses directional gradients to measure to what extent a user-defined concept influences a certain classification outcome. In a successive work, Ghorbani et al. (2019) propose a novel technique, called automated concept-based explanation, that aggregates related local image segments across diverse data to automatically extract visual concepts and is able to identify human-friendly concepts relevant to the network’s output predictions. However, both these methods consider specific concepts for each class, ignoring the fact that some of them may be shared by different categories. In this way, the same concept might be represented differently across classes, and this could negatively affect the concept’s importance for classification. To address this issue, Fang et al. (2020) present a novel visual concept mining algorithm. This approach comprises two main components: a potential concept generator to discover concepts by automatically searching and grouping important pixels via saliency map calculation; a visual concept extractor to learn the similarity and diversity of the concepts among different classes and quantify their correlation and unique contribution to each class.

Although they are useful, these post-hoc concept-based methods are based on the assumption that the representatives of different concepts lie in separate portions of the latent space, and this property may not hold (Chen et al., 2020). This difficulty is mitigated with CW, since it directly forces the network to produce latent representations (in the case of graphs, node, edge, and consequently graph embeddings) that allow discriminating samples based on their belonging to certain concept classes.

3 Methods

In this section, we first highlight the main similarities and differences between GCNs, GATs and GINs, and between the normalization types we use. Successively, we present CW and the strategy we adopt to adapt it to GNNs, introducing two new activation modes for updating the gradients within the CW layer. Finally, we illustrate the method for identifying the structural parts of the molecules that are relevant to a certain concept.

3.1 Graph neural networks

Graph neural networks are based on the functional mechanism of message passing, which is responsible for the generation of new node embeddings through the iterative aggregation and update of the nodes and edges information. In this section, we describe in more detail the architectures used in this work, namely GCNs, GATs, and GINs. A hidden layer of a GCN can be written as a nonlinear function f:

$$\begin{aligned} H^{(l+1)} = f(H^{(l)}, A) \end{aligned}$$
(1)

that takes as input the graph’s adjacency matrix \({\textbf {A}}\) and the latent node features \({\textbf {H}}\) for some layer l. A simple layer-wise propagation rule for a GCN can therefore be written as:

$$\begin{aligned} f(H^{(l)},A) = \sigma (AH^{(l)}W^{(l)}) \end{aligned}$$
(2)

where \({\textbf {W}}\) is a weight matrix for the l-th neural network layer and \(\sigma\) is a nonlinear activation function. By multiplying the weight matrix with the adjacency matrix, all the feature vectors of the immediate neighbours are aggregated for every node, but self-loops are not included, which means that the feature vector of the node itself is not considered. This issue is solved by Kipf and Welling (2017), who define a generic l-th layer of a GCN as:

$$\begin{aligned} H^{(l+1)} = \sigma (\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}H^{(l)}W^{(l)}) \end{aligned}$$
(3)

where \(H^{(l)}\) are the hidden features of the l-th layer, \(W^{(l)}\) are its learnable parameters, and \(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}\) is the symmetrically-normalized adjacency matrix with \(\tilde{A}=A+I\) being the adjacency matrix taking into account also the presence of self-loops, so that each node in the graph also includes its own features in the next representation, and \(\tilde{D}\) is the degree matrix of \(\tilde{A}\). By writing Eq. (3) in vector form, we get:

$$\begin{aligned} h_i^{(l+1)} = \sigma \left( \sum _{j} \, \frac{1}{c_{ij}}h_j^{(l)}W^{(l)}\right) \end{aligned}$$
(4)

where j is the index of the neighboring node of node i and \(c_{ij}\) is a normalization constant for the edge connecting nodes i and j, which is obtained using the symmetrically normalized adjacency matrix \(D^{-\frac{1}{2}}A^{-\frac{1}{2}}\). At this point, by choosing an appropriate non-linearity and initializing the weight matrix such that it is orthogonal, this update rule becomes stable, also thanks to the normalization with \(c_{ij}\).

In GATs, self-attention is performed by applying an attention function, \(\textit{a}\) which produces attention scores:

$$\begin{aligned} e_{ij}= \textit{a}({\textbf {W}}h_i, {\textbf {W}}h_j) \end{aligned}$$
(5)

that represents the importance of the features of node j to node i. Successively, the coefficients are normalized for every choice of j with the softmax function to facilitate comparisons between coefficients of different nodes, thus obtaining:

$$\begin{aligned} \alpha _{ij}={\textit{softmax}}_j(e_{ij})=\frac{{\textit{exp}}(e_{ij})}{\sum _{k\in N_i}\,{\textit{exp}}(e_{ik})} \end{aligned}$$
(6)

These normalized attention coefficients are used to compute a linear combination of the nodes features, to obtain the new embedding for each node. A non-linearity is also usually applied, thus getting the following update rule:

$$\begin{aligned} h_i^{(l+1)} = \sigma \left( \sum _{j\in N_i} \, \alpha _{ij}h_j^{(l)}W^{(l)}\right) \end{aligned}$$
(7)

Finally, in GINs the aggregation of the features of neighbouring nodes and the update of each node’s embedding is implemented as follows:

$$\begin{aligned} h_i^{(l+1)} = {\textit{MLP}}^{(l+1)} \left( (1+\epsilon ^{(l+1)}) \cdot h_i^{(l)} + \sum _{j\in N_i}h_j^{(l)}\right) \end{aligned}$$
(8)

where \(\epsilon ^{(l+1)}\) is a learnable parameter and \({\textit{MLP}}\) is a multi-layer perceptron with non-linearity.

Since molecules that are tested as potential candidate drugs are usually small, GNNs that are adopted in drug discovery are generally made up of just a few convolutional layers, that are used to generate the latent representation of the nodes. GNNs can provide node-, edge-, and graph-level predictions, but in this work we will just focus on graph classification. To this aim, a readout layer is needed to obtain a representation for the whole graph and it is followed by a final classification layer to obtain predictions.

3.1.1 Normalization layers for GNNs

Cai et al. (2021) analyzes the effectiveness of different types of normalization for GNNs, by adapting some existing methods, including BatchNorm, LayerNorm, and InstanceNorm, to the graph domain, and proposing a novel one, called GraphNorm.

Given a set of samples \(x_1,\ldots , x_n\), a normalization operation shifts each \(x_i\) by the mean \(\mu\), and scales them down by the standard deviation \(\sigma\): \(x_i \rightarrow \gamma \frac{x_i-\mu }{\sigma }+\beta\), with \(\gamma\) and \(\beta\) being learnable parameters. What differs among the various normalization methods is the set of feature values the normalization is applied to. BatchNorm normalizes all values in a given feature dimension across the nodes of all graphs in the batch. LayerNorm, instead, normalizes values across different dimensions of each node. InstanceNorm normalizes values across all nodes for each individual graph. Finally, GraphNorm adds a learnable parameter \(\alpha\), multiplying \(\mu\), to automatically control which proportion of the mean should be kept in the shift operation.

3.2 Concept whitening

CW is a module inserted into a neural network that aligns the axes of the latent space with known concepts of interest and facilitates their extraction. Thus, CW allows learning an inherently interpretable model, since it can show how a concept is represented at a given layer of the network. CW works similarly to batch whitening (Huang et al., 2018b), as it decorrelates and normalizes each axis of the latent space, thus transforming the post-convolution latent space so that the covariance matrix between channels is the identity. However, CW also provides an extra step involving a rotation matrix used to match the concepts to the axes of the latent space. This matrix is optimized using Cayley-transform-based curvilinear search algorithms (Wen & Yin, 2013).

More formally, suppose that \({\textbf {x}}_1, {\textbf {x}}_2,\ldots , {\textbf {x}}_n \in \mathcal {X}\) are dataset samples and \(y_1, y_2,\ldots , y_n \in \mathcal {Y}\) are the corresponding labels. A deep neural network classifier \(f: \mathcal {X} \rightarrow \mathcal {Y}\) can be split into two parts, namely a feature extractor \(\Phi : \mathcal {X} \rightarrow \mathcal {Z}\) with parameters \(\theta\), and a classifier \(g: \mathcal {Z} \rightarrow \mathcal {Y}\) with parameters \(\omega\). Then, \({\textbf {z}} = \Phi ({\textbf {x}};\theta )\) is the latent representation of \({\textbf {x}}\), and \(f({\textbf {x}})=g( \Phi ({\textbf {x}};\theta );\omega )\) is the predicted label. For each \(k \in [1,K]\), with K being the number of concepts, we need to define an auxiliary dataset \({\textbf {X}}_{c_k}\). Exploiting CW, we want to simultaneously learn \(\Phi\) and g, such that the classifier gives accurate predictions and the jth dimension \(z_j\) of the latent representation \({\textbf {z}}\) aligns with concept \(c_j\). By doing this, samples in \({\textbf {X}}_{c_j}\) should have larger values of \(z_j\) than other samples.

Now, let \({\textbf {Z}}_{d \times n}\) be the latent representation matrix of n samples, where each column \({\textbf {z}}_i \in \mathbb {R}^d\) contains the latent features of the ith samples. The CW module consists of two parts, a whitening and an orthogonal transformation. The whitening transformation decorrelates and standardizes the data, and it is defined as:

$$\begin{aligned} \psi ({\textbf {Z}}) = {\textbf {W}} ({\textbf {Z}}-\mu {\textbf {1}}_{n \times 1}^T) \end{aligned}$$
(9)

where \(\mu =\frac{1}{n} \sum _{i=1}^{n} {\textbf {z}}_i\) is the sample mean and \({\textbf {W}}_{d \times d}\) is the whitening matrix such that \({\textbf {W}}^T {\textbf {W}} = \Sigma ^{-1}\), with \(\Sigma\)\(_{d \times d} = \frac{1}{n}({\textbf {Z}}-\mu {\textbf {1}}^T)({\textbf {Z}}-\mu {\textbf {1}}^T)^T\) being the covariance matrix. The whitening matrix is computed as in zero-phase component analysis (ZCA) (Huang et al., 2018a):

$$\begin{aligned} {\textbf {Z}} = {\textbf {D}} \Lambda ^{-\frac{1}{2}} {\textbf {D}}^T \end{aligned}$$
(10)

where \(\Lambda _{d \times d}\) and \({\textbf {D}}_{d \times d}\) are respectively the eigenvalue diagonal matrix and the eigenvector matrix given by the eigenvalue decomposition of the covariance matrix, \(\Sigma = {\textbf {D}}\Lambda {\textbf {D}}^T\).

Once the latent space has been mean-centered and decorrelated, samples are rotated in their latent space so that those that are related to concept \(c_j\), \({\textbf {X}}_{c_j}\), are highly activated on the \(j_{th}\) axis. In particular, the orthogonal matrix \({\textbf {Q}}_{d \times d}\), whose column \({\textbf {q}}_j\) is the \(j_{th}\) axis, is obtained by optimizing the following objective:

$$\begin{aligned} \max \limits _{{\textbf {q}}_1, {\textbf {q}}_2,\ldots ,{\textbf {q}}_k} \, \sum _{j=1}^{k} \, \frac{1}{n_j} \, {\textbf {q}}_j^T \, \psi ({\textbf {Z}}_{c_j}) \, {\textbf {1}}_{n_j \times 1} \quad s.t. \quad {\textbf {Q}}^T{\textbf {Q}}={\textbf {I}}_d \end{aligned}$$
(11)

where \({\textbf {Z}}_{c_j}\) is a \(d \times n_j\) matrix denoting the latent representation of \({\textbf {X}}_{c_j}\). During training, two different objectives are optimized alternately. The main objective is the one related to the classification accuracy:

$$\begin{aligned} \min \limits _{\theta , \omega , W, \mu } \, \frac{1}{n} \, \sum _{i=1}^{n} \, l(g({\textbf {Q}}^T \psi (\Phi ({\textbf {x}}_i;\theta ); {\textbf {W}},\mu );\omega ),y_i) \end{aligned}$$
(12)

where \(\Phi\) and \(\psi\) are the layers before and after the CW module, parametrized by \(\theta\) and \(\omega\) respectively. The actual CW module is represented by \({\textbf {Q}}^T\psi\), while l is any differentiable loss, e.g., cross-entropy loss. The second objective is the concept alignment loss:

$$\begin{aligned} \max \limits _{{\textbf {q}}_1, {\textbf {q}}_2,\ldots ,{\textbf {q}}_k} \, \sum _{j=1}^{k} \, \frac{1}{n_j} \, \sum _{x_i^{c_j} \in X_{c_j}} \, {\textbf {q}}_j^T \, \psi (\Phi ({\textbf {x}}_i^{c_j};\theta );{\textbf {W}},\mu ) \quad s.t. \quad {\textbf {Q}}^T{\textbf {Q}}={\textbf {I}}_d \end{aligned}$$
(13)

Q is fixed while training for the main objective, while the other parameters are fixed when training for Q. The second optimization problem with the orthogonality constraint is solved by gradient-based approaches on the Stiefel manifold. At each step t in which the second objective is handled, the orthogonal matrix Q is updated by the Cayley transform:

$$\begin{aligned} {\textbf {Q}}^{(t+1)} = \left( I + \frac{\eta }{2}{} {\textbf {A}}\right) ^{-1} \, {\textbf {Q}}^{(t+1)} = \left( I + \frac{\eta }{2}{} {\textbf {A}}\right) {\textbf {Q}}^{(t)} \end{aligned}$$
(14)

where \({\textbf {A}} = {\textbf {G}}({\textbf {Q}}^{(t)})^T - {\textbf {Q}}^{(t)}{} {\textbf {G}}^T\) is a skew-symmetric matrix, \({\textbf {G}}\) is the gradient of the loss function and \(\eta\) is the learning rate. The optimization procedure is also accelerated by curvilinear search at each step (Wen & Yin, 2013). Since in (14) the stationary points are reached when \({\textbf {A}} = {\textbf {0}}\), there are multiple solutions that lie in a high-dimensional space, so the stationary points are likely to be saddle points. To address this issue, stochastic gradient descent (SGD) is used, and momentum has been exploited to accelerate and stabilize the training.

Concerning implementation details, it is important to highlight that each channel within one layer is used to represent a specific concept. This is done by reshaping the output of each convolutional layer \(Z_{n\times d \times h \times w}\) into a matrix \(Z_{d\times (hwn)}\), with d being the number of channels. In this way, after performing CW, we still have a matrix with shape \(d\times (hwn)\) and, by reshaping it to \(n\times d \times h \times w\), we obtain that each feature map in the resulting tensor now represents whether an important concept is detected at each location in the image for the considered layer. Finally, an activation value for each \(h \times w\) feature map is computed considering different activation modes:

  • mean computes the mean of all feature map values;

  • max takes the maximum over all the feature map values;

  • pos_mean computes the mean of all positive feature map values;

  • max_pool calculates the mean of the down-sampled feature map obtained by max pooling. This is the activation mode that was used in the experiments in (Chen et al., 2020) since it is able to capture both high-level and low-level concepts.

3.3 Adaptation of CW to Conv-GNNs

Concept-based explanation methods are particularly suited for interpreting QSAR models because they allow leveraging domain-specific knowledge by focusing on molecular properties that are known to affect bioactivity. Due to the lack of any such type of approaches for graph data, we adapt CW to Conv-GNNs. In particular, we follow the procedure of Chen et al. (2020), using the CW module to replace the BatchNorm layer straight after a convolutional one.

The mathematical formulation of the whitening transformation and the optimization problem that allows finding the orthogonal matrix described in Sect. 3.2 remains unaltered while applying them to GNNs. Consequently, the basic functioning of the CW module is identical to the case in which it is added to a CNN. However, the data is completely different, and therefore the input shapes of the transformations, i.e., the output shapes of the convolutional layers, change accordingly. In fact, while the output of a 2D convolutional layer has shape \(n \times d \times h \times w\), with n, d, h, w being respectively the batch size, the dimension of the latent space, and the image height and width, the output of a graph convolutional layer has shape \(N \times d\), where N is the number of nodes and d is again the dimension of the latent space. These represent the shapes of the tensors that are given as input to the concept whitening layer. As explained in Sect. 3.2, in the case of CNNs, each feature map obtained from the convolution of one filter is reshaped so that, for each filter, the output of a convolutional layer \(Z_{n \times d \times h \times w}\) is reshaped into a matrix \(Z_{(g \times d) \times (hwn)}\), where g is the number of channels used to represent each concept and hwn corresponds to the total number of features. Since one channel is used to represent each concept, this reduces to \(Z_{d \times (hwn)}\). This operation can be easily transferred to the graph domain, by changing the dimension of the output of each convolutional layer from \(Z_{N \times d}\) to \(Z_{g \times d \times N}\). The subsequent computations remain exactly the same as before, and after the CW layer, each channel represents a specific concept. We clarify that the CW module necessarily needs to be inserted in place of a normalization layer, after a convolutional layer. The input shape to the CW module is therefore the output shape of the convolutional layer. Since the shape of the transformations that compose the CW module is inferred from the shape of the input data, the module is able to automatically adapt to varying inputs in the case of Conv-GNNs. Similarly, if we change the dimension of the convolutional layer, the shape of the transformations in the CW module will change based on the new shape of the convolutional output.

The only aspect that cannot be directly adapted to GNNs concerns one of the activation modes we presented in Sect. 3.2: max_pool. In fact, this consists in performing 2D pooling and unpooling operations, which cannot be performed on graph data. In this work, we propose two alternative activation modes that exploit the top-k pooling operator presented by Gao and Ji (2019). Instead of clustering “similar” nodes, top-k pooling propagates only part of the input, that is not uniformly sampled from the input itself. By specifying a pooling ratio, \(k \in (0,1]\), we can select just some parts of the input graph, by keeping just \(\lceil kN \rceil\) nodes out of the initial N. This selection is done by projecting node features onto the direction of a trainable vector, \({\textbf {p}}\), and keeping the nodes with the highest projection scores. In fact, the scalar projection of the i-th node’s feature vector, \({\textbf {x}}_i\), on \({\textbf {p}}\), computed as \(y_i = \frac{{\textbf {x}}_i{\textbf {p}}}{{\textbf {p}}}\), indicates how much information is retained after the projection onto p and we want to preserve as much information as possible. To make \({\textbf {p}}\) learnable by back-propagation, the projection scores are used as gating values to control how much information to keep from the retained nodes. This last property of top-k pooling was exploited to actually develop two different activation modes, called topk_pool and weighted_topk_pool. The first one is obtained by just computing the mean of the node embeddings of the down-sampled graph. The second one, instead, is obtained by making a weighted average of the node embeddings of the down-sampled graph, using as weights the projection scores returned by top-k pooling.

3.3.1 Structural information related to concept activations

Together with providing conceptual explanations thanks to the adaptation of the CW module, we analyze the concept-structure relationship by combining CW with a XAI post-hoc method such as GNNExplainer. More generally, being the CW layer differentiable, any post-hoc method can be used to understand the structural motifs that modulate the concept activation. In this way, we can additionally obtain structural explanations. The use of a post-hoc method for this further step is necessary because some of the molecular properties that we use as concepts are “abstract”. With this adjective, we mean that it is not possible to directly derive the input attributions from the concept’s value. Consequently, we use GNNExplainer to extract the portion of the molecular graphs that most contributes to the concept latent value. GNNExplainer, in fact, is a perturbation based method that optimizes an edge mask such that the mutual information between the GNN’s output and the distribution of possible sub-graphs is maximized.

4 Experiments

In this section, after introducing the datasets and the concepts we use, we report our experimental setup to make results reproducible. Then, we start our analysis by comparing the classification performances obtained using GCN, GAT and GIN. In particular, we show how using different activation modes within the CW layers leads to different results. Moreover, we compare the performances obtained using different types of normalization in the black-box models. Subsequently, we study how concepts are represented within the CW layers and analyze the concept-structure relationships. Finally, we compute quantitative metrics to evaluate the improvement in interpretability.

4.1 Datasets

We train and test all the different architectures on four molecule datasets for graph classification. Molecules are represented as graphs, in which nodes and edges represent atoms and bonds, respectively. The first dataset we used is BBBP (Martins et al., 2012), which addresses blood-brain barrier penetration. This is a crucial aspect in the development of drugs targeting the central nervous system. The second one is BACE (Subramanian et al., 2016), which has as target beta-secretase 1. This protein is essential for the generation of beta-amyloid peptide in neural tissue, a component of amyloid plaques widely believed to be involved in the development of Alzheimer’s disease. The third one is ClinTox (Wu et al., 2018), which compares drugs approved by the FDA and drugs that have failed clinical trials for toxicity reasons. The last one is the HIV dataset,Footnote 1 which contains 40,000 compounds, tested for their ability to inhibit HIV replication, that are associated to binary labels indicating whether they are active or inactive.

Table 1 Concepts selected for each tested dataset with the chosen threshold
Full size table

4.2 Concept selection

As previously mentioned, we select the concepts by taking into account the molecular properties that are known to be relevant for each of the studied tasks. More specifically, we build each concept’s dataset by keeping all the molecules that present a value for the corresponding molecular property within a predefined interval. In order to select the most appropriate concepts, we follow the work of Sakiyama et al. (2021) and Subramanian et al. (2016) for BBBP and BACE, respectively. For ClinTox we select the concepts among the ones used for BBBP and BACE that led to the greatest improvement when used alone within the CW layers. For the HIV dataset, instead, we follow the work of Sirois et al. (2005) and Kiralj and Ferreira (2003). Table 1 reports the concepts selected for each dataset, together with the corresponding threshold values. For more details on the meaning of the concepts and the threshold selection, please refer to Appendix A.

Table 2 Hyperparameters used to train the models on the three considered datasets
Full size table

4.3 Experimental setup

All the code was developed in PyTorch (Paszke et al., 2019), using PyTorch Geometric library (Fey & Lenssen, 2019) (PyG). Each model used in the experiments is made up of three convolutional layers, which can be GCNConv, GATConv, or GINConv layers, with 128 units and a dense layer with 128 units. In GATConv multi-head attention layers, the number of attention heads is set to 2. Instead, the MLP in GINConv layers (see Eq. (8)) is designed as a single linear layer with the input and output dimensions equal to the number of units in the previous and following convolutional layers, respectively. The convolutional and dense layers have ReLU activation function. Additionally, there is a normalization layer after each convolutional layer, which can be a BatchNorm, LayerNorm, InstanceNorm, or GraphNorm layer. The CW layers are substituted to these normalization layers. Finally, the readout layer is represented by a global sum pooling in the case of BBBP and HIV and a global max pooling in the case of BACE and ClinTox, and it is followed by a simple dense layer that performs the classification.

For all the black-box models, we have implemented early stopping with a patience of 20 epochs. After the addition of CW, we found out that training the models for a maximum of 50 epochs with early stopping with patience 5 allows obtaining the best performance. Each experiment was run 15 times to compare different seeds for statistical significance. In Table 2, we summarize the values of the hyperparameters that were used for BBBP, BACE, ClinTox, and HIV, respectively.

Table 3 Performance on BBBP over 15 runs before and after implementing early stopping (ES), together with the epoch at which on average early stopping occurs
Full size table

4.4 Hyperparameters tuning

In order to choose the number of epochs and to decide whether or not to add early stopping, we have performed hyperparameters tuning. In Table 3 we report the performance of the network on the validation set before and after implementing early stopping on BBBP dataset. We also report the epoch at which on average early stopping occurs. For all the architectures, early stopping occurs pretty soon during training. Moreover, by training the models for the number of epochs specified in Table 2 without early stopping the performances decrease, meaning that the models are overfitting. After training the black-boxes, we tried to fine-tune the models with CW layers for just one additional epoch. However, this led to very low results, both in terms of accuracy and ROC-AUC, and that is why we set the maximum number of epochs to 50 but, following the same procedure we have just described, we set early stopping patience to 5.

Table 4 Mean ROC-AUC over 15 runs before and after the addition of the three concept whitening layers for BBBP, BACE, ClinTox, and Tox21
Full size table
Table 5 Mean ROC-AUC over 15 runs on all tested datasets before and after the addition of the three concept whitening layers using different normalization layers in the baseline models corresponding to the best-performing interpretable models
Full size table
Fig. 1
figure 1

Comparison between the performance of each black-box model and the best corresponding interpretable model. The ROC-AUC values obtained with CW are equal or higher than those obtained with the black-boxes

Full size image

4.5 Classification performances

In this section, we verify how the substitution of the BatchNorm layers of a pre-trained model with CW layers affects its performance. In Table 4, we present the mean ROC-AUC values obtained using GCN, GAT and GIN on BBBP, BACE, ClinTox, and HIV, respectively. In particular, we compare the performances obtained by the black-box models with BatchNorm and their interpretable versions, while using different activation modes. For each dataset, there is at least one activation mode within the CW layers that allows to equal or, in most cases, improve the ROC-AUC with respect to their black-box versions for all the architectures, as shown in Fig. 1. In particular, max mode is the one that guarantees the best results for all the architectures on BBBP and HIV, and the highest accuracy and ROC-AUC values are obtained with GAT architecture. On the contrary, the activation mode that gave the worst results for both GCN and GAT on BBBP and HIV is weighted_topk_pool, which is instead the best one in the case of GCN architecture on BACE and GIN architecture on ClinTox. Despite the good performance of GCN on BACE, the best results on this dataset were obtained with GAT and topk_pool activation mode. The best results on ClinTox were obtained using GCN architecture, with mean or pos_mean activation modes leading to similar performances. We impute the higher performances of the interpretable models to the ability of the CW layers to force the node embeddings produced by the models to represent relevant information in terms of the nodes’ belonging to each concept’s class, which attributes such representations a greater discriminative power.

Another important consideration is that the activation modes we propose, namely topk_pool and weighted_topk_pool, allow obtaining comparable performances with respect to the already existing ones, even improving them in some cases.

The table we have just described also contains the average performance of three known baselines: a random forest, a multi-layer perceptron (MLP) and a MPNN. Overall, the results obtained with these models are comparable or, in most cases, lower than those reached by our black-box models and always worse than those obtained with our interpretable models. Just in the case of the HIV dataset, MLP performs particularly well, overcoming the performance of the best of our interpretable models.

In Table 5, we compare the results obtained in terms of ROC-AUC by training the black-box model corresponding to the best-performing architecture in the previous experiments (GAT for BBBP, BACE, and HIV, and GCN for ClinTox) with different types of normalization. The best black-box model is the one with BatchNorm layers for all datasets. Moreover, BatchNorm is the type of normalization that allowed obtaining the best results after the addition of CW both in terms of accuracy and ROC-AUC on BBBP and ClinTox. However, this is not true for BACE, on which InstanceNorm and BatchNorm guaranteed the best performances, and HIV, on which LayerNorm and InstanceNorm gave the best results.

In Appendix B, we also report the accuracy values for all the experiments we have just described, both comparing different architectures in Table 8 and different normalization types in Table 9. In general, accuracies are in accordance with ROC-AUC values.

Fig. 2
figure 2

Concepts importance measured at the three CW layers

Full size image

4.6 Concept representations

Since the main purpose of CW is to provide an easy way to understand which type of features are captured at a certain level of the network and to what extent each concept is relevant for the final prediction, it is useful to analyze the different importance of each concept at each layer of the network. In Fig. 2, we report the concepts importance at each of the CW layers for BBBP dataset. The contribution of each concept is computed as the sum of the positive directional derivatives of the gradients along the channel representing that concept. There are significant differences across layers. At layer 0, all importance scores are below 0.5, with the exception of logP, which is slightly above the threshold, and they are all quite similar across concepts. At layer 1, we start to notice a greater differentiation among concepts, and the importance score for NOCount reaches 0.6. Finally, the importance scores become well-separated at layer 2. The most relevant concept is QED, followed by \(\#\) Heteroatoms and NOCount. On the contrary, TPSA and logP seem to be quite irrelevant. These results are in accordance with the observations made by Sakiyama et al. (2021). In fact, QED, NOCount, and \(\#\) Heteroatoms are the only concepts among the five we selected that appear in all the descriptor sets studied by Sakiyama et al. (2021) resulting in the best performance in BBBP classification using a DL model. Finally, it is important to notice that the importance of the last two concepts, NOCount and \(\#\) Heteroatoms, is usually in agreement. This is due to the fact that the two concepts are strongly related, since oxygen and nitrogen atoms are heteroatoms themselves.

Fig. 3
figure 3

Trajectory showing how the percentile rank for the activation values on the concepts QED and NOCount for the molecule on the left changes when the CW layers are inserted at different depths

Full size image

To better understand what type of information is captured at different depths, we computed the percentile rank for the activation values for the concepts QED and NOCount at the three CW layers in the best-performing model on each dataset. Figure 3 shows an example from BBBP dataset. The trajectory confirms that the network first learns atom-level information, thus giving a higher percentile rank for the activations on the concept NOCount. Going deeper in the network, larger neighborhoods are considered, and therefore it is able to encode graph-level information, giving a higher percentile rank for the concept QED, which estimates the drug-likeness.

Fig. 4
figure 4

Comparison between normalized intra-concept and inter-concept similarities, obtained using the best-performing interpretable model on BBBP (right) and its corresponding black-box (left). In the black-box model, the last convolutional layer is followed by a BatchNorm layer, while in the interpretable model it is followed by a CW module

Full size image

Finally, we analyze normalized intra- and inter-concept similarities, as computed in the paper that presents CW (Chen et al., 2020). Specifically, intra-concept similarity for concept i is defined as:

$$\begin{aligned} d_{ii} = \frac{1}{n^2} \left( \sum \limits _{j=1}^{n} \sum \limits _{k=1}^{n} \frac{{{\textbf {x}}}_{ij} \cdot {{\textbf {x}}}_{ik}}{\Vert {{\textbf {x}}}_{ij}\Vert _2 \; \Vert {{\textbf {x}}}_{ik}\Vert _2} \right) \end{aligned}$$
(15)

where n is the total number of samples belonging to concept i and \({\textbf {x}}_{ij}\) is the representation for sample j of concept i. Inter-concept similarity between two concepts p and q, instead, is computed as:

$$\begin{aligned} d_{pq} = \frac{1}{nm} \, \left( \sum \limits _{j=1}^{n} \sum \limits _{k=1}^{m} \, \frac{{{\textbf {x}}}_{pj} \cdot {{\textbf {x}}}_{qk}}{\Vert {{\textbf {x}}}_{pj}\Vert _2 \; \Vert {{\textbf {x}}}_{qk}\Vert _2} \right) \end{aligned}$$
(16)

where n and m are the number of samples belonging to concepts q and p, respectively. In the plot in Fig. 4, the value in cell (i, j) is obtained as follows:

$$\begin{aligned} Q_{ij} = \frac{d_{ij}}{\sqrt{d_{ii}d_{jj}}} \end{aligned}$$
(17)

In Fig. 4, we notice that, in the BBBP dataset, models employing CW achieve greater separability between dissimilar concepts, more specifically NOCount and TPSA and #Heteroatoms and TPSA. At the same time, with CW the network has a greater ability to recognize the similarity between QED, TPSA, and LogP, and between NOCount and #Heteroatoms, which are indeed strictly related concepts.

4.7 Structural information related to concepts activations

Here, we show how to obtain a structural visualization of the concept activation using post-hoc explainability methods. In particular, we analyze the concept-structure relationship highlighted by GNNExplainer for the concept \(\#\) Heteroatoms (Fig. 5) in the case of BBBP dataset.

It is interesting to observe that the atoms that more strongly influence the concept activation are indeed heteroatoms, most of the time oxygen and nitrogen atoms. These results suggest that the network is correctly identifying the structural sub-parts of the molecules that determine their belonging to a particular concept dataset.

These findings confirm that this method allows to understand the structural relationships of the molecules to descriptor-based concepts. Such a relationship could be exploited for the optimization of the molecules’ biological activities in order to design novel drugs.

Fig. 5
figure 5

Analysis of the concept-structure relationship concerning the number of heteroatoms through GNNExplainer

Full size image

4.8 Improvement in interpretability

Since our aim is to propose self-interpretable QSAR models to be exploited in the field of drug discovery, we conceived interpretability as the ability to identify the structural parts of the molecules to which we need to drive chemical modifications to increase their potency. In this view, the ability to compute the importance of certain molecular properties (concepts) in order to obtain a desired type of biological activity and the possibility of using post-hoc approaches to identify the structural properties that are relevant for each concept represent by themselves an improvement in the interpretability of the models. By considering the definition of each concept, we can indeed make sure that post-hoc approaches are correctly highlighting the right atoms.

Table 6 Concepts selected for each tested dataset with the chosen threshold
Full size table

Additionally, we quantitatively evaluate the improvement in interpretability using Fidelity+ (Pope et al., 2019). This metric is computed as the difference between the originally predicted probabilities and those obtained after masking out the important input features identified through GNNExplainer. This can be written as:

$$\begin{aligned} \textit{Fidelity+} = \frac{1}{N} \, \sum \limits _{i=1}^{N} \, (f(G_i)_{y_i} - f(G_i^{1-m_i})_{y_i}) \end{aligned}$$
(18)

where \(G_i\) is the i-th input graph and \(f(\cdot )\) is the model to be evaluated. \(m_i\) is the importance map in which important input features correspond to 1 and all the others to 0. Consequently, \(G_i^{1-m_i}\) is the graph we obtain by masking out input features according to the complementary mask \(1-m_i\). Since QED and logP are abstract concepts, which cannot be directly associated to structural properties of the molecules, we need to use GNNExplainer to perform the input masking needed to compute fidelity scores.

For each dataset, we have computed the fidelity score for the best-performing interpretable GAT model and the corresponding black-box. The results are reported in Table 6. Overall, the greatest improvements in fidelity are registered for BBBP, HIV, and ClinTox. For the latter, we notice that even the interpretable model is identifying input properties whose removal brings an increase in the model’s performance. This may be due to the fact that the selection of the concepts in the case of ClinTox has been performed by an experimental evaluation of those used for BBBP and BACE. Although the selected concepts proved to be useful in performing the prediction, more relevant concepts could be identified by domain experts in order to guarantee a positive fidelity score. Finally, in the case of BACE CW allows a reduction in standard deviation among fidelity scores.

5 Conclusions

This work proposes an adaptation of CW to spatial Conv-GNNs in order to develop inherently interpretable QSAR models. Thanks to CW, we obtain conceptual explanations, which allow identifying the concepts that mostly influence the output predictions by studying the evolution of the concept importance across layers. Additionally, we also provide structural explanations by combining CW with a post-hoc explanation method, namely GNNExplainer. In this way, we are able to identify the structural parts of the molecules that are relevant to a certain concept, i.e., we can retrieve input attributions. Based on them, we show an improvement in the fidelity score when using CW. We also report an improvement in terms of classification performances of the models when using CW layers. Using normalization types other than BatchNorm in the black-box can in some cases benefit the performance of the corresponding interpretable model. Finally, we propose two new activation modes, topk_pool and weighted_topk_pool, that guarantee comparable or, in some cases, better results than those obtained with max, mean and pos_mean.

Future works might try to use structural properties of the molecules, such as pharmacophoric points, as concepts. Additionally, it would be interesting to analyze whether changing small parts of the network leads to specific changes in the concepts’ representation and how this influences the classification performance of the model. Finally, future research might further investigate the use of CW in multi-label classification tasks.