Imputation of clinical covariates in time series

Abstract

Missing data is a common problem in longitudinal datasets which include multiple instances of the same individual observed at different points in time. We introduce a new approach, MedImpute, for imputing missing clinical covariates in multivariate panel data. This approach integrates patient specific information into an optimization formulation that can be adjusted for different imputation algorithms. We present the formulation for a K-nearest neighbors model and derive a corresponding scalable first-order method med.knn. Our algorithm provides imputations for datasets with both continuous and categorical features and observations occurring at arbitrary points in time. In computational experiments on three real-world clinical datasets, we test its performance on imputation and downstream predictive tasks, varying the percentage of missing data, the number of observations per patient, and the mechanism of missing data. The proposed method improves upon both the imputation accuracy and downstream predictive performance relative to the best of the benchmark imputation methods considered. We show that this edge is consistently present both in longitudinal and electronic health records datasets as well as in binary classification and regression settings. On computational experiments on synthetic data, we test the scalability of this algorithm on large datasets, and we show that an efficient method for hyperparameter tuning scales to datasets with 10,000’s of observations and 100’s of covariates while maintaining high imputation accuracy.

1 Introduction

Machine learning applied to healthcare data can generate actionable insights ranging from predicting the onset of disease to streamlining hospital operations. Statistical models that leverage the variety and richness of clinical data are still relatively rare and offer an exciting avenue for further research (Callahan and Shah 2017). As an increasing amount of information becomes available the medical field expects machine learning to become an indispensable tool for clinicians (Obermeyer and Emanuel 2016).

This information will come from various clinical and epidemiological sources. Claims records, clinical trials, and data from longitudinal studies have been an invaluable resource for medical research over the past decades. In many of these datasets, data from individual subjects is gathered over time via continuous or repeated monitoring of both risk factors and health outcomes. For example, longitudinal cohort studies are used to discover relationships between exposures of interest and long term health effects including adverse events and chronic disease. By design, these studies mitigate recall bias in participants by collecting data prospectively and prior to knowledge of a possible subsequent event (Caruana et al. 2015).

Another valuable source of clinical data are Electronic Health Records (EHR). Over the past years, widespread uptake of EHR has generated massive datasets that contain quantitative, qualitative, and transactional data (Murdoch and Detsky 2013). Their hospital adoption has skyrocketed in part due to the Health Information Technology for Economic and Clinical Health (HITECH) Act of 2009, which provided $30 billion in incentives for hospitals and physician practices to adopt EHR systems (Birkhead et al. 2015). While primarily designed for archiving patient information and performing administrative healthcare tasks, many researchers have found secondary use of these records for various clinical informatics applications (Shickel et al. 2018). Because heterogeneous labs, measurements, and notes are recorded for patients during each visit, EHR data has a rich and complex structure with time series information.

However, it is algorithms and not merely datasets that will prove transformative for the medical field (Obermeyer and Emanuel 2016). To make progress, we need to develop new statistical tools tailored to clinical applications which address the challenges and leverage common structure encountered in healthcare data. One of the most important issues is the ubiquitous presence of missing time series data (Pedersen et al. 2017), particularly for variables requiring complex, time-sensitive, or resource-intensive procedures to collect. There are many reasons for “missingness”, including missed study visits, patients lost to follow-up, missing information in source documents, lack of availability (e.g., laboratory tests that were not performed), and clinical scenarios preventing collection of certain variables (e.g., missing coma scale data in sedated patients) (Newgard and Lewis 2015). Thus, creating a consistent dataset for individuals over multiple visits even at the same healthcare organization for a fixed set of covariates remains a challenge. Even in longitudinal studies, where a set of covariates is collected over time, missing data are pervasive and complete ascertainment of all variables is rare (Landrum and Becker 2001).

The presence of missing data poses considerable challenges in the analyses and interpretation of clinical investigations’ results (Wood et al. 2004), potentially weakening their validity and leading to biased inferences. Their presence may complicate interpretation or even invalidate an otherwise important study (Ware et al. 2012). Many methods commonly used for handling missing values during data analysis can yield biased results, decrease study power, or lead to underestimates of uncertainty, all reducing the chance of drawing valid conclusions (Newgard and Lewis 2015). As many statistical models and machine learning algorithms rely on complete datasets, it is key to handle the missing data appropriately.

1.1 Review of methods for handling missing values

In this section, we present some of the most common approaches for missing data imputation. First, we introduce fairly simple and intuitive techniques that do not require the use of sophisticated machine learning methods. We then provide brief descriptions of advanced missing data imputation algorithms, both general purpose methods as well as approaches tailored to medical records and time series.

Excluding observations that contain missing values has been a standard practice for clinical research, primarily due to the lack of interpretable, accurate machine learning methods that can be easily applied by medical researchers (Sterne et al. 2009; Janssen et al. 2010). Unsurprisingly, complete case analysis may suffer from severe bias and the reduced sample size results in lower study power (Newgard and Lewis 2015). Recent advances in machine learning have allowed missing values to be accurately imputed prior to running statistical analyses on the complete dataset. The benefit of the latter approach is that once a set (or multiple sets) of complete data has been generated, practitioners can easily apply their own learning algorithms to the imputed dataset. In healthcare settings, often times those datasets contain numerous visits of the same person corresponding to various patterns of missing data. This special structure challenges state-of-the-art missing data methods which do not consider the connection of multiple observations to the same individual (Che et al. 2018).

A variety of machine learning approaches have been introduced in the literature to impute missing values ignoring the potential dependency between observations of the same individual. The simplest approach is the mean imputation that uses the mean of the observed values to replace those missing for the same covariate (Little and Rubin 2019). However, mean imputation underestimates the variance, ignores the correlation between the features leading to poor imputation outcomes.

Another common method called bpca uses the singular value decomposition (SVD) of the data matrix and information from a Bayesian prior distribution on the model parameters to impute missing values. This method outperforms basic SVD methods (Oba et al. 2003). In cases where the level of missing data is above 30%, we have found that this method reduces to mean imputation, leading to similar biases (Faria et al. 2018).

Joint modeling assumes the existence of a joint distribution on the entire dataset and a parametric density function on the data given model parameters. Current implementations of the method estimate the model parameters using an Expectation-Maximization (EM) approach in order to maximize the likelihood function. One widely used software package which implements this approach, Amelia I, assumes that data are drawn from a multivariate normal distribution (Honaker et al. 1999). In practice, healthcare data typically violate this condition (Sterne et al. 2009).

Recent review articles indicate that single imputation methods can lead to seriously misleading results and advise us to consider multiple imputation (Janssen et al. 2010; Little and Rubin 2019). This approach, implemented in the software package mice, allows for uncertainty about the missing data by creating several different plausible imputed datasets and appropriately combining results obtained from each of them (Schafer and Olsen 1998). The Amelia I package was extended to multiple imputation in the Amelia II algorithm (Honaker et al. 2011). Multiple imputation entails two stages: (1) generating replacement values for missing data and repeating this procedure many times, resulting in many datasets with replaced missing information, and (2) analyzing the many imputed datasets and combining the results (Li et al. 2015). As a result, multiple imputation methods are slower and require pooling results, which may not be appropriate for certain applications. For example, in clinical applications, where the interpretability of the underlying model matters, a single imputed dataset and simple predictive model may be preferred.

Most recently, Bertsimas et al. (Bertsimas et al. 2018b) proposed a general optimization framework with a predictive model-based cost function that can explicitly handle both continuous and categorical variables and can be used to generate single, as well as multiple, imputations. This optimization perspective has led to new scalable algorithms for more accurate data imputation. We describe this method OptImpute in more detail in Sect. 2.2, which we use as a foundation for the imputation method proposed in this paper.

The algorithms above are not tailored to multivariate time series datasets despite the fact that covariates may be strongly correlated over time (Lipton et al. 2016). Preliminary work has been done demonstrating their performance in that setting (Zhang 2016). Recurrent Neural Network approaches have also been employed to handle missing values in time series among the covariates for a particular prediction task (Lipton et al. 2016; Che et al. 2018). However, these approaches differ from traditional imputation methods because they also use features derived from the missing pattern itself, and they require that the downstream learning method is a neural network. In contrast, our method produces a single imputed dataset that can be used as training data for any supervised learning method which is preferred for the downstream task.

In practice, simpler techniques are more commonly applied in the panel data setting. Researchers often opt for a moving average approach with a fixed time window using previous observations from the same individual (Flores et al. 2019). For example, the last-observation-carried-forward method is used to impute a present missing value by carrying only the last non-missing value forward for a defined time period (Siddiqui and Ali 1998). However, these techniques ignore the correlation between covariates which is leveraged by other more advanced imputation methods. There have been a few methods that give weights to instances of the same patient in temporal data. For example, this approach has been applied to adverse drug events monitoring (Zhao and Henriksson 2016). In addition, similar methods have been applied in the political science and economics fields where time-series cross-sectional data are quite common (Shor et al. 2007).

1.2 Contributions

Given multivariate time series data, we develop a novel imputation method that utilizes optimization and machine learning techniques and outperforms state-of-the-art algorithms. Our contributions are as follows:

• 1. We formulate the problem of missing data imputation with time series information under the MedImpute framework, extending the OptImpute framework proposed by Bertsimas et al. (2018b). Our approach can be adjusted to account for different imputation models based on predictive methods such as K-NN, SVM, and trees. We focus on a K-NN formulation to solve the problem and derive a corresponding fast first-order algorithm med.knn. This method provides imputations for datasets with both continuous and categorical features and observations occurring at arbitrary points in time.

• 2. We design a series of computational experiments on three real-world sets of data with direct clinical implications. We consider the Framingham Heart Study (FHS) and the Parkinson’s Progression Markers Initiative (PPMI), two longitudinal datasets with rich time series data recorded at regular time intervals, and Electronic Health Record (EHR) data from the Dana Farber Cancer Institute (DFCI), which is less structured and more sparse time series data. We provide a comprehensive framework for our experiments that tests the performance of our method across a diverse range of scenarios, varying parameters including: (1) the percentage of missing data, (2) the number of observations per individual, and (3) the mechanism of missing data. For the latter, we consider different mechanisms for the longitudinal and EHR datasets corresponding to the different patterns of missing data which are typically observed in real-world datasets. We demonstrate that med.knn obtains the best predictive performance and lowest imputation error as we vary the missing percentage from 10% to 50%. In addition, we show that for all datasets, the relative performance of med.knn improves as we increase the number of observations per individual. Finally, we demonstrate that med.knn performs well on missing patterns commonly encountered in practice for both longitudinal studies and EHR data. These improvements are relative to the best of the comparator methods among amelia, moving average, mean, bpca, mice, and opt.knn, which are described in Sect. 3.

• 3. We propose a new custom tuning procedure to efficiently learn the hyperparameters in the optimization problem avoiding the use of traditional approaches such as Grid Search. Our methodology allows for decoupling the problem into multiple parts, enabling parallel computation that can decrease the run time. We create synthetic EHR data to test the scaling performance of the algorithm as we increase the number of observations and features. Our results show that the custom tuning approach leads to both superior scaling performance and better imputation accuracy compared to standard cross-validation. The tuning procedure is described in Sect. 2.4 and the scaling experiments with synthetic data are provided in Sect. 4.

The structure of the paper is as follows. In Sect. 2, we describe our framework for imputation of clinical covariates in time series and proposed method med.knn. In Sect. 3, we describe computational experiments on three real-world datasets evaluating both imputation and prediction accuracy. In Sect. 4, we present scaling experiments on simulated clinical datasets. In Sect. 5, we discuss properties of our algorithm and key insights from our experiments. We conclude our work in Sect. 6.

2 Methods

In this section, we describe our proposed method for imputation. In Sect. 2.1, we define variables and notation that we use in this paper. In Sect. 2.2, we review the OptImpute framework for missing data imputation. In Sect. 2.3, we introduce our new framework for imputation MedImpute which directly models clinical covariates in time series, and we present the K-Nearest Neighbors (K-NN) based formulation. In Sect. 2.4, we describe a custom tuning procedure to efficiently learn the hyperparameters in the optimization problem. Finally, in Sect. 2.5 we provide the detailed steps of the first-order method med.knn that can be used to find high-quality solutions.

2.1 Variables and notation

In this paper, we consider the single imputation problem for which our task is to fill in the missing values of dataset $\mathbf {X} \in {\mathbb {R}}^{n \times p}$ with n observations (rows) and p features (columns). Without loss of generality, we assume that the first $p_0$ features are continuous and that the next $p_1 = p - p_0$ features are categorical, and the missing and known indices are specified by the following sets:

$$\begin{aligned} \begin{aligned} \mathcal {M}_0&= \{(i,d) : \text {entry}~x_{id}~\text {is missing}, ~1 \le d \le p_0, {~1 \le i \le n} \}, \\ \mathcal {N}_0&= \{(i,d) : \text {entry}~x_{id}~\text {is known}, ~1 \le d \le p_0, {~1 \le i \le n}\},\\ \mathcal {M}_1&= \{(i,d) : \text {entry}~x_{id}~\text {is missing}, ~p_0 + 1 \le d \le p_0 + p_1, {~1 \le i \le n}\},\\ \mathcal {N}_1&= \{(i,d) : \text {entry}~x_{id}~\text {is known}, ~p_0 + 1 \le d \le p_0 + p_1, {~1 \le i \le n}\},\\ \mathcal {I}&= \{i : \mathbf {x}_i~\text {has one or more missing values}\}. \end{aligned} \end{aligned}$$

(1)

Here, $\mathcal {M}_0$, $\mathcal {M}_1$ are the sets of indices of the missing values in the continuous and categorical variables, respectively. Similarly, $\mathcal {N}_0$, $\mathcal {N}_1$ are the sets of indices of the known values in the continuous and categorical variables, respectively. $\mathcal {I}$ is the set of rows which contains at least one missing value.

We suppose that all of the continuous variables are normalized with unit SD and that the dth categorical variable takes value among $k_d$ classes. Given this data, we introduce the decision variables $\mathbf {W} \in {\mathbb {R}}^{n \times p_0}$, $\mathbf {V} \in \{1,\ldots ,k_{p_0 + 1}\} \times \ldots \times \{1, \ldots , k_{p_0 + p_1}\}$ to be the matrices of imputed continuous and categorical variables, respectively. For each entry $x_{id}$, $w_{id}$ is the imputed value if $d \in \{1,\ldots , p_0\}$, and $v_{id}$ is the imputed value if $d \in \{p_0 + 1,\ldots , p_0 + p_1\}$. We refer to the full imputation for observation $\mathbf {x}_i$ as $(\mathbf {w}_i, \mathbf{v}_i)$. For the MedImpute method, we also assume that each observation $\mathbf {x}_i$ corresponds to a particular patient with the unique ID $y_i$ observed at time-stamp $t_i$.

2.2 Review of OptImpute

Next, we review the OptImpute framework for general imputation which we use as a foundation for our method. In this approach, we formulate the missing data problem as an optimization problem in which all entries are simultaneously filled in and used as covariates to predict the other entries. Our key decision variables are the imputed values $\{w_{id}: (i,d) \in \mathcal {M}_0 \}$ and $\{v_{id}: (i,d) \in \mathcal {M}_1 \}$. We will also introduce auxiliary decision variables $\mathbf {Z}$. For any given set of imputed values and a corresponding data $\mathbf {X}$, we associate a cost function $c(\cdot )$ to it. Thus, our objective is to solve the following optimization problem:

$$\begin{aligned} \begin{aligned}&\begin{aligned} \min ~~ c(\mathbf {Z}, \mathbf {W}, \mathbf {V}; \mathbf {X}) \end{aligned}\\&\begin{aligned} \text {s.t.}~~~~~ w_{id}&= x_{id}&(i,d) \in \mathcal {N}_0,\\ v_{id}&= x_{id}&(i,d) \in \mathcal {N}_1,\\ (\mathbf {Z},&\mathbf {W}, \mathbf {V}) \in \mathcal {Z}, \\ \end{aligned} \end{aligned} \end{aligned}$$

(2)

where $\mathcal {Z}$ is the set of all feasible combinations $(\mathbf {Z}, \mathbf {W}, \mathbf {V})$ of auxiliary vectors and imputations. In this paper, we only consider an OptImpute formulation based upon K-Nearest Neighbors (K-NN), however it is also possible to consider formulations based upon SVM and trees (Bertsimas et al. 2018b).

In the K-NN formulation, the objective is to impute the missing values so that each point is as close to its K-nearest neighbors as possible. First, we define a distance metric on the dataset. Given two observations i and j, we say that the distance between them is:

$$\begin{aligned} d_{ij} := \sum _{d=1}^{p_0} (w_{id} - w_{jd})^2 + \sum _{d=p_0+1}^{p_0+p_1} \mathbb {1}_{\{v_{id} \ne v_{jd}\}}. \end{aligned}$$

(3)

In this distance metric, we weight the contributions from the continuous and categorical variables equally, but it is also possible to introduce a scaling factor to weight these terms differently. Given this distance metric, we introduce the binary variables $\mathbf {Z} \in \{0,1\}^{|\mathcal {I}| \times n}$, where

$$\begin{aligned} z_{ij} = \left\{ \begin{array}{ll} 1, &\quad \hbox {if}\,j\,\hbox {is among the}\,K-\hbox {nearest neighbors of } i\\ &\quad \text {with respect to distance metric}~(3), \\ 0, &\quad \text {otherwise.} \end{array} \right. \end{aligned}$$

(4)

The OptImpute formulation with the K-NN objective function is

$$\begin{aligned} \begin{aligned}&\begin{aligned} \min ~~ \sum _{i\in \mathcal {I}}\sum _{j=1}^n z_{ij}\left( \sum _{d=1}^{p_0} (w_{id}-w_{jd})^2 + \sum _{d=p_0+1}^{p_0+p_1} \mathbb {1}_{\{v_{id}\ne v_{jd}\}}\right) \end{aligned}\\&\begin{aligned} \text {s.t.}~~~~~ w_{id}&= x_{id}&(i,d) \in \mathcal {N}_0,\\ v_{id}&= x_{id}&(i,d) \in \mathcal {N}_1,\\ z_{ii}&= 0&i \in \mathcal {I}, \\ \sum _{j=1}^n z_{ij}&=K&i \in \mathcal {I},\\ \mathbf {Z}&\in \{0,1\}^{|\mathcal {I}| \times n}, \\ \end{aligned} \end{aligned} \end{aligned}$$

(5)

where $\mathcal {I} = \{i : \mathbf {x}_i~\text {has one or more missing values}\}$. Problem (5) is non-convex with integer constraints for the categorical variables. In order to solve this problem, the authors find near optimal feasible solutions using first-order methods with random and targeted warm starts, resulting in a new imputation algorithm called opt.knn (Bertsimas et al. 2018b).

At a high level, the opt.knn algorithm works as follows. The user provides as input an incomplete data matrix $\mathbf {X}$, a convergence threshold $\delta _0 > 0$, and a warm start imputation $(\mathbf {W}^0, \mathbf {V}^0)$. The output of the algorithm is the full matrix $\mathbf {X}^{imp}$ with the imputed variables. In each iteration, we alternate updating the auxiliary variables $\mathbf {Z}$ and the imputation $(\mathbf {W}, \mathbf {V})$ using either Coordinate Descent (CD) or Block Coordinate Descent (BCD). The problem of updating $\mathbf {Z}$ given an imputation reduces to a simple sorting procedure on the distances. To update $(\mathbf {W}, \mathbf {V})$ in CD, we locally optimize each imputed value ($w_{id}$ or $v_{id}$) one at a time. To update $(\mathbf {W}, \mathbf {V})$ in BCD, for each continuous or categorical feature we solve a Quadratic Optimization problem or a Mixed-Integer Optimization problem, respectively. We continue updating these values until the objective value stops improving by a sufficiently large amount $\delta _0$. Notice that the objective function value is strictly decreasing by at least $\delta _0$ at every iteration until the algorithm terminates. As a result, the number of steps required for the algorithm termination is:

$$\begin{aligned} T = \frac{1}{\delta _0} c(\mathbf {Z}^0, \mathbf {W}^0, \mathbf {V}^0;\,\mathbf {X}), \end{aligned}$$

(6)

where $\mathbf {W}^0, \mathbf {V}^0$ are the warmstart values, $\mathbf {X}$ is data, and $\mathbf {Z}^0$ is the initialized auxiliary variables. There are no analytical guarantees that the algorithm will find the globaly optimal solution (Wright 2015). We repeat this process for multiple warm starts and take the solution with the best objective value to be the final imputation. The algorithm for a single warm start is summarized in Algorithm 1.

2.3 MedImpute

In this section, we present the MedImpute framework for imputation of clinical covariates in time series. We extend the general OptImpute framework by weighting instances of the same person in the imputation model. We focus on the K-NN classifier and provide the specific formulation to solve this problem. Our new framework takes into account the time series structure frequently encountered in healthcare data. In addition, unlike univariate time series methods, this approach leverages statistical correlations between multiple clinical covariates.

Suppose that we are given the same problem setup for single imputation as described in Sect. 2.2. In addition, assume that each observation i corresponds to an individual patient with unique identifier $y_i \in \{1,\ldots ,M\}$ recorded at a particular time point. For datasets with multiple observations of individuals over time, we have $M < n$. Define $t_i \in {\mathbb {R}}^+$ as the number of (days/months/years) after a reference date that observation i was recorded. It follows that $|t_i - t_j|$ is the time difference in (days/months/years) between observations i and j. Note that this framework captures the common structure of many clinical datasets collected over time, including longitudinal studies, insurance claims, and EHR data.

For each clinical covariate $d = 1,\ldots ,p$, we introduce the parameters $\alpha _d$, $h_d$. We learn $\alpha _d$ and $h_d$ via a custom tuning procedure which we describe in Sect. 2.4. The first learned parameter $\alpha _d \in [0,1]$ is the relative weight given to the time series component of the objective function for variable d. At the extremes, $\alpha _d = 0$ corresponds to imputing covariate d under the OptImpute objective, and $\alpha _d = 1$ corresponds to imputing covariate d using each individual’s time series information independently. The second learned parameter $h_d \in (0,\infty )$ is the halflife parameter for the covariate d. This parameter is called the “halflife” parameter because it is the halflife of an exponential decay function $f(x) = 2 ^ {-x / h_d}$ that we use to determine the relative weights for multiple observations of the same patient.

We introduce this parameter $h_d$ so that observations from the same individual at nearby points in time will be weighted most heavily in the imputation. We make this design decision under the assumption that each clinical covariate can be approximated as a continuous function which is relatively smooth over time. For example, Body Mass Index (BMI) is a clinical covariate with values that are relatively smooth over time. Under this model, we assume that a BMI measurement from one week ago is more predictive of a patient’s current BMI than a BMI measurement from one year ago. However, we do not make any assumptions about how much more/less predictive these different measurements are, only that their relative weights follow an exponential distribution. The halflife of this exponential distribution for covariate d is the modelling parameter that we refer to as $h_d$.

For each pair of observations i, j, covariate d, and corresponding halflife parameter $h_d$, define the two derived parameters:

$$\begin{aligned} \begin{aligned}&\begin{aligned} C_{ijd} = \left\{ \begin{array}{ll} 2^{-|t_i - t_j| / h_d}, &\quad \text {if}~y_i = y_j, \\ 0, &\quad \text {otherwise}, \\ \end{array} \right. \end{aligned}\\&\begin{aligned} {\overline{C}}_{ijd} = \frac{C_{ijd}}{ \displaystyle \sum \nolimits _{\{j' : y_i = y_{j'}, j' \ne i\}} C_{ijd} }. \end{aligned} \end{aligned} \end{aligned}$$

(7)

The first derived parameter $C_{ijd}$ is the relative weight that observation j is given for time-series based imputation of observation i in covariate d. Note that this parameters is only non-zero when $y_i = y_j$, i.e. i and j are observations from the same patient. For example, if $h_d = 7$ days, then past observations of covariate d from one week and two weeks ago from the same patient would be given relative weights 0.5 and 0.25, respectively. The second derived parameter, ${\overline{C}}_{ijd}$, is the normalized variation of $C_{ijd}$. In particular, ${\overline{C}}_{ijd}$ is the relative weight that observation j is given to impute observation i in covariate d, divided by the sum of all relative weights of observations from the same patient in covariate d.

The MedImpute formulation with the K-NN objective function is

$$\begin{aligned} \begin{aligned}&\begin{aligned} \min ~~ {\frac{1}{K}} \sum _{i\in \mathcal {I}} \sum _{j=1}^n z_{ij}\left( \sum _{d=1}^{p_0} (1 - \alpha _d) (w_{id}-w_{jd})^2 + \sum _{d=p_0+1}^{p_0+p_1} (1 - \alpha _d) \mathbb {1}_{\{v_{id}\ne v_{jd}\}}\right) \\ + \sum _{i\in \mathcal {I}} \sum _{j=1}^n\left( \sum _{d=1}^{p_0} \alpha _d {{\overline{C}}_{ijd}}(w_{id}-w_{jd})^2 + \sum _{d=p_0+1}^{p_0+p_1} \alpha _d {{\overline{C}}_{ijd}}\mathbb {1}_{\{v_{id}\ne v_{jd}\}}\right) \\ \end{aligned}\\&\begin{aligned} \text {s.t.}~~~~~ w_{id}&= x_{id}&(i,d) \in \mathcal {N}_0,\\ v_{id}&= x_{id}&(i,d) \in \mathcal {N}_1,\\ z_{ii}&= 0&i \in \mathcal {I}, \\ \sum _{j=1}^n z_{ij}&=K&i \in \mathcal {I},\\ \mathbf {Z}&\in \{0,1\}^{|\mathcal {I}| \times n}, \\ \end{aligned} \end{aligned} \end{aligned}$$

(8)

where $\mathcal {I} = \{i : \mathbf {x}_i~\hbox {has one or more missing values}\}\hbox { and }\alpha _d , {\overline{C}}_{ijd}$ are constants. This problem is equivalent to (5) plus a penalty term in the objective for each feature d with different weights $\alpha _d$ in order to account for instances of the same person in the dataset. At the optimal solution, the objective function is the sum of the distances from each point to its K-nearest neighbors with respect to distance metric (3), plus the sum of the distances from each point to other observations from the same individual.

We derive a fast algorithm to provide high quality solutions to this problem using first order methods with random restarts, alternatively updating the binary variables and the imputed values as in opt.knn (Bertsekas 1999). In Algorithm 2, we summarize the med.knn method for a single warm start. In the next section, we describe the steps of this algorithm in detail.

MedImpute provides a flexible framework that can be easily extended as well. For example, we may consider other predictive models besides K-NN such as support vector machines and decision tree based methods by adjusting the objective functions of the corresponding OptImpute formulations appropriately. We refer the reader to (Bertsimas et al. 2018b) for more discussion on these alternate formulations, which is a possible area of future work. In these cases, we add the same penalty term to the objective functions that we added in formulation (8), and we solve using first-order methods with random starts. In this manuscript, we focus on the K-NN formulation due to the method’s simplicity that is close to the medical practice. The idea of imputing a patient’s missing values using the mean or the mode of the covariates from the most similar individuals to that observation is intuitive. Various implementations of the heuristic K-NN approach are already widely accepted and used in practice (Crookston and Finley 2008). For these reasons, we decided to extend upon those combining the time series component and an optimization framework.

The method can also be adapted to a multiple imputation setting. However, while multiple imputation has been considered for several years to be the most accurate method for dealing with missing data (Rubin 1996), there is a tradeoff because single imputation is more interpretable. In particular, with single imputation we obtain one downstream predictive model that can be easily presented and explained to an entire clinical team, which is a critical step in the process of data-driven medical research (Shrive et al. 2006).

2.4 Learning $\alpha _d$ and $h_d$

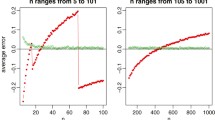
In this section, we describe a custom tuning procedure to efficiently learn $\alpha _d$ and $h_d$, which are hyperparameters in the optimization problem (8). We run this custom tuning procedure as a pre-processing step before the med.knn algorithm, which allows us to learn these parameters without using cross-validation. This is a heuristic procedure which decouples the problem into multiple parts, first learning $h_d$ for each covariate, and then learning $\alpha _d$ for each covariate. As a result, this custom tuning procedure is more computationally efficient and scales to larger problem sizes than cross-validation. In Sect. 4, we present the results from computational experiments comparing the speed and imputation accuracy of this custom tuning procedure against a traditional cross-validation method for selecting $\alpha _d$ and $h_d$.

In the first step of the custom tuning procedure, we learn the halflife parameter $h_d$ for each covariate. As in cross-validation, we tune the halflife parameters over a discrete range of values, denoted as $\mathcal H$. For example, in the computational experiments, we set $\mathcal H = \{1, 7, 30, 90, 365, 1000\}$, representing halflife values of 1 day, 1 week, 1 month, etc. For each covariate d, we compute the leave-one-out error for each halflife value $h_d \in \mathcal H$. In particular, to compute the leave-one-out error for the halflife value $h_d$, first we derive the weights ${\overline{C}}_{ijd}$, then we impute the known values in covariate d using these weights, and finally we compute the sum-of-squared errors. Afterwards, we select the halflife parameter $h_d$ which yields the lowest leave-one-out error.

For each continuous covariate $d \in \{1, \ldots , p_0\}$, the leave-one-out error is defined as:

$$\begin{aligned} \sum _{\{i: (i,d) \in \mathcal {N}_0\}} (x_{id} - {\hat{w}}_{id})^2, \end{aligned}$$

(9)

where:

$$\begin{aligned} {\hat{w}}_{id} := \sum _{j=1}^n {\overline{C}}_{ijd} x_{jd}. \end{aligned}$$

(10)

Here, ${\hat{w}}_{id}$ is equivalent to the MedImpute imputation of a continuous covariate $x_{id}$ when $\alpha _d = 1$. For each categorical covariate $d \in \{p_0 + 1, \ldots , p_0 + p_1\}$, the leave-one-out error is defined as:

$$\begin{aligned} \sum _{\{i: (i,d) \in \mathcal {N}_1\}} \mathbb {1}_{\{x_{id} \ne {\hat{v}}_{id}\}}, \end{aligned}$$

(11)

where:

$$\begin{aligned} {\hat{v}}_{id} := \arg \max _{v_{id}} \sum _{j=1}^n {\overline{C}}_{ijd} \mathbb {1}_{\{x_{jd} = v_{id}\}}. \end{aligned}$$

(12)

Intuitively, ${\hat{v}}_{id}$ is the weighted mode of covariate d, where the weights are ${\overline{C}}_{ijd}$. This is equivalent to the MedImpute imputation of the categorical covariate $x_{id}$ when $\alpha _d = 1$.

Note that we are able to learn $h_d$ independently from $\alpha _d$ because the selection of ${\overline{C}}_{ijd}$ which minimizes the objective function (8) for any fixed value of $\alpha _d$ also minimizes the objective function for any choice of $\alpha _d \in [0,1]$. Similarly, we can learn the halflife parameters $\{h_1, h_2, \ldots , h_p\}$ independently from one another, because the optimal choice of $h_d$ which minimizes the objective function (8) does not depend upon the values of $\{h_1, \ldots , h_{d-1}, h_{d+1}, \ldots , h_p\}$. Therefore, in this custom tuning procedure, we take advantage of this fact, and tune each of the halflife parameters as an initial step.

In the second step of the custom tuning procedure, we learn the MedImpute weight parameter $\alpha _d$ for each covariate. As in cross-validation, we tune the MedImpute weight parameters over a discrete range of values, denoted as $\mathcal {A}$. For example, in the computational experiments, we set $\mathcal {A} = \{0, 0.05, \ldots , 0.95, 1.0\}$, denoting relative MedImpute weights of 0%, 5%, ..., 100%, respectively. For each covariate d, we compute the k-fold error for each MedImpute weight value $\alpha _d \in \mathcal {A}$. In particular, to compute the k-fold error for the MedImpute weight value $\alpha _d$, first we split the dataset into k subsets (aka “folds”), next we impute each data subset using the rest of the subsets as training data, and finally we compute the total sum-of-squared errors across all of the folds. We select the MedImpute weight parameter $\alpha _d$ which yields the lowest k-fold error. For continuous covariates, the k-fold error is defined as:

$$\begin{aligned} \sum _{\ell = 1}^k \sum _{\{i: (i,d) \in \mathcal {N}_0^\ell \}} (x_{id} - {\hat{w}}_{id}^\ell )^2, \end{aligned}$$

(13)

where $\mathcal {N}_0^\ell$ are the known continuous values in the $\ell$th fold. The imputed values ${\hat{w}}_{id}^\ell$ are given by:

$$\begin{aligned} {\hat{w}}_{id}^\ell := (1 - \alpha _d) w^{\text {OPT}_\ell }_{id} + \alpha _d \sum _{\{i: (i,d) \in \mathcal {N}_0 \setminus \mathcal {N}_0^\ell \}} {\overline{C}}_{ijd} x_{jd}, \end{aligned}$$

(14)

where $w^{\text {OPT}_\ell }_{id}$ is the OptImpute imputation of $x_{id}$ using the data from the other $k-1$ folds, and $\mathcal {N}_0 \setminus \mathcal {N}_0^\ell$ are the known continuous values not in the $\ell$th fold. For categorical covariates, the k-fold error is defined as:

$$\begin{aligned} \sum _{\ell = 1}^k \sum _{\{i: (i,d) \in \mathcal {N}_1^\ell \}} \mathbb {1}_{\{x_{id} \ne {\hat{v}}^\ell _{id}\}}, \end{aligned}$$

(15)

where $\mathcal {N}_1^\ell$ are the known categorical values in the $\ell$th fold. The imputed values ${\hat{v}}_{id}^\ell$ are given by:

$$\begin{aligned} {\hat{v}}_{id}^\ell := \arg \max _{v_{id}} \left[ (1 - \alpha _d) \mathbb {1}_{\{v^{\text {OPT}_\ell }_{id} = v_{id}\}} + \alpha _d \sum _{\{i: (i,d) \in \mathcal {N}_0 \setminus \mathcal {N}_0^\ell \}} {\overline{C}}_{ijd} \mathbb {1}_{\{x_{jd} = v_{id}\}} \right] . \end{aligned}$$

(16)

where $v^{\text {OPT}_\ell }_{id}$ is the OptImpute imputation of $x_{id}$ using the data from the other $k-1$ folds, and $\mathcal {N}_1 \setminus \mathcal {N}_1^\ell$ are the known categorical values not in the $\ell$th fold. Intuitively, ${\hat{v}}_{id}^\ell$ is the weighted mode of the OptImpute value and the other known values of the same covariate, where the weights are $(1 - \alpha _d)$ and $\alpha _d {\overline{C}}_{ijd}$, respectively.

Finally, we note that there is another hyperparameter that we may tune for the med.knn algorithm, K, which is the number of nearest-neighbors. In the computational experiments, we fix $K = 10$, which works well for the datasets that we consider here. Previously, it has been shown that the OptImpute methods are relatively robust even if their hyperparameters are misspecified (Bertsimas et al. 2018b). Thus, while the accuracy of the med.knn algorithm can be improved slightly by tuning over K, the relative improvement in imputation accuracy is outweighed by the increased computational costs.

2.5 The med.knn algorithm

In this section, we provide details for the updates in the med.knn imputation algorithm. This is a first-order method to find locally optimal solutions to Problem (5). As in the opt.knn algorithm, in this algorithm we alternatively update $\mathbf {Z}$ and $(\mathbf {W}, \mathbf {V})$ until the solution converges. The update for $\mathbf {Z}$ is identical to the one for opt.knn, and is computed with a simple sorting procedure on the distances. However, the update for $(\mathbf {W}, \mathbf {V})$ is modified and depends upon the MedImpute parameters $\alpha _d$, $C_{ijd}$. As in opt.knn, we can update the values of $(\mathbf {W}, \mathbf {V})$ either with Block Coordinate Descent (BCD) or Coordinate Descent (CD) which are described in the following subsections. The opt.knn updates for both BCD and CD are equivalent to the corresponding med.knn updates when $\alpha _d = 0$ for all $d = 1,\ldots ,p$.

2.5.1 Block coordinate descent

In this approach, we update all of the imputed values at once. We call this approach BCD because we update the variables $(\mathbf {W}, \mathbf {V})$ as an entire block, keeping $\mathbf {Z}$ fixed. Our formulation Problem (8) decomposes by dimension into $p_0$ Quadratic Optimization problems for the continuous features and $p_1$ Mixed Integer Optimization problems for the categorical features. To update the imputed values $\mathbf {w}^d$ for continuous feature $d = 1,\ldots ,p_0$, we solve:

$$\begin{aligned} \begin{aligned}&\begin{aligned} \min _{\mathbf {w}^d}~~ \sum _{i \in \mathcal {I}}\sum _{j=1}^n z_{ij} (1 - \alpha _d)(w_{id}-w_{jd})^2 + \sum _{i \in \mathcal {I}}\sum _{j=1}^n \alpha _d {{\overline{C}}_{ijd}} (w_{id}-w_{jd})^2 \\ \end{aligned}\\&\begin{aligned} \text {s.t.}~~~~~ w_{id}&= x_{id}&(i,d) \in \mathcal {N}_0.\\ \end{aligned} \end{aligned} \end{aligned}$$

(17)

Taking the partial derivative of the objective function with respect to $w_{id}$ for some missing entry $(i,d) \in \mathcal {M}_0$ and setting it to zero, we obtain after some simplifications:

$$\begin{aligned} \begin{aligned} 0 =&\bigg ((1-\alpha _d)K + \alpha _d + \sum _{j \in \mathcal {I}}[(1 - \alpha _d)z_{ji} + \alpha _d {\overline{C}}_{jid}]\bigg )w_{id}\\&- \sum _{(j,d)\in \mathcal {M}_0} [(1 - \alpha _d)(z_{ij} + z_{ji}) + \alpha _d ({\overline{C}}_{ijd} + {\overline{C}}_{jid})]w_{jd}\\&- \sum _{(j,d) \in \mathcal {N}_0} [(1 - \alpha _d)(z_{ij} + \mathbb {1}_{\{j \in \mathcal {I}\}} z_{ji}) + \alpha _d({\overline{C}}_{ijd} + \mathbb {1}_{\{j \in \mathcal {I}\}} {\overline{C}}_{jid})]x_{jd}. \end{aligned} \end{aligned}$$

(18)

This follows directly from equation (9) in (Bertsimas et al. 2018b). For each feature $d = 1,\ldots ,p_0$, we have a system of equations of the above form which we can solve to determine the optimal imputed values $w_{id}, (i,d) \in \mathcal {M}_0$. Simplifying the notation, suppose that the missing values for the dimension d are $\widetilde{\mathbf {w}}^d:= (w_{1d}, \ldots , w_{ad})$ and the known values are $\mathbf {x}^d:=(x_{(a+1)d}, \ldots , x_{nd})$. Then the set of optimal imputed values $w_{id}^d, (i,d) \in \mathcal {M}_0$ is the solution to the linear system

$$\begin{aligned} ((1-\alpha _d)\mathcal {Q}+\alpha _d \mathbf {P})\widetilde{\mathbf {w}}^d = ((1-\alpha _d)\mathcal {R}+\alpha _d \mathbf {Y})\mathbf {x}^d, \end{aligned}$$

(19)

where the matrices $\mathcal {Q}$, $\mathbf {P}$, $\mathcal {R}$, and $\mathbf {Y}$ are defined as

$$\begin{aligned} \mathcal {Q}&= \begin{bmatrix} K + \sum _{j \in \mathcal {I}}z_{j1} - 2z_{11} & -z_{12}-z_{21} & \ldots & -z_{1a} -z_{a1} \\ -z_{21}-z_{12} & K + \sum _{j \in \mathcal {I}}z_{j2}- 2z_{22} & \ldots & -z_{2a} -z_{a2} \\ \vdots & \vdots & \ddots & \vdots \\ -z_{a1}-z_{1a}& -z_{a2}-z_{2a} & \ldots & K + \sum _{j \in \mathcal {I}}z_{ja} - 2z_{aa} \end{bmatrix},\end{aligned}$$

(20)

$$\begin{aligned} \mathbf {P}&= \begin{bmatrix} \sum _{j \in \mathcal {I}}{\overline{C}}_{j1d} - 2{\overline{C}}_{11d} & -{\overline{C}}_{12d}-{\overline{C}}_{21d} & \ldots & - {\overline{C}}_{1ad}-{\overline{C}}_{a1d} \\ -{\overline{C}}_{21d}-{\overline{C}}_{12d} & \sum _{j \in \mathcal {I}} {\overline{C}}_{j2d} - 2{\overline{C}}_{22d} & \ldots & - {\overline{C}}_{2ad}-{\overline{C}}_{a2d} \\ \vdots & \vdots & \ddots & \vdots \\ -{\overline{C}}_{a1d}-{\overline{C}}_{1ad}& -{\overline{C}}_{a2d} - {\overline{C}}_{2ad} & \ldots & \sum _{j \in \mathcal {I}}{\overline{C}}_{jad}- 2{\overline{C}}_{aad} \end{bmatrix}, \end{aligned}$$

(21)

$$\begin{aligned} \mathcal {R}&= \begin{bmatrix} z_{1(a+1)} + \mathbb {1}_{\{(a+1)\in \mathcal {I}\}}z_{(a+1)1}\ldots z_{1n} + \mathbb {1}_{\{n \in \mathcal {I}\}}z_{n1} \\ \vdots \quad \quad \quad \quad \vdots \\ z_{a(a+1)} + \mathbb {1}_{\{(a+1)\in \mathcal {I}\}}z_{(a+1)a}\ldots z_{an} + \mathbb {1}_{\{n \in \mathcal {I}\}}z_{na} \\ \end{bmatrix}, \end{aligned}$$

(22)

$$\begin{aligned} \mathbf {Y}&= \begin{bmatrix} {\overline{C}}_{1(a+1)d} + \mathbb {1}_{\{(a+1)\in \mathcal {I}\}}{\overline{C}}_{(a+1)1d}\ldots {\overline{C}}_{1nd} + \mathbb {1}_{\{n \in \mathcal {I}\}}{\overline{C}}_{n1d} \\ \vdots \quad \quad \quad \quad \vdots \\ {\overline{C}}_{a(a+1)d} + \mathbb {1}_{\{(a+1)\in \mathcal {I}\}}{\overline{C}}_{(a+1)ad} \ldots {\overline{C}}_{and} + \mathbb {1}_{\{n \in \mathcal {I}\}}{\overline{C}}_{nad} \\ \end{bmatrix}. \end{aligned}$$

(23)

Without loss of generality, there exists a closed-form solution

$$\begin{aligned} \widetilde{\mathbf {w}}^d = ((1 - \alpha _d)\mathcal {Q}+\alpha _d \mathbf {P})^{-1}((1 - \alpha _d)\mathcal {R}+\alpha _d \mathbf {Y}) \mathbf {x}^d \end{aligned}$$

(24)

to this system of equations for each feature $d = 1,\ldots ,p_0$. To update the imputed values $\mathbf{v}^d$ for each categorical feature $d = (p_0+1),\ldots ,p$, we solve the following mixed-integer optimization problem:

$$\begin{aligned} \begin{aligned}&\begin{aligned}&{\min _{\mathbf{v}^d}}&\sum _{i \in \mathcal {I}}\sum _{j=1}^n ((1 - \alpha _d)z_{ij} + \alpha _d {{\overline{C}}_{ijd}}) y_{ij} \end{aligned}\\&\begin{aligned} \text {s.t.}~~~&v_{id} = x_{id}&(i,d) \in \mathcal {N}_1, \\&v_{id} - v_{jd} \le y_{ij}k_d&i=1,\ldots ,n, j=1,\ldots ,n,\\&v_{jd} - v_{id} \le y_{ij}k_d&i=1,\ldots ,n, j=1,\ldots ,n,\\&y_{ij} \in \{0,1\}^{|\mathcal {I}| \times n}.\\ \end{aligned} \end{aligned} \end{aligned}$$

(25)

This is a Mixed Integer Optimization problem, which is practically solvable as the BCD update for opt.knn. Since the BCD update step requires inverting a matrix with $O(n^2)$ entries and solving an optimization problem with $O(n^2)$ binary variables, this method works best for smaller problem sizes $n \le 10,000$.

2.5.2 Coordinate descent

In CD, we update the imputed values one at a time. In order to update the imputed value for $x_{id}$, we fix all of the variables in Problem (8) except for $w_{id}$ or $v_{id}$ and solve the corresponding one-dimensional optimization problem. This results in fast, closed-form updates for both the continuous and categorical variables. Each $w_{id}, (i,d)\in \mathcal {M}_0$ is imputed as the minimizer of the following:

$$\begin{aligned} \begin{aligned} \min _{w_{id}}~~ \sum _{r\in \mathcal {I}}\sum _{j=1}^n z_{rj}\sum _{d=1}^{p_0} (1 - \alpha _d)(w_{rd}-w_{jd})^2 + \sum _{r\in \mathcal {I}}\sum _{j=1}^n\sum _{d=1}^{p_0} \alpha _d {{\overline{C}}_{rjd}}(w_{rd}-w_{jd})^2. \end{aligned} \end{aligned}$$

(26)

Solving the above gives the closed-form solution for every $(i,d)\in \mathcal {M}_0$:

$$\begin{aligned} w_{id} = \frac{\sum _{j=1}^n ((1 - \alpha _d)z_{ij} + \alpha _d {\overline{C}}_{ijd})w_{jd} + \sum _{j \in \mathcal {I}}((1 - \alpha _d)z_{ji}+ \alpha _d {\overline{C}}_{jid})}{K + \sum _{j=1}^n \alpha _d {\overline{C}}_{ijd}+ \sum _{j \in \mathcal {I}}((1 - \alpha _d)z_{ji}+\alpha _d {\overline{C}}_{jid})}. \end{aligned}$$

(27)

Similarly, each categorical variable $v_{id}, (i,d) \in \mathcal {M}_1$ is imputed as the minimizer of the following:

$$\begin{aligned} \begin{aligned} \min _{v_{id}}~~ \sum _{r\in \mathcal {I}}\sum _{j=1}^n z_{rj}\sum _{d=p_0+1}^{p_0+p_1} (1 - \alpha _d)\mathbb {1}_{\{v_{rd}\ne v_{jd}\}} + \sum _{r\in \mathcal {I}}\sum _{j=1}^n\sum _{d=p_0+1}^{p_0+p_1} \alpha _d {{\overline{C}}_{rjd}}\mathbb {1}_{\{v_{rd}\ne v_{jd}\}}. \end{aligned} \end{aligned}$$

(28)

Suppose that the value of categorical variable $v_{id}$ is one of $k_d$ distinct categories $\{1, 2,\ldots , k_d\}$. Then, the solution to problem (28) is

$$\begin{aligned} \arg \max _{k \in \{1,\ldots ,k_d\}} \Bigg [\sum _{j=1}^n \bigg ((1 - \alpha _d)z_{ij}+\alpha _d {{\overline{C}}_{ijd}}\bigg )\mathbb {1}_{\{v_{jd} =k\}} + \sum _{j\in \mathcal {I}} \bigg ((1 - \alpha _d)z_{ji}+\alpha _d {{\overline{C}}_{ijd}}\bigg )\mathbb {1}_{\{v_{jd} =k\}}\Bigg ]. \end{aligned}$$

(29)

Here, we set the imputed variable to be the value with the highest frequency in the neighborhood, with instances of the same person i receiving additional weight calibrated by the parameters $\{{\overline{C}}_{ijd}\}_{j=1}^n$ and $\alpha _d$.

This approach scales to large problem sizes (n in the 100,000’s), and it is the method that we implement for the computational experiments.

3 Computational experiments on real-world clinical datasets

In this section, we run a series of computational experiments testing the performance of med.knn imputing missing values in real-world clinical datasets. In Sect. 3.1, we provide an overview of the three datasets and their baseline characteristics. In Sect. 3.2, we describe the mechanisms for generating Missing Not at Random (MNAR) data that are used in some of the experiments. In Sect. 3.3, we describe the setup of the computational experiments, and we describe the imputation methods that we run for comparison across all of the computational experiments. In Sect. 3.4, we report the results of the experiments on the imputation tasks. In Sect. 3.5, we report the results of the experiments on the downstream predictive tasks. In Sect. 3.6 we discuss the results and major takeaways from the computational experiments.

3.1 Description of real-world clinical datasets

In this section we describe the three real-world clinical datasets used in the computational experiments. In Sect. 3.1.1, we describe the FHS dataset. In Sect. 3.1.2, we describe the DFCI dataset. Finally, in Sect. 3.1.3, we describe the PPMI dataset.

3.1.1 Framingham heart study (FHS) dataset

The FHS was started in 1948 with the goal of observing a large population of healthy adults over time to better understand the factors that lead to cardiovascular disease. Over 80 variables were collected from 5209 people at a time for more than 40 years. The FHS is arguably the most influential longitudinal study in the field of cardiovascular and cerebrovascular research. This data has now been used in more than 2400 studies and is considered one of the top 10 cardiology advances of the twentieth century alongside the electrocardiogram and open-heart surgery (Daniel Levy 2006).

In our computational experiments, we consider all individuals from the FHS Original Cohort (National Heart, Lung, and Blood Institute, Boston University 2012) with 10 or more observations, which includes $M = 1107$ unique patients. For each patient, we take the 10 most recent observations, so the dataset has $n = 11{,}070$ observations total. We include $p = 13$ continuous (Age, Body Mass Index, Systolic Blood Pressure, High-Density Lipoproteins, Hematocrit, Blood Glucose levels) and categorical covariates (Gender, Smoking, presence of Cardiovascular Disease, presence of Atrial Fibrillation, presence of diabetes, currently under prescription of antihypertensive medication, presence of Left Ventricular Hypertrophy from ECG results).

Overall, there are 12.56% missing values in the FHS dataset. The percentage of missing values in each covariate is shown in Table 5 in Appendix 7.1. Due to the design of the longitudinal study, the 10 observations for each patient occur at regular intervals spaced 2 years apart, for a total span of 18 years. For the imputation tasks, we add in additional missing values to the FHS dataset, and evaluate the accuracy of med.knn and comparison methods against the ground-truth values. For the downstream tasks, we evaluate classification models which predict 10-year risk of stroke given the imputed training data.

3.1.2 Dana farber cancer institute (DFCI) dataset

The DFCI dataset was obtained from a recently published work on predicting mortality in late-stage cancer patients (Bertsimas et al. 2018a). In this study, the authors retrospectively obtained patient data from EHR and linked Social Security Administration mortality data for cancer patients at the Dana Farber Cancer Institute / Brigham and Women’s Cancer Center from 2004 through 2014. Predictive models were fit for the entire population and individual cancers, including breast, lung, colorectal, kidney, and prostate cancer. Study eligibility required adult patients that have received at least one anticancer treatment over the course of their care, including chemotherapy, immunotherapy, and targeted therapy.

In our computational experiments, we consider all patients with late-stage breast cancer from the DFCI dataset. Each observation corresponds to a patient initiating an anticancer regimen which was systematically recorded in the hospital’s database. As a result, for every patient who followed more than one regimen, multiple observations were collected. For each patient, we include all of their observations in either the training set or testing set, respectively. In total, we have 12,206 observations that correspond to 5987 unique patients. This includes 3228 individuals who have just one line of therapy and therefore only appear once in this dataset. For each observation, there are 106 covariates which describe the patient at that point in time, including demographics, lab tests, vital signs, current medications, medical history, biomarkers, and variables derived from the patient’s temporal EHR history.

Overall, there are 10.79% missing values in the DFCI dataset. The percentage of missing values in each covariate is shown in Table 6 in Appendix 7.1. Due to the nature of this observational study, the observations for each patient occur at irregular intervals, which correspond to hospital visits. In addition, in the dataset each patient has anywhere from 1 to 12 observations. In Appendix 7.1, we provide some more details on the DFCI dataset, including the distribution of observations per patient (see Fig. 13) and summary statistics of the time intervals between each visit (see Table 8). For the imputation tasks, we add in additional missing values to the DFCI dataset, and evaluate the accuracy of med.knn and comparison methods against the ground-truth values. For the downstream tasks, we evaluate classification models which predict 60-day risk of mortality given the imputed training data.

3.1.3 Parkinson’s progression markers initiative (PPMI) dataset

The PPMI (Marek et al. 2011) was a landmark observational clinical study with the aim to comprehensively evaluate patient cohorts using imaging, biologic sampling as well as clinical and behavioral data to identify biomarkers of Parkinson’s disease progression.

In our computational experiments, we consider data from the PPMI baseline examination as well as the following three years of follow-up. In this longitudinal study, 20 patients appeared only in one follow-up examination, 33 in two while the rest of the population participated in all 352 clinical evaluations. As a result, in total we have 1547 observations corresponding to 405 distinct patients. For each observation, there are 116 covariates which describe the demographic characteristics, the results of behavioral tests, clinical test results, as well as the presence or absence of genetic mutations related to the disease.

Overall, there are 2.61% missing values in the PPMI dataset. The percentage of missing values in each covariate is shown in Table 7 in Appendix 7.1. Due to the design of the longitudinal study, the 4 observations for each patient occur at regular intervals spaced 1 year apart, for a total span of 4 years. For the imputation tasks, we add in additional missing values to the PPMI dataset, and evaluate the accuracy of med.knn and comparison methods against the ground-truth values. For the downstream tasks, we evaluate regression models which predict the Montreal Cognitive Assessment (MoCA) score one year in advance. The MoCA score is a rapid screening instrument for mild cognitive dysfunction, a clinical state that often progresses to dementia (Nasreddine et al. 2005).

3.2 Mechanisms for generating missing not at random (MNAR) data

Missing data can either be Missing Completely At Random (MCAR), Missing At Random (MAR), or Missing Not At Random (MNAR) (Little and Rubin 2019). The type of missingness can be determined through an understanding of the specific feature and what systematic biases may exist in its collection process. Different types of missingness must be treated differently for meaningful analysis. In reality, missing data are most commonly associated with the MNAR category where the presence of unknown values is systematically related to unobserved factors.

In this section, we describe mechanisms for generating Missing Not at Random (MNAR) data for our computational experiments. We consider different mechanisms for the longitudinal and EHR datasets corresponding to the different patterns of missing data which are typically observed in real-world datasets. In Sect. 3.2.1, we describe the missing data mechanism that we use for the MNAR experiments on the two longitudinal datasets: FHS and PPMI. In Sect. 3.2.2, we describe the missing data mechanism that we use for the MNAR experiments on the EHR dataset: DFCI.

For all MNAR experiments, the total percentage of missing data is fixed to $30\%$. For each individual experiment, we assume that the dataset is ($\gamma 30$% MNAR, $(1-\gamma )30\%$ MCAR), where $\gamma$ is a constant that we select between 0 and 1. To generate the missing data patterns, first we generate the $\gamma 30\%$ MNAR patterns, and then we randomly select an additional $(1-\gamma )30\%$ subset of the data to be Missing Completely at Random (MCAR). In the following two sections, we describe the specific ways that we generate MNAR data for longitudinal studies and EHR data, which are influenced by real-world missing data mechanisms.

3.2.1 MNAR mechanism for data from longitudinal studies

In longitudinal studies, missing data patterns often result from changes in the experiment design. Researchers may decide to include an additional set of variables as the study progresses over time due to new information from other investigations. Thus, it is common for feature d to be missing for the first $t_d$ rounds of long-term longitudinal studies. For example, ECG results were only first recorded in the FHS study 14 years after the study began (D’Agostino et al. 2013; Mahmood et al. 2014).

To generate $\gamma$30% MNAR patterns under this mechanism, we use the following process. First, we randomly select a covariate d and a discrete uniform random variable $t_d \in \{1,2,\ldots ,N\}$, where $N = 10$ for the FHS dataset and $N = 4$ for the PPMI dataset. The value $t_d$ corresponds to the last round of the longitudinal study that covariate d is missing. For example, if $t_d = 2$ for the covariate “Left Ventricular Hypertrophy” (LVH), then the value for LVC will be missing for all observations in the two first clinical examinations. We continue this process until we have introduced $\gamma 30\%$ MNAR missing values. Afterwards, we introduce additional MCAR missing values to the remaining dataset in order to obtain the final dataset with 30% missing values.

3.2.2 MNAR mechanism for data from EHR

In EHR data, missing data patterns may be correlated with the severity of patient’s condition. Consider the case of a patient whose physician suspects the existence of chronic kidney disease. The associated record is more likely to have a recorded value for Glomerular Filtration Rate since it is a direct indication of the kidney’s functional status (Levey et al. 2005). Therefore, observed values are more likely to be below the threshold of $60 \text {mL/min/1.73 m}^2$ since they correspond to sicker patients.

To generate $\gamma 30\%$ MNAR patterns under this mechanism, we suppose that missing indicators are independent Bernoulli random variables where the probability that entry $x_{id}$ is missing equals the probability that a normal random variable $N(x_{id}, \epsilon )$ is greater than a particular threshold for covariate d. The threshold for each covariate d is the quantile of $\mathbf {X}^d$ which corresponds to the desired missing percentage level $\gamma 30\%$. Then, we introduce additional MCAR missing values to the remaining dataset in order to obtain the final dataset with 30% missing values total for this experiment.

3.3 Experimental setup

In this section, we describe the setup of computational experiments that compare med.knn to other state-of-the-art imputation methods. We use data from three distinct sources to test the performance of our algorithm on both longitudinal cohort study and EHR datasets. The codebase for the computational experiments is publicly available at https://github.com/colin78/medimpute_computational_experiments.

In our experiments, we take the full dataset to be the ground truth. First, we normalize the data so that each continuous covariate has mean zero and SD equal to one. Then, we run some of the most commonly-used and state-of-the-art methods for imputation to predict the missing values and compare against med.knn. The methods that we compare are as follows:

• 1. Mean (mean) This is the simplest method. For each continuous feature, we impute the mean of the observed values and, for each categorical feature, we impute the mode of the observed values (Little and Rubin 2019).

• 2. Moving average (moving.avg) This method takes into account only observations of the same entity (i.e., patient) and imputes their averages under a given time window. In cases where only one observation per entity is available, the method reduces to the mean. For each dataset, we consider a different time horizon depending on the relative scale of the data (i.e, years, months, or days). Implemented in the Julia programming language.

• 3. Bayesian principal component analysis (bpca) This method takes a singular value decomposition (SVD) of the data matrix and information from a Bayesian prior distribution on the model parameters to impute missing values (Oba et al. 2003). Implemented using the pcaMethods package in the R programming language.

• 4. Multivariate imputation via chained equations (mice) In this multiple imputation method, we begin from m random starts and iteratively update each one to produce m independent imputations. In each iteration, we update the imputed values in feature d by drawing from a distribution conditional on all other features (van Buuren and Groothuis-Oudshoorn 2011). We use Classification Trees for the categorical features and Regression Trees for the continuous features. Implemented using the mice package in in the R programming language.

• 5. Multiple imputation with boostrap expectation maximization (Amelia II) This is another multiple imputation method that builds upon the Amelia I framework, which assumes that the data is jointly distributed as multivariate normal and uses an expectation-maximization (EM) algorithm with bootstrapping (Honaker et al. 2011; King et al. 2001). In addition, a newer version of the method allows for the imputation of cross-sectional time series data. It can build a general model of patterns within variables across time by creating a sequence of polynomials of the time index. Thus, it is able to capture variables that are recorded over time within a cross-sectional unit and are observed to vary smoothly over time. Implemented using the amelia package in the R programming language.

• 6. OptImpute under K-NN objective (opt.knn) This method finds a high quality solution to Problem (5) minimizing the sum of distances from each point to its K-Nearest Neighbors (Bertsimas et al. 2018b). We find solutions to this problem using Algorithm 1 with the CD update. Fixing $K = 10$, we use several warm and random restarts and select the imputation with the best objective value. Implemented using the OptImpute package in the Julia programming language.

• 7. MedImpute under K-NN objective (med.knn) This method finds a high quality solution to Problem (8) minimizing the sum of distances from each point to its K-Nearest Neighbors and other instances of the same individual. We find solutions to this problem using Algorithm 2 with the CD update. For each feature d, we perform cross-validation to tune the parameters $\alpha _d, h_d$ with the rest of the MedImpute parameters set equal to zero. Fixing $K = 10$, we use several warm and random restarts and select the imputation with the best objective value. Implemented in the Julia programming language.

For each experiment, we evaluate the imputation accuracy of each method using the Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) metrics, which are extended to accommodate both continuous and categorical covariates. Let $\mathcal {M}_0^{test}$, $\mathcal {M}_1^{test}$ be the hold-out sets for the missing continuous and categorical covariates, respectively. We define the MAE and RMSE metrics to be:

$$\begin{aligned}&\text {MAE} := \frac{1}{|\mathcal {M}_0^{test}|} \sum _{(i,d) \in \mathcal {M}_0^{test}} |w_{id} - x_{id}| + \frac{1}{|\mathcal {M}_1^{test}|} \sum _{(i,d) \in \mathcal {M}_1^{test}} \mathbb {1}_{\{v_{id} \ne x_{id}\}}, \end{aligned}$$

(30)

$$\begin{aligned}&\text {RMSE} := \sqrt{\frac{1}{|\mathcal {M}_0^{test}|} \sum _{(i,d) \in \mathcal {M}_0^{test}} (w_{id} - x_{id})^2 + \frac{1}{|\mathcal {M}_1^{test}|} \sum _{(i,d) \in \mathcal {M}_1^{test}} \mathbb {1}_{\{v_{id} \ne x_{id}\}}}. \end{aligned}$$

(31)

In addition to comparing the accuracy of each method on the imputation task, we also compare their performance on downstream predictive tasks which are tailored for each dataset. In these experiments, we use the imputation methods to fill in the missing values of the datasets, and then we train machine learning models with the data from completed datasets. By comparing the accuracy of the predictive models on the downstream tasks, we can see the relative impact of using one imputation method versus another in a machine learning pipeline. For the FHS dataset, the downstream task is to predict 10-year risk of stroke, a classification task. For the DFCI dataset, the downstream task is to predict 60-day risk of mortality, which is also a classification task. For the PPMI dataset, the downstream task is to predict the Montreal Cognitive Assessment (MoCA) score for next year, which is a regression task.

To evaluate the accuracy on the downstream predictive task, first we split the patients from the completed dataset into a training and testing set using a 75%/25% ratio. For the longitudinal datasets (FHS and PPMI) we include only one visit per patient, the most recent one. Thus, the time series component of the dataset is only present in the missing data imputation process but not in the supervised learning part of the experiment. This setup allows us to quantify the relative benefit of med.knn per individual. For the EHR dataset (DFCI), we include all of the observations from each patient in either the training or testing set for the supervised learning task.

Next, we train predictive models on the training set and report the out-of-sample accuracy on the testing set. For the classification tasks, we train $\ell _1$-regularized logistic regression models and report the out-of-sample Area Under the Receiver Operator Characteristic Curve (AUC). For the regression task, we train $\ell _1$-regularized linear regression models and report the out-of-sample Mean Absolute Error (MAE). These two metrics are commonly used evaluation criteria in machine learning (Hastie et al. 2009). We repeat all experiments for 25 random seeds and average the results. Each iteration corresponds to a different random split of the patients into the training and testing sets, a random warmstart, and a randomly generated missing data pattern. In particular, we note that the patient IDs and the time stamps corresponding to each row of the dataset are maintained across the different random seeds, so that the temporal sequence of the records remains the same as the original dataset.

We artificially created missing data under different mechanisms and random patterns to compare the imputation accuracy of the proposed method. The missing data generation process was independently applied to each column. For a fixed missing percentage $f\%$, we remove the necessary number of known values for each feature to reach the $f\%$ target. The patient ID $y_i$ was not factored in the missing data generation process and all rows were considered independent observations. If the existing percent of missing data for a column was higher than the target $f\%$, we do not generate any artificial missing values for the covariate, and thus the feature does not contribute to the estimation of the imputation accuracy metrics.

Given this framework for evaluating imputation methods on both imputation and downstream tasks, we conduct a variety of experiments which vary the pattern of the missing data. In particular, we conduct three different types of experiments that correspond to variations in the form of missing data that we frequently encounter in medical datasets:

• 1. Percentage of missing data We generate patterns of missing data for various percentages ranging from 10 to 50% under the missing completely at random (MCAR) mechanism. Given a target proportion of missing data f (i.e., $f = 20\%$), we generate among all observed data f missing values at each column independently from the rest completely at random.

• 2. Number of observations per patient With the missing percentage fixed at 50% MCAR, we vary the time frame during which patient observations are included in the imputation task. Our goal is to quantify the effect of the time series component as we vary its intensity.

• 3. Mechanism of missing data With the missing percentage fixed at 30%, we vary the missing data mechanism from Missing Completely At Random (MCAR) to Missing Not At Random (MNAR) on a gradient scale. In particular, we suppose that the missing pattern is ($\gamma$30% MNAR, ($1 - \gamma$)30% MCAR), where $\gamma$ varies from 0 to 1. We consider two different MNAR mechanisms that correspond to distinct missing data patterns observed in longitudinal studies and EHR.

The objective of the first set of experiments is to determine which imputation methods perform best at high and low levels of missing data. For these experiments, we also report the results from statistical hypothesis tests (Friedman Rank and pairwise t-tests) to evaluate whether the rankings and differences between the imputation algorithms are statistically significant. The objective of the second set of experiments is to determine how the performance of med.knn and other imputation methods varies as the amount of time series information available on each patient fluctuates. Finally, the objective of the third set of experiments is to determine how robust each imputation method is with respect to the missing data mechanism. In the previous section, we describe the two mechanisms for generating MNAR data for the third set of experiments. Below, we summarize all of the steps required to run one of the computational experiments for a single random seed:

• 1. Fix a random seed s, a dataset, a desired missingness percentage level $f\%$, a missing data imputation method, and a value for the $\gamma$ parameter.

• 2. Generate a random missing data pattern in the given dataset using the targeted percentage of missing values $f\%$, the random seed s, and the value of the $\gamma$ parameter.

• 3. Impute the missing values in the provided dataset using the specified algorithm (i.e. med.knn, mean, bpca).

• 4. Calculate the imputation error using the MAE and RMSE metrics (see Eqs. 30, 31) on the artificially generated missing data.

• 5. Split the patients in the dataset into a training and testing set using a 75%/25% ratio. For the longitudinal datasets, only include the most recent observation from each individual in the training and testing sets. For the EHR (DFCI) dataset, include all of the observations from each individual in the training or testing set.

• 6. Train a downstream predictive model on the training set using the cv.glmnet function from the R glmnet package (Friedman et al. 2009). For the FHS and DFCI datasets which have binary outcomes variables, train a logistic regression model with $l_1$ regularization. For the PPMI dataset which has a continuous outcome variable, train a linear regression model with $l_1$ regularization.

• 7. Report the out-of-sample performance of the trained model on the testing set. For the classification tasks, report the out-of-sample AUC, and for the regression task, report the out-of-sample MAE.

3.4 Imputation results

In this section, we provide the results from all experiments on the imputation tasks. In particular, we present the imputation results from the (1) percentage of missing data, (2) number of observations per patient, and (3) mechanism of missing data experiments.

Percentage of missing data

In Fig. 1, we show the MAE imputation accuracy results from the first set of experiments in which we vary the percentage of missing data from 10 to 50%, and the missing data mechanism is fixed to MCAR. We present the exact values and standard errors in this plot in the Appendix in Table 9. Across all of the datasets, med.knn achieves the lowest average MAE for all of the missing percentages tested. On the FHS longitudinal dataset with 50% MCAR data, med.knn has an average MAE of 0.289 compared to the next best method opt.knn with an average MAE of 0.503, a 42.54% reduction. Similarly, on the PPMI longitudinal dataset with 50% MCAR data, med.knn has an average MAE of 1.286 compared to the next best method opt.knn with an average MAE of 1.99, a 35.37% reduction. On the DFCI dataset with 50% MCAR data, med.knn has an average MAE of 3.568 compared to the next best method mean with an average MAE of 4.367, a 22.39% reduction.

Fig. 1

Imputation errors for each method using the MAE metric on the FHS, DFCI, and PPMI datasets, varying the percentage of missing data from 10 to 50%. The missing data mechanism is fixed to MCAR

In Fig. 2, we present the RMSE imputation accuracy results. In general, the results are similar to the MAE imputation accuracy results, and med.knn produces the imputation with the lowest RMSE across all experiments. One notable difference is on the DFCI dataset, the relative improvement of med.knn compared to bpca, moving.avg, and mean is much smaller. Because the mean imputation method performs relatively well, this suggests that there are some difficult-to-impute covariates in the DFCI dataset which are resulting in large RMSE values for all of the more complex methods.

Fig. 2

Imputation errors for each method using the RMSE metric on the FHS, DFCI, and PPMI datasets, varying the percentage of missing data from 10 to 50%. The missing data mechanism is fixed to MCAR

In Table 1, we present the results from the Friedman Rank test for each of the Missing Data imputation experiments. In this statistical test, we compare the relative rank of med.knn against the relative ranks of the comparator methods for each of the 25 random seeds. These results demonstrate that the med.knn method is consistently ranked higher than the others across each of the experiments.

Table 1 The Friedman rank test results for the imputation tasks varying the percentage of missing data from 10 to 50% MCAR, using either the MAE or RMSE metric for comparison

In Table 2, we present the results from the pairwise t-test for each of the experiments. In this statistical test, we evaluate the differences in MAE between med.knn and each of the comparison methods. In all of the experiments, we observe that the differences in MAE are statistically significant with p-values less than 0.001. In most cases, we observe that the relative improvement of med.knn decreases as the percentage of missing data increases. This is because the comparator methods perform similarly across all levels of missing data from 10-50%, while the med.knn performs best at the lowest missing percentages. One exception is mice on the PPMI dataset, which declines in performance rapidly as the percentage of missing data increases. Another exception is the bpca method, which surprisingly improves in performance as the percentage of missing data increases for the DFCI and PPMI datasets. One explanation for these results could be that bpca is overfitting on the datasets which have few missing values.

In the “Appendix”, we present the MedImpute hyperparameters which were selected in Missing Percentage experiments for the FHS dataset. In Table 15, we show the median halflife parameters that were selected for each covariate at each missing percentage. We observe that most of the halflife parameters are consistent across different levels of missing data, and for many of the covariates the highest halflife parameter of 1000 days was selected. This suggests that for these covariates, a measurement from 1000 days ago may be used to significantly inform the measurement for the same patient today. In addition, we may be able to improve the performance of this method by considering even longer halflife values. In Table 16, we show the median alpha parameters that were selected for each covariate at each missing percentage, from the validation. In all cases, the alpha parameter is at least 0.5, and in many cases equals 1. This suggests that for these covariates, the time series part of the objective function is more important for the imputation than the K-nearest neighbors part of the objective function. In addition, we observe that the alpha parameter selected generally decreases or remains the same as the percentage of missing data increases. This suggests that as the percentage of missing data increases, the time series part of the objective function should be weighted less heavily in the imputation because there is less time series information available for each observation in the dataset.

Table 2 Pairwise t-tests between med.knn and benchmark methods for imputation tasks varying the percentage of missing data from 10-50% MCAR, using the MAE metric for comparison

Number of observations per patient

In Fig. 3, we present the MAE imputation accuracy results from the experiments in which we vary the number of observations per patient. We present the exact values and standard errors in this plot in the Appendix in Table 11. Across all of the experiments, we observe that as the time horizon increases, the performance of med.knn generally improves. This is expected, because as the time horizon increases, we include more observations per patient in the dataset, so there is more time series information that can be leveraged during the imputation process.

Similarly, the imputation accuracy of the moving.avg method generally improves as the time horizon increases. One notable exception is in the FHS dataset, the MAE of the moving.avg method increases as the time horizon increases from 10 to 20 years, while the MAE of med.knn remains relatively constant. From this, we can deduce that past observations of patients in the FHS dataset from 10 to 20 years prior have little predictive power for the other imputed values, which causes simple time series methods such as moving.avg to perform worse with more data. In contrast, the med.knn method has an exponential halflife parameter that we can tune so that observations from 10+ years ago are weighted less heavily in the imputation, so the performance remains about the same with the additional data.

One surprising trend that we observe in these graphs is the performance of amelia, which is another imputation method that takes into account time series information. On the DFCI dataset, as the time horizon increases, the imputation error increases. In addition, on the FHS dataset, as time horizon increases, the imputation error remains about the same. Only in the PPMI dataset does the performance of amelia noticeably improve as the time horizon increases.

Fig. 3

Imputation errors for each method using the MAE metric on the FHS, DFCI, and PPMI datasets, varying the time horizon which determines the number of observations per patient. The missing data mechanism is fixed to MCAR, and the total percentage of missing data is fixed to 50%

In Fig. 4, we present the RMSE imputation accuracy results for the Observations Per Patient experiments. The results are similar to the MAE imputation accuracy results, and med.knn produces the imputation with the lowest RMSE across all experiments. One characteristic of the RMSE results is that they are much noisier, and in particular on the DFCI dataset the RMSE values do not decrease monotonically in a smooth fashion. Since the RMSE metric is more sensitive to outliers than the MAE metric, this suggests that there may be some outliers in the DFCI data which are added into the dataset at different time horizons.

Fig. 4

Imputation errors for each method using the RMSE metric on the FHS, DFCI, and PPMI datasets, varying the time horizon which determines the number of observations per patient. The missing data mechanism is fixed to MCAR, and the total percentage of missing data is fixed to 50%

In addition to evaluating the imputation accuracy of med.knn on datasets with varying numbers of observations per patient, we can also evaluate the imputation accuracy on subsets of patients within the DFCI dataset which have varying numbers of observations. In Fig. 5, we present the imputation errors for med.knn on the DFCI dataset with 30% MCAR missing data, for subgroups of patients which have $1,2,\ldots ,12$ observations per patient in the dataset. Overall, the MAE for the entire dataset is 3.331. For patients with one visit, and therefore one observation in the dataset, the average MAE is almost 3.5. In contrast, for patients with 10 or more visits, the average MAE is below 2.5. This suggests that in datasets with heterogeneous numbers of observations per patient, the med.knn imputation may be most accurate for the patients with the most observations in the dataset.

Fig. 5

Imputation errors for med.knn on the DFCI dataset with 30% MCAR missing data for subgroups of patients which have varying numbers of visits in the dataset

Overall, from the Observations Per Patient experiments, we can conclude that med.knn method performs best with the additional time series information. As the time horizon increases, the imputation accuracy of med.knn generally improves or remains the same, while in a few cases the other time series methods moving.avg and amelia perform significantly worse with additional time series data. In addition, the imputation accuracy of the methods which do not take into account time series information (bpca, mean, mice, opt.knn) remains relatively constant as the time horizon varies. Furthermore, within a dataset that has heterogeneous numbers of observations per patient, such as EHR datasets, we may expect med.knn to most accurately impute values for the patients with the most observations in the dataset.

In the “Appendix”, we present the MedImpute hyperparameters which were selected in Observations Per Patient experiments for the FHS dataset. First, in Table 17, we show the median halflife parameters that were selected for each covariate for each experiment. For OPP $\le 2$, the selection of the halflife parameter does not impact the imputation, so the halflife parameter is set to 1 for each covariate. For OPP $\ge 3$, the halflife parameters remain relatively constant for each covariate as the observations per patient varies. In Table 18, we show the median alpha parameters that were selected for each covariate. When the OPP $= 1$, there is no time series information in the dataset, so the alpha parameter is set to 0 for each covariate. For OPP $\ge 2$, the alpha parameters selected remain relatively constant for each covariate, with a few gradual trends for some of the covariates. For some covariates such as Age, Body Mass Index, and Systolic Blood Pressure, the selected alpha parameter gradually increases as OPP increases, and for other covariates such as Blood Glucose and High-Density Lipoproteins, the selected alpha parameter gradually decreases as OPP increases. This suggests that the addition of more time series data may change the med.knn imputation of each covariate differently.

Mechanism of missing data

In Fig. 6, we present the MAE imputation accuracy results from the experiments in which we vary the mechanism of missing data. We present the exact values and standard errors in this plot in the Appendix in Table 13. Across all of these experiments, we observe that med.knn has the best average MAE values by a significant margin.

In general, the imputation accuracy of all of the imputation methods increases or remains the same as the proportion of MNAR data increases. Two exceptions are the moving.avg method on the FHS dataset and the amelia method on the DFCI experiments, which both improve in performance at first as a small proportion of MNAR data is added. One possible explanation for this is that the MNAR data acts as a regularizer which helps these methods avoids overfitting to the dataset. However, in most cases the imputation error increases or remains constant as the percentage of MNAR data increases.

In the FHS MNAR experiments, the performance of all of the methods remains relatively constant, however the imputation error of moving.avg improves at $\gamma = 0.1$. Because moving.avg is the second-best performing method in these experiments, this means that the edge of the med.knn method slightly decreases in these experiments. In the PPMI MNAR experiments, the imputation error of all methods increases approximately linearly as the proportion of MNAR data increases. In the DFCI MNAR experiments, the imputation error for all methods except for amelia increases sharply at $\gamma = 0.1$, and then increases linearly afterwards as $\gamma$ increases. As a result, for the experiments on the DFCI and PPMI datasets, the absolute improvement of med.knn over the comparator methods remains about the same as the proportion of MNAR data increases.

Fig. 6

Imputation errors for each method using the MAE metric on the FHS, DFCI, and PPMI datasets, varying the ratio of the missing data mechanism from $\gamma = 0$ (30% MCAR, 0% MNAR) to $\gamma = 1$ (0% MCAR, 30% MNAR). The total percentage of missing data is fixed to 30%

In Fig. 7, we present the RMSE imputation accuracy results for the missing data mechanism experiments. The results are largely consistent with the MAE imputation accuracy results. In particular, med.knn produces the imputation with the lowest RMSE by a significant margin across all experiments.

Fig. 7

Imputation errors for each method using the RMSE metric on the FHS, DFCI, and PPMI datasets, varying the ratio of the missing data mechanism from $\gamma = 0$ (30% MCAR, 0% MNAR) to $\gamma = 1$ (0% MCAR, 30% MNAR). The total percentage of missing data is fixed to 30%

Overall, these experiments demonstrate that the med.knn method performs well relative to the other imputation methods even as the mechanism of missing data changes. In the MNAR experiments for the longitudinal datasets, FHS and PPMI, the relative imputation accuracy of the comparator methods remains approximately the same with the med.knn method performing best, with the exception of the moving.avg method which performs significantly worse. Thus, we can conclude that the med.knn method is well suited for imputing missing values according to the particular MNAR mechanism designed for longitudinal datasets which is described in Sect. 3.2.1. In the MNAR experiments for the EHR dataset DFCI, the relative imputation accuracy of the comparator methods remains approximately the same with the med.knn method performing best, with the exception of the amelia method which performs significantly better. Therefore, we can also conclude that the med.knn is suitable for imputing missing values according to the MNAR mechanism for EHR datasets which is described in Sect. 3.2.2.

In the “Appendix”, we present the MedImpute hyperparameters which were selected in Mechanism of Missing Data experiments for the FHS dataset. In Tables 19 and 20, we show the median halflife and alpha parameters that were selected for each covariate for each experiment, respectively. Across all of the experiments, we observe that the parameters selected during the validation procedure remain almost exactly constant. We conclude that varying the missing data mechanism for the FHS dataset according to the approach outlined in Sect. 3.2.1 has little impact on the med.knn imputation for this dataset.

3.5 Prediction results

In this section, we provide the results from all experiments on the downstream prediction tasks. In particular, we present the downstream prediction results from the 1) Percentage of Missing Data, 2) Number of Observations Per Patient, and 3) Mechanism of Missing Data experiments. For the FHS and DFCI datasets, in which we train and evaluate classification models, we report the average out-of-sample AUC results. For the PPMI dataset, in which we train and evaluate regression models, we report the average out-of-sample MAE results.

Percentage of missing data

In Fig. 6, we present the performance on the downstream tasks from the experiments in which we vary the percentage of missing data. We present the exact values and standard errors in this plot in the Appendix in Table 10. Across all of the datasets, the med.knn method performs best, and the downstream performance of all methods generally declines as the missing level increases. In particular, the AUC values generally decrease for the classification tasks and the MAE values generally increase for the regression tasks as the percentage of missing data increases.

For the FHS dataset, while the downstream performance of all methods declines as the percentage of missing data increases, the downstream performance of med.knn declines least rapidly. In particular, with $20\%$ missing data, the downstream AUC of med.knn is 0.897, compared to downstream AUC of 0.861 from the second-best method bpca and the baseline AUC of 0.901 with no additional missing data. With $50\%$ missing data, the downstream AUC of med.knn is 0.864, compared to 0.826 for the second-best method moving.avg.

Similarly, for the DFCI dataset, the med.knn method performs best across all levels of missing data, and the downstream AUC values generally decrease as the missing level increases. The only exception is for the amelia method, where we do not observe a smooth trend because this method does not converge in some cases. In addition, the relative improvement of med.knn compared to the other imputation methods is lower for this dataset. At $50\%$ missing data, the downstream AUC of med.knn is 0.889, compared to 0.884 for the second-best method bpca and the baseline AUC of 0.92 with no additional missing data.

Lastly, in the PPMI dataset, we observe the same trends that the med.knn method performs best, and the performance of all methods declines as the missing level increases. In this case, the downstream MAE for each method increases as the percentage of missing data increases. Across all levels of missing data, med.knn achieves the lowest downstream MAE. At $50\%$ missing data, the downstream MAE of med.knn is 1.917, compared to 2.092 for the second-best method opt.knn and the baseline MAE of 1.170 with no additional missing data.

Fig. 8

Downstream accuracy results for each method on the FHS, DFCI, and PPMI datasets, varying the percentage of missing data from 10 to 50% according to the MCAR mechanism. On each plot, we overlay the downstream accuracy of a baseline model trained with no additional missing data as a dotted blue line (shaded with standard error bars)

In Table 3, we present the results from the Friedman Rank tests for each of the downstream predictive tasks varying the percentage of missing data. Similar to Friedman Rank tests for the imputation tasks, each test is significant with a p-value less than 0.001. These results demonstrate that the med.knn method is consistently ranked higher than the others for each of the downstream predictive tasks.

Table 3 The Friedman Rank test results for the downstream predictive tasks varying the percentage of missing data from 10 to 50% MCAR

In Table 4, we present the results from the pairwise t-tests for each of the experiments. In this statistical test, we evaluate the differences in downstream predictive performance between med.knn and each of the comparison methods. We consider the differences in downstream AUC for the classification tasks, and we consider the differences in downstream MAE for the regression tasks. In most of the experiments, we observe that the differences in downstream AUC/MAE are statistically significant with p-values less than 0.001. These results demonstrate that the relative improvement in imputation accuracy for the med.knn method carries over to a relative improvement in performance on the downstream predictive tasks with different levels of MCAR data. Between the two classification tasks, we observe that the med.knn gives larger improvements in AUC on the FHS dataset than the DFCI dataset. In addition, we observe that as the percentage of missing data increases, the relative improvement of med.knn increases in general. These results are expected because as the percentage of missing data increases, the impact of the imputation method on the training data and the final prediction task increases as well. Since med.knn provides substantial improvements in imputation accuracy for all levels of missing data, having larger amounts of missing data generally leads to larger gains in downstream predictive accuracy. There are a few exceptions to this, for example amelia, bpca, mean, and opt.knn on the PPMI dataset, and moving.avg on the DFCI dataset. In these cases, the largest improvement for med.knn occurs at the 10% missing level. For these several examples, it follows that med.knn does a much better job at simulating the training dataset with 10% missing data, but the other methods begin to catch up as the percentage of missing data increases.

Table 4 Pairwise t-tests between med.knn and benchmark methods for imputation tasks varying the percentage of missing data from 10 to 50% MCAR

Number of observations per patient

In Fig. 9, we present the performance on the downstream tasks from the experiments in which we vary the time horizon which determines the number of observations per patient. We present the exact values and standard errors in this plot in the Appendix in Table 12. Across all of the experiments, we observe that the downstream performance of med.knn tends to improve as the time horizon increases, so that the dataset includes more observations per patient. However, for each dataset, after a certain point there are diminishing returns, so that adding more observations per patient to the dataset does not improve the performance on the downstream task.

For the FHS dataset, in which the task is to predict 10-year risk of stroke, the downstream AUC of med.knn plateau starts to plateau at a time horizon of 6 years. For the DFCI dataset, in which the task is to predict 60-day risk of mortality, the downstream AUC of med.knn starts to plateau around 3 years. Similarly, for the PPMI dataset, in which the task is to predict the next year MoCA score, the downstream MAE reaches a minimum value at 3 years.

In comparison to the other methods, we observe that med.knn tends to perform relatively better with more observations per patient in the dataset. This indicates that the med.knn method is able to leverage the additional time series information more efficiently than the other methods. The only exception to this is amelia on the DFCI dataset, which outperforms med.knn with time horizons of 3 and 5 years, respectively. However, we observe that the amelia method is more unstable, and med.knn outperforms this method for the longest time horizon of 10 years.

Fig. 9

Downstream accuracy results for each method on the FHS, DFCI, and PPMI datasets, varying the time horizon which determines the number of observations per patient. In these experiments, the missing data mechanism is fixed to MCAR, and the total percentage of missing data is fixed to 50%. On each plot, we overlay the downstream accuracy of a baseline model trained with no additional missing data as a dotted blue line (shaded with standard error bars) (Color figure online)

Mechanism of missing data

In Fig. 10, we present the performance on the downstream tasks from the experiments in which we vary the mechanism of missing data. We present the exact values and standard errors in this plot in the Appendix in Table 14. In all of the experiments, we observe that the med.knn acheives the best downstream accuracy, typically by a substantial margin.

In the FHS dataset, the average AUC for med.knn remains around 0.89 and above across all proportions of MNAR data, while the second-best performing method moving.avg has an average AUC below 0.87. In the PPMI dataset, the downstream MAE values for all of the methods increases approximately linearly as the ratio of MNAR data increases. As a result, the relative improvement of med.knn on downstream tasks remains large for all of the MNAR experiments on longitudinal datasets.

On the other hand, the relative improvement of med.knn on downstream tasks is more varied for the MNAR experiments on EHR data. In the DFCI dataset, the downstream AUC values for each of the methods increases significantly when gamma = 0.1, and then decreases gradually as gamma increases further. These results are somewhat counterintuitive because the imputation errors for most of these methods increase significantly at gamma = 0.1, and then increase gradually afterwards. One possible explanation is that the DFCI dataset has some outlier values that tend to be missing under the MNAR mechanism for electronic health record data (described in Sect. 3.2.2), which typically skew the downstream prediction results. At the peak when gamma = 0.1, the relative improvement of med.knn is very small, with a downstream AUC of 0.916 compared to the next best method mice which has a downstream AUC of 0.915. At the extreme when gamma = 1, the downstream AUC of med.knn is 0.912 compared to 0.904 for the next best methods (mice and bpca).

Fig. 10

Downstream accuracy results for each method on the FHS, DFCI, and PPMI datasets, varying the ratio of the missing data mechanism from $\gamma = 0$ (30% MCAR, 0% MNAR) to $\gamma = 1$ (0% MCAR, 30% MNAR). On each plot, we overlay the downstream accuracy of a baseline model trained with no additional missing data as a dotted blue line (shaded with standard error bars) (Color figure online)

3.6 Discussion of the computational experiments on real-world clinical datasets

In this section, we discuss the major takeaways from the computational experiments on real-world clinical datasets. For each dataset, we consider downstream models to predict patient outcomes that are clinically relevant, in order to simulate the performance of med.knn in practical applications. For the FHS and PPMI datasets, which are longitudinal studies, the clinical outcomes of interest are 10-year risk of stroke and next year MoCA score, which can be predicted using the most recent observation for each patient. For the DFCI dataset, which is an EHR dataset, the clinical outcome of interest is 60-day risk of mortality for late-stage cancer patients, which requires us to train models using all of the observations from each patient (using the latest observation for each patient would bias the results). As a result, the evaluation of the downstream models is different between the datasets. Furthermore, we conduct non-identical experiments on each dataset due to inherent dissimilarities in the time series structure.

Due to the significant differences between each dataset, we can draw separate conclusions from each one as a separate case study. The FHS dataset is a long term longitudinal study with many patients, few covariates, and a downstream classification task. In contrast, the PPMI dataset is a shorter longitudinal study with fewer patients, more covariates, and a downstream regression task. Finally, the DFCI dataset is an EHR dataset with irregularly recorded observations, the most patients, the most covariates, and a downstream classification task. The results from the computational experiments demonstrate that med.knn performs well across this range of diverse case studies. In particular, we show that this method performs well on datasets with: (1) large or small numbers of patients, (2) large or small numbers of covariates, and (3) regularly or irregularly recorded observations. Moreover, the application of med.knn for imputation led to improved downstream predictive performance on two binary classification tasks and one regression task.

Prior to training the downstream models, we do not perform any further preprocessing on the imputed data, so we preserve the correlation structure of the original dataset. As a result, since these are real-world datasets, there may be unexpected correlations between the predictors which impact the accuracy of the downstream models. One could apply PCA or another dimensionality-reduction method to transform the feature space prior to training downstream models on the imputed datasets. However, this analysis is outside of the scope of this set of computational experiments.

In the Percentage of Missing Data experiments, we observe that increased imputation accuracy does not always translate into increased downstream model accuracy. For example, on the DFCI dataset, bpca performs poorly on the imputation task (see Fig. 1), but is one of the top-performing methods on the downstream predictive task (see Fig. 8). This is possible because in the downstream predictive task, some features are more significant than others, so having a large imputation error on the insignificant features may only result in a small decline in downstream model accuracy. However, we also observed that in all datasets, med.knn consistently performed best on both the imputation and downstream tasks, by a significant margin in most cases. These results suggest that for all three of the real-world datasets considered here, med.knn leads to improvements in imputation accuracy on the clinically significant covariates in each downstream model.

In the OPP experiments, the major trend that we observe is that the med.knn method performs significantly better with more time series data. For example, in the FHS dataset, the imputation accuracy and downstream performance of med.knn improves dramatically as OPP increases from one to four. This makes sense because as we include more observations per patient in the dataset, there is more relevant information available to impute the missing covariates for each patient. We expect that this explains why the relative improvement of med.knn is less significant on the DFCI dataset for several of the experiments. In this dataset, over half of the patients have a single observation, so there is limited time series available to fill in the missing values for these patients. In contrast, in the FHS dataset, every patient has 10 observations in the full dataset, so there is more data available to aid the imputation.

In the MNAR experiments, we demonstrate that med.knn works under missing data mechanisms that are frequently encountered in practice. Longitudinal studies often contain systematic missing information on some clinical examinations based on decisions made by the designers of the study. For example, the Framingham Heart Study dataset has expanded over time as clinicians have incorporated more and more variables that are suspected to be correlated with heart disease (Mahmood et al. 2014). However, since some of these variables were not recorded initially, they are systematically missing from this dataset. In EHR datasets, clinical covariates recorded for each visit typically vary based the health condition of the patient. Patients at higher risk are likely to undergo more detailed medical examinations, resulting in fewer missing values. Through the MNAR experiments for each case study, we show that med.knn is an effective method for imputing missing values under these specific mechanisms of missing data for longitudinal studies and EHR datasets.

4 Scaling experiments on simulated clinical datasets

In this section, we present scaling experiments on simulated clinical datasets. In Sect. 4.1, we describe the data generation process which allows us to construct simulated longitudinal clinical datasets with 10,000’s of observations and 100’s of features. In Sect. 4.2, we describe the experimental setup of the scaling experiments, which considers two variations of the med.knn method. In Sect. 4.3, we report the results of the scaling experiments, including the imputation accuracy and timing results.

4.1 Simulated data: Synthea

We create synthetic EHR to test the performance of the algorithm in higher instances of both the number of observations and the number of features using the Synthea synthetic patient population simulator. It constitutes an open-source, synthetic patient generator that aims to model the medical history of patients using specific demographic information (Walonoski et al. 2018). Patient records are generated using simulation processes that follow disease progression patterns published in the medical literature. For each synthetic patient, Synthea data contains a complete medical history, including medications, allergies, medical encounters, and social determinants of health. We pre-processed the records combining them into a single dataset that contains a summary of all the information available at each visit.

Since we leverage this data source for experiments testing the scalability of the algorithm, we do not limit the amount of observations to a specific number. Each patient in the data is associated on average with 20 distinct visits (observations). We aggregate the EHR into 344 distinct features. Each experiment randomly samples a subset of these features to compare the computational time needed by the algorithm. The covariates that comprise the data include demographic characteristics, diagnosis and procedure codes, medical prescriptions, and lab test results. We do not include any downstream prediction task.

4.2 Experimental setup for the scaling experiments

In this section, we go over the experimental setup for the scaling experiments. We use synthetically generated data for EHR varying both the number of observations n and the number of features p. Our goal is to evaluate the scaling performance and accuracy of the algorithm comparing the two proposed methods for tuning the hyperparameters $\alpha _d$ and $h_d$.

One of the most well-established approach for hyperparameter tuning in machine learning is K-fold cross-validation (Kohavi et al. 1995). In the time series setting, Bergmeir et al. (2018) showed that this technique is applicable for time series models, in particular for the case of autoregression models. However, due to the large number of combinations of different values for $\alpha _d$ and $h_d$, in the case of med.knn, the computation time for the K-fold cross-validation scales at an quadratic rate as the number of covariates increases. For this reason, we propose a custom tuning procedure to select the hyperparameters. We conduct a series of experiments comparing the following hyperparameter selection processes:

• 1. Grid search This approach uses the well-established ten-fold cross-validation process to determine the hyperparameters $h_d$ and $\alpha _d$ for every variable. Prior to solving the algorithm, 10% of the values of each feature are artificially removed. A set of values is defined and all their combinations are evaluated for each feature individually when solving the reduced version of the dataset. The grid for $\alpha _d$ was set to $[0.0, 0.1,\ldots ,1.0]$ and for $h_d$ to [90, 180, 365, 1000].

• 2. Custom tuning The custom tuning procedure proposed in Sect. 2.4. This is a heuristic method to decompose the problem into multiple parts, first learning $h_d$ for each covariate, and then learning $\alpha _d$ for each covariate. This approach does not involve cross-validation and allows for parallel computations as the problem is fully decoupled.

For each experiment, we evaluate the imputation accuracy of each approach using the MAE and RMSE metrics, as defined in Equations 30 and 31. In addition, we also compare their scaling performance by measuring the average time needed for completion. In these experiments, we did not consider the prediction task as in Sect. 3. Here, we limit the types of experiments only to Percentage of Missing Data following the experimental set up of Sect. 3.3.

We vary the number of features between [50, 100, 200, 300] and the number of observations between [1000, 12, 500, 25, 000, 50, 000, 75, 000]. These bounds were chosen as they represent the most common spectra of problem sizes that we encounter in healthcare applications. We repeat all experiments for five random seeds and average the results.

4.3 Results of the scaling experiments

In this section, we present the results from the scaling experiments. In Fig. 11, we demonstrate the timing results. While both the methods scale to the largest problem size with $n = 75{,}000$ observations and $p = 300$ features, the Custom Tuning procedure is − 60.42% faster than Grid Search; the traditional cross-validation procedure. Across all experiments, Custom Tuning is on average − 87.05% faster than Grid Search. We notice that for the lower problem sizes, the Custom Tuning approach leads almost instantaneous algorithm completion while Gridsearch requires up to 12 h to solve.

Fig. 11

Average time for MedImpute methods to complete imputation tasks on the Synthea dataset using different procedures for hyperparameter tuning, with varying numbers of observations n and features p in the dataset

Figure 12 presents the results referring to imputation accuracy. The two procedures lead to minimal differences in imputation performance. Across all experiments, the Custom Tuning procedure is slightly more accurate than the GridSearch procedure, with an average improvement of − 4.36% in MAE. The gap between the two processes is larger when $n \in [25{,}000, 50{,}000]$ leading to an average reduction of − 8.81% of the imputation error. We also note that only when $n=1000$, GridSearch as the MAE is increased on average by 2.82% by the new method. In all other combinations, Custom Tuning leads to more accurate results with the maximum improvement reaching a reduction of 10.48% ($n=50{,}000$, $p=100$). Detailed results for the RMSE metric are provided in Fig. 14 at the “Appendix”.

Fig. 12

Average MAE imputation errors for MedImpute methods on the Synthea dataset using different procedures for hyperparameter tuning, with varying numbers of observations n and features p in the dataset

4.4 Discussion of the scaling experiments on simulated clinical datasets

The results from the scaling experiments demonstrate that the custom tuning procedure for the MedImpute hyperparameters $\alpha _d$ and $h_d$ is highly effective and efficient. In particular, the proposed method significantly reduces the computational time required, while also giving a slight improvement in imputation accuracy as well compared to traditional cross-validation. Using the methodology, we are able to scale the algorithm to higher problem instances without sacrificing its imputation performance.

An analysis of the runtime complexity of the two hyperparameter selection methods provides further insights into these results. The key bottleneck of the med.knn algorithm is computing the K-NN assignment on $\mathbf {X}$ to update $\mathbf {Z}$ in each coordinate descent step, which requires ${\mathcal {O}}(n \log n)$ operations. The Grid Search procedure requires ${\mathcal {O}}(p^2)$ iterations to identify the best values for $\alpha _d$ and $h_d$, so the complete runtime for this method is ${\mathcal {O}}(n p^2 \log n)$. On the other hand, the Custom tuning procedure only requires ${\mathcal {O}}(p)$ iterations because each hyperparameter for each covariate can be computed independently of the remaining covariates. As a result, this method scales in a linear fashion with respect to the number of covariates, and the full runtime is ${\mathcal {O}}(n p \log n)$.

Despite these theoretical asymptotic runtime guarantees, we recognize that the med.knn method with the Custom Tuning procedure for hyperparameter tuning still takes up to 16 h in datasets with $n\sim$ 50,000 observations. However, given that the imputation task usually takes place once in the pre-processing part of the data analysis, we believe that the time cost is not significantly high. Moreover, the Custom tuning process allows for decoupling the problem in smaller instances. Thus, the application of parallel computing techniques can further improve the scaling performance of the algorithm.

5 Discussion

MedImpute is an extension of the OptImpute framework introduced by Bertsimas et al. (2018b). MedImpute uses the same optimization approach to solving the missing data problem. However, the optimization formulation is significantly different and more general than the OptImpute formulations in order to incorporate additional time series information present in cross-sectional data. The new formulation provides a structured way of accounting for observations from the same entity and re-weighting the objective function to incorporate time series information. As a result, the resulting imputation algorithm med.knn from the MedImpute framework outperforms opt.knn from the OptImpute framework and other benchmark imputation methods on real-world clinical datasets with patients observed over time.

In the MedImpute formulation, two new parameters are introduced, $\alpha _d, h_d$, that are specific to each covariate d. The proposed Custom Tuning procedure allows for learning the values of these parameters more efficiently compared to a traditional Grid Search approach. In addition, these parameters are interpretable in a clinical context, yielding insights regarding the significance of time in their determination. For example, in the FHS dataset, we learn different values of $\alpha _d$ for chronic disease indicators such as Type 2 Diabetes Mellitus (T2DM) and lab values such as Systolic Blood Pressure (SBP). It is likely that an individual diagnosed with T2DM will continue to have this diagnosis regardless of the other covariates (American 2010), so MedImpute finds $\alpha _{\text {d}}$ relatively close to 1 for this feature. On the other hand, the lab measurement of SBP may vary significantly during a single day (Millar-Craig et al. 1978), so previous observations of this covariate from the same individual provide relatively less information. For this feature, MedImpute finds $\alpha _d$ closer to 0 so that the K-nearest neighbors are weighted more heavily in the imputation. In addition, we learn $h_d$ to determine the relative weights that we give to observations of feature d from the same individual based on time elapsed. MedImpute selects higher values of $h_d$ for features that change slowly over time such as the Body Mass Index and lower values for features that change rapidly over time such as SBP.

Beyond the healthcare setting, cross-sectional datasets are also quite common in other areas such as finance and economics. Our algorithm can be generalized and applied to any data where there is a time series component and multiple observations are tied to the same entity. The entity may represent a patient, as we portray in this work, or something else that is observed over time such as a financial organization, region, or country. Therefore, the MedImpute imputation framework and the associated med.knn algorithm may be applied to impute missing values in other domains as well.

6 Conclusions

In this paper, we propose the optimization framework MedImpute that addresses the missing data problem for multivariate data in time series encountered in medical applications. We introduce a new imputation algorithm med.knn that yields high quality solutions using optimization techniques combined with fast first-order methods. Through computational experiments on three real-world clinical datasets, including two longitudinal studies and one EHR dataset, we show that med.knn offers statistically significant gains in imputation quality over state-of-the-art imputation methods, which leads to improved out-of-sample performance on downstream tasks. Through scaling experiments on a synthetic EHR dataset, we demonstrate that med.knn can be applied to complete datasets with 10,000’s of observations and 100’s of features. As a flexible, accurate, and intuitive approach, MedImpute has the potential to become an indispensable tool for applications with longitudinal missing data. Promising areas for future work include: (1) applications of this method to longitudinal datasets that are not related to healthcare, (2) additional experiments to assess the performance on downstream predictive tasks with transformed feature spaces, (3) extensions of the optimization framework to incorporate more specialized structure that is present in longitudinal healthcare datasets.

Appendix

1.1 Detailed properties of real-world clinical datasets

In this section, we provide additional details regarding the real-world clinical datasets which are used in the computational experiments. In Tables 5, 7, and 6, we show the percentage of missing data in each covariate for the FHS, PPMI, and the DFCI datasets, respectively. In Fig. 13, we show a histogram of the number of observations per patient in the DFCI dataset. Table 8 shows summary statistics of inter-visit time intervals (in days) for the DFCI dataset.

Table 5 Percentage of missing data in each covariate in the original FHS dataset

Table 6 Percentage of missing data in each covariate in the original DFCI dataset

Table 7 Percentage of missing data in each covariate in the original PPMI dataset

Fig. 13

Histogram of the number of observations per patient in the DFCI dataset

Table 8 Summary statistics of inter-visit time intervals (in days) for the DFCI dataset, where $t_i$ is the time of visit i and $t_1$ corresponds to the most recent visit for each patient

1.2 Supplemental experimental results

This section provides detailed results from the computational experiments on the real-world datasets. Each table refers to either the imputation accuracy or downstream predictive performance for all FHS, DFCI, and PPMI. Tables 9 and 10 refer to the MCAR experiments when we vary the percentage of missing data from 10 to 50%. Tables 11 and 12 show the performance of all methods when we vary the number of observations per patient. Tables 13 and 14 focus on the experiments where we vary the ratio of the missing data mechanism from $\gamma = 0$ (30% MCAR, 0% MNAR) to $\gamma = 1$ (0% MCAR, 30% MNAR).

Table 9 Imputation errors for each method using the MAE metric on the FHS, DFCI, and PPMI datasets, varying the percentage of missing data from 10 to 50%.

Table 10 Downstream accuracy results for each method on the FHS, DFCI, and PPMI datasets, varying the percentage of missing data from 10 to 50% according to the MCAR mechanism. For an illustration, see Fig. 8

Table 11 Imputation errors for each method using the MAE metric on the FHS, DFCI, and PPMI datasets, varying the time horizon which determines the number of observations per patient

Table 12 Downstream accuracy results for each method on the FHS, DFCI, and PPMI datasets, varying the time horizon which determines the number of observations per patient

Table 13 Imputation errors for each method on the FHS, DFCI, and PPMI datasets, varying the ratio of the missing data mechanism from $\gamma = 0$ (30% MCAR, 0% MNAR) to $\gamma = 1$ (0% MCAR, 30% MNAR)

Table 14 Downstream accuracy results for each method on the FHS, DFCI, and PPMI datasets, varying the ratio of the missing data mechanism from $\gamma = 0$ (30% MCAR, 0% MNAR) to $\gamma = 1$ (0% MCAR, 30% MNAR)

1.3 Medimpute hyperparameter tuning results for FHS experiments

In this section, we present the MedImpute hyperparameters which were selected for the FHS experiments. These hyperparameters were tuned via the custom procedure described in Sect. 2.4. The covariates in the FHS dataset are:

• 1. Afib Boolean whether or not the patient has a diagnosis of Atrial Fibrillation.

• 2. Age Age of the patient (in years).

• 3. AHT Boolean whether or not the patient has a diagnosis of Arterial Hypertension.

• 4. BMI Body mass index of the patient.

• 5. CVD Boolean whether or not the patient has a diagnosis of cardiovascular disease.

• 6. Diabetes Boolean whether or not the patient has a diagnosis of Diabetes.

• 7. Gender Gender of the patient.

• 8. Glucose_bl Blood glucose level of the patient.

• 9. HDL High-density lipoproteins level of the patient.

• 10. LVH Boolean whether or not the patient has a diagnosis of left ventricular hypertrophy.

• 11. SBP Systolic blood pressure of the patient.

• 12. Smoking Categorical variable describing the smoking behavior of the patient.

Table 15 Median halflife parameter selected for each covariate in the FHS dataset in the MCAR missing percentage experiments with 10 observations per patient

Table 16 Median alpha parameter selected for each covariate in the FHS dataset in the MCAR Missing Percentage experiments with 10 observations per patient

Table 17 Median halflife parameter selected for each covariate in the FHS dataset in the MCAR OPP experiments with 50% missing data

Table 18 Median alpha parameter selected for each covariate in the FHS dataset in the MCAR OPP experiments with 50% missing data

Table 19 Median halflife parameter selected for each covariate in the FHS dataset in the MNAR experiments with 50% missing data and 10 observations per patient

Table 20 Median alpha parameter selected for each covariate in the FHS dataset in the MNAR experiments with 50% missing data and 10 observations per patient

1.4 Supplemental synthetic experiments results

Figure 14 provides a direct comparison between the Custom Tuning and Grid Search parameter selection processes. We provide results with respect to the imputation error using the RMSE metric.

Fig. 14

Average RMSE imputation errors for MedImpute methods on the Synthea dataset using different procedures for hyperparameter tuning, with varying numbers of observations n and features p in the dataset

1.5 Nemenyi critical diagrams

In this section, we show Nemenyi Critical Diagrams (Ismail Fawaz et al. 2019) for the results from the Percentage of Missing Data experiments which are presented in Sect. 3. These graphs highlight statistically significant differences in the overall rankings of the methods. To generate these diagrams, first the Friedman Rank Test was performed to compare the relative performance of the different imputation methods in each experiment. Second, the Wilcoxon-Holm method was performed to detect pairwise significance. In the diagram for a single experiment, each imputation method is plotted according to its average relative rank on a number line from one to seven. Methods which do not have statistically significant differences in their overall rankings are joined by a horizontal line.

In Figs. 15 and 16, we show the Nemenyi Critical Diagrams comparing the methods on the imputation tasks under the MAE and RMSE metrics, respectively. For the FHS and PPMI datasets, we observe that med.knn is consistently the top ranked method across all of the experiments. For the DFCI dataset, med.knn is consistently top ranked method under the MAE metric, however med.knn outperforms the benchmark methods by a smaller margin under the RMSE metric.

In Fig. 17, we show the Nemenyi Critical Diagrams comparing the methods on the downstream predictive tasks. Our results demonstrate the edge of the proposed algorithm over the other missing data imputation methods considered. The performance gap is wider in the longitudinal datasets (FHS, PPMI) compared to the DFCI dataset. Nevertheless, even in the latter case, we notice that med.knn improves upon the other best performing methods (mean and bpca).

Fig. 15

Nemenyi critical diagrams comparing the relative ranking of all methods on the imputation tasks varying the percentage of missing data with respect to the MAE metric. Diagrams are shown for the FHS, DFCI, and PPMI datasets (right to left) and varying levels of missing data from 10 to 50% (top to bottom). In each diagram, imputation methods are plotted according to their average relative rankings on a number line from one to seven. Methods which do not have statistically significant differences in their overall rankings are joined by a horizontal line

Fig. 16

Nemenyi Critical Diagrams comparing the relative ranking of all methods on the imputation tasks varying the percentage of missing data with respect to the RMSE metric. Diagrams are shown for the FHS, DFCI, and PPMI datasets (right to left) and varying levels of missing data from 10 to 50% (top to bottom). In each diagram, imputation methods are plotted according to their average relative rankings on a number line from one to seven. Methods which do not have statistically significant differences in their overall rankings are joined by a horizontal line

Fig. 17

Nemenyi Critical Diagrams comparing the relative ranking of all methods on the downstream predictive tasks varying the percentage of missing data. For the FHS and DFCI datasets, rankings are based upon the out-of-sample AUC metric, and for the PPMI dataset, rankings are based upon the out-of-sample MAE metric. Diagrams are shown for the FHS, DFCI, and PPMI datasets (right to left) and varying levels of missing data from 10 to 50% (top to bottom). In each diagram, imputation methods are plotted according to their average relative rankings on a number line from one to seven. Methods which do not have statistically significant differences in their overall rankings are joined by a horizontal line

1.6 Additional statistical significance tests for the percentage of missing data experiments

In this section, we present the results from statistical tests comparing the performance of the med.knn method at different levels of missing data. In particular, we run Welch two-sided t-tests evaluating whether med.knn leads to higher imputation error and lower downstream model accuracy as we increase the percentage of missing data. We run statistical tests for the following pairs of missing percentages: 10% versus 20%, 20% versus 30%, 30% versus 40%, and 40% versus 50%.

The results from the t-tests comparing the imputation errors are summarized in Table 21. We observe that in all of the experiments, the imputation error significantly increases going from 40 to 50% missing values. Similarly, the imputation error significantly increases going from 30 to 40% missing values with the exception of the DFCI dataset. For the MAE metric, most of the differences are not significant for percentage shifts below 30%. On the other hand, most of the differences for the percentage shifts below 30% are significant for the RMSE metric, with the exception of two cases where the opposite trend is observed.

Table 21 Results from Welch two-sided t-tests comparing the imputation error of the med.knn algorithm for varying pairs of missing percentages under the MCAR missing data mechanism

The results from the t-tests comparing the downstream model performance are summarized in Table 22. In all but one case, we observe that the downstream model performance significantly declines as the percentage of missing data increases.

Table 22 Results from Welch two-sided t-tests comparing the downstream model accuracy of the med.knn algorithm for varying pairs of missing percentages under the MCAR missing data mechanism