Introduction

In comparison with silicate or borate glasses, phosphate glasses possess interesting functional properties, mainly the higher refractive indexes, the lower melting temperature, and thermal expansion coefficients, and high transparency in the ultraviolet range [1, 2]. On the other hand, phosphate glasses have poor chemical durability. The chemical durability and additional properties of phosphate glasses can be improved by the addition of various metal ions into the phosphate network [3, 4]. Due to this compositional variability, phosphate glasses can be used for metal sealing applications, photonics, radioactive waste vitrification, medical applications, etc. [5,6,7].

The SVTDM enables the interpretation of the relationships between the composition, structure, and properties [8,9,10,11,12,13,14,15]. The validity of the model has to be confirmed by the comparison of its results with the available structural data [13,14,15,16]. In our previous work [16,17,18,19], we showed that the statistical analysis of the compositional and temperature series of Raman spectra validated the SVTDM thermodynamic model for the Na2O–B2O3, CaO–P2O5, and ZnO–P2O5 binary glass systems. The main aim of this work is to produce a thermodynamic model to describe the structure for the BaO–P2O5 binary glasses.

Method

Thermodynamic model of Shakhmatkin and Vedishcheva

SVTDM was successfully applied to the study of silicate glasses [8,9,10,11,12,13,14,15,16]. This model uses the assumption that glasses and melts are ideal solutions formed from products of equilibrium chemical reactions between the simple chemical entities (oxides, halogenides, etc.) and from the original un-reacted entities. The model only uses the molar Gibbs energies of pure crystalline compounds and the analytical composition of the system that is being considered. The equilibrium molar amount of each of the systems species is obtained by minimization of the system’s Gibbs energy constrained by the overall system composition [20]. SVTDM can be applied to most multicomponent glasses using crystalline state data. The contemporary databases of thermodynamic properties (e.g., FACT database [21, 22]) enable the routine construction of the SVTDM for various multicomponent systems.

Malfait’s decomposition of Raman spectra

The basic assumption of Malfait’s method [23,24,25] is that the Raman spectra can be expressed as the sum of partial Raman spectra (PRS) of individual system components multiplied by its equilibrium amount. The linear vector space with the dimensionality given by the number of species with different PRS that independently vary their abundance is spanned by the Raman spectra obtained for series of glasses with different compositions. Arbitrary scaling is used when recording each experimental spectrum. The number of independent components can be determined by principal component analysis (PCA) of the set of experimental Raman spectra [26, 27]. It is worth noting that the field of thermal analysis finds the PCA to be very advantageous [28].

Multivariate curve resolution

The set of experimental Raman spectra can be decomposed by the multivariate curve resolution (MCR) method [29, 30] on the spectra of quasi-pure components (loadings) and relative abundances of these components (scores). The comparison of MCR with PRS of Malfait’s decomposition based on the SVTDM can be used for confirmation/validation of SVTDM.

Experimental

The compositional series of binary barium phosphate glasses containing 30, 35, 40, 45, and 50 mol% of BaO, abbreviated as 70P30B, 65P35B, 60P40B, 55P45B, and 50P50B were studied. The glass batches were prepared from analytical grade ammonium dihydrogen phosphate (NH4H2PO4) and barium carbonate (BaCO3). Stoichiometric quantities of BaCO3 and NH4H2PO4 were placed into an alumina crucible after being mixed in an agate mortar. In order to remove the water, ammonia, and carbon dioxide, the sample was slowly heated to 700 °C in an electrical furnace. Subsequently, the calcination products were melted at the temperature range of 1100–1200 °C, depending on their chemical composition. The resulting melt was poured onto a preheated (300 °C) brass mold and annealed for 2 h at the temperature that was approximately 5 °C below the glass transition temperature (Tg). The values of the glass transition temperature and the thermal expansion coefficient of glass, αg, taken from the work of Lee and Taylor [31] are summarized in Table 1.

Table 1 Glass transition temperature Tg [31], thermal expansion coefficient of glass αg [31], and results of SVTDM with corresponding Q-distribution for studied glasses
Full size table

Raman spectra were recorded using RENISHAW inVia Reflex Raman spectrometer with Leica DM2500 microscope. The semiconductor laser (532 nm, 28.5 mW) was used as the excitation source with the spot of about 1 mm diameter. After the baseline subtraction, the spectra were corrected by the Böse–Einstein population factor [32]:

$$I_{\text{cor}} = I_{\exp } \nu \nu_{0}^{3} \frac{{1 - \exp \left[ { - hc\nu /kT} \right]}}{{\left( {\nu_{0} - \nu } \right)^{4} }}$$
(1)

where Iexp and Icor are observed and corrected Raman intensities, ν and ν0 are the Raman shift and the wavenumber of the excitation laser, and h, k, c, and T represent Planck’s constant, Boltzmann’s constant, the speed of light, and thermodynamic temperature. Furthermore, all spectra were normalized to the height of the highest peak [33].

Results and discussion

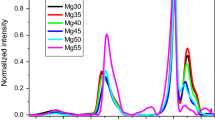
The set of five baseline subtracted and thermally corrected Raman spectra of xBaO·(1 − x) P2O5 (x = 0.30, 0.35, 0.40, 0.45, and 0.50) glasses was analyzed (Fig. 1). The spectra were recorded with a wavenumber step of 2 cm−1 in the range (150–1500) cm−1.

Fig. 1
figure 1

Normalized and thermally corrected Raman spectra

Full size image

MATLAB software was used for the principal component analysis [27]. The real error of 2.6% approaches the experimental error for two components. The PCA analysis resulted in two independent components. This is because the indicator function [26, 27] had a minimum (Fig. 2), and the Malinowski significance fell to 8%, when using two components.

Fig. 2
figure 2

PCA—indicator function—reaches minimum for two components

Full size image

The SVTDM was evaluated well above Tg at a temperature of 1000 K (Fig. 3). The seven following system components, which are defined as stable crystalline phases of the BaO–P2O5 binary phase diagram, were considered: BaO, P2O5, 4BaO·P2O5 (B4P), 3BaO·P2O5 (B3P), 2BaO·P2O5 (B2P), BaO·P2O5 (BP), and BaO·2 P2O5 (BP2). The FACT database was used to gather the molar Gibbs energies of the components listed above [21]. The thermodynamic model behaves like a quasi-binary system at temperatures above Tg (i.e., maximum two system components can be found with nonzero abundance). Therefore, the mass conservation law can be used to evaluate the equilibrium molar quantities of system components for all studied glass compositions at their Tg. For example, when applied to the xBaO·(1 − x) P2O5 glass composition we obtain the following relation:

Fig. 3
figure 3

Thermodynamic model of Shakhmatkin and Vedishcheva (SVTDM)—equilibrium molar amounts of system components at temperature T = 1000 K

Full size image

  • for 0 ≤ x ≤ 1/3, only P and BP2 are present with a non-negligible equilibrium molar content, ni.

    $$n\left( {{\text{BP}}2} \right) = x$$
    (2)
    $$n\left( {\text{P}} \right) = 1 - 3x$$
    (3)

  • for 1/3 ≤ x ≤ 0.5, only BP2 is present with non-negligible equilibrium molar content ni. The mass conservation law gives us:

    $$n\left( {{\text{BP}}2} \right) = 1 - 2x$$
    (4)
    $$n\left( {\text{BP}} \right) = 3x - 1$$
    (5)

The resulting equilibrium molar amounts and the corresponding Q-distributions are summarized in Table 1. It is shown that only two Q-units are present in the studied glass compositions. Only two system components (i.e., BP2 and BP) are present in nonzero equilibrium molar amounts for all studied glasses, with the exception of the xg(BaO) = 0.3 glass, where a small amount of P2O5 was found. This result is in agreement with the result PCA analysis of the experimental Raman spectra. The compositional dependence of Q2 equilibrium molar amount is similar to the compositional dependence of glass transition temperature and coefficient of thermal expansion αg (Tg and αg values were taken from the work of Lee and Taylor [31]). That is, with increase in content of BaO the Q2 equilibrium molar amount as well as Tg and αg values increases (Fig. 2).

Therefore, in the next step, Malfait’s spectral decomposition was performed with our own FORTRAN program JaneDove, by using the BP2 and BP equilibrium molar amounts. Such way, two PRS were obtained—the first one corresponding to BP2 with small admixture of P and the second one corresponding to BP. The calculated spectra reproduced the experimental spectra with high accuracy (Fig. 4). The obtained partial Raman spectra of BP2 and BP are plotted in Fig. 5 where they are compared with the corresponding MCR loadings.

Fig. 4
figure 4

Comparison of experimental and Malfait’s method calculated Raman spectra

Full size image
Fig. 5
figure 5

Comparison of normalized partial Raman spectra BP2 and BP with corresponding normalized MCR loadings

Full size image

MCR [29, 30] performed for two independent components resulted in the Raman spectra (loadings) and relative abundances (scores) of both components (Figs. 4, 5). 98.93% of the spectral data variance was reproduced using the MCR method. Based on the high positive correlation between equilibrium molar amounts and scores, the particular loadings were attributed to the particular system components. In this way, Loading 1 was attributed to BP2, and Loading 2 to BP. It can be seen that normalized MCR loadings are very similar to the normalized PRS (Fig. 5). The MCR results are not unique. All experimental spectra and loadings (i.e., the spectra of “pure” component) can be scaled by multiplying or dividing them by an arbitrary positive constant. Such scaling of the experimental spectra and loadings is shown in the corresponding change of the scores. In this way, scores can be adjusted to reproduce the equilibrium molar amounts of system components. Adjustment of the scores is based on the minimization of the sum of the squares of the differences between scores and their corresponding equilibrium molar amounts. A good agreement between the adjusted scores and equilibrium molar amounts of BP2 and BP system components is illustrated in Fig. 6.

Fig. 6
figure 6

Comparison of adjusted scores and equilibrium molar amounts of BP and BP2

Full size image

Conclusions

PRS calculated from the SVTDM by the Malfait’s method coincide with the loadings calculated by the MCR method. MCR and Malfait’s results are based on the results of SVTDM and reproduced the experimental spectra with high accuracy. Such way, the obtained results confirm the SVTDM.