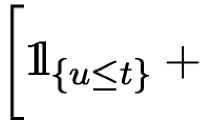1 Introduction

Let \(\mu \) be a probability distribution on \({\mathbb {R}}\) and \(n\in {\mathbb {N}}\). We say that \(\mu \) is n-completely mixable if there exists a random vector \(X=(X_1,X_2,\dots ,X_n)\) such that for each \(i=1,2,\dots ,n\) the random variable \(X_i\sim \mu \) (i.e., \(X_i\) has distribution \(\mu \)) and \(\sum _{i=1}^n X_i\) is a.s. constant. If such a vector X exists, then it is called a complete mix (or a mix for short). The number \(C=\frac{1}{n}\sum _{i=1}^n X_i\) is called the center of the mix.

The problem of n-complete mixability is mostly theoretical in nature but it became popular because of its connections with applications, especially with risk theory. For more details, see, e.g., [1, 2, 4, 6].

Obviously, only one-point probability distributions are 1-completely mixable and each symmetric distribution is 2-completely mixable (the symmetry is the necessary and sufficient condition for 2-complete mixability). However, for \(n\ge 3\) the problem of characterizing n-complete mixability is only partially solved and is still an object of thorough research (see [9] for an exhaustive list of references). In particular, the following sufficient conditions for n-complete mixability have been established:

If \(\mu \) has a symmetric and unimodal density, then \(\mu \) is n-completely mixable for all \(n\ge 2\) ( [7]).

If \(\mu \) has a density, which is monotone on its support \([a,b]\subset {\mathbb {R}}\), then \(\mu \) is n-completely mixable if and only if the expected value \(E(\mu )\) is in \([a+\frac{b-a}{n},b-\frac{b-a}{n}]\) ([8]).

If \(\mu \) has a density, which is concave on its support, then \(\mu \) is n-completely mixable for all \(n\ge 3\) ( [5]).

If \(\mu \) has a density f on a finite interval [a, b] and \(f(x)\ge \frac{3}{n(b-a)}\), then \(\mu \) is n-completely mixable ([6]).

For a long time, it was not known whether the center of the mix is always unique for an n-completely mixable probability distribution (for \(n\ge 3\)). The problem was recently solved in [3]. The center of the mix is not necessarily unique. In our paper, we use that fact to prove that for each \(d\in {\mathbb {N}}\) and each non-empty bounded Borel set \(B\subset {\mathbb {R}}^d\) there exists a d-dimensional probability distribution \(\varvec{\mu }\) satisfying what follows: For each \(n\ge 3\) and each probability distribution \(\varvec{\nu }\) on B, there exist d-dimensional random vectors \({\textbf{X}}_{\varvec{\nu },1},{\textbf{X}}_{\varvec{\nu },2},\dots ,{\textbf{X}}_{\varvec{\nu },n}\) such that \(\frac{1}{n}({\textbf{X}}_{\varvec{\nu },1}+{\textbf{X}}_{\varvec{\nu },2}+\dots +{\textbf{X}}_{\varvec{\nu },n})\sim \varvec{\nu }\) and \({\textbf{X}}_{\varvec{\nu },i}\sim \varvec{\mu }\) for \(i=1,2,\dots ,n\) (see Theorem 1). The assumption about the boundedness of the support of measure \(\varvec{\nu }\) can be replaced with the weaker assumption about the concentration of measure \(\varvec{\nu }\) (see Theorem 2 and Corollary 1).

Our results have connections with both risk theory and statistics. Namely, if we have a number of observations from some unknown probability distribution \(\mu \), and if we do not know anything about the dependence structure of these observations, then the sample mean is not a good statistic for inference about \(\mu \). For the connections with risk theory, see [1, 2, 4, 6].

In Sect. 2, we prove Theorems 1 and 2, and Corollary 1, but first we present some lemmas. The results presented in Sect. 3 show that certain generalizations of Theorem 1 are not possible.

2 The Main Results

Before proving our main results (Theorems 1 and 2), we need to present some auxiliary results.

Lemma 1

(See [3, Example 2.6].) Let N and M be independent random variables such that \(P(M=0)=P(M=1)=\frac{1}{2}\) and \(P(N=2^n)=\frac{1}{2^{n+1}}\) for \(n=0,1,\dots \). We define random variables \(U_0=V_0=N\), \(W_0=W_1=-2N\), \(U_1=2(1-M)N+M\) and \(V_1=2MN+1-M\). Then, \(U_0\sim U_1\), \(V_0\sim V_1\), and \(W_0\sim W_1\) and

$$\begin{aligned} U_0+V_0+W_0=0,\qquad U_1+V_1+W_1=1. \end{aligned}$$

Moreover, if X is any of random variables \(U_0\), \(U_1\), \(V_0\), \(V_1\), \(W_0\), and \(W_1\), then

$$\begin{aligned} \frac{1}{2(x+1)}<P(|X|>x)<\frac{2}{x}\quad \text {for }x>0. \end{aligned}$$

In particular, \(E|X|=\infty \) and \(E|X|^\alpha <\infty \) for each \(\alpha \in (0,1)\).

Now, we use Lemma 1 and binary representations of numbers from [0, 1] to obtain the following proposition.

Proposition 1

There exist random variables \(U_t\), \(V_t\), \(W_t\) with \(t\in [0,1]\), such that

$$\begin{aligned} U_t + V_t + W_t = t\quad \text {for each}t\in [0,1] \end{aligned}$$

and the distributions of \(U_t\), \(V_t\), and \(W_t\) each do not depend on t.

Proof

Let \((U_{0,j}, V_{0,j}, W_{0,j}, U_{1,j}, V_{1,j}, W_{1,j})\) for \(j=1,2,\dots \) be a sequence of independent copies of the random vector defined in Lemma 1. We define

$$\begin{aligned} U_t=\sum _{j=1}^\infty \frac{U_{t_j,j}}{2^j},\qquad V_t=\sum _{j=1}^\infty \frac{V_{t_j,j}}{2^j},\qquad W_t=\sum _{j=1}^\infty \frac{W_{t_j,j}}{2^j}, \end{aligned}$$
(1)

where \(t=\sum _{j=1}^\infty \frac{t_j}{2^j}\) is a binary representation of t, and \(t_1,t_2,\dots \in \{0,1\}\).

All the above series are almost surely convergent. Indeed, by Lemma 1, we have

$$\begin{aligned} \sum _{j=1}^\infty P\left( \left| \frac{U_{t_j,j}}{2^j}\right|>\frac{1}{2^{j/2}}\right) =\sum _{j=1}^\infty P(|U_{t_j,j}|>2^{j/2})<\sum _{j=1}^\infty \frac{2}{2^{j/2}}<\infty , \end{aligned}$$

and by the Borel–Cantelli lemma, we obtain that \(\left| \frac{U_{t_j,j}}{2^j}\right| \le \frac{1}{2^{j/2}}\) for all but finitely many \(j=1,2,\dots \). It follows that \(\sum _{j=1}^\infty \frac{U_{t_j,j}}{2^j}\) is almost surely absolutely convergent. The same holds for \(\sum _{j=1}^\infty \frac{V_{t_j,j}}{2^j}\) and \(\sum _{j=1}^\infty \frac{W_{t_j,j}}{2^j}\).

The distribution of \(U_t\) does not depend on t. Indeed, if \(s=\sum _{j=1}^\infty \frac{s_j}{2^j}\) and \(t=\sum _{j=1}^\infty \frac{t_j}{2^j}\), then \((U_{s_j,j}:j\in {\mathbb {N}})\sim (U_{t_j,j}:j\in {\mathbb {N}})\) since both sequences are i.i.d. with the same marginal distribution. Hence, \(U_s\sim U_t\). A similar argument shows that the distributions of \(V_t\) and \(W_t\) do not depend on t. For later use, we denote these distributions as follows: \(U_t\sim \mu _U\), \(V_t\sim \mu _V\), and \(W_t\sim \mu _W\).

Finally, for each \(t\in [0,1]\) we have

$$\begin{aligned} U_t+V_t+W_t=\sum _{j=1}^\infty \frac{U_{t_j,j}+V_{t_j,j}+W_{t_j,j}}{2^j}=\sum _{j=1}^\infty \frac{t_j}{2^j}=t. \end{aligned}$$

\(\square \)

Theorem 1

Let \(d\in {\mathbb {N}}\) and \(B\subset {\mathbb {R}}^d\) be a non-empty bounded Borel subset of the d-dimensional Euclidean space. There exists a d-dimensional probability distribution \(\varvec{\mu }\) satisfying what follows: For each \(n\ge 3\) and each probability distribution \(\varvec{\nu }\) on B, there exist d-dimensional random vectors \({\textbf{X}}_{\varvec{\nu },1},{\textbf{X}}_{\varvec{\nu },2},\dots ,{\textbf{X}}_{\varvec{\nu },n}\) such that \(\frac{1}{n}({\textbf{X}}_{\varvec{\nu },1}+{\textbf{X}}_{\varvec{\nu },2}+\dots +{\textbf{X}}_{\varvec{\nu },n})\sim \varvec{\nu }\) and \({\textbf{X}}_{\varvec{\nu },i}\sim \varvec{\mu }\) for \(i=1,2,\dots ,n\).

Proof

Without loss of generality, we may assume that \(B\subset [0,1]^d\). (If \(B\not \subset [0,1]^d\), then we may apply an affine transformation to each of the d coordinates of \({\mathbb {R}}^d\) to put B into \([0,1]^d\).)

Let \(\varvec{\mu }\) be the probability distribution on \({\mathbb {R}}^d\) such that all d marginals of \(\varvec{\mu }\) are independent and equal to the convolution of the distributions \(\mu _U\), \(\mu _V\), and \(\mu _W\) defined in the proof of Proposition 1 (i.e., \(\varvec{\mu }=\mu \otimes \dots \otimes \mu \), where \(\mu =\mu _U*\mu _V*\mu _W\)).

We fix an arbitrary \(n\ge 3\). Let \(\varvec{\nu }\) be any probability distribution on B and let \({\textbf{T}}=(T^{(1)},T^{(2)},\dots ,T^{(d)})\) be a random vector satisfying \({\textbf{T}}\sim \varvec{\nu }\). Using the binary representation of \(T^{(1)},T^{(2)},\dots ,T^{(d)}\), we define random variables \(T_j^{(m)}\) with \(m=1,2,\dots ,d\), and \(j=1,2,\dots \), such that \(T^{(m)}=\sum _{j=1}^\infty \frac{T_j^{(m)}}{2^j}\) for \(m=1,2,\dots ,d\), and random variables \(T_j^{(m)}\) take values in \(\{0,1\}\). Let \((U_{0,j}^{(m),k}, V_{0,j}^{(m),k}, W_{0,j}^{(m),k}, U_{1,j}^{(m),k}, V_{1,j}^{(m),k}, W_{1,j}^{(m),k})\) (with \(m=1,2,\dots ,d\), \(k=0,1,\dots ,n-1\) and \(j = 1,2,\dots \)) be a system of independent copies of the random vector defined in Lemma 1. We assume that this system is independent of \({\textbf{T}}\).

For \(k=0,1,\dots ,n-1\), let \({\textbf{U}}_{{\textbf{T}}}^k=(U_{{\textbf{T}}}^{(1),k},U_{{\textbf{T}}}^{(2),k},\dots ,U_{{\textbf{T}}}^{(d),k})\), \({\textbf{V}}_{{\textbf{T}}}^k=(V_{{\textbf{T}}}^{(1),k},V_{{\textbf{T}}}^{(2),k},\dots ,V_{{\textbf{T}}}^{(d),k})\) and \({\textbf{W}}_{{\textbf{T}}}^k=(W_{{\textbf{T}}}^{(1),k},W_{{\textbf{T}}}^{(2),k},\dots ,W_{{\textbf{T}}}^{(d),k})\) be given by

for \(m=1,2,\dots ,d\)

We define the requested random vectors \({\textbf{X}}_{\varvec{\nu },i}=(X_{\varvec{\nu },i}^{(1)},X_{\varvec{\nu },i}^{(2)},\dots ,X_{\varvec{\nu },i}^{(d)})\) as follows:

$$\begin{aligned} {\textbf{X}}_{\varvec{\nu },i}= {\textbf{U}}_{{\textbf{T}}}^{i\text { mod }n} +{\textbf{V}}_{{\textbf{T}}}^{(i+1)\text { mod }n} +{\textbf{W}}_{{\textbf{T}}}^{(i+2)\text { mod }n}. \end{aligned}$$

Now, we use the property that for each \(t\in \{0,1\}\) and each m, j and k, we have \(U_{t,j}^{(m),k}+V_{t,j}^{(m),k}+W_{t,j}^{(m),k}=t\). As a consequence, we obtain that for \(m=1,2,\dots ,d\), we have

It follows that \(\frac{1}{n}({\textbf{X}}_{\varvec{\nu },1}+{\textbf{X}}_{\varvec{\nu },2}+\dots +{\textbf{X}}_{\varvec{\nu },n})={\textbf{T}}\sim \varvec{\nu }\).

It remains to show that for each \(i=1,2,\dots ,n\), we have \({\textbf{X}}_{\varvec{\nu },i}\sim \varvec{\mu }\). First, we observe that the conditional distribution of \(X_{\varvec{\nu },i}^{(m)}= U_{{\textbf{T}}}^{(m),i\text { mod }n} +V_{{\textbf{T}}}^{(m),(i+1)\text { mod }n} +W_{{\textbf{T}}}^{(m),(i+2)\text { mod }n}\), given T, is \(\mu =\mu _U*\mu _V*\mu _W\). Moreover, the coordinates \(X_{\varvec{\nu },i}^{(1)}\), \(X_{\varvec{\nu },i}^{(2)}\), ...,\(X_{\varvec{\nu },i}^{(d)}\) are conditionally independent (given T). It follows that \({\textbf{X}}_{\varvec{\nu },i}\sim \varvec{\mu }=\mu \otimes \dots \otimes \mu \), conditionally. Since this distribution does not depend on the condition, we obtain that \({\textbf{X}}_{\varvec{\nu },i}\sim \varvec{\mu }\) unconditionally. \(\square \)

In the following results, we strengthen Theorem 1 by replacing the assumption about the boundedness of the support of measure \(\varvec{\nu }\) with the weaker assumption about the concentration (small tails) of measure \(\varvec{\nu }\).

Theorem 2

Let \(d\in {\mathbb {N}}\), \(B_1\subset B_2\subset \dots \subset {\mathbb {R}}^d\) be non-empty bounded Borel sets and \(0\le p_1\le p_2\le \dots \) be a sequence of real numbers satisfying \(\lim _{k\rightarrow \infty }p_k=1\). There exists a d-dimensional probability distribution \(\varvec{\mu }\) satisfying what follows: For each \(n\ge 3\) and each probability distribution \(\varvec{\nu }\) on \({\mathbb {R}}^d\) satisfying \(\varvec{\nu }(B_k)\ge p_k\) for \(k=1,2,\dots \), there exist d-dimensional random vectors \({\textbf{X}}_{\varvec{\nu },1},{\textbf{X}}_{\varvec{\nu },2},\dots ,{\textbf{X}}_{\varvec{\nu },n}\) such that \(\frac{1}{n}({\textbf{X}}_{\varvec{\nu },1}+{\textbf{X}}_{\varvec{\nu },2}+\dots +{\textbf{X}}_{\varvec{\nu },n})\sim \varvec{\nu }\) and \({\textbf{X}}_{\varvec{\nu },i}\sim \varvec{\mu }\) for \(i=1,2,\dots ,n\).

Proof

If \(p_k=1\) for some k, then the result follows by Theorem 1 applied to the Borel set \(B=B_k\). In the sequel, we assume that \(p_k<1\) for each k. We may also assume that the sequence \((p_k)\) is strictly increasing. Indeed, if \(p_k=p_{k+1}\), then we can exclude both \(p_{k+1}\) and \(B_{k+1}\) from the respective sequences.

We put \(p_0=0\) and \(B_0=\emptyset \). For \(k=1,2,\dots \) let \(\varvec{\mu }_k\) be the probability measure given by Theorem 1 for the Borel set \(B=B_k\) and let \(\varvec{\mu }=\sum _{k=1}^\infty (p_k-p_{k-1})\varvec{\mu }_k\).

Given the measure \(\varvec{\nu }\), we will define a sequence \((\varvec{\nu }_k)\) of measures on \({\mathbb {R}}^d\) by formula \(\varvec{\nu }_k=\sum _{l=1}^kA_{k,l}\cdot \varvec{\nu }|_{B_l{\setminus } B_{l-1}}\), where \(A_{k,l}=\prod _{j=l}^{k-1}(\varvec{\nu }(B_j)-p_j)/\prod _{j=l}^k(\varvec{\nu }(B_j)-p_{j-1})\) for \(1\le l\le k\), and the restriction \(\varvec{\nu }|_B\) is defined by \(\varvec{\nu }|_B(A)=\varvec{\nu }(A\cap B)\) for each Borel set \(A\subset {\mathbb {R}}^d\). It is easy to verify that for each \(1\le l\le k\) we have \(A_{k,l}\ge 0\), \(\sum _{l=1}^kA_{k,l}\cdot (\varvec{\nu }(B_l)-\varvec{\nu }(B_{l-1}))=1\), and \(\sum _{k=l}^\infty A_{k,l}\cdot (p_k-p_{k-1})=1\). Consequently, \(\varvec{\nu }_k\) is a probability measure on \(B_k\), and \(\sum _{k=1}^\infty (p_k-p_{k-1})\varvec{\nu }_k=\sum _{(l,k):1\le l\le k}(p_k-p_{k-1})A_{k,l}\varvec{\nu }|_{B_l{\setminus } B_{l-1}}=\sum _{l=1}^\infty \varvec{\nu }|_{B_l{\setminus } B_{l-1}}=\varvec{\nu }\).

Now, for each \(k=1,2,\dots \) let \({\textbf{X}}_{\varvec{\nu }_k,1},{\textbf{X}}_{\varvec{\nu }_k,2},\dots ,{\textbf{X}}_{\varvec{\nu }_k,n}\) be d-dimensional random vectors given by Theorem 1. Moreover, let L be a random variable, independent of these vectors, such that \(P(L=k)=p_k-p_{k-1}\) for \(k=1,2,\dots \). We define \({\textbf{X}}_{\varvec{\nu },i}={\textbf{X}}_{\varvec{\nu }_L,i}\) for \(i=1,2,\dots ,n\). The conditional distribution of \({\textbf{X}}_{\varvec{\nu },i}\) (under the condition \(L=k\)) is \(\varvec{\mu }_k\). Consequently, \({\textbf{X}}_{\varvec{\nu },i}\sim \sum _{k=1}^\infty (p_k-p_{k-1})\varvec{\mu }_k=\varvec{\mu }\). Similarly, \(\frac{1}{n}({\textbf{X}}_{\varvec{\nu },1}+{\textbf{X}}_{\varvec{\nu },2}+\dots +{\textbf{X}}_{\varvec{\nu },n})\sim \sum _{k=1}^\infty (p_k-p_{k-1})\varvec{\nu }_k=\varvec{\nu }\). \(\square \)

We recall that for two probability distributions \(\mu \) and \(\nu \) on \({\mathbb {R}}\), we say that \(\mu \) is stochastically dominated by \(\nu \) (denoted by \(\mu \le _{st}\nu \)) when their cumulative distribution functions satisfy the inequality \(F_\mu (u)\ge F_\nu (u)\) for each \(u\in {\mathbb {R}}\). Equivalently, \(\mu \le _{st}\nu \) if and only if there exist random variables \(X\sim \mu \) and \(Y\sim \nu \) satisfying \(X\le Y\).

Corollary 1

Let \(d\in {\mathbb {N}}\), \(f:{\mathbb {R}}^d\rightarrow {\mathbb {R}}\) be a Borel function such that \(\lim _{{\textbf{x}}\rightarrow \infty }f({\textbf{x}})=+\infty \), and \(\nu _0\) be a fixed probability distribution on \({\mathbb {R}}\). We consider a family \(\varvec{{\mathcal {V}}}\) consisting of probability distributions of all d-dimensional random vectors \({\textbf{Z}}\) such that the distribution of \(f({\textbf{Z}})\) is stochastically dominated by \(\nu _0\).

There exists a d-dimensional probability distribution \(\varvec{\mu }\) satisfying what follows: For each \(n\ge 3\) and each probability distribution \(\varvec{\nu }\in \varvec{{\mathcal {V}}}\), there exist d-dimensional random vectors \({\textbf{X}}_{\varvec{\nu },1},{\textbf{X}}_{\varvec{\nu },2},\dots ,{\textbf{X}}_{\varvec{\nu },n}\) such that \(\frac{1}{n}({\textbf{X}}_{\varvec{\nu },1}+{\textbf{X}}_{\varvec{\nu },2}+\dots +{\textbf{X}}_{\varvec{\nu },n})\sim \varvec{\nu }\) and \({\textbf{X}}_{\varvec{\nu },i}\sim \varvec{\mu }\) for \(i=1,2,\dots ,n\).

The case when f is the Euclidean norm in \({\mathbb {R}}^d\) and \(\nu _0\) is a probability distribution on \((0,\infty )\) seems to be the most useful.

Proof

For \(k=1,2,\dots \) let \(B_k=\{{\textbf{x}}\in {\mathbb {R}}^d:f({\textbf{x}})\le k+a\}\), where \(a\in {\mathbb {R}}\) is chosen in such a way that the sets \(B_k\) are non-empty and let \(p_k=\nu _0((-\infty ,k+a])\). By the assumption about the limit of f at infinity, the sets \(B_k\) are bounded. Applying Theorem 2 for sequences \((B_k)\) and \((p_k)\) completes the proof of the corollary. \(\square \)

3 Some Necessary Conditions for the Center of the Mix

In this section, we present some necessary conditions that should be satisfied by each complete mix. In particular, we show that we can neither replace the [0, 1] interval in Proposition 1 nor skip the boundedness assumption about set B in Theorem 1. (However, we can weaken the assumptions about the distribution \(\varvec{\nu }\) as in Theorem 2 and Corollary 1.) We also generalize the following necessary condition for a probability distribution to be n-completely mixable, formulated by Wang and Wang in 2011:

Proposition 2

( [8], see also [5, 6, 9]) Suppose the probability distribution \(\mu \) is n-completely mixable, centered at C. Let \(a=\inf \{x:\mu ((-\infty ,x])>0\}\) and \(b=\sup \{x:\mu ((-\infty ,x])<1\}\). If one of a and b is finite, then the other one is finite, and \(a+\frac{b-a}{n}\le C\le b-\frac{b-a}{n}\).

The following proposition and Corollary 2 significantly strengthen the above result (cf. Remark 1).

Proposition 3

Let \(\nu \) be a probability distribution on \({\mathbb {R}}\). If \(X_1,X_2,\dots ,X_n\) are random variables satisfying \(X_1+X_2+\dots +X_n\sim \nu \), then for each \(a_1,a_2,\dots ,a_n\in {\mathbb {R}}\) and \(i=1,2,\dots ,n\) we have

$$\begin{aligned} P\left( X_i>a_i\right) -\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^nP(X_j<a_j)\le \nu \left( \left( \sum \nolimits _{j=1}^na_j,\infty \right) \right) \le \sum _{j=1}^nP(X_j>a_j) \end{aligned}$$

and

$$\begin{aligned} P\left( X_i<a_i\right) -\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^nP(X_j>a_j)\le \nu \left( \left( -\infty ,\sum \nolimits _{j=1}^na_j\right) \right) \le \sum _{j=1}^nP(X_j<a_j). \end{aligned}$$

Proof

We show the first inequality. Using the implication \((\forall _j\ X_j\le a_j)\Rightarrow \sum _{j=1}^nX_j\le \sum _{j=1}^na_j\), we obtain

$$\begin{aligned} \nu \left( \left( \sum \nolimits _{j=1}^na_j,\infty \right) \right){} & {} =P\left( \sum _{j=1}^nX_j>\sum _{j=1}^na_j\right) \le P\left( \bigcup _{j=1}^n(X_j>a_j)\right) \\{} & {} \le \sum _{j=1}^nP(X_j>a_j). \end{aligned}$$

Similarly, by \((\sum _{j=1}^nX_j\le \sum _{j=1}^na_j,\ \forall _{j\ne i}\ -X_j\le -a_j)\Rightarrow X_i\le a_i\) we obtain

$$\begin{aligned} \begin{aligned} P(X_i>a_i)\le&P\left( \left( \sum _{j=1}^nX_j>\sum _{j=1}^na_j\right) \cup \bigcup _{\begin{array}{c} j=1\\ j\ne i \end{array}}^n(-X_j>-a_j)\right) \\ \le&\nu \left( \left( \sum \nolimits _{j=1}^na_j,\infty \right) \right) +\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^nP(X_j<a_j). \end{aligned} \end{aligned}$$

The proof of the second inequality is analogous. \(\square \)

If we put \(\nu =\delta _t\) (the one-point probability distribution concentrated at \(t\in {\mathbb {R}}\)) and \(a_i=t-\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^na_j\) into Proposition 3, then we obtain the following corollary.

Corollary 2

If \(X_1,X_2,\dots ,X_n\) are random variables satisfying \(X_1+X_2+\dots +X_n=t\in {\mathbb {R}}\), then for each \(a_1,a_2,\dots ,a_n\in {\mathbb {R}}\) and \(i=1,2,\dots ,n\) we have

$$\begin{aligned} \sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^nP(X_j<a_j)\ge P\left( X_i>t-\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^na_j\right) \end{aligned}$$
(2)

and

$$\begin{aligned} \sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^nP(X_j>a_j)\ge P\left( X_i<t-\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^na_j\right) . \end{aligned}$$
(3)

If \(\sum _{j=1}^n a_j<t\), then \(\sum _{j=1}^nP(X_j>a_j)\ge 1\). If \(\sum _{j=1}^n a_j>t\), then \(\sum _{j=1}^nP(X_j<a_j)\ge 1\).

Remark 1

We will show that Corollary 2 is a generalization of Proposition 2.

Let \(X_1,X_2,\dots ,X_n\) be random variables satisfying \(X_1,X_2,\dots ,X_n\sim \mu \) and \(\frac{1}{n}(X_1+X_2+\dots +X_n)=C\). We recall that \(a=\inf \{x:\mu ((-\infty ,x])>0\}\) and \(b=\sup \{x:\mu ((-\infty ,x])<1\}\).

Assume that a is finite. Then, for each \(j=1,2,\dots ,n\) we have \(P(X_j<a)=\mu ((-\infty ,a))=0\). By (2) applied to \(a_1=a_2=\dots =a_n=a\) and \(t=nC\) we obtain \(P(X_i>nC-(n-1)a)=0\). Consequently, b is finite and \(b\le nC-(n-1)a\), which is equivalent to \(a+\frac{b-a}{n}\le C\).

Now, assume that b is finite. Then, for each \(i=1,2,\dots ,n\) we have \(P(X_i>b)=\mu ((b,\infty ))=0\). By (3) applied to \(a_1=a_2=\dots =a_n=b\) and \(t=nC\) we obtain \(P(X_i<nC-(n-1)b)=0\). Consequently, a is finite and \(a\ge nC-(n-1)b\), which is equivalent to \(C\le b-\frac{b-a}{n}\).

As a consequence of Corollary 2, we immediately obtain the following corollary.

Corollary 3

Let \(\mu _1,\mu _2,\dots ,\mu _n\) be probability distributions. If there exist random variables \(X_1\sim \mu _1\), \(X_2\sim \mu _2,\dots \), \(X_n\sim \mu _n\) and \(t\in {\mathbb {R}}\) such that \(X_1+X_2+\dots +X_n=t\), then

$$\begin{aligned}{} & {} -\infty<\sup \left\{ \sum _{j=1}^na_j:\sum _{j=1}^n\mu _j((-\infty ,a_j))<1\right\} \le t\\{} & {} \quad \le \inf \left\{ \sum _{j=1}^na_j:\sum _{j=1}^n\mu _j((a_j,\infty ))<1\right\} <\infty . \end{aligned}$$

Corollary 3 shows that we cannot replace the [0, 1] interval in Proposition 1 by any unbounded set. Additionally, it shows that we cannot skip the assumption that the set B is bounded in Theorem 1. (Indeed, Corollary 3 implies that the projection of B onto each coordinate has to be bounded.)