Abstract
We introduce the notion of a conditional distribution to a zero-probability event in a given direction of approximation and prove that the conditional distribution of a family of independent Brownian particles to the event that their paths coalesce after the meeting coincides with the law of a modified massive Arratia flow, defined in Konarovskyi (Ann Probab 45(5):3293–3335, 2017. https://doi.org/10.1214/16-AOP1137).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of classical systems of interacting particles is the Arratia flow or coalescing Brownian particles, proposed by R. Arratia in [1] (see also [3, 39, 40]). It is the family of one-dimensional Brownian motions with the same diffusion rate starting at every point of the real line and moving independently until their meeting. When two particles collide, they coalesce and move together. The model was obtained as a scaling limit of a continuous analog of a family of coalescing random walks on the real line, and the initial interest of the study was its connection with a voter model [1, 2]. Later the Arratia flow and its generalization, Brownian web [22], appear as scaling limits of seemingly disconnected models like true self-repelling motion [53], Hastings-Levitov planer aggregation models [44], oriented percolation [50], isotropic stochastic flows of homeomorphisms in \(\mathbb {R}\) [46], solutions to evolutionary stochastic differential equations [14], etc. In particular, this leads to the intensive study of the properties of the Arratia flow. We refer to [15,16,17,18, 22, 25, 43, 47, 51, 54, 55] for more details.
However the classical Arratia flow does not take into account the physical characteristics of particles like mass, spin, charge, etc., which can influence the particle behavior. In [34, 37], the first author proposed a physical improvement called a modified massive Arratia flow (shortly MMAF), where the diffusion rate of particles depends inversely proportional on their mass. More precisely, every particle carries a mass that obeys the conservation law, i.e., the mass of a new particle that appeared after the coalescing equals the sum of the colliding particles. This type of interaction makes the particle system more natural from a physical point of view and leads to a new local phenomena [33]. It turns out that the MMAF is closely related with the geometry of the Wasserstein space of probabilities measures on the real line [37] and also is a non-trivial solution to the Dean-Kawasaki equation for supercooled liquids appearing in macroscopic fluctuation theory or models for glass dynamics in non-equilibrium statistical physics [4, 9,10,11,12,13, 19, 24, 30, 31, 35, 36, 41, 48, 49, 52, 56]. For the regularized versions of the Dean-Kawasaki equation see also [7, 8, 21]. This makes the model of a reasonable candidate for a Brownian motion on the Wasserstein space.
The main goal of this paper is to show that the MMAF appears by the conditioning of independent Brownian particles (more precisely, a cylindrical Wiener process) to the event that particle paths “coalesce” after their meeting. To be more precise, we will justify that the conditional law of a cylindrical Wiener process in \(L_2[0,1]\) starting at some non-decreasing function g to the event of coalescence is the law of a MMAF. But we will pay the prize of having to investigate more carefully the notion of conditional law to a zero-probability event, allowing to define it only in some directions of approximation. First of all, this observation would explain some similarities of the particle model with a Wiener process in the Euclidian space. For instance, the rate function in the large deviation principle for the MMAF has a similar form as the rate function for a usual Wiener process (see [38, Theorem 2.1] for a finite particle system and [37, Theorem 1.4] for the MMAF starting from all points of an interval). Secondary, we hope this result will shed some light on the uniqueness of the distribution of the MMAF, which is one of the biggest problems.
We first introduce a definition of a conditional distribution along a direction, which allows to interpret a value of the commonly used notion of regular conditional probability at a fixed point (see e.g [26, Theorem I.3.3] and [29, Theorem 6.3] for the existence of the regular conditional probability).
Let \(\textbf{E}\) be a Polish space, \({\mathcal {B}}(\textbf{E})\) denote the Borel \(\sigma \)-algebra on \(\textbf{E}\) and \({\mathcal {P}}(\textbf{E})\) be the space of probability measures on \((\textbf{E},{\mathcal {B}}(\textbf{E}))\) endowed with the topology of weak convergence. In general, given a random element X in \(\textbf{E}\) and \(C \in {\mathcal {B}}(\textbf{E})\) such that \({\mathbb {P}} \left[ X \in C \right] =0\), defining the conditional probability \({\mathbb {P}} \left[ X \in \cdot | X \in C \right] \) has no sense if we consider \(\{X \in C \}\) as an isolated event. However, one can make a proper definition with the help of regular conditional probability if C is given by \(C= \text {T}^{-1} (\{ z_0 \})\), where \(z_0\) belongs to a metric space \(\textbf{F}\) and \(\text {T}: \textbf{E}\rightarrow \textbf{F}\) is some measurable map. Let \(p: {\mathcal {B}}(\textbf{E}) \times \textbf{F}\rightarrow [0,1]\) be a regular conditional probabilityFootnote 1 of X given \(\text {T}(X)\). If \(p(\cdot ,z)\), \(z\in \textbf{F}\), is continuous in \(z_0\), then one can define \({\mathbb {P}} \left[ X \in C \right] \) to be equal to \(p(\cdot ,z_0)\). But in general case, the regular conditional probability p is well defined for only \({\mathbb {P}}^{\text {T}(X)}\)-almost every \(z \in \textbf{F}\), where \({\mathbb {P}}^{\text {T}(X)}\) denotes the law of \(\text {T}(X)\). Therefore, we will introduce a notion of the value of p at a fixed point along a (random) direction.
Definition 1.1
Let \(\{ \xi ^n\}_{n\ge 1}\) be a sequence of random elements in \(\textbf{F}\) such that
- (B1):
-
for each \(n \ge 1\), the law of \(\xi ^n\) is absolutely continuous with respect to the law of \(\text {T}(X)\);
- (B2):
-
\(\{\xi ^n\}_{n\ge 1}\) converges in distribution to \(z_0\) in \(\textbf{F}\).
A probability measure \(\nu \) on \((\textbf{E},{\mathcal {B}}(\textbf{E}))\) is the value of the conditional distribution of X to the event \(\{ \text {T}(X)=z_0\}\) along the sequence \(\{ \xi ^n \}\) if for every \(f \in {\mathcal {C}}_b(\textbf{E})\)
where p is a regular conditional probability of X given \(\text {T}(X)\). We denote this measure by \(\nu = Law_{\{\xi ^n\}}(X | \text {T}(X)=z_0)\).
We remark that the measure \(\nu \) does not depend on the version of the regular conditional probability p. In Sect. 2, we explain that the above definition generalizes the case where p is continuous at \(z_0\) and that it is very close to the intuitive definition of the conditional probability \({\mathbb {P}} \left[ X \in \cdot \ | X \in C \right] \) by approximation of the set C. Furthermore, we introduce in Sect. 2 a method to construct \(\nu \).
In order to formulate the main result of the paper, we remind the definition of the MMAF.Footnote 2 Let \(D((0,1),{\mathcal {C}}[0,\infty ))\) denote the space of càdlàg functions from (0, 1) to \({\mathcal {C}}([0,\infty ), \mathbb {R})\). Let \(g:[0,1] \rightarrow \mathbb {R}\) be a non-decreasing càdlàg function such that \(\int _0^1 |g(u)|^p \text {d}u < \infty \) for some \(p>2\).
Definition 1.2
A random element  in the space \(D((0,1),{\mathcal {C}}[0,\infty ))\) is called modified massive Arratia flow (shortly MMAF) starting at g if it satisfies the following properties
in the space \(D((0,1),{\mathcal {C}}[0,\infty ))\) is called modified massive Arratia flow (shortly MMAF) starting at g if it satisfies the following properties
-
(E1)
for all \(u \in (0,1)\) the process
 is a continuous square-integrable martingale with respect to the filtration
is a continuous square-integrable martingale with respect to the filtration  (1.2)
(1.2) -
(E2)
for all \(u \in (0,1)\),
 ;
; -
(E3)
for all \(u<v\) from (0, 1) and \(t\ge 0\),
 ;
; -
(E4)
for all \(u,v \in (0,1)\), the joint quadratic variation of
 and
and  is
is 
where
 and
and  .
.
Intuitively, the massive particles  , for each \(u \in (0,1)\), evolve like independent Brownian particles with diffusion rates inversely proportional to their masses, until two of them collide. When two particles meet, they coalesce and form a new particle with the mass equal to the sum of masses of the colliding particles.
, for each \(u \in (0,1)\), evolve like independent Brownian particles with diffusion rates inversely proportional to their masses, until two of them collide. When two particles meet, they coalesce and form a new particle with the mass equal to the sum of masses of the colliding particles.
The random element  can be identified with an \(L_2^{\uparrow }\)-valued process
can be identified with an \(L_2^{\uparrow }\)-valued process  , \(t \ge 0\), where \(L_2^{\uparrow }\) is the subset of \(L_2[0,1]\) consisting of all functions which have non-decreasing versions. There exists a cylindrical Wiener process
, \(t \ge 0\), where \(L_2^{\uparrow }\) is the subset of \(L_2[0,1]\) consisting of all functions which have non-decreasing versions. There exists a cylindrical Wiener process  in \(L_2[0,1]\) starting at g such that
in \(L_2[0,1]\) starting at g such that

where for any \(f \in L_2^{\uparrow }\), \(pr_f\) is the orthogonal projection operator in \(L_2[0,1]\) onto the subspace of \(\sigma (f)\)-measurable functions. Those results will be recalled with further details and references in Sect. 3.
Our main results consists in the construction of the following objects and in the following theorem.
- (S1):
-
We start from
 , a MMAF starting at a strictly increasing map g.
, a MMAF starting at a strictly increasing map g. - (S2):
-
Thus there exists a cylindrical Wiener process
 in \(L_2[0,1]\) starting at g satisfying (1.3).
in \(L_2[0,1]\) starting at g satisfying (1.3).  can be seen as the coalescing part of
can be seen as the coalescing part of  .
. - (S3):
-
Given
 , we decompose
, we decompose  into
into  and a non-coalescing part
and a non-coalescing part  , so that
, so that  is completely determined by
is completely determined by  and
and  . We postpone to Sect. 3.3 the precise definition of the map \(\text {T}\). We are interested in the conditional distribution of
. We postpone to Sect. 3.3 the precise definition of the map \(\text {T}\). We are interested in the conditional distribution of  to the event
to the event  , which is the event where
, which is the event where  coincides with its coalescing part
coincides with its coalescing part  .
. - (S4):
-
For every \(n \ge 1\), \(\xi ^n\) is defined as a sequence \(\{\xi ^n_j\}_{j \ge 1}\) of independent Ornstein–Uhlenbeck processes such that \(\{ \xi ^n\}_{n\ge 1}\) converges in distribution to zero in the space \({\mathcal {C}}[0,\infty )^{\mathbb {N}}\), equipped with the product topology, and the law of \(\xi ^n\) is absolutely continuous with respect to the law of
 , which is the law of a sequence of independent standard Brownian motions.
, which is the law of a sequence of independent standard Brownian motions.
Theorem 1.3
The value of the conditional distribution of  to the event
to the event  along \(\{\xi ^n\}\) is the law of
along \(\{\xi ^n\}\) is the law of  .
.
Unfortunatly, we cannot prove the result for any sequence \(\{\xi ^n\}\) satisfying (B1)-(B2), and this seems to be not achievable and possibly even not true. Nevertheless, a sequence of Ornstein–Uhlenbeck processes seems a reasonable choice of \(\{\xi ^n\}\) satisfying (B1)-(B2). We refer to Theorem 3.11 for a more precise statement after having carefully defined \(\text {T}\) and \(\{ \xi ^n\}_{n\ge 1}\) among others.
Our second result is the fact that  coupled by equation (1.3) is uniquely determined by the law of
coupled by equation (1.3) is uniquely determined by the law of  . It does not impy the uniqueness of the distribution of
. It does not impy the uniqueness of the distribution of  . However, we hope that it could be a first step in the proof that
. However, we hope that it could be a first step in the proof that  is a unique solution the the SDE (1.3).
is a unique solution the the SDE (1.3).
Theorem 1.4
Let  , \(t \ge 0\), be a MMAF starting at g. Let
, \(t \ge 0\), be a MMAF starting at g. Let  and
and  be cylindrical Wiener processes in \(L_2\) starting at g and such that
be cylindrical Wiener processes in \(L_2\) starting at g and such that  and
and  satisfy Eq. (1.3). Then
satisfy Eq. (1.3). Then  .
.
Theorem 1.4 has an interest which is independent of the conditional distribution problem, but it is proved using the same techniques as for Theorem 1.3. Moreover, as a corollary, one can see that steps (S1) and (S2) in the statement of the main result can be replaced by starting from any pair  coupled by (1.3), which is a stronger result.
coupled by (1.3), which is a stronger result.
Content of the paper. In Sect. 2, we propose a method for the construction of a conditional distribution according to Definition 1.1. In Sect. 3, we recall needed properties of the MMAF and define the non-coalescing map \(\text {T}\), using a construction of an orthonormal basis in \(L_2[0,1]\) which is tailored for the MMAF. Finally in that section, we state the main result in Theorem 3.11. Sections 4, and 5 are devoted to the proofs of Theorem 3.11 and Theorem 1.4, respectively.
2 On Conditional Distributions
Definition 1.1 is consistent with the continuous case. Indeed, if the map \(z \mapsto p(\cdot ,z)\) is continuous at \(z_0\), then by the continuous mapping theorem \(p(\cdot ,z_0) = Law_{\{\xi ^n\}}(X | \text {T}(X)=z_0)\) for any sequence \(\{ \xi ^n\}_{n\ge 1}\) satisfying (B1) and (B2). Actually, it is an equivalence, as the following lemma shows.
Lemma 2.1
Let \(z_0\) belong to the support of \({\mathbb {P}}^{\text {T}(X)}\). There exists a probability measure \(\nu \) such that \(\nu = Law_{\{\xi ^n\}}(X | \text {T}(X)=z_0)\) along any sequence \(\{\xi ^n\}_{n\ge 1}\) satisfying (B1) and (B2) if and only if there exists a version of p which is continuous at \(z_0\in \textbf{F}\). In this case, \(\nu \) is equal to the value of the continuous version of p at \(z_0\).
We postpone the proof of the lemma to Sect. A.2 in Appendix.
Remark 2.2
Definition 1.1 extends the intuitive definition of the conditional distribution of X given \(\{X \in C\}\) as the weak limit
where C is a closed subset of \(\textbf{E}\) and \(C_\varepsilon \) denotes its \(\varepsilon \)-extension, that is, \(C_{\varepsilon }=\left\{ x \in \textbf{E}:\ d_{\textbf{E}}(C,x)<\varepsilon \right\} \). We assume \({\mathbb {P}} \left[ X \in C_\varepsilon \right] >0\) for any \(\varepsilon >0\). Then \(\text {T}\) can be defined by \(\text {T}(x):=d_{\textbf{E}}(C,x)\). We note that \( \{X \in C\} = \{ \text {T}(X)=0\}\) and \(\{X \in C_\varepsilon \} = \{ \text {T}(X)<\varepsilon \}\) for all \(\varepsilon >0\). The sequence \(\{\xi ^n\}\) could then be defined by
One can easily check that \(\{\xi ^n\}\) satisfies conditions (B1) and (B2) with \(z_0=0\), and that
Therefore, the weak limit of the sequence \(( {\mathbb {P}} \left[ X \in \cdot \ |X \in C_{1/n} \right] )_{n\ge 1}\) coincides with the measure \(Law_{\{\xi ^n\}}(X | \text {T}(X)=0)\) if it exists.
We next introduce an idea to build a conditional distribution of X given \(\{\text {T}(X)=z_0\}\) along a sequence \(\{\xi ^n\}\). The idea is to split the random element X into two independent parts, Y and Z, so that Z has the same law as \(\text {T}(X)\). More precisely, we assume that there exists a quadruple \((\textbf{G},\varPsi ,Y,Z)\) satisfying the following conditions
- (P1):
-
\(\textbf{G}\) is a measurable space;
- (P2):
-
Y and Z are independent random elements in \(\textbf{G}\) and \(\textbf{F}\), respectively;
- (P3):
-
\(\varPsi : \textbf{G}\times \textbf{F}\rightarrow \textbf{E}\) is a measurable map such that \(\text {T}(\varPsi (Y,Z))=Z\) a.s.;
- (P4):
-
X and \(\varPsi (Y,Z)\) have the same distribution.
Proposition 2.3
Let \((\textbf{G},\varPsi ,Y,Z)\) be a quadruple satisfying (P1)-(P4). The map p defined by
is a regular conditional probability of X given \(\text {T}(X)\).
Moreover, if \(\{\xi ^n\}_{n \ge 1}\) is a sequence of random elements in \(\textbf{F}\) independent of Y and satisfying (B1) and (B2) of Definition 1.1, then \(\varPsi (Y, \xi ^n)\) converges in distribution to the measure \(Law_{\{\xi ^n\}}(X | \text {T}(X)=z_0)\).
Proof
Since \(\varPsi \) is measurable, p defined by (2.1) satisfies properties (R1) and (R2) of Definition A.1. Furthermore, for every \(A \in {\mathcal {B}}(\textbf{E})\) and \(B \in {\mathcal {B}}(\textbf{F})\)
Moreover, since X and \(\varPsi (Y,Z)\) have the same law, \(\text {T}(X)\) and \(Z=\text {T}(\varPsi (Y,Z))\) have the same law too, so \({\mathbb {P}}^Z={\mathbb {P}}^{\text {T}(X)}\). This concludes the proof of (R3).
Let \(f \in {\mathcal {C}}_b(\textbf{E})\). By (2.1) and Proposition A.2, we know that for any regular conditional probability p of X given \(\text {T}(X)\), the equality \(\int _\textbf{E}f(x) p(\text {d}x,z)= {\mathbb {E}} \left[ f(\varPsi (Y, z)) \right] \) holds for \({\mathbb {P}}^{\text {T}(X)}\)-almost all \(z \in \textbf{F}\). It also holds \({\mathbb {P}}^{\xi ^n}\)-almost everywhere by Property (B1). By independence of \(\xi ^n\) and Y and Fubini’s theorem,
By (1.1), the last term tends to \(\int _\textbf{E}f(x) \nu (\text {d}x)\), where \(\nu =Law_{\{\xi ^n\}}(X | \text {T}(X)=z_0)\). This concludes the proof of the convergence in distribution. \(\square \)
3 Precise Statement of the Main Result
In the introduction, we announced the construction of several objects, including a modified massive Arratia flow (MMAF) and a non-coalescing remainder map \(\text {T}\). The main part of this construction will be the definition of an orthonormal basis of \(L_2[0,1]\) which is tailored for the MMAF. In this section, we will follow the steps (S1)-(S4) from the introduction and finally, we will state again Theorem 1.3 in a more precise form, see Theorem 3.11.
3.1 MMAF and Set of Coalescing Paths
In this section, we define the set \(\textbf{Coal}\) of coalescing trajectories in an infinite-dimensional space and we recall important properties of the MMAF introduced in Definition 1.2 to show that it takes values almost surely in \(\textbf{Coal}\). Since they are not the central issue of this paper, the proofs of this section will be succinct, but we will refer to previous works or to Appendix for the detailed versions.
Fix g belonging to the set \(L_{2+}^{\uparrow }\) that consists of all non-decreasing càdlàg functions \(g:(0,1) \rightarrow \mathbb {R}\) satisfying \(\int _0^1 |g(u)|^{2+\varepsilon } \text {d}u <\infty \) for some \(\varepsilon >0\). Let \(\text {St}\) denote the set of non-decreasing step functions \(f:[0,1) \rightarrow \mathbb {R}\) of the form
where \(n \ge 1\), \(f_1< \dots < f_n\) and \(\{\pi _1, \dots \pi _n\}\) is an ordered partition of [0, 1) into half-open intervals of the form \(\pi _j=[a_j,b_j)\). The natural number n is denoted by N(f) and is by definition finite for every \(f \in \text {St}\). Recall that \(L_2:=L_2[0,1]\) and that \(L_2^{\uparrow }\) is the subset of \(L_2\) consisting of all functions which have non-decreasing versions.
Definition 3.1
We define \(\textbf{Coal}\) as the set of functions y from \({\mathcal {C}}([0,\infty ),L_2^{\uparrow })\) such that
-
(G1)
y has a version in \(D((0,1), {\mathcal {C}}[0,\infty ))\), the space of càdlàg functions from (0, 1) to \({\mathcal {C}}([0,\infty ), \mathbb {R})\);
-
(G2)
\(y_0= g\);
-
(G3)
for each \(t>0\), \(y_t \in \text {St}\);
-
(G4)
for each \(u,v \in (0,1)\) and \(s\ge 0\), \(y_s(u)=y_s(v)\) implies \(y_t(u)=y_t(v)\) for every \(t\ge s\);
-
(G5)
\(t \mapsto N(y_t)\), \(t\ge 0\), is a càdlàg non-increasing integer-valued function with jumps of height one and which is constant equal to 1 for sufficiently large time.
We can interpret y as a deterministic particle system, where \(y_t(u)\), \(t \ge 0\), describes the trajectory of a particle labeled by u. Condition (G3) means that there is only a finite number of particles at each positive time. By Condition (G4), two particles coalesce when they meet. Moreover, by Condition (G5), there can be at most one coalescence at each time, and the number of particles is equal to one for large time.
Note that, according to Lemma B.2 in Appendix, the set \(\textbf{Coal}\) is measurable in \({\mathcal {C}}([0,\infty ),L_2^{\uparrow })\). We will also consider \(\textbf{Coal}\) as a metric subspace of \({\mathcal {C}}([0,\infty ),L_2^{\uparrow })\).
Recall the following existence property of modified massive Arratia flow.
Proposition 3.2
Let \(g \in L_{2+}^{\uparrow }\). There exists a MMAF starting at g.
Proof
See [33, Theorem 1.1]. \(\square \)
Equivalently, we may also define a MMAF as an \(L_2^{\uparrow }\)-valued process, in the following sense. For every \(f \in L_2^{\uparrow }\), \(pr_f\) denotes the orthogonal projection operator in \(L_2\) onto the subspace of \(\sigma (f)\)-measurable functions.
Lemma 3.3
Let \(g \in L_{2+}^{\uparrow }\) and  be a MMAF starting at g. Then the process
be a MMAF starting at g. Then the process  , \(t\ge 0\), defined by
, \(t\ge 0\), defined by  , \(t\ge 0\), satisfies
, \(t\ge 0\), satisfies
-
(M1)
 , \(t\ge 0\), is a continuous \(L_2^{\uparrow }\)-valued process with
, \(t\ge 0\), is a continuous \(L_2^{\uparrow }\)-valued process with  , \(t\ge 0\);
, \(t\ge 0\); -
(M2)
for every \(h \in L_2\) the \(L_2\)-inner product
 , \(t\ge 0\), is a continuous square-integrable martingale with respect to the filtration generated by
, \(t\ge 0\), is a continuous square-integrable martingale with respect to the filtration generated by  , \(t\ge 0\), that trivially coincides with
, \(t\ge 0\), that trivially coincides with  ;
; -
(M3)
the joint quadratic variation of
 , \(t\ge 0\), and
, \(t\ge 0\), and  , \(t\ge 0\), equals
, \(t\ge 0\), equals  , \(t\ge 0\).
, \(t\ge 0\).
Furthermore, if a process  , \(t\ge 0\), starting at g satisfies (M1)-(M3), then there exists a MMAF
, \(t\ge 0\), starting at g satisfies (M1)-(M3), then there exists a MMAF  such that
such that  in \(L_2\) a.s. for all \(t \ge 0\).
in \(L_2\) a.s. for all \(t \ge 0\).
Proof
The first part of the statement follows directly from Lemma B.3 in Appendix, for Property (M1), and from [37, Lemma 3.1], for properties (M1) and (M2). As regards the second part of the lemma, it is proved in [33, Theorem 6.4]. \(\square \)
According to Lemma 3.3, we may identify the modified massive Arratia flow  and the \(L_2^{\uparrow }\)-valued martingale
and the \(L_2^{\uparrow }\)-valued martingale  , \(t\ge 0\), using both notations for the same object.
, \(t\ge 0\), using both notations for the same object.
Lemma 3.4
The process  , \(t\ge 0\), belongs almost surely to \(\textbf{Coal}\).
, \(t\ge 0\), belongs almost surely to \(\textbf{Coal}\).
Proof
By construction, the process satisfies properties (G1) and (G2). Properties (G3) and (G4) were proved in [33], propositions 6.2 and 2.3 ibid, respectively. Property (G5) is stated in Lemma B.4 in Appendix. \(\square \)
3.2 MMAF and Cylindrical Wiener Process
The goal of this section is the precise construction of a cylindrical Wiener process  for which the equality (1.3) holds for a given MMAF
for which the equality (1.3) holds for a given MMAF  . This will complete step (S2) from the introduction.
. This will complete step (S2) from the introduction.
For every \(f \in L_2^{\uparrow }\), let \(L_2(f)\) denote the subspace of \(L_2\) consisting of \(\sigma (f)\)-measurable functions. In particular, if f is of the form (3.1), then \(L_2(f)\) consists of all step functions which are constant on each \(\pi _j\). For any \(f \in L_2^{\uparrow }\), let \(pr_f\) (resp. \(pr_{f}^{\bot }\)) denote the orthogonal projection in \(L_2\) onto \(L_2(f)\) (resp. onto \(L_2(f)^{\bot }\)). Moreover, for any progressively measurable process \(\kappa _t\), \(t\ge 0\), in \(L_2\) and for any cylindrical Wiener process B in \(L_2\), we denote
where \(K_t=(\kappa _t,\cdot )_{L_2}\), \(t\ge 0\).
Proposition 3.5
Let \(g \in L_{2+}^{\uparrow }\) and  , \(t\ge 0\), be a MMAF starting at g. Let \(B_t\), \(t\ge 0\), be a cylindrical Wiener process in \(L_2\) starting at 0 defined on the same probability space and independent of
, \(t\ge 0\), be a MMAF starting at g. Let \(B_t\), \(t\ge 0\), be a cylindrical Wiener process in \(L_2\) starting at 0 defined on the same probability space and independent of  . Then the process
. Then the process  , \(t \ge 0\), defined by
, \(t \ge 0\), defined by

is a cylindrical Wiener process in \(L_2\) starting at g, where equality (3.2) should be understoodFootnote 3 as follows:

Moreover,  satisfies Eq. (1.3).
satisfies Eq. (1.3).
Proof
It follows from Property (M3) and from [23, Corollary 2.2] that there exists a cylindrical Wiener process \({\tilde{B}}\) in \(L_2\) starting at 0 (possibly on an extended probability space also denoted by \((\varOmega ,{\mathcal {F}},{\mathbb {P}})\)) such that

Moreover, we may assume that \({\tilde{B}}\) is independent of B. It is trivial that the map  defined by (3.2) is linear. Let \(({\mathcal {F}}_t)_{t\ge 0}\) be the natural filtration generated by \({\tilde{B}}\) and B. Let us check that
defined by (3.2) is linear. Let \(({\mathcal {F}}_t)_{t\ge 0}\) be the natural filtration generated by \({\tilde{B}}\) and B. Let us check that  , \(t\ge 0\), is an \(({\mathcal {F}}_t)\)-Brownian motion starting at \((g,h)_{L_2}\) with diffusion rate \(\Vert h\Vert _{L_2}^2\) for any \(h \in L_2\). Using the independence of \({\tilde{B}}\) and B, we have that
, \(t\ge 0\), is an \(({\mathcal {F}}_t)\)-Brownian motion starting at \((g,h)_{L_2}\) with diffusion rate \(\Vert h\Vert _{L_2}^2\) for any \(h \in L_2\). Using the independence of \({\tilde{B}}\) and B, we have that  , \(t\ge 0\), is a continuous \(({\mathcal {F}}_t)\)-martingale with quadratic variation
, \(t\ge 0\), is a continuous \(({\mathcal {F}}_t)\)-martingale with quadratic variation

This implies that  is a cylindrical Wiener process.
is a cylindrical Wiener process.
Moreover, for every \(h \in L_2\) and \(t \ge 0\),

Therefore  , which is equality (1.3). \(\square \)
, which is equality (1.3). \(\square \)
Note that it is not obvious whether each cylindrical Wiener process  in \(L_2\) starting at g and satisfying (1.3) is necessary of the form (3.2). Actually, this is the result of Theorem 1.4 and will be proved in Sect. 5.
in \(L_2\) starting at g and satisfying (1.3) is necessary of the form (3.2). Actually, this is the result of Theorem 1.4 and will be proved in Sect. 5.
3.3 Construction of Non-coalescing Remainder Map
Up to now and until the end of Sect. 4, we fix a strictly increasing function g in \(L_{2+}^{\uparrow }\) and  , where
, where  , \(t \ge 0\), is a modified massive Arratia flow starting at g and
, \(t \ge 0\), is a modified massive Arratia flow starting at g and  , \(t \ge 0\), is defined by (3.2). In particular, the assumption on g implies that \(L_2(g)=L_2\). In this section, we consider step (S3) from the introduction.
, \(t \ge 0\), is defined by (3.2). In particular, the assumption on g implies that \(L_2(g)=L_2\). In this section, we consider step (S3) from the introduction.
Let us introduce for every \(y \in \textbf{Coal}\) the corresponding coalescence times:
Since g is a strictly increasing function, one has that \(N(g)=+\infty \), and therefore, the family \(\{\tau ^y_k,\ k \ge 0\}\) is strictly decreasing for all \(y \in \textbf{Coal}\), i.e.,
by Condition (G5).
Now we are going to define an orthonormal basis \(\{ e_{k}^y,\ k\ge 0 \}\) in \(L_2\) which depends on \(y \in \textbf{Coal}\). Since \(y_t\), \(t\ge 0\), is an \(L_2\)-valued continuous function and \(L_2(g)=L_2\) due to the strong increase of g, it is easily seen that the closure of \(\bigcup _{ k=1 }^{ \infty } L_2(y_{\tau _{k}^y})\) coincides with \(L_2\). Let \(H_k^y\) be the orthogonal complement of \(L_2(y_{\tau _{k}^y})\) in \(L_2\), \(k\ge 1\).
Lemma 3.6
For each \(y \in \textbf{Coal}\) there exists a unique orthonormal basis \(\{e_l^y,\ l \ge 0\}\) of \(L_2\) such that
-
(1)
the family \(\{ e_l^y,\ 0\le l< k \}\) is a basis of \(L_2(y_{\tau _{k}^y})\) for each \(k\ge 1\);
-
(2)
\((e_l^y, \mathbb {1}_{[0,u]})_{L_2} \ge 0\) for every \(u \in (0,1)\).
Moreover, the family \(\left\{ e_{l}^y,\ l\ge k \right\} \) is a basis of \(H_k^y\) for each \(k\ge 1\).
In other words, the map \(t \mapsto pr_{y_t}\) is a projection map onto a subspace which decreases from exactly one dimension whenever a coalescence of y occurs, and the basis \(\{e_l^y,\ l \ge 0\}\) is adapted to that decreasing sequence of subspaces.
Proof
Let us construct the family \(\{ e_k^y,\ k\ge 0\}\) explicitly. Since \(y_{\tau _1^y}\) is constant on [0, 1], the only choice is \(e_0^y=\mathbb {1}_{[0,1]}\).
We say that an interval I is a step of a map f if f is constant on I but not constant on any interval strictly larger than I. At time \(\tau _{k}^y\) a coalescence occurs. So there exist \(a<b<c\) such that [a, b) and [b, c) are steps of \(y_{\tau _{k+1}^y}\), and [a, c) is a step of \(y_{\tau _{k}^y}\). We call b the coalescence point of \(y_{\tau _{k}^y}\). The only possible choice for \(e_k^y\) so that it has norm 1, it belongs to \(L_2(y_{\tau _{k+1}^y})\), it is orthogonal to every element of \(L_2(y_{\tau _{k}^y})\) and it satisfies Condition 2) is:
Since \(\overline{\bigcup _{ k=1 }^{ \infty } L_2(y_{\tau _k^y})}=L_2\), we get that \(\{ e_k^y,\ k\ge 0\}\) form a basis of \(L_2\).
The last part of the statement follows from the fact that for each \(k \ge 1\), \(H_k^y = L_2(y_{\tau _{k}^y})^{\bot }\). \(\square \)
Remark 3.7
The construction of the basis \(\left\{ e_k^y,\ k\ge 0 \right\} \) in the above proof easily implies that the map \(\textbf{Coal}\ni y\mapsto e_k^y \in L_2\) is measurable for any \(k\ge 0\), where \(\textbf{Coal}\) is endowed with the induced topology of \({\mathcal {C}}([0,\infty ),L_2^{\uparrow })\). Moreover, by (3.4), for every \(k\ge 1\), \(e_k^y\) is uniquely determined by \(y_{\cdot \wedge \tau _k^y}\).
According to step (S3), given  , we will define now the non-coalescing part
, we will define now the non-coalescing part  of
of  . Note that
. Note that  are
are  -stopping times for all \(k\ge 0\), where
-stopping times for all \(k\ge 0\), where  is the complete right-continuous filtration generated by the MMAF
is the complete right-continuous filtration generated by the MMAF  . Furthermore, Remark 3.7 yields that
. Furthermore, Remark 3.7 yields that  is an
is an  -measurable random element in \(L_2\). To simplify the notation, we will write \(e_k\) and \(\tau _k\) instead of
-measurable random element in \(L_2\). To simplify the notation, we will write \(e_k\) and \(\tau _k\) instead of  and
and  , respectively.
, respectively.
Recall that  is defined by equality (3.2). In particular, the real-valued process
is defined by equality (3.2). In particular, the real-valued process  , \(t\ge 0\), satisfies
, \(t\ge 0\), satisfies

because  . By construction of \(e_k\) in Lemma 3.6,
. By construction of \(e_k\) in Lemma 3.6,  vanishes for all \(t \ge \tau _k\). Thus, we note that for \(t \in [0, \tau _k]\),
vanishes for all \(t \ge \tau _k\). Thus, we note that for \(t \in [0, \tau _k]\),  and that
and that  , whereas for \(t \ge \tau _k\),
, whereas for \(t \ge \tau _k\),  . Since B is independent of
. Since B is independent of  and thus of \(e_k\), \(B_t(e_k)\) is well defined by \( B_t(e_k)=\int _{ 0 }^{ t }e_k \cdot \text {d}B_s\), \(t\ge 0\). To recap, in space direction \(e_k\), the projection of
and thus of \(e_k\), \(B_t(e_k)\) is well defined by \( B_t(e_k)=\int _{ 0 }^{ t }e_k \cdot \text {d}B_s\), \(t\ge 0\). To recap, in space direction \(e_k\), the projection of  is equal to the projection of its coalescing part
is equal to the projection of its coalescing part  before stopping time \(\tau _k\), and is equal to the projection of a noise B which is independent of
before stopping time \(\tau _k\), and is equal to the projection of a noise B which is independent of  after \(\tau _k\). Therefore, we define formally
after \(\tau _k\). Therefore, we define formally  as follows:
as follows:

More rigorously,Footnote 4 we define \(\xi _t\) as a map from the Hilbert space \(L_2^0:=L_2\ominus span\{\mathbb {1}_{[0,1]}\}\) to \(L_2(\varOmega )\). We set

Proposition 3.8
For every \(h \in L_2^0\) the sum (3.5) converges almost surely in \({\mathcal {C}}[0,\infty )\). Moreover, \(\xi _t\), \(t \ge 0\), is a cylindrical Wiener process in \(L_2^0\) starting at 0 that is independent of the MMAF  .
.
In order to prove the above statement, we start with the following lemma.
Lemma 3.9
The processes  , \(k\ge 1\), are independent standard Brownian motions that do not depend on the MMAF
, \(k\ge 1\), are independent standard Brownian motions that do not depend on the MMAF  .
.
Proof
Let us denote

We fix \(n\ge 1\) and show that the processes  , \(\eta _k\), \(k \in [n]\), are independent and that \(\eta _k\), \(k \in [n]\), are standard Brownian motions. Let
, \(\eta _k\), \(k \in [n]\), are independent and that \(\eta _k\), \(k \in [n]\), are standard Brownian motions. Let
be bounded measurable functions. By strong Markov property of B and the independence of B and  , \(B_{\cdot +\tau _k}-B_{\tau _k}\) is also independent of
, \(B_{\cdot +\tau _k}-B_{\tau _k}\) is also independent of  . Moreover for every \(y \in \textbf{Coal}\),
. Moreover for every \(y \in \textbf{Coal}\),
are independent standard Brownian motions. Therefore, we can compute

where \(w_k\), \(k \in [n]\), are independent standard Brownian motions that do not depend on  . This completes the proof of the lemma. \(\square \)
. This completes the proof of the lemma. \(\square \)
Proof of Proposition 3.8
Let \(h \in L_2^0\) and \(y \in \textbf{Coal}\) be fixed. For every \(n \in \mathbb {N}\) we define
where \(\eta _k\), \(k \ge 1\), are defined by (3.6). By Lemma 3.9, \(\eta _k\), \(k\ge 1\), are independent standard Brownian motions, hence \(M_t^{y, n} (h)\), \(t\ge 0\), is a continuous square-integrable martingale with respect to the filtration \(({\mathcal {F}}^{\eta }_t)_{t\ge 0}\) generated by \(\eta _k\), \(k\ge 1\), with quadratic variation \( \langle M^{y, n} (h) \rangle _t = \sum _{k=1}^n (e_k^y, h)_{L_2}^2t\), \(t\ge 0\). Moreover, for each \(T>0\) the sequence of processes \(\{M^{y,n}(h)\}_{n \ge 1}\) restricted to the interval [0, T] converges in \(L_2(\varOmega , {\mathcal {C}}[0,T])\). Indeed, for each \(m < n\), by Doob’s inequality
The sum \(\sum _{k=1}^n (e_k^y, h)_{L_2}^2\) converges to \(\Vert h\Vert _{L_2}^2\) because \(\{e_k^y,\ k \ge 1\}\) is an orthonormal basis of \(L_2^0\). Thus, \(\{M^{y,n}(h)\}_{n \ge 1}\) is a Cauchy sequence in the space \(L_2(\varOmega , {\mathcal {C}}[0,T])\), and hence, it converges to a limit denoted by \(M^y(h)= \sum _{k =1}^\infty (e_k^y, h)_{L_2} \eta _k\). Trivially, \(M^y_t(h)\) can be well defined for all \(t\ge 0\), and, by [6, Lemma B.11], \(M^y_t(h)\), \(t \ge 0\), is a continuous square-integrable \(({\mathcal {F}}^{\eta }_t)\)-martingale with quadratic variation \(\langle M^y(h) \rangle _t= \lim _{n \rightarrow \infty } \langle M^{y, n} (h) \rangle _t= \Vert h\Vert ^2_{L_2} t\), \(t\ge 0\).
Remark that \(\sum _{k=1}^{\infty } (e_k^y, h)_{L_2} \eta _k\) is a sum of independent random elements in \({\mathcal {C}}[0, T]\). Thus, by Itô-Nisio’s Theorem [27, Theorem 3.1], \(\{M^{y, n} (h)\}_{n\ge 1}\) converges almost surely to \(M^y(h)\) in \({\mathcal {C}}[0, T]\) for every \(T>0\), and therefore, in \({\mathcal {C}}[0,\infty )\). Recall that by Lemma 3.9, the sequence \(\{\eta _k\}_{k\ge 1}\) is independent of  , and by Lemma 3.4,
, and by Lemma 3.4,  belongs to \(\textbf{Coal}\) almost surely. Then \(\sum _{k=1}^{\infty } (e_k, h)_{L_2}\eta _k\) also converges almost surely in \({\mathcal {C}}[0, \infty )\) to a limit that we have called \(\xi (h)\).
belongs to \(\textbf{Coal}\) almost surely. Then \(\sum _{k=1}^{\infty } (e_k, h)_{L_2}\eta _k\) also converges almost surely in \({\mathcal {C}}[0, \infty )\) to a limit that we have called \(\xi (h)\).
Moreover, similarly as the proof of Lemma 3.9, we show that the processes  and \(\{\xi (h_i),\ i \in [n]\}\) for every \(h_i \in L_2^0\), \(i \in [n]\), \(n\ge 1\), are independent. We conclude that \(\xi \) is independent of
and \(\{\xi (h_i),\ i \in [n]\}\) for every \(h_i \in L_2^0\), \(i \in [n]\), \(n\ge 1\), are independent. We conclude that \(\xi \) is independent of  .
.
Let us show that \(\xi \) is a cylindrical Wiener process. Obviously, \(h \mapsto \xi (h)\) is a linear map. We denote  , \(t\ge 0\). We need to check that for every \(h \in L_2^0\), \(\xi (h)\) is an
, \(t\ge 0\). We need to check that for every \(h \in L_2^0\), \(\xi (h)\) is an  -Brownian motion. According to Lévy’s characterization of Brownian motion [26, Theorem II.6.1], it is enough to show that \(\xi (h)\) is a continuous square-integrable
-Brownian motion. According to Lévy’s characterization of Brownian motion [26, Theorem II.6.1], it is enough to show that \(\xi (h)\) is a continuous square-integrable  -martingale with quadratic variation \(\Vert h\Vert _{L_2}^2t\). So, we take \(n\ge 1\) and a bounded measurable function
-martingale with quadratic variation \(\Vert h\Vert _{L_2}^2t\). So, we take \(n\ge 1\) and a bounded measurable function
Then using Lemma 3.9 and the fact that \(M^y(h)\) is an \(({\mathcal {F}}^{\eta }_t)\)-martingale, we have for every \(s<t\)

Hence, \(\xi (h)\) is an  -martingale. Similarly, one can prove that \(\xi _t(h)^2-\Vert h\Vert _{L_2}^2t\), \(t\ge 0\), is also an
-martingale. Similarly, one can prove that \(\xi _t(h)^2-\Vert h\Vert _{L_2}^2t\), \(t\ge 0\), is also an  -martingale. This proves that \(\xi (h)\) is a continuous square-integrable
-martingale. This proves that \(\xi (h)\) is a continuous square-integrable  -martingale with quadratic variation \(\Vert h\Vert _{L_2}^2t\), \(t\ge 0\). The equality \({\mathbb {E}} \left[ \xi _t(h_1)\xi _t(h_2) \right] =t ( h_1,h_2 )_{L_2}\), \(t\ge 0\), trivially follows from the polarization equality and the fact that \(\xi (h_1)\) and \(\xi (h_2)\) are martingales with respect to the same filtration
-martingale with quadratic variation \(\Vert h\Vert _{L_2}^2t\), \(t\ge 0\). The equality \({\mathbb {E}} \left[ \xi _t(h_1)\xi _t(h_2) \right] =t ( h_1,h_2 )_{L_2}\), \(t\ge 0\), trivially follows from the polarization equality and the fact that \(\xi (h_1)\) and \(\xi (h_2)\) are martingales with respect to the same filtration  . Thus, \(\xi \) is an
. Thus, \(\xi \) is an  -cylindrical Wiener process in \(L_2^0\) starting at 0. This finishes the proof of the proposition. \(\square \)
-cylindrical Wiener process in \(L_2^0\) starting at 0. This finishes the proof of the proposition. \(\square \)
We conclude this section by defining properly the space \(\textbf{E}\) on which the random element  take values and the non-coalescing remainder map \(\text {T}: \textbf{E}\rightarrow \textbf{F}\) needed to achieve step (S3) from the introduction. However, as we already noted, the cylindrical Wiener process
take values and the non-coalescing remainder map \(\text {T}: \textbf{E}\rightarrow \textbf{F}\) needed to achieve step (S3) from the introduction. However, as we already noted, the cylindrical Wiener process  is not a random element in \({\mathcal {C}}([0,\infty ),L_2)\). So we define \(\textbf{E}:={\mathcal {C}}([0,\infty ),L_2^{\uparrow })\times {\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\) and \(\textbf{F}:={\mathcal {C}}_0[0,\infty )^{\mathbb {N}}\). Here, \({\mathcal {C}}[0,\infty )\) is the space of continuous functions from \([0, \infty )\) to \(\mathbb {R}\) equipped with its usual Fréchet distance, \({\mathcal {C}}_0[0,\infty )\) denotes the subspace of all functions vanishing at 0 and \(\mathbb {N}_0:= \mathbb {N}\cup \{0\}\). Equipped with the metric induced by the product topology, \(\textbf{E}\) is a Polish space.
is not a random element in \({\mathcal {C}}([0,\infty ),L_2)\). So we define \(\textbf{E}:={\mathcal {C}}([0,\infty ),L_2^{\uparrow })\times {\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\) and \(\textbf{F}:={\mathcal {C}}_0[0,\infty )^{\mathbb {N}}\). Here, \({\mathcal {C}}[0,\infty )\) is the space of continuous functions from \([0, \infty )\) to \(\mathbb {R}\) equipped with its usual Fréchet distance, \({\mathcal {C}}_0[0,\infty )\) denotes the subspace of all functions vanishing at 0 and \(\mathbb {N}_0:= \mathbb {N}\cup \{0\}\). Equipped with the metric induced by the product topology, \(\textbf{E}\) is a Polish space.
Now, we fix an orthonormal basis \(\{h_j,\ j\ge 0\}\) of \(L_2\) such that \(h_0=\mathbb {1}_{[0,1]}\). In particular, \(\{h_j,\ j\ge 1\}\) is an orthonormal basis of \(L_2^0\). We identify the cylindrical Wiener process  with the following random element in \({\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\):
with the following random element in \({\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\):

Indeed  and
and  are related by
are related by  , for all \(t\ge 0\) and \(h \in L_2\), where the series converges in \({\mathcal {C}}[0,\infty )\) almost surely for every \(h \in L_2\).
, for all \(t\ge 0\) and \(h \in L_2\), where the series converges in \({\mathcal {C}}[0,\infty )\) almost surely for every \(h \in L_2\).
Similarly, we identify \(\xi \) with \({\widehat{\xi }}_t=\left( {\widehat{\xi }}_j(t)\right) _{j\ge 1}:=\left( \xi _t(h_j)\right) _{j\ge 1}\), \(t\ge 0\), and  with
with  , \(t\ge 0\). By equality (3.5), \({\widehat{\xi }}\) and
, \(t\ge 0\). By equality (3.5), \({\widehat{\xi }}\) and  are related by
are related by

We define  , which is a random element on in \(\textbf{E}\). By (3.7), there exists a measurable map \({\widehat{\text {T}}}: \textbf{E}\rightarrow \textbf{F}\) such that
, which is a random element on in \(\textbf{E}\). By (3.7), there exists a measurable map \({\widehat{\text {T}}}: \textbf{E}\rightarrow \textbf{F}\) such that

almost surely.
3.4 Statement of the Main Result
Let us clarify step (S4) from the introduction. According to Definition 1.1, we need to define a random sequence \(\{\xi ^n\}_{n \ge 1}\) in \(\textbf{F}={\mathcal {C}}_0[0,\infty )^{\mathbb {N}}\) converging to 0 in distribution and such that \({\mathbb {P}}^{\xi ^n}\) is absolutely continuous with respect to the law of  . By (3.8) and Proposition 3.8,
. By (3.8) and Proposition 3.8,  is the law of a sequence of independent Brownian motions.
is the law of a sequence of independent Brownian motions.
Let for each \(n \ge 1\), \(\xi ^n:=(\xi ^n_j)_{j \ge 1}\) be the sequence of Ornstein–Uhlenbeck processes, independent of  , that are strong solutions to the equations
, that are strong solutions to the equations
where \(\{\alpha _j^n,\ n,j \ge 1\}\) is a family of non-negative real numbers such that
-
(O1)
for every \(n\ge 1\) the series \(\sum _{ j=1 }^{ \infty } (\alpha _j^n)^2< +\infty \);
-
(O2)
for every \(j\ge 1\), \(\alpha _j^n \rightarrow +\infty \) as \(n\rightarrow \infty \).
Remark 3.10
-
(i)
Using Kakutani’s theorem [28, p. 218] and Jensen’s inequality, it is easily seen that Condition (O1) guaranties the absolute continuity of \({\mathbb {P}}^{\xi ^n}\) with respect to \({\mathbb {P}}^{{\widehat{\xi }}}\) on \({\mathcal {C}}[0,\infty )^\mathbb {N}\). The indicator function in the drift is important, otherwise the law is singular. Hence, Assumption (B1) of Definition 1.1 is satisfied by the sequence \(\{ \xi ^n \}_{n\ge 1}\).
-
(ii)
Condition (O2) yields the convergence in distribution of \(\{\xi ^n\}_{n\ge 1}\) to 0 in \({\mathcal {C}}[0,\infty )^\mathbb {N}\) (see Lemma 4.6 below). Thus Assumption (B2) is also satisfied.
The following theorem is the main result of the paper.
Theorem 3.11
The value of the conditional distribution of  to the event
to the event  along \(\{\xi ^n\}\) is the law of
along \(\{\xi ^n\}\) is the law of  .
.
The event  , which equals to \(\{ {\widehat{\xi }}=0\}\), is by construction the event where the non-coalescing part of
, which equals to \(\{ {\widehat{\xi }}=0\}\), is by construction the event where the non-coalescing part of  vanishes.
vanishes.
Remark 3.12
For simplicity, we assumed in Sects. 3.3 and 3.4 that the initial condition g is strictly increasing. Actually, everything remains true if g is an arbitrary element of \(L_{2+}^{\uparrow }\), up to replacing the space \(L_2\) by the space \(L_2(g)\). In particular, if g is a step function, then \(L_2(g)\) has finite dimension, equal to N(g), and the orthonormal basis constructed in Lemma 3.6 and the sum in the definition of \({\widehat{\xi }}\) consists of finitely many summands.
4 Proof of the Main Theorem
In order to prove Theorem 3.11, we follow the strategy introduced in Sect. 2. We start by the construction of a quadruple \((\textbf{G},\varPsi ,Y,Z)\) satisfying (P1)-(P4). The idea behind the construction of \(\varPsi \) is inspired by the result of Proposition 3.5, stating that  can be build from the MMAF
can be build from the MMAF  and some independent process.
and some independent process.
4.1 Construction of Quadruple
Define \(\textbf{G}:=\textbf{Coal}\),  and \(Z:={\widehat{{\mathcal {Z}}}}\), where \({\mathcal {Z}}\) is a cylindrical Wiener process in \(L_2^0\) starting at 0 that is independent of
and \(Z:={\widehat{{\mathcal {Z}}}}\), where \({\mathcal {Z}}\) is a cylindrical Wiener process in \(L_2^0\) starting at 0 that is independent of  . By the same identification as previously, for the same basis \(\{h_j,\ j\ge 0\}\), \({\widehat{{\mathcal {Z}}}}_t=\left( {\widehat{{\mathcal {Z}}}}_j(t)\right) _{j\ge 1}:=\left( {\mathcal {Z}}_t(h_j)\right) _{j\ge 1}\), \(t \ge 0\), is a sequence of independent standard Brownian motions and is a random element in \(\textbf{F}\). Therefore, properties (P1) and (P2) are satisfied.
. By the same identification as previously, for the same basis \(\{h_j,\ j\ge 0\}\), \({\widehat{{\mathcal {Z}}}}_t=\left( {\widehat{{\mathcal {Z}}}}_j(t)\right) _{j\ge 1}:=\left( {\mathcal {Z}}_t(h_j)\right) _{j\ge 1}\), \(t \ge 0\), is a sequence of independent standard Brownian motions and is a random element in \(\textbf{F}\). Therefore, properties (P1) and (P2) are satisfied.
We define

where  is a map from \(L_2\) to \(L_2(\varOmega )\) defined by
is a map from \(L_2\) to \(L_2(\varOmega )\) defined by

for all \(t\ge 0\) and \(h \in L_2\). As in the proof of Lemma 3.9, one can show that \({\mathcal {Z}}(e_k)\), \(k\ge 1\), are independent standard Brownian motions that do not depend on  .
.
Lemma 4.1
For each \(h \in L_2\), the sum in (4.1) converges almost surely in \({\mathcal {C}}[0, \infty )\). Furthermore,  is a cylindrical Wiener process in \(L_2\) starting at g and the law of
is a cylindrical Wiener process in \(L_2\) starting at g and the law of  is equal to the law of
is equal to the law of  .
.
Remark 4.2
Before giving the proof of the lemma, remark that the map \(\varphi \) constructs a cylindrical Wiener process from  , by adding to
, by adding to  some non-coalescing term. Actually, for each \(y \in \textbf{Coal}\), \(\varphi (y,z)\) belongs to \(\textbf{Coal}\) if and only if \(z=0\). This statement is proved in Lemma B.9.
some non-coalescing term. Actually, for each \(y \in \textbf{Coal}\), \(\varphi (y,z)\) belongs to \(\textbf{Coal}\) if and only if \(z=0\). This statement is proved in Lemma B.9.
Proof of Lemma 4.1
Let us first show that the sum in (4.1) converges almost surely in \({\mathcal {C}}[0,\infty )\). Fixing \(y \in \textbf{Coal}\) and \(h \in L_2\), we define for every \(n \ge 1\)
Since \({\mathcal {Z}}(e_k)\), \(k\ge 1\), are independent standard Brownian motions, one can easily check that \(R^{y,n}_t (h)\), \(t\ge 0\), is a continuous square-integrable martingale with respect to the filtration generated by \({\mathcal {Z}}_{t-\tau _k^y}(e_k)\), \(k\ge 1\). As in the proof of Proposition 3.8, one can show that the sequence of partial sums \(\{R^{y,n}(h)\}_{n\ge 1}\) converges in \({\mathcal {C}}[0,\infty )\) almost surely for each \(y \in \textbf{Coal}\). By the independence of \({\mathcal {Z}}(e_k)\), \(k\ge 1\), and  , one can see that the series
, one can see that the series

also converges almost surely in \({\mathcal {C}}[0,\infty )\).
Next, we claim that there exists a cylindrical Wiener process \(\theta _t\), \(t \ge 0\), in \(L_2^0\) starting at 0 independent of  such that
such that

Indeed, by Proposition 3.5, there is a cylindrical Wiener process \(B_t\), \(t \ge 0\), in \(L_2\) starting at 0 independent of  and satisfying Eq. (3.2). Taking \(\theta \) equal to the restriction of B to the sub-Hilbert space \(L_2^0\), we easily check that
and satisfying Eq. (3.2). Taking \(\theta \) equal to the restriction of B to the sub-Hilbert space \(L_2^0\), we easily check that  , \(t\ge 0\), since for all \(s \ge 0\),
, \(t\ge 0\), since for all \(s \ge 0\),  almost surely. Furthermore, almost surely
almost surely. Furthermore, almost surely

For each fixed \(y \in \textbf{Coal}\), the family
has the same distribution as
Therefore, using the independence of  and \(\theta \) on the one hand and the independence of
and \(\theta \) on the one hand and the independence of  and \({\mathcal {Z}}\) on the other hand, we get the equality
and \({\mathcal {Z}}\) on the other hand, we get the equality

This relation and equalities (4.1) and (4.2) yield that the law of  is equal to the law of
is equal to the law of  . In particular,
. In particular,  is a cylindrical Wiener process in \(L_2\) starting at g. \(\square \)
is a cylindrical Wiener process in \(L_2\) starting at g. \(\square \)
Moreover, there exists a measurable map \({\widehat{\varphi }}: \textbf{E}\rightarrow {\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\) such that

almost surely. Let us define \(\varPsi :\textbf{G}\times \textbf{F}\rightarrow \textbf{E}\) by
It follows from the last two equalities and from Lemma 4.1 that
Corollary 4.3
The laws of  and of
and of  are the same.
are the same.
Hence Property (P4) is satisfied. It remains to check (P3). By equalities (3.7) and (3.8), we compute  :
:

Proposition 4.4
Almost surely  .
.
Proof
By continuity in t of  and \({\widehat{{\mathcal {Z}}}}_j(t)\), it is enough to show that for each \(t \ge 0\) and \(j \ge 1\) almost surely
and \({\widehat{{\mathcal {Z}}}}_j(t)\), it is enough to show that for each \(t \ge 0\) and \(j \ge 1\) almost surely  . Since \(\{h_i,\ i\ge 1\}\) is an orthonormal basis of \(L_2^0\), we have
. Since \(\{h_i,\ i\ge 1\}\) is an orthonormal basis of \(L_2^0\), we have

By (4.1) and Lemma 3.6, we have

Hence, almost surely

because \(\{e_k,\ k \ge 1\}\) is an orthonormal basis of \(L_2^0\). \(\square \)
Thus, Property (P3) holds. Hence, by Proposition 2.3, the probability kernel p defined by

for all \(A \in {\mathcal {B}}(\textbf{E})\) and \(z \in \textbf{F}\), is a regular conditional probability of  given
given  .
.
4.2 Value of p Along a Sequence of Ornstein–Uhlenbeck Processes
According to Proposition 2.3, it remains to show the following to complete the proof of Theorem 3.11. Let \(\left\{ \xi ^n\right\} _{n\ge 1}\) be the sequence defined by (3.9) and independent of  . Let \(\varPsi \) be defined by (4.3). Then
. Let \(\varPsi \) be defined by (4.3). Then  converges in distribution to
converges in distribution to  .
.
For \(y \in \textbf{Coal}\) we consider
where the map \({\widehat{\varphi }}:\textbf{E}\rightarrow {\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\) was defined in Sect. 4.1. Since for every \(n\ge 1\) the law of \(\xi ^n\) is absolutely continuous with respect to \({\mathbb {P}}^{{\widehat{\xi }}}\) (which is equal to \({\mathbb {P}}^{{\widehat{{\mathcal {Z}}}}}\)), we have that for almost all \(y \in \textbf{Coal}\) with respect to 
for each \(j\ge 0\), where the series converges in \({\mathcal {C}}[0,\infty )\) almost surely. Without loss of generality, we may assume that equality (4.5) holds for all \(y \in \textbf{Coal}\). Otherwise, we can work with a measurable subset of \(\textbf{Coal}\) of  -measure one for which equality (4.5) holds.
-measure one for which equality (4.5) holds.
Proposition 4.5
Let \(\varepsilon \in (0,1)\) and \(y \in \textbf{Coal}\) be such that \(\sum _{k=1}^\infty (\tau _k^y)^{1-\varepsilon }< \infty \). Then the sequence of processes \(\varPsi (y,\xi ^n)\), \(n \ge 1\), converges in distribution to \((y,{\widehat{y}})\) in \(\textbf{E}={\mathcal {C}}([0, \infty ), L_2^{\uparrow }) \times {\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\), where \({\widehat{y}}=(( y_{\cdot },h_j )_{L_2})_{j\ge 0}\).
Let us fix \(y \in \textbf{Coal}\) satisfying the assumption of Proposition 4.5. Before starting the proof, we define for all \(j\ge 0\)
and \(R_t^n:=(R^n_j(t))_{j\ge 0}\), \(t\ge 0\). Remark that \(R^n_0=0\). Note that it is sufficient to prove that
Indeed, this will imply that
Let us first prove some auxiliary lemmas.
Lemma 4.6
The sequence of random elements \(\{ \xi ^n \}_{n\ge 1}\) converges in distribution to 0 in \({\mathcal {C}}[0,\infty )^\mathbb {N}\).
Proof
In order to prove the lemma, we first show that the sequence \(\{ \xi ^n \}_{n\ge 1}\) is tight in \({\mathcal {C}}[0,\infty )^\mathbb {N}\). This will imply that the sequence \(\{ \xi ^n \}_{n\ge 1}\) is relatively compact, by Prohorov’s theorem. Then we will show that every (weakly) convergent subsequence of \(\{ \xi ^n \}_{n\ge 1}\) converges to 0. This will immediately yield that \(\xi ^n {\mathop {\rightarrow }\limits ^{d}}0\) in \({\mathcal {C}}[0,\infty )^\mathbb {N}\).
According to [20, Proposition 3.2.4], the tightness of \(\{ \xi ^n \}_{n\ge 1}\) will follow from the tightness of \(\{ \xi ^n_j \}_{n\ge 1}\) in \({\mathcal {C}}[0,\infty )\) for every \(j\ge 1\). So, let \(j\ge 1\) and \(T>0\) be fixed. Since the covariance of Ornstein–Uhlenbeck processes is well known, one can easily check that for every \(n \ge 1\) and every \(0\le s\le t\le n\),
where \( \frac{1}{ 0 }:=+\infty \). Since \(\xi ^n_j\) is a Gaussian process, it follows that for every \(0\le s\le t\le T\) and every \(n \ge T\),
Moreover, \(\xi ^n_j(0)=0\). Hence, by Kolmogorov–Chentsov tightness criterion (see, e.g., [29, Corollary 16.9]), the sequence of processes \(\{ \xi ^n_j \}_{n\ge 1}\) restricted to [0, T] is tight in \({\mathcal {C}}[0,T]\). Since \(T>0\) was arbitrary, we get that \(\{ \xi ^n_j \}_{n\ge 1}\) is tight in \({\mathcal {C}}[0,\infty )\). Hence, \(\{ \xi ^n \}_{n\ge 1}\) is tight in \({\mathcal {C}}[0,\infty )^\mathbb {N}\).
Next, let \(\{ \xi ^n \}_{n\ge 1}\) converges in distribution to \(\xi ^\infty \) in \({\mathcal {C}}[0,\infty )^\mathbb {N}\) along a subsequence \(N \subseteq \mathbb {N}\). Then for every \(t\ge 0\) and \(j\ge 1\) \(\{ \xi ^n_j(t) \}_{n\ge 1}\) converges in distribution to \(\xi ^\infty _j(t)\) in \(\mathbb {R}\) along N. But on the other hand, for each \(n \ge t\),
by (4.7) and Assumption (O2) in Sect. 3.4. Hence, \(\xi ^\infty _j(t)=0\) almost surely for all \(t\ge 0\) and \(j\ge 1\). Thus, we have obtained that \(\xi ^\infty =0\), and therefore, \(\xi ^n {\mathop {\rightarrow }\limits ^{d}} 0\) in \({\mathcal {C}}[0,\infty )^\mathbb {N}\) as \(n\rightarrow \infty \). \(\square \)
To prove that \(\{ R^n \}_{n\ge 1}\) converges to 0, we will use the same argument as in the proof of Lemma 4.6. So, we start from the tightness of \(\{ R^n \}\).
Lemma 4.7
Under the assumption of Proposition 4.5, the sequence \(\{R^n\}_{n\ge 0}\) is tight in \({\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\).
Proof
Again, according to [20, Proposition 3.2.4], it is enough to check that the sequence \(\{R^n_j\}_{n\ge 1}\) is tight in \({\mathcal {C}}[0,\infty )\) for every \(j\ge 0\). For \(j=0\), \(R^n_0=0\) so the result is obvious. So, let \(j\ge 1\) be fixed. We set
and
Then \(R^n_j=R^{n,1}_j+R^{n,2}_j\). We will prove the tightness separately for \(\{ R^{n,1}_j \}_{n\ge 1}\) and \(\{ R^{n,2}_j \}_{n\ge 1}\).
Tightness of \(\{R^{n,1}_j\}_{n\ge 1}\). Using the fact that \(\{ e_k^y,\ k\ge 1\}\) and \(\{ h_l,\ l\ge 1\}\) are bases of \(L_2^0\), a simple computation shows that almost surely
Due to the absolute continuity of the law of \(\xi ^n\) with respect to the law of \({\widehat{\xi }}\) and the equality \(\varGamma _j(\xi ^n)=R^{n,1}_j\), we get that \(R^{n,1}_j=\xi _j^n\). Hence it follows from Lemma 4.6 that \(R^{n,1}_j\) converges in distribution to 0 in \({\mathcal {C}}[0,\infty )\). In particular, \(\{ R^{n,1}_j \}_{n\ge 1}\) is tight in \({\mathcal {C}}[0,\infty )\), according to Prohorov’s theorem.
Tightness of \(\{R^{n,2}_j\}_{n\ge 1}\).
Step I. For any \(t\in [0,n]\), the vector
belongs almost surely to \(L_2^0\) and \({\mathbb {E}} \left[ \Vert V^n_t \Vert _{L_2}^2 \right] \le \sum _{k=1}^\infty (t \wedge \tau _k^y) < \infty \).
Indeed, by Parseval’s equality (with respect to the orthonormal family \(\{e_k^y,\ k\ge 1\}\)) and by the independence of \(\{\xi ^n_l\}_{l\ge 1}\),
where \(E^n_{k,l}(t):={\mathbb {E}} \left[ \left( \mathbb {1}_{\left\{ t \ge \tau _k^y \right\} }\xi ^n_l(t - \tau _k^y) - \xi ^n_l(t) \right) ^2 \right] \). Since \(\xi ^n_l(0)=0\), we have
By inequality (4.7), we can deduce that
Therefore,
by Parseval’s identity (with respect to the orthonormal family \(\{h_l,\ l\ge 1\}\)). Moreover, \(\sum _{k=1}^\infty (t \wedge \tau _k^y) \le t^\varepsilon \sum _{k=1}^\infty ( \tau _k^y)^{1-\varepsilon } < \infty \). Therefore, for any \(t \in [0,n]\), \(V^n_t\) belongs to \(L_2^0\) almost surely. In particular, for every \(t\in [0,n]\) the inner product \((V^n_t,h_j)_{L_2}\) is well defined, and almost surely \(R^{n,2}_j(t)=( V^n_t,h_j )_{L_2}\).
Step II. Let \(T>0\). There exists \(C_{y, \varepsilon }\) depending on y and \(\varepsilon \) such that for all \(0\le s \le t\le T\) and \(n \ge T\),
Indeed, proceeding as in Step I, we get
where we use as previously inequality (4.7). The series \(\sum _{k=1}^\infty ( \tau _k^y )^{1-\varepsilon }\) converges by assumption on y, so the proof of Step II is achieved.
Step III. There exists \(\alpha >0\), \(\beta >0\) and \(C_{y, \varepsilon }\) depending on y and \(\varepsilon \) such that for all \(0\le s \le t\le T\) and \(n \ge T\),
Indeed, for any \(s \le t\) from [0, T], \(R^{n,2}_j(t)-R^{n,2}_j(s)\) is a random variable with normal distribution \({\mathcal {N}} (0, \sigma ^2)\). By Step II, \(\sigma ^2 \le C_{y, \varepsilon } (t-s)^{\varepsilon }\). Therefore, for any \(p \ge 1\),
The statement of Step III follows by choosing p larger than \(\frac{1}{\varepsilon }\).
Step IV. By Kolmogorov–Chentsov tightness criterion (see e.g. [29, Corollary 16.9]), it follows from Step III and the equality \(R^{n,2}_j(0)=0\), \(n \ge 1\), that the sequence of processes \(\{R^{n,2}_j\}_{n\ge 1}\) restricted to [0, T] is tight in \({\mathcal {C}}[0,T]\) for every \(T>0\). Hence, \(\{ R^{n,2}_j \}_{n\ge 1}\) is tight in \({\mathcal {C}}[0,\infty )\).
Conclusion of the proof. As the sum of two tight sequences, the sequence \(\{R^n_j\}_{n\ge 1}\) is tight in \({\mathcal {C}}[0, \infty )\) for any \(j\ge 1\). Since \({\mathcal {C}}[0,\infty )^\mathbb {N}\) is equipped with the product topology, it follows from [20, Proposition 3.2.4] that the sequence \(\{R^n\}_{n\ge 1}\) is tight in \({\mathcal {C}}[0,\infty )^\mathbb {N}\). \(\square \)
Lemma 4.8
For every \(j \ge 1\) and \(t\ge 0\), \({\mathbb {E}} \left[ (R^n_j(t))^2 \right] \rightarrow 0\) as \(n \rightarrow \infty \).
Proof
Let \(j \ge 1\) and \(t\ge 0\) be fixed. We recall that \(R^n_j=R^{n,1}_j + R^{n,2}_j\). Remark that \(R^{n,1}_j= \xi ^n_j\) almost surely. Thus, \({\mathbb {E}} \left[ \left( R^{n,1}_j(t)\right) ^2 \right] \rightarrow 0\) follows immediately from inequality (4.7).
Due to the equality \(R^{n,2}_j(t) = (V^n_t,h_j)_{L_2}\), we can estimate for \(n\ge t\)
By (4.9) and (4.7), we have for every \(k,l\ge 1\)
Therefore, inequalities (4.10) and (4.11) and the dominated convergence theorem imply that \({\mathbb {E}} \left[ \left\| V^n_t \right\| _{L_2}^2 \right] \rightarrow 0\). This concludes the proof. \(\square \)
Proof of Proposition 4.5
Lemma 4.7 and Prohorov’s theorem yield that the sequence \(\{R^n\}_{n\ge 1}\) is relatively compact in \({\mathcal {C}}[0,\infty )^{\mathbb {N}_0}\). Moreover, by Lemma 4.8, we deduce that each weakly convergent subsequence of \(\{R^n\}_{n\ge 1}\) converges in distribution to 0. It implies convergence (4.6), which achives the proof of the proposition. \(\square \)
Proof of Theorem 3.11
By lemmas 3.4 and B.6,  belongs almost surely to \(\textbf{Coal}\) and the series
belongs almost surely to \(\textbf{Coal}\) and the series  converges almost surely for each \(\varepsilon \in (0,\frac{1}{2})\). Therefore, Proposition 4.5 and the independence of
converges almost surely for each \(\varepsilon \in (0,\frac{1}{2})\). Therefore, Proposition 4.5 and the independence of  and \(\{\xi ^n\}_{n \ge 1}\) imply that
and \(\{\xi ^n\}_{n \ge 1}\) imply that  , \(n \ge 1\), converges in distribution to
, \(n \ge 1\), converges in distribution to  in \(\textbf{E}\). By Proposition 2.3, the same sequence converges in distribution to the conditional law
in \(\textbf{E}\). By Proposition 2.3, the same sequence converges in distribution to the conditional law  . Thus
. Thus  . \(\square \)
. \(\square \)
5 Coupling of MMAF and Cylindrical Wiener Process
We have already seen, in Proposition 3.5 and its proof, that for every MMAF  starting at g there exists a cylindrical Wiener process
starting at g there exists a cylindrical Wiener process  in \(L_2\) starting at g such that equation (1.3) holds. However, it is unknown whether equation (1.3) has a strong solution.
in \(L_2\) starting at g such that equation (1.3) holds. However, it is unknown whether equation (1.3) has a strong solution.
In Proposition 3.5, we considered a process  defined by (3.2) and we proved that the pair
defined by (3.2) and we proved that the pair  satisfies (1.3). The reverse statement holds true, in the following sense.
satisfies (1.3). The reverse statement holds true, in the following sense.
Proposition 5.1
Let  , \(t\ge 0\), be a MMAF and
, \(t\ge 0\), be a MMAF and  , \(t\ge 0\) be a cylindrical Wiener process in \(L_2\) both starting at g and such that
, \(t\ge 0\) be a cylindrical Wiener process in \(L_2\) both starting at g and such that  satisfies (1.3). Then there exists a cylindrical Wiener process \(B_t\), \(t\ge 0\), in \(L_2\) starting at 0 independent of
satisfies (1.3). Then there exists a cylindrical Wiener process \(B_t\), \(t\ge 0\), in \(L_2\) starting at 0 independent of  such that for every \(h \in L_2\) almost surely
such that for every \(h \in L_2\) almost surely

Proposition 5.1 directly implies the statement of Theorem 1.4. Before we prove Proposition 5.1, we will show several auxiliary statements.
Recall that we denote  and
and  , and that for every \(k\ge 1\), the random element \(e_{k}\) is
, and that for every \(k\ge 1\), the random element \(e_{k}\) is  -measurable. Let
-measurable. Let  be the complete right-continuous filtration generated by
be the complete right-continuous filtration generated by  .
.
For every \(k\ge 1\) we remark that  , \(t\ge 0\), is a cylindrical Wiener process starting at 0 independent of
, \(t\ge 0\), is a cylindrical Wiener process starting at 0 independent of  . Moreover, if \(l \ge k\), then \(\tau _l \le \tau _k\) almost surely and the random element \(e_l\) is
. Moreover, if \(l \ge k\), then \(\tau _l \le \tau _k\) almost surely and the random element \(e_l\) is  -measurable, hence also
-measurable, hence also  -measurable. Therefore, the process
-measurable. Therefore, the process

is well defined.
Lemma 5.2
The processes  ,
,  , \(k\ge 1\), are independent.
, \(k\ge 1\), are independent.
In order to prove that lemma, we start by some auxiliary definitions and results. The process

is a well-defined continuous \(L_2\)-valued  -martingale, because
-martingale, because  is
is  -measurable and
-measurable and  , is independent of
, is independent of  . Let \({\mathcal {G}}_k\) be the complete \(\sigma \)-algebra generated by
. Let \({\mathcal {G}}_k\) be the complete \(\sigma \)-algebra generated by  , \(t\ge 0\), and by \(\zeta _t^k\), \(t\ge 0\).
, \(t\ge 0\), and by \(\zeta _t^k\), \(t\ge 0\).
Lemma 5.3
For every \(k\ge 1\), the MMAF  is \({\mathcal {G}}_k\)-measurable as a map from \(\varOmega \) to \({\mathcal {C}}([0,\infty ),L_2^{\uparrow })\).
is \({\mathcal {G}}_k\)-measurable as a map from \(\varOmega \) to \({\mathcal {C}}([0,\infty ),L_2^{\uparrow })\).
Proof
In order to show the measurability of  with respect to \({\mathcal {G}}_k\), it is enough to show the measurability of
with respect to \({\mathcal {G}}_k\), it is enough to show the measurability of  , \(t\ge 0\).
, \(t\ge 0\).
By Corollary B.8, we know that for every \(g \in \text {St}\) and cylindrical Wiener process W, there exists a unique continuous \(L_2^{\uparrow }\)-valued process Y such that almost surely
where \(W_t^g=\int _{ 0 }^{ t } pr_{g}\text {d}W_s \), \(t\ge 0\).
Let us consider the equation

where  . We note that
. We note that  belongs to \(\text {St}\) almost surely and is independent of
belongs to \(\text {St}\) almost surely and is independent of  . Furthermore, the process
. Furthermore, the process  , \(t\ge 0\), is a strong solution to (5.3). Therefore, it is uniquely determined by \(\zeta ^k\) and
, \(t\ge 0\), is a strong solution to (5.3). Therefore, it is uniquely determined by \(\zeta ^k\) and  , and thus it is \({\mathcal {G}}_k\)-measurable. \(\square \)
, and thus it is \({\mathcal {G}}_k\)-measurable. \(\square \)
Lemma 5.4
Let \(y \in \textbf{Coal}\) and \(k \ge 1\). Then the processes

are independent standard Brownian motions that do not depend on

Proof
By Lemma 3.6, the family \(\{e^y_l, l \ge 0\}\) is orthonormal. Consequently,  , \(l \ge 0\), are independent Brownian motions. Moreover, by Lemma 3.6 again,
, \(l \ge 0\), are independent Brownian motions. Moreover, by Lemma 3.6 again,  , \(t \ge 0\), and thus it is independent to
, \(t \ge 0\), and thus it is independent to  , \(l \ge k\). \(\square \)
, \(l \ge k\). \(\square \)
Lemma 5.5
For every \(k\ge 1\) the processes  , \(l\ge k\), are independent Brownian motions and do not depend on \({\mathcal {G}}_k\). Furthermore, for each \(l>k\),
, \(l\ge k\), are independent Brownian motions and do not depend on \({\mathcal {G}}_k\). Furthermore, for each \(l>k\),  is \({\mathcal {G}}_k\)-measurable, where \(\tau _{k,l}:=\tau _k-\tau _l\).
is \({\mathcal {G}}_k\)-measurable, where \(\tau _{k,l}:=\tau _k-\tau _l\).
Proof
Let \(n\ge k\) and \(m\ge 1\) be fixed. Let \(h_j\), \(j\ge 0\), be an arbitrary orthonormal basis of \(L_2\). We consider bounded measurable functions
We then use the independence of  from
from  .
.

Then we apply Lemma 5.4 and we denote by \(w_l\), \(l=k,\dots ,n\), a family of standard independent Brownian motions that do not depend on  and
and  .
.

which achieves the proof of the first part of the statement.
Furthermore, for every \(l>k\), we remark that \(e_l\) and \(\tau _l\) are \({\mathcal {G}}_k\)-measurable because they are  -measurable and
-measurable and  . Then the process
. Then the process  , \(t\ge 0\), is \({\mathcal {G}}_k\)-measurable, and consequently,
, \(t\ge 0\), is \({\mathcal {G}}_k\)-measurable, and consequently,  is also \({\mathcal {G}}_k\)-measurable. This finishes the proof of the second part of the lemma. \(\square \)
is also \({\mathcal {G}}_k\)-measurable. This finishes the proof of the second part of the lemma. \(\square \)
Next, we define the gluing map \(\text {Gl}:{\mathcal {C}}_0[0,\infty )^2 \times [0,\infty ) \rightarrow {\mathcal {C}}_0[0,\infty )\) as follows:
where \(a^+:=a\vee 0\). It is easily seen that the map \(\text {Gl}\) is continuous and therefore measurable.
Since almost surely,  , \(t\ge 0\), for every \(l>k\ge 1\), a simple computation shows that for every \(l>k\ge 1\) almost surely
, \(t\ge 0\), for every \(l>k\ge 1\), a simple computation shows that for every \(l>k\ge 1\) almost surely

where \(\tau _{k,l}:=\tau _k-\tau _l\).
Proof of Lemma 5.2
In order to prove this lemma, it is enough to show that for each \(k \ge 1\),  is independent of
is independent of  ,
,  , \(l >k\).
, \(l >k\).
Let us denote by \({\mathcal {H}}_k\) be the complete \(\sigma \)-algebra generated by \({\mathcal {G}}_k\) and  , \(l >k\). By Lemma 5.5, the process
, \(l >k\). By Lemma 5.5, the process  is independent of \({\mathcal {H}}_k\).
is independent of \({\mathcal {H}}_k\).
Moreover for every \(l>k\), using Lemma 5.3,  and \(\tau _{k,l}\) are \({\mathcal {G}}_k\)-measurable, hence they are \({\mathcal {H}}_k\)-measurable. By Lemma 5.5 and by the definition of \({\mathcal {H}}_k\), we also see that
and \(\tau _{k,l}\) are \({\mathcal {G}}_k\)-measurable, hence they are \({\mathcal {H}}_k\)-measurable. By Lemma 5.5 and by the definition of \({\mathcal {H}}_k\), we also see that  and
and  are \({\mathcal {H}}_k\)-measurable. By (5.5), it follows that
are \({\mathcal {H}}_k\)-measurable. By (5.5), it follows that  is \({\mathcal {H}}_k\)-measurable for every \(l>k\). Therefore
is \({\mathcal {H}}_k\)-measurable for every \(l>k\). Therefore  ,
,  , \(l >k\), are independent of
, \(l >k\), are independent of  . \(\square \)
. \(\square \)
5.1 Proof of Proposition 5.1
Let \(\beta _k\), \(k \ge 0\), be independent standard Brownian motions, independent of  . Recall that
. Recall that  , \(t\ge 0\), is a right-continuous
, \(t\ge 0\), is a right-continuous  -adapted process in \(L_2\). Thus we can define for every \(k\ge 0\)
-adapted process in \(L_2\). Thus we can define for every \(k\ge 0\)

Since \(\tau _0=+\infty \), we have in particular \(B_0(t)= \beta _0(t)\), \(t \ge 0\).
Lemma 5.6
The processes \(B_k\), \(k\ge 0\), defined by (5.6), are independent standard Brownian motions.
Proof
The statement of this lemma directly follows from Lévy’s characterization of Brownian motion [26, Theorem II.6.1]. \(\square \)
We will now use the result of Lemma 5.2 to prove the following lemma.
Lemma 5.7
The processes  , \(B_k\), \(k\ge 0\), are independent.
, \(B_k\), \(k\ge 0\), are independent.
Proof
Since \(B_0=\beta _0\) is independent of  by definition and of \(B_k\), \(k\ge 1\), by Lemma 5.6, it is enough to prove that the processes
by definition and of \(B_k\), \(k\ge 1\), by Lemma 5.6, it is enough to prove that the processes  , \(B_k\), \(k \in [n]\), are independent, for any given n.
, \(B_k\), \(k \in [n]\), are independent, for any given n.
Putting together (5.2), (5.4) and (5.6), we have

Since \(\beta _k\), \(k \in [n]\), is independent of  and using Lemma 5.2, we deduce that the processes
and using Lemma 5.2, we deduce that the processes  , \(\beta _k\),
, \(\beta _k\),  , \(k\in [n]\), are independent. Moreover, \(\tau _k\), \(k\in [n]\), are measurable with respect to
, \(k\in [n]\), are independent. Moreover, \(\tau _k\), \(k\in [n]\), are measurable with respect to  . Let \(G_0:{\mathcal {C}}([0,\infty ),L_2^{\uparrow }) \rightarrow \mathbb {R}\), \(F_k:{\mathcal {C}}[0,\infty ) \rightarrow \mathbb {R}\), \(k\in [n]\), be bounded measurable functions. We have
. Let \(G_0:{\mathcal {C}}([0,\infty ),L_2^{\uparrow }) \rightarrow \mathbb {R}\), \(F_k:{\mathcal {C}}[0,\infty ) \rightarrow \mathbb {R}\), \(k\in [n]\), be bounded measurable functions. We have

Note that if \(w_1\) and \(w_2\) are independent standard Brownian motions and \(r>0\), then the process \(\text {Gl}(w_1,w_2,r)\) is a standard Brownian motion. It follows that for any fixed \(y \in \textbf{Coal}\),  , \(k\in [n]\), is a family of independent standard Brownian motions. Thus for every \(y \in \textbf{Coal}\),
, \(k\in [n]\), is a family of independent standard Brownian motions. Thus for every \(y \in \textbf{Coal}\),

where \(w_k\), \(k \in [n]\), denotes an arbitrary family of independent standard Brownian motions. This easily implies the statement of the lemma, because \(B_k\), \(k \in [n]\), are independent standard Brownian motions by Lemma 5.6. \(\square \)
Now, we finish the proof of Proposition 5.1.
Proof of Proposition 5.1
Define
Since \(B_k\), \(k\ge 0\), are independent Brownian motions that do not depend on  and hence on \(e_k\), \(k\ge 1\), one can show similarly to the proof of Lemma 3.9 that the series converges in \({\mathcal {C}}[0,\infty )\) almost surely for every \(h \in L_2\), and \(B_t\), \(t\ge 0\), is a cylindrical Wiener process in \(L_2\) starting at 0.
and hence on \(e_k\), \(k\ge 1\), one can show similarly to the proof of Lemma 3.9 that the series converges in \({\mathcal {C}}[0,\infty )\) almost surely for every \(h \in L_2\), and \(B_t\), \(t\ge 0\), is a cylindrical Wiener process in \(L_2\) starting at 0.
Moreover, B is independent of  . Indeed, for any \(n \ge 1\), for any \(h_1, \dots , h_n\) in \(L_2\), for any bounded and measurable functions \(F: {\mathcal {C}}[0, \infty ) ^n \rightarrow \mathbb {R}\) and \(G: {\mathcal {C}}([0,\infty ),L_2^{\uparrow }) \rightarrow \mathbb {R}\),
. Indeed, for any \(n \ge 1\), for any \(h_1, \dots , h_n\) in \(L_2\), for any bounded and measurable functions \(F: {\mathcal {C}}[0, \infty ) ^n \rightarrow \mathbb {R}\) and \(G: {\mathcal {C}}([0,\infty ),L_2^{\uparrow }) \rightarrow \mathbb {R}\),

where \(w_k\), \(k \in [n]\), denotes an arbitrary family of independent standard Brownian motions.
Moreover, since  , we easily check that
, we easily check that

for all \(t\ge 0\), which implies equality (5.1). \(\square \)
Data Availability
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Notes
See Definition A.1 in Appendix.
The process
 , \(t\ge 0\), does not take values in the space of Hilbert-Schmidt operators in \(L_2\). Therefore, the integral
, \(t\ge 0\), does not take values in the space of Hilbert-Schmidt operators in \(L_2\). Therefore, the integral  is not well defined but
is not well defined but  is.
is.Similarly as for the cylindrical Wiener process
 , \(\xi \) cannot be defined as a random process taking values in \(L_2\).
, \(\xi \) cannot be defined as a random process taking values in \(L_2\).
References
Arratia, R.A.: Coalescing Brownian motion on the line. ProQuest LLC, Ann Arbor, MI (1979). Thesis (Ph.D.)–The University of Wisconsin - Madison
Arratia, R.A.: Coalescing brownian motion and the voter model on \(\mathbb{Z}\). Unpublished partial manuscript (1981)
Berestycki, N., Garban, C., Sen, A.: Coalescing Brownian flows: a new approach. Ann. Probab. 43(6), 3177–3215 (2015). https://doi.org/10.1214/14-AOP957
Bertini, L., De Sole, A., Gabrielli, D., Jona-Lasinio, G., Landim, C.: Macroscopic fluctuation theory. Rev. Mod. Phys. 87, 593–636 (2015). https://doi.org/10.1103/RevModPhys.87.593
Blount, D., Kouritzin, M.A.: On convergence determining and separating classes of functions. Stoch. Process. Appl. 120(10), 1898–1907 (2010). https://doi.org/10.1016/j.spa.2010.05.018
Cherny, A.S., Engelbert, H.J.: Singular Stochastic Differential Equations. Lecture Notes in Mathematics, vol. 1858. Springer, Berlin (2005)
Cornalba, F., Shardlow, T., Zimmer, J.: A regularized Dean-Kawasaki model: derivation and analysis. SIAM J. Math. Anal. 51(2), 1137–1187 (2019). https://doi.org/10.1137/18M1172697
Cornalba, F., Shardlow, T., Zimmer, J.: From weakly interacting particles to a regularised Dean-Kawasaki model. Nonlinearity 33(2), 864–891 (2020). https://doi.org/10.1088/1361-6544/ab5174
Dean, D.S.: Langevin equation for the density of a system of interacting Langevin processes. J. Phys. A 29(24), L613–L617 (1996). https://doi.org/10.1088/0305-4470/29/24/001
Delfau, J.B., Ollivier, H., López, C., Blasius, B., Hernández-Garcí a, E.: Pattern formation with repulsive soft-core interactions: discrete particle dynamics and Dean-Kawasaki equation. Phys. Rev. E 94(4), 042120, 13 (2016)
de la Torre, J.A., Espanol, P., Donev, A.: Finite element discretization of non-linear diffusion equations with thermal fluctuations. J. Chem. Phys. 142(9), 094115 (2015). https://doi.org/10.1063/1.4913746
Donev, A., Fai, T.G., Vanden-Eijnden, E.: A reversible mesoscopic model of diffusion in liquids: from giant fluctuations to Fick’s law. J. Stat. Mech. Theory Exp. 2014(4), P04004 (2014)
Donev, A., Vanden-Eijnden, E.: Dynamic density functional theory with hydrodynamic interactions and fluctuations. J. Chem. Phys. 140(23), 234115 (2014). https://doi.org/10.1063/1.4883520
Dorogovtsev, A.A.: One Brownian stochastic flow. Theory Stoch. Process. 10(3–4), 21–25 (2004)
Dorogovtsev, A.A., Gnedin, A.V., Vovchanskii, M.B.: Iterated logarithm law for size of clusters in arratia flow. Theory Stoch. Process. 18(34)(2), 1–7 (2012)
Dorogovtsev, A.A., Korenovska, I.A., Glinyanaya, E.V.: On some random integral operators generated by an Arratia flow. Theory Stoch. Process. 22(2), 8–18 (2017)
Dorogovtsev, A.A., Ostapenko, O.V.: Large deviations for flows of interacting Brownian motions. Stoch. Dyn. 10(3), 315–339 (2010). https://doi.org/10.1142/S0219493710002978
Dorogovtsev, A.A., Riabov, G.V., Schmalfuß, B.: Stationary points in coalescing stochastic flows on \(\mathbb{R} \). Stoch. Process. Appl. 130(8), 4910–4926 (2020). https://doi.org/10.1016/j.spa.2020.02.005
Embacher, P., Dirr, N., Zimmer, J., Reina, C.: Computing diffusivities from particle models out of equilibrium. Proc. A. 474(2212), 20170694 (2018). https://doi.org/10.1098/rspa.2017.0694
Ethier, S.N., Kurtz, T.G.: Markov processes. Wiley Series in Probability and Mathematical Statistics: Probability and Mathematical Statistics. Wiley, New York (1986). https://doi.org/10.1002/9780470316658. Characterization and convergence
Fehrman, B., Gess, B.: Well-posedness of nonlinear diffusion equations with nonlinear, conservative noise. Arch. Ration. Mech. Anal. 233(1), 249–322 (2019). https://doi.org/10.1007/s00205-019-01357-w
Fontes, L.R.G., Isopi, M., Newman, C.M., Ravishankar, K.: The Brownian web: characterization and convergence. Ann. Probab. 32(4), 2857–2883 (2004). https://doi.org/10.1214/009117904000000568
Gawarecki, L., Mandrekar, V.: Stochastic differential equations in infinite dimensions with applications to stochastic partial differential equations. Probability and its Applications (New York). Springer, Heidelberg (2011)
Giacomin, G., Lebowitz, J.L., Presutti, E.: Deterministic and stochastic hydrodynamic equations arising from simple microscopic model systems. In: Stochastic partial differential equations: six perspectives, Math. Surveys Monogr., vol. 64, pp. 107–152. Amer. Math. Soc., Providence, RI (1999). https://doi.org/10.1090/surv/064/03
Glinyanaya, E.V., Fomichov, V.V.: Limit theorems for the number of clusters of the Arratia flow. Theory Stoch. Process. 23(2), 33–40 (2018). https://doi.org/10.1080/00029890.1916.11998164
Ikeda, N., Watanabe, S.: Stochastic differential equations and diffusion processes, North-Holland Mathematical Library, vol. 24, second edn. North-Holland Publishing Co., Amsterdam; Kodansha, Ltd., Tokyo (1989)
Itô, K., Nisio, M.: On the convergence of sums of independent Banach space valued random variables. Osaka Math. J. 5, 35–48 (1968)
Kakutani, S.: On equivalence of infinite product measures. Ann. Math. 2(49), 214–224 (1948). https://doi.org/10.2307/1969123
Kallenberg, O.: Foundations of Modern Probability, Probability and its Applications (New York), 2nd edn. Springer, New York (2002). https://doi.org/10.1007/978-1-4757-4015-8
Kawasaki, K.: Stochastic model of slow dynamics in supercooled liquids and dense colloidal suspensions. Physica A 208(1), 35–64 (1994). https://doi.org/10.1016/0378-4371(94)90533-9
Kipnis, C., Olla, S., Varadhan, S.R.S.: Hydrodynamics and large deviation for simple exclusion processes. Commun. Pure Appl. Math. 42(2), 115–137 (1989). https://doi.org/10.1002/cpa.3160420202
Konarovskiĭ, V.V.: On an infinite system of diffusing particles with coalescing. Teor. Veroyatn. Primen. 55(1), 157–167 (2010). https://doi.org/10.1137/S0040585X97984693
Konarovskyi, V.: On asymptotic behavior of the modified Arratia flow. Electron. J. Probab. 22, 19 (2017). https://doi.org/10.1214/17-EJP34
Konarovskyi, V.: A system of coalescing heavy diffusion particles on the real line. Ann. Probab. 45(5), 3293–3335 (2017). https://doi.org/10.1214/16-AOP1137
Konarovskyi, V., Lehmann, T., von Renesse, M.: On Dean-Kawasaki dynamics with smooth drift potential. J. Stat. Phys. 178(3), 666–681 (2020). https://doi.org/10.1007/s10955-019-02449-3
Konarovskyi, V., Lehmann, T., von Renesse, M.K.: Dean-Kawasaki dynamics: ill-posedness vs. triviality. Electron. Commun. Probab. 24, 8 (2019). https://doi.org/10.1214/19-ECP208
Konarovskyi, V., von Renesse, M.K.: Modified massive Arratia flow and Wasserstein diffusion. Commun. Pure Appl. Math. 72(4), 764–800 (2019). https://doi.org/10.1002/cpa.21758
Konarovskyi, V.V.: Large deviations principle for finite system of heavy diffusion particles. Theory Stoch. Process. 19(1), 37–45 (2014)
Le Jan, Y., Raimond, O.: Flows, coalescence and noise. Ann. Probab. 32(2), 1247–1315 (2004). https://doi.org/10.1214/009117904000000207
Le Jan, Y., Raimond, O.: Sticky flows on the circle and their noises. Probab. Theory Related Fields 129(1), 63–82 (2004). https://doi.org/10.1007/s00440-003-0324-9
Marconi, U.M.B., Tarazona, P.: Dynamic density functional theory of fluids. J. Chem. Phys. 110(16), 8032–8044 (1999). https://doi.org/10.1063/1.478705
Marx, V.: A new approach for the construction of a Wasserstein diffusion. Electron. J. Probab. 23, 124 (2018). https://doi.org/10.1214/18-EJP254
Munasinghe, R., Rajesh, R., Tribe, R., Zaboronski, O.: Multi-scaling of the \(n\)-point density function for coalescing Brownian motions. Commun. Math. Phys. 268(3), 717–725 (2006). https://doi.org/10.1007/s00220-006-0110-5
Norris, J., Turner, A.: Hastings-Levitov aggregation in the small-particle limit. Commun. Math. Phys. 316(3), 809–841 (2012). https://doi.org/10.1007/s00220-012-1552-6
Parthasarathy, K.R.: Probability measures on metric spaces. Probability and Mathematical Statistics, No. 3. Academic Press, Inc., New York-London (1967)
Piterbarg, V.V.: Expansions and contractions of isotropic stochastic flows of homeomorphisms. Ann. Probab. 26(2), 479–499 (1998). https://doi.org/10.1214/aop/1022855641
Riabov, G.V.: Random dynamical systems generated by coalescing stochastic flows on \(\mathbb{R}\). Stoch. Dyn. 18(4), 1850031 (2018). https://doi.org/10.1142/S0219493718500314
Rotskoff, G.M., Vanden-Eijnden, E.: Neural networks as interacting particle systems: Asymptotic convexity of the loss landscape and universal scaling of the approximation error. Preprint (2018). arXiv:1805.00915
Sadhu, T., Derrida, B.: Correlations of the density and of the current in non-equilibrium diffusive systems. J. Stat. Mech. Theory Exp. 2016(11), 113202 (2016)
Sarkar, A., Sun, R.: Brownian web in the scaling limit of supercritical oriented percolation in dimension \(1+1\). Electron. J. Probab. 18(21), 23 (2013). https://doi.org/10.1214/EJP.v18-2019
Shamov, A.: Short-time asymptotics of one-dimensional Harris flows. Commun. Stoch. Anal. 5(3), 527–539 (2011)
Spohn, H.: Large Scale Dynamics of Interacting Particles. Springer, Berlin (1991). https://doi.org/10.1007/978-3-642-84371-6
Tóth, B., Werner, W.: The true self-repelling motion. Probab. Theory Related Fields 111(3), 375–452 (1998). https://doi.org/10.1007/s004400050172
Tribe, R., Zaboronski, O.: Pfaffian formulae for one dimensional coalescing and annihilating systems. Electron. J. Probab. 16(76), 2080–2103 (2011). https://doi.org/10.1214/EJP.v16-942
Tsirelson, B.: Nonclassical stochastic flows and continuous products. Probab. Surv. 1, 173–298 (2004). https://doi.org/10.1214/154957804100000042
Velenich, A., Chamon, C., Cugliandolo, L.F., Kreimer, D.: On the Brownian gas: a field theory with a Poissonian ground state. J. Phys. A 41(23), 235002 (2008). https://doi.org/10.1088/1751-8113/41/23/235002
Acknowledgements
The authors are very grateful to Max von Renesse for very useful discussions and suggestions. The first author also thanks Andrey A. Dorogovtsev for his helpful comments and the interest to the studying problem. The first author was partly supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - SFB 1283/2 2021 - 317210226.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix: Regular Conditional Probability
1.1 Definition
Let \(\textbf{E}\) be a Polish space and \(\textbf{F}\) be a metric space. We consider random elements X and \(\xi \) in \(\textbf{E}\) and \(\textbf{F}\), respectively, defined on the same probability space \((\varOmega , {\mathcal {F}}, {\mathbb {P}})\). Let also \({\mathcal {B}}(\textbf{E})\) (resp. \({\mathcal {B}}(\textbf{F})\)) denote the Borel \(\sigma \)-algebra on \(\textbf{E}\) (resp. \(\textbf{F}\)) and \({\mathcal {P}}(\textbf{E})\) be the space of probability measures on \((\textbf{E},{\mathcal {B}}(\textbf{E}))\) endowed with the topology of weak convergence.
Definition A.1
A function \(p: {\mathcal {B}}(\textbf{E}) \times \textbf{F}\rightarrow [0,1]\) is a regular conditional probability of X given \(\xi \) if
- (R1):
-
for every \(z \in \textbf{F}\), \(p(\cdot ,z)\in {\mathcal {P}}(\textbf{E})\);
- (R2):
-
for every \(A \in {\mathcal {B}}(\textbf{E})\), \(z \mapsto p(A, z)\) is measurable;
- (R3):
-
for every \(A \in {\mathcal {B}}(\textbf{E})\) and \(B \in {\mathcal {B}}(\textbf{F})\),
$$\begin{aligned} {\mathbb {P}} \left[ X \in A,\ \xi \in B \right] =\int _B p(A,z)\; {\mathbb {P}}^\xi (\text {d}z), \end{aligned}$$where \({\mathbb {P}}^\xi :={\mathbb {P}} \circ \xi ^{-1}\) denotes the law of \(\xi \).
Recall the following existence and uniqueness result (see e.g. [29, Theorem 6.3]):
Proposition A.2
There exists a regular conditional probability of X given \(\xi \). Moreover, it is unique in the following sense: if p and \(p'\) are regular conditional probabilities of X given \(\xi \), then
1.2 Proof of Lemma 2.1
We first recall that the sufficiency of Lemma 2.1 immediately follows from the continuous mapping theorem.
We next prove the necessity. We first choose a family \(\{ f_k,\ k\ge 1 \}\subset {\mathcal {C}}_b(\textbf{E})\) which strongly separate points in \(\textbf{E}\). One can show that such a family exists since \(\textbf{E}\) is separable (see also [5, Lemma 2]). By [20, Theorem 4.5] (or [5, Theorem 6] for weaker assumptions on the space \(\textbf{E}\)), any sequence \(\{\mu _n\}_{n\ge 1}\) of probability measures on \(\textbf{E}\) converges weakly to a probability measure \(\mu \) if and only if
for all \(k\ge 1\).
We define the following sets
for all \(k\ge 1\) and \(m\ge 1\). Let also \(A_m^k=A_m^{k,+}\cup A_m^{k,-}\).
Lemma A.3
If for every \(k\ge 1\) and \(m\ge 1\) there exists \(\delta _m^k>0\) such that
where \(B_m^k\) is the ball in \(\textbf{F}\) with center \(z_0\) and radius \(\delta _m^k\), then p has a version continuous at \(z_0\). Moreover, it can be taken as
Proof
We first remark that according to (A.1), \(p'=p\) \({\mathbb {P}}^{{\text {T}(X)}}\)-a.e. Next, let \(z_n \rightarrow z_0\) in \(\textbf{F}\) as \(n \rightarrow \infty \). Without loss of generality, we may assume that \(z_n \not \in \bigcup _{ k,m=1 }^{ \infty }\left( A_m^k \cap B_m^k \right) \) for all \(n\ge 1\). Let \(m\ge 1\) and \(k\ge 1\) be fixed. Then there exists a number N such that \(z_n \in B_m^k\) for all \(n\ge N\). Consequently, \(z_n \not \in A_m^k\), \(\forall n\ge N\), that yields
for all \(n\ge N\). This finishes the proof of the lemma. \(\square \)
We come back to the proof of Lemma 2.1. Let us assume that p has no version continuous at \(z_0\). Then, according to Lemma A.3, there exists \(k\ge 1\) and \(m\ge 1\) such that for every \(\delta >0\)
where \(B_{\delta }\) denotes the ball with center \(z_0\) and radius \(\delta \). Without loss of generality, we may assume that \({\mathbb {P}}^{{\text {T}(X)}}\left[ A_m^{k,+} \cap B_{\delta } \right] >0\) for every \(\delta >0\). For every \(n\ge 1\), let \(\xi ^n\) be a random element in \(\textbf{F}\) with distribution
where
By the construction, \({\mathbb {P}}^{\xi ^n}\ll {\mathbb {P}}^{{\text {T}(X)}}\), \(n\ge 1\). Moreover, it is easy to see that \(\xi ^n \rightarrow z_0\) in distribution as \(n \rightarrow \infty \). But
Indeed, for every \(n\ge 1\) the random element \(\xi ^n\) takes values almost surely in \(A_m^{k,+}\), which implies that
We have obtained the contradiction with assumption (1.1). This finishes the proof of Lemma 2.1.
Some Properties of MMAF
1.1 Measurability of Coalescing Set
We recall that the set \(D((0,1),{\mathcal {C}}[0,\infty ))\) denotes the space of càdlàg functions from (0, 1) to \({\mathcal {C}}[0,\infty )\) equipped with the Skorokhod distance, which makes it a Polish space. Set
It is easily seen that \(D^{\uparrow }\) a closed subspace of \(D((0,1),{\mathcal {C}}[0,\infty ))\). So, we will consider \(D^{\uparrow }\) as a Polish subspace of \(D((0,1),{\mathcal {C}}[0,\infty ))\). Let
Lemma B.1
For every \(A\in {\mathcal {B}}(D^{\uparrow })\) the set \(A \cap D^{\uparrow }_2\) is a Borel measurable subset of \({\mathcal {C}}L_2^{\uparrow }:={\mathcal {C}}([0,\infty ),L_2^{\uparrow })\).
Proof
First we are going to show that \(D^{\uparrow }_2\) is a subset of \({\mathcal {C}}L_2^{\uparrow }\). So, we take \(y \in D^{\uparrow }_2\) and check that y is a continuous \(L_2\)-valued function. The continuity of y at 0 follows from the definition of \(D^{\uparrow }_2\). Let \(t>0\) and \(t_n \rightarrow t\) as \(n\rightarrow \infty \). Without loss of generality, we may assume that \(t_n \in [\frac{1}{ T },T]\) for some \(T \in \mathbb {N}\) and all \(n\ge 1\). We are going to show that \(y_{t_n} \rightarrow y_t\) in \(L_2\), \(n \rightarrow \infty \). Let us note that the sequence \(\{ y_{t_n} \}_{n\ge 1}\) is relatively compact, according to [33, Lemma 5.1] and the fact that \(y_{t_n} \in L_2^{\uparrow }\), \(n\ge 1\), are uniformly bounded in \(L_{2+\delta }\)-norm. This implies that there exists a subsequence \(N \subseteq \mathbb {N}\) and \(f \in L_2^{\uparrow }\) such that \(y_{t_n} \rightarrow f\) in \(L_2\) along N. On the other hand, \(y_{t_n} \rightarrow y_t\) pointwise, that implies the equality \(f=y_t\). Moreover, it yields that every convergent subsequence of \(\{y_{t_n}\}_{n\ge 1}\) converges to \(y_t\) in \(L_2\). Using the relatively compactness of \(\{ y_{t_n} \}_{n\ge 1}\), we can conclude that \(y_{t_n} \rightarrow y_t\) in \(L_2\) as \(n\rightarrow \infty \). Thus, \(y \in {\mathcal {C}}L_2^{\uparrow }\).
Next, we will check that the set \(D^{\uparrow }_2\) is measurable in \(D^{\uparrow }\). We fix \(t\ge 0\) and make the following observation. For every \(y \in D^{\uparrow }\) the real-valued function \(y_t\) is non-decreasing on (0, 1). This implies that it has at most countable number of discontinuous points. Hence, by [20, Proposition 3.5.3], the convergence \(y^n \rightarrow y\) in \(D^{\uparrow }\) implies the convergence of \(y^n_t \rightarrow y_t\) a.e. (with respect to the Lebesgue measure on [0, 1]). Using Fatou’s lemma, we get that the set
for every \(K\ge 0\), \(p\ge 2\) and \(f \in L_p\). Hence the set
is Borel measurable in \(D^{\uparrow }\). Using the standard argument and (B.1), one can check the measurability of \(D^2\). So, the set \(D^{\uparrow }_2=D^1 \cap D^2\) is Borel measurable in \(D^{\uparrow }\).
We claim that the identity map \(\varPhi :D^{\uparrow }_2\rightarrow {\mathcal {C}}L_2^{\uparrow }\) is Borel measurable. Indeed, let
Then the preimage
is a closed set in \(D^{\uparrow }\), by (B.1). Since the Borel \(\sigma \)-algebra on \({\mathcal {C}}L_2^{\uparrow }\) is generated by the family \(\left\{ B^T_r(y),\ T,r>0,\ y \in {\mathcal {C}}L_2^{\uparrow }\right\} \), \(\varPhi \) is a Borel measurable function. Moreover, it is an injective map. So, using the Kuratowski theorem (see [45, Theorem 3.9]) and the fact that \(A \cap D^{\uparrow }_2\in {\mathcal {B}}(D^{\uparrow })\), we obtain that the image \(\varPhi (A \cap D^{\uparrow }_2)=A \cap D^{\uparrow }_2\in {\mathcal {B}}({\mathcal {C}}L_2^{\uparrow })\) for every \(A \in {\mathcal {B}}(D^{\uparrow })\). \(\square \)
Lemma B.2
Let \(\textbf{Coal}\) be defined in Sect. 3.1. Then \(\textbf{Coal}\) is a Borel measurable subset of \({\mathcal {C}}L_2^{\uparrow }\).
Proof
Let \(\textbf{Coal}_D\) consists of all functions from \(D^{\uparrow }\) which satisfies conditions (G2)-(G5) of the definition of \(\textbf{Coal}\) in Sect. 3.1. Since every function \(f \in \text {St}\) has a finite \(L_p\)-norm for every \(p\ge 2\), it is easily seen that
Hence, according to Lemma B.1, the statement of the lemma will immediately follow from the measurability of \(\textbf{Coal}_D\) in \(D^{\uparrow }\). However, this follows from the fact that the set \(\textbf{Coal}_D\) can be determined via values of \(y(u) \in {\mathcal {C}}[0,\infty )\) for u from a countable set U. We leave a detailed proof for the reader. \(\square \)
1.2 Properties of MMAF
Let  be a MMAF starting at \(g \in L_{2+}^{\uparrow }\), and
be a MMAF starting at \(g \in L_{2+}^{\uparrow }\), and  , \(t\ge 0\).
, \(t\ge 0\).
Lemma B.3
If \(\Vert g\Vert _{L_{2+\varepsilon }}<\infty \) for some \(\varepsilon >0\), then for every \(T>0\) and \(\delta \in \left( 0,\frac{ \varepsilon }{ 2+\varepsilon } \right) \) there exists \(C_{T,\delta }\) such that

Proof
In order to check the estimate, one needs to repeat the proof of [33, Proposition 4.4] replacing the summation with the integration. \(\square \)
Recall that for every \(f \in \text {St}\), N(f) denotes the number of steps of f. We write \(N(f)= \infty \) for each non-decreasing càdlàg function f which does not belong to \(\text {St}\). For any \(y \in {\mathcal {C}}([0,\infty ),L_2^{\uparrow })\), define
The following lemma states that a MMAF satisfies almost surely Property (G5) of Definition 3.1.
Lemma B.4
Let  , \(t \ge 0\), be a MMAF starting at g. Then
, \(t \ge 0\), be a MMAF starting at g. Then

Proof
The proof of the statement follows from the fact that with probability one, three or more independent Brownian motions cannot meet at the same time, and from mathematical induction. \(\square \)
Lemma B.5
For every \(y \in \textbf{Coal}\), \(\beta >0\) and \(n\ge 1\), one has
Proof
For simplicity of notation, we will omit the superscript y in \(\tau _k^y\). We write for \(m>n\)
Hence, the statement of the lemma follows from the monotone convergence theorem. \(\square \)
Lemma B.6
Let  be a MMAF starting at \(g \in L_{2+}^{\uparrow }\). Then for every \(\beta > \frac{1}{ 2 }\),
be a MMAF starting at \(g \in L_{2+}^{\uparrow }\). Then for every \(\beta > \frac{1}{ 2 }\),  almost surely.
almost surely.
Proof
Let \(g \in L_{2+\varepsilon }\) for some \(\varepsilon >0\). In order to prove the lemma, we will use the estimate

from [33, Remark 4.6], where \(C_{\varepsilon ,T}\) is a constant depending on \(\varepsilon \) and \(T>0\). Take an arbitrary number \(T>0\) and estimate for \(\beta > \frac{1}{ 2 }\)

Thus  almost surely, for all \(T>0\). Since
almost surely, for all \(T>0\). Since  almost surely by (B.2),
almost surely by (B.2),  almost surely. Thus, the statement of the lemma follows directly from Lemma B.5. \(\square \)
almost surely. Thus, the statement of the lemma follows directly from Lemma B.5. \(\square \)
1.3 Uniqueness of Solutions to Deterministic Equation
Denote \(\textbf{E}^g:=\left\{ x \in {\mathcal {C}}\left( [0,\infty ),L_2(g)\right) :\ x_0=g\right\} \) and
Let \(g \in \text {St}\) be fixed and \(N(g)=n\). For functions \(x \in {\mathcal {C}}\left( [0,\infty ),L_2(g)\right) \) and \(y \in \textbf{Coal}^{\text {ex}}\), we introduce the integral
Lemma B.7
For every \(x \in {\mathcal {C}}\left( [0,\infty ),L_2(g)\right) \), there exists a unique \(y \in \textbf{Coal}^{\text {ex}}\) such that
Proof
Without loss of generality, we assume that \(x_0=g\). The function \(y \in \textbf{Coal}^{\text {ex}}\) can be constructed step by step. First take \(\sigma _0=0\) and \({\tilde{y}}^0_t=g\), \(t\ge 0\). Then set
and
for all \(k \in [n-1]\). Remark that \(\dim L_2({\tilde{y}}^k_{\sigma _k}) \in [n-k]\) for each \(0\le k \le n-1\). We set \(\sigma _n=+\infty \). The function y can be defined as
By construction, y belongs to \(\textbf{Coal}^{\text {ex}}\), satisfies (B.4) and is uniquely determined. \(\square \)
Corollary B.8
Let W be a cylindrical Wiener process in \(L_2(g)\) starting at g. Then there exists a unique \(({\mathcal {F}}^W_t)\)-adapted process \(Y_t\), \(t\ge 0\), such that
where \(({\mathcal {F}}^W_t)_{t\ge 0}\) is the filtration generated by W.
Proof
The statement of the lemma directly follows from Lemma B.7 and the fact that \(L_2^{\uparrow }\)-valued continuous martingales starting from g belongs to \(\textbf{Coal}\) almost surely (see [33, Proposition 2.2]). \(\square \)
1.4 On Map \(\varphi \)
In Remark 4.2, we announced the following result.
Lemma B.9
For every \(y \in \textbf{Coal}\) and \(z=(z_k)_{k \ge 1} \in {\mathcal {C}}_0[0, \infty )^\mathbb {N}\) define similarly to (4.1)
if the series converges in \({\mathcal {C}}([0,\infty ),L_2)\). Then for each \(y \in \textbf{Coal}\), \(\varphi (y,z)\) belongs to \(\textbf{Coal}\) if and only if \(z=0\).
Proof
It is obvious that \(\varphi (y,0)=y \in \textbf{Coal}\).
We assume now that \(\varphi (y,z)\) belongs to \(\textbf{Coal}\) and prove that \(z=0\). Set
and show that \(\gamma (y,z)=0\). This will immediately imply \(z=0\).
Step I. Let \(k \ge 1\) be fixed. By (3.4), there exist \(a<b<c\) such that
The goal of this step is to show that \(\varphi _{\tau _k^y}(y,z)(u) = y_{\tau _k^y}(u)\) for every \(u \in [a,c)\), in other words, that \(\gamma _{\tau _k^y}(y,z)\) is equal to zero on the interval [a, c).
By the construction of \(\tau _k^y\) and \(e_k^y\), \(y_{\tau _k^y}\) is constant on the interval [a, c). Furthermore, since \(\varphi (y,z) \in \textbf{Coal}\), \(\varphi _{\tau _k^y}(y,z)\) belongs to \(L_2^{\uparrow }\). Hence, we can deduce that \(\gamma _{\tau _k^y}(y,z) = \varphi _{\tau _k^y}(y,z) -y_{\tau _k^y}(y,z)\) is non-decreasing on [a, c), as a difference of a non-decreasing function and a constant function. Furthermore,
since \(z_k(0)=0\). Hence, \(\gamma _{\tau _k^y}(y,z)\) belongs to \(span\left\{ e_l^y,\ l \ge k+1 \right\} \), whereas \(\mathbb {1}_{[a,b)}\) and \(\mathbb {1}_{[a,c)}\) both belong to \(span\left\{ e_l^y,\ l \le k\right\} \). Indeed, \(\mathbb {1}_{[a,c)} \in L_2(y_{\tau _k^y})= span\left\{ e_l^y,\ l < k\right\} \), by Lemma 3.6, and \(\mathbb {1}_{[a,b)} \in span\left\{ \mathbb {1}_{[a,c)}, e_k^y\right\} \). Recall that \(\{e_l^y,\ l \ge 0\}\) is an orthonormal basis of \(L_2\). Thus,
So, we can deduce that \(u \mapsto (\gamma _{\tau _k^y}(y,z), \mathbb {1}_{[a,u)})_{L_2}\) is a convex function on [a, c] which vanishes at a, b and c. Thus, it is zero everywhere on [a, c]. In particular, \(\gamma _{\tau _k^y}(y,z)(u)=0\) for every \(u \in (a,c)\). Consequently, \(\varphi _{\tau _k^y}(y,z)(u) = y_{\tau _k^y}(u)\) for every \(u \in (a,c)\). The equality also holds for \(u=a\), by the right-continuity of \(\varphi _{\tau _k^y}(y,z)\) and \(y_{\tau _k^y}\).
Step II. Now let \(t >0\) be fixed. By Property (G3) of the definition of \(\textbf{Coal}\) in Sect. 3.1, \(y_t\) belongs to \(\text {St}\), and thus,
for pairwise distinct \(y_j\), \(j\in [n]\). Fix \(j \in [n]\). By coalescence Property (G4), there exists \(k \ge 1\) such that \(u \mapsto y_s(u)\) is constant on \([a_j,c_j)\) for every \(s \ge \tau _k^y\) and non-constant on \([a_j,c_j)\) for every \(s < \tau _k^y\). By Step I, \(y_{\tau _k^y}= \varphi _{\tau _k^y}(y,z)\) on \([a_j,c_j)\). Thus, \(\varphi _{\tau _k^y}(y,z)\) is constant on \([a_j,c_j)\). By Property (G4) again, now applied to \(\varphi (y,z)\), \(\varphi _t(y,z)\) is constant on \([a_j,c_j)\) due to \(t \ge \tau _k^y\). As the difference of two constant functions, \(\gamma _t(y,z)\) is also constant on \([a_j,c_j)\). Moreover, by the construction of \(\gamma \) and Lemma 3.6, \(\gamma _t(y,z)\) is orthogonal to \(L_2(y_t)\). Hence \(\gamma _t(y,z)\) is also orthogonal to \(\mathbb {1}_{[a_j,c_j)}\). Therefore, we can conclude that \(\gamma _t(y,z)= 0 \) on \([a_j,c_j)\). Since \(j \in [n]\) and \(t>0\) were arbitrary, we deduce that \(\gamma _t(y,z)=0\) on [0, 1) for every \(t >0\). This finishes the proof of the lemma. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Konarovskyi, V., Marx, V. On Conditioning Brownian Particles to Coalesce. J Theor Probab 36, 2126–2164 (2023). https://doi.org/10.1007/s10959-023-01267-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10959-023-01267-4
Keywords
- Regular conditional probability
- Modified massive Arratia flow
- Cylindrical Wiener process
- Coalescing Brownian motions



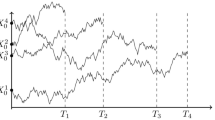
 is a continuous square-integrable martingale with respect to the filtration
is a continuous square-integrable martingale with respect to the filtration 
 ;
; ;
; and
and  is
is 
 and
and  .
. , a MMAF starting at a strictly increasing map g.
, a MMAF starting at a strictly increasing map g. in
in  can be seen as the coalescing part of
can be seen as the coalescing part of  .
. , we decompose
, we decompose  into
into  and a non-coalescing part
and a non-coalescing part  , so that
, so that  is completely determined by
is completely determined by  and
and  . We postpone to Sect.
. We postpone to Sect.  to the event
to the event  , which is the event where
, which is the event where  coincides with its coalescing part
coincides with its coalescing part  .
. , which is the law of a sequence of independent standard Brownian motions.
, which is the law of a sequence of independent standard Brownian motions. ,
,  ,
,  ,
,  ,
,  ;
; ,
,  ,
,  ,
,  ,
,  is not well defined but
is not well defined but  is.
is. ,
,