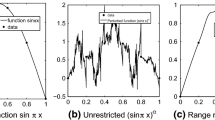
We study structural, integral, differential, variational, and fractal properties of a function f whose argument \( x={\Delta }_{\alpha_1{\alpha}_2\dots {\alpha}_n\dots}^{Q_s^{\ast }} \) is represented by a polybasic s-symbol \( {Q}_s^{\ast } \) -representation (1 < s ∈ N) and its corresponding value is expressed as follows: \( f\left(x={\Delta }_{\alpha_1{\alpha}_2\dots {\alpha}_n\dots}^{Q_s^{\ast }}\right)={a}^{\alpha_1{u}_1+{\alpha}_2{u}_2+\dots +{\alpha}_n{u}_n+\dots }, \) where u1 + u2 + … is a given convergent positive series and αn ∈ {0, 1, …, s - 1}.
Similar content being viewed by others
References
M. Pratsiovytyi and N. Vasylenko, “Fractal properties of functions defined in terms of Q-representation,” Int. J. Math. Anal. (Ruse), 7, No. 61-64, 3155–3167 (2013).
M. V. Prats’ovytyi, Fractal Approach to the Investigation of Singular Distributions [in Ukrainian], National Pedagogic University, Kyiv (1998).
M. V. Pratsiovytyi, Ya. V. Goncharenko, N. V. Dyvliash, and S. P. Ratushniak, “Inversor of digits of \( {Q}_s^{\ast } \) -representation of numbers,” Mat. Stud., 55, No. 1, 37–43 (2021).
M. V. Prats’ovytyi and S. P. Ratushnyak, “Distribution of values of a fractal function of random argument,” Nauk. Chasopys. Nats. Ped. Univ. Drahomanova, Ser. 1, Fiz.-Mat. Nauk., No. 16, 150–160 (2014).
M. V. Pratsiovytyi and S. P. Ratushnyak, “Continuous nowhere differentiable function with fractal properties defined in terms of Q2-representation,” Nelin. Kolyv., 23, No. 2, 231–252 (2020); English translation: J. Math. Sci., 258, No. 5, 670–697 (2021).
B. Sendov, “Binary self-similar fractal functions,” Fundam. Prykl. Mat., 5, No. 2, 589–595 (1999).
M. V. Pratsiovytyi, Ya. V. Goncharenko, S. O. Dmytrenko, I. M. Lysenko, and S. P. Ratushniak, “On one class of functions with fractal properties,” Bukov. Mat. Zh., 6, No. 1, 273–283 (2021).
N. O. Korsun’ and M. V. Pratsiovytyi, “On the set of partial sums of alternating series with one condition of homogeneity and a generalization of the binary representation of numbers,” Nauk. Chasopys. Nats. Ped. Univ. Drahomanova, Ser. 1, Fiz.-Mat. Nauk., No. 10, 28–39 (2009).
J. A. Guthrie and I. E. Nymann, “The topological structure of the set of subsums of an infinite series,” Collog. Math., 55, No. 2, 323–327 (1988).
V. P. Markitan, M. V. Prats’ovytyi, and I. O. Savchenko, “Superfractality of the set of incomplete sums of one positive series,” Ukr. Mat. Zh., 70, No. 10, 1403–1416 (2018); English translation: Ukr. Math. J., 70, No. 10, 1619–1634 (2019).
J. E. Nymann and R. A. Saenz, “On the paper of Guthrie and Nymann on subsums of infinite series. The topological structure of the set of subsums of an infinite series,” Collog. Math., 68, 259–264 (1995).
M. V. Pratsiovytyi, Ya. V. Goncharenko, I. M. Lysenko, and S. P. Ratushniak, “Fractal functions of exponential type that is generated by the \( {Q}_s^{\ast } \) -representation of argument,” Mat. Stud., 56, No. 2, 133–143 (2021).
S. Kakeya, “On the partial sums of an infinite series,” Tohoku Sci. Rep., 3, No. 4, 159–164 (1914).
Ya. Vynnyshyn, V. Markitan, M. Pratsiovytyi, and I. O. Savchenko, “Positive series for which the sets of subsums are Cantorvals,” in: Proc. Internat. Geom. Cent., 12, No. 2, 26–42 (2019); https://doi.org/10.15673/tmgc.v12i2.1455.
S. Albeverio, M. Pratsiovytyi, and G. Torbin, “Fractal probability distributions and transformations preserving the Hausdorff–Besicovitch dimension,” Ergodic Theory Dynam. Systems, 24, 1–16 (2004).
M. V. Pratsiovytyi, “Distributions of sums of random power series,” Dop. Nats. Akad. Nauk Ukr., No. 5, 32–37 (1996).
M. V. Pratsiovytyi, “Convolutions of singular distributions,” Dop. Nats. Akad. Nauk Ukr., No. 9, 36–42 (1997).
R. Salem, “On some singular monotonic functions which are strictly increasing,” Trans. Amer. Math. Soc., 53, 423–439 (1943).
G. Marsaglia, “Random variables with independent binary digits,” Ann. Math. Statist., 42, No. 2, 1922–1929 (1971).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Neliniini Kolyvannya, Vol. 24, No. 4, pp. 498–517, October–December, 2021.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Pratsiovytyi, M.V., Vovk, Y.Y., Lysenko, I.M. et al. Superpositions of Functions with Fractal Properties. J Math Sci 273, 248–270 (2023). https://doi.org/10.1007/s10958-023-06497-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-023-06497-9