Abstract
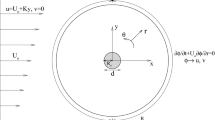
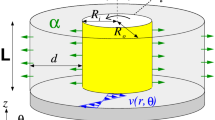
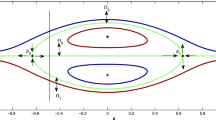
In the present work, we study various modes that arise after a circular Couette flow loses its stability in the presence of an axial flow due to a constant axial pressure gradient and a radial flow through the permeable walls of the cylinders. The basic object of our investigation is a nonlinear system of amplitude equations describing multiple flow bifurcations between permeable cylinders. Different bifurcations will be investigated theoretically with application of numerical methods.
Similar content being viewed by others
References
D. I. Takeuchi and D. F. Jankowski, “Numerical and experimental investigation of the stability of spiral Poiseuille flow,” J. Fluid Mech., 102, 101–126 (1981).
H. A. Snyder, “Experiments on the stability of spiral flow at low axial Reynolds numbers,” Proc. Roy. Soc. London, Ser. A, 265, 198–214 (1962).
K. Min and R. M. Lueptow, “Circular Couette flow with pressure-driven axial flow and a porous inner cylinder,” Exp. Fluids, 17, No. 3, 190–197 (1994).
S. Wroński, E. Molga, and L. Rudniak, “Dynamic filtration in biotechnology,” Bioprocess Eng., 4, No. 3, 99–104 (1989).
K. H. Kroner and V. Nissinen, “Dynamic filtration of microbial suspensions using an axially rotating filter,” J. Membrane Sci., 36, 85-100 (1988).
E. C. Johnson and R. M. Lueptow, “Hydrodynamic stability of flow between rotating porous cylinders with radial and axial flow,” Phys. Fluids, 9, 3687 (1997); http://dx.doi.org/10.1063/1.869506
A. A. Kolyshkin and R. Vaillancourt, “Linear stability of Couette–Poiseuille flow between rotating permeable cylinders,” C. R. Math. Acad. Sci., Soc. R. Can., 18, No. 6, 263–268 (1996).
A. A. Kolyshkin and R. Vaillancourt, “Convective instability boundary of Couette flow between rotating porous cylinders with axial and radial flows,” Phys. Fluids, 9, No. 4, 910–918 (1997).
C.-H. Kong and C.-K. Lee, “Instability of Taylor vortex and nonaxisymmetric modes in flow between rotating porous cylinders,” J. Fluids Eng., 120, No. 4, 745–749 (1998).
S. K. Bahl, “Stability of viscous flow between two concentric rotating porous cylinders,” Defence Sci. J., 20, 89–96 (1970).
K. Min and R. M. Lueptow, “Hydrodynamic stability of viscous flow between rotating porous cylinders with radial flow,” Phys. Fluids, 6, 144 (1994); http://dx.doi.org/10.1063/1.868077
E. Serre, M. A. Sprague, and R. M. Lueptow, “Stability of Taylor-Couette flow in a finite-length cavity with radial throughflow,” Phys. Fluids, 20, No. 3, 034106–034106 (2008).
M.-H. Chang, “Hydrodynamic stability of Taylor-Dean flow between rotating porous cylinders with radial flow,” Phys. Fluids, 15, 1178 (2003); http://dx.doi.org/10.1063/1.1561283
P. Chossat and G. Iooss, “The Couette–Taylor problem,” Appl. Math. Sci., 102, Springer-Verlag, New York (1994).
V. V. Kolesov, “Calculation of auto-oscillations resulting from the loss of stability of a nonisothermal Couette flow,” Fluid Dynamics, 16, No. 3, 344–350 (1981).
V. V. Kolesov and V. I. Yudovich, “Calculation of oscillatory regimes in couette flow in the neighborhood of the point of intersection of bifurcations initiating taylor vortices and azimuthal waves,” Fluid Dynamics, 33, No. 4, 532–542.
V. V. Kolesov and A. G. Khoperskii, Simple regimes of fluid motion in the neighborhood of the intersection of bifurcations initiating nonisothermal taylor vortices and azimuthal waves,” Fluid Dynamics, 37, No. 2, 257–267.
V. Kolesov and L. Shapakidze, “On transitions near the intersection point of bifurcations in the flow between two rotating permeable cylinders,” Proc. A. Razmadze Math. Inst., 122, 79–91 (2000).
V. Kolesov and L. Shapakidze, “On oscillatory modes in viscous incompressible liquid flows between two counter-rotating permeable cylinders,” in: Trends in Applications of Mathematics to Mechanics (Nice, 1998), Chapman & Hall/CRC, Boca Raton, FL (2000), pp. 221–227.
L. Shapakidze, “On the numerical investigation of instability and transition in flow between two porous rotating cylinders with a transverse pressure gradient,” Proc. A. Razmadze Math. Inst., 148, 69–80 (2008).
V. Kolesov, S. Ovchinnikova, N. Petrovskaya, and V. Yudovich, Onset of chaos through intersections of bifurcations in a Couette–Taylor flow,” Z. Angew. Math. Mech., 76, Suppl. 4, 567–570 (1996).
P. Chossat, Y. Demay, and G. Iooss, “Interaction de modes azimutaux dans le problème de Couette–Taylor,” Arch. Rat. Mech. Anal., 99, No. 3, 213–248 (1987).
V. V. Kolesov and M. N. Romanov, “Calculation of the stationary, periodic, and quasi-periodic viscous fluid flows between two rotating permeable cylinders,” Fluid Dynamics 45, No. 6, 880–888 (2010).
V. V. Kolesov and L. D. Shapakidze, “Instabilities and transition in flows between two porous concentric cylinders with radial flow and a radial temperature gradient,” Phys. Fluids, 23, 014107 (2011); http://dx.doi.org/10.1063/1.3534026
V. V. Kolesov and A. G. Khoperskii, Nonisothermal Couette–Taylor Problem [in Russian], Rostovon-Don (2009).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Sovremennaya Matematika i Ee Prilozheniya (Contemporary Mathematics and Its Applications), Vol. 97, Proceedings of the International Conference “Lie Groups, Differential Equations, and Geometry,” June 10–22, 2013, Batumi, Georgia, Part 2, 2015.
Rights and permissions
About this article
Cite this article
Shapakidze, L. On the Nonlinear Dynamical System of Amplitude Equations Corresponding to Intersections of Bifurcations in the Flow Between Permeable Cylinders with Radial and Axial Flows. J Math Sci 218, 820–828 (2016). https://doi.org/10.1007/s10958-016-3070-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-016-3070-0