Skip to main content
SpringerLink
Log in

Perturbation Propagation in a Thin Layer of a Viscosity-Stratified Fluid

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

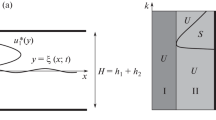
We consider a nonlinear system of equations governing the motion of a viscosity-layered fluid with a free surface in long-wave approximation. Using the semi-Lagrangian coordinates, we rewrite the governing equations in the integro-differential form and obtain necessary and sufficient hyperbolicity conditions. We approximate the integro-differential model by a finite-dimensional system of differential conservation laws and propose a model of propagation of nonlinear perturbations in a viscosity-stratified fluid.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. L. Kapitsa, “Wave flow of thin layers of a viscous fluid: I. Free flow” [in Russian], JETP, 18, 3–18 (1948); English transl.: Collected Papers of P.L. Kapitza, pp. 662–679 Pergamon, London etc. (1965).

  2. S. V. Alekseenko, V. E. Nakoryakov, and B. G. Pokusaev, Wave Flow of Liquid Films, Begell House, New York (1994).

    MATH  Google Scholar 

  3. H. C. Chang and E. A. Demekhin, Complex Wave Dynamics on Thin Films, Elsevier, San Diego (2002).

    Google Scholar 

  4. R. Govindarajan and K. C. Sahu, “Instabilities in viscosity-stratified flow,” Ann. Rev. Fluid Mech. 46, 331–353 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  5. P. Y. Lagrée, L. Staron, and S. Popinet, “The granular column collapse as a continuum: validity of a two-dimensional Navier – Stokes model with a μ(I)-rheology,” J. Fluid Mech. 686, 378–408 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  6. P. Jop, Y. Forterre, and O. Pouliquen, “A rheology for dense granular flows,” Nature 441, 727–730 (2006).

    Article  MATH  Google Scholar 

  7. O. Pouliquen and Y. Forterre, “A non-local rheology for dense granular flows,” Philos. Trans. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 367, No. 1909, 5091–5107 (2009).

    Article  MATH  Google Scholar 

  8. R. G. Bagnold, “Experiments of gravity-free dispersion of large solid spheres in a newtonian fluid under shear,” Proc. R. Soc. Lond., Ser. A 255, No. 1160, 49–63 (1954).

    Article  Google Scholar 

  9. V. M. Teshukov, “On hyperbolicity of long-wave equations” [in Russian], Dokl. Akad. Nauk SSSR 284, 555–559 (1985); English transl.: Sov. Math., Dokl. 32, 469–473 (1994).

  10. V. M. Teshukov, “Long waves in an eddying barotropic liquid” [in Russian], Prikl. Mekh. Tekh. Fiz. 35, No. 6, 823–831 (1994); English transl.: J. Appl. Mech. Tech. Phys. 35, No. 6, 17–26 (1994).

  11. I. I. Lipatov and V. M. Teshukov, “Nonlinear disturbances and weak discontinuities in a supersonic boundary layer” [in Russian], Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza No. 1, 110–125 (2004); English transl.: Fluid Dyn. 39, No. 1, 97–111 (2004).

  12. A. A. Chesnokov and P. V. Kovtunenko, “Weak discontinuities in solutions of long-wave equations for viscous flow,” Stud. Appl. Math. 132, No. 1, 50–64 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  13. D. J. Benney, “Some properties of long nonlinear waves,” Stud. Appl. Math. 52, 45–50 (1973).

    Article  MATH  Google Scholar 

  14. V. Yu. Liapidevskii and V. M. Teshukov, Mathematical Models of Propagation of Long Waves in a Non-Homogeneous Fluid [in Russian], Izd. SO RAN, Novosibirsk (2000).

    Google Scholar 

  15. V. E. Zakharov, “Benney equations and quasiclassical approximation in the method of the inverse problem” [in Russian], Funkts. Anal. Prilozh. 14, No. 2, 15–24 (1980); English transl.: Funct. Anal. Appl. 14, 89–98 (1980).

  16. V. Teshukov, G. Russo, and A. Chesnokov, “Analytical and numerical solutions of the shallow water equations for 2D rotational flows,” Math. Models Methods Appl. Sci. 14, No. 10, 1451–1479 (2004).

    Article  MathSciNet  MATH  Google Scholar 

  17. H. Nessyahu and E. Tadmor, “Non-oscillatory central differencing for hyperbolic conservation laws,” J. Comput. Phys. 87, No. 2, 408–463 (1990).

    Article  MathSciNet  MATH  Google Scholar 

  18. G. Russo, “Central schemes for conservation laws with application to shallow water equations,” In: Trends and Applications of Mathematics to Mechanics, pp. 225–246, Springer, Salerno (2005).

  19. A. Harten, B. Engquist, S. Osher, and S. Chakravarthy, “Uniformly high order accurate essentially non-oscillatory schemes. III,” J. Comput. Phys. 71, 231–303 (1987).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lavrent’ev Institute of Hydrodynamics SB RAS, 15, pr. Akad. Lavrent’eva, Novosibirsk, 630090, Russia

    P. V. Kovtunenko

  2. Novosibirsk State University, 2, ul. Pirogova, Novosibirsk, 630090, Russia

    P. V. Kovtunenko

Authors
  1. P. V. Kovtunenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. V. Kovtunenko.

Additional information

Translated from Vestnik Novosibirskogo Gosudarstvennogo Universiteta: Seriya Matematika, Mekhanika, Informatika 15, No. 2, 2015, pp. 38-50.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kovtunenko, P.V. Perturbation Propagation in a Thin Layer of a Viscosity-Stratified Fluid. J Math Sci 215, 499–509 (2016). https://doi.org/10.1007/s10958-016-2854-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-016-2854-6

Keywords

Search

Navigation