Turnpike Property in Optimal Microbial Metabolite Production

Abstract

We consider the problem of maximization of metabolite production in bacterial cells formulated as a dynamical optimal control problem (DOCP). According to Pontryagin’s maximum principle, optimal solutions are concatenations of singular and bang arcs and exhibit the chattering or Fuller phenomenon, which is problematic for applications. To avoid chattering, we introduce a reduced model which is still biologically relevant and retains the important structural features of the original problem. Using a combination of analytical and numerical methods, we show that the singular arc is dominant in the studied DOCPs and exhibits the turnpike property. This property is further used in order to design simple and realistic suboptimal control strategies.

1 Introduction

Microbial species seek to spread as much as possible, according to the availability of nutrients and resources in their surroundings, with the ultimate goal of invading their environment. As a result, when resources are limited, competition sets in between these single-cell organisms which naturally seek to keep themselves alive and develop faster than other competitors. This Darwinian adaptation capacity defines the fitness degree of each microorganism. Such a process can be formulated as a maximization problem of the microbial growth rate in order to outgrow the competitors. The microbial growth is described by ordinary differential equations and the so-called self-replicator model, which is commonly used to study the problems of resources allocation in microorganisms [14, 16, 24, 27], under the assumption that microbial species aim to optimally use their available energy to grow. This results in several applications in biotechnology, where the fitness of bacteria is used to optimize the production of high valuated compounds. Our work fits into this perspective, by developing novel theoretical and synthetic approaches for biotechnological applications. In this specific research area, optimal control theory has greatly contributed to achieving a better understanding of natural biological phenomena, and more importantly, to effectively controlling artificial cultures of microorganisms in biotechnological applications. Theoretical tools such as Pontryagin’s maximum principle (PMP, [19]) are usually combined with numerical ones like the shooting method or direct optimization approaches [3, 4], in order to provide satisfactory solutions to challenging optimization problems (DOCPs). The difficulty stems mainly from the strong nonlinearities of the models involving biological and chemical constraints. The turnpike phenomenon, which states that under some conditions the optimal solution of a given DOCP remains most of the time close to an optimal steady-state, solution of an associated static-OCP (see, e.g. [22]), is expected to provide new insights into the DOCP itself. In particular, the static solution is easier to determine and also to implement in practice. The concept of turnpike has been recently revisited in the literature and is gaining major attention within the area of optimal control [17, 20, 23, 29] due to its various applications and validity for different classes of problems. These phenomena have notably been reported in DOCP dealing with the growth of microorganisms in biotechnological systems [9, 12, 28]. Among various approaches that describe the turnpike behavior of the optimal solutions, one can cite measure type estimates as in [12] (measure turnpike) and exponential estimate as in [22] (exponential turnpike). In our case, we show that the exponential turnpike property hold and use it to devise suboptimal control strategies.

The contributions of the paper go in several directions. First, we show that the local exponential turnpike property holds on singular arcs. In contrast to known results on exponential turnpike in [22], we deal with singular trajectories. Using Pontryagin’s maximum principle and hyperbolic properties of the Hamiltonian system verified by extremals, we prove the turnpike property in the same manner as in [9, 18, 22]. Note that this result is in line with [9] where the turnpike property is shown for singular trajectories, but different since in our case the singular trajectories of the original model are of order two which strongly influences the extremal structure. Singular arcs play a major role in the solutions of the considered DOCP as was discussed in [26] and as can be seen on Fig. 5. Turnpike properties of singular arcs together with the stability of the static control allow us to construct a suboptimal control strategy by replacing the complicated singular control by a very simple constant control equal to the static control. The paper also deals with the Fuller phenomenon. It is well known (see, e.g. [30]) that the connection between bang arcs and singular arcs of intrinsic order two can only be achieved through chattering, that is by an infinite number of switchings between bang arcs over a finite time interval. This is problematic for applications and requires some approximation process, see for instance [7]. To tackle this issue we relax the problem to a simpler one which is biologically relevant and preserves most of the system structure while having the advantage of reducing the order of the single arcs by one. Consequently, the connections between the new optimal control regime no longer require chattering. Analysis of the reduced problem can be used to derive the turnpike property of the original problem since we also show that the singular flow of the two problems coincide. Thus, we construct a suboptimal open loop control law that exploits the turnpike property, with the benefits of avoiding chattering of the original solutions.

The paper is organized as follows. In Sect. 2, we introduce the full and reduced models of metabolite production and we state the DOCPs of interest. In Sect. 3, we present some numerical illustrations highlighting the turnpike feature of the optimal solutions. Then, in Sect. 4, we focus on the singular flow in the reduced DOCP, for which we prove the turnpike property along the singular trajectories. Section 5 is devoted to the turnpike property of singular trajectories in the full DOCP. Finally, we develop numerical algorithms in Sect. 6 to solve both problems that are based on singular arcs approximations by constant controls and provide numerical results in Sect. 7.

2 Model of Metabolite Production

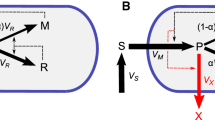
The extended self-replicator model that we consider was proposed by Giordano et al. [14], this is a coarse-grained model of resource allocation in bacteria. The cell dynamics comprises the gene expression machinery and the metabolic machinery including production of some metabolite of interest. The key elements in the reactions of the considered model are an external substrate S; a precursor metabolite P, which stands for the mass quantity of amino acids; a mass quantity of polymerase and ribosomes R, which represent the gene expression machinery; a mass quantity of enzymes involved in nutrient uptake and conversion to precursor M, which represent the metabolic machinery; a metabolite of interest X; and the volume ${\mathcal {V}}= \beta (M+R)$, where $\beta$ represents the inverse of the cytoplasmic density. The external substrate S is transformed into precursor metabolites P, which are then consumed by the gene expression and the metabolic machineries. Precursors M enable the conversion of external substrates into precursors, while R is responsible for the production of M and R itself. In addition, the model includes a metabolic pathway for the production of the metabolite of interest X. The allocation of resources over gene expression and metabolic machinery is modeled by the control function u(t), which indicates the proportional utilization of precursors for the synthesis of R and M.

For the sake of simplicity, the system variables are expressed per unit population volume, which are called concentrations, i.e. $p = \frac{P}{{\mathcal {V}}}$, $r = \frac{R}{{\mathcal {V}}}$, $m = \frac{M}{{\mathcal {V}}}$, $s = \frac{S}{{\mathcal {V}}_{\mathrm{ext}}}$, $x = \frac{X}{{\mathcal {V}}}$. The quantities p, r, m are intracellular concentrations of precursor metabolites, ribosomes and metabolic enzymes, respectively, s is the extracellular concentration of substrate with respect to a constant external volume ${\mathcal {V}}_{\mathrm{ext}}$. The m-dynamics can be expressed in terms of r and therefore is excluded from the analysis.

2.1 The Full Model

The general form of the model can be found in [14, 28]. Following the modeling steps in [14, 28], the synthesis rates in the dynamics are further taken as Michaelis–Menten kinetics. This leads to different models depending on environmental conditions. In our case we restrict our attention to the constant environmental conditions, when s is constant. We are led to the following control system with $u \in [0,1]$ the control function representing the proportion of resources allocated to gene expression (r), while $1-u$ is allocated to metabolism (m) which is excluded from the system,

$$\begin{aligned} { \begin{array}{l} {\dot{p}} = E_M(1-r) - k_1\frac{p {\left( 1 - r\right) }}{K_{1} + p} - (p+1)\frac{ p r}{K + p}, \\ {\dot{r}} = (u-r)\frac{p r}{K + p}, \\ {\dot{x}} = k_1 \frac{p {\left( 1-r\right) } }{K_{1} + p} - \frac{p r}{K + p}x, \\ {\dot{{\mathcal {V}}}} = \frac{p r}{K + p} {\mathcal {V}}, \\ \end{array}} \end{aligned}$$

(1)

with constant parameters $E_M, K, K_1, k_1$ and $p, r, x, {\mathcal {V}}$ satisfying $0< p,\ 0< x,\ 0 < {\mathcal {V}},\ 0 \le r \le 1$. The control u is assumed to be a measurable function $u: [0,T] \rightarrow [0,1]$. We denote by ${\mathcal {U}}$ the set of admissible controls. Thus, we are interested in maximization of the total quantity of the metabolite of interest X produced during time T using the resource allocation u. This amounts to maximizing the quantity $X(T) - X(0)$. By Yegorov et al. [28, Property 3.3], it is equivalent to maximization of $\ln X(T)$. Using the dynamics of $x, {\mathcal {V}}$ in (1), the cost can be expressed in variables (p, r, x) as follows (see [28] for details),

$$\begin{aligned} J_X = \ln X(T) + \mathrm {Const} = \int _0^T \frac{k_{1}}{x(t)} \frac{p(t) {\left( 1 - r(t)\right) } }{K_{1} + p(t)} \mathrm {d}t, \end{aligned}$$

(2)

where (p(t), r(t), x(t)) satisfy (1) for any $t \in [0,T]$. Notice that the dynamics of (p, r, x) do not depend on ${\mathcal {V}}$. We are led to the following optimal control problem. Find a control $u(\cdot ) \in {\mathcal {U}}$ which maximizes $J_X(u)$ for given T and (p, r, x) satisfying,

$$\begin{aligned} { \begin{array}{l} {\dot{p}} = E_M(1-r) - k_1\frac{p {\left( 1 - r\right) }}{K_{1} + p} - (p+1)\frac{ p r}{K + p}, \\ {\dot{r}} = (u-r)\frac{p r}{K + p}, \\ {\dot{x}} = k_1 \frac{p {\left( 1-r\right) } }{K_{1} + p} - \frac{p r}{K + p}x, \end{array}} \end{aligned}$$

(3)

with given initial point $(p_0, r_0, x_0)$ and free final point at final time T.

The existence of an optimal solution has already been shown in [28]. The analysis of optimal solutions made in [26, 28] shows that the singular arcs are of order two which suggests (cf. [30]) that any connection between bang and singular arcs is realized by chattering, that is, by an infinite number of switchings between bang arcs over a finite-time interval. The chattering phenomenon in optimal solution is delicate for applications because it cannot be directly implemented. To tackle this issue we propose to consider a reduced control system for which most of the structural properties still hold while the chattering phenomenon does not appear in optimal solutions. Notice first that in the model defined by (3) and (2), the control u only appears in the dynamics of r; moreover, at equilibrium we have $u=r$. In addition, r appears linearly in the dynamics of p, x and in the Lagrange cost (2).

2.2 The Reduced Model

Since r is the only variable whose time-derivative depends on the control, it is rather natural to consider the reduced system where r is no longer a state variable but a “cheap" control. This idea, similar to taking velocities as controls instead of forces for a mechanical systems, is standard [15] and also related to the Goh transformation [2]. Some authors call backstepping the process of deducing a feedback control for the full system from a feedback control for the reduced system [10]. The new state variables are (p, x) and the reduced system reads,

$$\begin{aligned} { \begin{array}{l} {\dot{p}} = E_M(1-r) - k_1\frac{p {\left( 1 - r\right) }}{K_{1} + p} - (p+1)\frac{ p r}{K + p}, \\ {\dot{x}} = k_1 \frac{p {\left( 1-r\right) } }{K_{1} + p} - x\frac{p r}{K + p}. \end{array}} \end{aligned}$$

(4)

As before, state (p, x) satisfies $0< p,\ 0 < x$ and control r satisfies $0 \le r \le 1$. The new DOCP (5) aims then to find the control r maximizing the cost (2) under the dynamical constraint (4), the state constraint $0< p,\ 0 < x$ and control constraint $0 \le r \le 1$. The initial position (p(0), x(0)) is fixed, while (p(T), x(T)) is free. So the problem is,

$$\begin{aligned} \max _{r \in {\mathcal {U}}_r} \int _0^T \frac{k_{1}}{x(t)} \frac{p(t) {\left( 1 - r(t)\right) } }{K_{1} + p(t)} \mathrm {d}t \end{aligned}$$

(5)

under the dynamical constraint (4) and $p(0) = p_0$, $x(0) = x_0$, $0 < p$, $0 < x$, where ${\mathcal {U}}_r = \{ r(\cdot ) \ \text {measurable} \ : \ 0 \le r(t) \le 1, \ t \in [0,T] \}$ is the set of admissible controls. We will call this optimal control problem the reduced problem. As a control, r is not expected to be absolutely continuous anymore but only essentially bounded. (As will be clear from the application of Pontryagin’s maximum principle, r will actually be discontinuous.) Accordingly, the reduced problem appears as a relaxation of the original one.

3 Numerical Examples Highlighting the Turnpike Features

In this section we provide numerical solutions obtained for both full and reduced models with a particular choice of parameters $E_M = k_1=K_1 = K=1$. These solutions serve as illustration for the following sections and show what turnpike property of a trajectory may look like. We anticipate on the next sections in the two following ways: (i) we say that an optimal solution is made of bang arcs, when the control is equal to either 1 or 0 (in both the reduced and full problems, the control takes values in [0, 1], where 0 and 1 are the boundary points), and singular arcs, when the control takes values in the interior of [0, 1]. In the obtained numerical solutions, we distinguish between singular or bang arcs by inspection. (ii) We use the notion of static optimal control problem which is defined in Sect. 4.2.

All the numerical solutions are obtained using direct numerical methods, which consist in solving a finite-dimensional optimization problem obtained by discretizing the optimal control problem; we use the bocop [21] software that efficiently automatizes this procedure. In bocop, both the state and control are discretized on fixed time grids. Depending on the numerical scheme chosen to approximate the dynamics (Crank–Nicolson, e.g.), these grids may coincide or not. Enforcing the pointwise state and control constraints at each grid point, one obtains a finite-dimensional optimization problem. This transformation of the original optimal control problem (described in -C++- and text files) into a nonlinear mathematical program is performed by bocop. The solver then relies on the very efficient code ipopt¹ to solve the optimization problem. A crucial step in the process is the generation of first and second order derivatives needed for the optimization; these differentials are obtained by automatic differentiation thanks to cppad.² The whole process is embedded in bocop; the v2 version of the code provides a GUI to plot the output, while v3 is part of the ct project³ and has a +python+ interface.

3.1 Turnpike Features in the Reduced Problem of Metabolite Production

In the reduced optimal control problem (5), we fix the initial condition to $x(0)=p(0)=1$. Optimal solutions have been computed⁴ For various values of T, the results are discussed in Figs. 1 and 2. See conclusions at the end of Sect. 3.2.

Fig. 1

On the left: the optimal control r(t), $t\in [0,15]$. On the right: the optimal control r(t), $t\in [0,30]$. The observed control structure is of type bang(1)-singular-bang(0); we call $t_1$ the time at the end of the first bang arc and $t_2$ the time at the end of the second and last one, they are marked on the graphics. One observes that increasing the total duration T seems to increase the duration $t_2-t_1$ of the singular arc without notably changing the durations $t_1$ and $T-t_2$ of the bang arcs. This tendency is confirmed in Fig. 2

Fig. 2

The same computation as in Fig. 1 has been repeated for various values of T between 10 and 320, $t_1$ and $t_2$ have been obtained for each T (see the table in Footnote 4) and we have plotted the values of $(t_2-t_1)/T$ against T. This confirms that the time spent on a singular arc becomes preponderant as T becomes large

Table 1 Values of the switching-instants $t_1$, $t_2$ for different time horizons [0, T], where T ranges from 10 to 320

3.2 Turnpike Features in the Full Problem of Metabolite Production

Let us now consider the initial DOCP (2)–(3). We define the associate static optimization problem.

$$\begin{aligned} \begin{aligned}&\max _{(p,r,x,u)} \quad \frac{k_{1}}{x} \frac{p {\left( 1 - r\right) } }{K_{1} + p}, \,&{\left\{ \begin{array}{ll} E_M(1-r) - k_1\frac{p {\left( 1 - r\right) }}{K_{1} + p} - (p+1) \frac{ p r}{K + p} = 0, \\ (u-r)\frac{p r}{K + p} = 0, \\ k_1 \frac{p {\left( 1-r\right) } }{K_{1} + p} - \frac{p r}{K + p}x = 0, \\ 0 \le {p}, \ 0 < {x}, \ 0 \le {r} \le 1, \ 0 \le {u} \le 1. \end{array}\right. } \end{aligned} \end{aligned}$$

(6)

Proposition 3.1

There exists a unique solution to (6) with parameters $E_M = k_1=K_1 = K=1$. This solution satisfies ${\overline{u}} = {\overline{r}}$, ${\overline{x}} = \frac{{\overline{p}}(1-{\overline{r}})}{{\overline{p}}{\overline{r}}}$, ${\overline{r}} = \frac{1}{{\overline{p}}^2+{\overline{p}}+1}$, where ${\overline{p}}$ is the unique $p>0$ maximizing $\frac{p}{(p+1)(p^2+p+1)}$.

Simple calculations give ${\overline{p}} = 0.5652$, ${\overline{x}} = 0.8846$ and ${\overline{r}} = {\overline{u}}= 0.5306$. The inequality constraints are not activated and can be disregarded in this case. The equality constraints are qualified. Thus, by the Lagrange necessary condition [13], there exists unique associated Lagrange multiplier ${\bar{\lambda }}$. For more details on the qualification of the constraints and the Lagrange necessary condition see [6]. Let us fix the initial conditions to $p(0)=x(0)=1$ and $r(0)=1/2$. The optimal trajectories (p(t), r(t), x(t)), obtained using the Bocop settings,⁵ are illustrated in Fig. 3 and the optimal control is given in Fig. 4. In Fig. 3, we observe that the optimal trajectories evolve around the static point over the time window where the control is singular (Fig. 4).

Fig. 3

The optimal trajectories for $t\in [0,40]$ in the numerical example of Sect. 3.2

Fig. 4

The optimal control u(t) for $t\in [0,40]$ in the example of Sect. 3.2

The numerical results suggest the following properties:

• the duration of the singular phase increases when we increase the final time T (Figs. 2 and 5 ),

• the duration of the singular phase increases much faster than the duration of the phase characterized by bang arcs when the time window [0, T] is large,

• for sufficiently large T, the optimal trajectories (Fig. 3) and the optimal control (Figs. 1 and 4) solutions of the reduced and the full DOCPs, stay most of the time close to the solution of the associated static-OCPs.

The fact that optimal trajectories stay most of the time near a steady state when the final time is large is known in control theory as the turnpike phenomenon. There exist different types of turnpikes, the most suitable in our case being the exponential turnpike property presented in [22]. At each time $t \in \left[ 0, T\right]$, the control u, the state z and the adjoint state $\lambda$ (defined in the next sections) satisfy the following estimate,

$$\begin{aligned} \Vert u(t) - {\bar{u}} \Vert + \Vert z(t) - {\bar{z}} \Vert + \Vert \lambda (t) - \bar{\lambda } \Vert \le C \left( {\mathrm{e}}^{-\mu t} + {\mathrm{e}}^{-\mu (T-t)}\right) , \end{aligned}$$

for some positive parameters $\mu , C$ independent from T and for time T large enough. In the following sections we will concentrate on proving the local exponential turnpike property of singular arcs.

Fig. 5

The singular arc becomes preponderant when T increases

4 Turnpike Property of the Singular Flow of the Reduced Problem

4.1 Reduced Problem

Let us start the analysis of the reduced problem defined by (2)–(4). Existence of an optimal solution follows from Filippov’s theorem [2]. Let us recall the PMP [19] as a necessary condition for optimality. Denoting by $z^r = (p,x)$ the state, by $(\lambda _0,\lambda ^r) = (\lambda _0,\lambda _p,\lambda _x) \in {\mathbb {R}}\times {\mathbb {R}}^2$ the adjoint state, and writing the cost (2) compactly $J_X = \int _0^T f^0(z,r)$, we denote by ${\mathcal {H}}^r$ the pseudo-Hamiltonian ${\mathcal {H}}^r(z^r, \lambda ^r, \lambda _0, r) = - \lambda _0 \,f_0 + \lambda _p\,{\dot{p}} + \lambda _x\,{\dot{x}}$.

Theorem 4.1

(Pontryagin’s maximum principle) If $z^r(\cdot )$ is a trajectory of (4) which maximizes the cost (2) then there exists a constant non-positive $\lambda _0$ and a map $\lambda ^r(\cdot )$, satisfying on [0, T] the following equations,

$$\begin{aligned}&{\dot{z}}^r = \frac{\partial }{\partial \lambda ^r} {\mathcal {H}}^r(z^r, \lambda ^r, \lambda _0, {\tilde{r}}), \nonumber \\&{\dot{\lambda }}^r = -\frac{\partial }{\partial z^r} {\mathcal {H}}^r(z^r, \lambda ^r, \lambda _0, {\tilde{r}}), \nonumber \\&{\mathcal {H}}^r(z^r, \lambda ^r, \lambda _0, {\tilde{r}}) = \max _{r \in \left[ 0, 1 \right] }{\mathcal {H}}^r(z^r, \lambda ^r, \lambda _0, r), \end{aligned}$$

(7)

and the transversality condition associated with the final condition $(p(T), x(T)) \in {\mathbb {R}}^n$ is $\lambda ^r(T) = 0$. A map $t\mapsto (z^r(t), \lambda ^r(t))$ that satisfies these conditions is called an extremal.

An extremal is called normal if the associated $\lambda _0$ satisfies $\lambda _0 < 0$ and abnormal if $\lambda _0 = 0$. System (7) is invariant under the rescaling of $(\lambda ^r(\cdot ),\lambda _0)$ by any positive constant and it is standard to fix $\lambda _0 = -1$ in case of normal extremals. As in [28], we note that since there is no terminal constraint for this Lagrange optimal control problem we are in the normal case. From now on we will write $H^r(z^r, \lambda ^r, r)$ for the normal pseudo-Hamiltonian associated with $\lambda _0 = -1$. The reduced control system (4) and $f^0(z,u)$ are affine in the control r. Thus, by applying the PMP the corresponding pseudo-Hamiltonian can be written ${H}^r (z^r, \lambda ^r, r) = H^r_0(z^r, \lambda ^r) + r\,H^r_1(z^r, \lambda ^r)$, where the switching function $H^r_1$ is as follows,

$$\begin{aligned} H^r_1= & {} \left( \frac{k_1p}{p + K_1} - \frac{(p + 1)p}{K + p} -E_M \right) \lambda _p \nonumber \\&- \left( \frac{k_1p}{p + K_1} + \frac{px}{K + p} \right) \lambda _x - \frac{k_1p}{x(p + K1)}. \end{aligned}$$

(8)

From maximization condition in PMP, it follows that the value of the optimal control depends on the values of the switching function $H^r_1$. The dependence is as follows. If $H^r_1(z^r(t), \lambda ^r(t)) > 0$ on some time interval $[a_1, b_1]$ then $r(t) = 1$ on $[a_1, b_1]$; if $H^r_1(z^r(t), \lambda ^r(t)) < 0$ on some time interval $[a_2, b_2]$ then $r(t) = 0$ on $[a_2, b_2]$. Finally, if $H^r_1(z^r(t), \lambda ^r(t)) = 0$ on some time interval $[a_3, b_3]$ then the corresponding control r is singular on $[a_3, b_3]$. The optimal control is then a concatenation of bang controls $u \equiv 1$, bang controls $u \equiv 0$ and singular controls.

From the transversality condition $\lambda ^r(T) = 0$, it follows that $\lambda _p(T) = \lambda _x(T) = 0$. Substituting $\lambda _p(T) = \lambda _x(T) = 0$ in (8) and taking into account $p,x > 0$, we deduce $H^r_1(z(T), \lambda (T)) \ne 0$. By continuity of $H^r_1(t)$, there exists $\epsilon > 0$ such that r is not singular on $[T-\epsilon , T]$ which means that any extremal ends with a bang arc. Moreover, from $H^r_1(T) = - \frac{k_1p}{x(p + K1)} < 0$, we deduce that the final bang control is $r \equiv 0$.

4.2 Static Problem

Now let us define the static problem corresponding to the reduced problem (5). In the static problem we are looking for the steady state of the dynamics (4) at which the cost (2) reaches its maximum. Let us denote the dynamics (4) of $z^r$ by $\dot{(z^r)} = f_r(z^r,r)$. The static problem is defined as follows.

$$\begin{aligned} \begin{aligned}&\max f^0(z^r,r), \,\,\, {\text {s.t.}} \,\,\, {\left\{ \begin{array}{ll} f_r(z^r,r)=0,&{} \\ 0 < p, x, &{} 0 \le r \le 1. \end{array}\right. } \end{aligned} \end{aligned}$$

(9)

Let us define in the same way the static problem corresponding to the original problem defined by (1), (2).

$$\begin{aligned} \begin{aligned}&\max f^0(z^r,r), \,\,\, {\text {s.t.}} \,\,\,&{\left\{ \begin{array}{ll} f_r(z^r,r)=0, &{}\quad (u-r)\frac{p r}{K + p} = 0, \\ 0 < p, x, &{}\quad 0 \le r,u \le 1. \end{array}\right. } \end{aligned} \end{aligned}$$

(10)

As $\frac{p}{K + p}$ is positive, the solution of (10) satisfies either $r=0$ or $u=r$. At $r=0$, we have $\dot{x} = \frac{k_1 p}{K_1 + p} \ne 0$ (here we avoid the case $k_1 = 0$ because in this case $f^0(z^r,r) \equiv 0$) and $f_r(z^r,r)=0$ is not satisfied. The solution of (10) satisfies therefore $r>0, \ u=r$. Both cost and equations in (10) do not depend on u, as a result, the value of r optimal for (10) coincides with the value optimal for (9). Hence, we proved the following result.

Proposition 4.1

Solution ($\bar{p}$, $\bar{x}$, $\bar{r}$) of the static problem (10) coincides with the solution of the static problem (9).

From the form of $f_r(z^r,r)$ given by (4), r and x can be expressed as rational functions of p and the problem of maximization of $f^0(z^r,r)$ can be reformulated as a problem of maximization of a rational function $f^0(z^r(p),r(p))$ on $p > 0$. It was shown in [28] that the value of p maximizing $f^0$ is unique in the domain $p>0$ for (10). As a consequence of Proposition 4.1, the same holds for (9). The solution of the static-OCP is called the static point. The inequality constraints are not activated and can be disregarded in both cases (9) and (10), the equality constraints are qualified at the optimum in both cases. With the same arguments as in [6], we can apply the Lagrange necessary condition [13] to (9), (10) and deduce the existence of the unique Lagrange multiplier. Here we are interested in the components of the Lagrange multiplier dual to the variables representing the state in the OCP counterparts of (9), (10). Thus we denote by ${\bar{\lambda }}$ the dual variables to $({{\bar{p}}}, {{\bar{x}}}, {{\bar{r}}})$ and ${\bar{\lambda }}^r$ the components of ${\bar{\lambda }}$ dual to $({{\bar{p}}}, {{\bar{x}}})$.

4.3 Singular Flow

Let us now consider in more details the singular control. First, we denote $H^r_{01} = \{H^r_0,H^r_1\}$ and by induction $H^r_{0i} = \{H^r_0,H^r_i\}$ and $H^r_{1i} = \{H^r_1,H^r_i\}$, where i is any sequence of 0s and 1s and $\{\cdot , \cdot \}$ is the Poisson bracket. The singular control is the control corresponding to the case $H^r_1(t) \equiv 0$ on some time interval. The value of singular control can be obtained by differentiating $H^r_1(t) = 0$, see [2, 5] for more details. The order of the control is the smallest number d such that the control u can be expressed from, $\frac{{\mathrm{d}}^{2d}}{{\mathrm{d}}t^{2d}} H^r_1(t) = 0.$ In the case of reduced problem, the control can be obtained from, $\frac{{\mathrm{d}}^{2}}{{\mathrm{d}}t^{2}} H^r_1(z^r, \lambda ^r) = H^r_{001}(z^r, \lambda ^r) + r H^r_{101}(z^r, \lambda ^r).$ Thus, the singular control is of order 1 and is defined by: $r_s = - \frac{H^r_{001}(z^r, \lambda ^r)}{H^r_{101}(z^r, \lambda ^r)}.$ According to [30], if the singular control is of order 1, then the connection between bang control and singular control is a simple connection: the chattering phenomenon does not occur in solutions to the reduced problem. The extremals associated with the singular control are called singular extremals; they stay in the singular surface: $\varSigma _r = \left\{ (z^r,\lambda ^r) \in {\mathbb {R}}^{4} \, | \, H^r_1 = 0, \ H^r_{01} = 0 \right\}$.

Proposition 4.2

In some neighborhood of $({\bar{p}}, {\bar{x}})$ solution of the static-OCP (9), the singular surface is a smooth surface defined by $(\lambda _p, \lambda _x) = (\lambda _p(p, x), \lambda _x(p, x))$ solution of the following nonsingular linear equation:

$$\begin{aligned} \begin{aligned}&a_1(p,x) \lambda _p + b_1(p,x) \lambda _x =c_1(p,x),\\&a_2(p,x) \lambda _p + b_2(p,x) \lambda _x =c_2(p,x), \end{aligned} \end{aligned}$$

(11)

with coefficients $a_1, a_2, b_1, b_2, c_1, c_2$ defined by,

$$\begin{aligned} \begin{aligned}&H_1(p,x,\lambda _p, \lambda _x) = a_1(p,x) \lambda _p + b_1(p,x) \lambda _x - c_1(p,x),\\&H_{01}(p,x,\lambda _p, \lambda _x) = a_2(p,x) \lambda _p + b_2(p,x) \lambda _x - c_2(p,x). \end{aligned} \end{aligned}$$

Proof

By definition of the singular surface, $(\lambda _p, \lambda _x)$ satisfy (11), which admits a unique solution if and only if the matrix $\varDelta = \left( {\begin{matrix} a_1 &{} b_1 \\ a_2 &{} b_2 \end{matrix}}\right)$ is invertible. Let $D = D(p,x)$ be the determinant of $\varDelta$. At an equilibrium of (4) we have,

$$\begin{aligned} \begin{aligned}&x = \frac{(p + 1) \mu _1}{E_M - \mu _1}\,\,\,\,\,\, \text {and} \,\,\,\,\,\, r = \frac{E_M - \mu _1}{E_M - \mu _1 +(p+1)\mu _2}, \end{aligned} \end{aligned}$$

(12)

with $\mu _1 = k_1 \, p\,/\,(K_1 + p)$ and $\mu _2 = p\,/\,(K + p)$. Substituting (12) into $\varDelta (p,x)$ and $f^0(p,r,x)$ yields, through symbolic computations conducted in Maple,

$$\begin{aligned} D(p, x(p)) \, f^0(p, r(p), x(p)) = \frac{p^2 (p + 1) E_M k_1 K_1}{(p+K)^2(p+K_1)^2}. \end{aligned}$$

Since the right-hand side is different from 0, we conclude that $D({{\bar{p}}},{{\bar{x}}}) \ne 0$. The function D(p, x) is continuous and thus it is different from zero in some neighborhood of $({{\bar{p}}},{{\bar{x}}})$, which implies existence of a unique solution of system (11). $\square$

Substitution of the singular control $r_s$ in (7) gives, with $H^r$ defined from ${\mathcal {H}}^r$ right after (7),

$$\begin{aligned} \dot{z^r} = \frac{\partial H^r}{\partial \lambda ^r}(z^r, \lambda ^r, r_s(z^r, \lambda ^r)), \qquad \dot{\lambda ^r} = - \frac{\partial H^r}{\partial z^r}(z^r, \lambda , r_s(z^r, \lambda ^r)). \end{aligned}$$

(13)

Defining the singular Hamiltonian by $H_s(z^r, \lambda ^r) = H^r(z^r, \lambda ^r, r_s(z^r, \lambda ^r))$, and since the derivative of H with respect to its third argument (control r) is zero on $\varSigma _r$, we can rewrite (13) as follows:

$$\begin{aligned} {\dot{z}}^r = \frac{\partial H_s}{\partial \lambda ^r}(z^r, \lambda ^r), \qquad \dot{\lambda ^r} = - \frac{\partial H_s}{\partial z^r}(z^r, \lambda ^r), \qquad (z^r, \lambda ^r) \in \varSigma _r\,, \end{aligned}$$

(14)

and we have the following result (Proof in “Appendix A”).

Proposition 4.3

The singular system (14) is the Hamiltonian system associated with the smooth Hamiltonian $H_s$ on the smooth submanifold $\varSigma _r$ in a neighborhood of $({\bar{p}}, {\bar{x}},\lambda _p({{\bar{p}}},{\bar{x}}), \lambda _x({{\bar{p}}}, {{\bar{x}}}))$.

By a straightforward adaptation of arguments from [6], we have the following relation between the equilibrium of singular Hamiltonian system and the static point.

Theorem 4.2

Point $({\bar{z}}^r,\bar{\lambda }^r)$ with $r_s({\bar{z}}^r,\bar{\lambda }^r) \in \left( 0,1 \right)$ is an equilibrium of the singular Hamiltonian system (14) if and only if $({\bar{z}}^r,{\bar{r}})$ with ${{\bar{r}}} = r_s({\bar{z}}^r,\bar{\lambda }^r)$ is an extremal value of the static problem (9).

4.4 Turnpike Theorem

The main result of this section is given by Theorem 4.3, in which we show local exponential turnpike property of a singular extremal, solution of (14). We assume that a solution of (14) is well defined on a time interval $[t_1, t_2]$.

Theorem 4.3

There exists $\epsilon >0$ such that, if $z^r(\cdot )$ is singular and satisfies (14) on $[t_1, t_2]$ , ${{\bar{z}}}_r$ is the solution of static OCP (9), and if

$$\begin{aligned} \Vert z^r(t_1) - {{\bar{z}}}_r \Vert + \Vert z^r(t_2) - {{\bar{z}}}^r \Vert \le \epsilon , \end{aligned}$$

then there exists $C>0$ such that for any $t \in \left[ t_1, t_2 \right]$ there holds

$$\begin{aligned} \Vert z^r(t) - {{\bar{z}}}_r \Vert + \Vert \lambda ^r(t) - {\bar{\lambda }}^r \Vert + | r_s(t) - {\bar{r}}| \le C \left( {\mathrm{e}}^{\mu (t_1-t)} + {\mathrm{e}}^{\mu (t-t_2)}\right) , \end{aligned}$$

(15)

where $\mu = {{\bar{p}}} \,{{\bar{r}}}\,/(K + {{\bar{p}}})\,$.

The singular arc belongs to 2-dimensional surface $\varSigma _r$ and, by Proposition 4.2, can be parameterized by (p, x) near the solution of the static problem $({\bar{p}}, {\bar{x}})$. Notice that the singular control of the reduced problem $r_s$ is a function only of p, and thus, we can rewrite the singular system as follows,

$$\begin{aligned} {\dot{p}} = f_p(p), \ {\dot{x}} = f_r(p) - \frac{p r(p)}{K+p} \, x. \end{aligned}$$

(16)

Let us introduce perturbations of the singular arc on ${\varSigma _r}$ near $({\bar{p}}, {\bar{x}})$, $\delta p = p(t) - {\bar{p}}, \ \delta x = x(t) - {\bar{x}}, \ \delta r = r(t) - {\bar{r}}$.

By definition, $(\delta p, \delta x)$ satisfy,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \begin{pmatrix} \delta p \\ \delta x\end{pmatrix} = {\mathbf {H}} \begin{pmatrix} \delta p \\ \delta x\end{pmatrix} + \begin{pmatrix} o_1(\delta p, \delta x) \\ o_2(\delta p, \delta x) \end{pmatrix} \quad \text {with} \quad {\mathbf {H}} = \begin{pmatrix} * &{}\quad 0 \\ * &{}\quad - \frac{{{\bar{p}}} {{\bar{r}}}}{K+ {{\bar{p}}}}\end{pmatrix}, \end{aligned}$$

(17)

and $o_1, o_2$ are $C^1$ functions on some neighborhood of $(0,0) \in {\mathbb {R}}^{2n}$ which have a little-o behavior. The linear part of (17) defines the linearized system,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \begin{pmatrix} \delta p \\ \delta x\end{pmatrix} = {\mathbf {H}} \begin{pmatrix} \delta p \\ \delta x\end{pmatrix}. \end{aligned}$$

(18)

Lemma 4.1

The matrix ${\mathbf {H}}$ is hyperbolic with opposite eigenvalues.

Proof

Consider the linearized system (18) in canonical coordinates,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \begin{pmatrix} \delta z_s \\ \delta \lambda _s\end{pmatrix} = {\mathbf {H}}_s \begin{pmatrix} \delta z_s \\ \delta \lambda _s\end{pmatrix}, \qquad {\mathbf {H}}_s = \begin{pmatrix}\frac{\partial ^2 h_s}{\partial \lambda _s \partial z_s}({\bar{z}}_s, \bar{\lambda }_s) &{}\quad \frac{\partial ^2 h_s}{\partial \lambda _s^2}({\bar{z}}_s, \bar{\lambda }_s) \\ \frac{\partial ^2 h_s}{\partial z_s^2}({\bar{z}}_s, \bar{\lambda }_s) &{}\quad -\frac{\partial ^2 h_s}{\partial \lambda _s \partial z_s}({\bar{z}}_s, \bar{\lambda }_s) \end{pmatrix}. \end{aligned}$$

(19)

The matrix ${\mathbf {H}}_s$ is traceless, and thus, so is ${\mathbf {H}}$. Therefore, eigenvalues of ${\mathbf {H}}$ are $\mu , \ -\mu$ with, $\mu = \dfrac{{{\bar{p}}} {{\bar{r}}}}{K+ {{\bar{p}}}} > 0$. $\square$

As ${\mathbf {H}}$ is hyperbolic, there exists a change of coordinates $A = (a_{i,j})$, $(g, h)^\top = A (\delta p, \delta x)^\top$, such that (18) in these coordinates takes the following form,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \begin{pmatrix} g \\ h\end{pmatrix} = \begin{pmatrix} -\mu &{}\quad 0 \\ 0 &{}\quad \mu \end{pmatrix} \begin{pmatrix} g \\ h\end{pmatrix} + \begin{pmatrix} {{\tilde{o}}}_1(g, h) \\ {{\tilde{o}}}_2(g, h) \end{pmatrix}. \end{aligned}$$

(20)

Lemma 4.2

[18] For any $T>0$ there exists $\rho > 0$ such that the following two statements hold.

• For any $(g_0, h_T) \in B(0, \frac{\rho }{K})$ there exists the unique $\left( g, h \right) \in C^1\left( \left[ 0,T \right] , {\mathbb {R}}^{2} \right)$ satisfying (20) and $g(0) = g_0, \ h(T) = h_T, \ \left| g(t) \right| + \left| h(t) \right| \le \rho , \ t \in [0,T].$

• The map $\varPhi$ defined by $\varPhi (g_0, h_T) = \left( g(\cdot ), h(\cdot ) \right)$ is continuous.

Lemma 4.3

[18] Let $\mu \in {\mathbb {R}}_+$ be the positive eigenvalue of ${\mathcal {H}}$. There exists ${r}_{\mu } \in (0, \infty )$ independent of $T \in (0, \infty )$ and functions $\theta _1, \theta _2 \in C_0\left( [0, {\bar{r}}_{\mu }]; {\mathbb {R}}_+ \right)$ satisfying $\theta _i(\beta ) \xrightarrow [\beta \ \rightarrow \ 0+]{} 0$ for $i = 1,2$, such that if (g, h) satisfies (20) and $\left| g(t)\right| + \left| h(t) \right| \le {r}_{\mu }, \ t \in [0, T]$, then for any $t \in [0, T]$ there holds

$$\begin{aligned}&\left| g(t) \right| \le C_{\mu } \left( \left| g(0)\right| \, {\mathrm{e}}^{-\mu t} + {\mathrm{e}}^{-\mu (T-t)} \, \left| h(T)\right| \, \theta _1(\Vert h\Vert _{c^0})\right) ,\nonumber \\&\left| h(t) \right| \le C_{\mu } \left( \left| h(T)\right| \, {\mathrm{e}}^{-\mu (T-t)} + {\mathrm{e}}^{-\mu t}\, \left| g(0)\right| \, \theta _2(\Vert g\Vert _{c^0})\right) . \end{aligned}$$

(21)

Proof of Theorem 4.3

By Proposition 4.2, there exists a neighborhood $V \subset {\mathbb {R}}^2$ of ${{\bar{z}}}_r$ such that in this neighborhood solutions of (14) can be parameterized by (p, x) and satisfy (16). Let us choose ${\tilde{\epsilon }}$ such that $z^r$ satisfying $\Vert z^r - {{\bar{z}}}_r \Vert \le {{\tilde{\epsilon }}}$ belong to V. We consider the perturbed system (18). Applying Lemmas 4.2 and 4.3 to the diagonalized system (20), we have existence of $r_{\mu }>0$ such that if

$$\begin{aligned} g(0)= & {} a_{1,1}\, \delta p(0) + a_{1,2}\, \delta x(0), \nonumber \\ h(T)= & {} a_{2,1}\, \delta p(T) + a_{2,2}\, \delta x(T) \end{aligned}$$

(22)

satisfy $\left| g(0) \right| + \left| h(T) \right| \le r_{\mu }$ then (g(t), h(t)) satisfy (21) for $t \in [0,T]$ and any final time T. Coming back to the initial coordinates $(\delta p, \delta x)$, if, $|\delta p(0)| + |\delta x(0)| + |\delta p(T)| + |\delta x(T)| \le \Vert A\Vert \, r_{\mu },$ then,

$$\begin{aligned} | \delta p(t) | + | \delta x(t) | \le \Vert A \Vert ^{-1} \left( | g(t) | + | h(t) |\right) , \end{aligned}$$

and as (21) applies, there exists a positive constant C such that,

$$\begin{aligned} \left| \delta p(t) \right| + \left| \delta x(t) \right| \le C \left( {\mathrm{e}}^{\mu (t_1-t)} + {\mathrm{e}}^{\mu (t-t_2)}\right) . \end{aligned}$$

Note that along the singular arc, r is a continuous functions of (p, x). By Proposition 4.2, $\lambda _s = \lambda _s(p,x)$ continuous near ${{\bar{z}}}_r$. As a conclusion, up to a change of constant C, we obtain (15) which ends the proof. $\square$

The obtained result concerns a singular arc. What about the whole solution? The numerical results obtained in Sect. 3.1 suggest that when the final time is large, any optimal solution contains a singular arc. Moreover, the singular arc constitutes the major part of a solution and this part grows relatively to the other part of trajectory when we increase the final time as in Fig. 1. These observations lead us to the following conjecture.

5 Turnpike Property of the Singular Flow of the Original Problem

Let us now come back to the original OCP given by dynamics (3) and cost (2). The first steps in the analysis of this OCP were done in [28]. In particular, they showed the existence of optimal solutions, the obtained numerical results showing signs of the turnpike behavior of solutions and analytic results showing the absence of the so-called exact turnpike (see [28] for more details). We will go further in the analysis of the turnpike property and show analytically that the singular arcs admit the local exponential turnpike property.

We denote by $z = (p,r,x)$ the state, by $\lambda = (\lambda _p,\lambda _r,\lambda _x) \in {\mathbb {R}}^3$ the adjoint state, and by ${\mathcal {H}}$ the pseudo-Hamiltonian associated with (3) and cost (2): ${\mathcal {H}}(z, \lambda , u) = f_0 + \lambda _p\,{\dot{p}} + \lambda _r\,{\dot{r}} + \lambda _x\,{\dot{x}}.$ We may also define as follows $H_0$ and $H_1$, in a unique way of expressing ${\mathcal {H}}$ as an affine function of the control: ${\mathcal {H}}(z, \lambda , u) = H_0(z, \lambda ) + u\,H_1(z, \lambda ).$ From PMP, each optimal $z(\cdot )$ satisfies, for some $\lambda (\cdot )$, the generalized Hamiltonian system,

$$\begin{aligned}&{\dot{z}} = \frac{\partial }{\partial \lambda } {\mathcal {H}}(z, \lambda , {\tilde{u}}), \nonumber \\&{\dot{\lambda }} = -\frac{\partial }{\partial z} {\mathcal {H}}(z, \lambda , {\tilde{u}}), \nonumber \\&{\mathcal {H}}(z, \lambda , {\tilde{u}}) = \max _{u \in \left[ 0, 1 \right] }{\mathcal {H}}(z, \lambda , u). \end{aligned}$$

(23)

Each solution of (23) is a concatenation of bang and singular arcs.

5.1 Singular Flow

Let us focus on the singular arcs. It was shown in [26, 28] that, at least in a neighborhood of the static equilibrium,

$$\begin{aligned} H_1=\frac{\lambda _r\,p\,r}{K+p}, \quad H_{101}=\frac{p}{K+p} H_{01}, \quad H_{10001}\ne 0. \end{aligned}$$

(24)

As a result, singular controls are of order 2 and are obtained from $\frac{{\mathrm{d}}^{4}}{{\mathrm{d}}t^{4}} H_1(t) = 0$:

$$\begin{aligned} u_s = - \frac{H_{00001}(z, \lambda )}{H_{10001}(z, \lambda )}. \end{aligned}$$

(25)

The corresponding singular extremals belong to the singular surface defined by,

$$\begin{aligned} \varSigma = \left\{ (z,\lambda ) \in {\mathbb {R}}^{6} \, | \, H_1 = 0, \ H_{01} = 0 , \ H_{001} = 0, \ H_{0001} = 0 \right\} . \end{aligned}$$

Notice that $H_1 = 0$ implies $\lambda _r = 0$, as we work locally near the static point. As in the reduced problem, we substitute the expression of $u_s$ as a function of $(z,\lambda )$ in ${\mathcal {H}}(z, \lambda , u)$ and obtain the singular Hamiltonian $H_s(z,\lambda ) = {\mathcal {H}}(z, \lambda , u_s(z,\lambda ))$. The system (23) becomes accordingly

$$\begin{aligned} {\dot{z}} = \frac{\partial H_s}{\partial \lambda }(z, \lambda )\,,\ \ {\dot{\lambda }} = - \frac{\partial H_s}{\partial z}(z, \lambda ) \,,\quad (z,\lambda )\in \varSigma \,. \end{aligned}$$

(26)

The flow of this system is called the singular flow. It is characterized by the following result, similar to Proposition 4.3, and whose proof is also deferred to “Appendix A”.

Proposition 5.1

$\varSigma$ is a smooth submanifold of co-dimension 4 and the singular system (26) is the Hamiltonian system on $\varSigma$ associated with the Hamiltonian $H_s$.

We will now establish a relation between the singular flow of the original optimal control problem given by dynamics (3) and cost (2) and the singular flow of the reduced problem (5).

Theorem 5.1

If the singular control $u_s$ given by (25) satisfies $0< u_s < 1$, then singular trajectory $(p(\cdot ), r(\cdot ), x(\cdot ))$ of OCP (1), (2) coincides with $({{\tilde{p}}}(\cdot ), {{\tilde{r}}}(\cdot ), {{\tilde{x}}}(\cdot ))$ where ${{\tilde{r}}}(\cdot )$ is the singular control and $({{\tilde{p}}}(\cdot ), {{\tilde{x}}}(\cdot ))$ is the singular trajectory of (5). Moreover, the singular surface of OCP (1), (2) can be written as follows

$$\begin{aligned} \varSigma = \left\{ (p,r,x,\lambda _p, \lambda _r, \lambda _x) \in {\mathbb {R}}^{6} \, | \, (p,x,\lambda _p, \lambda _x) \in \varSigma _r, \, \lambda _r = 0,\, r = r_s\right\} . \end{aligned}$$

(27)

Proof

A trajectory of (1), (2) is singular if and only if $\lambda _r = 0$. Notice that, ${\mathcal {H}} = H^r_0 + r \, H^r_1 + H_1 \left( u - r\right) ,$ and therefore,

$$\begin{aligned} \frac{\partial {\mathcal {H}}}{\partial r} = H^r_1 + \lambda _r \frac{p}{K+p}(u - 2r). \end{aligned}$$

(28)

Let us differentiate $\lambda _r = 0$ along singular solutions of (23). Using (28), we get,

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}}{{\mathrm{d}}t} \lambda _r = \left. -\frac{\partial {\mathcal {H}}}{\partial r} \right| _{\lambda _r = 0} = - H^r_1 = 0,\\&\frac{{\mathrm{d}}^2}{{\mathrm{d}}t^2} \lambda _r = \left. -\frac{{\mathrm{d}}}{{\mathrm{d}}t}\left( \frac{\partial {\mathcal {H}}}{\partial r}\right) \right| _{\lambda _r = 0, {{\dot{\lambda }}}_r = 0} = - \frac{{\mathrm{d}}}{{\mathrm{d}}t} \left( H^r_1 \right) = 0,\\&\frac{{\mathrm{d}}^3}{{\mathrm{d}}t^3} \lambda _r = \left. -\frac{{\mathrm{d}}^2}{{\mathrm{d}}t^2}\left( \frac{\partial {\mathcal {H}}}{\partial r}\right) \right| _{\lambda _r = 0, {{\dot{\lambda }}}_r = 0, \ddot{\lambda }_r = 0} = - \frac{{\mathrm{d}}^2}{{\mathrm{d}}t^2} \left( H^r_1 \right) = 0. \end{aligned} \end{aligned}$$

(29)

Now notice that the first two equations from (29) are equivalent to (11) and define the condition $(p,x,\lambda _p, \lambda _x) \in \varSigma _r$. The last equation from (29) can be written as, $\frac{{\mathrm{d}}^2}{{\mathrm{d}}t^2} \left( H^r_1 \right) = H_{001} + r \, H_{101}$, thus, r satisfying this equation is exactly the singular control $r_s$. On the other hand, the left-hand side of (29) together with $\lambda _r = 0$ defines the singular surface of the initial OCP problem and so we get (27). Finally, the dynamics of (p, x) in (1) does not depend on u, but depend on r which is given by $r=r_s$. $\square$

Proposition 5.2

At least for (p, x, r) close to the solution $({{\bar{p}}},{{\bar{x}}},{{\bar{r}}})$ of the static problem (9), (p, x) can be chosen as coordinates on the singular surface $\varSigma$, i.e. the latter has an equation of the form $r=r_s(p,x)$, $\lambda =A(p,x)$ with some smooth function A; in these coordinates, the equation for the singular extremals are:

$$\begin{aligned} \dot{z^r} = f_r(z^r, r_s(z^r)). \end{aligned}$$

Proof

By Proposition 4.2, $\lambda _p = \lambda _p (p, x), \lambda _x = \lambda _x(p,x)$ and $r = r_s(p,x)$, thus $\varSigma$ is parameterized by (p, x). $\square$

Remark 5.1

Symbolic calculations using Maple show that $r = r_s(p, x)$ is independent of x, that is $r_s = r_s(p)$.

The following counterpart of Theorem 4.2 states the relation between the static point and the equilibrium of the singular Hamiltonian system.

Theorem 5.2

Point $({\bar{z}},\bar{\lambda })$ with $u_s({\bar{z}},\bar{\lambda }) \in (0,1)$ is an equilibrium of the singular Hamiltonian system (26) if and only if $({\bar{z}},{\bar{u}})$ with ${{\bar{u}}} = u_s({\bar{z}},\bar{\lambda })$ is an extremal value of the static problem (10).

5.2 Turnpike Theorem

We are in position to prove the local exponential turnpike property of singular arcs of the original problem.

Theorem 5.3

There exists $\epsilon >0$ such that, if $z(\cdot )$ is singular and satisfies (26) on $[t_1, t_2] \subset [0,T]$, ${{\bar{z}}} = ({{\bar{z}}}_r, {{\bar{r}}})$ is the static point, solution of (9), and if

$$\begin{aligned} \Vert z(t_1) - {{\bar{z}}} \Vert + \Vert z(t_2) - {{\bar{z}}} \Vert \le \epsilon , \end{aligned}$$

(30)

then there exists $C>0$ such that for any $t \in \left[ t_1, t_2 \right]$ there holds

$$\begin{aligned}&\Vert z(t) - {{\bar{z}}} \Vert + |u_s(t) - {{\bar{u}}} | + \Vert \lambda (t) - {\bar{\lambda }} \Vert \nonumber \\&\quad \le C \left( {\mathrm{e}}^{\mu (t_1-t)} + {\mathrm{e}}^{\mu (t-t_2)}\right) , \end{aligned}$$

(31)

where $\mu = {{\bar{p}}} \,{{\bar{r}}}\,/(K + {{\bar{p}}})\,$.

Proof

By Theorem 5.1, the singular trajectories in the original problem (2)–(3) and the reduced problem (2)–(4) coincide. As a consequence on Theorem 4.3, condition (30) implies, $\Vert z_s(t) - {\bar{z}} \Vert + \Vert \lambda (t) - \bar{\lambda } \Vert + \left| r_s(t) - {\bar{r}} \right| \le C \left( {\mathrm{e}}^{\mu (t_1-t)} + {\mathrm{e}}^{\mu (t-t_2)}\right)$. We notice that $\lambda _r = 0$ and that the singular control $u_s$ is a continuous function of $(z, \lambda )$. This implies (31), up to some update of the constant C, which ends the proof. $\square$

In the case of optimal control problem (2)–(3), simulations show the predominance of the singular arcs and as a consequence, we observe the turnpike of the full solution as can be seen in Fig. 5 where the results are shown for increasing sequence of final times. As in the case of the reduced problem, we formulate a conjecture on the turnpike property of the optimal solutions of (2)–(3).

6 Suboptimal Control Strategies

6.1 Stability Properties

In this section we show stability properties of the dynamical systems obtained by taking the static value ${\bar{r}}$ in the reduced case and ${\bar{u}}$ in the complete case as a constant control. This control choice is particularly interesting because it provides a very simple but efficient approximation of the singular control. This approximation is further used in the design of numerical methods for both reduced and full problems. The stability properties justify the use of the constant control that will allow to reach the turnpike exponentially fast. (It would not be the case without stability.) Notice that in our case the singular control is given by a complicated rational function and the possibility to approximate this function by a simple constant control without a significant loss in the cost is particularly useful for applications.

6.1.1 Reduced Case

We start the analysis of the stability properties by considering the case of the reduced problem (4), (2).

Theorem 6.1

Assume $K = K_1$. Let $({{\bar{p}}}, {{\bar{x}}}, {{\bar{r}}})$ be the solution of the static problem (9) and let (p, x) be the solution of (4) corresponding to $r \equiv {\bar{r}}$ and the initial data $(p(0), x(0)) =(p_0, x_0)$. Then there exist constants $\beta = \beta (p_0) >0$ and $C = C(p_0, x_0) >0$ such that the following inequality holds for any $t>0$

$$\begin{aligned} \left| p(t) - {\bar{p}} \right| + \left| x(t) - {\bar{x}} \right| \le C\, {\mathrm{e}}^{- \beta t} . \end{aligned}$$

(32)

Proof

First, let us denote $\psi (p) = \frac{p}{p+K}$. This function is strictly increasing and positive for $p >0$. Recall if $r(t) = {\bar{r}}$ for $t \in [0, T]$ then $({{\bar{p}}}, {{\bar{x}}})$ is the equilibrium of (4). This permits to rewrite (4) in the following form

$$\begin{aligned} \begin{aligned} {\dot{p}}&= - \frac{1}{p+K} \left( \frac{K \left( k_1\left( 1 -{\bar{r}}\right) + {\bar{r}}\left( 1 +{\bar{p}}\right) \right) }{{\bar{p}}+K} + {\bar{r}} p \right) \left( p -{\bar{p}}\right) , \\ {\dot{x}}&= -{\bar{r}}\psi (p)\left( x -{\bar{x}}\right) , \end{aligned} \end{aligned}$$

(33)

which can be written in a simpler form as ${\dot{p}} = - d_1(p) \left( p -{\bar{p}}\right) , \ {\dot{x}} = -d_2(p)\left( x -{\bar{x}}\right)$. Coefficients $d_1, d_2$ satisfy $d_1(p) > d_1(0)$ for any $p > 0$ and $d_1(0) > 0$ and, in addition, $d_2(p(t))$ is such that $d_2(p(t)) > d_2(p_0)$ if $p_0 < {\bar{p}}$ and $d_2(p(t)) > d_2({\bar{p}})$ if $p_0 > {\bar{p}}$. Let us denote $V_p = \left| p(t) - {\bar{p}} \right|$, $V_x = \left| x(t) - {\bar{x}} \right|$. Outside $p={\bar{p}}$ and $x={\bar{x}}$, we have, $\dot{V}_p \le - d_1 V_p$, and $\dot{V}_x \le - d_2 V_x$, with $d_1 = d_1(0)$ and $d_2 = \min \{ d_2(p_0), d_2({\bar{p}})\}$. This implies (32). $\square$

In general there is no relation between $K, K_1$, so let us consider the case without assumptions on parameters.

Lemma 6.1

Point $({{\bar{p}}}, {{\bar{x}}})$ is the unique stable equilibrium of (4) with $r \equiv {\bar{r}}$ in $\varOmega$.

Proof

The uniqueness is a consequence of the uniqueness of the equilibrium $({{\bar{p}}}, {{\bar{r}}},{{\bar{x}}})$ of (1). The linearized matrix of (4) is of the following form

$$\begin{aligned} \begin{pmatrix} - ({{\bar{p}}}+1)\mu _2'({\bar{p}}, {\bar{r}}) - \mu _2({\bar{p}}, {\bar{r}}) - \mu _1'({\bar{p}}, {\bar{r}}) &{}\quad 0 \\ * &{}\quad - \mu _1({\bar{p}}, {\bar{r}})\end{pmatrix}, \end{aligned}$$

with $\mu _1 = \frac{k_1 p (1-r)}{K_1 + p}$ and $\mu _2 = \frac{p r}{K + p}$. As $\mu _1({\bar{p}}, {\bar{r}}), \mu _2({\bar{p}}, {\bar{r}}), \mu _1'({\bar{p}}, {\bar{r}}), \mu _2'({\bar{p}}, {\bar{r}})$ are positive, both eigenvalues of the matrix above are negative. Therefore, $({{\bar{p}}}, {{\bar{x}}})$ is a stable equilibrium. $\square$

Let us denote by $(p_{{\bar{r}}}, x_{{\bar{r}}})$ the solution of (4) with constant control $r = {\bar{r}}$ defined on some time interval $[ 0, {\widetilde{T}} ]$.

Lemma 6.2

There exist $\delta , \ {\overline{\mu }},\ {{\overline{C}}} > 0$ such that if, $\ |p_{{\bar{r}}}(0) - {\bar{p}} | + |x_{{\bar{r}}}(0) - {\bar{x}} | \le \delta ,$ then,

$$\begin{aligned} |p_{{\bar{r}}}(t) - {\bar{p}} | + |x_{{\bar{r}}}(t) - {\bar{x}} | \le {{\overline{C}}}\, {\mathrm{e}}^{- {\overline{\mu }} t}, \quad \text {for} \ t \in [ 0, {\widetilde{T}} ]. \end{aligned}$$

Corollary 6.2

There exist positive constants $\epsilon , T_0$ such that, if $t_2 - t_1 > T_0$ and,

$$\begin{aligned} \left| p_s(t_1) - {{\bar{p}}} \right| + \left| x_s(t_1) - {{\bar{x}}} \right| + \left| p_s(t_2) - {{\bar{p}}} \right| + \left| x_s(t_2) - {{\bar{x}}} \right| \le \epsilon , \end{aligned}$$

then there exists $C, C_J >0$ such that for any $t \in [ 0, {\widetilde{T}} ]$ there holds,

$$\begin{aligned} \begin{aligned}&\left| p_s(t) - p_{{\bar{r}}}(t) \right| + \left| x_s(t) - x_{{\bar{r}}}(t) \right| \le C \left( {\mathrm{e}}^{-\nu t} + {\mathrm{e}}^{-\nu ({\widetilde{T}}-t)}\right) , \\&\left| J(r_s) - J({{\bar{r}}}) \right| \le C_J \left( 1 - {\mathrm{e}}^{-\nu {\widetilde{T}}}\right) . \end{aligned} \end{aligned}$$

6.1.2 Complete Case (Full Model)

Similar properties hold for the initial OCP (2)–(3).

Lemma 6.3

Point $({{\bar{p}}}, {{\bar{r}}}, {{\bar{x}}})$ is the unique stable equilibrium of (3) with $u \equiv {\bar{u}}$ in $\varOmega$.

As before, we denote by $(p_{{\bar{u}}}, r_{{\bar{u}}}, x_{{\bar{u}}})$ the solution of (4) with constant control $u \equiv {\bar{u}}$ defined on $[ 0, {\widetilde{T}} ]$.

Lemma 6.4

There exist $\delta , \ {\overline{\mu }}_*,\ {{\overline{C}}} > 0$ s.t if, $|p_{{\bar{u}}}(0) - {\bar{p}} | + |r_{{\bar{u}}}(0) - {\bar{r}} | + |x_{{\bar{u}}}(0) - {\bar{x}} | \le \delta ,$ then, $|p_{{\bar{u}}}(t) - {\bar{p}} | + |r_{{\bar{u}}}(0) - {\bar{r}} | + |x_{{\bar{u}}}(t) - {\bar{x}} | \le {{\overline{C}}}\, {\mathrm{e}}^{- {\overline{\mu }}_* t}, \,\, \text {for} \ t \in [ 0, {\widetilde{T}} ].$

Corollary 6.3

There exist positive constants $\epsilon , T_0$ such that, if $t_2 - t_1 > T_0$ and,

$$\begin{aligned} \left| p_s(t_1) - {{\bar{p}}} \right| + \left| r_{s}(t_1) - {\bar{r}} \right| + \left| x_s(t_1) - {{\bar{x}}} \right| + \left| p_s(t_2) - {{\bar{p}}} \right| + \left| r_{s}(t_2) - {\bar{r}} \right| + \left| x_s(t_2) - {{\bar{x}}} \right| \le \epsilon , \end{aligned}$$

then there exist $C, C_J >0$ s.t. for any $t \in [ 0, {\widetilde{T}} ]$ the following holds:

$$\begin{aligned} \begin{aligned}&\left| p_s(t) - p_{{\bar{u}}}(t) \right| + \left| r_s(t) - r_{{\bar{u}}}(t) \right| + \left| x_s(t) - x_{{\bar{u}}}(t) \right| + \le C \left( {\mathrm{e}}^{-\nu t} + {\mathrm{e}}^{-\nu ({\widetilde{T}}-t)}\right) , \\&\left| J(u_s) - J({{\bar{u}}}) \right| \le C_J \left( 1 - {\mathrm{e}}^{-\nu {\widetilde{T}}}\right) . \end{aligned} \end{aligned}$$

6.2 Numerical Algorithm for the Reduced Problem

One of the practical applications of the turnpike property is the advantage in the development of the numerical methods. It can be used to improve the standard numerical methods: for improvements in direct and indirect numerical methods, see [8, 22]; for MPC in case of infinite horizon problems, see [11]. It was suggested much earlier in [25] for linear quadratic problem with fixed endpoints, and in [1] for general nonlinear OCPs with fixed endpoints, to approximate the solution by gluing the solutions of the corresponding backward and forward infinite horizon problems. In our case, we suggest an even simpler construction of a suboptimal control strategy which is easy to calculate and implement on the one hand and shows good approximation results on the other hand.

Numerical solutions of the reduced problem obtained using direct method implemented in Bocop software show that, for different parameters, initial data and final times, the obtained solutions are always with at most 3 arcs (see Sect. 3.1 for example in case $E_M = k_1=K_1 = K=1$). Moreover, the solutions with exactly 3 arcs are the most frequent solutions and occur when final time is large. For such solutions, the observed structure is Bang–Singular–Bang (B–S–B). We will take advantage of this observation and assume in following that solutions of the reduced problem have at most 3 arcs and the sequence of the arcs is a sub-sequence of B–S–B. With this assumption, we will construct a new algorithm to approximate the singular arc by a trajectory with the constant control $r = {\bar{r}}$, from the solution of the static problem (9). Let us define a new optimization problem associated with the reduced problem (5). We will use the notation $z^r = (p,x)$ and ${\dot{z}}^r = f_r(z^r, r)$ for the dynamics (4). We choose a control r in (4) in such a way that the dynamics takes the following form,

$$\begin{aligned} \begin{array}{ll} {\dot{z}}^r = f_r(z^r, r_1), &{} \quad t\in [0, T_1),\\ {\dot{z}}^r = f_r(z^r, {\bar{r}}),&{} \quad t\in [T_1, T_2),\\ {\dot{z}}^r = f_r(z^r, r_2), &{}\quad t\in [T_2, T],\\ \end{array} \end{aligned}$$

(34)

where ${\bar{r}}$ is the solution of the static–OCP (9), $r_1, r_2, T_1, T_2$ are parameters satisfying $0 \le r_1, r_2 \le 1$ and $0 \le T_1 \le T_2 \le T$. A reasonable next step is to find $r_1, r_2, T_1, T_2$ which maximize the cost (2) subject to (34). For this, we notice first that from the preliminary analysis in Sect. 4.1 it follows that the optimal control of the reduced OCP is zero during the final bang arc, meaning that $r \equiv 0$ on some time interval $[{{\tilde{t}}}, T]$. Therefore, we will set $r_2 = 0$, this will reduce the dimension of the optimization problem. Finally, the new optimization problem writes,

$$\begin{aligned} \begin{aligned}&\max \int _0^T \frac{k_{1}}{x(t)} \frac{p(t) {\left( 1 - r(t)\right) } }{K_{1} + p(t)} \mathrm {d}t \,&{\left\{ \begin{array}{ll} (p,x,r) \text { satisfy } (34), 0 \le r_1 \le 1, \ r_2 = 0, \\ 0 \le T_1 \le T_2 \le T. \end{array}\right. } \end{aligned} \end{aligned}$$

(35)

Proposition 6.1

There exists an optimal solution to the optimization problem (35).

Proof

Problem (35) can be rewritten as follows with $\left( p_{r_*}(\cdot ), x_{r_*}(\cdot ) \right)$ the flow of (4) with control r set to $r(\cdot ) \equiv r_*$,

$$\begin{aligned}&\max _{\begin{array}{c} 0 \le r_1 \le 1 \\ 0 \le T_1 \le T_2 \le T \end{array}} \ \int _0^{T_1} \frac{k_{1}}{x_{r_1}(t)} \frac{p_{r_1}(t) {\left( 1 - r_1\right) } }{K_{1} + p_{r_1}(t)} \mathrm {d}t + \int _{T_1}^{T_2} \frac{k_{1}}{x_{{{\bar{r}}}}(t)} \frac{p_{{{\bar{r}}}}(t) {\left( 1 - {{\bar{r}}}\right) } }{K_{1} + p_{{{\bar{r}}}}(t)}\mathrm {d}t \\&\quad + \int _{T_2}^{T} \frac{k_{1}}{x_{0}(t)} \frac{p_{0}(t) }{K_{1} + p_{0}(t)}\mathrm {d}t. \end{aligned}$$

Thus, we maximize a continuous function on a compact set $\{ (r_1, T_1, T_2) \ : \ 0 \le r_1 \le 1 , \ 0 \le T_1 \le T_2 \le T \}$. Such a maximization problem admits a solution. $\square$

The idea of replacing a complicated singular control by a simple constant control is important for applications. By solving (35), we choose, moreover, the best control values and switching times for such a control structure. By Lemma 6.2 and Corollary 6.2, the behavior of solutions of (4) with $r(\cdot ) \equiv 0$ is very similar to the turnpike behavior of the singular arc. Moreover, the error committed by setting the control $r(\cdot ) \equiv {{\bar{r}}}$ in place of $r(\cdot ) = r_s(\cdot )$ is bounded. The numerical simulations show even better results when compared to the solutions obtained using the standard direct optimization method, see Sect. 7. For the numerical solution of (35) we use Bocop software. In practice, this problem can be solved by any nonlinear programming solver. The discretization of the dynamical part of the constraint in (35) can be done in various ways just as in case of the direct methods for DOCPs (see [3] for direct methods in optimal control). We choose the approach of state and control discretization implemented in Bocop.

6.3 Numerical Algorithm for the Original Problem

The idea of approximating solutions with a simple piecewise constant control strategy which was described in case of the reduced problem applies in case of the original OCP (3), (2) with small modifications. From PMP it follows that $H_1(T) = 0$, so we cannot conclude on the exact value of the control during the final arc as it was done in the reduced case. Therefore, if we approximate a solution with 3 consecutive constant controls, the value of the last control remains an optimization parameter. We use the notation $z = (p, r, x)$ and ${\dot{z}} = f(z, u)$ for the dynamics (3). The 3-arc strategy leads to the following dynamics with ${\bar{u}}$ the corresponding value from the solution of the static problem.

$$\begin{aligned} \begin{array}{ll} {\dot{z}} = f(z, u_1), &{} \quad t\in [0, T_1)\\ {\dot{z}} = f(z, {\bar{u}}), &{}\quad t\in [T_1, T_2)\\ {\dot{z}} = f(z, u_2), &{}\quad t\in [T_2, T].\\ \end{array} \end{aligned}$$

(36)

The resulting optimization problem has the following form,

$$\begin{aligned} \!\!\!\max \int _0^T \frac{k_{1}}{x(t)} \frac{p(t) {\left( 1 - r(t)\right) } }{K_{1} + p(t)} \mathrm {d}t, \ \, {\text {s.t.}} \; {\left\{ \begin{array}{ll} (p,x,r) \text { satisfy } (36), \\ 0 \le u_1, u_2 \le 1, \ 0 \le T_1 \le T_2 \le T.\!\!\! \end{array}\right. } \end{aligned}$$

(37)

Using the same arguments as in the proof of Proposition 6.1, we get the existence of a solution of (37).

Proposition 6.2

There exists an optimal solution to the optimization problem (37).

The solution structure of the complete OCP (2)–(3) is more complicated than in the reduced case as the connection between bang arcs and singular arcs is achieved by chattering. Although it is standard to approximate chattering by a finite number of bang arcs in numerical methods (see, e.g. [31]), the method must be adapted to the concrete problem under consideration. Assume that all optimal solutions of problem (2)–(3) have only one singular arc. In this case, the 3-arc solution represents an approximation where all the bang-arcs, including chattering, before and after the singular arc are replaced by a single arc corresponding to a constant control, and the singular arc is approximated by an arc corresponding to the control $u = {\bar{u}}$. Notice that solution of (3) with $u = {\bar{u}}$ is exponentially close to the singular arc, just as in the reduced case as shown in Corollary 6.3. In the following numerical results we confirm that the numerical solution of (37) provide a very good approximation.

7 Numerical Results

In this section, we provide the numerical results showing the performance of the generic algorithms established in Sects. 6.2 and 6.3. For that, we use the open source optimal control toolbox Bocop. The results obtained using 3-arc algorithms are compared to the standard direct optimization approach implemented also in Bocop. Note that the introductory examples developed in Sect. 3 rely upon the same direct optimization method and are realized using Bocop. The idea of the direct numerical method [3] is based on the complete discretization of the OCP and formulation of the corresponding Nonlinear Program. This step is integrated in Bocop and below we specify the choice of the discretization methods in Footnotes 6, 7, 8; the NLP solver in Bocop is IPOPT.

Table 2 Values of the parameters in (4), used in Examples 7.1–7.2 for the reduced problem

Example 7.1

(Reduced self-replicator model) In the first numerical example, we use the parameters in Table 2 along with the Bocop settings⁶ and we provide the optimal state and co-state trajectories, along with the optimal control r(t), using a direct optimization method applied to the reduced DOCP. These solutions visually exhibit a turnpike behavior, as illustrated in Figs. 6 and 7.

Fig. 6

a The optimal state $p(t), \ r(t)$ on time interval [0, 100]. The initial states are given by $p(0)=x(0)=20$. b The optimal co-state $\lambda _{p}(t), \ \lambda _{r}(t)$ on time interval [0, 100], the transversality condition ($\lambda = 0$) is satisfied

Fig. 7

Optimal control r(t) on time interval [0, 100], compared to the 3-arcs approximation (Example 2), $t_1, t_2$, are the optimization parameters form the 3-arc algorithm

Fig. 8

suboptimal trajectories $p(t), \ x(t)$ obtained by the 3-arcs method, defined on [0, 100]. The initial conditions are $p(0)=x(0)=20$

Example 7.2

(Reduced self-replicator model—3-arc)

Now, we consider the numerical method based on the 3-arc approximation applied to the reduced problem, using the Bocop settings.⁷ The suboptimal control and the suboptimal trajectories obtained using the model parameters in Table 2 are shown in Figs. 7 and 8 . Next, we show the numerical results obtained for different final-times T, in order to compare the standard direct numerical approach and the approach by the 3-arc algorithm. The results are given in Table 3. The comparison is done by considering the relative error of the numerically obtained value functions of the two algorithms, that is the maximal cost value, for different final times, $\epsilon (T) = \frac{C_{3{\text {-arcs}}}(T) - C_{\mathrm{DOCP}}(T)}{C_{\mathrm{DOCP}}(T)},$ where $C_{\mathrm{DOCP}}(T)$ is the maximal value of the cost obtained using standard direct approach and $C_{3{\text {-arcs}}}(T)$ is the value obtained by the 3-arc algorithm, the both values are considered as functions of the final time T.

Table 3 The cost associated with the numerical methods: DOCP cost stands for the direct optimization solving the initial DOCP, and ${\text {Cost}}_{3{\text {-arcs}}}$ gives the cost of the 3-arc method

As illustrated in Table 3 and Fig. 9, the costs obtained by the two numerical approaches are substantially similar. These comparative results were obtained for equivalent numerical discretization methods and may slightly vary according to the selected ODE-discretization schemes.

Fig. 9

Using the data in Table 3, the relative error is represented for T varying between 20 and 280. The cost $C_{\mathrm{DOCP}}$ stands for the direct optimization in Bocop, while $C_{3{\text {-arcs}}}$ stands for the cost using the 3-arc approach

Let us now perform similar numerical examples based on the dynamics of the full model (3). The biological parameters in this case are given in Table 4. The results obtained in Examples 7.3–7.4 using appropriate Bocop settings are summarized in Table 5.

Table 4 Parameters used in Examples 7.3–7.4 for the original OCP (3), (2)

Example 7.3

(Full self-replicator model) First, we consider the numerical results obtained using a standard direct optimization method applied to the complete OCP (3), (2). A chattering phenomenon appears in the optimal control in Fig. 10. As in the reduced problem, these solutions visually exhibit the turnpike behavior, as illustrated in Figs. 10 and 11.

Fig. 10

The optimal control u(t) over [0, 70] in Example 3

Fig. 11

The optimal state (a) and co-state (b) trajectories obtained by standard direct approach in Bocop

Example 7.4

(Full self-replicator model—Solution with the 3-arc algorithm) Let us now consider the numerical results obtained using the 3-arc algorithm (37) applied to the complete OCP (3), (2). We perform numerical simulations for different final-times T, given in Table 4. The biological parameters are given in Table 4, implemented in Bocop along with the Bocop settings.⁸ The results when T varies from 70 to 470 are listed in Table 5.

Results for $T=70$: The suboptimal control and corresponding trajectories for $T = 70$ obtained by the 3-arc algorithm are given in Figs. 12 and 13, respectively.

Fig. 12

The suboptimal control u(t) for $t\in [0,70]$

Fig. 13

The suboptimal trajectories for $t\in [0,70]$

Using the data given in Table 5, we conclude that the relative error committed by the 3-arc approach is substantially minor, see the left graph of Fig. 14. The difference increases slowly when T is very large to the favor of the effective three arcs approximation. Indeed, we note that when T increases, the approximated 3-arc algorithm has better yields than the original DOCP (for equivalent discretization method and same time-steps in Bocop). On right graph of Fig. 14, you can also find $\Vert u_{\mathrm{bocop}}(t) - u_{3\mathrm{arcs}}(t) \Vert _2$, which shows how well the control obtain by the 3arc algorithm approximates the solution obtained by bocop. The observed results comfort the use of the simplest suboptimal control as an alternative effective control strategy.

Fig. 14

Left: the relative error in the costs committed when T varies from 70 to 470. Right: control error $\Vert u_{\mathrm{bocop}}(t) - u_{3\mathrm{arcs}}(t) \Vert _2$

8 Conclusion

We made the first steps in showing the role of the turnpike property for the optimization of metabolite production. We adapted the existing theoretical approach from [22] for the local exponential turnpike property to the singular arcs of order 1 and 2 appearing in our case. Pontryagin’s maximum principle together with numerical methods allowed us to deduce the structure of the solutions with predominance of the singular arc. In addition, the introduced reduced model permits to avoid the chattering phenomenon. Finally, we designed simple suboptimal open loop strategies for both reduced and complete models. These strategies are easier to implement from a biological and experimental point of view. The efficiency of the method was shown on numerical examples. For future work, we will further use the solution of the reduced OCP to construct control strategies for the original OCP. Another direction of research is to establish global turnpike behavior in the studied class of OCPs dedicated to bacterial growth, possibly trying to rely on dissipativity features [12, 17]. Whatever the order of the singular arcs coming into play, one expects that some turnpike property would hold not only along the singular arc, but also for the whole optimal trajectory where initial and terminal bang arcs (including those corresponding to the Fuller phenomenon) are only corrections made to accommodate boundary conditions.

Appendices

Proof of Propositions 4.3 and 5.1

Some notions of geometric control theory and differential forms are used in these proofs more heavily than in the rest of the paper; the unfamiliar reader is referred to [2]. Recall that a Hamiltonian vector field $\mathbf {H}$ on a manifold M is defined by a function $H:M\rightarrow {\mathbb {R}}$ (Hamiltonian) and a symplectic form $\omega$ (non-degenerate skew-symmetric closed differential form of degree 2); the vector field is then the only $\mathbf {H}$ such that $\mathrm {d}H=\omega (\mathbf {H},.)$. Recall also that the Poisson bracket of two smooth functions $H_1$ and $H_2$ satisfies: $\{H_1,H_2\}=\omega (\mathbf {H}_1,\mathbf {H}_2)=\mathbf {H}_1\, H_2=-\mathbf {H}_2\, H_1$. Let us now describe a general situation that encompasses both proofs.

Let M be a manifold of dimension 2n, $\omega$ a symplectic form on M, and consider $2p+1$ smooth functions $H,g_1,\ldots ,g_{2p}$ ($p>0$) from M to ${\mathbb {R}}$. Assume (i) that $N:=\{g_1=\cdots =g_{2p}=0\}$ is a smooth submanifold of M of co-dimension 2d, i.e. $\mathrm {d}g_1\wedge \cdots \wedge \mathrm {d}g_{2p}$ does not vanish on N, (ii) that the functions $\{H,g_1\}$, ..., $\{H,g_{2p}\}$ are identically zero on N (this means that the submanifold N is invariant by the flow of $\mathbf {H}$, because it translates into Lie derivatives: $\mathbf {H}\,g_1=\cdots =\mathbf {H}\,g_{2p}=0$), (iii) that the restriction $\omega |_N$ of the form $\omega$ to N is non-degenerate. Then the restriction $\mathbf {H}|_{N}$ of $\mathbf {H}$ to N is the Hamiltonian vector field (wrt. $\omega |_N$) on N associated with the Hamiltonian $H|_{N}$. Indeed, $\mathbf {H}|_{N}$ defines a vector field on N because (ii) implies that $\mathbf {H}(x)\in T_xN$ for all x in N; $\mathrm {d}(H|_{N})=(\omega |_{N})(\mathbf {H}|_{N},.)$ is true by restriction (even if $\omega |_{N}$ were degenerate), and does imply the above property because $\omega |_{N}$ is a symplectic form on N, being closed ($\mathrm {d}\omega =0$ follows automatically by restriction) and non-degenerate, as assumed in (iii). We now prove the propositions by checking that points (i), (ii) and (iii) hold in both cases.

Proof of Proposition 4.3

Let us apply the above when $p=1$, $H_0,H_1$ are two smooth functions, $g_1=H_1$, $g_2=\{H_{0},H_{1}\}=H_{01}$, $H_{101}=\{H_{1},H_{01}\}$ is assumed⁹ to not vanish on M, $H=H_0+u_s H_1$ with $u_s=-H_{001}/H_{101}$. Point (i) holds because $\mathrm {d}H_1,\mathrm {d}H_{01}$ are linearly independent at points where $H_{101}$ is nonzero (apply $\lambda _0\mathrm {d}H_1+\lambda _1\mathrm {d}H_{01}$ to the vector fields $\mathbf {H}_{1}$ and $\mathbf {H}_{01}$ successively). Point (ii) is satisfied because $\{H,g_1\}=\{H_0+u_sH_1,H_{1}\}=H_{01}+\{u_s,H_1\}\,H_1$ and

$$\begin{aligned} \{H,g_2\}=\{H_0+u_sH_1,H_{01}\}=\underbrace{H_{001}+u_s H_{101}}_{=0}+ \{u_s,H_{01}\}\,H_1, \end{aligned}$$

(38)

while $H_{1}$ and $H_{01}$ are zero on N. Point (iii) is satisfied because, for any x in N, $T_x N$, as a subspace of $T_x M$, is the annihilator of $\{\mathrm {d}H_1(x),\mathrm {d}H_{01}(x)\}$, or equivalently the $\omega$-orthogonal to the vector space L spanned by $\mathbf {H}_1(x),\mathbf {H}_{01}(x)$; the restriction of $\omega (x)$ to the 2-dimensional L is nondegenerate because $\omega (\mathbf {H}_1,\mathbf {H}_{01})=H_{101}\ne 0$, and this implies that the restriction to its $\omega$-orthogonal is nondegenerate as well. The precise case of Proposition 4.3 is retrieved for $n=2$, $M={\mathbb {R}}^4$ with coordinates $(p,x,\lambda _p,\lambda _x)$, N is $\varSigma _r$, $\omega =\mathrm {d}\lambda _p\wedge \mathrm {d}p+\mathrm {d}\lambda _x\wedge \mathrm {d}x$, and Hamiltonian $H_s$. $\square$

Proof of Proposition 5.1

Let us apply the above under the following assumptions that hold in Proposition 5.1 (in particular according to (24)): take $p=2$, $H_0,H_1$ two smooth functions, $g_1=H_1$, $g_2=\{H_{0},H_{1}\}=H_{01}$, $g_3=\{H_{0},H_{01}\}=H_{001}$, $g_4=\{H_{0},H_{001}\}=H_{0001}$, assume that $H_{10001}=\{H_{1},H_{0001}\}$ does not vanish on M, and define $H=H_0+u_s H_1$ with $u_s=-H_{00001}/H_{10001}$. We also assume that there are two smooth functions $a_1,a_2$ such that $H_{101}=a_1\,H_1+a_2\,H_{01}$. Point (i) holds because $\mathrm {d}H_1,\mathrm {d}H_{01},\mathrm {d}H_{001},\mathrm {d}H_{0001}$ are linearly independent at points where $H_{10001}$ is nonzero (apply $\lambda _1\mathrm {d}H_1+\lambda _2\mathrm {d}H_{01}+\lambda _3\mathrm {d}H_{001}+\lambda _4\mathrm {d}H_{0001}$ to the vector fields $\mathbf {H}_{1}$, $\mathbf {H}_{01}$, $\mathbf {H}_{001}$ and $\mathbf {H}_{0001}$, successively). Point (ii) is obvious for $g_1,g_2,g_3$, and $\{H,g_4\}=\{u_s,H_{0001}\}\,H_1$, similarly to (38). Let us turn to point (iii). For any x in N, as a subspace of $T_x M$, $T_x N$ is the annihilator of $\{\mathrm {d}H_1(x),\mathrm {d}H_{01}(x)$, $\mathrm {d}H_{001}(x),\mathrm {d}H_{0001}(x)\}$, or equivalently the $\omega$-orthogonal of the vector space generated by $\mathbf {H}_1(x),\mathbf {H}_{01}(x)$, $\mathbf {H}_{001}(x),\mathbf {H}_{0001}(x)$. The restriction of $\omega (x)$ to this vector space is non-degenerate because its matrix in the previous basis is

$$\begin{aligned} \left( \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad H_{10001}(x) \\ 0&{}\quad 0&{}\quad -H_{10001}(x)&{}\quad * \\ 0&{}\quad H_{10001}(x) &{}\quad 0&{}\quad * \\ -H_{10001}(x)&{}\quad *&{}\quad *&{}\quad 0 \end{array}\right) , \end{aligned}$$

where the Jacobi identity, the relation $H_{101}=a_1\,H_1+a_2\,H_{01}$, and the fact that $H_1,\ldots ,H_{0001}$ vanish on N have been used to obtain the upper triangular structure. The precise case of Proposition 5.1 is retrieved for $n=3$, $M={\mathbb {R}}^6$ with coordinates $(p,x,r,\lambda _p,\lambda _x,\lambda _r)$, N is $\varSigma$, $\omega =\mathrm {d}\lambda _p\wedge \mathrm {d}p+\mathrm {d}\lambda _x\wedge \mathrm {d}x+\mathrm {d}\lambda _r\wedge \mathrm {d}r$, and Hamiltonian $H_s$. $\square$

3-Arc Optimization Results in the Full-Model

See Table 5.

Table 5 Here we use the optimization method based on the 3 arcs, where $u_2$ is fixed to the static solution $u_2={\overline{u}}$ (where ${\overline{u}}=0.58$ is the solution of the static-OCP in the full model, corresponding to the parameters in Table 4), while $u_1$ and $u_3$ are free