Motion Controller Design of Wheeled Inverted Pendulum with an Input Delay Via Optimal Control Theory

Abstract

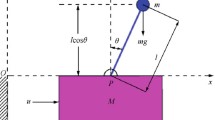
This paper investigates the control of Back-and-Forth motion to fetch object and Lower-Raise-Head motion to avoid obstacle of the wheeled inverted pendulum system with an input delay. In controlling the Back-and-Forth motion, the linear optimal control theory is used because the tilt angle of the pendulum is forced to be small enough by minimizing a quadratic performance criterion with large weight of tilt angle error, and the controller is represented by using predictor-based feedback. In controlling the Lower-Raise-Head motion, linearized models do not work due to the strong nonlinearity caused by big tilt angle for avoiding obstacle. Without considering yaw movement, the wheeled inverted pendulum system is decoupled, the subsystem governing the state of the tilt angle is transformed into a simple linear system by using feedback linearization. With a properly chosen trajectory tracking target, the control of Lower-Raise-Head motion is solved on the basis of optimal trajectory tracking control for linear subsystems with an input delay. Numerical simulations illustrate the effectiveness of the proposed approaches.

Appendix: Derivation of Equation (12)

Consider the optimal control problem of system (10) that minimizes the performance criterion (11). Firstly, let consider the special case of $\tau =0$, the augmented quadratic performance criterion can be defined as

$$\begin{aligned} \bar{J}= & {} \frac{1}{2}\mathbf{Y }^\mathrm{T}(t_f)\mathbf{Q }_0\mathbf{Y }(t_f)+\frac{1}{2}\int _0^{t_f}\left[ \mathbf{Y }^\mathrm{T}(t)\mathbf{Q }\mathbf{Y }(t)+u_{2}^\mathrm{T}(t)\mathbf{R }u_2(t)\right] \mathrm{d}t\\&+\int _0^{t_f}\left[ \varvec{\lambda }^\mathrm{T}(t)(\mathbf{A }\mathbf{Y }(t)+\mathbf{B }u_2(t)+\varvec{\omega }(t)-\dot{\mathbf{Y }}(t))\right] \mathrm{d}t, \end{aligned}$$

and the Hamiltonian function is defined by

$$\begin{aligned} H(\mathbf{Y },u_2,\varvec{\lambda },t)=\frac{1}{2}\mathbf{Y }^\mathrm{T}(t)\mathbf{Q }\mathbf{Y }(t)+\frac{1}{2}u_{2}^\mathrm{T}(t)\mathbf{R }u_2(t) +\varvec{\lambda }^\mathrm{T}(t)(\mathbf{A }\mathbf{Y }(t)+\mathbf{B }u_2(t)+\varvec{\omega }(t)). \end{aligned}$$

(20)

Then, $\bar{J}$ can be rewritten in the form of

$$\begin{aligned} \bar{J}= & {} \frac{1}{2}\mathbf{Y }^\mathrm{T}(t_f)\mathbf{Q }_0\mathbf{Y }(t_f)-\varvec{\lambda }^\mathrm{T}(t_f)\mathbf{Y }(t_f)+\varvec{\lambda }^\mathrm{T}(0)\mathbf{Y }(0)\\&+\int _0^{t_f}\left[ H(\mathbf{Y },u_2,\varvec{\lambda },t)+\dot{\varvec{\lambda }}^\mathrm{T}\mathbf{Y }(t)\right] \mathrm{d}t. \end{aligned}$$

Consider the variation of $\bar{J}$ due to the variables $u_2$ and $\mathbf{Y }$, we have

$$\begin{aligned} \delta \bar{J}=\delta \mathbf{Y }^\mathrm{T}(t_f)\mathbf{Q }_0\mathbf{Y }(t_f)-\delta \mathbf{Y }^\mathrm{T}(t_f)\varvec{\lambda }(t_f) +\int _0^{t_f}\left[ \delta \mathbf{Y }^\mathrm{T}\left( \frac{\partial H}{\partial \mathbf{Y }}+\dot{\varvec{\lambda }}\right) +\delta u_2^\mathrm{T}\frac{\partial H}{\partial u_2}\right] \mathrm{d}t \end{aligned}$$

By setting $\delta \bar{J}=0$, the necessary conditions for the minimum value problem are

$$\begin{aligned} \dot{\varvec{\lambda }}=-\frac{\partial H}{\partial \mathbf{Y }}, ~~ \dot{\mathbf{Y }}=\frac{\partial H}{\partial \varvec{\lambda }}, ~~ \frac{\partial H}{\partial u_2}=0 , ~~ \varvec{\lambda }(t_f)=\mathbf{Q }_0\mathbf{Y }(t_f). \end{aligned}$$

(21)

From (20) and (21), the optimal control of linear system (10) minimizes performance criterion (11) is given by

$$\begin{aligned} u_2^{*}(t)=-\mathbf{R }^{-1}\mathbf{B }^\mathrm{T}\varvec{\lambda }(t), \end{aligned}$$

(22)

where $\varvec{\lambda }(t)$ is determined by the following differential equations

$$\begin{aligned} -\dot{\varvec{\lambda }}= & {} \mathbf{Q }\mathbf{Y }+\mathbf{A }^\mathrm{T}\varvec{\lambda }, ~~~~~~\varvec{\lambda }(t_f)=\mathbf{Q }_0\mathbf{Y }(t_f) ,\end{aligned}$$

(23)

$$\begin{aligned} \dot{\mathbf{Y }}= & {} \mathbf{A }\mathbf{Y }-\mathbf{S }\varvec{\lambda }+\varvec{\omega },~~~~ \mathbf{Y }(0)=\mathbf X (0)-\bar{\mathbf{X }}(0), \end{aligned}$$

(24)

where $\mathbf{S }=\mathbf{B }\mathbf{R }^{-1}\mathbf{B }^\mathrm{T}$. According to (22), (23), and (24), we have

Lemma 5.1

When $\tau =0$, the optimal control of the linear system (10) that minimizes (11) is given by

(25)

where $\mathbf{P }_{0}(t)\in {\mathbb {R}}^{n\times n}$ and $\mathbf b _{0}(t)\in {\mathbb {R}}^{n}$ are the solutions of the Riccati differential equations

(26)

(27)

Proof

Firstly, let

$$\begin{aligned} \varvec{\lambda }(t)=\mathbf{P }_{0}\mathbf{Y }(t)+\mathbf b _{0}(t). \end{aligned}$$

(28)

Differentiating at the both sides of (28), combining (23) and (24) lead to

$$\begin{aligned} \dot{\varvec{\lambda }}=\dot{\mathbf{P }}_0\mathbf{Y }+\mathbf{P }_0 \dot{\mathbf{Y }}+\dot{\mathbf{b }}_0 =\dot{\mathbf{P }}_0\mathbf{Y }+\mathbf{P }_0(\mathbf{A }\mathbf{Y }-\mathbf{S }\varvec{\lambda }+\varvec{\omega })+\dot{\mathbf{b }}_0 =-\mathbf{Q }\mathbf{Y }-\mathbf{A }^\mathrm{T}\varvec{\lambda }. \end{aligned}$$

(29)

Equating the corresponding coefficients of both sides of (29), one has the Riccati equations (26) and (27).$\square$

From Lemma 5.1, the optimal control $u_2^{*}(t)$ consists of two parts, $-\mathbf{R }^{-1}\mathbf{B }^\mathrm{T}\mathbf{P }_0(t)\mathbf{Y }(t)$ is a feedback control that is determined by the current state, and the rest $-\mathbf{R }^{-1}\mathbf{B }^\mathrm{T}\mathbf b _0(t)$ is a feedforward that is determined by the tracking target.

When $\tau \ne 0$, let us introduce a new integral state transformation as follows:

$$\begin{aligned} \mathbf Z (t)=\mathbf{Y }(t)+\int _{t-\tau }^t\mathrm{e}^{-\mathbf{A }(s-t+\tau )}[\mathbf{B }u_2(s)+\varvec{\omega }(s+\tau )]\mathrm{d}s. \end{aligned}$$

(30)

Then, with $\mathbf{B }_0=\mathrm{e}^{-\mathbf{A }\tau }\mathbf{B }, \mathbf G (t)=\mathrm{e}^{-A\tau }\varvec{\omega }(t+\tau )$, the system (10) is changed to a delay-free form

$$\begin{aligned} \dot{\mathbf{Z }}(t)=\mathbf{A }\mathbf Z (t)+\mathbf{B }_0u_2(t)+\mathbf G (t). \end{aligned}$$

(31)

Equation (10) has an equivalent form as follows:

$$\begin{aligned} \mathbf{Y }(t)=\mathrm{e}^{\mathbf{A }t}\mathbf{Y }(0)+\int _{0}^t\mathrm{e}^{\mathbf{A }(t-s)}[\mathbf{B }u_2(s-\tau )+\varvec{\omega }(s)]\mathrm{d}s, \end{aligned}$$

and the solution $\mathbf{Y }(t)$ satisfies

$$\begin{aligned} \begin{aligned} \mathbf{Y }(t+\tau )&=\mathrm{e}^{\mathbf{A }\tau }\left( \mathbf{Y }(t)+\int _{t}^{t+\tau }\mathrm{e}^{\mathbf{A }(t-s)}[\mathbf{B }u_2(s-\tau )+\varvec{\omega }(s)]\mathrm{d}s\right) \\&=\mathrm{e}^{\mathbf{A }\tau }\left( \mathbf{Y }(t)+\int _{t-\tau }^t\mathrm{e}^{-\mathbf{A }(s-t+\tau )}[\mathbf{B }u_2(s)+\varvec{\omega }(s+\tau )]\mathrm{d}s\right) =\mathrm{e}^{\mathbf{A }\tau }\mathbf Z (t). \end{aligned} \end{aligned}$$

(32)

Thus, the initial condition $\mathbf{Y }(0)=\mathbf{Y }_{0}$ for system (10) is changed into $\mathbf Z (0)=\mathrm{e}^{-\mathbf{A }\tau }\mathbf{Y }(\tau )$.

The quadratic performance criterion $J$ for system (11) can be decomposed by $J=J_1+J_2,$ where $J_1=\frac{1}{2}\int _0^{\tau }\mathbf{Y }^\mathrm{T}\mathbf{Q }\mathbf{Y }\mathrm{d}t$ is fixed because the control does not take effect when $t\in [0,\tau [$, and

$$\begin{aligned} J_2=\frac{1}{2}\mathbf{Y }^\mathrm{T}(t_f)\mathbf{Q }_0\mathbf{Y }(t_f)+\frac{1}{2}\int _0^{t_{f}-\tau }\left[ \mathbf{Y }^\mathrm{T}(t+\tau )\mathbf{Q }\mathbf{Y }(t+\tau )+u_2^\mathrm{T}(t)\mathbf{R }u_2(t)\right] \mathrm{d}t. \end{aligned}$$

(33)

Hence, $J_d=J_1+J_2=\min$ if and only if $J_2=\min$. By substituting (32) into (33), the criterion $J_2$ takes the form

$$\begin{aligned} J_2=\frac{1}{2}\mathbf Z ^\mathrm{T}(t_{f}-\tau )\tilde{\mathbf{Q }}_0\mathbf Z (t_{f}-\tau ) +\frac{1}{2}\int _0^{t_{f}-\tau }\left[ \mathbf Z ^\mathrm{T}(t)\tilde{\mathbf{Q }}\mathbf Z (t)+u_2^\mathrm{T}(t)\mathbf{R }u_2(t)\right] \mathrm{d}t, \end{aligned}$$

where $\tilde{\mathbf{Q }}=\left( \mathrm{e}^{\mathbf{A }\tau }\right) ^\mathrm{T}\mathbf{Q }\mathrm{e}^{\mathbf{A }\tau },\tilde{\mathbf{Q }}_0=\left( \mathrm{e}^{\mathbf{A }\tau }\right) ^\mathrm{T}\mathbf{Q }_0\mathrm{e}^{\mathbf{A }\tau }$. Thus the original optimal control problem can be converted into the optimal control problem for linear delay-free system (31) associated with the performance criterion $J_2$.

According to Lemma 5.1, the optimal control for linear system (31) that minimizes $J_2$ is given by

$$\begin{aligned} u_2^*(t)=-\mathbf{R }^{-1}\mathbf{B }_0^\mathrm{T}[\mathbf{P }_d(t)\mathbf Z (t)+\mathbf b _d(t)], \end{aligned}$$

(34)

where $\mathbf{P }_d(t)\in {\mathbb {R}}^{n\times n}$ and $\mathbf b _{d}(t)\in {\mathbb {R}}^{n}$ are the solutions of the Riccati differential equations

$$\begin{aligned} \dot{\mathbf{P }_d}= & {} -\mathbf{P }_d\mathbf{A }-\mathbf{A }^\mathrm{T}\mathbf{P }_d+\mathbf{P }_d\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_0^\mathrm{T}\mathbf{P }_d-\tilde{\mathbf{Q }}, ~~~~\mathbf{P }_{d}(t_f-\tau )=\tilde{\mathbf{Q }}_0 ,\end{aligned}$$

(35)

$$\begin{aligned} \dot{\mathbf{b }}_{d}= & {} -[\mathbf{A }-\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_{0}^\mathrm{T}\mathbf{P }_{d}]^\mathrm{T}\mathbf b _{d}-\mathbf{P }_{d}\mathbf G (t), ~~~~\mathbf b _{d}(t_f-\tau )=0. \end{aligned}$$

(36)

By substituting (32) into (34), the delayed optimal control of system (10) can be expressed in terms of the state $\mathbf{Y }(t)$, rather than $\mathbf Z (t)$, in the form of

$$\begin{aligned} u_2^{*}(t-\tau )=-\mathbf{R }^{-1}(\mathrm{e}^{-\mathbf{A }\tau }\mathbf{B })^\mathrm{T}\left[ \mathbf{P }_d(t-\tau )\mathrm{e}^{-\mathbf{A }\tau }\mathbf{Y }(t)+\mathbf b _d(t-\tau )\right] . \end{aligned}$$

(37)

Lemma 5.2

Let $u_2^*(t-\tau )$ be the delayed optimal control of system (10), $u_{20}^*(t)$ be the optimal control of system (10) with $\tau =0$, then

$$\begin{aligned} u_2^{*}(t-\tau )=u_{20}^{*}(t)=-\mathbf{R }^{-1}\mathbf{B }^\mathrm{T}[\mathbf{P }_0(t)\mathbf{Y }(t)+\mathbf b _0(t)],~~(t\in [\tau ,t_f]), \end{aligned}$$

where $\mathbf{P }_{0}(t)\in {\mathbb {R}}^{n\times n}$ and $\mathbf b _{0}(t)\in {\mathbb {R}}^{n}$ are the solutions of the Riccati differential equations (26) and (27).

Proof

According to Lemma 5.1, the optimal control of the linear system (10) with $\tau =0$ can be given by (25). Multiplying (26) by $(\mathrm{e}^{\mathbf{A }\tau })^\mathrm{T}$ from the left and by $\mathrm{e}^{\mathbf{A }\tau }$ from the right, respectively, one see that $\mathbf W (t)=(\mathrm{e}^{\mathbf{A }\tau })^\mathrm{T}{\mathbf{P }_{0}}(t)\mathrm{e}^{\mathbf{A }\tau }$ is the solution of the following differential equation

$$\begin{aligned} \dot{\mathbf{W }}(t)=-\mathbf W (t)\mathbf{A }-\mathbf{A }^\mathrm{T}\mathbf W (t)+\mathbf W (t)\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_0^\mathrm{T}\mathbf W (t)-\tilde{\mathbf{Q }}, \end{aligned}$$

subject to $\mathbf W (t_f)=\tilde{\mathbf{Q }}_0$. Replacing $t$ with $t-\tau$ in (35) leads to

$$\begin{aligned} \dot{\mathbf{P }_d}(t-\tau )=-\mathbf{P }_d(t-\tau )\mathbf{A }-\mathbf{A }^\mathrm{T}\mathbf{P }_d(t-\tau ) +\mathbf{P }_d(t-\tau )\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_0^\mathrm{T}\mathbf{P }_d(t-\tau )-\tilde{\mathbf{Q }}, \end{aligned}$$

subject to $\mathbf{P }_{d}(t_f-\tau )=\tilde{\mathbf{Q }}_0$. It follows that both $\mathbf W (t)$ and $\mathbf{P }_d(t-\tau )$ satisfy the same differential equation under the same terminal condition. Thus, $\mathbf W (t)$ and $\mathbf{P }_d(t-\tau )$ must be the same, namely

$$\begin{aligned} \mathbf{P }_{d}(t-\tau )=\left( \mathrm{e}^{\mathbf{A }\tau }\right) ^\mathrm{T}\mathbf{P }_{0}(t)\mathrm{e}^{\mathbf{A }\tau }. \end{aligned}$$

(38)

Similarly, multiplying (27) by $(\mathrm{e}^{A\tau })^\mathrm{T}$ from the left, $\mathbf V (t)=(\mathrm{e}^{\mathbf{A }\tau })^\mathrm{T}\mathbf{b _{0}}$ is the solution of

$$\begin{aligned} \dot{\mathbf{V }}(t)=-\left[ \mathbf{A }-\mathrm{e}^{-\mathbf{A }\tau }\mathbf{S }\mathbf{P }_{0}\mathrm{e}^{\mathbf{A }\tau }\right] ^\mathrm{T}\mathbf V (t)-\left( \mathrm{e}^{\mathbf{A }\tau }\right) ^\mathrm{T}\mathbf{P }_{0}\varvec{\omega }, ~~\mathbf V (t_f)=0. \end{aligned}$$

By substituting (38) into (36) and replacing $t$ with $t-\tau$ leads to

$$\begin{aligned} \dot{\mathbf{b }}_d(t-\tau )=-\left[ \mathbf{A }-\mathrm{e}^{-\mathbf{A }\tau }\mathbf{S }\mathbf{P }_{0}\mathrm{e}^{\mathbf{A }\tau }\right] ^\mathrm{T}\mathbf b _{d}(t-\tau )-\left( \mathrm{e}^{\mathbf{A }\tau }\right) ^\mathrm{T}\mathbf{P }_{0}\varvec{\omega },~~ \mathbf b _{d}(t_f-\tau )=0. \end{aligned}$$

Hence, $\mathbf V (t)$ and $\mathbf b _d(t-\tau )$ must be the same, namely

$$\begin{aligned} \mathbf b _{d}(t-\tau )=\left( \mathrm{e}^{\mathbf{A }\tau }\right) ^\mathrm{T}\mathbf b _{0}(t). \end{aligned}$$

(39)

By substituting (38) and (39) into (37), the following simple relationship holds for $t\in [\tau ,t_f]$

$$\begin{aligned} u_2^{*}(t-\tau )=-\mathbf{R }^{-1}\mathbf{B }^\mathrm{T}[\mathbf{P }_{0}(t)\mathbf{Y }(t)+\mathbf b _0(t)]=u_{20}^{*}(t). \end{aligned}$$

This completes the proof. $\square$

Lemma 5.2 implies that the input delay does not affect the optimal control, when the system has no state delay, the optimal control of the delay-free system fully determines the optimal control of the corresponding system with an input delay, no matter how large the delay is.

When $t_f\rightarrow +\infty$, because the control takes effect only when $t\ge \tau$, the $J$ can be simplified as follows:

$$\begin{aligned} J=&\,\frac{1}{2}\int _0^{+\infty }\left[ \mathbf{Y }^\mathrm{T}(t)\mathbf{Q }\mathbf{Y }(t)+\nu ^\mathrm{T}(t-\tau )\mathbf{R }\nu (t-\tau )\right] \mathrm{d}t \\ =&\,\frac{1}{2}\int _0^{+\infty }\mathbf{Y }^\mathrm{T}(t)\mathbf{Q }\mathbf{Y }(t)\mathrm{d}t\\&+\frac{1}{2}\int _0^{\tau }\nu ^\mathrm{T}(t-\tau )\mathbf{R }\nu (t-\tau )\mathrm{d}t +\frac{1}{2}\int _{\tau }^{+\infty }\nu ^\mathrm{T}(t-\tau )\mathbf{R }\nu (t-\tau )\mathrm{d}t \\ =&\,\frac{1}{2}\int _0^{+\infty }\left[ \mathbf{Y }^\mathrm{T}(t)\mathbf{Q }\mathbf{Y }(t)+\nu ^\mathrm{T}(t)\mathbf{R }\nu (t)\right] \mathrm{d}t, \end{aligned}$$

and (26) becomes algebraic equation, then, we have

$$\begin{aligned}&-\mathbf{P }_0\mathbf{A }-\mathbf{A }^\mathrm{T}\mathbf{P }_0+\mathbf{P }_0\mathbf{B }\mathbf{R }^{-1}\mathbf{B }^\mathrm{T}\mathbf{P }_0-\mathbf{Q }=\mathbf 0 ,\end{aligned}$$

(40)

$$\begin{aligned}&\dot{\mathbf{b }}_{0}=-\left[ \mathbf{A }-\mathbf{B }\mathbf{R }^{-1}\mathbf{B }^\mathrm{T}\mathbf{P }_{0}\right] ^\mathrm{T}\mathbf b _{0}-\mathbf{P }_{0}\varvec{\omega },~~~~\mathbf b _{0}(t_f)=0. \end{aligned}$$

(41)

In this case, the matrix $\mathbf{P }_0$ is time independent and the Riccati equation becomes easy to solve. That is why the case of infinite time horizon is more often studied in practice.