Phase Diagram and Specific Heat of a Nonequilibrium Curie–Weiss Model

Abstract

Adding activity or driving to a thermal system may modify its phase diagram and response functions. We study that effect for a Curie–Weiss model where the thermal bath switches rapidly between two temperatures. The critical temperature moves with the nonequilibrium driving, opening up a new region of stability for the paramagnetic phase (zero magnetization) at low temperatures. Furthermore, phase coexistence between the paramagnetic and ferromagnetic phases becomes possible at low temperatures. Following the excess heat formalism, we calculate the nonequilibrium thermal response and study its behaviour near phase transitions. Where the specific heat at the critical point makes a finite jump in equilibrium (discontinuity), it diverges once we add the second thermal bath. Finally, (also) the nonequilibrium specific heat goes to zero exponentially fast with vanishing temperature, realizing an extended Third Law.

A Example: \(N = 2\)

When the system consists of two spins, the magnetization becomes $m^{N = 2} = \frac{\sigma _1+\sigma _2}{2} \in \{-1,0,1\}$, and energy $E(\sigma ) = -J_g\frac{1+\sigma _1 \sigma _2}{2} \in \{0,-J_g\}$, where $J_g = J \big ( 1 + \frac{g}{2} \big )$. Therefore, the process reduces to a two-level switch where g only affects the energy difference.

First, the heat fluxes (11), $P_{a,N=2}(\sigma )$ become

$$\begin{aligned} P_{a,N}(1,1) = P_{a,N}(-1,-1)&= -\frac{2J_g \nu }{(J_g\beta _{a})^n} e^{- \beta _{a} \frac{J_g}{2}}, \\ P_{a,N}(1,-1) = P_{a,N}(-1,1)&= \frac{2J_g \nu }{(J_g\beta _{a})^n} e^{\beta _{a} \frac{J_g}{2}} \end{aligned}$$

Fig. 9

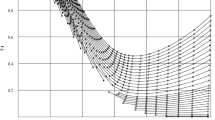
Heat capacities vs $\frac{1}{\beta } = \big ( J_g \frac{\beta _1 + \beta _2}{2} \big )^{-1}$ for $n = 3$ and $\delta = J_g \big ( \beta _2 - \beta _1 \big ) = 1$. The graphs stop at $\beta = \frac{\delta }{2}$ where $\beta _1 = 0$. We plot the total equilibrium result $C_{\text {eq, tot}}$ with a dashed line. (Made using Mathematica version 13.1.0.0 [35].)

The quasipotential $V_a^{(N=2)}$ in (13) takes the form $V_a^{(N = 2)}= (V_{a1}, V_{a2}, V_{a2}, V_{a1})$ with

$$\begin{aligned} V_{a1}&= - v_{ab} \ e^{-\frac{1}{2} \left( 2 \beta _a+\beta _b\right) J_g} \left( e^{\frac{\beta _a J_g}{2}} \beta _a^n+e^{\frac{\beta _b J_g}{2}} \beta _b^n\right) \\ V_{a 2}&= v_{ab} \ e^{-\frac{\beta _a J_g}{2}} \left( e^{\frac{\beta _b J_g}{2}} \beta _a^n+e^{\frac{\beta _a J_g}{2}} \beta _b^n\right) \\ v_{ab}&= J_g \left( e^{\beta _a J_g}+1\right) \beta _b^n \left( 2 \beta _1^n \cosh \left( \frac{\beta _2 J_g}{2}\right) +2 \beta _2^n \cosh \left( \frac{\beta _1 J_g}{2}\right) \right) ^{-2} \end{aligned}$$

where $a \ne b$. That, from (15), leads to the heat capacities,

$$\begin{aligned}&C_{aa}^{(N = 2)} =k_B \ {\tilde{C}}_{ab} \ \beta _a \ \beta _b^{2 n} \left( J_g \beta _a \beta _b^n + J_g \cosh {\frac{J_g}{2} (\beta _a-\beta _b)} - 2 \ n \ \beta _a^n \sinh {\frac{J_g}{2} (\beta _a-\beta _b)} \right) \\&C_{ab}^{(N = 2)} = k_B \ {\tilde{C}}_{ab} \ \beta _a^n \ \beta _b^{n+1} \left( J_g \beta _a^n \beta _b + J_g \beta _b^{n+1} \cosh {\frac{J_g}{2} (\beta _a-\beta _b)} + 2 \ n \ \beta _b^n \sinh {\frac{J_g}{2} (\beta _a-\beta _b)} \right) \\&{\tilde{C}}_{a b} = \frac{J_g}{4} \cosh {\frac{J \beta _a}{2}} \left( \beta _1^n \cosh \left( \frac{\beta _2 J_g}{2}\right) + \beta _2^n \cosh \left( \frac{\beta _1 J_g}{2}\right) \right) ^{-3} \end{aligned}$$

where again $a \ne b$. In equilibrium $\beta _2 = \beta _1$, all of them reduce to

$$\begin{aligned} C_{\text {eq,}ab}^{(N = 2)} = k_B\frac{\beta _1^2 J_g^2 e^{\beta _1 J_g}}{4 \left( e^{\beta _1 J_g}+1\right) ^2} \end{aligned}$$

which is a quarter of the total equilibrium heat capacity $C_\text {eq,tot}$ for a two-level system [36].

The heat capacities are plotted in Fig. 9, where some are seen to obtain negative values, here for $n = 3$. As discussed in [37], this happens due to a negative correlation between the quasipotential $V_a^{(N)}$ and the change in stationary distribution $\rho ^s$.