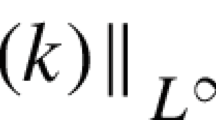Entropy Anomaly in Langevin–Kramers Dynamics with a Temperature Gradient, Matrix Drag, and Magnetic Field

Abstract

We investigate entropy production in the small-mass (or overdamped) limit of Langevin–Kramers dynamics. The results generalize previous works to provide a rigorous derivation that covers systems with magnetic field as well as anisotropic (i.e. matrix-valued) drag and diffusion coefficients that satisfy a fluctuation–dissipation relation with state-dependent temperature. In particular, we derive an explicit formula for the anomalous entropy production which can be estimated from simulated paths of the overdamped system. As a part of this work, we develop a theory for homogenizing a class of integral processes involving the position and scaled-velocity variables. This allows us to rigorously identify the limit of the entropy produced in the environment, including a bound on the convergence rate.

Appendices

Appendix A: Material from [47, 49]

In this appendix, we give a list of properties that, as shown in [47, 49], are sufficient to guarantee that Theorems 1 and 2 hold for the solutions to the SDE Eqs. (4)–(5).

Let ${\mathcal {F}}^W_t$ be the natural filtration of $W_t$ and ${\mathcal {C}}$ be any sigma sub-algebra of ${\mathcal {F}}$ that is independent of ${\mathcal {F}}^W_\infty$. Define ${\mathcal {G}}^{W,{\mathcal {C}}}_t\equiv \sigma ({\mathcal {F}}^W_t\cup {\mathcal {C}})$ and complete it with respect to $({\mathcal {G}}^{W,{\mathcal {C}}}_\infty ,P)$ to form $\overline{{\mathcal {G}}^{W,{\mathcal {C}}}_t}$. Note that $(W_t,\overline{{\mathcal {G}}^{W,{\mathcal {C}}}_t})$ is still a Brownian motion on $(\varOmega ,\overline{{\mathcal {G}}^{W,{\mathcal {C}}}}_\infty ,P)$ and this space satisfies the usual conditions [52].

For the result Eq. (22), we relied on the assumption that our filtered probability space is

$$\begin{aligned} (\varOmega ,{\mathcal {F}},{\mathcal {F}}_t,P)\equiv (\varOmega , \overline{{\mathcal {G}}^{W,{\mathcal {C}}}}_\infty ,\overline{{\mathcal {G}}^{W,{\mathcal {C}}}_t} ,P). \end{aligned}$$

(121)

We also need to assume:

• 1. V is $C^2$, $\gamma$ is $C^2$, $\psi$ is $C^3$, and, letting $\alpha$ denote a multi-index, the following are bounded:

  • (a) $\nabla _qV$,

  • (b) $\partial _{q^\alpha }\psi$ if $1\le |\alpha |\le 3$,

  • (c) $\partial _{q^\alpha }\partial _t\psi$ if $0\le |\alpha |\le 2$,

  • (d) $\partial _{q^\alpha }\gamma$ if $1\le |\alpha |\le 2$,

  • (e) $\partial _{q^\alpha }\partial _t\gamma$ if $0\le |\alpha |\le 1$.

• 2. There exists $a,b\ge 0$ s.t. ${\tilde{V}}(t,q)\equiv a+b\Vert q\Vert ^2+V(t,q)$ is non-negative.

• 3. There exist $C>0$ and $M>0$ such that

  $$\begin{aligned} |\partial _t V(t,q)|\le M+C\left( \Vert q\Vert ^2+{\tilde{V}}(t,q)\right) . \end{aligned}$$

  (122)

• 4. $\gamma$ is symmetric with eigenvalues bounded below by some $\lambda >0$.

• 5. $\varSigma \equiv \sigma \sigma ^T$ has eigenvalues bounded below by $\mu >0$.

• 6. $\gamma$, ${\tilde{F}}$, $\partial _t\psi$, and $\sigma$ are continuous and bounded.

• 7. The initial conditions satisfy the following:

  • (a) There exists $C>0$ such that the (random) initial conditions satisfy $\Vert u^m_0\Vert ^2 \le C m$ for all $m>0$ and all $\omega \in \varOmega$.

  • (b) Given any $p>0$ we have $E[\Vert q_0^m\Vert ^p]<\infty$ for all $m>0$, $E[\Vert q_0\Vert ^p]<\infty$, and $E[\Vert q_0^m-q_0\Vert ^p]^{1/p}=O(m^{1/2})$.

• 8. $\nabla _q V$ and ${\tilde{F}}$ are Lipschitz in x uniformly in t.

• 9. $\sigma$ is Lipschitz in (t, q).

Appendix B: Homogenization of Integral Processes

In this appendix, we develop the techniques necessary to investigate the entropy production in the underdamped system, Eq. (54), in the limit $m\rightarrow 0$.

General homogenization results about the $\epsilon \rightarrow 0^+$ limit of integral processes of the form $\int _0^t G(s,x_s^\epsilon ,z_s^\epsilon )ds$, where $x_s^\epsilon$ come from solving some family of Hamiltonian system parametrized by $\epsilon >0$ (analogous to m), can be found in [54]. Here we summarize and expand on the previous technique to derive explicit formulas for the limit in the case where the integrand is multi-linear in z, as well as cover processes of the form $m^{-1/2}\int _s^t z^m_r\cdot K(r,q_r^m,z^m_r)dr$, an important case that was not treated previously.

As a starting point, let $\chi (t,q,z):[0,\infty )\times {\mathbb {R}}^{n}\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}$ be $C^{1,2}$, meaning $\chi$ is $C^1$ and, for each t, q, $\chi (t,q,z)$ is $C^2$ in z with second derivatives continuous jointly in all variables.

Using the definitions from Sect. 1.1, define the operator L and its formal adjoint, $L^*$, by

$$\begin{aligned} (L\chi )(t,q,z)=&\,\frac{1}{2} \varSigma _{kl}(t,q)(\partial _{z_k}\partial _{z_l}\chi )(t,q,z)-{\tilde{\gamma }}_{kl}(t,q)\delta ^{li}z_i(\partial _{z_k}\chi )(t,q,z), \end{aligned}$$

(123)

$$\begin{aligned} (L^*h)(t,q,z)=&\,\partial _{z_k}\bigg (\frac{1}{2} \varSigma _{kl}(t,q)\partial _{z_l}h(t,q,z)+{\tilde{\gamma }}_{kl}(t,x)\delta ^{li}z_ih(t,q,z)\bigg ). \end{aligned}$$

(124)

As in [54], Itô’s formula can be used to compute

$$\begin{aligned}&\int _s^t(L\chi )(s,q_r^m,z_r^m)dr =m^{1/2} (R_1^m)_{s,t}+m\left( \chi (t,q_t^m,z_t^m)-\chi (s,q_s^m,z_s^m)+ (R^m_2)_{s,t}\right) ,\nonumber \\ \end{aligned}$$

(125)

where we define

$$\begin{aligned} (R_1^m)_{s,t}=&-\int _s^t(\nabla _q\chi )(r,q_r^m,z_r^m)\cdot z_r^m dr -\int _s^t (\nabla _z\chi )(r,q_r^m,z_r^m) \nonumber \\&\cdot \left[ (-\partial _r\psi (r,q_r^m)+{\tilde{F}}(r,q_r^m)-\nabla _qV(r,q_r^m))dr+\sigma (r,q^m_r) dW_r\right] \end{aligned}$$

(126)

and

$$\begin{aligned} (R^m_2)_{s,t}=&-\int _s^t\partial _r \chi (r,q_r^m,z_r^m)dr. \end{aligned}$$

(127)

Our strategy for homogenizing processes of the form $\int _s^t G(r,q_r^m,z_r^m)dr$ is to find a function ${\tilde{G}}(t,q)$ and a $C^{1,2}$ function $\chi (t,q,z)$ such that

$$\begin{aligned} L\chi =G-{\tilde{G}}. \end{aligned}$$

(128)

A problem of this type is termed a cell problem. It also appears in formal asymptotic methods for solving the backward Kolmogorov equation as a series in $\sqrt{m}$ (see Chapter 11 in [55]), as well as in rigorous homogenization results (see Chapter 18 in [55]), and so its appearance as a tool here is not too surprising.

Assuming ${\tilde{G}}$ and $\chi$ exist and don’t grow too fast in z, we will be able to use Eq. (125) to prove

$$\begin{aligned} \int _s^tG(r,q_r^m,z_r^m)dr\rightarrow \int _s^t{\tilde{G}}(r,q_r)dr \end{aligned}$$

(129)

as $m\rightarrow 0$. A solution, h, to the adjoint problem, $L^*h=0$, with $\int h(t,q,z)dz=1$, gives us a formula for ${\tilde{G}}$ as follows. First multiply Eq. (128) by h and integrate by parts. Assuming the boundary terms are negligible, one obtains

$$\begin{aligned} {\tilde{G}}(t,q)=\int h(t,q,z)G(t,q,z)dz. \end{aligned}$$

(130)

We will be able to make the above formal derivation rigorous under the following assumptions.

Assumption B1

From this point on, we assume:

• 1. The fluctuation–dissipation relation, Assumption 1, holds.

• 2. The properties from Appendix A hold.

• 3. ${\tilde{F}}$ is independent of p.

• 4. $\nabla _q\beta$ and ${\tilde{F}}$ are $C^2$.

• 5. For any $T>0$ and multi-index $\alpha$, the following are polynomially bounded in q, uniformly in $t\in [0,T]$:

  • (a) $\partial _{q^\alpha } \beta$ if $1\le |\alpha |\le 3$,

  • (b) $\partial _{q^\alpha }\partial _t \beta$ if $0\le |\alpha |\le 2$,

  • (c) $\partial _t^2 \beta$,

  • (d) $\partial _{q^\alpha }\partial _t^2 \psi$ if $0\le |\alpha |\le 1$,

  • (e) $\partial _{q^\alpha } {\tilde{F}}$ if $1\le |\alpha |\le 2$,

  • (f) $\partial _{q^\alpha } \partial _t{\tilde{F}}$ if $0\le |\alpha |\le 1$,

  • (g) $\partial _{q^\alpha } \partial _t V$ if $0\le |\alpha |\le 1$,

  • (h) $\partial _{q^\alpha } V$ if $|\alpha |=2$,

  i.e. there exists ${\tilde{C}}>0$, ${\tilde{p}}>0$ such that

  $$\begin{aligned} \sup _{t\in [0,T]}|\partial _t\beta (t,q)|\le {\tilde{C}}(1+\Vert q\Vert ^{{\tilde{p}}}) \end{aligned}$$

  (131)

  and so on.

With this assumption, $L^*h=0$ is solved by the Gibbs distribution (pointwise in (t, q)),

$$\begin{aligned} h(t,q,z)=\left( \frac{\beta (t,q)}{2\pi }\right) ^{n/2}e^{-\beta (t,q)\Vert z\Vert ^2/2}. \end{aligned}$$

(132)

The integral processes we wish to homogenize are sums of multi-linear functions in z i.e. they are sums of terms of the form

$$\begin{aligned} G(t,q,z)=B^{i_1,\ldots ,i_k}(t,q)z_{i_1}\ldots z_{i_k}. \end{aligned}$$

(133)

The solution to the cell problem, Eq. (128), for G’s of this form in detailed in Appendix C.

Using Lemma  C3 we obtain the following general convergence result, which is used to derive entropy homogenization theorems in Sect. 4.1. As tools, we will primarily employ the Burkholder–Davis–Gundy inequalities, Hölder’s inequality, and Minkowski’s inequality for integrals (see, for example, Theorem 3.28 in [52] for the former, and Theorems 6.2 and 6.19 in [56] for the latter two). In essence, these are all generalizations of the triangle or Cauchy-Schwarz inequalities to (stochastic) integrals and are all used to decompose the norm of the difference between the m-dependent process and its purported limit into pieces, each of which we can show is negligible as $m\rightarrow 0$.

Theorem B5

Let Assumption B1 hold, $T>0$ and $B(t,q):{\mathbb {R}}\times {\mathbb {R}}^n\rightarrow T^k({\mathbb {R}}^n)$ (rank k tensors) be $C^1$ and polynomially bounded in q with polynomially bounded first derivatives, all uniformly in $t\in [0,T]$.

For $0\le s\le t\le T$, consider the family of processes

$$\begin{aligned} J_{s,t}^m=\int _s^t B^{i_1,\ldots ,i_k}(r,q_r^m) (z_r^m)_{i_1}\ldots (z_r^m)_{i_k} dr. \end{aligned}$$

(134)

Define

$$\begin{aligned} J_{s,t}=\int _s^t B^{i_1,\ldots ,i_k}(r,q_r) \left( \int h(r,q_r,z) z_{i_1}\ldots z_{i_k} dz \right) dr, \end{aligned}$$

(135)

where h is given by Eq. (132). Then for any $p>0$ we have

$$\begin{aligned} \sup _{0\le s\le t\le T}E\left[ \left| J_{s,t}^m-J_{s,t}\right| ^p\right] ^{1/p}=O(m^{1/2}) \end{aligned}$$

(136)

as $m\rightarrow 0$.

Proof

Lemma C3 implies that for each value of B, ${\tilde{\gamma }}$, and $\beta$ there exists $A_j\in T^{k-2j}({\mathbb {R}}^n)$, $j=0,\ldots ,\lfloor (k-1)/2\rfloor$ such that

$$\begin{aligned} \chi (z)=\sum _{j=0}^{\lfloor (k-1)/2\rfloor }A_j^{i_1,\ldots ,i_{k-2j}}z_{i_1}\ldots z_{i_{k-2j}} \end{aligned}$$

(137)

solves

$$\begin{aligned} (L\chi )(z)=B(z,\ldots ,z)-\left( \frac{\beta }{2\pi }\right) ^{n/2}\int B({\tilde{z}},\ldots ,{\tilde{z}})e^{-\beta \Vert {\tilde{z}}\Vert ^2/2}d{\tilde{z}}, \end{aligned}$$

(138)

where L is given by Eq. (123). Considered as functions of $(\beta ,{\tilde{\gamma }},B)$, Lemma C3 also shows that the $A_j$ are $C^\infty$, linear in B, and every derivative with respect to any number of the $\beta$ and ${\tilde{\gamma }}$ variables is bounded by ${\tilde{C}}\Vert B\Vert$ for some ${\tilde{C}}>0$ on any open set of the form

$$\begin{aligned} U_{\epsilon ,R}=\{(\beta ,{\tilde{\gamma }},B): \beta >\epsilon , \hbox { the symmetric part of } {\tilde{\gamma }} \hbox { has spectrum in } (\epsilon ,R)\}, \end{aligned}$$

(139)

where $R>\epsilon >0$.

Assumptions 1 and B1 imply that $(\beta (t,q),{\tilde{\gamma }}(t,q),B(t,q))$ map $[0,T]\times {\mathbb {R}}^n$ into a region of the above form. Therefore

$$\begin{aligned} \chi (t,q,z)\equiv \chi (\beta (t,q),{\tilde{\gamma }}(t,q),B(t,q),z) \end{aligned}$$

(140)

is $C^{1,2}$ and there exists ${\tilde{C}},{\tilde{p}}>0$ such that

$$\begin{aligned}&\sup _{t\in [0,T]}\max \{|\chi (t,q,z)|,|\partial _t\chi (t,q,z)|,\Vert \nabla _q\chi (t,q,z)\Vert ,\Vert \nabla _z\chi (t,q,z)\Vert \}\nonumber \\&\quad \le {\tilde{C}}(1+\Vert q\Vert ^{{\tilde{p}}})(1+\Vert z\Vert ^k). \end{aligned}$$

(141)

The fact that $\chi (t,q,z)$ is $C^{1,2}$ allows us to apply Eq. (125) to obtain

$$\begin{aligned}&J^m_{s,t}-\int _s^t B^{i_1,\ldots ,i_k}(r,q^m_r) \left( \int h(r,q^m_r,z) z_{i_1}\ldots z_{i_k} dz \right) dr =\int _s^t(L\chi )(r,q_r^m,z_r^m)dr\nonumber \\&\quad =m^{1/2}\bigg (-\int _s^t(\nabla _q\chi )(r,q_r^m,z_r^m)\cdot z_r^m dr -\int _s^t (\nabla _z\chi )(r,q_r^m,z_r^m)\nonumber \\&\qquad \cdot \left[ (-\partial _r\psi (r,q_r^m)+{\tilde{F}}(r,q_r^m)-\nabla _q V(r,q_r^m))dr+\sigma (r,q^m_r) dW_r\right] \bigg )\nonumber \\&\qquad +m\left( \chi (t,q_t^m,z_t^m)-\chi (s,q_s^m,z_s^m)-\int _s^t\partial _r \chi (r,q_r^m,z_r^m)dr\right) . \end{aligned}$$

(142)

Therefore, for any $p\ge 2$, using the Burkholder–Davis–Gundy inequalities, Minkowski’s inequality for integrals, Hölder’s inequality, and Assumption B1, and letting the constant ${\tilde{C}}$ vary from line to line, we obtain

$$\begin{aligned}&E\left[ \left| J^m_{s,t}-\int _s^t B^{i_1,\ldots ,i_k}(r,q^m_r) \left( \int h(r,q^m_r,z) z_{i_1}\ldots z_{i_k} dz \right) dr\right| ^p\right] ^{1/p}\nonumber \\&\quad \le m^{1/2}\bigg ( E\left[ \left| \int _s^t(\nabla _q\chi )(r,q_r^m,z_r^m)\cdot z_r^m + (\partial _{z^j}\chi )(r,q_r^m,z_r^m)\right. \right. \nonumber \\&\qquad \quad \left. \left. \times (- \partial _r\psi +\tilde{F}-\nabla _qV)^j (r,q_r^m)dr\right| ^p\right] ^{1/p}\nonumber \\&\qquad \quad +E\left[ \left| \int _s^t (\nabla _z\chi )(r,q_r^m,z_r^m) \cdot \sigma (r,q^m_r) dW_r\right| ^p\right] ^{1/p}\bigg )\nonumber \\&\qquad \quad +m\bigg (E\left[ \left| \chi (t,q_t^m,z_t^m) \right| ^p\right] ^{1/p} +E\left[ \left| \chi (s,q_s^m,z_s^m) \right| ^p\right] ^{1/p}\nonumber \\&\qquad \quad +E\left[ \left| \int _s^t\partial _r \chi (r,q_r^m,z_r^m)dr \right| ^p\right] ^{1/p}\bigg )\nonumber \\&\quad \le {\tilde{C}}m^{1/2}\bigg ( \int _s^t E\left[ (1+\Vert q_r^m\Vert ^{{\tilde{p}}})^p(1+\Vert z_r^m\Vert ^{k+1})^p\right] ^{1/p}dr\nonumber \\&\qquad \quad + E\left[ \left( \int _s^t \Vert (\nabla _z\chi )(r,q_r^m,z_r^m) \cdot \sigma (r,q^m_r)\Vert ^2dr \right) ^{p/2}\right] ^{1/p}\bigg )\nonumber \\&\qquad \quad +{\tilde{C}} m\left( E\left[ (1+\Vert q_t^m\Vert ^{{\tilde{p}}})^p (1+\Vert z_t^m\Vert ^k)^p\right] ^{1/p}+ E\left[ (1+\Vert q_s^m\Vert ^{{\tilde{p}}})^p(1+\Vert z_s^m\Vert ^k)^p\right] ^{1/p}\right. \nonumber \\&\qquad \quad \left. + \int _s^t E\left[ (1+\Vert q_r^m\Vert ^{{\tilde{p}}})^p(1+\Vert z_r^m\Vert ^k)^p\right] ^{1/p}dr \right) . \end{aligned}$$

(143)

From this we can use Theorem 1 to find

$$\begin{aligned}&\sup _{0\le s\le t\le T}E\left[ \left| J^m_{s,t}-\int _s^t B^{i_1,\ldots ,i_k}(r,q^m_r) \left( \int h(r,q^m_r,z) z_{i_1}\ldots z_{i_k} dz \right) dr\right| ^p\right] ^{1/p}\nonumber \\&\quad \le {\tilde{C}}( m^{1/2}T+ m(2+T)+m^{1/2} T^{1/2}) \sup _{r\in [0,T]} E\left[ (1+\Vert q_r^m\Vert ^{{\tilde{p}}})^{2p}\right] ^{1/(2p)}\nonumber \\&\qquad \times E\left[ (1+\Vert z_r^m\Vert ^{k+1})^{2p}\right] ^{1/(2p)} =O(m^{1/2}). \end{aligned}$$

(144)

We can now compute

$$\begin{aligned}&\sup _{0\le s\le t\le T}E\left[ \left| J_{s,t}^m-J_{s,t}\right| ^p\right] ^{1/p}\nonumber \\&\quad \le O(m^{1/2})+\sup _{0\le s\le t\le T}E\left[ \left| \int _s^t B^{i_1,\ldots ,i_k}(r,q^m_r) \left( \int h(r,q^m_r,z) z_{i_1}\ldots z_{i_k} dz \right) dr\right. \right. \nonumber \\&\qquad \left. \left. - \int _s^t B^{i_1,\ldots ,i_k}(r,q_r) \left( \int h(r,q_r,z) z_{i_1}\ldots z_{i_k} dz \right) dr\right| ^p\right] ^{1/p}\nonumber \\&\quad \le O(m^{1/2})+C_{i_1\ldots i_k} \int _0^T E\left[ \left| (B^{i_1,\ldots ,i_k}\beta ^{-k/2})(r,q_r^m) - (B^{i_1,\ldots ,i_k}\beta ^{-k/2})(r,q_r) \right| ^p\right] ^{1/p}dr \end{aligned}$$

(145)

where

$$\begin{aligned} C_{i_1\ldots i_k}=\left( \frac{1}{2\pi }\right) ^{n/2}\int e^{-\Vert w\Vert ^2/2} w_{i_1}\ldots w_{i_k} dw. \end{aligned}$$

(146)

The assumptions imply $B^{i_1,\ldots ,i_k}\beta ^{-k/2}$ are $C^1$ with polynomially bounded first derivatives, and therefore the fundamental theorem of calculus can be used to show that

$$\begin{aligned} \sup _{t\in [0,T]}|(B^{i_1,\ldots ,i_k}\beta ^{-k/2})(t,q)-B^{i_1,\ldots ,i_k}\beta ^{-k/2}(t,{\tilde{q}}))|\le {\tilde{C}}(1+\Vert q\Vert ^{{\tilde{p}}}+\Vert q-{\tilde{q}}\Vert ^{{\tilde{p}}})\Vert q-{\tilde{q}}\Vert \end{aligned}$$

(147)

for some ${\tilde{C}},{\tilde{p}}>0$.

Therefore, again using Theorem 1, we find

$$\begin{aligned}&\sup _{0\le s\le t\le T}E\left[ \left| J_{s,t}^m-J_{s,t}\right| ^p\right] ^{1/p}\nonumber \\&\quad \le O(m^{1/2})+{\tilde{C}} T\sup _{r\in [0,T]} E\left[ (1+\Vert q_r\Vert ^{{\tilde{p}}}+\Vert q_r-{\tilde{q}}_r^m\Vert ^{{\tilde{p}}})^{2p}\right] ^{1/(2p)}E\left[ \Vert q_r^m-q_r\Vert ^{2p}\right] ^{1/{2p}}\nonumber \\&\quad =O(m^{1/2}). \end{aligned}$$

(148)

The result for general $p>0$ then follows from Hölder’s inequality. $\square$

Corollary B3

If the tensor rank, k, is odd then $J_{s,t}=0$ and hence

$$\begin{aligned} \sup _{0\le s\le t\le T}E\left[ \left| J_{s,t}^m\right| ^p\right] ^{1/p}=O(m^{1/2}) \end{aligned}$$

(149)

as $m\rightarrow 0$.

Processes of the form $m^{-1/2}J^m_{s,t}$ for k is odd do appear in the expression for the entropy production, Eq. (54). The above corollary proves that they don’t explode in the $L^p$ norm as $m\rightarrow 0$. In fact, we will now prove that their expected values have a well behaved limit.

Theorem B6

Let Assumption B1 hold, $T>0$, k be odd, and $B:{\mathbb {R}}\times {\mathbb {R}}^n\rightarrow T^k({\mathbb {R}}^n)$ be $C^2$ with B, $\partial _t B$, $\partial _{q^i} B$, $\partial _t\partial _{q^i}B$, and $\partial _{q^j}\partial _{q^i}B$ polynomially bounded in q, uniformly in $t\in [0,T]\times {\mathbb {R}}^n$ and consider the family of processes

$$\begin{aligned} J_{s,t}^m=\int _s^t B^{i_1,\ldots ,i_k}(r,q_r^m) (z_r^m)_{i_1}\ldots (z_r^m)_{i_k} dr \end{aligned}$$

(150)

for $0\le s\le t\le T$. Then, as $m\rightarrow 0$, we have

(151)

where h is given by Eq. (132) and $\chi$ is defined from B as in Eq. (137).

Proof

The hypotheses of Theorem B5 hold, so we can follow its proof up to Eq. (142) to obtain

$$\begin{aligned}&m^{-1/2}J^m_{s,t} =-\int _s^t(\nabla _q\chi )(r,q_r^m,z_r^m)\cdot z_r^m dr\nonumber \\&\qquad -\int _s^t (\nabla _z\chi )(r,q_r^m,z_r^m) \cdot \left[ (-\nabla _q V(r,q_r^m)-\partial _r\psi (r,q^m_r)+{\tilde{F}}(r,q_r^m))dr+\sigma (r,q^m_r) dW_r\right] \nonumber \\&\qquad +m^{1/2}\left( \chi (t,q_t^m,z_t^m)-\chi (s,q_s^m,z_s^m)-\int _s^t\partial _r \chi (r,q_r^m,z_r^m)dr\right) , \end{aligned}$$

(152)

where $\chi$ is defined in Eq. (137).

The following computation shows that

$$\begin{aligned} M_{s,t}\equiv \int _s^t (\nabla _z\chi )(r,q_r^m,z_r^m) \cdot \sigma (r,q^m_r) dW_r \end{aligned}$$

(153)

is a martingale (see [52]):

$$\begin{aligned}&E\left[ \int _s^t\Vert (\nabla _z\chi )(r,q_r^m,z_r^m) \cdot \sigma (r,q^m_r)\Vert ^2 dr\right] \nonumber \\&\quad \le {\tilde{C}}\Vert \sigma \Vert ^2_{\infty } E\left[ \int _s^t (1+\Vert q_r^m\Vert ^{{\tilde{p}}})^2(1+\Vert z_r^m\Vert ^{k})^2dr\right] \nonumber \\&\quad \le {\tilde{C}}\Vert \sigma \Vert ^2_{\infty } (t-s)\sup _{r\in [0,t]} E\left[ (1+\Vert q_r^m\Vert ^{{\tilde{p}}})^4\right] ^{1/2} E\left[ (1+\Vert z_r^m\Vert ^{k-1})^4\right] ^{1/2}<\infty , \end{aligned}$$

(154)

where we used Eq. (141), Assumption B1, and Theorem 1.

Therefore

$$\begin{aligned} m^{-1/2}E[J^m_{s,t}]&= -E\left[ \int _s^t (\nabla _z\chi )(r,q_r^m,z_r^m) \cdot (-\nabla _q V(r,q_r^m)-\partial _r\psi (r,q_r^m)+{\tilde{F}}(r,q_r^m))dr\right] \nonumber \\&\qquad -E\left[ \int _s^t(\nabla _q\chi )(r,q_r^m,z_r^m)\cdot z_r^m dr\right] +O(m^{1/2}), \end{aligned}$$

(155)

where we used the same reasoning as in the proof of Eq. (143) to bound the last term.

$\nabla _z\chi (t,q,z) \cdot (-\nabla _q V(t,q)-\partial _t\psi (t,q)+{\tilde{F}}(t,q))$ and $z\cdot \nabla _q\chi (t,q,z)$ are both finite sums of multi-linear functions of z. Tracing the definition Eq. (137), one can see that each tensor in the sum is a $C^1$ function of (t, q) and has zeroth and first derivatives that are polynomially bounded in q, uniformly in $t\in [0,T]$. Therefore Theorem B5 applies to these integrals, giving

(156)

and

$$\begin{aligned}&E\left[ \int _s^t(\nabla _q\chi )(r,q_r^m,z_r^m)\cdot z_r^m dr\right] =E\left[ \int _s^t \int \left( (\nabla _q\chi )(r,q_r,z)\cdot z\right) h(r,q_r,z)dzdr\right] +O(m^{1/2}). \end{aligned}$$

(157)

This completes the proof. $\square$

Appendix C: The Cell Problem

This appendix details the solution to the cell problem, Eq. (128), a certain inhomogeneous linear partial differential equation that is useful for homogenizing integral processes. Specifically, we provide an explicit solution for the case where the inhomogeneity is a multi-linear function.

We will need the following lemma bounding the spectrum of a matrix. See, for example, Appendix A in [47] for a proof.

Lemma C1

Let A be an $n\times n$ real or complex matrix with symmetric part $A^s=\frac{1}{2}(A+A^*)$. If the eigenvalues of $A^s$ are bounded above (resp. below) by $\alpha$ then the real parts of the eigenvalues of A are bounded above (resp. below) by $\alpha$.

We will also need the following result, which solves a kind of generalized Lyapunov equation.

Lemma C2

Let V be a finite dimensional vector space over ${\mathbb {C}}$, $C:V\rightarrow V$ be linear, and $B:V^k\rightarrow {\mathbb {C}}$ be multi-linear (i.e. $B\in T^k(V)$). If the eigenvalues of C all have negative real parts then there exists a unique $A\in T^k(V)$ that satisfies $\sum _i A(\cdot ,\ldots ,\cdot ,C\cdot ,\cdot ,\ldots ,\cdot )=-B$ (i.e. for the ith term in the sum, the ith input is composed with C). A is given by

$$\begin{aligned} A(v_1,\ldots ,v_k)=\int _0^\infty B(e^{tC}v_1,\ldots ,e^{tC}v_k) dt. \end{aligned}$$

(158)

Proof

The eigenvalue bound implies the existence of ${\tilde{C}}>0$, $\mu >0$ such that $\Vert e^{tC}\Vert \le {\tilde{C}}e^{-\mu t}$, therefore the integral Eq. (158) exists. We have

$$\begin{aligned}&\sum _i A(v_1,\ldots ,Cv_i,\ldots ,v_k)=\sum _i \int _0^\infty B(e^{tC}v_1,\ldots ,e^{tC}Cv_i,\ldots ,e^{tC}v_k) dt\nonumber \\&\quad =\int _0^\infty \frac{d}{dt}B(e^{tC}v_1,\ldots ,e^{tC}v_i,\ldots ,e^{tC}v_k) dt =-B(v_1,\ldots ,v_k). \end{aligned}$$

(159)

Therefore Eq. (158) provides the desired solution.

To prove uniqueness, it suffices to show that $A=0$ is the unique solution corresponding to $B=0$. To this end, suppose $\sum _i A(\cdot ,\ldots ,\cdot ,C\cdot ,\cdot ,\ldots ,\cdot )=0$. Let $\lambda _i$ be eigenvalues of C and $e^i_j$ be a basis of generalized eigenvectors, where $\{e^i_j\}_j$ is a basis for the eigenspace corresponding to $\lambda _i$ and $C e^i_j=\lambda _ie^i_j+e^i_{j-1}$ ($e_{-1}\equiv 0)$. Then

$$\begin{aligned} 0=\sum _l A(e^{i_1}_{0},\ldots ,Ce^{i_l}_{0},\ldots ,e^{i_k}_0)=\left( \sum _l \lambda _{i_l} \right) A(e^{i_1}_0,\ldots ,e^{i_k}_0). \end{aligned}$$

(160)

The coefficient is non-zero since the real parts of the $\lambda _i$ are all negative. Therefore

$$\begin{aligned} A(e^{i_1}_0,\ldots ,e^{i_k}_0)=0. \end{aligned}$$

(161)

We now show $A(e^{i_1}_{j_1},\ldots ,e^{i_k}_{j_k})=0$ for all choices of i’s and j’s. This will prove that $A=0$ by multi-linearity and the fact that the $e^{i}_j$’s form a basis. We induct on $N=\sum _{l} j_l$. We showed it above for $N=0$. Suppose it holds for $N-1$. Given $j_l$ with $\sum _l j_l=N$ we have

$$\begin{aligned} 0=&\sum _l A(e^{i_1}_{j_1},\ldots ,Ce^{i_l}_{j_l},\ldots ,e^{i_k}_{j_k})\nonumber \\ =&\left( \sum _l \lambda _{i_l} \right) A(e^{i_1}_{j_1},\ldots ,e^{i_k}_{j_k})+\sum _lA(e^{i_1}_{j_1},\ldots ,e^{i_l}_{j_l-1},\ldots ,e^{i_k}_{j_k}). \end{aligned}$$

(162)

$j_1+\ldots +(j_l-1)+\ldots +j_k=N-1$, so the last term vanishes by the induction hypothesis. As before, $\sum _l \lambda _{i_l}\ne 0$, hence $A(e^{i_1}_{j_1},\ldots ,e^{i_k}_{j_k})=0$. This proves the claim by induction. $\square$

Finally, the following lemma details the solution to the cell problem, Eq. (128).

Lemma C3

Consider the differential operator L defined by

$$\begin{aligned} (L\chi )(z)=&\beta ^{-1} \gamma _{\xi \zeta }(\partial _{z_\xi }\partial _{z_\zeta }\chi )(z)-{\tilde{\gamma }}_{\xi \eta }\delta ^{\eta \zeta }z_\zeta (\partial _{z_\xi }\chi )(z) \end{aligned}$$

(163)

where $\gamma$, the symmetric part of ${\tilde{\gamma }}$, is positive definite and $\beta >0$.

Let $k\ge 1$ and $B\in T^k({\mathbb {R}}^n)$. For $j=0,\ldots ,\lfloor (k-1)/2\rfloor$ define $A_j \in T^{k-2j}({\mathbb {R}}^n)$ inductively by

$$\begin{aligned} A_0(v_1,\ldots ,v_k)=-\int _0^\infty B(e^{-t{\tilde{\gamma }}}v_1,\ldots ,e^{-t{\tilde{\gamma }}}v_k)dt \end{aligned}$$

(164)

and

$$\begin{aligned} A_{j}(v_1,\ldots ,v_{k-2j})=\int _0^\infty 2\beta ^{-1} \sum _{\alpha =1}^{k-2(j-1)-1} \sum _{\delta >\alpha } A_{j-1}^{\alpha \delta } (e^{-t{\tilde{\gamma }}}v_1,\ldots ,e^{-t{\tilde{\gamma }}}v_{k-2j})dt, \end{aligned}$$

(165)

where $A_j^{\alpha \delta }\in T^{{k-2(j+1)}}({\mathbb {R}}^n)$ is the multi-linear map with components $A_j^{i_1,\ldots ,i_{k-2j}} \gamma _{i_\alpha i_\delta }$ and, for the purposes of taking the operator exponential, ${\tilde{\gamma }}$ is to be thought of as the linear map with action $z_\xi \rightarrow {\tilde{\gamma }}_{\xi \eta }\delta ^{\eta \zeta }z_\zeta$.

Then

$$\begin{aligned} \chi (z)=\sum _{j=0}^{\lfloor (k-1)/2\rfloor } A_j(z,\ldots ,z) \end{aligned}$$

(166)

is a solution to the cell problem

$$\begin{aligned} (L\chi )(z)=B(z,\ldots ,z)-\left( \frac{\beta }{2\pi }\right) ^{n/2}\int B({\tilde{z}},\ldots ,{\tilde{z}})e^{-\beta \Vert {\tilde{z}}\Vert ^2/2}d{\tilde{z}}. \end{aligned}$$

(167)

Note that, if k is odd, the integral in Eq. (167) vanishes.

Consider the components $A_j^{i_1,\ldots ,i_{k-2j}}$ to be functions of $(\beta ,{\tilde{\gamma }},B)$, defined on the domain where $\beta >0$, ${\tilde{\gamma }}$ has positive definite symmetric part, and $B\in T^k({\mathbb {R}}^n)$. The $A_j^{i_1,\ldots ,i_{k-2j}}$ are $C^\infty$ jointly in all of their variables on this domain and are linear in B.

Let $U_{\epsilon , R}$ be the open set defined by $\beta >\epsilon$ and the symmetric part of ${\tilde{\gamma }}$ having eigenvalues in the interval $(\epsilon ,R)$. Given $B\in T^k({\mathbb {R}}^n)$, any order derivative (including the zeroth) of $(\beta ,{\tilde{\gamma }})\rightarrow A_j^{i_1,\ldots ,i_{k-2j}}(\beta ,{\tilde{\gamma }},B)$ with respect to any combination of its variables is bounded by ${\tilde{C}} \Vert B\Vert$ on $U_{\epsilon ,R}$ for some ${\tilde{C}}>0$ (${\tilde{C}}$ depends on $\epsilon$, R, and the choice of derivatives, but not on B).

Proof

For $j=0,\ldots ,\lfloor (k-1)/2\rfloor$ let $A_j \in T^{k-2j}({\mathbb {R}}^n)$ be defined by Eq. (164)-Eq. (165). Note that Lemma C1 implies that the real parts of the eigenvalues of $-{\tilde{\gamma }}$ are negative, and hence the integrals in the definitions exist.

Define

$$\begin{aligned} \chi (z)=\sum _{j=0}^{\lfloor (k-1)/2\rfloor } A_j(z,\ldots ,z). \end{aligned}$$

(168)

We have

$$\begin{aligned} (\partial _{z_\xi } A_j)(z,\ldots ,z)=&\sum _{\alpha =1}^{k-2j} A_j^{i_1,\ldots ,i_{k-2j}}z_{i_1}\ldots z_{i_{\alpha -1}} \delta _{i_\alpha }^\xi z_{i_{\alpha +1}}\ldots z_{i_{k-2j}},\nonumber \\ (\partial _{z_\zeta }\partial _{z_\xi } A_j)(z,\ldots ,z)=&A_j^{i_1,\ldots ,i_{k-2j}} \sum _{\alpha =1}^{k-2j-1} \sum _{\delta >\alpha } \left( \delta _{i_\alpha }^{ \xi } \delta _{i_\delta }^\zeta + \delta _{i_\delta }^\xi \delta _{i_\alpha }^\zeta \right) \prod _{\rho \ne \alpha ,\delta }z_{i_{\rho }}, \end{aligned}$$

(169)

and so

$$\begin{aligned} (L\chi )(z)=&\sum _{j=0}^{\lfloor (k-1)/2\rfloor } \left( \beta ^{-1} \gamma _{\xi \zeta }(\partial _{z_\xi }\partial _{z_\zeta }A_j)(z)-{\tilde{\gamma }}_{\xi \eta }\delta ^{\eta \zeta }z_\zeta (\partial _{z_\xi }A_j)(z)\right) \nonumber \\ =&\sum _{j=0}^{\lfloor (k-1)/2\rfloor } \left( 2\beta ^{-1} \sum _{\alpha =1}^{k-2j-1} \sum _{\delta >\alpha } A_j^{\alpha \delta } (z,\ldots ,z)-\sum _{\alpha =1}^{k-2j} A_j(z,\ldots ,z,{\tilde{\gamma }} z,z,\ldots ,z)\right) , \end{aligned}$$

(170)

where $A_j^{\alpha \delta }\in T^{{k-2(j+1)}}({\mathbb {R}}^n)$ is the multi-linear map with components $A_j^{i_1,\ldots ,i_j} \gamma _{i_\alpha i_\delta }$ and it is the $\alpha$’th input of $A_j(z,\ldots ,z,{\tilde{\gamma }} z,z,\ldots ,z)$ that equals ${\tilde{\gamma }} z$ in the above sum.

Collecting terms involving tensors of the same degree, we have

$$\begin{aligned}&(L \chi )(z)-B(z,\ldots ,z)\nonumber \\&\quad =\sum _{j=1}^{\lfloor (k-1)/2\rfloor }\left( 2\beta ^{-1} \sum _{\alpha =1}^{k-2(j-1)-1} \sum _{\delta>\alpha } A_{j-1}^{\alpha \delta } (z,\ldots ,z)-\sum _{\alpha =1}^{k-2j} A_j(z,\ldots ,z,{\tilde{\gamma }} z,z,\ldots ,z)\right) \nonumber \\&\qquad - \left( \sum _{\alpha =1}^{k} A_0(z,\ldots ,z,{\tilde{\gamma }} z,z,\ldots ,z)+B(z,\ldots ,z)\right) \nonumber \\&\qquad +2\beta ^{-1} \sum _{\alpha =1}^{k-2\lfloor (k-1)/2\rfloor -1} \sum _{\delta >\alpha } A_{\lfloor (k-1)/2\rfloor }^{\alpha \delta } (z,\ldots ,z). \end{aligned}$$

(171)

Recalling the definition of $A_0$ and $A_j$ from Eqs. (164) and (165), Lemma C2 implies that they satisfy

$$\begin{aligned}&\sum _{\alpha =1}^{k} A_0(z,\ldots ,z,{\tilde{\gamma }} z,z,\ldots ,z)=-B(z,\ldots ,z), \end{aligned}$$

(172)

$$\begin{aligned}&\sum _{\alpha =1}^{k-2j} A_j(z,\ldots ,z,{\tilde{\gamma }} z,z,\ldots ,z)= 2\beta ^{-1} \sum _{\alpha =1}^{k-2(j-1)-1} \sum _{\delta >\alpha } A_{j-1}^{\alpha \delta }(z,\ldots ,z),~~ j\ge 1. \end{aligned}$$

(173)

Therefore

$$\begin{aligned}&(L \chi )(z)-B(z,\ldots ,z)=2\beta ^{-1} \sum _{\alpha =1}^{k-2\lfloor (k-1)/2\rfloor -1} \sum _{\delta >\alpha } A_{\lfloor (k-1)/2\rfloor }^{\alpha \delta } (z,\ldots ,z). \end{aligned}$$

(174)

If k is odd then $k-2\lfloor (k-1)/2\rfloor =1$ and therefore the second summation in Eq. (174) is empty. This gives $L\chi (z)=B(z,\ldots ,z)$ as claimed. If k is even then $k-2\lfloor (k-1)/2\rfloor =2$ and $A_{\lfloor (k-1)/2\rfloor }^{\alpha \delta }\in T^0({\mathbb {R}}^k)={\mathbb {R}}$. Therefore the right hand side of Eq. (174), call it ${\tilde{B}}$, is a constant.

The value of ${\tilde{B}}$ can be computed by integrating both sides against

$$\begin{aligned} h(z)=\left( \frac{\beta }{2\pi }\right) ^{n/2}e^{-\beta \Vert z\Vert ^2/2}. \end{aligned}$$

(175)

Using the fact that $\int h(z)dz=1$ results in

$$\begin{aligned} {\tilde{B}}=\int (L\chi )({\tilde{z}}) h({\tilde{z}}) d{\tilde{z}}-\int B({\tilde{z}},\ldots ,{\tilde{z}}) h({\tilde{z}})d{\tilde{z}}. \end{aligned}$$

(176)

Integrating by parts, observing that the boundary terms vanish at infinity, and using $L^*h=0$, where $L^*$ is the formal adjoint of L we find

$$\begin{aligned} {\tilde{B}}=-\int B({\tilde{z}},\ldots ,{\tilde{z}}) h({\tilde{z}})d{\tilde{z}} \end{aligned}$$

(177)

as claimed.

We now prove the claimed smoothness and boundedness properties. Let U be the subset of the $n\times n$ real matrices such that all of the eigenvalues of the symmetric part of the matrix are negative. This is an open set and the functions $G^{i_1\ldots i_l}_{j_1\ldots .j_l}:U\rightarrow \mathbb {{\mathbb {R}}}$,

$$\begin{aligned} G^{i_1\ldots i_l}_{j_1\ldots .j_l}(A)=\int _0^\infty (e^{tA})^{i_1}_{j_1}\ldots (e^{tA})^{i_l}_{j_l}dt, \end{aligned}$$

(178)

are smooth and can be differentiated under the integral. Restricted to the subset where the eigenvalues of the symmetric part are less than $-\epsilon <0$, $G^{i_1\ldots i_l}_{j_1\ldots .j_l}$ and its derivatives are all bounded. These facts can be proven by using the dominated convergence theorem, along with the formula for the derivative of the matrix exponential found in [57].

Therefore

$$\begin{aligned} A_0^{i_1,\ldots ,i_k}(\beta ,{\tilde{\gamma }},B)=-B^{j_1,\ldots ,j_k}G^{i_1\ldots i_k}_{j_1\ldots .j_k}(-{\tilde{\gamma }}) \end{aligned}$$

(179)

which is linear in B, smooth in $(B,{\tilde{\gamma }})$, and it, along with its derivatives, are bounded by ${\tilde{C}}\Vert B\Vert$, on the domain where the symmetric part of ${\tilde{\gamma }}$ has eigenvalues contained in $(\epsilon ,R)$.

Now, assume $A_{j-1}$ satisfies the desired properties. Then one can easily verify that

$$\begin{aligned}&A_{j}^{i_1,\ldots ,i_{k-2j}}(\beta ,{\tilde{\gamma }},B)\nonumber \\&\quad =2\beta ^{-1} \sum _{\alpha =1}^{k-2(j-1)-1} \sum _{\delta >\alpha } A_{j-1}^{l_1\ldots l_{\alpha -1} \eta l_{\alpha }\ldots . l_{\delta -2} \xi l_{\delta -1}\ldots l_{k-2j}}(\beta ,{\tilde{\gamma }},B)\frac{1}{2} ({\tilde{\gamma }}_{\eta \xi }+{\tilde{\gamma }}_{\xi \eta })G_{i_1\ldots i_{k-2j}}^{l_1\ldots l_{k-2j}}(-{\tilde{\gamma }}) \end{aligned}$$

(180)

does as well. Therefore the claim holds for all j by induction. $\square$