A General Fluctuation–Response Relation for Noise Variations and its Application to Driven Hydrodynamic Experiments

Abstract

The effect of a change of noise amplitudes in overdamped diffusive systems is linked to their unperturbed behavior by means of a nonequilibrium fluctuation–response relation. This formula holds also for systems with state-independent nontrivial diffusivity matrices, as we show with an application to an experiment of two trapped and hydrodynamically coupled colloids, one of which is subject to an external random forcing that mimics an effective temperature. The nonequilibrium susceptibility of the energy to a variation of this driving is an example of our formulation, which improves an earlier version, as it does not depend on the time-discretization of the stochastic dynamics. This scheme holds for generic systems with additive noise and can be easily implemented numerically, thanks to matrix operations.

Appendices

Appendix 1: Stationary Distribution

Here we briefly sketch the calculation of the stationary distribution of the system, for the sake of completeness.

With a drift $a(x)=-\mu \kappa x$ linear in $x$, the equation of motion (1) describes an Ornstein-Uhlenbeck process, which we rewrite here as

$$\begin{aligned} \dot{x} = - \Omega x+ \sqrt{2D} \xi \ , \end{aligned}$$

(38)

with $\Omega = \mu \kappa$. According to the corresponding Fokker–Planck equation, $\dot{\rho } = -\partial _i J_i$, stationarity requires the ensemble current $J = -\rho \Omega x- D\nabla \rho$ to be divergenceless, yielding

$$\begin{aligned} 0 = \rho \Omega _{ii} + \Omega _{ij} x_j \partial _i \rho +D_{ij} \partial _i \partial _j \rho \ . \end{aligned}$$

(39)

Clearly, a Gaussian distribution of the form

$$\begin{aligned} \rho (x) = Z^{-1} e^{-\frac{1}{2} x^\dagger Gx} \end{aligned}$$

(40)

satisfies the zero divergence condition above. To find the inverse covariance matrix $G$, one substitutes the ansatz, upon which a few lines of algebra implies the condition

$$\begin{aligned} \Omega G^{-1} + G^{-1} \Omega ^\dagger = 2 D\ . \end{aligned}$$

(41)

This is a system of linear equations in the elements of the covariance matrix $G^{-1}$, which can be solved, for instance, by rewriting it in terms of a vector composed of the columns of $G^{-1}$. Here, we simply quote the resulting matrix: Recalling $\Omega = \mu \kappa$ with $\kappa$ diagonal and $\mu$ given in Eq. (3), and $D$ given in Eq. (6), one finds

$$\begin{aligned} G^{-1} = \begin{bmatrix} \frac{T+(1-\varepsilon ^2)\Delta T}{\kappa _{11}} + \frac{\varepsilon ^2\Delta T}{\kappa _{11}+\kappa _{22}}&\frac{\varepsilon \Delta T}{\kappa _{11} + \kappa _{22}} \\ \frac{\varepsilon \Delta T}{\kappa _{11} + \kappa _{22}}&\frac{T}{\kappa _{22}} + \frac{\varepsilon ^2\Delta T}{\kappa _{11}+\kappa _{22}} \end{bmatrix} \ . \end{aligned}$$

(42)

Inversion of this matrix thus determines the stationary distribution (40).

Appendix 2: Form of the Perturbation Parameter

Even though it may sometimes be more convenient mathematically to work in terms of the noise amplitude $B$, it is the diffusivity matrix $D$ which is physically relevant, since the noise amplitude is fixed only up to an orthogonal transformation. Hence the perturbation parameter, $h= \delta B\tilde{B}^{-1}$, defined in Sec. 3.1 in terms of the noise amplitude should eventually be expressed in terms of a perturbation of the diffusivity. With $D= \tilde{D}+ \delta D$ and $B= \tilde{B}+ \delta B$, in line with Sec. 3.1, the definitions $2 D= BB^\dagger$ and $2 \tilde{D}= \tilde{B}\tilde{B}^\dagger$ imply that

$$\begin{aligned} 2 \delta D= \tilde{B}\delta B^\dagger + \delta B\tilde{B}^\dagger \ . \end{aligned}$$

(43)

Note that one should not expect to solve this equation for $\delta B$ uniquely given a specific $\delta D$; many noise coefficient matrices $B$ map into the same diffusion matrix $D$.

The relation above can now be used to express the perturbation parameter $h= \delta B\tilde{B}^{-1}$ in terms of $\tilde{D}$ and $\delta D$, but not uniquely, which is not a problem. Multiplying Eq. (43) by $\tilde{D}^{-1}$ from the left and right, one easily finds

$$\begin{aligned} \tilde{D}^{-1} \delta D\tilde{D}^{-1} = \tilde{D}^{-1} h+ h^\dagger \tilde{D}^{-1}\ . \end{aligned}$$

(44)

The left hand side of this equation is equal to $-\delta D^{-1}$ (verified easily by varying the identity $1 = DD^{-1}$) which is determined by the physical description of the perturbation. Meanwhile, the right hand side of the equation is twice the symmetric part of $\tilde{D}^{-1} h$. In other words, it is only the symmetric part of $\tilde{D}^{-1} h$ that is fixed by the physical form of the perturbation, and the antisymmetric part is left undetermined. It therefore behooves one to choose $\tilde{D}^{-1} h$ to be purely symmetric, whence one obtains $-\delta D^{-1} = 2 \tilde{D}^{-1} h$, or

$$\begin{aligned} h= -\tfrac{1}{2} \tilde{D}\delta D^{-1} = -\tfrac{1}{2} D\delta D^{-1} \ , \end{aligned}$$

(45)

where the second equality is valid due to the overarching first order approximation of linear response.

Appendix 3: Asymptotic Values of the Susceptibility

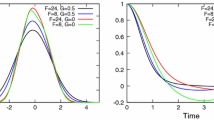
In this appendix, we sketch how the asymptotic values for the susceptibilities in Figs. 2 and 3 were obtained.

One can derive a host of relations valid in the stationary regime by requiring that time derivatives of state observables vanish [28]. For the present discussion, the relevant observable is the tensor $x_i x_j$, i.e.,

$$\begin{aligned} 0 = \frac{\mathrm{d}}{\mathrm{d}t} \langle x_i x_j \rangle = \langle \mathbb {L}x_i x_j \rangle \ , \end{aligned}$$

(46)

with the backward generator $\mathbb {L}= a_i \partial _i + D_{ij} \partial _i \partial _j$. (One should keep in mind that the average is in the stationary regime, although we leave it unlabeled). When evaluated explicitly, with $a= \mu F$, one finds the relation

$$\begin{aligned} 0 = \mu \langle Fx^\dagger \rangle + \langle xF^\dagger \rangle \mu + 2 D\ . \end{aligned}$$

(47)

This matrix relation entails a set of equations for the independent components of the tensor $\langle x_i F_j \rangle$, of which there are 3 in our case with 2 degrees of freedom.

We note that for our system, $U(x) = -(1/2) \mathrm{Tr}(Fx)$. Thus, multiplying Eq. (47) from the left by $\mu ^{-1}$ and taking the trace, we find the stationary average of the potential energy to be

$$\begin{aligned} \langle U(x) \rangle = -\frac{1}{2} \mathrm{Tr}\langle Fx \rangle = \frac{1}{2} \mathrm{Tr}(\mu ^{-1} D) \ . \end{aligned}$$

(48)

Hence, the stationary (asymptotic) value for the susceptibility is found as

$$\begin{aligned} \frac{\partial \langle U \rangle }{\partial \Delta T} = \frac{1}{2} \mathrm{Tr}\! \left( \mu ^{-1} \frac{\partial D}{\partial \Delta T}\right) = \frac{1}{2} \ , \end{aligned}$$

(49)

which was evaluated using Eq. (6) for the diffusion matrix. This asymptotic value for $\chi$ was indicated in Fig. 2.

The susceptibility of the energy of the second particle $U_2 (x_2) = -(1/2) F_2 x_2$ can be extracted similarly from Eq. (47), with the exception that one has to go through the tedium of actually solving for the component $\langle F_2 x_2 \rangle$. We quote only the result of this straightforward exercise:

$$\begin{aligned} \frac{\partial \langle U_2 \rangle }{\partial \Delta T} =&-\frac{1}{2} \frac{\partial }{\partial \Delta T} \langle F_2 x_2 \rangle = \frac{\varepsilon ^2}{2\left( 1+\frac{\kappa _{11}}{\kappa _{22}}\right) } \ . \end{aligned}$$

(50)

This was evaluated as 0.01899 for the actual experimental values of $\kappa _{11} = {3.3745} \,\mathrm{pN}/\upmu \mathrm{m}$, $\kappa _{22} = {3.3285} \,\mathrm{pN}/\upmu \mathrm{m}$, and $\varepsilon = 0.2766$, and indicated in Fig. 3 as the asymptotic value of the susceptibility $\chi$.