A proven optimal result for a benchmark instance of the uncapacitated examination timetabling problem

Abstract

Examination timetabling is a problem well known to the scheduling community. Its simplest version, which is the uncapacitated examination timetabling problem, is easily described and comprehended. Nevertheless, proof of optimality is notoriously difficult even for moderate size problems. In this paper, we describe the effort that our team exercised in finally proving the optimality of the sta83 instance of Carter’s dataset. The problem was decomposed naturally in three parts and for each part a different approach managed to prove optimality of the currently best known solution. This work also presents optimal solutions to subproblems that exist in various public datasets problems and two best known solutions of such problems.

1 Introduction

Timetabling problems arise in several domains including health-care, education, call centers, airlines and others. Rostering and scheduling are also commonly used terms to describe timetabling problems. In this paper we study the uncapacitated examination timetabling problem (UETP). UETP is the problem of scheduling university examinations to periods (time-slots) in such a way that no student should be examined at the same period for more than one course. Furthermore, the schedule of each student should allow enough time for studying between successive examinations. The problem is uncapacitated in the sense that no room capacities or availabilities are considered.

Our contribution to UETP is twofold. Firstly, we present a way of decomposing and reducing the sizes of the problems that results in obtaining two new best known solutions for benchmark instances. Secondly, and most noteworthy we propose a novel way of approaching a certain known instance of the Carter’s dataset (Carter et al., 1996) of the UETP that results in actually proving the optimal value of the instance.

An outline of the paper follows. Section 2 provides a succinct description of the problem. Section 3 presents a glimpse of the broad bibliography for university examination problems capacitated or not. The next section describes our efforts to cleanse and decompose the problem instances so as to reduce their sizes, in an effort to feed various solution approaches with easier to digest problems. Section 5 is devoted to attacking the UETP problem instances with three specific methods that are later used in Sect. 6 to prove optimality for problem instance sta83 of the well-known Carter’s dataset. Next, our conclusions follow.

2 Problem description

Each UETP instance contains information about the set of examinations that each student is enrolled in. Each instance has a specific number of periods that can be used to schedule the examinations to. The single hard constraint is that no student is allowed to participate in more than one examination per period. To allow time for each student to study between his examinations, for each student s, for each pair of examinations taken by s, a penalty of 16 is imposed if the two examinations occur in adjacent time slots (called distance 1), penalty 8 is imposed for distance 2, 4 for distance 3, 2 for distance 4, and 1 for distance 5.

The natural way to represent an instance is as a pair consisting of the number of available periods P and an undirected weighted graph ${\mathbb {G}} = ({\mathbb {V}},{\mathbb {E}})$ where each vertex in ${\mathbb {V}}$ is an examination and each edge in ${\mathbb {E}}$ connects two examinations with common students. The weight of each edge is the number of common students for the examinations it connects.

3 Related work

The field of educational timetabling is very active. Several papers are typically published every year regarding course timetabling (Babaei et al., 2015) (post-enrollment and curriculum-based), examination timetabling (Carter et al., 1996), high school timetabling (Schaerf, 1999), thesis defense timetabling (Battistutta et al., 2020) and others. Several surveys regarding the field have been published and present the challenges that such problems pose (Schaerf, 1999; Kristiansen & Stidsen, 2013). The survey by Qu et al. (2009) focuses on examination timetabling that is the subject of our work too. Recent surveys by Tan et al. (2021) and Ceschia et al. (2022) demonstrate the strong interest of the timetabling community for educational timetabling problems. In Ceschia et al. (2022) focus is given on “standard” formulations and benchmark instances that are also used in our work are presented. Another recent work, this time for real world examination timetabling problems, is the paper from Battistutta et al. (2020).

Members of our team are also active in educational timetabling. In Gogos et al. (2021) a novel way of estimating lower bounds for UETP instances was proposed. Ideas about symmetry elimination, problem decomposition and cleansing of the instances were also presented there. The current paper serves as a follow-up and provides experimental results based on those ideas.

4 Preprocessing

Before solving each problem, we perform a cleansing process through which we remove problem components that are irrelevant to the optimization. By solving the cleansed problem, we will still be able to find optimal solutions that will be optimal for the original problem. Furthermore, we identify independent subproblems that exist in each problem. Such subproblems can be solved independently and the solution to the original problem can be stitched by using the solutions of the subproblems. The main ideas that we use for cleansing and decomposing the problems are more extensively described in Gogos et al. (2021).

Initially, we remove obvious noise students and examinations (Alefragis et al., 2021). This occurs by removing from the problem students enrolled in a single examination since such students cannot contribute to the cost because cost incurs for pairs of examinations for the same student. Moreover, if all enrollments of an examination are students enrolled only in this examination, then we can safely remove the examination too. Then, we identify subgraphs of the graph that can be handled independently. Note that a subgraph of a graph ${\mathbb {G}}$ is a connected component of ${\mathbb {G}}$, and that it can be handled independently because none of its examinations and students appear anywhere outside the component. The size of a subgraph refers to the number of its nodes which is equal to the number of the corresponding subproblem’s exams. Subgraphs of size lower than $\lfloor \frac{P-1}{6} \rfloor + 1$, where P is the number of periods, are identified as noise. This can be justified by the fact that we can spread the examinations of such subgraphs to the P available periods with zero penalty. Examinations with degree lower than $\frac{P}{11}$ are also noise since they can be always positioned with zero penalty. Then, any student that has a single non-noise examination and an arbitrary amount of noise examinations is also considered as noise. The process repeats until no more examinations or students can be marked as noise. A description of the procedure is given in Algorithm 1.

Another form of preprocessing involves the identification of interchangeable examinations that was proposed in Gogos et al. (2021). These examinations have the same neighborhoods, as defined in graph ${\mathbb {G}}$, and the same number of common students for each neighbor. As these examinations are practically the same we can enforce them to either be in the same period if they are not in conflict or to follow a specific sequence of appearance in the final schedule if they have common students. By eliminating this type of symmetry of the problem, MIP/CP solvers are able to better explore the solution space.

4.1 Datasets

The standard benchmark dataset for UETP is Carter’s dataset (a.k.a. Toronto dataset). Those instances were contributed in Carter et al. (1996) back in 1996 and since then were used in many papers. Recently, 20 new instances that are modified versions of other more complex formulations, were added by Bellio et al. (2021) who proposed a new dataset obtained by translating real instances from other examination timetabling problems (i.e., 12 instances of the Track 1, ITC-2007 and 8 instances from various Italian universities) into the uncapacitated formulation. All of them are publicly available in https://opthub.uniud.it/ (OPTHUB) which is a site that hosts definitions, datasets and solutions of several timetabling problems that have attracted the interest of the timetabling community.

The characteristics of the instances used in this paper are shown in Table 1. Conflict density is a metric that is computed by dividing the number of edges of the problem’s corresponding graph by $n(n-1)/2$, where n is the number of vertices. Values for noise students and examinations are computed based on Algorithm 1. Moreover, the table presents the best known values that were obtained by solutions that we have downloaded from OPTHUB in April 2022. Costs assume integer values and since the problem is of minimization nature, lower values are favored. Normalized costs are shown in the rightmost column of the table and are computed by dividing each integer cost by the corresponding number of students. The star symbol ($*$) in best known cost (95947) of instance sta83 indicates that this cost is optimal. In Sect. 6, we show that this is indeed the case. We consider it as the highlight of our work, since it is the first instance among the Carter’s dataset for which it is proven that an optimal solution has been reached. It should be noted that the table has symbol $\dagger$ for the best known costs of two instances, ITC2007_9 and ITC2007_10. These best known values were contributed by our team and were obtained by exploiting the concept of noise examinations and students and the decomposition of problems to subproblems that enabled us to use optimal solutions to independent subproblems and search for good solutions using the Variable Neighborhood Search approach described in Alefragis et al. (2021). Note that all other best known values included in Table 1 are values from solutions contributed by other researchers to OPTHUB.

Table 1 Instances-descriptive statistics-noise examinations and noise students-best known costs

4.2 Decomposed instances

After applying Algorithm 1, some problems are decomposed to subproblems. For most instances, a number of examinations and students are removed since they are in effect noise. The resulting subproblems are presented in Table 2. The name of each subproblem follows the pattern d_i_(Ex_Sy_IDz), where d is the name of the originating instance, i is a number that assumes value 1 for the smallest subproblem and is incremented by 1 for each subsequent subproblem (subproblems are ordered by size = number of exams), x is the number of examinations, y is the number of students and z is the smallest examination number that exists in the subproblem. Number z is needed in order to differentiate among subproblems having the same number of examinations and same number of students. This is indeed the case for subproblems D1-2-17_1 and D1-2-17_2 that both have 8 examinations and 1 student, but in the first case the identifying examination is 217 while for the second case the identifying examination is 257. Note that in Table 2 the number of examinations and the number of students exclude noise examinations and noise students, respectively. Again, the presence of symbol $*$ denotes that the corresponding integer cost is optimal. It should be also noted that the normalized cost is computed by dividing the integer cost by the number of students (including noise ones) that exists in the originating instance. We opt to use two values for the cost (i.e., an exact integer one and an approximate decimal one) since the values in the relevant bibliography are decimal, but the integer cost is needed for precise results.

Table 2 Problems resulted by decomposed instances of Table 1—all noise examinations and noise students are removed

5 Optimality proving tools

We have identified three different approaches to prove optimality for certain instances, and we present them below. Under certain conditions (number of exams, conflict density, current best known solution, number of periods) these approaches may be able to prove that a solution is indeed optimal.

5.1 Mixed integer programming

As optimality is our main concern, the first thoughts that come to mind are linear programming and mixed integer programming. The mathematical model described below can solve an UETP instance, provided that the instance size is manageable. For a graph ${\mathbb {G}} = ({\mathbb {V}},{\mathbb {E}})$ where vertices ${\mathbb {V}}$ serve as the exams, each edge in ${\mathbb {E}}$ means that two examinations have common students. The weight of an edge $W_{v_1, v_2}$ connecting vertices $v_1$ and $v_2$ is equal to the number of common students these examinations have. P is the number of available periods.

The integer decision variables $p_v$ in Eq. 1 denote the period each examination v will take place while the derived binary decision variables in Eq. 2 help us to activate or deactivate penalties in the objective function in Eq. 3. In particular variable, $y16_{v_1, v_2}$ assumes value 1 when examinations $v_1$ and $v_2$ are positioned 1 period away from each other or 0 otherwise. Likewise, $y8_{v_1, v_2}$, $y4_{v_1, v_2}$, $y2_{v_1, v_2}$ and $y1_{v_1, v_2}$ are for distances of 2, 3, 4 and 5 periods correspondingly, between examinations $v_1$ and v2. The constraint in Eq. 4 forces examinations with common students to take place in different periods. Equation 5 forces binary decision variables in Eq. 2 to indicate the distance between two exams. Equations 4 and 5 are obviously nonlinear, so we used the logical constraints feature of IBM ILOG CPLEX (IBM, 2022) to model both of them. In particular, for Eq. 4 we directly used operator != having meaning “different from”, while for Equation  5 we used operator == meaning “equivalence”. IBM ILOG CPLEX uses a method called logical constraints extraction that automatically transforms logical constraints into equivalent linear formulations. This transformation involves automatic creation of new variables and constraints. Note that for each equality of Eq. 5, the right part consists of adding two equivalences that could not possible be both true at the same time (i.e., the equivalences have the same left part but different right parts). This ensures that the variable at the left part of the equality assumes a binary value. Equation 6 allows only one of the penalty indicating variables in Eq. 2 to be active at any time. This constraint is redundant, but its presence seems to help the solver in reaching better solutions.

$$\begin{aligned}{} & {} p_{v} \in [0, P) \quad \forall v \in {\mathbb {V}} \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \begin{aligned} \quad y16_{v_1, v_2} \in \lbrace 0, 1 \rbrace \quad \forall (v_1, v_2) \in {\mathbb {E}} \\ \quad y8_{v_1, v_2} \in \lbrace 0, 1 \rbrace \quad \forall (v_1, v_2) \in {\mathbb {E}} \\ \quad y4_{v_1, v_2} \in \lbrace 0, 1 \rbrace \quad \forall (v_1, v_2) \in {\mathbb {E}} \\ \quad y2_{v_1, v_2} \in \lbrace 0, 1 \rbrace \quad \forall (v_1, v_2) \in {\mathbb {E}} \\ \quad y1_{v_1, v_2} \in \lbrace 0, 1 \rbrace \quad \forall (v_1, v_2) \in {\mathbb {E}} \\ \end{aligned} \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \begin{aligned} \text {min} \quad&16*\sum _{v_1, v_2 \in {\mathbb {E}}} W_{v_1, v_2}*y16_{v_1, v_2} \\&+ 8*\sum _{v_1, v_2 \in {\mathbb {E}}} W_{v_1, v_2}*y8_{v_1, v_2}\\&+ 4*\sum _{v_1, v_2 \in {\mathbb {E}}} W_{v_1, v_2}*y4_{v_1, v_2} \\&+ 2*\sum _{v_1, v_2 \in {\mathbb {E}}} W_{v_1, v_2}*y2_{v_1, v_2} \\&+ \sum _{v_1, v_2 \in {\mathbb {E}}} W_{v_1, v_2}*y1_{v_1, v_2} \end{aligned} \end{aligned}$$

(3)

Subject to:

$$\begin{aligned} p_{v_1} \ne p_{v_2} \quad \forall (v_1, v_2) \in {\mathbb {E}} \end{aligned}$$

(4)

$$\begin{aligned} \begin{aligned} y16_{v_1, v_2} = (p_{v_1}-p_{v_2}=1) + (p_{v_1}-p_{v_2}=-1) \quad \forall (v_1, v_2) \in {\mathbb {E}}\\ y8_{v_1, v_2} = (p_{v_1}-p_{v_2}=2) + (p_{v_1}-p_{v_2}=-2) \quad \forall (v_1, v_2) \in {\mathbb {E}}\\ y4_{v_1, v_2} = (p_{v_1}-p_{v_2}=3) + (p_{v_1}-p_{v_2}=-3) \quad \forall (v_1, v_2) \in {\mathbb {E}}\\ y2_{v_1, v_2} = (p_{v_1}-p_{v_2}=4) + (p_{v_1}-p_{v_2}=-4) \quad \forall (v_1, v_2) \in {\mathbb {E}}\\ y1_{v_1, v_2} = (p_{v_1}-p_{v_2}=5) + (p_{v_1}-p_{v_2}=-5) \quad \forall (v_1, v_2) \in {\mathbb {E}}\\ \end{aligned} \end{aligned}$$

(5)

$$\begin{aligned} \begin{aligned}&y16_{v_1, v_2} + y8_{v_1, v_2} + y4_{v_1, v_2} + y2_{v_1, v_2} + y1_{v_1, v_2}\\&\le 1 \quad \forall (v_1, v_2) \in {\mathbb {E}}\\ \end{aligned} \end{aligned}$$

(6)

Finally, let ${\mathbb {I}}^+$ be the set of sets of interchangeable examinations as defined in Gogos et al. (2021). In order to break a symmetry of the problem, we enforce an order over the examinations belonging to each set. This is formulated in Eq. 7, where members of each set ${\mathbb {S}}$ of the sets in ${\mathbb {I}}^+$ are ordered among each other.

$$\begin{aligned} v_i \le v_{i+1} \quad \forall v_i \in {\mathbb {S}}: i \in 1 \dots {\mathbb {S}}-1, \quad \forall {\mathbb {S}} \in {\mathbb {I}}^{+} \end{aligned}$$

(7)

Other formulations of the mathematical model have been proposed in the past. An example is the work in Bellio et al. (2021) that uses the so-called channeling constraints that were originally proposed in Aardal et al. (2007). A difference in our model is that we employ the concept of interchangeable examinations that are embedded in the formulation. Moreover, the objective function is constructed equivalently, but differently, in our case.

5.2 Intelligent enumeration

Some of the instances have a comparatively small number of available periods. It is noteworthy that even small sub-problems with a few periods and a relatively low number of examinations are hard to optimally solve by current state of the art mixed integer programming solvers. A new method was developed to handle such instances, and this method, depending on the number of examinations, available periods and the conflict density of the corresponding graph is able to solve some problems to optimality. Moreover, the same method can be exploited and reach good solutions for bigger instances.

To best describe this process, we will use a toy example with its graph representation pictured in Fig. 1. Let the available periods for this problem to be four. The problem consists of five examinations with a varying number of common students between certain pairs of exams. Note that exams 1, 2, 3 form a non-trivial clique, e.g., they are a complete sub-graph of the graph. As no student is allowed to participate in more than one examination per period, those three examinations will end up in three different periods. Also, examination 5 with a weighted degree of just 2 does not seem to play a major part in the grander scheme of things. Note that an optimal solution puts examinations 1, 2, 3, 4, 5 at periods 2, 3, 0, 0, 3, respectively, and assumes a cost of 4008.

Fig. 1

Toy example for demonstrating the intelligent enumeration scheme

The method can be used to either search for a good solution or to prove optimality, based on characteristics of the problem in question. The main idea remains the same for both cases. Firstly, we reduce the problem size by removing some of its exams. Then, we generate partial solutions, evaluate their cost and if it falls under some cutoff limit, which could be the cost of the best known solution, we fill the missing examinations to form a complete solution. This process is expected to act as a filter and has the potential to be computationally faster than a full enumeration.

The main idea of the method is to exploit a clique in the graph. In selecting a clique, it usually makes sense to choose the maximum clique. In the toy example, the maximum clique is the set of examinations $\{1, 2, 3\}$. It is guaranteed that the clique’s examinations will end up on different periods which, for convenience, we name after them, $\{P_1, P_2, P_3\}$ correspondingly. Since we have four available periods we will name the period that will not be occupied by any of them as $P_E$. The remaining examinations $\{4, 5\}$ can be easily checked in this small example about their possible final positions. So, examination 4 can be placed in any of $\{P_2, P_3, P_E\}$ and examination 5 can join any period $\{P_1, P_2, P_3, P_E\}$.

Since examinations for the clique are fixed in periods $\{P_1, P_2, P_3\}$ the possible assignments for examinations 4 and 5 are $(4:P_2, 5:P_1), (4:P_2, 5:P_3), (4:P_2, 5:P_E), (4:P_3, 5:P_1), (4:P_3, 5:P_2), (4:P_3, 5:P_E), (4:P_E, 5:P_1), (4:P_E, 5:P_2), (4:P_E, 5:P_3)$ while $(4:P_2, 5:P_2), (4:P_3, 5:P_3), (4:P_E, 5:P_E)$ are infeasible as examinations 4 and 5 are in conflict. In total, there are 9 feasible schedules. If we had opted to leave examination 5 out, there would be just 3 feasible schedules $(4:P_2), (4:P_3), (4:P_E)$.

Initially, we ignore examination 5 and we examine all possible permutations of $\{P_1, P_2, P_3, P_E\}$. We complement every permutation with each of the 3 possible partial schedules $(4:P_2), (4:P_3), (4:P_E)$. Since each schedule and its reverse have exactly the same objective value, we can skip mirrored permutations, effectively cutting off half of the search space, thus eliminating this kind of symmetry. Nevertheless, for large numbers of periods, it is unrealistic to traverse all possible permutations, even by considering half of them. In the toy example, we evaluate $4!/2*3 = 36$ partial solutions (i.e., 4!/2 equals the permutations of the available periods after removing reverse symmetries, and 3 are the possible periods that examination 4 might end to) and we keep those that have cost under a cutoff barrier. The unscheduled examination 5 has a weighted degree of just 2, while other examinations have weighted degrees ranging from 52 to 350. So, most of the partial solutions should be filtered out.

Examination 5 of the toy example was initially ignored. A similar decision must be taken for each problem, about the examinations that will be initially ignored too. Unfortunately, this is not a trivial task. We cannot remove examinations of the chosen clique, should we wish to do so we should pick another clique. Intuitively, we want to initially ignore examinations with low degrees and weighted degrees, as they are able to appear in more periods. Consequently, they allow for more possible outcomes while at the same time their impact on the objective function is minor. It should be noted that not all partial solutions (solutions with ignored examinations still unscheduled) may lead to feasible solutions. So, for the case that full enumeration is unrealistic, quick feasibility checks can reveal unpromising partial solutions that are meaningless to be completed. The method is tuned by balancing the number of possible partial schedules generated with respect to the impact that the selected examinations have on the objective. The tuning is guided by selecting, through sampling, suitable examinations that will hopefully result in cutting-off many possible solutions. For the toy example, the costs of these partial solutions are depicted in Table 3. Note that the table contains only 12 rows, instead of 24, since we choose to apply $P_1 < P_2$ to eliminate reverse timetable symmetry. Assuming that we already have a schedule with cost 4008, the costs of the partial schedules that are not cutoff are shown in bold in Table 3. This means that only these partial solutions have the potential to be completed to full ones having cost 4008.

Table 3 Permutations and partial solutions costs for the toy example in Fig. 1

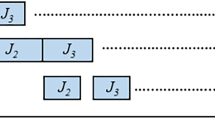
To further augment our filter while keeping computational cost low, it is possible for partial solutions that are under the cutoff barrier to calculate the minimum cost each unscheduled examination can possibly introduce to the partial solution. If the sum of those minimum costs plus our partial solutions cost is under the cutoff barrier, the partial solution may lead to a desired complete solution. This process can be seen as a multi-layer filter like the one depicted in Fig. 2.

Fig. 2

Filter process

Another way to view the process is as a carefully organized tree search, aiming at a solution of minimum cost. During the process branches of the search space are pruned based on cutoff values. Moreover, an A* style lookahead search is employed that calculates the minimum cost each unscheduled examination can possibly introduce to the partial solution.

5.3 Estimating lower bounds

Each students schedule is also an UETP sub-problem where his examinations are a complete graph where all edges have a weight of 1. This problem can be solved optimally for almost all instances, especially for those with a low number of periods.

Summing up those minimum penalties for all students can provide us with a lower bound. In the rare occasion that a solution’s objective function is equal to this bound then this solution is optimal.

6 sta83 optimal solution

No optimality has ever been proven for any Carter’s dataset instance until now. In this section, we show that the solution for sta83 having value 95947 (95947/611=157.0327 in decimal value, where 611 is the total number of students for sta83) which appears in many papers (e.g., (Burke & Bykov, 2006; Demeester et al., 2012; Leite et al., 2018) ) is indeed optimal.

Instance sta83 consists of 139 exams, 13 periods and has a relatively low conflict density of value 0.14. The instance has no noise examinations and no noise students as defined in Sect. 4. The instance is comprised of 3 disconnected components as shown in Fig. 3.

Fig. 3

Disconnected components of sta83. The weight of each edge is indicated by its thickness

The problem is divided into three independent subproblems, since these components are disconnected. Provided that we can optimally solve each one of them, joining these solutions would result to an optimal solution for the whole problem. Motivated by the prospect of proving optimality for a Carter’s dataset instance, we focused our attention on this task, and we managed to solve each subproblem to optimality using a different approach, resulting in a novel way of handling high conflict-density components.

All experiments were run on a Windows 11 workstation equipped with a i7-11700 - 8 cores CPU and 16GB RAM. The version of the IBM ILOG CPLEX used was 22.1.1.

6.1 Component sta83_62

This is the largest component of sta83, having 62 examinations and a conflict density of 0.36. We tried to solve it using the model described in Sect. 5.1 using the IBM ILOG CPLEX IP solver. Unfortunately, after several hours the solver was unable to prove optimality. We tried to warm start the solution with the current best solution and have set the MIP emphasis parameter first to “emphasize optimality over feasibility” and then to “emphasize moving best bound”. Both attempts were unsuccessful.

We noticed that the component has a special structure. It contains 10 sets of examinations with each set consisting of exactly 5 interchangeable examinations. These examinations amount for 50 of the 62 examinations that the component has in total. Details of these sets are presented in Table 4. Since interchangeable examinations can freely swap places with each other while keeping the objective value unchanged, the introduction of the symmetry breaking constraints of Eq. 6 greatly improved the solver’s efficiency in proving the optimal solution.

We also noticed that 3 examinations existed (72, 133, 136) in the graph that had connections with all other exams. So, we tried an approach that fixed these 3 examinations in specific periods and then tried to solve the remaining problem using IBM ILOG CPLEX. This time, the result was successful, the solver was able to return a result, either optimal or infeasible in a few minutes. It should be noted that infeasibility occurs because the cost of the best known solution is used as a cutoff constraint. So, we had only to try all possible places for positioning the 3 examinations and then solve the resulting problem. Since there are only 13 periods in instance sta83, this would mean that only ${13 \atopwithdelims ()3}=286$ configurations existed that should be multiplied by $\frac{3!}{2}$ since the 3 examinations can occupy the fixed periods in any order (divided by 2 due to the inherent symmetry of the problem).

By exploiting the above observations, IBM ILOG CPLEX IP solver was able to solve each subproblem in a few minutes. After solving all subproblems, the optimal solution for sta83_62 was proven to be 32695. This solution occurred when examinations 72, 133 and 136 were fixed to periods 3, 6 and 8, respectively. The symmetric solution also exists and is produced by fixing examinations 72, 133 and 136 to periods 9, 6 and 4. Of course, many more symmetric solutions exist due to the interchangeable exams.

Table 4 Component sta83_62, sets of interchangeable examinations and their characteristics

6.2 Component sta83_47

This component proved to be the easy part. It consists of 47 examinations and has a conflict density of 0.35. As described in Sect. 5.3, we can estimate a lower bound by adding the minimum cost each student’s schedule could possibly inflict. So, for each student in isolation, an IP model is formulated that given only the number of periods and the number of examinations that this student participates, decides about the schedule that results to the minimum possible cost. Of course, since each student is considered in isolation if two students share the same number of examinations then the problem needs to be solved just once. In practice, this is the case for several students. By adding minimum penalties of all students we have a lower bound for this component, which is 47250. The best known solution turns out to have cost equal to the lower bound obtained in this manner. Thus, the optimal solution for this component is 47250.

6.3 Component sta83_30

This was the last component to solve. It is the smallest one with just 30 examinations but a high conflict density of 0.72. With high hopes since just the smallest piece of the puzzle was missing, we were surprised to find out that to the best of our ability our MIP models were not able to prove an optimal solution. We have tried the same trick that we have used successfully in component sta83_62. We noticed that in the case of sta83_30 there is only one examination (134) that is connected to every other one. So, we tried to fix this examination to each period in turn and then to solve the remaining problems using IBM ILOG CPLEX. Unfortunately, this did not helped the solver to prove the optimality of the solution. Each subproblem seemed to run forever.

By observing closely the high density graph of this component we came up with the idea of separating examinations with high degrees and examinations with relatively low degrees. A similar idea has been exploited by Rahman et al. (2009) and others in constructing timetables giving precedence to high degree examinations and leaving for a later phase the low degree ones. In our approach, we isolated the maximum clique, which for this particular instance contains 12 examinations and tried to arrange those examinations to the 13 periods leaving one period empty for each possible arrangement.

A significant observation is that regardless of the periods that the clique occupies, the possible placements for the remaining examinations will be the same because their possible positions are constrained by the examinations of the clique. By multiplying the number of those possibilities with the number of permutations of the periods we were able to count all possible solutions to be $13! * 109152$ where 13! is the number of possible period permutations and 109152 is the number of possible ways to schedule the remaining examinations for the specific component. This number is still quite large so we exploited the method described in Sect. 5.2. We aim to find a set of examinations that has minor impact on the cost but at the same time possible final positions of the sets’ examinations might be disproportionate large. Figure 4 which shows the degrees and weighted degrees of examinations was used as a visual aid for identifying the examinations needed. These examinations should reside at the lower left corner and should have the desirable characteristics. For sta83_30 a good set of examinations proven to be $\{5, 131, 28, 48, 76\}$ that manages to lower multiplier 109152 to just 47.

Fig. 4

Scatter plot of sta83_30 that gives insight about the set of examinations that should be scheduled last

The unscheduled examinations weighted degree is comparatively low and so the method has the potential of working effectively. By keeping in the set of initially unscheduled examinations, examinations that can easily move around the schedule, the number of possible partial solutions becomes quite low. Moreover, the low weighted degree that these examinations have prohibits from heavy impacts on the objective function. So, the filtering process is working. For the case of sta83_30 this “intelligent” search resulted in 13 distinct optimal solutions (and their symmetric ones) all having the same cost, 16002. The search was implemented in Bezanson et al. (2017) using its parallel computing features for the CPU. Five high end workstations were simultaneously running the experiment and the time needed was about 12 h.

7 Conclusions

This work was about the uncapacitated examination timetabling problem. It continues previous work of members of our team. A key observation is that even for this rather simple scheduling problem that is only an abstraction of the corresponding real-life problem, the proof that a given solution is optimal is definitely not trivial. Nevertheless, our team succeeded in proving the optimality of a certain instance, namely sta83 of the Carter’s dataset. In order for this to happen we had to decompose the problem into independent subproblems. Having 3 problems of moderate size gave us the opportunity of experimenting with various approaches. No method was able to solve all three subproblems. After many experiments and carefully analyzing the components, we finally discovered three approaches that were able to prove optimality. Each subproblem was solved by a different approach and the optimal solution for sta83 was proven. The other problem instances of Carter’s dataset and 20 more problem instances publicly available were unable to be solved to optimality using the same approach. This likely occurred because proving optimality becomes very challenging when the number of periods is big and when the number of examinations (i.e., nodes in the problem’s graph) are relatively large. Nevertheless, by following the procedure of removing noise students, identifying and solving independently connected components (subgraphs of the problem’s graph) we were able to contribute two new best solutions to public dataset problems, alongside with several optimal solutions to subproblems that exist in various problem instances.